 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hole theory as a prediction tool for Brownian diffusive motion in binary mixtures of liquids†
Carmine D'Agostino
Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge CB3 0AS, UK. E-mail: cd419@cam.ac.uk; Tel: +44 (0)1223-335245
First published on 8th November 2017
Abstract
The hole theory of liquids has been around for a long time since its development. This theory assumes that a liquid can be seen as a continuum permeated by holes and was developed with the aim of explaining thermal and viscous properties in liquids at equilibrium. It has often been used as a predictive tool for viscosity of liquids, including molten metals, ionic and molecular liquids. However, a direct link to actual transport properties in liquids, i.e., molecular diffusion, has never been fully shown nor validated. This work explores the application of hole theory as a simple tool to understand and predict molecular diffusion at equilibrium in liquids. In particular, a wide range of binary liquid mixtures, ranging from ideal to highly non-ideal, has been assessed by calculating the average hole diffusivity as a function of composition and comparing these values to experimental values of molecular diffusivity at equilibrium. The results show that the average motion of the holes describes very well the average motion of the diffusing species in the mixture and this is ascribed to an inter-diffusion process between the molecular species and the holes. The findings reported here are of importance as they establish a direct link between hole theory and transport properties and validate the use of the theory as an effective and novel way of estimating molecular diffusivity in liquids, which may be challenging to measure or often unavailable, by knowing surface tension and viscosity data, which are widely available in the literature or easier to measure.
Introduction
The hole theory of liquids developed by Fürth1–3 regards a liquid as a continuum permeated by a large number of holes with the number of holes being comparable to the number of particles in the liquids. This theory aims at explaining thermal and viscous properties of liquids in a state of equilibrium based on the motion of the holes within the continuum liquid. For example, it has been suggested that variation of the viscosity and thermal conductivity of liquids can be related to the average life of the holes,4 which is the time for which a hole lasts before it is destroyed by evaporation of molecules into it. The amount of free volume in liquids seems also to be important in determining transport properties. Tracer diffusion studies in liquid zinc5 showed that the presence of voids of molecular or ionic volume is required for diffusion. Experimental values of the diffusion coefficient of zinc ions were seen to correlate well with the Cohen–Turnbull theory,6 which relates the diffusion coefficient in a liquid of hard spheres to the free volume available. Based on the work of Fürth,3 Abbott7 has used the hole theory to explain viscosity changes in ionic compounds and some molecular liquids. In his work he used the hole theory to calculate viscosities of ionic and molecular liquids and then compared these values with measured values of viscosity. A correlation valid for both ionic and molecular liquids was observed. Based on these results, Abbott concluded that the hole theory, whilst currently approximate, provides a simple model to explain mobility in fluids, by means of predicting viscosity. In another work, the hole theory has been used to explain viscosity and ionic conductivity in ferrocene-based ionic liquids.8 The results of this work suggested that the dominant mode of charge transport in these liquids was via the mobility of holes.It is clear that most of the work on assessing the validity of the hole theory of liquids to explain transport properties has been focused on understanding viscosity, mostly in molten metals and ionic liquids, whereas a direct link with transport properties, i.e., molecular diffusion due to Brownian motion, has not yet been observed in full details.
Some preliminary studies have highlighted the importance of the hole motion in liquids. For example, a previous study on ionic liquids has suggested that the size of the hole seems to be the dominant factor in controlling mass transport in ionic liquids, although further details were not given.9 A similar conclusion was reached by observing that the correlation length in ferrocene ionic liquids gives an indication of the hole size.8 Whilst these results seem to suggest the validity of the hole theory in determining transport in ionic liquids, to the best of the author's knowledge, a conclusion on the validity of this approach is far from being reached, particularly for the case of molecular liquids, and there is not yet a clear evidence on to what extent the theory can be used to describe molecular motion.
In these work, a systematic study aiming at assessing to what extent the hole theory is able to predict molecular mobility in liquids is conducted. In particular, the hole theory is used to calculate the average diffusion of the holes in a variety of binary liquid mixtures, with different thermodynamic properties, as a function of composition, which is then compared to the average molecular diffusion of the species at equilibrium. The findings are then discussed and critically assessed.
Methodology
The hole theory assumes that a liquid contains empty spaces or holes, which arise from thermally generated fluctuations in local density.4,7 The holes are randomly distributed and the radius 〈rH〉 of the average sized hole is related to the surface tension, γ, by the following equation:10
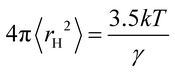 | (1) |
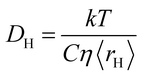 | (2) |
The hole theory was developed to explain properties of a liquid in a state of equilibrium. Therefore, in order to compare the mobility of the holes with that of the species in the binary mixture, a diffusion parameter describing the molecular motion of the species at equilibrium is required. For this purpose, the arithmetic average proposed by Darken11 is considered, which has been extensively used to calculate the average value of diffusivity at equilibrium,12–14 i.e., in the absence of a gradient of chemical potential, and has also been validated using molecular dynamics simulations.15 Other correlations, such as the geometric average proposed by Vignes,16 have been proposed. It is important to note that in the case of the mixtures studied here, the tracer diffusivities of species 1 and 2 are similar, which implies that the use of either the arithmetic or geometric average leads to essentially the same results. This aspect has also been discussed in more details elsewhere.13
The Darken relation allows to calculate the average diffusivity at equilibrium, that is, in the absence of a chemical potential gradient, in a binary mixture according to:11
| D12 = x2D1 + x1D2 | (3) |
Several mixtures have been investigated, for which data on surface tension, viscosity and tracer diffusivity at the same temperature as a function of composition are known. The details of the mixtures used are reported in Table 1, together with the references used to obtain the data.
| Mixture | Surface tension γ [N m−1] | Viscosity η [Pa s] | Diffusivity D [m2 s−1] | Temperature T [K] |
|---|---|---|---|---|
| a CT is carbon tetrachloride, TEA is trimethylamine and NMP is N-methylpyrrolidine. | ||||
| Acetone/benzene | 19 | 20 | 21 | 298.15 |
| Acetone/chloroform | 22 | 23 | 21 | 298.15 |
| Acetone/water | 24 | 25 | 21 | 298.15 |
| Acetone/CTa | 26 | 26 | 27 | 298.15 |
| n-Heptane/benzene | 26 | 28 | 29 | 298.15 |
| n-Hexane/nitrobenzene | 30 | 31 | 13 | 303.15 |
| TEA/watera | 32 | 33 | 34 | 289.15 |
| Methanol/water | 35 | 36 | 37 | 298.15 |
| NMP/watera | 38 | 39 | 40 | 293.15 |
| n-Heptane/n-octane | 41 | 42 | 13 | 293.15 |
Results and discussion
In order to start the analysis, eqn (1) is used to obtain the average hole size, 〈rH〉, as a function of mole fraction for the various mixtures; typical hole sizes calculated using eqn (1) are in the range 1–3 Å, which agrees with values previously reported when studying ionic and molecular liquids.7 More details on the calculated hole radii are reported in the ESI, Table S1.† Once 〈rH〉is known, eqn (2) is then used to calculate the diffusion coefficient of the hole, DH.The values of DH for the various mixtures as a function of mole fraction are reported in Fig. 1–10 and compared with the molecular mobility factor, D12, calculated using eqn (3). It is noted that the errors on those values are difficult to obtain as they will depend on a combination of errors on viscosity, surface tension and tracer diffusivity, which are often not available in the literature. Typical relative errors on bulk liquid tracer diffusivity values calculated using NMR diffusion techniques are reported to be approximately in the range 2–3%.43 Therefore, an assumption of a 5% relative error on such values seems a reasonable conservative assumption.
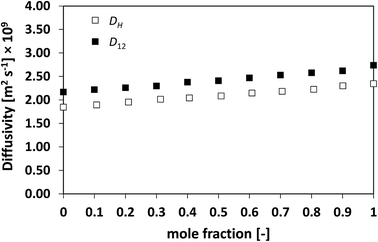 | ||
| Fig. 1 Average hole diffusivity, DH, and species diffusivity, D12, in n-heptane/n-octane mixtures as a function of n-heptane mole fraction. | ||
The discussion starts with the simplest mixture assessed, the binary ideal system of n-heptane/n-octane, for which the activity coefficients are equal to the unity. It can be seen from Fig. 1 as the average diffusivity of the two species in the mixture, D12, increases in a linear fashion as the concentration of n-heptane increases. This is typically the case for ideal mixtures of hydrocarbons, which show what is usually defined as a milder, well-behaved composition dependence.13,44
From the figure it is clear as the hole average diffusivity, DH, shows essentially the same trend as that observed for D12, with values that are fairly close between the two different diffusivities, although such a difference is deemed to be above the experimental error stated in the methodology section. This first result already suggests that the average diffusivity of the species in the mixtures, D12, and that of the holes, DH, are related and show similar values.
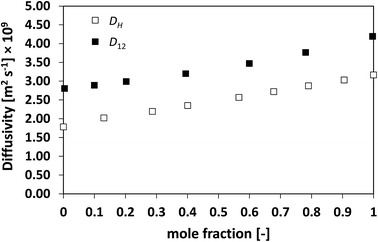
In order to assess whether this relationship between the two diffusivities has a more general validity, the approach has been extended to a series of more challenging cases, namely, slightly non-ideal, non-ideal and highly non-ideal binary mixtures. In this way, a wide range of cases is assessed and a better conclusion can therefore be made. Fig. 2 and 3 show the plots for D12 and DH as a function of composition for the systems n-heptane/benzene and acetone/benzene, respectively, which are moderate non-ideal mixtures with fairly well-behaved composition dependence of D12, showing positive deviations, i.e., activity coefficients greater than one.
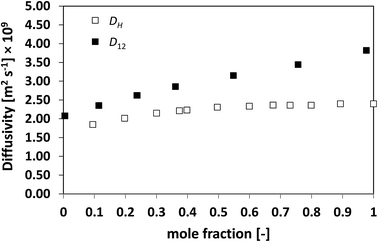 | ||
| Fig. 2 Average hole diffusivity, DH, and species diffusivity, D12, in n-heptane/benzene mixtures as a function of n-heptane mole fraction. | ||
 | ||
| Fig. 3 Average hole diffusivity, DH, and species diffusivity, D12, in acetone/benzene mixtures as a function of acetone mole fraction. | ||
Similarly to what observed for the ideal system n-heptane/n-octane, also in this case D12 and DH have similar trends, with values of diffusivity that are different but again not far apart from each other. For the n-heptane/benzene mixture there seems to be a divergence between the two values at higher n-heptane mole fraction; however, the trends are well-defined. It is also noted as DH is systematically lower than D12 at all compositions, similar for the n-heptane/n-octane mixtures. Similar observations can be made when analysing the acetone/water system, Fig. 4, acetone/CT system, Fig. 5, and acetone/chloroform system, Fig. 6. The latter is interesting to assess as, unlike the other systems presented so far, it shows negative deviations from ideality, i.e., activity coefficients lower than one.
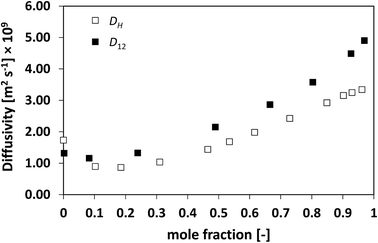 | ||
| Fig. 4 Average hole diffusivity, DH, and species diffusivity, D12, in acetone/water mixtures as a function of acetone mole fraction. | ||
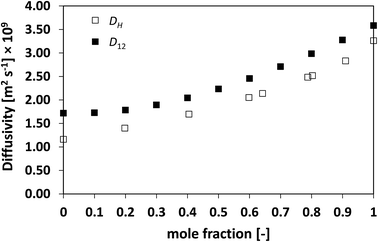 | ||
| Fig. 5 Average hole diffusivity, DH, and species diffusivity, D12, in acetone/CT mixtures as a function of acetone mole fraction. | ||
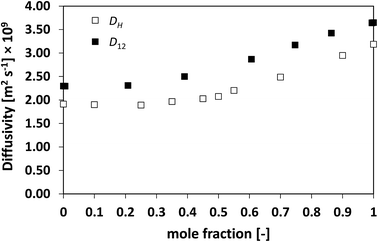 | ||
| Fig. 6 Average hole diffusivity, DH, and species diffusivity, D12, in acetone/chloroform mixtures as a function of acetone mole fraction. | ||
Also in these two cases, the trend in D12 is reflected very well in DH, including the presence of the plateau at low acetone mole fractions.
We now assess non-ideal mixtures whereby the behaviour of D12 as a function of composition shows marked minima. This is the case of the methanol/water, Fig. 7, and the NMP/water system, Fig. 8, which show positive and negative deviations from ideality, respectively. The presence of such minima on the average mobility of the species in these systems has been ascribed to water–solute complexes, which reduce molecular mobility in concentrated solutions.40,45
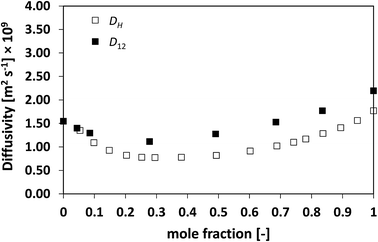 | ||
| Fig. 7 Average hole diffusivity, DH, and species diffusivity, D12, in methanol/water mixtures as a function of methanol mole fraction. | ||
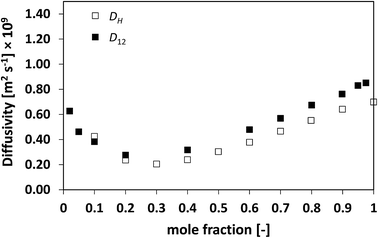 | ||
| Fig. 8 Average hole diffusivity, DH, and species diffusivity, D12, in NMP/water mixtures as a function of NMP mole fraction. | ||
Analysing the behaviour of DH for the systems a very similar trend to that of D12 is again observed. As for the previous cases, also for these systems the values of DH are generally lower than D12, although the differences are not large, particularly for the water/NMP system. It is remarkable to note as the DH trend is able to pick in details the main features of the D12 trend, including the presence and position of minima.
The results presented so far begin to unravel a very interesting finding, that is, the holes formed in the liquid move in a very similar fashion and at a similar rate to the actual diffusing species. To further test this theory, systems with high deviations from ideality have also been assessed. Fig. 9 shows the D12 and DH plots for the n-hexane/nitrobenzene system, which shows highly positive deviations with formation of an upper consolute point.13
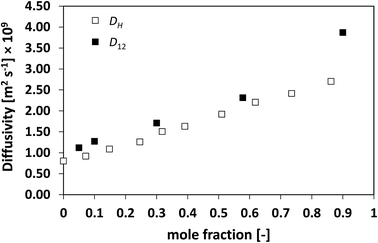 | ||
| Fig. 9 Average hole diffusivity, DH, and species diffusivity, D12, in n-hexane/nitrobenzene mixtures as a function of n-hexane mole fraction. | ||
Also in this case, a very similar trend between D12 and DH is observed, with values that are close with each other, particularly at low n-hexane mole fraction and again with DH systematically lower than D12.
Finally, the system TEA/water has also been investigated, which is shown in Fig. 10. This is a particularly complex system, with a peculiar thermodynamic behaviour46 and formation of a lower consolute point, where water and TEA are thought to form hydrogen bonding that leads to a minimum in the average diffusivity D12 as a function of composition.34 From Fig. 10 it is clear as D12 and DH have a remarkably similar behaviour, with DH reflecting very well the changes in D12 as a function of composition, including the presence of a minimum at low TEA mole fraction.
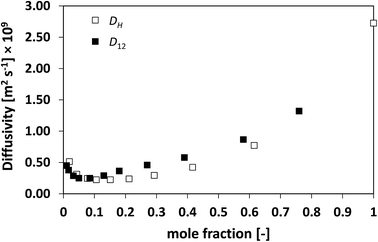 | ||
| Fig. 10 Average hole diffusivity, DH, and species diffusivity, D12, in TEA/water mixtures as a function of TEA mole fraction. | ||
Based on the results presented here, one can conclude that the average diffusivity of the holes formed in a binary mixture of two molecular liquids describes very well the diffusion behaviour at equilibrium of the species as a function of composition, suggesting that the movement of the holes in the liquid is intimately linked to that of the species diffusing. The observation of this phenomenon for a wide range of molecular binary liquid mixtures ranging from ideal to highly non-ideal strongly suggest that the hole theory is a simple but effective approach to study molecular mobility in liquids and liquid mixtures. The findings of this work are in line with preliminary observations, mostly done on ionic liquids, and extend the application of this theory to a wide variety of molecular liquid systems. Importantly, whilst previous work on ionic liquids has shown the validity of such a theory by investigating viscosity, here a direct link between the mobility of the holes and a translational dynamic property of the species, that is, diffusivity, is established. Hence, knowing surface tension and viscosity data, which are widely available in the literature, and using such a theory it is possible to predict with a good approximation behaviour and values of average tracer diffusivities for mixtures as a function of composition, which are often not available or in some cases difficult to measure.
It is important to note that the results presented in Fig. 1–10 for DH, which systematically underpredicts D12, assume a no-slip condition, with a friction constant C = 6π used in eqn (2), which is the classical version of the Stokes-Einstein relation. This assumption is often used for viscous fluids but is not always accurate, which may well be the case here as the diffusion process is that of “empty” holes diffusing in a viscous fluid. Hence, one may expect a lower friction constant. If this factor becomes a variable, it becomes possible to obtain an optimised value of C such that DH ≈ D12. The optimised value of C for the different mixtures studied in this work is shown in Table 2.
| Mixture | Optimised C value |
|---|---|
| Acetone/benzene | 4.4π |
| Acetone/chloroform | 4.9π |
| Acetone/water | 4.6π |
| Acetone/CT | 5.0π |
| n-Heptane/benzene | 4.4π |
| n-Hexane/nitrobenzene | 4.9π |
| TEA/water | 4.6π |
| Methanol/water | 4.4π |
| NMP/water | 5.2π |
| n-Heptane/n-octane | 5.2π |
It is interesting to note as the optimal values of the friction constant C are similar for all the mixtures studied here, with an average overall value across all the systems of C ≈ 4.8π, well within the range C = 4π − 6π, which are the boundary conditions of the Stokes-Einstein equation for slip and no-slip condition, respectively.47 Therefore, the meaningful values of the optimised friction constant C validate eqn (2) as a physically meaningful model, which allows an accurate calculation of the average molecular mobility at equilibrium in binary mixtures from viscosity and surface tension data. It is interesting to note as well that such value of C is indeed lower than that for the no-slip condition, which agrees on the previous discussion onto why a no-slip condition systematically underpredicts D12.
It is worth to discuss a possible explanation as to why the average diffusion rate of the holes generated in the liquid is close to that of the species. In the case of ionic liquids, it has been suggested that diffusion of ionic species may occur via ions moving from one vacancy to another9 and this is attributed to the observation that the typical hole size in ionic liquids is comparable to the size of the ions, hence, it is relatively easy for a small ion to move into a vacant site.7 Typical hole radii for the mixtures studied here are in the range 1–3 Å, which is comparable to the molecular radius of the diffusing species. Hence, one may speculate a sort of mutual or inter-diffusion process between the liquid species and the holes, which results in DH ≈ D12. At this point it is worth noting that indeed, in a theoretical work on dilute metallic solutions,48 it has been suggested that a move by a hole is identical with a move by an atom, but in the opposite sense, which is indeed the concept of mutually diffusing species. Hence, assuming the hole theory is valid, this further support the idea proposed here of a mutual diffusion process between the liquid species and the holes formed in molecular liquids, as the results also suggest.
Conclusions
The work reported here has shown that the hole theory of liquids describes well molecular diffusion and is able to give accurate predictions of the average molecular mobility of species in binary mixtures at equilibrium. A clear link between the theory and molecular diffusion is therefore established. In particular, using the Stokes-Einstein equation and the average hole radius with an optimised, physically meaningful, friction constant, it is possible to calculate with a good degree of accuracy, values of the average mobility of the diffusing species as a function of composition, often difficult to measure experimentally or not available, by knowing viscosity and surface tension data, which are straightforward to measure and widely available in the literature. It is suggested that the similar values in the average hole and species diffusivities, DH and D12, respectively, are due to an inter-diffusion process between the liquid species and the holes, which results in DH ≈ D12.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Carmine D'Agostino is grateful to Wolfson College, Cambridge, for supporting his research activities. Pierre Bräuer is acknowledged for useful discussion on the topic.References
- R. Fürth, Proc. Cambridge Philos. Soc., 1941, 37, 252–275 CrossRef.
- R. Fürth, Proc. Cambridge Philos. Soc., 1941, 37, 276–280 CrossRef.
- R. Fürth, Proc. Cambridge Philos. Soc., 1941, 37, 281–290 CrossRef.
- F. C. Auluck and D. S. Kothari, Nature, 1944, 153, 777 CrossRef CAS.
- N. H. Nachtrieb, C. Wahl and E. Fraga, J. Phys. Chem., 1963, 67, 2353–2355 CrossRef CAS.
- M. H. Cohen and D. Turnbull, J. Chem. Phys., 1959, 31, 1164–1169 CrossRef CAS.
- A. P. Abbott, ChemPhysChem, 2004, 5, 1242–1246 CrossRef CAS PubMed.
- A. W. Taylor, P. Licence and A. P. Abbott, Phys. Chem. Chem. Phys., 2011, 13, 10147–10154 RSC.
- A. P. Abbott, R. C. Harris, K. S. Ryder, C. D'Agostino, L. F. Gladden and M. D. Mantle, Green Chem., 2011, 13, 82–90 RSC.
- J. O. Bockris and A. K. N. Reddy, Modern Electrochemistry, Plenum Press, New York. U.S.A., 1970 Search PubMed.
- L. S. Darken, Trans. Am. Inst. Min., Metall. Pet. Eng., 1948, 175, 184–201 Search PubMed.
- T. Allie-Ebrahim, Q. Zhu, P. Brauer, G. D. Moggridge and C. D'Agostino, Phys. Chem. Chem. Phys., 2017, 19, 16071–16077 RSC.
- C. D'Agostino, M. D. Mantle, L. F. Gladden and G. D. Moggridge, Chem. Eng. Sci., 2011, 66, 3898–3906 CrossRef.
- X. Liu, T. J. H. Vlugt and A. Bardow, Ind. Eng. Chem. Res., 2011, 50, 10350–10358 CrossRef CAS.
- R. Krishna and J. M. van Baten, Ind. Eng. Chem. Res., 2005, 44, 6939–6947 CrossRef CAS.
- A. Vignes, Industrial & Engineering Chemistry Fundamentals, 1966, vol. 5, pp. 189–199 Search PubMed.
- Q. Zhu, C. D'Agostino, M. Ainte, M. D. Mantle, L. F. Gladden, O. Ortona, L. Paduano, D. Ciccarelli and G. D. Moggridge, Chem. Eng. Sci., 2016, 147, 118–127 CrossRef CAS.
- J. H. Wang, J. Am. Chem. Soc., 1952, 74, 1182–1186 CrossRef CAS.
- W. E. Shipp, J. Chem. Eng. Data, 1970, 15, 308–311 CrossRef CAS.
- R. K. Nigam and B. S. Mahl, Indian J. Chem., 1971, 9, 1255–1258 CAS.
- D. K. Anderson, J. R. Hall and A. L. Babb, J. Phys. Chem., 1958, 62, 404–409 CrossRef CAS.
- S. A. Levichev, in Fiziko-chimiceskie svojstva rastvorov, ed. A. Rusanov, 1964, pp. 219–226 Search PubMed.
- K. Ramamoorthy, Indian J. Pure Appl. Phys., 1973, 11, 556–559 CAS.
- S. Enders, H. Kahl and J. Winkelmann, J. Chem. Eng. Data, 2007, 52, 1072–1079 CrossRef CAS.
- R. A. Stairs, in Thermodynamic Behavior of Electrolytes in Mixed Solvents, American Chemical Society, 1976, vol. 155, pp. 332–342 Search PubMed.
- B. I. Konobeev and V. V. Lyapin, Russ. J. Appl. Chem., 1970, 43, 806–813 Search PubMed.
- R. Haase and W. Engels, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1983, 38, 281–283 Search PubMed.
- S. Kouris and C. Panayiotou, J. Chem. Eng. Data, 1989, 34, 200–203 CrossRef CAS.
- K. R. Harris, C. K. N. Pua and P. J. Dunlop, J. Phys. Chem., 1970, 74, 3518–3529 CrossRef CAS.
- V. Ramakrishna and M. Patel, Indian J. Chem., 1970, 8, 256–260 CAS.
- E. F. Zhuravlev, Zh. Obshch. Khim., 1961, 31, 363–367 CAS.
- A. N. Campbell, Can. J. Chem., 1981, 59, 127–131 CrossRef CAS.
- N. Hafaiedh, A. Toumi and M. Bouanz, J. Chem. Eng. Data, 2009, 54, 2195–2199 CrossRef CAS.
- C. D'Agostino, M. D. Mantle, L. F. Gladden and G. D. Moggridge, Chem. Eng. Sci., 2012, 74, 105–113 CrossRef.
- R. Belda Maximino, Phys. Chem. Liq., 2009, 47, 475–486 CrossRef.
- P. S. Nikam and A. B. Nikumbh, J. Chem. Eng. Data, 2002, 47, 400–404 CrossRef CAS.
- Z. J. Derlacki, A. J. Easteal, A. V. J. Edge, L. A. Woolf and Z. Roksandic, J. Phys. Chem., 1985, 89, 5318–5322 CrossRef CAS.
- A. García-Abuín, D. Gómez-Díaz, J. M. Navaza and I. Vidal-Tato, J. Chem. Eng. Data, 2008, 53, 2671–2674 CrossRef.
- A. García-Abuín, D. Gómez-Díaz, M. D. La Rubia and J. M. Navaza, J. Chem. Eng. Data, 2011, 56, 646–651 CrossRef.
- L. Ambrosone, G. D'Errico, R. Sartorio and V. Vitagliano, J. Chem. Soc., Faraday Trans., 1995, 91, 1339–1344 RSC.
- D. L. Katz and W. Saltman, Ind. Eng. Chem. Res., 1939, 31, 91–94 CrossRef CAS.
- A. Aucejo, M. C. Burguet, R. Munoz and J. L. Marques, J. Chem. Eng. Data, 1995, 40, 141–147 CrossRef CAS.
- C. D'Agostino, J. Mitchell, L. F. Gladden and M. D. Mantle, J. Phys. Chem. C, 2012, 116, 8975–8982 Search PubMed.
- R. Krishna, Phys. Chem. Chem. Phys., 2015, 17, 27428–27436 RSC.
- R. Li, C. D'Agostino, J. McGregor, M. D. Mantle, J. A. Zeitler and L. F. Gladden, J. Phys. Chem. B, 2014, 118, 10156–10166 CrossRef CAS PubMed.
- K. W. Chun, T. C. Clinkscales and R. R. Davison, J. Chem. Eng. Data, 1971, 16, 443–446 CrossRef CAS.
- Y. Ishii and N. Ohtori, Phys. Rev. E, 2016, 93, 050104 CrossRef PubMed.
- R. P. Johnson, Phys. Rev., 1939, 56, 814–818 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10787k |
| This journal is © The Royal Society of Chemistry 2017 |
