Cryptic post-transition state bifurcations that reduce the efficiency of lactone-forming Rh-carbenoid C–H insertions

Abstract

Byproducts of chemical reactions are generally thought to result from the competition between two reaction pathways, each with its own rate-determining transition state structure. We show here, however, that pathways with a single transition state structure followed by a post-transition state bifurcation may also be a source of undesired products, especially those whose appearance is unexpected. The viability of this scenario for intramolecular C–H insertion reactions affording β-lactones via Rh-carbenoid intermediates is assessed through quantum chemical calculations on potential energy surfaces and quasi-classical molecular dynamics simulations. It appears that, in these cases, the rhodium catalyst is to blame for the accessibility of a second, unintended, pathway following the transition state structure for β-lactone formation that leads to fragmentation to a ketene and carbonyl compound. If an unexpected product is formed via a post-transition state bifurcation, conventional strategies for suppressing its formation are unlikely to succeed. Guidelines for recognizing the presence of a post-transition state bifurcation are described here, along with hints at means for controlling product distributions.

---

Introduction

Unexpected and unwanted products of synthetic organic reactions are almost universally ascribed to competition from chemical processes with activation barriers similar to or lower than that for the process leading to the desired product. In some scenarios, the transition state structures for selectivity-determining steps are different from the rate-determining transition state structure(s), making predicting product distributions especially difficult.¹ We show here that another source of undesired products is possible—a post-transition state bifurcation (PTSB) that occurs en route to the desired product that opens up a barrierless path toward a second product. We demonstrate the importance of such a scenario through an illustrative example taken from the realm of C–H activation chemistry, and we briefly describe several related systems that point to the potential generality of the concept in the C–H activation field. We speculate that such a scenario may well be to blame for the failure of many other synthetic reactions as well. While PTSBs have been invoked to rationalize selectivity for a growing number of organic reactions,^2–5 the potential importance of recognizing a PTSB during optimization of the synthetic utility of a reaction has not been given sufficient attention.

The Rh(II)-catalyzed C–H insertion reaction has been a standard method for generating new C–C bonds for several decades.^6–10 Regio-,¹¹ diastereo-,¹² and enantioselective^13–15 variants of this reaction have been developed, demonstrating the utility of Rh-based catalysts in accessing a large region of chemical space.^7,16 Though Rh-catalyzed C–H insertion reactions have been used extensively in synthesis, there have been a relatively small number of computational studies on mechanisms and the origins of regio- and stereoselectivity for these reactions.^17–20 In particular, computational studies focusing on reactions of α-diazocarbonyl compounds have been limited, despite the extensive use of these substrates for intramolecular C–H insertion reactions to afford cyclic esters and ketones (e.g., Fig. 1 and 2).^21–24

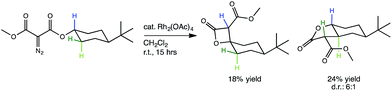Fig. 1 A lactone-forming C–H insertion reaction: the experimentally studied reaction under investigation in this computational study.³⁰ Though a particular diastereomer of the γ-lactone has been drawn, the relative stereochemistry of the two diastereomers of γ-lactone products (seen in a ratio of 6 : 1) was not reported.

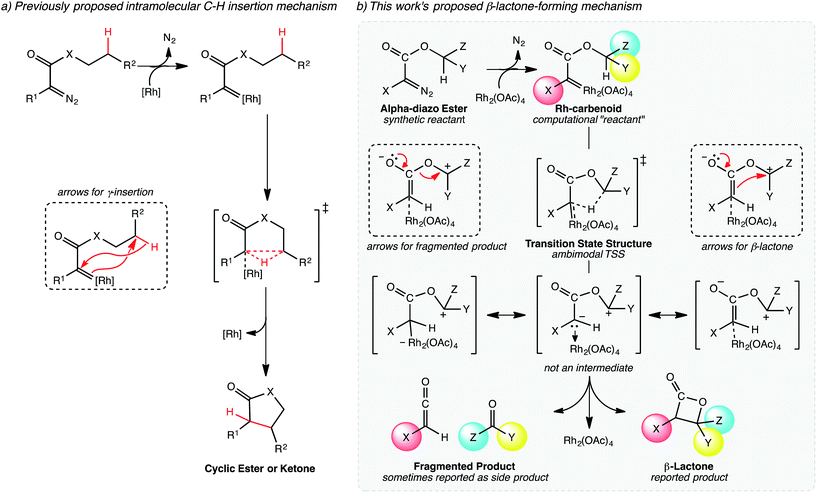Fig. 2 Mechanisms of lactone-forming C–H insertion reactions. (a) The previously proposed mechanism for five-membered ring formation proposed by Yoshikai and Nakamura.^17,18 (b) Our proposed mechanism for β-lactone formation, involving a PTSB.

Here we aim to call attention to a new, and potentially general, type of PTSB that plays a key role in determining the product distribution in Rh(II)-catalyzed lactonization reactions.^2,3,25–29 Our hope is that the results of this study will help to shed light on a phenomenon rarely considered in the design of transition metal (and other) catalysts.

The representative Rh-promoted intramolecular C–H insertion reaction on which we will focus, reported previously by Lee, et al.,³⁰ is shown in Fig. 1. In this reaction, a 4-t-butylcyclohexyl diazomalonate is exposed to a catalytic quantity of Rh₂(OAc)₄. We initially sought a rationalization for the β/γ selectivity shown, but along the way, a new PTSB involved in the β-lactone-forming reactions was uncovered (Fig. 2b). Detailed examination of this PTSB led to a series of general guidelines for recognizing the presence of a PTSB.

Results and discussion

Mechanistic problems

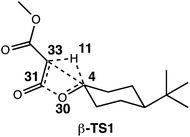
The generally accepted single-step mechanism for lactone formation^17,18 (Fig. 2a) was investigated for the reaction shown in Fig. 1 (see Methods section for computational details). Competing transition state structures (TSSs) for β- and γ-lactone formation were located using systematic conformational searches (see Methods). The lowest energy TSS found appeared to correspond to formation of the β-lactone, which does not agree with the reported product ratio, where the γ-lactone was the major product—24% yield versus 18% yield of β-lactone. Surprisingly, though the geometry of the C/H/C bond-making/breaking array was extremely similar in all TSSs found, the intrinsic reaction coordinate (IRC; minimum energy path from TSS to product) for the apparent β-lactone-forming TSS (β-TS1) actually led to the product of a retro-ene-like reaction (labeled “fragmented product” in Fig. 2b, where X is a methyl ester and Y and Z are methylene groups of 4-t-butylcyclohexanone). A TSS corresponding to a [2+2]-cycloaddition between the resultant fragments, methyl-3-oxoacrylate (a ketene) and 4-t-butylcyclohexanone, was located, revealing a possible new pathway to β-lactone formation. However, this step of the mechanism was calculated to have too high of a free energy barrier (approximately 50 kcal mol⁻¹) to be feasible under the experimental conditions (room temperature, 15 h). TSSs with catalyst coordination to the ketene oxygen or ketone oxygen were investigated, but no arrangement led to a barrier that was low enough for a room temperature reaction (see ESI†).

Bifurcating pathways

It was at this point that we considered the possibility of a PTSB following β-TS1. A pathway with a PTSB involves a single TSS that leads directly to two products without any intervening minima (referred to as an ambimodal³¹ TSS).^{2–5,25–29,32} In such a case, traditional transition state theory (TST),^33–36 where barriers to formation of two competing products are compared, cannot be used to predict experimental product distributions, because the two products share a TSS for their formation. PTSBs have been reported previously for some Au-catalyzed reactions,^37–46 as well as a Rh-promoted C–H insertion reaction where the PTSB leads to both the direct insertion product and the product of a C–H activation/Cope rearrangement sequence.⁴ Examination of structures along the IRC for the fragmentation reaction suggests that the reaction is asynchronous, with hydride transfer preceding C–O bond breaking (see ESI†). In effect, an enolate with an appended oxonium ion is formed (Fig. 2b, not an intermediate), but this enolate can either eliminate a carbonyl while forming a ketene or attack the carbon of the oxonium ion to form a β-lactone, neither process having a barrier on the potential energy surface (PES). While the PTSB we describe here has some unique features (vide infra), we suspect that PTSBs may be more common in transition metal catalyzed reactions than generally appreciated.

Upon reexamination of the table of experimental results in the Lee et al. report,³⁰ we noticed (now that we were pondering the possibility of fragmentation via bifurcation) a footnote stating that 4-t-butylcyclohexanone was obtained in 50% yield. While we speculate that this footnote may have been included to explain the relatively low yields of the expected lactone products, the result mentioned can be rationalized by a PTSB, since 4-t-butylcyclohexanone is one of the fragmentation products that would be produced via one exit channel from β-TS1!

Dynamic behavior

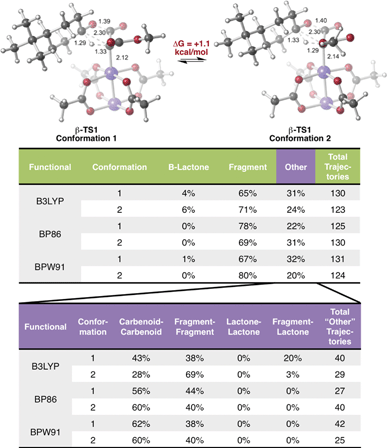
Encouraged by this discovery, we shifted our attention to the observed ratio of 4-t-butylcyclohexanone to β-lactone, products that we now hypothesize to be derived from the same TSS. Quasi-classical “downhill” molecular dynamics simulations were conducted,^29,47–50 starting from the optimized β-TS1 (see Methods). To ensure that the conformation of the TSS at the start of dynamics trajectories did not influence the results, we performed trajectory calculations for the two lowest energy conformations of the TSS, which differ by rotation around the C–C bond to the ester moiety (Fig. 3, top). Conformation 1, where the carbonyl groups in the substrate are trans to one another, is predicted to be 1.1 kcal mol⁻¹ lower in free energy than conformation 2, where the carbonyl groups are cis to one another (calculated at the B3LYP/6-31G(d), LANL2DZ level of theory). Additionally, both TSS conformations were optimized with three different functionals (see Methods) to check that our results were not functional-dependent. These TSSs were then used for dynamics simulations, where the same functional used in the TSS optimization was used to calculate forces during the trajectories.

Fig. 3 Dynamic behavior. Top: β-TS1 conformations used to initiate molecular dynamics. A free energy difference of 1.1 kcal mol⁻¹ was calculated at the B3LYP/6-31G(d), LANL2DZ level of theory, favoring conformation 1. Middle: results of quasi-classical molecular dynamics simulations for trajectories initiated from the two conformations of β-TS1. Bottom: a breakdown of results in the “other” category.

As shown in Fig. 3, in all cases the dominant product was the IRC product (i.e., from fragmentation). While these results do predict the experimentally observed major product to be 4-t-butylcyclohexanone, the experimental and computational product ratios do not match quantitatively. Additionally, simulations with the BP86 functional did not lead to any β-lactone product and simulations with the BPW91 functional produced only one trajectory connecting the Rh-carbenoid to the β-lactone product. These results will likely be improved by running molecular dynamics simulations in explicit solvent, since solvent cage effects are expected to discourage fragmentation; such simulations are challenging,^51,52 but are being pursued, and results will be described in due course.

In a large number of trajectories, pathways connecting the Rh-carbenoid with products (of C–H insertion or fragmentation) were not observed. Fig. 3, bottom, shows a breakdown of these trajectories. With the BP86 and BPW91 functionals, all of these trajectories corresponded to recrossing, where both sides of each trajectory connected to the Rh-carbenoid or both sides connected to the fragmented products. Unexpectedly, one conformation of the TSS modeled with B3LYP had a large portion of the trajectories connected to the fragmented product on one side and the β-lactone product on the other—an unusual outcome considering the TSS from which dynamics simulations were initiated should connect product(s) to the Rh-carbenoid reactant. How can this result be rationalized?

Saddles, ridges and monkeys

To investigate the origins of this phenomenon, a relaxed PES scan over two bond distances was conducted (Fig. 4). Note that this surface corresponds to the system in the absence of catalyst. The coordination of the catalyst to different atoms of the substrate during the generation of the surface for the catalyzed reaction resulted in discontinuities, and we felt that we could not make accurate assumptions about the location of the catalyst at all points on the PES. The C4–C33 and O30–C31 bond distances were chosen as relevant geometric parameters, since both distances being large corresponds to the fragmented product region of the PES, and both distances being small corresponds to the β-lactone region of the PES. The locations of β-TS1 and β-TS2 with respect to these two bond distances are marked on this surface by solid blue dots for the catalyzed system and unfilled dots for the uncatalyzed system. The β-TS1_cat geometry and IRC plotted are those of the lowest energy conformation (conformation 1, Fig. 3). The IRC paths for the catalyzed and uncatalyzed systems also are shown on this surface by solid and dashed blue lines, respectively. While the energies of stationary points and IRC points for the uncatalyzed reaction could be compared directly to the PES energies, the energies of stationary points for the catalyzed reaction and associated IRC, which led to the fragmented product, are plotted by equating the energy of the lowest energy point of the surface in the fragment region to the endpoint of the β-TS1_cat IRC.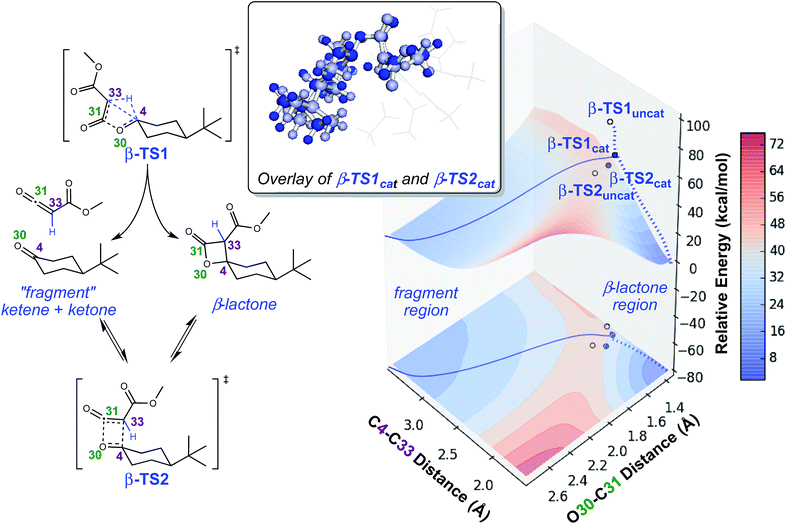

Fig. 4 Potential energy surface for lactone formation/fragmentation. Results of a relaxed PES scan along two bond distances in the uncatalyzed system (left) calculated at the B3LYP/6-31G(d) level of theory. A contour plot of the surface is projected onto the plane beneath the 3-dimensional plot. Energies reported are electronic energies, not including zero-point corrections. The locations of β-TS1 and β-TS2 with respect to the two distances plotted for the catalyzed and uncatalyzed reactions are labeled with solid blue dots and unfilled dots, respectively. The locations of the IRCs for both the catalyzed and uncatalyzed reactions are drawn with solid and dashed blue lines, respectively. The β-TS1_cat structure plotted is “conformation 1” in Fig. 3, the lowest energy conformation found. An overlay of β-TS1_cat and β-TS2_cat is included (top, center) to show the geometric similarity of these two structures with respect to the C4–C33 and O30–C31 bond distances.

There are several remarkable features of this surface. First, the energy of β-TS1_uncat is significantly above the surface. This is due to the fact that the hydride-shifting event that occurs in the TSS is not captured by the energy of the surface at this spot, as the only two geometric parameters constrained in generating the surface are the C4–C33 and O30–C31 distances. Though the location of β-TS1_cat is not quantitatively accurate, it appears that the energy gap between the TSS for the catalyzed reaction and the surface is not as large as that for the uncatalyzed reaction, which could point to the role of the rhodium catalyst in facilitating C–H insertion. The influence of the catalyst is also seen in the IRC plots for the catalyzed and uncatalyzed reactions, which define the minimum energy pathways to products from the TSS. The IRC pathway switches from one connected directly to the β-lactone product for the uncatalyzed reaction to one connected directly to the fragmented product once the catalyst is introduced. For the uncatalyzed system to take this path, a slight energetic ridge (Fig. 4, red) would need to be traversed. Thus, it appears that the rhodium catalyst is specifically aiding in the generation of the ketene and ketone fragments. Consistent with this contention, 100% of molecular dynamics trajectories initiated from β-TS1_uncat formed the carbene on one side of the TSS and the β-lactone on the other, matching the IRC behavior. Finally, the locations of the β-TS1_cat and β-TS2_cat structures are quite close to one another on the surface. The geometric similarity of β-TS1_cat and β-TS2_cat (see overlay in Fig. 4) is likely the primary reason that a substantial number of trajectories (8/130) connected the fragmented and β-lactone products to each other (rather than to the reactant). In the sampling of geometries near β-TS1_cat to initiate trajectories, some structures were probably very close to β-TS2_cat. In the extreme case that the geometries of the two TSSs are the same, the TSS region of the PES would be considered a “monkey saddle,” where a single point on the PES connects three separate minima.⁵³

Potential generality and markers for bifurcations

Does the scenario described above apply to other C–H insertion reactions? Indeed it does. We have found several additional Rh-catalyzed C–H insertion reactions with analogous PTSBs. Two such systems are described briefly here. First, Davies et al. recently showed that particular carbenoid precursors containing ortho-bromophenyl groups preferentially form β-lactones over γ-lactones (Fig. 5).¹³ Interestingly, when the other substituent on the carbenoid was an ethyl ester group, there was a preference for forming the trans β-lactone product, but when this same substituent was a benzyl ester group, the preference switched to the cis diastereomer. Second, Wamser and Bach also noticed a preference for β-lactone over γ-lactone formation with the presence of an ortho-bromo substituent on the phenyl ring attached to the Rh-carbenoid (Fig. 5), but in these experiments, Rh₂(OAc)₄ was used as catalyst.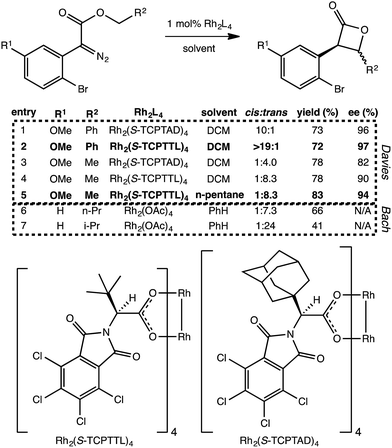

Fig. 5 Additional β-lactone-forming reactions with post-transition state bifurcations. Selected reactions from Davies, et al.¹³ and Wamser and Bach.¹¹ The Davies entries, 1–5, show a switch in diastereoselectivity for different R² substituents, as well as an increase in yield and enantioselectivity with a switch to a less polar solvent. The structures of the catalyst's chiral ligands are also shown, though the catalyst modeled computationally was Rh₂(OAc)₄. The Bach results shown here (entries 6 and 7) show an increase in diastereoselectivity (for the trans product) with the change from n-propyl to isopropyl at R², but a decrease in yield. We propose that these reactions involve PTSBs that could be decreasing the yield of the desired β-lactone products formed.

First, minima and TSSs relevant to Davies' reactions were modeled with a Rh₂(OAc)₄ catalyst to facilitate direct comparison to the other experimental systems. Using the B3LYP functional, it was found that IRCs for both the cis and trans configurations when R² is a methyl group (e.g., Fig. 5, entry 5) led directly to the β-lactone product. However, IRCs for both cis and trans configurations when R² is a phenyl (e.g., entry 2) led directly to the fragmented products. For Bach's systems, where R² was always an alkyl substituent, IRCs again led to the β-lactone product. This substituent-induced switch in IRC behavior is consistent with the involvement of PTSBs.

To our surprise, it was found that the conformation of the TSS also could influence IRC behavior. A higher energy conformation of the trans TSS where R² is a phenyl group led directly to the β-lactone product, in contrast to the IRC behavior of the lowest energy conformation, which led to the fragmented products. This higher energy conformation (7.6 kcal mol⁻¹ higher in free energy than the lowest energy conformation, calculated at the B3LYP/6-31G(d), LANL2DZ level of theory) only differs from the lowest energy conformation by rotation of the substituted phenyl ring (Fig. 6). The analogous higher energy conformation of the cis TSS had an IRC that led to the fragmented product, again in contrast to the trans TSS with the same substituted phenyl ring orientation. This conformation-dependent IRC behavior not only points to involvement of PTSBs, but also hints at the potential to increase β-lactone product formation by controlling the conformation of the substrate, i.e., the ligands on the catalyst could influence the preferred conformation of the substrate, thereby favoring particular exit channels from bifurcating pathways (and maybe already do in the case of the bulky, chiral ligands used in Davies' studies).

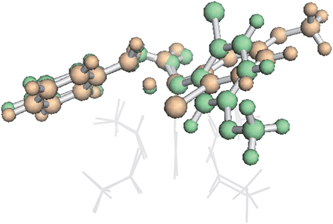Fig. 6 Conformational dependence of IRC behaviour. An overlay of two conformations of β-TS1 for formation of the trans product for the substrates in entries 1 and 2 in the table inset in Fig. 5.⁵⁴ The lowest energy conformation (orange, IRC leading to the fragmented product) and the higher energy conformation (green, IRC leading to the β-lactone product) differ only by rotation of the substituted phenyl ring. The Rh₂(OAc)₄ catalyst is represented as gray lines for clarity. Both structures were optimized at the B3LYP/6-31G(d), LANL2DZ level of theory.

In some cases, the functional used to locate the TSS and calculate its IRC also had an influence on the product to which the IRC led. In contrast to results using the B3LYP functional just described, when the higher energy conformation of the trans TSS for entry 2 (Fig. 4) was optimized with the BP86 functional, its IRC led to the fragmented products. We take this sort of inconsistency as another marker of a PTSB.

Molecular dynamics simulations initiated from each of the TSSs examined for Davies' and Bach's systems favored the IRC product in each case, but a significant amount of the non-IRC product was formed in all cases, further validating the contention that PTSBs are involved. We hypothesize that these systems result in good, rather than excellent, yields (issues of chemist, climate, etc. aside) due to the presence of the PTSB that provides a second exit channel from the pathway following the TSS.

Conclusions and prospects

Using DFT calculations (both static and dynamic), we were able to qualitatively reproduce the regioselectivity seen experimentally for several Rh-carbenoid promoted intramolecular C–H insertion reactions. Most importantly, our results are consistent with pathways to β-lactones that have PTSBs that are responsible for byproduct formation.

The results of these studies have revealed several phenomena a computational chemist can use to diagnose for the presence of a PTSB. While it was suggested previously that the formation of two (or more) products in dynamics simulations initiated from a TSS^1,25 and “shoulders” along IRCs (i.e., transitions from a low gradient to a high gradient) can be indicative of PTSBs,^3,55 the results of the current study suggest that changes to the IRC product with (1) relatively minor functional group substitutions on the substrate, (2) the relative stereochemistry of the TSS, (3) the conformation of the TSS, and/or (4) the functional used to locate the TSS and compute its IRC, may also point to PTSBs.

In general, one can expect to find a PTSB when the structure corresponding to the putative intermediate in a proposed two step mechanism is actually a TSS (or close to it), e.g., the oxonium/enolate described here (Fig. 2), secondary carbocations in terpene-forming cyclization/rearrangements,^3,26 π-complexes in Au-promoted cyclizations.^37–46 One should not only interrogate reactions of interest for the presence of this scenario, but reactions with PTSBs also, in principle, can be designed by looking for (and rationally manipulating) putative intermediates expected to reside in extremely shallow energy wells that can be accessed from high energy TSSs. It is time to stop bumping into bifurcations and instead actively pursue both of these directions. We are doing so and we hope others will do the same.

Methods

DFT calculations were completed using the Gaussian 09 program package.⁵⁶ All energies reported are Gibbs free energies at 298 K unless otherwise noted. Transition state structures (TSSs) were each verified as such by a frequency calculation that predicted exactly one imaginary frequency, while minima showed zero imaginary frequencies. To verify that a TSS is connected to the expected minima, intrinsic reaction coordinate (IRC)^25,57,58 calculations were run in both the forward and reverse directions. Molecular geometries were optimized with the B3LYP,^59,60 BP86,^61,62 and BPW91 (ref. 61–63) functionals with 6-31G(d)⁶⁴ for C, H and O and LANL2DZ⁶⁵ for Rh as the basis set in all cases [a basis set that is referred to here as 6-31G(d), LANL2DZ]. All three levels of theory have been used previously on related systems involving Rh catalysts.¹⁹ All stationary points were also optimized using B3LYP paired with a larger basis set [6-31+G(d,p)⁶⁴ for C, H, and O and SDD⁶⁶ for Rh; see ESI† for structures and energies] to validate relative energies and molecular geometries along the reaction pathway. While TSS barriers were consistently 2 to 3 kcal mol⁻¹ higher using the larger basis set, relative barriers heights and exergonicities did not change compared to 6-31G(d), LANL2DZ and there were no notable changes in geometries. Three-dimensional molecular images were created using CYLview software.⁶⁷

Early on in this study, we examined the possibility of structures with triplet electronic character, as well as the possibility of unpaired electrons in an overall singlet system by running unrestricted calculations with the keywords “guess = (mix, always)”. Using the B3LYP functional, triplet structures were consistently higher in energy than their singlet counterparts (see ESI†) and the optimized unrestricted singlet structures exhibited no radical character.

To ensure that the lowest energy conformations of the TSSs were found, after an initial TSS was optimized, a relaxed PES scan was performed in which two dihedral angles, corresponding to (1) rotation around the C–C bond of the methyl ester group and (2) rotation about the Rh-carbenoid bond, were varied. The three distances between the three atoms involved in bond making/breaking during the C–H insertion (the carbenoid carbon and the atoms of the C–H bond) were constrained to their distances in the initially optimized TSS. The lowest energy structures found as a result of this conformational search were then fully optimized to TSSs. The initial conformational search was conducted with the B3LYP functional, and the resulting lowest energy structures then were optimized with BP86 and BPW91.

These three levels of theory were also utilized in direct dynamics calculations.^68,69 Quasi-classical molecular dynamics simulations were conducted using Singleton's progdyn script package.⁴⁷ Progdyn interfaces with Gaussian 09 to calculate force constants at each step of a trajectory. Trajectories were initialized starting from an optimized TSS. Each trajectory was given a random amount of initial kinetic and potential energy and then propagated in both forward and reverse directions, defined by the phase of the imaginary vibrational mode of the TSS. In all cases, the 10 lowest energy vibrational modes (which were always less than 100 cm⁻¹) were not given any initial displacement. This is because the Rh-containing system is relatively large, which makes finding a starting structure that has the desired total energy difficult when including the displacement of these low energy modes. Trajectories were terminated when they reached structures that closely resembled minima on the PES, as defined by the following stop criteria: the Rh-carbenoid reactant was considered to have formed when the C4–H11 distance was less than 1.10 Å, the β-lactone product was considered to have been formed when the C33–H11 distance was less than 1.10 Å and the C4–C33 distance was less than 1.56 Å, and the fragmented products were considered to have been formed when the C33–H11 distance was less than 1.10 Å and the O30–C31 distance was greater than 2.50 Å (numbering below). Though omitted from the picture below for clarity, Rh₂(OAc)₄ was coordinated to C33 at the start of the dynamics trajectories.

Acknowledgements

We gratefully acknowledge support from the National Science Foundation (CHE-1565933 and the XSEDE program via CHE-030089) and the Department of Education's Graduate Assistance in Areas of National Need (GAANN) fellowship.

References

1. H. Mayr and A. R. Ofial, Angew. Chem., Int. Ed., 2006, 45, 1844–1854.
2. D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Çelebi-Ölçüm and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601.
3. Y. J. Hong and D. J. Tantillo, Nat. Chem., 2014, 6, 104–111.
4. J. H. Hansen, T. M. Gregg, S. R. Ovalles, Y. Lian, J. Autschbach and H. M. Davies, J. Am. Chem. Soc., 2011, 133, 5076–5085.
5. A. Patel, Z. Chen, Z. Yang, O. Gutierrez, H. W. Liu, K. N. Houk and D. A. Singleton, J. Am. Chem. Soc., 2016, 138, 3631–3634.
6. D. E. Olson and J. Du Bois, J. Am. Chem. Soc., 2008, 130, 11248–11249.
7. F. J. Lombard and M. J. Coster, Org. Biomol. Chem., 2015, 13, 6419–6431.
8. A. Padwa and Y. Zou, J. Org. Chem., 2015, 80, 1802–1808.
9. N. V. Rostovskii, M. S. Novikov, A. F. Khlebnikov, V. A. Khlebnikov and S. M. Korneev, Tetrahedron, 2013, 69, 4292–4301.
10. M. P. Doyle, Chem. Rev., 1986, 86, 919–939.
11. M. Wamser and T. Bach, Synlett, 2014, 25, 1081–1084.
12. C. Liang, F. Collet, F. Robert-Peillard, P. Müller, R. H. Dodd and P. Dauban, J. Am. Chem. Soc., 2008, 130, 343–350.
13. L. Fu, H. Wang and H. M. Davies, Org. Lett., 2014, 16, 3036–3039.
14. S. Chuprakov, J. A. Malik, M. Zibinsky and V. V. Fokin, J. Am. Chem. Soc., 2011, 133, 10352–10355.
15. M. P. Doyle, Aldrichimica Acta, 1996, 29, 3–11.
16. D. F. Taber and S.-E. Stiriba, Chem.–Eur. J., 1998, 4, 990–992.
17. E. Nakamura, N. Yoshikai and M. Yamanaka, J. Am. Chem. Soc., 2002, 124, 7181–7192.
18. N. Yoshikai and E. Nakamura, Adv. Synth. Catal., 2003, 345, 1159–1171.
19. T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586.
20. X. Zhang, H. Xu and C. Zhao, J. Org. Chem., 2014, 79, 9799–9811.
21. Z. Zhang and J. Wang, Tetrahedron, 2008, 64, 6577–6605.
22. B. S. Balaji and B. M. Chanda, Tetrahedron Lett., 1998, 39, 6381–6382.
23. D. F. Taber and R. E. Ruckle, J. Am. Chem. Soc., 1986, 108, 7686–7693.
24. M. P. Doyle and M. A. McKervey, Chem. Commun., 1997, 983–989.
25. S. Maeda, Y. Harabuchi, Y. Ono, T. Taketsugu and K. Morokuma, Int. J. Quantum Chem., 2015, 115, 258–269.
26. Y. J. Hong and D. J. Tantillo, Nat. Chem., 2009, 1, 384–389.
27. Z. C. Kramer, B. K. Carpenter, G. S. Ezra and S. Wiggins, J. Phys. Chem. A, 2015, 119, 6611–6630.
28. P. Collins, B. K. Carpenter, G. S. Ezra and S. Wiggins, J. Chem. Phys., 2013, 139, 154108.
29. S. R. Hare and D. J. Tantillo, Beilstein J. Org. Chem., 2016, 12, 377–390.
30. E. J. Lee, K. Woon and K. Y. Seong, Tetrahedron Lett., 1990, 31, 1023–1026.
31. H. V. Pham and K. N. Houk, J. Org. Chem., 2014, 79, 8968–8976.
32. J. Rehbein and B. K. Carpenter, Phys. Chem. Chem. Phys., 2011, 13, 20906–20922.
33. P. Pechukas, Annu. Rev. Phys. Chem., 1981, 32, 159–177.
34. K. J. Laidler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664.
35. D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800.
36. H. Eyring, J. Chem. Phys., 1935, 3, 107.
37. D. Garayalde, E. Gomez-Bengoa, X. Huang, A. Goeke and C. Nevado, J. Am. Chem. Soc., 2010, 132, 4720–4730.
38. Z. J. Wang, D. Benitez, E. Tkatchouk, W. A. Goddard, III and F. D. Toste, J. Am. Chem. Soc., 2010, 132, 13064–13071.
39. E. L. Noey, X. Wang and K. N. Houk, J. Org. Chem., 2011, 76, 3477–3483.
40. M. M. Hansmann, M. Rudolph, F. Rominger and A. S. Hashmi, Angew. Chem., Int. Ed., 2013, 52, 2593–2598.
41. Y. Wang, A. Yepremyan, S. Ghorai, R. Todd, D. H. Aue and L. Zhang, Angew. Chem., Int. Ed., 2013, 52, 7795–7799.
42. M. H. Vilhelmsen and A. S. Hashmi, Chemistry, 2014, 20, 1901–1908.
43. M. M. Hansmann, S. Tsupova, M. Rudolph, F. Rominger and A. S. Hashmi, Chemistry, 2014, 20, 2215–2223.
44. S. V. C. Vummaleti, L. Falivene, A. Poater and L. Cavallo, ACS Catal., 2014, 4, 1287–1291.
45. E. Tudela, J. Gonzalez, R. Vicente, J. Santamaria, M. A. Rodriguez and A. Ballesteros, Angew. Chem., Int. Ed., 2014, 53, 12097–12100.
46. L. Zhang, Y. Wang, Z. J. Yao, S. Wang and Z. X. Yu, J. Am. Chem. Soc., 2015, 137, 13290–13300.
47. D. A. Singleton, C. Hang, M. J. Szymanski and E. E. Greenwald, J. Am. Chem. Soc., 2003, 125, 1176–1177.
48. U. Lourderaj, K. Park and W. L. Hase, Int. Rev. Phys. Chem., 2008, 27, 361–403.
49. B. K. Carpenter, Annu. Rev. Phys. Chem., 2005, 56, 57–89.
50. U. Lourderaj and W. L. Hase, J. Phys. Chem. A, 2009, 113, 2236–2253.
51. Z. Yang, C. Doubleday and K. N. Houk, J. Chem. Theory Comput., 2015, 11, 5606–5612.
52. Z. Chen, Y. Nieves-Quinones, J. R. Waas and D. A. Singleton, J. Am. Chem. Soc., 2014, 136, 13122–13125.
53. D. M. Birney, Curr. Org. Chem., 2010, 14, 1658–1668.
54. The PyMOL Molecular Graphics System, Version 1.8, Schrödinger, LLC.
55. D. H. Nouri and D. J. Tantillo, J. Org. Chem., 2006, 71, 3686–3695.
56. M. J. T. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Naka, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
57. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
58. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
59. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
60. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
61. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
62. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
63. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
64. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
65. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
66. G. Igel-Mann, H. Stoll and H. Preuss, Mol. Phys., 1988, 65, 1321–1328.
67. C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, 2009.
68. C. Doubleday, K. Bolton and W. L. Hase, J. Am. Chem. Soc., 1997, 119, 5251–5252.
69. M. Paranjothy, R. Sun, Y. Zhuang and W. L. Hase, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 296–316.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed molecular dynamics information, Cartesian coordinates, intrinsic reaction coordinates (IRCs), and 3-dimensional CYLview images of all optimized structures (PDF). See DOI: 10.1039/c6sc03745c

---