Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The interplay between fluorescence and phosphorescence with luminescent gold(I) and gold(III) complexes bearing heterocyclic arylacetylide ligands†
Kaai Tung
Chan
a,
Glenna So Ming
Tong
*a,
Wai-Pong
To
a,
Chen
Yang
a,
Lili
Du
b,
David Lee
Phillips
b and
Chi-Ming
Che
*ac
aState Key Laboratory of Synthetic Chemistry, Institute of Molecular Functional Materials, Department of Chemistry, The University of Hong Kong, Pokfulam Road, Hong Kong SAR, China. E-mail: tongsm@hku.hk; cmche@hku.hk
bDepartment of Chemistry, The University of Hong Kong, Hong Kong, China
cDepartment of Chemistry, HKU Shenzhen Institute of Research and Innovation, Shenzhen 518053, China
First published on 5th December 2016
Abstract
The photophysical properties of a series of gold(I) [LAu(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] (L = PCy3 (1a–4a), RNC (5a), NHC (6a)) and gold(III) complexes [Au(C^N^C)(C
CR)] (L = PCy3 (1a–4a), RNC (5a), NHC (6a)) and gold(III) complexes [Au(C^N^C)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] (1b–4b) bearing heterocyclic arylacetylide ligands with narrow band-gap are compared. The luminescence of both series are derived from an intraligand transition localized on the arylacetylide ligand (ππ*(C
CR)] (1b–4b) bearing heterocyclic arylacetylide ligands with narrow band-gap are compared. The luminescence of both series are derived from an intraligand transition localized on the arylacetylide ligand (ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)) but 1a–3a displayed prompt fluorescence (τPF = 2.7–12.0 ns) while 1b–3b showed mainly phosphorescence (τPh = 104–205 μs). The experimentally determined intersystem crossing (ISC) rate constants (kISC) are on the order of 106 to 108 s−1 for the gold(I) series (1a–3a) but 1010 to 1011 s−1 for the gold(III) analogues (1b–3b). DFT/TDDFT calculations have been performed to help understand the difference in the kISC between the two series of complexes. Owing to the different oxidation states of the gold ion, the Au(I) complexes have linear coordination geometry while the Au(III) complexes are square planar. It was found from DFT/TDDFT calculations that due to this difference in coordination geometries, the energy gap between the singlet and triplet excited states (ΔEST) with effective spin–orbit coupling (SOC) for Au(I) systems is much larger than that for the Au(III) counterparts, thus resulting in the poor ISC efficiency for the former. Time-resolved spectroscopies revealed a minor contribution (<2.9%) of a long-lived delayed fluorescence (DF) (τDF = 4.6–12.5 μs) to the total fluorescence in 1a–3a. Attempts have been made to elucidate the mechanism for the origins of the DF: the dependence of the DF intensity with the power of excitation light reveals that triplet–triplet annihilation (TTA) is the most probable mechanism for the DF of 1a while germinate electron–hole pair (GP) recombination accounts for the DF of 2a in 77 K glassy solution (MeOH/EtOH = 4
CR)) but 1a–3a displayed prompt fluorescence (τPF = 2.7–12.0 ns) while 1b–3b showed mainly phosphorescence (τPh = 104–205 μs). The experimentally determined intersystem crossing (ISC) rate constants (kISC) are on the order of 106 to 108 s−1 for the gold(I) series (1a–3a) but 1010 to 1011 s−1 for the gold(III) analogues (1b–3b). DFT/TDDFT calculations have been performed to help understand the difference in the kISC between the two series of complexes. Owing to the different oxidation states of the gold ion, the Au(I) complexes have linear coordination geometry while the Au(III) complexes are square planar. It was found from DFT/TDDFT calculations that due to this difference in coordination geometries, the energy gap between the singlet and triplet excited states (ΔEST) with effective spin–orbit coupling (SOC) for Au(I) systems is much larger than that for the Au(III) counterparts, thus resulting in the poor ISC efficiency for the former. Time-resolved spectroscopies revealed a minor contribution (<2.9%) of a long-lived delayed fluorescence (DF) (τDF = 4.6–12.5 μs) to the total fluorescence in 1a–3a. Attempts have been made to elucidate the mechanism for the origins of the DF: the dependence of the DF intensity with the power of excitation light reveals that triplet–triplet annihilation (TTA) is the most probable mechanism for the DF of 1a while germinate electron–hole pair (GP) recombination accounts for the DF of 2a in 77 K glassy solution (MeOH/EtOH = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Both 4a and 4b contain a BODIPY moiety at the acetylide ligand and display only 1IL(ππ*) fluorescence with negligible phosphorescence being observed. Computational analyses attributed this observation to the lack of low-lying triplet excited states that could have effective SOC with the S1 excited state.
1). Both 4a and 4b contain a BODIPY moiety at the acetylide ligand and display only 1IL(ππ*) fluorescence with negligible phosphorescence being observed. Computational analyses attributed this observation to the lack of low-lying triplet excited states that could have effective SOC with the S1 excited state.
Introduction
Phosphorescence is a distinctive photophysical property of transition-metal complexes, which has widespread applications in diverse areas. As it is derived from the ‘forbidden’ radiative relaxation of a triplet-excited state to the singlet ground state, it is featured by long emission lifetime (in μs) and reduced emission energy compared to fluorescence commonly encountered in organic luminophores. Electronic transitions associated with a change of spin are prohibited by the spin-selection rule. However, transition-metal ions that have high atomic number and hence, large spin–orbit coupling constant (ξ), usually lead to efficient spin–orbit coupling (SOC) that relaxes the spin selection rule. Fast intersystem crossing (ISC) in the sub-picosecond to picosecond time regime1 leads to rapid depletion of a singlet excited state to a triplet excited state instead of fluorescence as fluorescence radiative lifetime is typically in the nanosecond range. Thus, in transition-metal complexes, phosphorescence normally prevails in their luminescence spectra.However, in recent years, there are an increasing number of reports on transition-metal complexes which display slow ISC rate with lifetimes ranging from hundreds of ps to ns. For instance, 2,5-bis(arylethynyl)rhodacyclopentadiene complexes (ξRh = 1260 cm−1)2 were reported to display exclusively prompt fluorescence with high emission quantum yields of 0.3–0.7 and lifetimes of 1–3 ns, corresponding to ISC rate constants of ∼108 s−1.3 In addition, transition-metal complexes containing fused aromatic systems such as perylene, perylene diimide, pyrene and tetracene also show ligand-dominated fluorescence (see Fig. 1).4 Hence, it has become clear that the presence of heavy elements does not guarantee fast ISC rate; the molecular structure and the nature of the ligands may play more critical roles in determining the ISC rate.
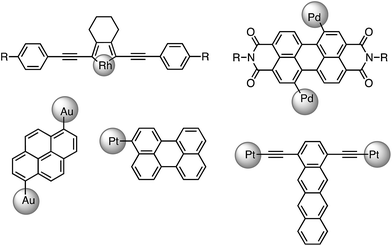 | ||
| Fig. 1 Selected examples of transition-metal complexes that display dominant fluorescence instead of phosphorescence. Auxiliary ligands coordinated to the metal ions are omitted. | ||
Luminescent Au(I) complexes are well documented to display rich photophysical properties. Although Au(I) complexes generally display phosphorescence owing to the large SOC constant of Au(I) ion (ξAu ∼ 5100 cm−1),2 ligand-centered fluorescence has also been reported in a number of gold(I) complexes. For example, as revealed by the luminescence of [TEE(AuPCy3)4] and [TEB(AuPCy3)3] (TEE = tetraethynylethene; TEB = 1,3,5-triethynylbenzene), subtle changes in the electronic structure of the bridging alkynyl ligand leads to intense phosphorescence (Φem = 0.46, τ = 285 μs) in the latter but solely fluorescence (Φem = 0.22, τ < 0.05 μs) in the former.5 In both cases, the luminescence originates from the ligand-centered transition mainly localized on the bridging alkynyl ligands. Che and co-workers also reported a series of Au(I)-conjugated acetylides, [(Cy3P)Au(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C6H4)n−1(C
C–C6H4)n−1(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh)] (n ≥ 2), which display dual fluorescence (prompt and delayed) and phosphorescence.6 Both the Φem and ratio of fluorescence versus phosphorescence were found to depend on the conjugation length (number of repeating units n) and the substitution pattern of arylacetylide ligands.
CPh)] (n ≥ 2), which display dual fluorescence (prompt and delayed) and phosphorescence.6 Both the Φem and ratio of fluorescence versus phosphorescence were found to depend on the conjugation length (number of repeating units n) and the substitution pattern of arylacetylide ligands.
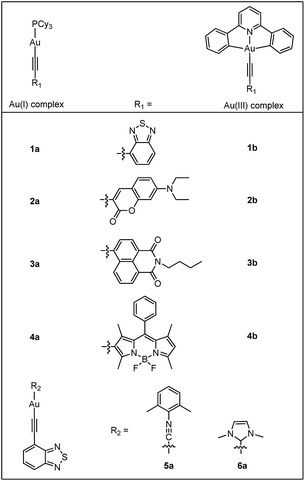
As a continuous effort to elucidate the ligand effects on the photophysics of luminescent gold complexes, heterocyclic arylacetylide ligands containing narrow band-gap moieties (benzothiadiazole (L1), coumarin (L2), naphthalimide (L3) and boron-dipyrromethene (referred to as Bodipy) (L4); Chart 1) were chosen in this study. A series of Au(I) heterocyclic arylacetylide complexes, 1a–4a, were synthesized. Tricyclohexylphosphine (PCy3) was used as the auxiliary ligand in these complexes because (1) it is optically transparent at wavelength >250 nm so that it is not involved in the emissive excited states in the UV-visible spectral region and (2) its steric bulkiness would prevent the gold ions from coming into close contact that could lead to low-lying excited states originated from metal–metal and π–π interactions. It is worth mentioning that several recently reported Au(I) alkynyl complexes bearing similar benzothiadiazole,7 coumarin8 and naphthalimide9 derivatives also show similar luminescence properties as our Au(I) complexes.10,11 The effects of auxiliary ligands on the photophysical properties of Au(I) complexes were also studied by comparing 1a with two derivatives containing 2,6-dimethylphenyl isocyanide (RNC, 5a) and 1,3-dimethylimidazol-2-ylidene (NHC, 6a) instead of the phosphine auxiliary ligand, respectively.
The effects of the oxidation state of the metal ion on the photophysical behaviours of transition-metal complexes are relatively unexplored. Herein, an analogous series of Au(III)-acetylides supported by the cyclometalated [C^N^C] ligand (1b–4b; HC^N^CH = 2,6-diphenylpyridine) were also prepared and their photophysical properties were compared with those of the Au(I) counterparts. The photophysical properties of both Au(I) and Au(III) complexes were investigated by steady-state and time-resolved spectroscopic measurements. DFT/TDDFT calculations were performed on the pairs (1a, 1b) and (4a, 4b) in order to understand the origin of the dramatic difference in ISC efficiencies between these Au(I) and Au(III) complexes.
Results
Synthesis and characterization
The gold(I) alkynyl complexes 1a–6a were synthesized in 53–79% yields following the protocol of base deprotonation (NaOMe) of terminal alkynes and substitution of chloride ion of the corresponding Au(I) precursors.5a,6a,b,12 As these complexes were observed to show signs of decomposition on SiO2 column, column chromatography was not used for their purification. Analytically pure 1a–6a were obtained by recrystallization from CH2Cl2/hexane mixtures. The Au(III) complexes 1b–4b were synthesized by copper-catalyzed Sonogashira coupling between terminal alkynes and [Au(C^N^C)Cl] using deoxygenated CH2Cl2 as the solvent, with NEt3 added to initiate the deprotonation of alkynes.13 These complexes were purified by chromatography on SiO2 column using dichloromethane and hexane as eluent. The yields were 51–84%.All complexes have been characterized by 1H and 13C NMR, mass spectrometry (FAB+) and elemental analyses. Ligands L1–L4 were characterized by 1H NMR and MS-EI. The complexes are stable in the solid state and in solution under ambient conditions. Complexes 1a–6a are highly soluble in CH2Cl2 and THF but are less soluble in alcoholic solvents such as MeOH. Complexes 1b–4b have lower solubility compared with their Au(I) counterparts. All of these gold complexes appear as yellow or orange solids except for 4a and 4b that are purplish red. The 31P signals of 1a–4a occur at ca. δ 56.3 as a singlet, characteristic of the 31P signals of the Au–PCy3 moiety that usually appear in the range of δ 56.0–58.0.6a,b,12 In the 13C NMR spectra, two doublets are observed at ca. δ 131.2–146.2 (2JCP ≈ 130 Hz) and 94.6–98.4 (3JCP ≈ 24 Hz) which can be assigned to the α and β-acetylenic carbons.6a,b,12b In 6a, the carbene carbon ligated to gold occurs at δ 187.7.14
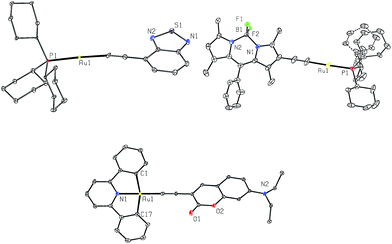
X-Ray crystallography
Crystals of 1a, 4a and 2b were obtained by layering hexane over concentrated CH2Cl2 solutions. Their crystal data and selected bond lengths and angles are given in ESI.†Fig. 2 shows the structures of 1a and 4a (top panel). The P1–Au1–C(acetylide) angles of 1a and 4a are 175.0(13) and 178.1(2)° and Au1–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C angles are 170.9(4) and 177.6(5)°, respectively, revealing slight deviation from linear coordination geometry. The Au1–C(acetylide) distances of 2.049(4) and 2.001(5) Å and C
C angles are 170.9(4) and 177.6(5)°, respectively, revealing slight deviation from linear coordination geometry. The Au1–C(acetylide) distances of 2.049(4) and 2.001(5) Å and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C distances of 1.146(7) and 1.191(8) Å for 1a and 4a, respectively, are comparable with those of other reported gold(I) acetylide complexes.6a,b,12a,b The crystal packing diagrams of 1a and 4a are shown in ESI (Fig. S1†). In both cases, there are no short intermolecular contacts; the closest Au⋯Au distances are 5.9715(5) and 5.2726(4) Å for 1a and 4a, respectively.
C distances of 1.146(7) and 1.191(8) Å for 1a and 4a, respectively, are comparable with those of other reported gold(I) acetylide complexes.6a,b,12a,b The crystal packing diagrams of 1a and 4a are shown in ESI (Fig. S1†). In both cases, there are no short intermolecular contacts; the closest Au⋯Au distances are 5.9715(5) and 5.2726(4) Å for 1a and 4a, respectively.
The crystal structure of 2b (Fig. 2, bottom) shows a slightly distorted square-planar geometry with C1–Au1–C17 angle of 162.44(14)°. The Au1–C(acetylide) and C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C distances are 1.969(4) and 1.197(5) Å, respectively. These parameters are similar to those found in related cyclometalated Au(III) arylacetylide complexes.13 The torsional angle between the Au(C^N^C) and arylacetylide planes is approximately 72.6°. This non-planarity gives rise to negligible π–π stacking between molecules as shown in Fig. S2 in ESI.†
C distances are 1.969(4) and 1.197(5) Å, respectively. These parameters are similar to those found in related cyclometalated Au(III) arylacetylide complexes.13 The torsional angle between the Au(C^N^C) and arylacetylide planes is approximately 72.6°. This non-planarity gives rise to negligible π–π stacking between molecules as shown in Fig. S2 in ESI.†
Electrochemical properties
The electrochemical properties of selected complexes, 1a–4a and 1b–4b, were investigated by cyclic voltammetry. The electrochemical data are summarized in Table 1. The cyclic voltammograms of the Au(I) complexes and their Au(III) counterparts are shown in Fig. S3, ESI.† Except for 1a and 2a, both classes of complexes display both irreversible oxidation (Epa = +0.6 to +1.4 V) and quasi-reversible/irreversible reduction waves (Epc = −1.5 to −1.8 V) attributed to the redox process localized on the arylacetylides. For the pairs [2a, 2b] and [4a, 4b], the Epa occur at relatively low potential of ca. +0.6 and +0.7 V, respectively, suggesting higher HOMO level of the conjugated coumarin and Bodipy than the other heterocyclic moieties. For the Au(III) complexes, other than the redox reactions occurring at the arylacetylide ligands at potentials similar to the Au(I) counterparts, there are also irreversible reduction waves at ca. −1.9 to −2.0 V attributable to reduction of the [C^N^C] ligands.| Complex | E pc /V | E pa /V |
|---|---|---|
| a Values determined in CH2Cl2 (Cp2Fe+/0 occurs at E1/2 = +0.15–0.16 V) at 298 K; values reported versus Ag/AgNO3 reference electrode; electrolyte: 0.1 M nBu4NPF6; scan rate = 100 mV s−1. b Cathodic peak potential (Epc) of irreversible wave. c Anodic peak potential of (Epa) irreversible wave. d E 1/2 = Epa + Epc of quasi-reversible wave. | ||
| 1a | −1.79d | — |
| 2a | — | 0.61, 0.95 |
| 3a | −1.61d | 1.44 |
| 4a | −1.50d | 0.71, 1.14 |
| 1b | −1.82, −2.03 | 1.25 |
| 2b | −1.89 | 0.59, 1.02 |
| 3b | −1.59, −1.95 | 1.42 |
| 4b | −1.49d, −2.02 | 0.74 |
UV-vis absorption spectroscopy
All photophysical data of the gold complexes and the free ligands L1–L4 are listed in Table 2.| UV/Vis absorption, λmax/nm (103ε/M−1 cm−1) | Emission | |||||||
|---|---|---|---|---|---|---|---|---|
| Medium | λ F/nm | λ Ph/nm | τ PF /ns | τ DF /μs | τ phos/μs | Φ em | ||
a Data were obtained from steady-state measurements with degassed CH2Cl2 solutions (2 × 10−5 M) unless specified. Measurements with glassy solutions were performed in EtOH/MeOH (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture at 77 K.
b Emission lifetimes of prompt fluorescence (τPF) were determined by time-correlated single photon counting (TCSPC) measurement.
c Emission lifetimes of delayed fluorescence (τDF) were obtained from fitting the decay of the time-resolved emission (TRE) as a mono-exponential decay in the delay time range of 0–40 ns and 1–46 μs, respectively. Measurements were performed in degassed CH2Cl2 (5 × 10−5 M) solutions.
d Emission quantum yields (Φem) were obtained using quinine sulfate in degassed 0.5 M H2SO4 (Φ = 0.546) as the standard unless specified. Φem measured in steady state is the overall emission quantum yield, i.e. Φem = ΦPF + ΦDF for 1a–3a and 5a–6a.
e Obtained from time-resolved emission spectra.
f Emission lifetime was not determined (n.d.) due to weak emission signal.
g Determined from time-resolved emission spectra in degassed CH2Cl2 (1 × 10−5 M) solutions.
h Determined from fs-TRF spectra.
i Emission quantum yields (Φem) were obtained using [Ru(bpy)3][PF6]2 in degassed acetonitrile as the standard (Φ = 0.062). 1) mixture at 77 K.
b Emission lifetimes of prompt fluorescence (τPF) were determined by time-correlated single photon counting (TCSPC) measurement.
c Emission lifetimes of delayed fluorescence (τDF) were obtained from fitting the decay of the time-resolved emission (TRE) as a mono-exponential decay in the delay time range of 0–40 ns and 1–46 μs, respectively. Measurements were performed in degassed CH2Cl2 (5 × 10−5 M) solutions.
d Emission quantum yields (Φem) were obtained using quinine sulfate in degassed 0.5 M H2SO4 (Φ = 0.546) as the standard unless specified. Φem measured in steady state is the overall emission quantum yield, i.e. Φem = ΦPF + ΦDF for 1a–3a and 5a–6a.
e Obtained from time-resolved emission spectra.
f Emission lifetime was not determined (n.d.) due to weak emission signal.
g Determined from time-resolved emission spectra in degassed CH2Cl2 (1 × 10−5 M) solutions.
h Determined from fs-TRF spectra.
i Emission quantum yields (Φem) were obtained using [Ru(bpy)3][PF6]2 in degassed acetonitrile as the standard (Φ = 0.062).
|
||||||||
| 1a | 265 (14.1), 275 (14.6), 305 (9.3), 311 (9.8), 319 (12.4), 379 (6.9) | CH2Cl2 298 K | 467 | — | 12.0 | 11.9 | — | 0.91 |
| Glassy 77 K | 442 | 630, 688e | n.d.f | 109e | ||||
| Solid 298 K | 504 | — | 5.3 | — | ||||
| Solid 77 K | 492 | — | 11.6 | — | ||||
| 2a | 271 (13.9), 316 (3.2), 331 (3.2), 410 (40.0), 423 (3.7, br) | CH2Cl2 298 K | 466 | 596, 652e | 2.7 | 4.6 | n.d.f | 0.70 |
| 11.8g | 13.6g | |||||||
| Glassy 77 K | 460, 481 | 596, 653e | 243e | 203e | ||||
| Solid 298 K | 405 (weak), 480 (sh), 515 (max) | 598, 652 (sh)e | 15.0e | 24.6e | ||||
| Solid 77 K | 409 (weak), 487 (max), 517 (sh) | 597, 654(sh)e | 9.4e | 12.0e | ||||
| 3a | 283 (12.2), 333 (5.6), 350 (11.3), 380 (23.8), 397 (25.5) | CH2Cl2 298 K | 441 | 613, 670e | 2.8 | 2.6, 12.5 | n.d.f | 0.78 |
| 31.5g | 61.9g | |||||||
| Glassy 77 K | 418, 439, 462 (sh) | 569, 609, 666e | n.d.f | 530e | ||||
| Solid 298 K | 403 (sh), 503 | 610, 668e | 29.1 | 64.9e | ||||
| Solid 77 K | 404 (sh), 504 | 627, 680e | 35.1 | 92.3e | ||||
| 4a | 280 (13.5), 325 (4.5), 412 (10.1), 553 (40.2) | CH2Cl2 298 K | 593 | — | 0.8 | — | — | 0.04 |
| 5a | 266 (18.6), 279 (15.8), 294 (12.5), 305 (11.2), 311 (10.1), 319 (12.7), 371 (7.1) | CH2Cl2 298 K | 456 | — | 11.0 | 6.8 | — | 0.90 |
| 6a | 259 (18.3), 280 (17.5), 298 (7.8), 305 (10.7), 311 (11.4), 319 (14.2), 383 (8.3) | CH2Cl2 298 K | 476 | — | 14.0 | 7.4 | — | 0.84 |
| 1b | 283 (20.4), 310 (24.1), 318 (26.8), 369 (13.0), 381 (13.8) | CH2Cl2 298 K | 461h | 630, 671 (sh) | 13.8h | — | 104 | 0.003i |
| Glassy 77 K | 610, 668 | n.d.f | ||||||
| 2b | 312 (13.9), 406 (35.9, br), 432 (40.7) | CH2Cl2 298 K | 473h | 592, 642 (sh) | 9.0h | — | 124 | 0.01i |
| Glassy 77 K | 585, 605, 643 | 1200 | ||||||
| Solid 298 K | 530, 601, 660 | 1.4 | ||||||
| 3b | 312 (12.7), 325 (11.9), 379 (26.6), 395 (29.5) | CH2Cl2 298 K | 459h | 603, 659 (sh) | 5.2h | — | 205 | 0.04i |
| Glassy 77 K | 598, 614 (sh), 652 | 2200 | ||||||
| 4b | 312 (12.1), 320 (12.0), 366 (7.6), 384 (9.6), 401 (10.7), 515 (24.0, br), 546 (41.7) | CH2Cl2 298 K | 583 | — | 2.1 | — | — | 0.13 |
| L1 | 303 (8.7), 309 (9.7), 316 (11.9), 341 (4.1) | CH2Cl2 298 K | 412 | — | 1.0 | — | — | 0.07 |
| L2 | 260 (15.9), 326 (4.7), 405 (24.0, br), 417 (24.7) | CH2Cl2 298 K | 455 | — | 3.6 | — | — | 0.94 |
| L3 | 333 (14.6), 350 (22.4), 367 (20.6) | CH2Cl2 298 K | 378, 398, 419 (sh) | — | 0.5 | — | — | 0.11 |
| L4 | 321 (3.9, br), 376 (5.3, br), 486 (14.8, sh), 517 (45.4) | CH2Cl2 298 K | 533 | — | 6.4 | — | — | 0.83 |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)) with some charge-transfer character. Similar assignments were also made for other Au(I) alkynyl complexes in the literature.6,7,8a Bathochromic shifts of 1IL transitions of arylacetylides are observed upon coordination of the arylacetylides to the Au(I) ion and are ascribed to π-interaction between Au(I) 5d orbitals and the ligand π-orbitals (see MO surfaces in Fig. 9 and 10).
CR)) with some charge-transfer character. Similar assignments were also made for other Au(I) alkynyl complexes in the literature.6,7,8a Bathochromic shifts of 1IL transitions of arylacetylides are observed upon coordination of the arylacetylides to the Au(I) ion and are ascribed to π-interaction between Au(I) 5d orbitals and the ligand π-orbitals (see MO surfaces in Fig. 9 and 10).
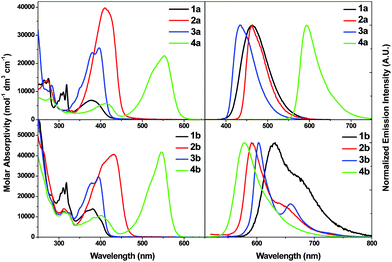 | ||
| Fig. 3 UV-vis absorption spectra (left) and emission spectra (right) of 1a–4a (top) and 1b–4b (bottom) in CH2Cl2 at 298 K (2 × 10−5 M). | ||
Replacing the neutral auxiliary ligand PCy3 in 1a with 2,6-dimethylphenyl isocyanide (RNC, 5a) and 1,3-dimethylimidazol-2-ylidene (NHC, 6a) results in a slight change in λmax of the lowest energy absorption band (λmax = 371 nm (5a, RNC) and 383 nm (6a, NHC) cf. λmax = 379 nm (1a, PCy3)) (Fig. S6 in ESI†).
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) transitions. Comparisons of the absorption spectra of 1a–4a and 1b–4b at λ ≤ 300 nm revealed that the absorption bands in this spectral region are more intense in 1b–4b with ε values of ca. 4 × 104 mol−1 dm3 cm−1 and these high energy absorption bands likely involve intraligand 1ππ*(C^N^C) transitions (Fig. S7 in ESI†).
CR) transitions. Comparisons of the absorption spectra of 1a–4a and 1b–4b at λ ≤ 300 nm revealed that the absorption bands in this spectral region are more intense in 1b–4b with ε values of ca. 4 × 104 mol−1 dm3 cm−1 and these high energy absorption bands likely involve intraligand 1ππ*(C^N^C) transitions (Fig. S7 in ESI†).
Steady-state emission spectroscopy
All of the complexes are luminescent in degassed CH2Cl2 at room temperature and in 77 K glassy solutions (EtOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH = 4
MeOH = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) upon excitation at the corresponding lowest-energy absorption λmax. As depicted in Table 2, there is a distinct difference between the two classes of complexes: the Au(I) complexes 1a–6a display predominantly fluorescence while the Au(III) complexes, 1b–3b, exhibit exclusively weak phosphorescence. Complex 4b, on the other hand, shows fluorescence only.
1) upon excitation at the corresponding lowest-energy absorption λmax. As depicted in Table 2, there is a distinct difference between the two classes of complexes: the Au(I) complexes 1a–6a display predominantly fluorescence while the Au(III) complexes, 1b–3b, exhibit exclusively weak phosphorescence. Complex 4b, on the other hand, shows fluorescence only.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited states, with some charge transfer character, which probably arise from mixings of metal-to-ligand charge-transfer (MLCT) character. Solvent effects on the emissions of 1a–3a can be found in Fig. S10, ESI.† There is no discernible phosphorescence for 1a–4a under steady-state conditions in solutions at either room temperature or 77 K (Fig. S9, ESI†).
CR) excited states, with some charge transfer character, which probably arise from mixings of metal-to-ligand charge-transfer (MLCT) character. Solvent effects on the emissions of 1a–3a can be found in Fig. S10, ESI.† There is no discernible phosphorescence for 1a–4a under steady-state conditions in solutions at either room temperature or 77 K (Fig. S9, ESI†).
Comparing the three Au(I) complexes bearing the benzothiadiazole moiety, the emission energies (λmax = 467, 456 and 476 nm for 1a (PCy3), 5a (RNC) and 6a (NHC), respectively (Fig. S11 in ESI†)) and emission lifetimes (τPF ∼ 11–14 ns) are similar, indicating that the auxiliary ligand plays an insignificant role in modification of the electronic structures of the excited states.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1), structured emission profiles, and long emission lifetimes, the emissions of 1b–3b could be attributed to 3ππ*(C
400 cm−1), structured emission profiles, and long emission lifetimes, the emissions of 1b–3b could be attributed to 3ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited states with negligible mixings of MLCT and LLCT character (LLCT = ligand-to-ligand charge transfer). Solvent effects on the emissions of 1b can be found in Fig. S12, ESI.† On the contrary, 4b shows emission with a small Stokes shift of 920 cm−1 and emission lifetime of only 2.1 ns. Thus, the emission of 4b is derived from fluorescence with 1ππ*(C
CR) excited states with negligible mixings of MLCT and LLCT character (LLCT = ligand-to-ligand charge transfer). Solvent effects on the emissions of 1b can be found in Fig. S12, ESI.† On the contrary, 4b shows emission with a small Stokes shift of 920 cm−1 and emission lifetime of only 2.1 ns. Thus, the emission of 4b is derived from fluorescence with 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CBodipy) parentage.
CBodipy) parentage.
Time-resolved spectroscopies for the gold(I) complexes
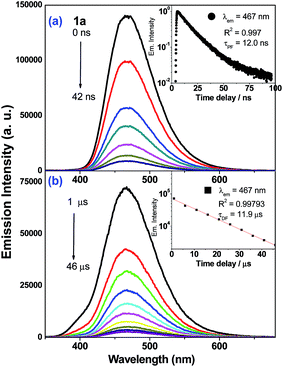
Nanosecond time-resolved emission (ns-TRE) spectra of the Au(I) complexes in degassed CH2Cl2 solutions at 298 K (5 × 10−5 M) are measured at different time delays and are presented in Fig. 4 (1a) and ESI (2a–3a, 5a–6a; Fig. S13†). There are two components in the emission decay: a major component which decays within nanoseconds (τ1 = 12.0 (1a), 2.7 (2a), 2.8 (3a), 11.0 (5a) and 14.0 ns (6a)) and a minor component with microsecond decay lifetime (τ2 = 11.9 (1a), 4.6 (2a), 2.6, 12.5 (3a), 6.8 (5a) and 7.4 μs (6a)). For each of these Au(I) complexes, both decay components have identical emission profile and peak energy and so, the short-lived one (τ1) is assigned to be prompt fluorescence (PF) while the long-lived one (τ2) is delayed fluorescence (DF) of 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) character. In the case of 4a, only PF (τPF = 0.8 ns) is observed. The proportion of DF and PF constituting the total emission of 1a–3a have been estimated (Table 3): the intensity of DF is minute (<3%) when compared with that of PF (>97%). It is noted that delayed fluorescence in the microsecond time regime is indicative of the emission generated from a long-lived excited state. This is further supported by nanosecond transient absorption (ns-TA) measurements that reveal the presence of long-lived absorbing species in the microsecond timescale (vide infra).
CR) character. In the case of 4a, only PF (τPF = 0.8 ns) is observed. The proportion of DF and PF constituting the total emission of 1a–3a have been estimated (Table 3): the intensity of DF is minute (<3%) when compared with that of PF (>97%). It is noted that delayed fluorescence in the microsecond time regime is indicative of the emission generated from a long-lived excited state. This is further supported by nanosecond transient absorption (ns-TA) measurements that reveal the presence of long-lived absorbing species in the microsecond timescale (vide infra).
| Complex | % PF | % DF |
|---|---|---|
| a % PF and % DF are estimated by integrating the emission intensity of degassed CH2Cl2 (5 × 10−5 M) in the spectral region of λ = 350–700 nm over the time range: 0–500 ns and 800 ns to 999 μs, respectively (λexc = 355 nm). | ||
| 1a | 99.2 | 0.81 |
| 2a | 99.9 | 0.1 |
| 3a | 97.1 | 2.9 |
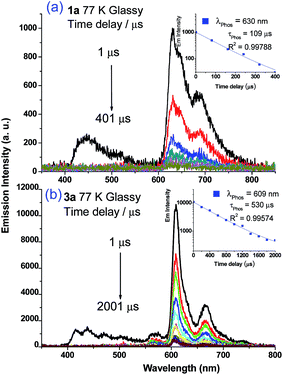
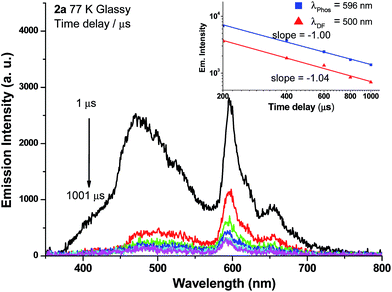
Weak phosphorescence bands were observed for 1a–3a under different conditions. For dilute CH2Cl2 solutions (1 × 10−5 M) at 298 K, dominant emissions were observed in the spectral region of 440–470 nm, which correspond to fluorescence (Fig. S14, left panel in ESI†). In addition, weak emission peaks at ca. 600 nm become discernible for 2a and 3a and the lifetimes measured are 13.6 and 61.9 μs, respectively (Fig. S13, right panel in ESI†). Cooling to 77 K gives more resolved phosphorescence bands with vibrational progression spacings of 1300–1400 cm−1 for all three complexes (Fig. 5 and 6). For 1a, contrary to the ns-TRE spectra recorded in degassed CH2Cl2 at room temperature (Fig. 4 (5 × 10−5 M); Fig. S14, ESI† (1 × 10−5 M)) where only DF could be observed over the time range 1–46 μs, in 77 K glassy solution, phosphorescence at 630 nm is dominant and the weak DF at 467 nm vanishes after 80 μs (Fig. 5a). The phosphorescence band decays with first-order kinetics at τphos = 109 μs. Similarly, the low-temperature ns-TRE spectra of 3a is dominated by phosphorescence at 609 nm and DF vanishes after 200 μs (Fig. 5b). The phosphorescence band also decays mono-exponentially with τphos = 530 μs. The photodynamics of 2a at 77 K, however, is different from that of 1a and 3a: both DF and phosphorescence of 2a are of comparable intensities initially (∼1 μs) in the 77 K ns-TRE spectra (Fig. 6); in addition, DF and phosphorescence do not follow first-order kinetics but decay according to the power law (I ∝ t−1) in the time interval 1 μs to 1.2 ms (inset of Fig. 6). The thermally induced Stokes shifts (ΔEs = E00 (77 K) − E00 (298 K)), being ∼0 (2a) and ∼107 cm−1 (3a), are small, thus supporting that the phosphorescence bands are originated from 3IL.15 Moreover, as the emission energies and profiles of the low-energy bands are similar to those of the steady-state emission spectra of the Au(III) analogues, the low-energy emission bands of 1a–3a are assigned to be from phosphorescence decay of the 3ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited state.
CR) excited state.
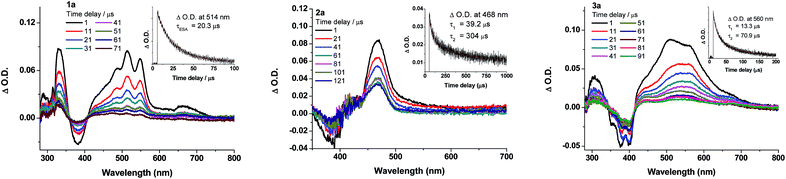
Nanosecond transient absorption (ns-TA) difference spectra of 1a–3a (Fig. 7) and 5a–6a (Fig. S15 in ESI†) have been recorded in deoxygenated CH2Cl2 at a gate delay of 1 μs after excitation at λ = 355 nm. The ns-TA spectra are characterized by an intense positive signal due to excited-state absorption (ESA) within the spectral range 400–700 nm. The decay time constants of the lowest-energy ESA (τESA) are 20.3 (1a), 39.2; 304 (2a), and 13.3; 70.9 μs (3a) (insets of Fig. 7). Changing the auxiliary ligand from PCy3 (1a) to RNC (5a) and NHC (6a) results in negligible changes in the ns-TA spectra and τESA (Fig. 7vs. S15†), suggesting that auxiliary ligand has little effect on the photophysics of the gold(I) arylacetylide complexes.
Time-resolved spectroscopies for the gold(III) complexes
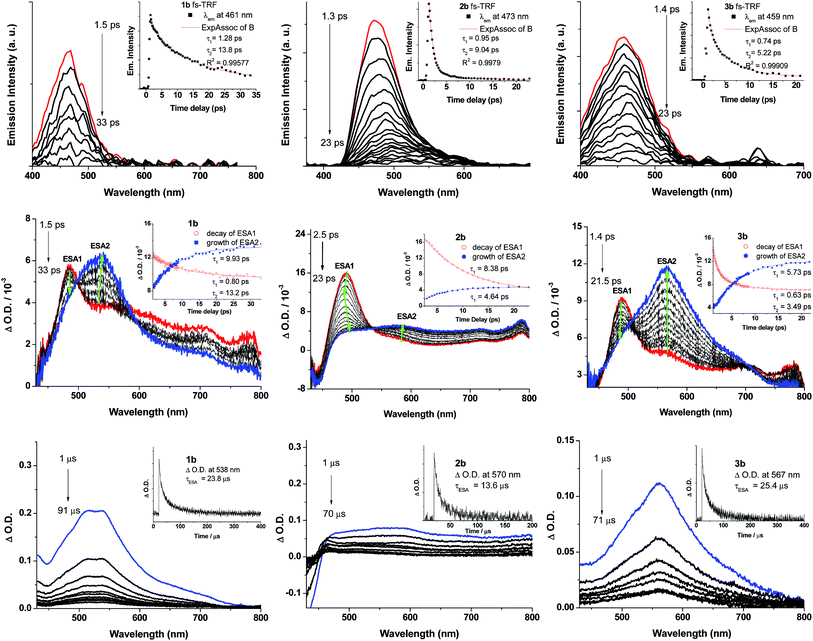
ns-TRE and ns-TA difference spectra of 1b–3b have been recorded in degassed CH2Cl2 solutions at 298 K at a gate delay of 1 μs. The ns-TRE spectra of 1b–3b (Fig. S16 in ESI†) have the same emission profiles and peak positions as the corresponding steady-state phosphorescence spectra and exhibit single exponential decay lifetimes of 20.8 (1b), 9.7 (2b) and 18.3 μs (3b). For the ns-TA difference spectra of 1b–3b (Fig. 8, bottom panel), a broad positive ESA band was observed in the spectral region 450–800 nm; this ESA signal follows first-order kinetics with lifetimes determined to be 23.8 (1b), 13.6 (2b) and 25.4 μs (3b), in reasonable agreement with the phosphorescence decay lifetimes determined from their respective ns-TRE spectra, thus indicating that the broad ESA is derived from T1 → Tn absorption.To probe the early excited state dynamics of the gold(III) complexes, in particular the events associated with ISC, femtosecond time-resolved fluorescence (fs-TRF) and transient absorption difference spectra (fs-TA) of 1b–3b have been recorded. Fig. 8 depicts the fs-TRF (top panel) and fs-TA spectra (middle panel) of complexes 1b–3b in CH2Cl2 solution at various time intervals after 400 nm excitation at 298 K. Promptly (<2 ps) after photo-excitation, an unstructured fluorescence band peaking at 461 (1b), 473 (2b) and 459 nm (3b) appears and decays completely within 100 ps. As the TRF emission peaks and profiles closely resemble those of their Au(I) analogues, 1a–3a, these TRF spectra are suggested to be originated from the 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited state. Fitting of the kinetic traces at their peaking wavelengths reveals that bi-exponential functions are required for 1b–3b with τ1 and τ2 being 1.28 and 13.8 ps for 1b, 0.95 and 9.04 ps for 2b, and 0.74 and 5.22 ps for 3b.
CR) excited state. Fitting of the kinetic traces at their peaking wavelengths reveals that bi-exponential functions are required for 1b–3b with τ1 and τ2 being 1.28 and 13.8 ps for 1b, 0.95 and 9.04 ps for 2b, and 0.74 and 5.22 ps for 3b.
In the fs-TA of 1b–3b (Fig. 8, middle panel), all three complexes displayed similar spectral transformations: the initially formed (∼1.4–2.5 ps) excited state absorption peaking at ∼490 nm (ESA1) decays with a concomitant growth of a broad band covering a spectral region 450–800 nm (ESA2) and is fully developed within 40 ps and persists up to 2.7 ns (the longest time recorded in the fs measurements). Clear isosbestic points could be observed at ∼500 nm (1b), 530 nm (2b) and ∼500 and 700 nm (3b) during the temporal evolution. Such kind of spectral conversion points to a precursor–successor relationship between ESA1 and ESA2. Kinetic analyses at representative wavelengths of these TA spectra reveals that ESA1 of 1b and 3b decay bi-exponentially with τ1 and τ2 being 0.80 and 13.2 ps for 1b and 0.63 and 3.49 ps for 3b, respectively, whereas ESA1 of 2b decays with a single exponential time constant of τ2 = 8.38 ps. ESA2, on the other hand, grows with first-order kinetics for all three complexes 1b–3b with time constants τESA2 = 9.93 (1b), 4.64 (2b) and 5.73 ps (3b). Given the similar decay time constants between the fs-TRF and ESA1 in fs-TA of 1b–3b, the spectral dynamics for both time-resolved spectra should be originated from the same S1 excited state, namely, the 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited state as revealed in the fs-TRF. On the other hand, comparing the ESA2 in fs-TA spectra at the longest time recorded with the corresponding ns-TA spectra for each Au(III) complex (Fig. 8, bottom panel), the two spectra are similar, indicating that ESA2 is derived from T1 → Tn absorption. Because there is a precursor–successor relationship between the ESA1 (S1 → Sn absorption) and ESA2 (T1 → Tn absorption), τ2 of ESA1 is assigned to ISC from the S1 excited state to a receiving triplet excited state, which then internally converted to the T1 excited state with an ultrafast time scale. Thus, τISC = 13.2 ps (1b), 8.38 ps (2b) and 3.49 ps (3b). The short τ1 = 0.80/1.28 (1b), 0.95 ps (2b) and 0.63/0.74 ps (3b) of ESA1/TRF may likely correspond to the S1 vibrational relaxation.
CR) excited state as revealed in the fs-TRF. On the other hand, comparing the ESA2 in fs-TA spectra at the longest time recorded with the corresponding ns-TA spectra for each Au(III) complex (Fig. 8, bottom panel), the two spectra are similar, indicating that ESA2 is derived from T1 → Tn absorption. Because there is a precursor–successor relationship between the ESA1 (S1 → Sn absorption) and ESA2 (T1 → Tn absorption), τ2 of ESA1 is assigned to ISC from the S1 excited state to a receiving triplet excited state, which then internally converted to the T1 excited state with an ultrafast time scale. Thus, τISC = 13.2 ps (1b), 8.38 ps (2b) and 3.49 ps (3b). The short τ1 = 0.80/1.28 (1b), 0.95 ps (2b) and 0.63/0.74 ps (3b) of ESA1/TRF may likely correspond to the S1 vibrational relaxation.
Intersystem crossing rate
The spectroscopically determined intersystem crossing rate constants (kISC) and the corresponding time constants (τISC) for both Au(I) and Au(III) complexes studied herein are tabulated in Table 4. For 1a–3a and 5a–6a, assuming that the major non-radiative decay of the S1 excited state is ISC, i.e. knr ≈ kISC, an upper bound approximation of the kISC values could be obtained by eqn (1):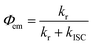 | (1) |
| Complex | k ISC /107 s−1 | τ ISC /ns | Complex | k ISC /1010 s−1 | τ ISC /ps |
|---|---|---|---|---|---|
| a k ISC for 1a–3a, 5a–6a are calculated according to eqn (1). b τ ISC = 1/kISC. c τ ISC of 1b–3b is estimated from τ2 obtained from the fs-TA spectra of ESA1. | |||||
| 1a | <0.75 | 133 | 1b | 7.57 | 13.2 |
| 2a | <11.1 | 9.0 | 2b | 11.9 | 8.38 |
| 3a | <7.9 | 12.7 | 3b | 28.7 | 3.49 |
| 5a | <0.91 | 110 | |||
| 6a | <1.14 | 87.5 | |||
The estimated kISC for the gold(I) complexes are 7.5 × 106 to 1.1 × 108 s−1 and the intersystem crossing time constants (τISC) are 9.0–133 ns. These τISC are much larger than those of many phosphorescent transition-metal complexes (τISC in the femtosecond to picosecond timescale). For 1b–3b, the τISC values are more than three orders of magnitude faster than their gold(I) analogues; these ISC rates, nevertheless, are comparable to other transition-metal complexes where S1 → T1 ISC is mediated by a higher-lying Tn triplet excited state.16,17
Computational study
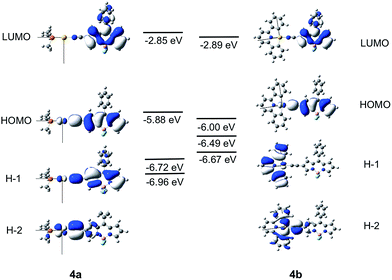
The different luminescence behaviors between the Au(I) and Au(III) systems were investigated by DFT/TDDFT calculations. The pair (1a, 1b) was chosen as a representative example to examine why the Au(I) complexes studied herein display only fluorescence while the Au(III) counterparts exhibit exclusively phosphorescence. As the Bodipy-functionalized complexes give fluorescence for both Au(I) and Au(III) complexes, DFT/TDDFT calculations were also performed on the pair, (4a, 4b). To save computational time, the cyclohexyl groups of the phosphine ligands in 1a and 4a were replaced by methyl groups.Calculations on 1a and 1b
The frontier MO diagrams of 1a and 1b are shown in Fig. 9. The HOMO and LUMO for both complexes 1a and 1b are predominantly localized on the arylacetylide ligand. For 1b, a considerable contribution (17%) from the C^N^C moiety to the LUMO is also noted. The energy gap between HOMO and H−1 in 1a is approximately 0.88 eV. For 1a, the H−1 is comprised of the antibonding combinations of Au(dxy) and π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) orbitals with little involvement of the phosphine ligand. For 1b, H−1 is composed of Au(dxz) and the π(C^N^C) orbitals; the energy gap between HOMO and H−1 in 1b is only 0.2 eV. The H−2 of 1b is made up of an antibonding combination of the Au(dxy), π(C
C) orbitals with little involvement of the phosphine ligand. For 1b, H−1 is composed of Au(dxz) and the π(C^N^C) orbitals; the energy gap between HOMO and H−1 in 1b is only 0.2 eV. The H−2 of 1b is made up of an antibonding combination of the Au(dxy), π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) and σ(C^N^C) orbitals, with a HOMO/H−2 orbital energy gap of only ∼0.4 eV. Clearly, the cyclometalated [C^N^C] ligand has a role in destabilizing the Au(d) orbitals. Therefore, the HOMO and H−1/H−2 energy gaps in 1b are much smaller than that in 1a.
C) and σ(C^N^C) orbitals, with a HOMO/H−2 orbital energy gap of only ∼0.4 eV. Clearly, the cyclometalated [C^N^C] ligand has a role in destabilizing the Au(d) orbitals. Therefore, the HOMO and H−1/H−2 energy gaps in 1b are much smaller than that in 1a.
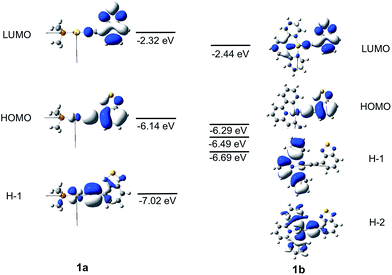 | ||
| Fig. 9 Frontier MOs of 1a and 1b at the optimized S0 geometries. Orbital energies are also given in eV. | ||
The energies of the singlet and triplet excited states and the associated nature and composition for 1a and 1b at their respective optimized singlet ground state geometries are obtained by TDDFT and are shown in Table S5 and S6 in ESI.† For 1a, there is only one triplet excited state (T1) which is more than 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 below S1. In addition, both S1 and T1 excited states are of the same parentage and are derived from HOMO → LUMO transition (∼90%) and thus, there would be no effective SOC between them. The triplet excited states above S1 were also considered; the closest lying Tm excited state with efficient SOC is when m = 4, which is derived from a H−1 to LUMO transition (90% H−1 → L). However, the energy separation ΔE(S1–T4) is −3180 cm−1, which is too large to be overcome by thermal activation.
000 cm−1 below S1. In addition, both S1 and T1 excited states are of the same parentage and are derived from HOMO → LUMO transition (∼90%) and thus, there would be no effective SOC between them. The triplet excited states above S1 were also considered; the closest lying Tm excited state with efficient SOC is when m = 4, which is derived from a H−1 to LUMO transition (90% H−1 → L). However, the energy separation ΔE(S1–T4) is −3180 cm−1, which is too large to be overcome by thermal activation.
On the other hand, for 1b, there are four triplet excited states which are lower-lying than S1, of which the closest-lying T4 excited state is only ∼70 cm−1 below the S1 excited state. Thus, thermal energy at room temperature assists facile ISC, even though SOC is small between the S1 and T4 excited states (|<S1|HSOC|T4>|2 ∼ 1.5 cm−2). In addition, among the triplet excited states above S1, there is a close-lying T5 excited state derived from the H−2 → LUMO transition (79%) which lies only 390 cm−1 above the S1 excited state and ISC from S1 to T5 could be thermally activated. Besides, owing to the different orientations of the d-orbitals in HOMO and H−2, the S1 and T5 excited states could have effective SOC (|<S1|HSOC|T5>|2 ∼ 4.1 × 103 cm−2).
Calculations on 4a and 4b
The Frontier MOs for 4a and 4b are shown in Fig. 10. Relative to 1a and 1b, the HOMO is destabilized and the LUMO is stabilized for 4a and 4b. Even for 4b, which contains a cyclometalated [C^N^C] ligand, the LUMO is predominantly localized on the Bodipy-functionalised arylacetylide ligand. The HOMO is composed of an antibonding combination of the Au(dyz) and π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CBodipy) orbitals. The energies and compositions of the singlet and triplet excited states of 4a and 4b at their respective optimized singlet ground state geometries were obtained by TDDFT and are collected in Tables S7 and S8 in ESI.† For this pair, (4a, 4b), the two triplet excited states, T1 and T2, are more than 2000 cm−1 below the S1 excited state and are all composed of Au(dyz) orbitals. As SOC between the coupling singlet and triplet excited states would be ineffective with d-orbitals of the same orientation, ISC from S1 to T2 (or T1) for 4a and 4b would be sluggish.
CBodipy) orbitals. The energies and compositions of the singlet and triplet excited states of 4a and 4b at their respective optimized singlet ground state geometries were obtained by TDDFT and are collected in Tables S7 and S8 in ESI.† For this pair, (4a, 4b), the two triplet excited states, T1 and T2, are more than 2000 cm−1 below the S1 excited state and are all composed of Au(dyz) orbitals. As SOC between the coupling singlet and triplet excited states would be ineffective with d-orbitals of the same orientation, ISC from S1 to T2 (or T1) for 4a and 4b would be sluggish.
 | ||
| Fig. 10 Frontier MOs of 4a and 4b at their optimized S0 geometries. Orbital energies are also given in eV. | ||
For 4a, the T3 excited state is the closest-lying triplet excited state that could have effective SOC with the S1 excited state due to a minor contribution of the H−5 → LUMO transition to the T3 excited state (H−5 is composed of the Au(dz2) orbital); however, ΔE(S1–T3) is −2955 cm−1 (negative sign indicates that T3 lies above S1) which is much larger than the thermal energy. For 4b, the T3 excited state is also the closest-lying triplet excited state that could have effective SOC with the S1 excited state due to a minor contribution of H−1 → LUMO transition in the T3 excited state (the d-orbitals of the Au(III) ion at the HOMO and H−1 of 4b are of different orientations, Fig. 10). However, the singlet–triplet gap, ΔE(S1–T3) = −1192 cm−1, is also much larger than the thermal energy. Thus, the pair (4a, 4b) is expected to have slow ISC rates, when taking into consideration both the singlet–triplet energy gaps and SOC.
Discussion
General remarks on the photophysical properties
The emissions of the Au(I) complexes, 1a–6a are attributable to 1IL ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) excited states. Pronounced red shifts in emission λmax of arylacetylides can be observed upon their coordination to Au(I) ion (e.g. λmax = 412 nm (L1) vs. 467 nm (1a)). Considering the complexes 1a, 5a and 6a, which have different neutral auxiliary ligands (phosphine (PCy3, 1a), isocyanide (RNC, 5a) and N-heterocyclic carbene (NHC, 6a)) but the same acetylide ligand with a benzothiadiazole moiety, the lowest energy emission λem red shifts with the auxiliary ligand from 456 nm (RNC) to 467 nm (PCy3) to 476 nm (NHC). A rationalization would be that the NHC, being the strongest σ-donor ligand among the auxiliary ligands in the three complexes, destabilizes the Au(d) orbital to the greatest extent. From DFT calculations, the HOMO is comprised of a Au(d) orbital and π(C
CR) excited states. Pronounced red shifts in emission λmax of arylacetylides can be observed upon their coordination to Au(I) ion (e.g. λmax = 412 nm (L1) vs. 467 nm (1a)). Considering the complexes 1a, 5a and 6a, which have different neutral auxiliary ligands (phosphine (PCy3, 1a), isocyanide (RNC, 5a) and N-heterocyclic carbene (NHC, 6a)) but the same acetylide ligand with a benzothiadiazole moiety, the lowest energy emission λem red shifts with the auxiliary ligand from 456 nm (RNC) to 467 nm (PCy3) to 476 nm (NHC). A rationalization would be that the NHC, being the strongest σ-donor ligand among the auxiliary ligands in the three complexes, destabilizes the Au(d) orbital to the greatest extent. From DFT calculations, the HOMO is comprised of a Au(d) orbital and π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) (Fig. 9). Thus, the more electron-donating the auxiliary ligand, the more destabilized the HOMO, and hence, the smaller the HOMO–LUMO gap and the 1ππ*(C
CR) (Fig. 9). Thus, the more electron-donating the auxiliary ligand, the more destabilized the HOMO, and hence, the smaller the HOMO–LUMO gap and the 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) energy. A similar trend in the lowest energy absorption λabs can also be observed on changing the auxiliary ligand from RNC (371 nm) to PCy3 (379 nm) and NHC (383 nm).
CR) energy. A similar trend in the lowest energy absorption λabs can also be observed on changing the auxiliary ligand from RNC (371 nm) to PCy3 (379 nm) and NHC (383 nm).
Most of the reported luminescent cyclometalated Au(III) complexes display phosphorescence that comes from the 3ππ* IL excited state localized on the cyclometalated ligands.13 For the Au(III) complexes studied herein, 1b–3b, the lowest-energy triplet excited states are of 3ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) in nature, with λmax = 630, 592 and 603 nm respectively. These complexes, however, exhibit rather weak phosphorescence, with Φem values in the range of 0.003–0.04. It is noted that in 77 K glassy solutions, the phosphorescence lifetimes are significantly increased compared with those obtained in degassed CH2Cl2 at RT (e.g. 205 μs at RT to 2.2 ms at 77 K for 3b). Since low temperature and rigid glassy matrix can impede structural distortion, the lifetimes obtained at 77 K could reflect the intrinsic radiative lifetime of the complexes. The especially long emission lifetimes can reflect the predominant localization of the emitting T1 excited state on the arylacetylide ligand, i.e.3ππ*(C
CR) in nature, with λmax = 630, 592 and 603 nm respectively. These complexes, however, exhibit rather weak phosphorescence, with Φem values in the range of 0.003–0.04. It is noted that in 77 K glassy solutions, the phosphorescence lifetimes are significantly increased compared with those obtained in degassed CH2Cl2 at RT (e.g. 205 μs at RT to 2.2 ms at 77 K for 3b). Since low temperature and rigid glassy matrix can impede structural distortion, the lifetimes obtained at 77 K could reflect the intrinsic radiative lifetime of the complexes. The especially long emission lifetimes can reflect the predominant localization of the emitting T1 excited state on the arylacetylide ligand, i.e.3ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) with little participation of the metal ion. This is also corroborated by the small thermally induced Stokes shifts (ΔEs = E00 (77 K) − E00 (298 K)) of less than 600 cm−1 (Table 2).
CR) with little participation of the metal ion. This is also corroborated by the small thermally induced Stokes shifts (ΔEs = E00 (77 K) − E00 (298 K)) of less than 600 cm−1 (Table 2).
Intersystem crossing in gold(I) and gold(III) complexes
ISC is usually fast in transition-metal complexes with time constants (τISC) in the fs to ps time regimes. In the literature, there are numerous examples which show ultrafast ISC,1,18–25e.g. [M(bpy)3]2+ (M = Ru or Fe, τISC = 30 fs),19a,b [Re(L)(CO)3(bpy)] (τISC = 100–140 fs),20 [Ir(piq)3] (piq: 1-phenylisoquinoline; τISC = 70 fs),21b [Pt(PBu3)2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CPh)2] (τISC = 70 fs),22 and [Cy3PAu(2-naphthyl)] (τISC = 230 fs)23etc. These τISC correspond to rates of intersystem crossing (kISC) in the range of 1012 to 1013 s−1. The fast kISC in transition-metal complexes is traditionally attributed to a large spin–orbit coupling (SOC) constant inherited from the heavy metal atom. However, there are increasing number of reports revealing slow ISC rate (kISC ∼ 108 s−1) in spite of the presence of heavy transition metal, such as the cases of Rh(I)- and Ir(III)-bis(arylethynyl)cyclopentadiene,3 Au(I)-pyrene,4b Pt(II)-perylene/4c tetracene,4e and Pd(II)-perylene diimide;4f all these complexes contain highly conjugated ligand systems and display ligand-dominated 1ππ* fluorescence. There are also cases where comparable kISC and kr of S1 → S0 leads to the observation of dual fluorescence–phosphorescence under steady-state condition, e.g., [Pt(L)(acac)] and [Ir(L)(acac)] (L = 2-(oligothienyl)pyridine);26 [Os(L)(CO)3X] (L = 8-quinolinolate27 or isoquinoline-triazole),28 and [Bu4N]4[Pt2(μ-P2O5(BF2)2)4],29etc.
CPh)2] (τISC = 70 fs),22 and [Cy3PAu(2-naphthyl)] (τISC = 230 fs)23etc. These τISC correspond to rates of intersystem crossing (kISC) in the range of 1012 to 1013 s−1. The fast kISC in transition-metal complexes is traditionally attributed to a large spin–orbit coupling (SOC) constant inherited from the heavy metal atom. However, there are increasing number of reports revealing slow ISC rate (kISC ∼ 108 s−1) in spite of the presence of heavy transition metal, such as the cases of Rh(I)- and Ir(III)-bis(arylethynyl)cyclopentadiene,3 Au(I)-pyrene,4b Pt(II)-perylene/4c tetracene,4e and Pd(II)-perylene diimide;4f all these complexes contain highly conjugated ligand systems and display ligand-dominated 1ππ* fluorescence. There are also cases where comparable kISC and kr of S1 → S0 leads to the observation of dual fluorescence–phosphorescence under steady-state condition, e.g., [Pt(L)(acac)] and [Ir(L)(acac)] (L = 2-(oligothienyl)pyridine);26 [Os(L)(CO)3X] (L = 8-quinolinolate27 or isoquinoline-triazole),28 and [Bu4N]4[Pt2(μ-P2O5(BF2)2)4],29etc.
In this work, the luminescence behaviour of the Au(I) and Au(III) complexes are drastically different, even though they have the same metal and arylacetylide ligands. Ligand-dominated fluorescence has been observed with the Au(I) complexes, 1a–3a and 5a–6a, with kISC estimated to range from 7.5 × 106 to 1.1 × 108 s−1. The Au(III) complexes 1b–3b, on the other hand, display phosphorescence, with kISC estimated to be larger than 1010 s−1. The major difference between the two series of gold complexes is the oxidation state of Au ion, that dictates the coordination geometry, i.e. a linear geometry for the Au(I) complexes, 1a–6a, and a square-planar geometry for Au(III) complexes, 1b–4b. The coordination geometry has a significant impact on the relative energies of the frontier orbitals (specifically, the d-orbital energies) and hence the relative energies of the singlet and triplet excited states, which subsequently affect the kISC.
The two factors that determine the kISC are (1) the SOC matrix element <Sn|HSOC|Tm>, and (2) the energy gap (ΔEST) between the coupling singlet (Sn) and triplet (Tm) excited states. The larger the HSOC and the smaller the energy gap (ΔEST), the faster will be kISC. For effective SOC, this requires the metal d-orbitals of the coupling singlet and triplet excited states to have different orientations. For example, if Sn is derived from a metal-to-ligand charge transfer (MLCT) excited state where Au(dxz) orbital is involved, HSOC would be zero if the triplet excited state is also an MLCT state that involves Au(dxz) orbital because of symmetry reasons.
The pair (1a, 1b) has been chosen as a representative example to illustrate the different photophysical properties exhibited by the Au(I) and Au(III) arylacetylide complexes studied in this work. From the DFT/TDDFT calculations, it is revealed that owing to the inherent linear coordination geometry of the Au(I) complex, the d-orbitals of the gold(I) ion is mainly destabilized by the arylacetylide ligand (Fig. 9 and Table S9 in ESI†). On the other hand, as Au(III) complexes are assumed to have a square-planar four-coordinated geometry, thus, in addition to the antibonding interactions with the arylacetylide ligand, the d-orbitals of gold(III) ion could also be destabilized by the cyclometalated [C^N^C] ligand (both π-type, e.g. H−1, and σ-type, e.g. H−2 in 1b; Fig. 9 and Table S9 in ESI†); these latter interactions result in smaller d-orbital splittings in the Au(III) series than the Au(I) series. In effect, S1 and S2 excited states are ∼4200 cm−1 apart for 1a while the analogous splitting (between S1 and S3 excited states) is only ∼1300 cm−1 for 1b. As S2 of 1a is derived from 1[Au(dxy) → π*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)]/1[π(C
CR)]/1[π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) → π*(C
C) → π*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] (1MLCT/1ILCT) and S3 of 1b from 1[Au(dxy) → π*(C
CR)] (1MLCT/1ILCT) and S3 of 1b from 1[Au(dxy) → π*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)]/1[π(C
CR)]/1[π(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) → π*(C
C) → π*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)]/1[π(C^N^C) → π*(C
CR)]/1[π(C^N^C) → π*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] (1MLCT/1ILCT/1LLCT), i.e., both are of charge-transfer type excited states, the singlet–triplet energy gaps for this type of transitions are small (ΔE(S2–T4) ∼ 1000 cm−1 for 1a and ΔE(S3–T5) ∼ 900 cm−1 for 1b) (T4 (1a) and T5 (1b) are the triplet counterpart of S2 (1a) and S3 (1b) respectively). As depicted in Fig. 11, the S1/T5 energy gap for 1b is small but the S1/T4 energy gap for 1a is large. In other words, the oxidation state of the gold ion affects the coordination geometry of the complex, which in turn change the interactions between the metal d-orbitals and ligand orbitals, giving rise to different d-orbital splitting and subsequently the singlet–triplet splitting (ΔEST) of the two coupling excited states in the gold complexes.
CR)] (1MLCT/1ILCT/1LLCT), i.e., both are of charge-transfer type excited states, the singlet–triplet energy gaps for this type of transitions are small (ΔE(S2–T4) ∼ 1000 cm−1 for 1a and ΔE(S3–T5) ∼ 900 cm−1 for 1b) (T4 (1a) and T5 (1b) are the triplet counterpart of S2 (1a) and S3 (1b) respectively). As depicted in Fig. 11, the S1/T5 energy gap for 1b is small but the S1/T4 energy gap for 1a is large. In other words, the oxidation state of the gold ion affects the coordination geometry of the complex, which in turn change the interactions between the metal d-orbitals and ligand orbitals, giving rise to different d-orbital splitting and subsequently the singlet–triplet splitting (ΔEST) of the two coupling excited states in the gold complexes.
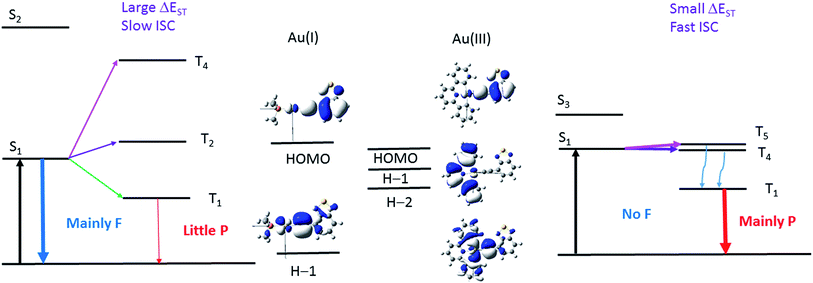 | ||
| Fig. 11 Illustration of the low-lying singlet and triplet excited states of Au(I) (left) and Au(III) (right) complexes that accounts for the different photophysical behaviour of the Au(I) and Au(III) complexes investigated in this work. S1 and T1 for both complexes are derived from HOMO → LUMO transitions; S2 and T4 excited states of 1a are derived from 1,3[H−1 → LUMO] transitions while S3 and T5 excited states of 1b are derived from 1,3[H−2 → LUMO] transitions. The d-orbitals involved in the T2 of 1a and T4 of 1b have the same orientations as their respective S1 excited state (see Tables S5, S6 and S9 in ESI†). The wavy blue arrows indicate internal conversion (IC) from the T5 to T1 excited state. F = fluorescence and P = phosphorescence. | ||
Moreover, DFT/TDDFT calculations also revealed that there is a triplet excited state (T4) almost isoenergetic with the S1 excited state (<70 cm−1 below the S1 excited state) in 1b such that even though the SOC between S1 and T4 is small due to the similar d-orbital orientations involved in both excited states, thermal energy could promote facile ISC. With 1a, the closest triplet excited state (T2) to the S1 excited state is more than 500 cm−1 above the S1 excited state, which is more than twice the thermal energy at room temperature and SOC is also small between these two excited states as the d-orbitals involved are also of the same orientations. Thus, taken together both the SOC and ΔEST, 1b should have a much faster kISC than 1a.
On the other hand, for the Bodipy-functionalized complexes, 4a and 4b, only 1ππ*(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CBodipy) fluorescence with no long-lived species are observed under ns-TRE and ns-TA measurements. The photophysical behavior of the Bodipy-functionalized complexes can be attributed to the intrinsically small band-gap of the Bodipy moiety. Due to the highly conjugated structure of Bodipy, the HOMO is much destabilized and there is a wide orbital energy gap between the HOMO and other occupied MOs, even in the case of 4b which contains a [C^N^C] ligand. As a result, the HOMO/H−x orbital energy gap is the largest among the four arylacetylide ligands studied herein (H−x is the other occupied orbitals lower in energy than the HOMO; x = 1, 2, …). In effect, the closest Tm excited state that could have effective SOC with S1 is more than 1000 cm−1 above the S1 excited state. With such a large ΔE(S1–Tm), thermal energy would be insufficient to promote ISC. Therefore, similar to the scenario in the case of 1a (Fig. 11, left), ISC is sluggish for Au(I) and Au(III) arylacetylide complexes bearing Bodipy.
CBodipy) fluorescence with no long-lived species are observed under ns-TRE and ns-TA measurements. The photophysical behavior of the Bodipy-functionalized complexes can be attributed to the intrinsically small band-gap of the Bodipy moiety. Due to the highly conjugated structure of Bodipy, the HOMO is much destabilized and there is a wide orbital energy gap between the HOMO and other occupied MOs, even in the case of 4b which contains a [C^N^C] ligand. As a result, the HOMO/H−x orbital energy gap is the largest among the four arylacetylide ligands studied herein (H−x is the other occupied orbitals lower in energy than the HOMO; x = 1, 2, …). In effect, the closest Tm excited state that could have effective SOC with S1 is more than 1000 cm−1 above the S1 excited state. With such a large ΔE(S1–Tm), thermal energy would be insufficient to promote ISC. Therefore, similar to the scenario in the case of 1a (Fig. 11, left), ISC is sluggish for Au(I) and Au(III) arylacetylide complexes bearing Bodipy.
Mechanism for the generation of delayed fluorescence
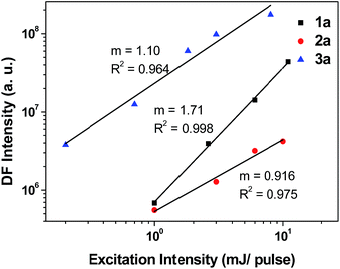
From the ns-TRE measurements of 1a–3a, DF contributes to the total fluorescence, though only a minute proportion (<3%, Table 3). In general, the mechanism of DF could be inferred from the dependence of the DF intensity (IDF) with the power of excitation light.30 According to Bässler, a quadratic dependence of excitation power with the DF intensity indicates that the mechanism of the DF is TTA with dominant phosphorescence.30b On the other hand, a linear dependence of DF intensity with excitation power could be due to three possible mechanisms: TTA with dominant delayed-fluorescence, TADF, and GP-recombination. As depicted in Fig. 12, the plot of IDF against excitation intensity in double-logarithm scale gave a slope of 1.71 ≈ 2 for 1a; this nearly quadratic dependence is most consistent with the TTA mechanism with dominant phosphorescence. However, for 2a and 3a (slope = 0.916 and 1.10), both display nearly linear dependence between IDF and excitation intensity. Therefore, it is not possible to confirm the mechanism for DF in the case of 2a and 3a by solely considering the excitation power dependence.Time-dependence of IDF and phosphorescence intensity (IP) could also give hints to the DF mechanism.30,31 For TTA with dominant DF, phosphorescence intensity decays with a power law, IP ∝ t−1 while IDF is approximately constant at short time and IDF ∝ t−2 at longer time. For the GP-recombination mechanism, both DF and phosphorescence decay in accordance with the power law, IDF ∝ t−1, at both short and long times.30a In the case of 2a in 77 K glassy solution, both DF and phosphorescence decayed according to the power law: I ∝ t−1 over the time intervals investigated (1 μs to 1.2 ms) (Fig. 6, inset), suggesting that the DF mechanism under this condition is most likely the GP-recombination mechanism. As for 3a, there is no power law decay relation with both DF and phosphorescence and so it seems unlikely that GP-recombination is the mechanism for the generation of DF in 3a. There is still not enough information to conclude on the DF mechanism for 3a.
Conclusion
A series of gold complexes with different oxidation states, gold(I) complexes [LAu(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] and gold(III) complexes [Au(C^N^C)(C
CR)] and gold(III) complexes [Au(C^N^C)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)] bearing the same heterocyclic arylacetylides with narrow bandgap were synthesized and characterized. The photophysical behaviors with the gold ion in different oxidation states are strikingly different: fluorescence dominates the luminescence of the Au(I) complexes while phosphorescence takes over in the Au(III) complexes. Detailed computational studies by DFT/TDDFT have accounted for these phenomena as a result of different coordination environments inherited from the gold ion in a particular oxidation state: a linear coordination geometry for Au(I) and a square-planar coordination geometry for Au(III). This difference in coordination geometry subtly affects the energy separation between the coupling singlet and triplet excited states, leading to smaller ΔEST of the Au(III) complexes than the Au(I) complexes and hence, larger kISC in the Au(III) complexes than the Au(I) complexes. For the complexes bearing Bodipy-functionalized acetylide ligand, they only display prompt fluorescence. Computational analyses revealed that, due to the especially narrow bandgap of Bodipy, the ΔEST is still large even in the Au(III) complex so that kISC could not compete with fluorescence radiative decay. Additionally, the mechanisms for the generation of DF in Au(I) complexes have been explored. To the best of our knowledge, this is the first report which systematically studies the effects of the metal ion oxidation state on the photophysical behaviours of transition-metal complexes.
CR)] bearing the same heterocyclic arylacetylides with narrow bandgap were synthesized and characterized. The photophysical behaviors with the gold ion in different oxidation states are strikingly different: fluorescence dominates the luminescence of the Au(I) complexes while phosphorescence takes over in the Au(III) complexes. Detailed computational studies by DFT/TDDFT have accounted for these phenomena as a result of different coordination environments inherited from the gold ion in a particular oxidation state: a linear coordination geometry for Au(I) and a square-planar coordination geometry for Au(III). This difference in coordination geometry subtly affects the energy separation between the coupling singlet and triplet excited states, leading to smaller ΔEST of the Au(III) complexes than the Au(I) complexes and hence, larger kISC in the Au(III) complexes than the Au(I) complexes. For the complexes bearing Bodipy-functionalized acetylide ligand, they only display prompt fluorescence. Computational analyses revealed that, due to the especially narrow bandgap of Bodipy, the ΔEST is still large even in the Au(III) complex so that kISC could not compete with fluorescence radiative decay. Additionally, the mechanisms for the generation of DF in Au(I) complexes have been explored. To the best of our knowledge, this is the first report which systematically studies the effects of the metal ion oxidation state on the photophysical behaviours of transition-metal complexes.
Acknowledgements
This work was funded by the National Key Basic Research Program of China (No. 2013CB834802), the Area of Excellence Program (AoE/P-03/08) and the Hong Kong Research Grants Council (HKU 700812P, 17300614). This work is also conducted in part using the research computing facilities and/or advisory services offered by Information Technology Services, the University of Hong Kong. D. L. Phillips acknowledges the University Development Fund grant 2014–15 for the “New Ultrafast Spectroscopy Experiments for Shared Facilities” from the University of Hong Kong.Notes and references
- M. Chergui, Acc. Chem. Res., 2015, 48, 801 CrossRef CAS PubMed.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press, USA, 2006, 3rd edn Search PubMed.
- (a) A. Steffan, M. G. Tay, A. S. Batsanov, J. A. K. Howard, A. Beedy, K. Q. Vuong, X.-Z. Sun, M. W. George and T. B. Marder, Angew. Chem., Int. Ed., 2010, 49, 2349 CrossRef PubMed; (b) A. Steffan, R. M. Ward, M. G. Tay, R. M. Edkins, F. Seeler, M. van Leeuwen, L.-O. Palsson, A. Beeby, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Chem.–Eur. J., 2014, 20, 3652 CrossRef PubMed; (c) A. Steffan, K. Costuas, A. Boucekkine, M.-H. Thibault, A. Beeby, A. S. Batsanov, A. Charaft-Eddin, D. Jacquemin, J.-F. Halet and T. B. Marder, Inorg. Chem., 2014, 53, 7055 CrossRef PubMed.
- (a) H. Weissman, E. Shirman, T. Ben-Moshe, R. Cohen, G. Leitus, L. J. W. Shimon and B. Rybtchinski, Inorg. Chem., 2007, 46, 4790 CrossRef CAS PubMed; (b) W. Y. Heng, J. Hu and J. H. K. Yip, Organometallics, 2007, 26, 6760 CrossRef CAS; (c) S. Lentijo, J. A. Miguel and P. Espinet, Inorg. Chem., 2010, 49, 9169 CrossRef CAS PubMed; (d) V. Prusakova, C. E. McCusker and F. Castellano, Inorg. Chem., 2012, 51, 8589 CrossRef CAS PubMed; (e) M.-H. Nguyen, C.-Y. Wong and J. H. K. Yip, Organometallics, 2013, 32, 1620 CrossRef CAS; (f) S. Lentijo, G. Aullon, J. A. Miguel and P. Espinet, Dalton Trans., 2013, 42, 6353 RSC.
- (a) W. Lu, N. Zhu and C.-M. Che, J. Organomet. Chem., 2003, 670, 11 CrossRef CAS; (b) G. S. M. Tong, P. K. Chow and C.-M. Che, Angew. Chem., Int. Ed., 2010, 49, 9206 CrossRef CAS PubMed.
- (a) H.-Y. Chao, W. Lu, Y. Li, M. C. W. Chan, C.-M. Che, K.-K. Cheung and N. Zhu, J. Am. Chem. Soc., 2002, 124, 14696 CrossRef CAS PubMed; (b) W. Lu, W.-M. Kwok, C. Ma, C. T.-L. Chan, M.-X. Zhu and C.-M. Che, J. Am. Chem. Soc., 2011, 133, 14120 CrossRef CAS PubMed; (c) C. Ma, C. T.-L. Chan, W.-M. Kwok and C.-M. Che, Chem. Sci., 2012, 3, 1883 RSC.
- A. Möller, P. Bleckenwegner, U. Monkowius and F. Mohr, J. Organomet. Chem., 2016, 813, 1 CrossRef.
- (a) J. Arcau, V. Andermark, E. Aguiló, A. Gandioso, A. Moro, M. Cetina, J. C. Lima, K. Rissanen, I. Ott and L. Rodríguez, Dalton Trans., 2014, 43, 4426 RSC; (b) A. J. Moro, B. Rome, E. Aguiló, J. Arcau, R. Puttreddy, K. Rissanen, J. C. Lima and L. Rodríguez, Org. Biomol. Chem., 2015, 13, 2026 RSC.
- E. E. Langdon-Jones, D. Lloyd, A. J. Hayes, S. D. Wainwright, H. J. Mottram, S. J. Coles, P. N. Horton and S. J. A. Pope, Inorg. Chem., 2015, 54, 6606 CrossRef CAS PubMed.
- A. Meyer, C. P. Bagowski, M. Kokoschka, M. Stefanopoulou, H. Alborzinia, S. Can, D. H. Vlecken, W. S. Sheldrick, S. Wölfl and I. Ott, Angew. Chem., Int. Ed., 2012, 51, 8895 CrossRef CAS PubMed.
- E. E. Langdon-Jones and S. J. A. Pope, Chem. Commun., 2014, 50, 10343 RSC.
- (a) C.-M. Che, H.-Y. Chao, V. M. Miskowski, Y. Li and K.-K. Cheung, J. Am. Chem. Soc., 2001, 123, 4985 CrossRef CAS PubMed; (b) W. Lu, H.-F. Xiang, N. Zhu and C.-M. Che, Organometallics, 2002, 21, 2343 CrossRef CAS; (c) W. Lu, N. Zhu and C.-M. Che, J. Am. Chem. Soc., 2003, 125, 16081 CrossRef CAS PubMed.
- (a) V. W.-W. Yam, K. M.-C. Wong, L.-L. Hung and N. Zhu, Angew. Chem., Int. Ed., 2005, 44, 3107 CrossRef CAS PubMed; (b) V. K.-M. Au, K. M.-C. Wong, D. P.-K. Tsang, M.-Y. Chan, N. Zhu and V. W.-W. Yam, J. Am. Chem. Soc., 2010, 132, 14273 CrossRef CAS PubMed; (c) D.-A. Roşca, D. A. Smith and M. Bochmann, Chem. Commun., 2012, 48, 7247 RSC; (d) W.-P. To, G. S.-M. Tong, W. Lu, C. Ma, J. Liu, A. L.-F. Chow and C.-M. Che, Angew. Chem., Int. Ed., 2012, 51, 2654 CrossRef CAS PubMed; (e) W.-P. To, K. T. Chan, G. S. M. Tong, C. Ma, W.-M. Kwok, X. Guan, K.-H. Low and C.-M. Che, Angew. Chem., Int. Ed., 2013, 52, 6648 CrossRef CAS PubMed.
- (a) A. L.-F. Chow, M.-H. So, W. Lu, N. Zhu and C.-M. Che, Chem.–Asian J., 2011, 6, 544 CrossRef CAS PubMed; (b) J. Gil-Rubio, V. Cámara, D. Bautista and J. Vicente, Organometallics, 2012, 31, 5414 CrossRef CAS.
- I. E. Pomestchenko and F. N. Castellano, J. Phys. Chem. A, 2004, 108, 3485 CrossRef CAS.
- R. A. Vogt, M. A. Peay, T. G. Gray and C. E. Crespo-Hernández, J. Phys. Chem. Lett., 2010, 1, 1205 CrossRef CAS.
- F. Frei, A. Rondi, D. Espa, M. L. Mercuri, L. Pilia, A. Serpe, A. Odeh, F. V. Mourik, M. Chergui, T. Feurer, P. Deplano, A. Vlček Jr and A. Cannizzo, Dalton Trans., 2014, 43, 17666 RSC.
- K.-C. Tang, K. L. Liu and I.-C. Chen, Chem. Phys. Lett., 2004, 386, 437 CrossRef CAS.
- (a) A. Cannizzo, F. van Mourik, W. Gawelda, G. Zgrablic, C. Bressler and M. Chergui, Angew. Chem., Int. Ed., 2006, 45, 3174 CrossRef CAS PubMed; (b) W. Gawelda, A. Cannizzo, V.-T. Pham, F. van Mourik, C. Bressler and M. Chergui, J. Am. Chem. Soc., 2007, 129, 8199 CrossRef CAS PubMed.
- A. Cannizzo, A. M. Blanco-Rodríguez, A. El Nahhas, J. Šebera, S. Záliš, A. Viček Jr and M. Chergui, J. Am. Chem. Soc., 2008, 130, 8967 CrossRef CAS PubMed.
- (a) G. J. Hedley, A. Ruseckas and I. D. W. Samuel, Chem. Phys. Lett., 2008, 450, 292 CrossRef CAS; (b) G. J. Hedley, A. Ruseckas and I. D. W. Samuel, J. Phys. Chem. A, 2009, 113, 2 CrossRef CAS PubMed.
- G. Ramakrishna, T. Goodson III, J. E. Rogers-Haley, T. M. Cooper, D. G. McLean and A. Urbas, J. Phys. Chem. C, 2009, 113, 1060 CAS.
- R. A. Vogt, T. G. Gray and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2012, 134, 14808 CrossRef CAS PubMed.
- O. Bräm, F. Messina, E. Baranoff, A. Cannizzo, M. K. Nazeeruddin and M. Chergui, J. Phys. Chem. C, 2013, 117, 15958 Search PubMed.
- (a) K. Li, G. Cheng, C. Ma, X. Guan, W.-M. Kwok, Y. Chen, W. Lu and C.-M. Che, Chem. Sci., 2013, 4, 2630 RSC; (b) G. Cheng, S. C. F. Kui, W.-H. Ang, M.-Y. Ko, P.-K. Chow, C.-L. Kwong, C.-C. Kwok, C. Ma, X. Guan, K.-H. Low, S.-J. Su and C.-M. Che, Chem. Sci., 2014, 5, 4819 RSC.
- D. N. Kozhevnikov, V. N. Kozhevnikov, M. Z. Shafikov, A. M. Prokhorov, D. W. Bruce and J. A. G. Williams, Inorg. Chem., 2011, 50, 3804 CrossRef CAS PubMed.
- Y.-M. Cheng, Y.-S. Yeh, M.-L. Ho and P.-T. Chou, Inorg. Chem., 2005, 44, 4594 CrossRef CAS PubMed.
- C.-C. Hsu, C.-C. Lin, P.-T. Chou, C.-H. Lai, C.-W. Hsu, C.-H. Lin and Y. Chi, J. Am. Chem. Soc., 2012, 134, 7715 CrossRef CAS PubMed.
- T. Hofbeck, Y. C. Lam, M. Kalbáč, S. Záliš, A. Vlček Jr and H. Yersin, Inorg. Chem., 2016, 55, 2441 CrossRef CAS PubMed.
- (a) K. Hensel and H. Bässler, Adv. Mater. Opt. Electron., 1992, 1, 179 CrossRef CAS; (b) A. Hayer, H. Bässler, B. Falk and S. Schrader, J. Phys. Chem. A, 2002, 106, 11045 CrossRef CAS; (c) A. Köhler and H. Bässler, Mater. Sci. Eng., R, 2009, 66, 71 CrossRef.
- M. Aydemir, V. Jankus, F. B. Dias and A. Monkman, Phys. Chem. Chem. Phys., 2014, 16, 21543 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details of synthesis, characterization, photophysical data and additional computational details. CCDC 1499919–1499921. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc03775e |
| This journal is © The Royal Society of Chemistry 2017 |