Open Access Article
Open Access ArticleContinuous variables logic via coupled automata using a DNAzyme cascade with feedback†
S.
Lilienthal
a,
M.
Klein
a,
R.
Orbach
a,
I.
Willner
a,
F.
Remacle
ab and
R. D.
Levine
*ac
aInstitute of Chemistry, The Hebrew University of Jerusalem, Jerusalem 91904, Israel. E-mail: rafi@fh.huji.ac.il
bDepartment of Chemistry, University of Liege, B6c, 4000 Liege, Belgium
cDepartment of Molecular and Medical Pharmacology, David Geffen School of Medicine, Department of Chemistry and Biochemistry, University of California, Los Angeles, CA 90095, USA
First published on 1st December 2016
Abstract
The concentration of molecules can be changed by chemical reactions and thereby offer a continuous readout. Yet computer architecture is cast in textbooks in terms of binary valued, Boolean variables. To enable reactive chemical systems to compute we show how, using the Cox interpretation of probability theory, one can transcribe the equations of chemical kinetics as a sequence of coupled logic gates operating on continuous variables. It is discussed how the distinct chemical identity of a molecule allows us to create a common language for chemical kinetics and Boolean logic. Specifically, the logic AND operation is shown to be equivalent to a bimolecular process. The logic XOR operation represents chemical processes that take place concurrently. The values of the rate constants enter the logic scheme as inputs. By designing a reaction scheme with a feedback we endow the logic gates with a built in memory because their output then depends on the input and also on the present state of the system. Technically such a logic machine is an automaton. We report an experimental realization of three such coupled automata using a DNAzyme multilayer signaling cascade. A simple model verifies analytically that our experimental scheme provides an integrator generating a power series that is third order in time. The model identifies two parameters that govern the kinetics and shows how the initial concentrations of the substrates are the coefficients in the power series.
Introduction
Modern digital logic uses the very same switching hardware to solve a great variety of problems. Each switch has two values, on and off. One limitation is the use of binary logic so that a number specified to several digits in base ten needs a long binary representation and many step processing. Physicochemical measurements typically provide a continuous readout and we would like to directly use those continuous variables without binning the readout interval into two or more discrete regions. Therefore, ideally we would like to define and implement logic operations on continuous variables. This will reduce memory requirements and the number of cycles necessary to process information. However, in addition we would like to retain the simplicity, reliability and generality of switching (i.e., Boolean) hardware.We aim here to show that a network of coupled chemical reactions can be transcribed into a series of cascaded Boolean logic gates. The set of gates that is provided by chemical kinetics is functionally complete in the sense of logic1,2 and therefore can be used to implement any other gate. An additional significant point is that these Boolean gates accept and deliver continuous variables. To demonstrate our ideas in a concrete setting we report explicit experimental results for a physicochemical system whose continuous change provides the numerical solution to a problem that is usually solved using digital means. Furthermore we show that the solution can be cast in terms of Boolean logic as used in computer architecture. We further show that the assembled machine is a computing circuit that is modular, that can be cascaded, that incorporates feedback and that is programmable. It is the feedback that endows our component logic units with their individual built-in memory.
Computing with molecules3–7 often has a raw output that is a continuous signal. This signal is usually binned into few ranges, often just two, sometimes three or four. Multilevel logic,5,8–12 which is more compact, is enabled by discretizing into more than two bins. However, there is an inherent loss of information in binning continuous variables. Furthermore, with three or more value logic variables there is the question of which algebra to use or which set of gates is functionally complete. The present approach, valid for networks of chemical reactions, remains Boolean but using continuous input and output.
Computer circuits achieve their remarkable abilities by the concatenation of small logic units. We show that for us concatenation is possible using kinetic networks because a species that is an output of one gate is recognized as an input by another appropriate gate. Biochemical networks13,14 are concatenated by the same principle. The implementation of concatenation by chemical kinetics requires that one can reliably recognize different species as being different.
To demonstrate our approach in a concrete setting we take advantage of the exceptional recognition properties of oligonucleotides.15 The structural and functional information within the oligonucleotide sequence has been widely used to develop computing circuits.7,15–19 Different DNA automata have been reported using toehold-mediated strand displacement,20 the application of DNAzymes11,21–24 or the use of sequence-specific restriction enzymes.25,26 For example, the strand-displacement principle has been implemented to use DNA as a universal material for controlling the dynamic behavior of coupled chemical reactions with non linear couplings,27 and systems implementing large scale feedback digital logic28 and algorithmic functions29 have been demonstrated.
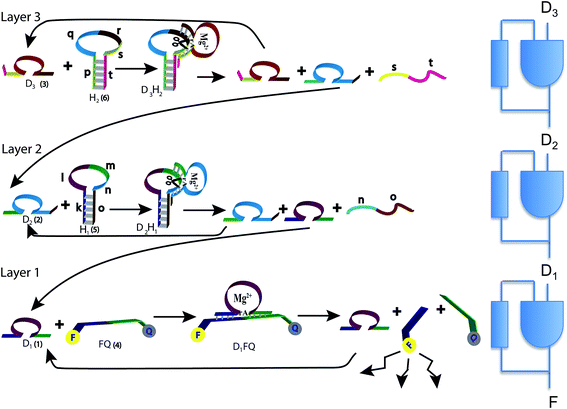
In the present study we designed a cascade of three Mg2+-dependent DNAzymes that act as a third order polynomial function generator. The reaction scheme uses tailored effector hairpins, predesigned functional sequences (see Table S1 of the ESI,†), that exist in a stable hairpin structure at 20 °C and include a single stranded loop to be cleaved by the respective DNAzyme. The hybrid of the DNAzyme and the hairpin (see Fig. 1), catalyzed by the Mg2+ ions, dissociates to regenerate the DNAzyme.
The theoretical idea that enables continuous logic is, as we suggested before,30 the use of the Cox point of view31–33 of probability theory as propositional logic.34 In the simple Boolean approach a proposition is either true or false so the logic is two-valued. The Cox approach allows us to assign a continuous number, the probability, to a proposition while retaining the structure of logic. For an axiomatic approach that allows using continuous variables for Boolean logic see ref. 35 and 36. Another route to continuous variables is to generalize from a Boolean description, for example ref. 37 and 38. Specifically, using the Cox approach, we show how the Boolean AND and OR logic operations1,2 applied to chemical reactions can be assigned inputs that are continuous and which vary with time. Our machines do not use the base sequence of DNA as inputs or outputs and as such are different from automata where the data structure is a base sequence.39,40 Our scheme works with variables that are concentrations that change with time in the manner of chemical kinetics. Each stage of the complete machine produces an intermediate that is fed forward to the next stage. Each stage also produces a feedback and thereby we have a machine with a built in memory. Such a machine can therefore be called an automaton.1 As an end product our machines produce a fluorescence that is monitored, and this is the final output.
Experimental
Implementation and readout of a three layered DNAzyme cascade
The operation of the three layer DNAzyme cascade and its equivalent logic circuit is schematically presented in Fig. 1. More details are in the section Materials and methods, and in Table S1 of the ESI,†. The detailed sequences corresponding to the composite given in Fig. 1 are described in Table S1, ESI.† Note that the colors in the respective sequence domains are identical to the colored domains of the schematic constituents shown in Fig. 1. The reaction system consists of three different Mg2+-dependent DNAzymes, D1, D2 and D3, labeled (1), (2) and (3) in Fig. 1, respectively. The reaction mixture also includes the fluorophore/quencher-functionalized ribonucleobase-modified DNA strand FQ (4), acting as the substrate for D1 and two hairpin structures, H1 (5) and H2 (6), acting as effector units for the conjugation of the DNAzymes D2 and D3. In the first reaction layer D1 catalyzes the cleavage of its substrate, the fluorophore-modified strand (4). This cleavage results in the fluorescence of the fluorophore released from the substrate (4) and provides the readout signal. This signal is shown as F in the logic scheme.There are two reaction paths that generate D1, as shown in Fig. 1. D1 can be generated in the first layer, and this is the feedback shown in the logic scheme. This feedback is slightly delayed because the reaction is not instantaneous, but it is fast on the macroscopic time scale. In a second path D1 can be generated in layer 2. In this way, D1 is the signal from layer 2 communicated to the layer 1 implementing cascade. The input of D1 from layer 2 to layer 1 is also shown in the logic diagram on the right of Fig. 1 as a D1 input to the lowest continuous state machine. H1 (5) acts as the effector unit for the second reaction layer. It is designed to implement two functions. Domains k, l and m in the stem region correspond to the sequence of D1 and thereby the signal to be delivered to the layer below will be generated. Domains m, n and part of o represent the substrate-sequence for the D2 DNAzyme. The caging of the D1 sequence in hairpin H1 deactivates its catalytic activities. In the presence of D2 and Mg2+ ions, the hairpin H1 is cleaved, yielding D1 and regenerating D2. The sequence n, o is a waste product. The D2-mediated generation of D1 delivers D1 to the first layer. If layer 2 is operating there is no need for an initial concentration of D1 to cleave (4). Similarly, hairpin H2 (6) includes the domains p and t in the stem region and domains q, r and s as parts of the loop. The domains p + q + r correspond to the caged sequence of D2, while the domains r, s and part of t provide the substrate sequence for D3. In the presence of D3 and Mg2+-ions, hairpin H2 is cleaved to yield free D2 and regenerate D3, while generating the sequence s + t as waste product. The cleavage of H2 restores the concentration of D2 in layer 2 of the system.
The fluorophore-labeled fragmented substrate generated in the different DNAzyme layered structures provided a readout signal for the activity of the respective DNAzyme cascade.
In summary, the operation of the bottom layer, layer 1, alone provides a first order reaction with the fluorophore-labeled fragmented substrate providing a readout signal. The directly read fluorescence output vs. time at three different temperatures is shown in Fig. 2. There is a short induction time until the concentration of D1 becomes steady and then the signal increases linearly with time. Beyond that first layer, layer 1 + layer 2 couple the D2 and D1 DNAzymes and generate a second order cascade where the fluorophore-labeled fragmented substrate generated in layer 1 provides the readout signal. Similarly, coupling of D3 to D2 and D1 generates a third order catalytic cascade. The average over three replicas of the directly read fluorescence output vs. time for all three layers is shown in Fig. 3 as dots. The continuous curves in Fig. 3 are a numerical fit using the kinetic scheme discussed below and in Section I of the ESI.† The numerical integration of the non-linear rate equations was done using a Runge–Kutta fifth order scheme. In the kinetics there are a number of conserved quantities, for example the sum of the free and bound concentration of D3 (conserved sums are identified in the analytical results shown in Sections II and III of the ESI†). During the numerical integration we did not impose any of those conserved quantities but rather used the computed sums to check that they are indeed conserved as the integration proceeds. The time step in the Runge–Kutta numerical integration was chosen to be small enough that the conservation was better than one part in a million.
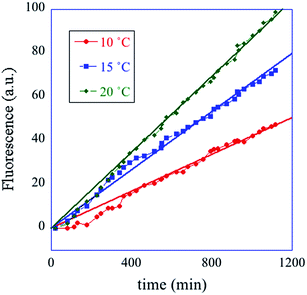 | ||
| Fig. 2 A one layer operation. The measured fluorescence at three different temperatures, cited in degrees C (see inset) vs. time. The straight lines are fits to the data. The kinetic scheme (eqn (1)) shows (see Section II of the ESI†) that after an induction period the fluorescence increases linearly with time with a rate constant that increases with temperature. | ||
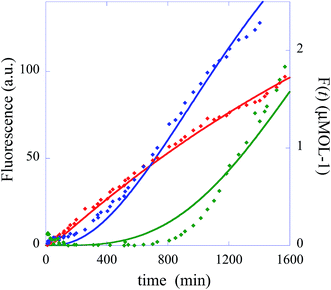 | ||
| Fig. 3 The experimentally measured fluorescence for the one layer system (red diamonds), the two layer system (blue diamonds) and the three layer system (green diamonds). Also shown as continuous curves are numerical fits using the kinetic scheme (eqn (1)), one layer, and of Section I of the ESI.† The numerical integration of the non-linear rate equations was done using a Runge–Kutta fifth order scheme. The values of initial concentrations are as in the experiments and the rate constants are from Table 1. Each point shown as experimental is an average over three measurements. The initial concentrations (in μmol) are: one layer system [D1(t = 0)] = 0.66 and [FQ(t = 0)] = 4, two layer system: [D1(t = 0)] = 0, [D2(t = 0)] = 0.66, [FQ(t = 0)] = 4, [H1(t = 0)] = 4, three layer system: [D1(t = 0)] = 0, [D2(t = 0)] = 0, [D3(t = 0) = 0.66], [FQ(t = 0)] = 4, [H1(t = 0)] = 4, [H2(t = 0) = 4]. | ||
Results
A kinetic scheme fits the data
The reaction scheme shown in Fig. 1 allows us to write a conventional kinetic scheme where each layer has a bimolecular hybridization step followed by a unimolecular fragmentation. The full scheme is shown in Section I of the ESI.† Shown here in eqn (1) is the scheme for just the first layer, where the square brackets denote concentrations. If layer 1 is a stand-alone as in the results shown in Fig. 2 then the feed forward term from layer 2 is absent. In this case it is necessary to have a finite initial concentration of the DNAzymes (1), D1, to start the reaction. In the general case one need not do this and can instead rely on the feed forward from layer 2. If there is no initial concentration of D1 then the feed forward will result in an induction time before layer 1 will fluoresce. After this short initial time the feedback built into layer 1 will replenish D1 | (1) |
In the experiment the initial concentration of the fluorophore/quencher FQ is in excess, and in the numerical fit of the data to the kinetic scheme we allow its concentration to depend on time. The result of the fit is that layer 1 promptly reaches a steady state where the concentration of the adduct D1FQ reaches a steady value. Once steady state is reached the fluorescence increases linearly with time as seen in Fig. 2. The kinetic scheme for the three layer system is discussed further in Section I of the ESI.†
In the numerical integration of the kinetic scheme to fit to the experimental results the rate constants for hybridization and fragmentation, k− and k+, are allowed to have different values for each layer. The results of the numerical fit for the rate constants, given in detail in Table 1, are fairly similar values for the three layers. The values of a few hundreds mol−1 min−1 for k− and about 6 × 10−2 min−1 for k+ are consistent with estimates41 based on the, here short, length of the strand that participates in the hybridization and other known rates.41,42 The kinetic characterization of the specific Mg2+-dependent DNAzyme was previously reported.41,42 The fit to the experimental data is shown in Fig. 3 as continuous curves. Possibly the fit could be improved by allowing a reaction that is the reverse of hybridization, but the number of fitting parameters becomes excessive. For the case when the initial concentration of the DNAzyme is not zero only for the topmost layer, the fit shows that the topmost layer is the first to reach a steady state. A short time later the next layer reaches a steady state, etc. When we have three layers (green curve) as in Fig. 1, layer 3 delivers a steady feed through of D2 to layer 2. Since layer 2 is being pumped linearly in time it produces D1 with a rate that increases linearly with time. Then the fluorophore F is produced with a rate that is quadratic in time. The fluorescence output rises as a cubic function.
| Layer/rate constant | k − (mol−1 min−1) | k + (min−1) |
|---|---|---|
| Layer 1 | 600.0 | 0.02 |
| Layer 2 | 1000.0 | 0.05 |
| Layer 3 | 200.0 | 0.04 |
To show analytically that the system produces a polynomial that is third order in time and, in particular to show that a special case is that this is an ‘integrator’ of the inputs of the DNAzymes, we discuss a simplified model (where the rate constants of each layer are identical, see below) that admits an analytical solution. By an ‘integrator’ we mean that the system integrates a function (of time) once, and then another time and yet one more time etc. Each such integration step accepts an input from the previous step and delivers an output to the next step, and we have already discussed how this feed forward is implemented, Fig. 1. For a three layer system the output in terms of the initial concentrations of the DNAzymes and of any initial concentration of a free fluorophore is
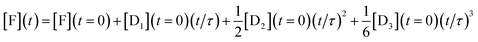 | (2) |
This expression clearly shows how the different terms depend linearly on the initial concentrations of the different DNAzymes, concentrations that can be independently varied. An explicit expression for the time scale τ is obtained from the kinetic model as discussed below, τ = 1/xκ. 1/κ is the duration of the induction period after which eqn (2) is valid. So we need to operate under conditions such that x < 1 to observe the power series output. The numerical solution for the kinetics shows that the initial concentrations govern the output of the three layers even when the simplifying assumptions of the model are not made, with an example shown in Fig. S1 of the ESI.† Also shown in the ESI is Fig. S2†, which exhibits the concentrations of the outputs of three concatenated layers at the first seven time steps of an Euler style integration of the differential equations of the model. That the system acts as an integrator is quite general; the model assumptions are necessary, however, to get the same time scale for the three layers. The operation of an integrator performing the same way as in eqn (2) but through an analog electronic circuit is shown using conventional symbols of electronic circuits in Fig. S3 of the ESI.†
An analytical model
The model is a limiting case designed to allow for an analytical solution. We take the rate constants for hybridization and dissociation to be the same for all three steps and take the concentrations of the three substrates, H1, H2 and FQ to be equal and to be in considerable excess such that effectively they are not changing with time. The key reason for the shortcoming of the model is the assumption that the rate constants for dissociation and for hybridization have the same value for the three layers. The fit to the experimental data, see Table 1, shows that this is only roughly the case.The model identifies a time constant of the problem, κ, common to all three layers
| κ = k+ + k−[substrate] | (3) |
In terms of the numerical fit to the experimental data we have that κ ≃ 0.022 min−1. The model identifies 1/κ as the induction time until the system settles to a steady operation.
A dimensionless variable that characterizes the steady state is K = k−[substrate]/k+. In the model the value of K is taken to be the same for all three layers. In terms of K we define the dimensionless fraction x,
 | (4) |
An analytic solution for the fluorescence vs. time when only layer 1 acts is derived in Section II of the ESI† with the final result
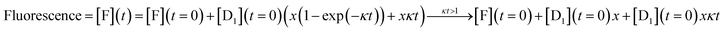 | (5) |
| Fluorescence = [F](t) = [F](t = 0) + [D1](t = 0)xκt | (6) |
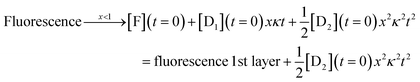 | (7) |
The complete solution is given in eqn (S3) of the ESI.†
For the third layer the limit of longer times, xκt > 1 and fast induction times, x < 1, which defines the three layer integrator (compare to eqn (2)) is
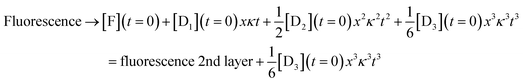 | (8) |
Eqn (6)–(8) show the capabilities of the integrator within the model. Fig. S6† shows the close agreement of the analytical model and the numerical solution. Fig. S7† shows the behavior after an induction period. Lastly, Fig. S8† shows the solution when we solve the kinetic equations numerically or using the model results in the regime that K, K = k−[substrate]/k+, is larger than 1. A high value of K also leads to x < 1 as shown in Fig. S4.† The difference between the two ranges, K < 1 and K > 1, is in the strength of binding of the DNAzyme and its substrate. When K is larger than 1 hybridization is favored, while when K is small the adduct rapidly dissociates so that the substrate is in excess. Either limiting case leads to x < 1, which is what we need for the model to accurately mimic the real kinetics. Fig. S8† shows the close agreement of the two for K = 15.98.
The analytical solution of the model shows explicitly the mapping of the chemical kinetics to a different mathematical problem. In actuality, the experimental results are more robust than the analytical model because even when the limiting conditions, such as having the same rate constants for the different layers, are not fulfilled, the output is a polynomial of the third order with coefficients that can be controlled as shown for example in Fig. S1 of the ESI.†
Discussion
Programmability
The computational program that the experimental system implements is versatile because one can change both the inputs and the kinetic parameters. In particular we have the option of cascading different automata, leading the way to modular design. The diversity and generality of this paradigm are also achieved by controlling the substrate recognition sequences and by the implementation of many different metal ion-dependent DNAzymes.43–47 Different power series can be generated by varying the initial concentrations of the DNAzymes. The concentrations of the hairpins can also be used to change the power series. The role of the two kinds of concentrations is by no means equivalent. As seen from the kinetic scheme, forming a fluorescing molecule consumes a molecule of a DNAzyme and a molecule of its substrate. But the DNAzyme is recovered and the substrate is not. The substrate is continuously consumed and unless its initial concentration is high enough the operation will soon cease. One can vary initial concentrations of the DNAzyme and its substrate independently. For the system to operate as an integrator one needs for the variations to remain in the range where the ratio of concentrations of DNAzyme to its substrate is small. The initial temperature can only be varied in a limited range but (see Fig. 2) the rate constant, the slope in the plot, shows quite measurable variation with temperature. As discussed below the rate constant is an input to the AND logic operation. Fig. 2 shows how temperature provides a control variable for a system with only one layer (eqn (6)). Ionic strength is another useful control variable through its effect41 on the rate of hybridization reactions.Continuous logic
The concentration of a species is effectively a continuous variable. Typically even a small volume contains a very large number of molecules. So a single sampling is sufficient because a second sampling will, within experimental error, yield the same value. Sampling measures the mean number of molecules. P(A) is the probability of identifying a molecule as species A and in chemical stoichiometry its value equals the mole fraction of A. If the system is a pure substance P(A) = 1 if all molecules are A and P(A) = 0 if none are. Chemical reactions change the number of molecules of different species. The most common reaction is the bimolecular reaction, which requires the encounter of two molecules, say A and B. This very description defines an AND operation because reaction occurs if and only if both A and B are present. To a classical chemist identifying a molecule as species A and identifying a molecule as B are mutually exclusive events. In other words, a molecule has an identity in the sense of the Aristotlean principle of identity. To distinguish between the chemical symbol and the logic proposition we use bold face characters such that A is the proposition identifying a molecule of the system as species A. Then, since A and B are independent the probability of identifying a pair as molecule A and molecule B is P(AB) = P(A)P(B). This is a well known definition of probability theory for two independent propositions. We show in Scheme 1 an interpretation of the result P(AB) = P(A)P(B) from a molecular level view of a bimolecular reaction taking place during successive infinitesimal instants of time. On the macroscopic time scale many additions take place during an infinitesimal instant of time δt. On a molecular scale, at successive instants A is a sequence of 0's and 1's. P(A) is the fraction of 1's in a very long such sequence. On a molecular time scale P(A) fluctuates between 0 and 1. On the macroscopic time scale P(A) changes monotonically and slowly in time in accordance with the equations of chemical kinetics. Similarly B is a sequence of 0's and 1's. A Boolean logic ‘AND’ operation of A and B is shown below. Clearly the long time fraction of 1's in the sequence C that is the result of the multiplication is P(C) ≡ P(AB) = P(A)P(B). | ||
| Scheme 1 A microscopic view of an AND between two molecules implemented by the progress of a bimolecular event. | ||
Sometime ago Cox31,32 showed how to assign a continuous number to the results of operations of Boolean algebra such as AND within the framework of inductive logic. Cox showed that his rules of operations on assertions are equivalent to probability theory. In particular the probability of A and B is P(AB) = P(A)P(B). Cox intended his axioms to cover the situation where probability encodes a state of knowledge. But as Cox emphasized the most accurate estimation of a numerical value for a probability is when it is the frequency of realizing the proposition in a long run of repeating identical experiments. Thereby Cox enables us to relate the ‘and’ of kinetics to the AND operation of Boolean logic. To conclude, P(A) is the frequency with which molecule A is observed in a long sequence of independent repeated samplings of molecules. Chemical kinetics as usually understood is particularly suitable to implement the frequency interpretation of probability because any sample involves a very large number of molecules so that the measured frequency of identifying a molecule as A is the probability P(A). This is, of course, not the case for very small systems in which case there can be fluctuations.
The other binary definition that Boole used in his algebra is OR. Boole used an exclusive disjunction or, in a current terminology, an exclusive OR, denoted XOR. This excludes the two events C and D from occurring simultaneously so that P(C + D) = P(C) + P(D). The exclusive OR logic operation is just what we need for chemical kinetics because, for example, an adduct A can dissociate into product C or product D. Here too we use the result, obvious to a chemist, that a molecule has an identity, it is either C or D.
We also need the XOR because in general, more than one reaction can contribute to a change of concentration. The logic XOR and the chemical kinetics ‘or’ play corresponding roles because the two manners of changing the concentration are mutually exclusive, which is why the two reaction rates add as shown in eqn (1). In the next instant of macroscopic time the concentration of a molecule is changing by this reaction or by that reaction.
The operation of an integrator exhibits a XOR when, say, the concentration of a DNAzyme in the second layer, D2, is changed either by the ongoing reactions or by an addition from the outside. Thereby the fluorescence output is a sum of terms.
Depending on the process, reactions can also act in an opposite direction, which is how we represent the Boolean negation. AND, XOR and NOT are together sufficient to generate all possible logical operations.
The bimolecular reaction rate of A and B is proportional to the product of the two concentrations, as shown for the hybridization processes in eqn (1). Relating the reaction rate and the concentrations there is the reaction rate constant. This arises because for reaction to take place, it is necessary for A and B to be both present, but this is not sufficient. The two molecules need to encounter and they need to react. The reaction rate constant bears dimensions, so we need to discuss how to input it as a proposition. Consider first the simpler case of a unimolecular reaction, for example the dissociation of the adduct D1FQ as shown in eqn (1). We aim to show that the probability that D1FQ dissociates in the short time interval δt is the dimensionless quantity k+δt. In the kinetic scheme the only fate of D1FQ is dissociation. So its concentration changes as [D1FQ](t + δt) = [D1FQ](t)(1 − k+δt). In words, the probability of identifying D1FQ at the time t + δt equals the probability of identifying D1FQ at times t multiplied by (where this multiplication is equivalent to an AND operation) the probability that it did not dissociate in the time interval t to t + δt. In the kinetic eqn (1) the term −k+[D1FQ](t)δt is the probability of identifying D1FQ at the time t multiplied by (≡AND) the probability that it does dissociate in the time interval t to t + δt. For a bimolecular reaction, say the hybridization of D1 and FQ to form D1FQ, we can first AND D1 and FQ and then AND the identification of the pair with the probability k−δt to hybridize in the time interval t to t + δt. What we conclude is that in a short time interval monitoring the progress of a unimolecular reaction in a macroscopic system mimics an AND gate with two inputs. Monitoring a bimolecular reaction implements an AND gate with three inputs. In both cases one of the inputs is determined by the relevant reaction rate constant. Changing the rate constant by changing the temperature, as is shown in Fig. 2,is changing an input to the logic.
Conclusions
On the molecular scale of space and time, a bimolecular reaction occurs when single molecules A and B meet and react. Such an experiment can be realized in a crossed molecular beams experiment.48 A single isolated A + B collision implements a binary AND gate. On the macroscopic level a chemical reaction is when billions upon billions of individual collisions occur independently and simultaneously on the macroscopic time scale. This is the continuous AND gate that we discuss here. It is a single macroscopic gate acting as very many microscopic gates operating independently in parallel. The XOR gate is implemented by a reaction branching into mutually exclusive products. The negation operation, NOT, is a unary gate. It is ‘not identifying the molecule as A’. The different molecules are mutually exclusive. Using a bar to denote negation we can write P(Ā) = 1 − P(A).An essential ingredient in computing circuits is the ability to transmit the output of one stage as input to the next stage. Chemical kinetic networks are inherently able to do this feed forward. A more specific chemical mechanism is the feedback, which allows the system to respond taking into account its present state. This enables a so called automaton logic operation. The feedback is also continuously variable so it mimics a continuous state machine, rather than a finite state one. We used the unique recognition and catalytic properties of nucleic acids to design and implement the concatenated automata. This allowed the construction of a machine where the output is easily monitored and where the response of individual layers can also be measured. We demonstrate that the cascade implements an integrator. The continuous logic elements that are introduced here could be implemented in biological systems14 such as biochemical and/or signaling networks.
Experimental
Materials and methods
The operation of the third-order DNAzyme three layer cascade is schematically presented in Fig. 1. The experiments were performed in 10 mM HEPES buffer solution (50 mM NaCl, 25 mM MgCl2, pH 7) at 20 °C (or other temperatures as indicated in Fig. 2). The oligonucleotides were dissolved in distilled water (pH = 7) to yield stock solutions of 100 μM. All oligonucleotides were purchased from Integrated DNA Technologies (IDT).The concentrations of the hairpin structures, the concentration of the inputs and the concentration of the substrates were varied and specifically indicated in the figure captions of the respective experiment. The initial concentration of the fluorophore-quencher, 4 × 10−6 M, was the same in all experiments. The progress of the 1st, 2nd and 3rd order cascaded layers was probed by following the time-dependent fluorescence changes upon cleavage of the fluorophore-quencher modified substrate (λex = 494 nm λem = 519 nm).
All DNA sequences were designed to minimize undesired cross hybridization using NUPACK (http://www.nupack.org/). The sequences are given in Table S1 of the ESI.†
Conflict of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the EC FP7-funded BAMBI Project 618024 and by the EC FP7-funded MULTI Project 317707. FR is a director of research with FNRS (Fonds National de la Recherche Scientifique), Belgium.References
- Z. Kohavi and N. K. Jha, Switching and finite automata theory, Cambridge University Press, Cambridge, 2010 Search PubMed.
- M. M. R. Mano, C. R. Kime and T. Martin, Logic and Computer Design Fundamentals, Pearson Education, Upper Saddle River, NJ, 2016 Search PubMed.
- J. Andreasson and U. Pischel, Chem. Soc. Rev., 2015, 44, 1053–1069 RSC.
- G. de Ruiter and M. E. van der Boom, Acc. Chem. Res., 2011, 44, 563–573 CrossRef CAS PubMed.
- A. P. deSilva, Molecular Logic-based Computation, RSC, Cambridge, 2012 Search PubMed.
- K. He, Y. Li, B. Xiang, P. Zhao, Y. Hu, Y. Huang, W. Li, Z. Nie and S. Yao, Chem. Sci., 2015, 6, 3556–3564 RSC.
- DNA computing and Molecular Programming, ed. D. Stefanovic and A. Tuberfield, Springer, Berlin, 2012 Search PubMed.
- J. Cervera and S. Mafé, ChemPhysChem, 2010, 11, 1654–1658 CrossRef CAS PubMed.
- B. Fresch, M. Cipolloni, T.-M. Yan, E. Collini, R. D. Levine and F. Remacle, J. Phys. Chem. Lett., 2015, 6, 1714–1718 CrossRef CAS PubMed.
- M. Klein, S. Rogge, F. Remacle and R. D. Levine, Nano Lett., 2007, 7, 2795–2799 CrossRef CAS PubMed.
- R. Orbach, S. Lilienthal, M. Klein, R. D. Levine, F. Remacle and I. Willner, Chem. Sci., 2015, 6, 1288–1292 RSC.
- E. Torres, K. L. Kompa, F. Remacle and R. D. Levine, Chem. Phys., 2008, 347, 531–545 CrossRef CAS.
- U. Alon, An Introduction to Systems Biology, CRC Press, Boca Raton, FL, 2007 Search PubMed.
- F. C. Simmel, ACS Nano, 2013, 7, 6–10 CrossRef CAS PubMed.
- F. Wang, C. H. Lu and I. Willner, Chem. Rev., 2014, 114, 2881–2941 CrossRef CAS PubMed.
- R. Orbach, F. Remacle, R. D. Levine and I. Willner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21228–21233 CrossRef CAS PubMed.
- A. J. Genot, J. Bath and A. J. Turberfield, J. Am. Chem. Soc., 2011, 133, 20080–20083 CrossRef CAS PubMed.
- M. N. Stojanovic, T. E. Mitchell and D. Stefanovic, J. Am. Chem. Soc., 2002, 124, 3555–3561 CrossRef CAS PubMed.
- M. N. Stojanovic and D. Stefanovic, Nat. Biotechnol., 2003, 21, 1069–1074 CrossRef CAS PubMed.
- D. Y. Zhang, A. J. Turberfield, B. Yurke and E. Winfree, Science, 2007, 318, 1121–1125 CrossRef CAS PubMed.
- J. Elbaz, O. Lioubashevski, F. Wang, F. Remacle, R. D. Levine and I. Willner, Nat. Nanotechnol., 2010, 5, 417–422 CrossRef CAS PubMed.
- M. Kahan-Hanum, Y. Douek, R. Adar and E. Shapiro, Sci. Rep., 2013, 3, 1535 Search PubMed.
- R. Orbach, F. Remacle, R. D. Levine and I. Willner, Chem. Sci., 2014, 5, 1074–1081 RSC.
- R. Orbach, B. Willner and I. Willner, Chem. Commun., 2015, 51, 4144–4160 RSC.
- R. Adar, Y. Benenson, G. Linshiz, A. Rosner, N. Tishby and E. Shapiro, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9960–9965 CrossRef CAS PubMed.
- Y. Benenson, B. Gil, U. Ben-Dor, R. Adar and E. Shapiro, Nature, 2004, 429, 423–429 CrossRef CAS PubMed.
- D. Soloveichik, G. Seelig and E. Winfree, in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), LNCS, 2009, vol. 5347, pp. 57–69 Search PubMed.
- C. W. Brown, M. R. Lakin, E. K. Horwitz, M. L. Fanning, H. E. West, D. Stefanovic and S. W. Graves, Angew. Chem., Int. Ed., 2014, 53, 7183–7187 CrossRef CAS PubMed.
- L. Qian and E. Winfree, Science, 2011, 332, 1196–1201 CrossRef CAS PubMed.
- F. Remacle and R. D. Levine, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12091–12095 CrossRef CAS PubMed.
- R. T. Cox, Am. J. Phys., 1946, 17, 1–13 CrossRef.
- R. T. Cox, in The Maximum Entropy Formalism, ed. R. D. Levine and M. Tribus, MIT Press, Cambridge, Mass., 1979, pp. 119–167 Search PubMed.
- D. J. C. MacKay, Information Theory, Inference and Learning Algorithms, Cambridge University Press, Cambridge, 2004 Search PubMed.
- S. Givant and P. Halmos, Introduction to Boolean Algebra, Springer, New York, 2009 Search PubMed.
- E. V. Huntington, Proc. Natl. Acad. Sci. U. S. A., 1932, 32, 179–180 CrossRef.
- E. V. Hutington, Transactions of the American Mathematical Society, 1933, 35, 274–304 Search PubMed.
- D. M. Wittmann, J. Krumsiek, J. Saez-Rodriguez, D. A. Lauffenburger, S. Klamt and F. J. Theis, BMC Syst. Biol., 2009, 3, 1–21 CrossRef PubMed.
- R. Thomas and R. D'Ari, Biological Feedback, CRC Press, Boca Raton, 1990 Search PubMed.
- C. H. Bennett, Int. J. Theor. Phys., 1982, 21, 905–940 CrossRef CAS.
- S. Shoshani, T. Ratner, R. Piran and E. Keinan, Isr. J. Chem., 2011, 51, 67–86 CrossRef CAS.
- J. G. Wetmur, Crit. Rev. Biochem. Mol. Biol., 1991, 26, 227–259 CrossRef CAS PubMed.
- J. G. Wetmur and N. Davidson, J. Mol. Biol., 1968, 31, 349–370 CrossRef CAS PubMed.
- R. R. Breaker and G. F. Joyce, Chem. Biol., 1994, 1, 223–229 CrossRef CAS PubMed.
- R. R. Breaker and G. F. Joyce, Chem. Biol., 1995, 2, 655–660 CrossRef CAS PubMed.
- J. C. Hogan Jr, Nat. Biotechnol., 1997, 15, 328–330 CrossRef CAS PubMed.
- J. Liu and Y. Lu, J. Am. Chem. Soc., 2007, 129, 9838–9839 CrossRef CAS PubMed.
- A. Roth and R. R. Breaker, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 6027–6031 CrossRef CAS.
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, Cambridge, 2004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc03892a |
| This journal is © The Royal Society of Chemistry 2017 |