Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism of photocatalytic water oxidation on small TiO2 nanoparticles†
Mikko
Muuronen
 *a,
Shane M.
Parker
*a,
Shane M.
Parker
 a,
Enrico
Berardo
a,
Enrico
Berardo
 bc,
Alexander
Le
a,
Martijn A.
Zwijnenburg
bc,
Alexander
Le
a,
Martijn A.
Zwijnenburg
 c and
Filipp
Furche
c and
Filipp
Furche
 *a
*a
aDepartment of Chemistry, University of California, 1102 Natural Sciences II, Irvine, CA 92697-2025, USA. E-mail: mmuurone@uci.edu; filipp.furche@uci.edu; Fax: +1 949 824 8571; Tel: +1 949 824-5051
bDepartment of Chemistry, Imperial College London, South Kensington, London, SW7 2AZ, UK
cDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
First published on 7th December 2016
Abstract
We present the first unconstrained nonadiabatic molecular dynamics (NAMD) simulations of photocatalytic water oxidation by small hydrated TiO2 nanoparticles using Tully surface hopping and time-dependent density functional theory. The results indicate that ultrafast electron–proton transfer from physisorbed water to the photohole initiates the photo-oxidation on the S1 potential energy surface. The new mechanism readily explains the observation of mobile hydroxyl radicals in recent experiments. Two key driving forces for the photo-oxidation reaction are identified: localization of the electron–hole pair and stabilization of the photohole by hydrogen bonding interaction. Our findings illustrate the scope of recent advances in NAMD methods and emphasize the importance of explicit simulation of electronic excitations.
Introduction
TiO2 is the prototypical redox photocatalyst because it is inexpensive, abundant, versatile, and non-toxic.1,2 Ever since the ability of TiO2 to split water was discovered in 1972,3 the use of TiO2 for solar fuel generation has been intensely studied. However, the efficiency of TiO2-based photocatalysts has remained moderate, which was attributed to a lack of mechanistic understanding and models to inform synthetic improvements.4 Apart from sample preparation, heterogeneity, and system size, a key challenge of mechanistic studies of TiO2 photocatalysis are ultra-fast processes involving nonadiabatic transitions between electronic states, which are exceedingly difficult to characterize experimentally and theoretically.Here we propose a detailed mechanistic model for photocatalytic water oxidation on TiO2 nanoparticles. Our model explicitly accounts for exciton dynamics, nonadiabatic transitions, and bond breaking for the first time, and is based on recent methodological developments of on-the-fly non-adiabatic molecular dynamics (NAMD) simulations.5–8
The high kinetic barrier for photolytic water splitting on TiO2 surfaces is caused by the oxygen evolution reaction (OER),9–12
| 2H2O + 4h+ → O2 + 4H+. | (1) |
The first of the four one-electron oxidation steps is likely rate-limiting;10,12–14 however, the mechanism of this step is controversial and several conflicting models have been proposed. The earliest models based on spectroscopic experiments suggested that the photohole (h+) oxidizes a surface bound hydroxyl group ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH,15,16
TiIV–OH,15,16
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH + h+ → TiIV–OH + h+ → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–(·OH)+. TiIV–(·OH)+. | (2) |
This mechanism was challenged by the results of density functional theory (DFT) calculations suggesting that ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH groups trap electrons, not holes.17 An alternative mechanism,
TiIV–OH groups trap electrons, not holes.17 An alternative mechanism,
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH2 + h+ → TiIV–OH2 + h+ → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–(·OH) + H+, TiIV–(·OH) + H+, | (3) |
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH2 instead of
TiIV–OH2 instead of ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH by the photohole.10 The high barrier of this step can be lowered by deprotonation of
TiIV–OH by the photohole.10 The high barrier of this step can be lowered by deprotonation of ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH2 with base, resulting a barrierless hole transfer.12,18,19 The resulting proton-coupled electron transfer (PCET) mechanism, where a strongly localized photohole h+ is transferred from a bridging oxygen Obr to the
TiIV–OH2 with base, resulting a barrierless hole transfer.12,18,19 The resulting proton-coupled electron transfer (PCET) mechanism, where a strongly localized photohole h+ is transferred from a bridging oxygen Obr to the ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–(OH)− species, is consistent with the observed pH dependence of the OER.9,20 However, the recent experimental detection of mobile rather than surface bound OH radicals in three different experiments casts doubts on the hypothesis that the oxidized water is bound to the TiO2 surface.21–24 Based on scanning tunneling microscopy (STM) experiments, Hou and co-workers suggested that mobile ·OH species result from protonated Obr sites as a reaction intermediate:22
TiIV–(OH)− species, is consistent with the observed pH dependence of the OER.9,20 However, the recent experimental detection of mobile rather than surface bound OH radicals in three different experiments casts doubts on the hypothesis that the oxidized water is bound to the TiO2 surface.21–24 Based on scanning tunneling microscopy (STM) experiments, Hou and co-workers suggested that mobile ·OH species result from protonated Obr sites as a reaction intermediate:22![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–OH2 + h+ → TiIV–OH2 + h+ → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIV–(ObrH)+–TiIV TiIV–(ObrH)+–TiIV![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) + ·OH. + ·OH. | (4) |
Recent Ehrenfest NAMD simulations of periodic TiO2 surfaces also considered this mechanism,25 but the simulation times were too short (up to 20 fs) to be conclusive. Nakato and coworkers suggested that nucleophilic attack of water on a Obr, activated by h+, might initiate the OER,26,27
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Obr(h+) + H2O(l) → Obr(h+) + H2O(l) → ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) ·ObrOH + H+, ·ObrOH + H+, | (5) |
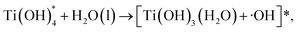 | (6) |
Methods
The PBE0 (ref. 29) hybrid functional and polarized double-ζ valence def2-SVP30 basis sets were used for NAMD simulations. To account for van der Waals interactions, D3 dispersion corrections were employed.31 The forces on the S1 and S0 potential energy surfaces (PESs) and the non-adiabatic couplings between them were computed analytically at each time step.32,33 The nuclear dynamics used Tully's surface hopping algorithm and a leapfrog–Verlet integrator with time-step of 40 a.u. (1 fs).34,35 115 trajectories were initiated with random nuclear velocities consistent with a 350 K thermal ensemble, and the trajectories were propagated for up to 1 ps. To describe homolytic bond cleavage, the spin symmetry was allowed to break if triplet instability was found for the reference state. We recently showed that this methodology can treat both closed and open shell pathways semiquantitatively in photodissociation of acetaldehyde.8 To avoid convergence and stability problems close to the conical intersections (CIs), a surface hop was forced if the S1–S0 gap is below 0.5 eV.6,36 All computations were performed using a local development version based on Turbomole 7.1.37 See ESI† for benchmark results and further details.Results and discussion
To compare the reactivity of surface-bound vs. physisorbed water, we simulated small hydrated (TiO2)4(OH)4 nanoparticles with two, four, eight or ten additional water molecules, see Fig. 1 and S3.† These models can accommodate all proposed mechanisms (2)–(6) with the exception of mechanisms requiring deprotonation of water by added base, and enabled total simulation times up to 60 ps. Even though the initial one-electron oxidation is much faster, these long simulation times were necessary to capture reactive trajectories without imposing artificial bias on the system.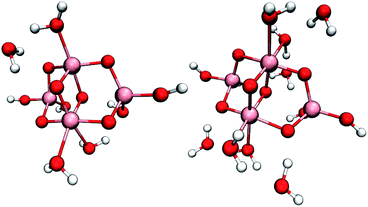 | ||
| Fig. 1 Studied (TiO2)4(OH)4 nanoparticles with four (left) and eight (right) additional water molecules. Pink, red and white spheres represent titanium, oxygen and hydrogen atoms, respectively. | ||
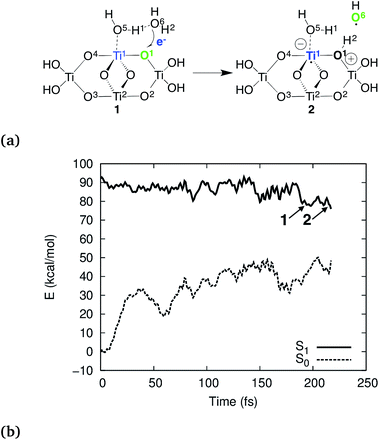
According to our simulations, the reaction starts by electron–proton transfer (EPT) from physisorbed water to the photohole strongly localized on Obr as depicted in Fig. 2a. In (TiO2)4(OH)4(H2O)8, this reaction occurs on the S1 potential energy surface (PES), close to the S1–S0 conical intersection (CI), see Fig. 2b. The reactive intermediate 1 forms approximately 200 fs after the trajectory was initiated and undergoes hydrogen-transfer reaction within 20 fs to form intermediate 2.
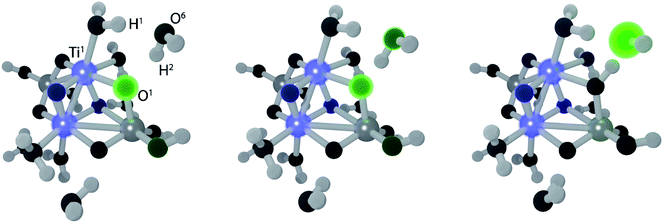
The electron transfer reaction is displayed in Fig. 3 for (TiO2)4(OH)4(H2O)8. At 200 fs, the photohole (green) is localized strongly on bridging oxygen O1, forming the intermediate 1. The hole is transferred to physisorbed water at 213 fs and intermediate 2 forms at 219 fs via concerted proton transfer without substantial nuclear reorientation. Intermediate 2 subsequently decays rapidly to S0 through a CI and forms a stable ground state intermediate followed by dissociation of the hydroxyl radical (see ESI†).
The structure of the intermediate observed in the NAMD simulations is in close agreement with STM measurements.22 Moreover, our mechanism yields mobile OH radicals, in accordance with several recent experiments.21,23,24 The charge-transfer (CT) reactivity seen in our simulations is indirectly supported by a TS study of Ti(OH)428 and NAMD simulations of the oxidation of chemisorbed methanol on a TiO2 surface.38
To further analyze the exciton dynamics and the resulting EPT, we consider the difference in atomic natural bonding orbital39 (NBO) charges between the S1 and the S0 states, see Fig. 4a. Positive values of the population difference indicate hole charge, i.e., loss of electron density on atoms relative to the ground state, and negative values indicate electron charge, i.e., gain of electron density relative to the ground state. In the Franck–Condon geometry, the hole is shared between all bridging oxygens, O1–O4, and the electron is distributed equally to Ti1 and Ti2. During the first 100 fs, the hole localizes strongly on the bridging oxygen O1 until EPT from the physisorbed water H2O6 occurs at 213 fs. The other bridging oxygens, O2–O4, gain electron density and thus act as electron traps. This allows them to hydrogen bond with liquid water more efficiently, but does not lead to any reactivity. A consequence of the hole localization is the subsequent localization of the electron on Ti1 adjacent to the reactive O1,
 | (7) |
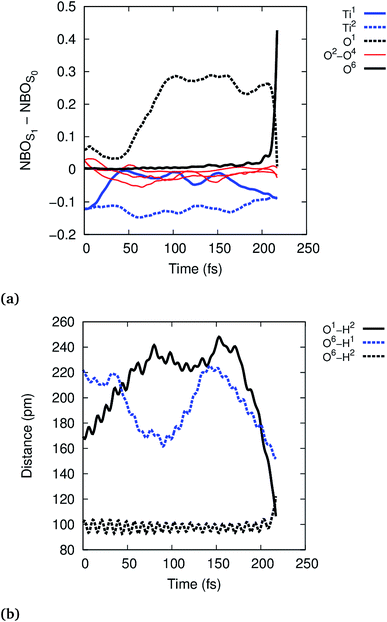 | ||
| Fig. 4 Time-evolution of the exciton according to NBO population analysis (a) and of the selected O–H distances (b) in the reactive trajectory for (TiO2)4(OH)4(H2O)8 nanoparticle. | ||
The localization of the two opposite charges provides coulombic stabilization of the exciton and drives the reaction
[![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIII–Obr(h+)–TiIV TiIII–Obr(h+)–TiIV![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) ]* + H2O(l) → [ ]* + H2O(l) → [![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIII–(ObrH)+–TiIV TiIII–(ObrH)+–TiIV![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) + ·OH]* + ·OH]* | (8) |
![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) TiIII–(ObrH)+–TiIV
TiIII–(ObrH)+–TiIV![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) species, which are stable on a picosecond timescale in ab initio molecular dynamics simulations.40 While less confinement may increase the exciton size, the energy gain from localization also increases in larger particles. Larger rutile hydrated and hydroxylated (TiO2)23 nanoparticles exhibit exciton localization after self-trapping (i.e. at the S1 PES minimum) on a similar scale as the ones studied here,41 suggesting that the self-trapped exciton size may not depend strongly on the particle size.
species, which are stable on a picosecond timescale in ab initio molecular dynamics simulations.40 While less confinement may increase the exciton size, the energy gain from localization also increases in larger particles. Larger rutile hydrated and hydroxylated (TiO2)23 nanoparticles exhibit exciton localization after self-trapping (i.e. at the S1 PES minimum) on a similar scale as the ones studied here,41 suggesting that the self-trapped exciton size may not depend strongly on the particle size.
Photohole localization is not the only driving force of the reaction, however, since EPT only occurs 100 fs after the photohole localizes: starting at ∼150 fs, the reactive physisorbed water hydrogen bonds more strongly with the Ti1 bound water (O6–H1 distance decreases from 220 pm to 170 pm), see Fig. 4b; concurrently, the electron starts to localize on Ti1, see Fig. 4a. The EPT follows these changes as seen in the O1–H2 and O6–H2 distances. This suggests that the localized electron on Ti1 also favors EPT by some electron transfer to the water bound to Ti1. The electron rich water then stabilizes the nascent H2O+ by solvating the hole, thus facilitating the reaction. This interpretation is also supported by the observation that the reaction is faster in the smaller (TiO2)4(OH)4(H2O)4 model: Ti1 is bound to only one water instead of two in (TiO2)4(OH)4(H2O)8, which facilitates electron localization and concomitant stabilization of the photohole by hydrogen bonding interaction. Intermediate 1 is formed approximately at 150 fs in the reactive trajectory for (TiO2)4(OH)4(H2O)4, similar to the reactivity observed for the larger (TiO2)4(OH)4(H2O)8 particle (Fig. S5 and S6†).
Why did previous simulations not show the present mechanism? These simulations were based on free charge carriers, i.e., cationic and anionic species in the electronic ground state, which do not include electron–hole interaction. For (TiO2)4(OH)4(H2O)8, the reaction is exothermic by approximately 10 kcal mol−1 compared to the Franck–Condon geometry on the S1 PES (Fig. 2b). On the other hand, for a free hole the reaction is endothermic by approximately 7 kcal mol−1 (ESI†). This 17 kcal mol−1 difference is mainly due to coulombic stabilization of the exciton (“exciton binding energy”), of the H2O+ species, and of the protonated bridging oxygen O1 by the electron component of the exciton. This was confirmed by BOMD simulations for free holes which did not show any reactivity up to 135 ps of total simulation time. Explicit simulation of both, the electron and the hole and their interaction, i.e., electronic excitation beyond the single-particle picture, is necessary to explain the reactivity. Furthermore,the oxidation occurs only after relaxation of the S1 state, and thus the reactivity cannot be rationalized from the Franck–Condon geometry.
Conclusions
The first unconstrained NAMD simulations of water oxidation by small TiO2 nanoparticles show EPT from physisorbed liquid water to a strongly localized hole on Obr. This mechanism is consistent with STM experiments,22 and generates mobile hydroxyl radicals in accordance with recent experiments based on three different fluorescence probe methods and total internal reflection fluorescence microscopy.21,23,24 The calculations reveal two key driving forces of the oxidation reaction: (i) localization of the exciton with close proximity of the electron and hole charges leads to a gain of coulombic stabilization. (ii) Simultaneously, hydrogen bonding stabilizes the emerging H2O+ species, which is deprotonated to free OH in the excited state.These results provide a rationale for the low catalytic activity of TiO2 in water splitting: while exciton localization is necessary to drive the reaction, it can also promote recombination of the electron and hole charges, i.e., non-radiative decay to the ground state. This is seen in the vast majority of our trajectories. Similarly, the effective stabilization of the photohole by hydrogen bonding requires a specific orientation of surface bound water, which has a large entropic penalty. While additional validation of the proposed mechanism is desirable, e.g., by exploring the effects of the particle size and bulk solvation, the present results could inform future efforts to increase the water splitting activity of TiO2-based photocatalysts by targeted synthetic modification.
Acknowledgements
This material is based upon work supported by the U.S. Department of Energy under Award DE-SC0008694. SMP is supported by an Arnold O. Beckman Postdoctoral Fellowship, and EB would like to thank the Thomas Young Centre for a Junior Research Fellowship which allowed him to visit University of California, Irvine. MZ acknowledges the UK Engineering and Physical Sciences Research Council (EPSRC) for funding (Grant EP/I004424/1). Helpful discussions with Shane A. Ardo are also acknowledged.References
- K. Hashimoto, H. Irie and A. Fujishima, Jpn. J. Appl. Phys., 2005, 44, 8269–8285 CrossRef CAS.
- M. Kapilashrami, Y.-S. Zhang, Y. S. Liu, A. Hagfeldt and J. Guo, Chem. Rev., 2014, 114, 9662–9707 CrossRef CAS PubMed.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- J. Schneider, Chem. Rev., 2014, 114, 9919–9986 CrossRef CAS PubMed.
- M. Barbatti, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 620–633 CrossRef CAS.
- E. Tapavicza, G. D. Bellchambers, J. C. Vincent and F. Furche, Phys. Chem. Chem. Phys., 2013, 15, 18336–18348 RSC.
- F. Furche, B. T. Krull, B. D. Nguyen and J. Kwon, J. Chem. Phys., 2016, 144, 174105 CrossRef PubMed.
- J. C. Vincent, M. Muuronen, K. C. Pearce, L. N. Mohanam, E. Tapavicza and F. Furche, J. Phys. Chem. Lett., 2016, 7, 4185–4190 CrossRef CAS PubMed.
- J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885–13891 CrossRef CAS PubMed.
- Á. Valdés, Z.-W. Qu, G.-J. Kroes, J. Rossmeisl and J. K. Nørskov, J. Phys. Chem. C, 2008, 112, 9872–9879 Search PubMed.
- Á. Valdés, J. Brillet, M. Gratzel, H. Gudmundsdottir, H. A. Hansen, H. Jonsson, P. Klupfel, G.-J. Kroes, F. Le Formal, I. C. Man, R. S. Martins, J. K. Nørskov, J. Rossmeisl, K. Sivula, A. Vojvodic and M. Zach, Phys. Chem. Chem. Phys., 2012, 14, 49–70 RSC.
- J. Chen, Y. Li, P. Sit and A. Selloni, J. Am. Chem. Soc., 2013, 135, 18774–18777 CrossRef CAS PubMed.
- Á. Valdés and G.-J. Kroes, J. Phys. Chem. C, 2010, 114, 1701–1708 Search PubMed.
- Y. Li, Z. Liu, L. Liu and W. Gao, J. Am. Chem. Soc., 2010, 132, 13008–13015 CrossRef CAS PubMed.
- R. H. Wilson, J. Electrochem. Soc., 1980, 127, 228–234 CrossRef CAS.
- M. R. Hoffman, S. T. Martin, W. Choi and D. W. Bahnemann, Chem. Rev., 1995, 95, 69–96 CrossRef.
- C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803 CrossRef PubMed.
- W.-N. Zhao and Z.-P. Liu, Chem. Sci., 2014, 5, 2256–2264 RSC.
- Y.-F. Li and A. Selloni, ACS Catal., 2016, 6, 4769–4774 CrossRef CAS.
- A. Imanishi, T. i. Okamura, N. Ohashi, R. Nakamura and Y. Nakato, J. Am. Chem. Soc., 2007, 129, 11569–11578 CrossRef CAS PubMed.
- T. Hirakawa, K. Yawata and Y. Nosaka, Appl. Catal., A, 2007, 325, 105–111 CrossRef CAS.
- S. Tan, H. Feng, Y. Ji, Y. Wang, J. Zhao, A. Zhao, B. Wang, Y. Luo, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2012, 134, 9978–9985 CrossRef CAS PubMed.
- J. Zhang and Y. Nosaka, J. Phys. Chem. C, 2014, 118, 10824–10832 CAS.
- W. Kim, T. Tachikawa, G. h. Moon, T. Majima and W. Choi, Angew. Chem., 2014, 126, 14260–14265 CrossRef.
- G. A. Tritsaris, D. Vinichenko, G. Kolesov, C. M. Friend and E. Kaxiras, J. Phys. Chem. C, 2014, 118, 27393–27401 CAS.
- R. Nakamura and Y. Nakato, J. Am. Chem. Soc., 2004, 126, 1290–1298 CrossRef CAS PubMed.
- R. Nakamura, T. Tanaka and Y. Nakato, J. Phys. Chem. B, 2004, 108, 10617–10620 CrossRef CAS.
- A. Kazaryan, R. van Santen and E. J. Baerends, Phys. Chem. Chem. Phys., 2015, 17, 20308–20321 RSC.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433 CrossRef CAS.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061 CrossRef CAS.
- S. D. Elliott, R. Ahlrichs, O. Hampe and M. M. Kappes, Phys. Chem. Chem. Phys., 2000, 2, 3415–3424 RSC.
- B. G. Levine, C. Ko, J. Quenneville and T. J. Martínez, Mol. Phys., 2006, 104, 1039–1051 CrossRef CAS.
- F. Furche, R. Ahlrichs, C. Hättig, W. Klopper, M. Sierka and F. Weigend, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 91–100 CrossRef CAS.
- G. Kolesov, D. Vinichenko, G. A. Tritsaris, C. M. Friend and E. Kaxiras, J. Phys. Chem. Lett., 2015, 6, 1624–1627 CrossRef CAS PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS.
- S. Selcuk and A. Selloni, Nat. Mater., 2016, 15, 1107–1112 CrossRef CAS PubMed.
- E. Berardo and M. A. Zwijnenburg, J. Phys. Chem. C, 2015, 119, 13384–13393 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Full details on computational methodology, analysis of reactive trajectory for (TiO2)4(OH)4(H2O)4 and of non-adiabatic transitions. See DOI: 10.1039/c6sc04378j |
| This journal is © The Royal Society of Chemistry 2017 |