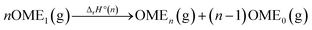Highly correlated ab initio thermodynamics of oxymethylene dimethyl ethers (OME): formation and extension to the liquid phase†
Received
27th January 2017
, Accepted 14th April 2017
First published on 20th April 2017
Abstract
Oxymethylene dimethyl ethers, of the structure CH3(OCH2)nOCH3, denoted as OMEn are receiving increasing interest (where n = 2–5) in a range of important applications including as sustainable fuels and solvents (e.g. as derived from green methanol). However, limited thermodynamic information from computational studies exists in the literature regarding their formation in the gas and liquid phases. In this context, this report describes the principal thermodynamic functions of gaseous and liquid phase OME formation derived from B3LYP-D3(BJ)/def2-TZVPP optimised structures and a series of CCSD(T) and MP2 calculations. The generated total energies are almost of CCSD(T)/A′VQZ quality, the “gold standard” of computational chemistry. Thermal corrections to enthalpy and entropy were included on the basis of analytical BP86-D3(BJ)/def-TZVP frequencies and empirical corrections for low anharmonic C–O–C–O torsional vibrations/hindered rotations and due to the neglect of other conformers/enantiomers. This yielded corrected values for the standard entropy S° of gaseous OMEn (n = 2–7). With the well-established experimental formation enthalpies of dimethyl ether (i.e. OME0) and OME1, the formation enthalpies of OME2–7 were obtained from those and the isodesmic reaction enthalpy of nOME1 → OMEn + (n − 1)OME0. Overall, an error bar on those gas phase values of <1 kJ mol−1 is assigned. From the known and extra- or interpolated phase change thermodynamics, the standard formation enthalpy H°, and the standard entropy S°, as well as the heat capacity cp were established for the liquid mixture of OME2–7. The internal consistency of these data was assessed based on the plots of H°/S° vs. n, presenting linear regressions and correlation coefficients very close to unity. Data quality was also evaluated against published combustion energies, suggesting our values are currently the most reliable, internally consistent dataset that should be used in future investigations for the design of sustainable ether-based fuels and chemicals.
Introduction
Oxymethylene dimethyl ethers (OMEn) of the chemical structure CH3(–OCH2–)nO–CH3 are an attractive class of non-toxic oligomeric compounds that are receiving increasing interest as potential sustainable platform chemicals with a multitude of possible applications. Amongst others, the following uses of OMEn have been discussed: as a solvent (e.g. as a substitute for carcinogenic THF), in the absorption of CO2 or synthesis of fine chemicals (OME1 is already industrially applied1,2), as potential combustion additives for natural gas or methanol engines (OME2), and – most importantly – directly as soot-free diesel fuel (OME3–5).3 For a review on soot-free diesel fuel see ref. 4. However, currently the established syntheses of larger OMEn with n = 2–5 are based on the reaction of 1,3,5-trioxane and OME1 or aqueous formaldehyde and methanol.5,6 These syntheses neither are from an economical, nor from a sustainability point of view converged. The main reason for this is that typical synthesis routes are performed in the aqueous phase that leads to equilibria from which only <50% are the desired OMEn. As a consequence, a number of mechanistic and kinetic investigations regarding these equilibrium mixtures have been published.7 In this context, we have recently reported a combined multicomponent thermodynamic vapour–liquid equilibrium model for OMEn synthesis, based on methanol (CH3OH) as the educt and source of formaldehyde (H2CO; denoted henceforth as FA).8 Some recent considerable progress was reported on a website.‡ Yet, reliable experimental, thermodynamic data on OMEn are scarcely available.9 With the advent of increasing computer power and thus affordable ab initio compound schemes to get near to the basis set and correlation limit, systematic investigations on computational grounds are now accessible. Interestingly, the computational investigation of OMEn was hitherto restricted to a few simple DFT calculations with small basis sets.10 In this regard, the following report describes a series of compound calculations approximating the CCSD(T)/A′VQZ level and associated investigations with the aim to establish the standard formation enthalpy ΔfH°, and the standard entropy S° as well as the heat capacity cp, for gaseous and liquid OME2–7.
Method section
General
All calculations were performed with TURBOMOLE.12 DFT optimisations were carried out at the BP86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13-D3(BJ)/def-TZVP14 level with RI-J auxiliary bases15 and D3
13-D3(BJ)/def-TZVP14 level with RI-J auxiliary bases15 and D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 (BJ)17 dispersion correction and with B3LYP-D3(BJ)/def2-TZVPP18 and corresponding RI-J19 auxiliary bases. Vibrational frequencies were calculated analytically at the BP86-D3(BJ)/def-TZVP level with the AOFORCE20 module and all structures represented true minima without imaginary frequencies on the respective hypersurface. Thermal contributions to ab initio reaction energies (see below) were calculated with inclusion of zero point energy, thermal contributions to the enthalpy/entropy (FREEH tool; unscaled§ BP86-D3(BJ)/def-TZVP vibrational frequencies).
16 (BJ)17 dispersion correction and with B3LYP-D3(BJ)/def2-TZVPP18 and corresponding RI-J19 auxiliary bases. Vibrational frequencies were calculated analytically at the BP86-D3(BJ)/def-TZVP level with the AOFORCE20 module and all structures represented true minima without imaginary frequencies on the respective hypersurface. Thermal contributions to ab initio reaction energies (see below) were calculated with inclusion of zero point energy, thermal contributions to the enthalpy/entropy (FREEH tool; unscaled§ BP86-D3(BJ)/def-TZVP vibrational frequencies).
Ab initio calculations
MP2/A′VXZ and CCSD(T)/A′VXZ single point calculations with correlation-consistent basis sets were done with A′VXZ = cc-pVXZ for H,21 aug-cc-pVXZ for 2nd row elements,22 (X = D, Q) and corresponding RI-C auxiliary bases. The structures used for the single point calculations had B3LYP-D3(BJ)/def2-TZVPP quality.
Results and discussion
The minimum structures of the most relevant OMEn in this publication are displayed (Fig. 1).
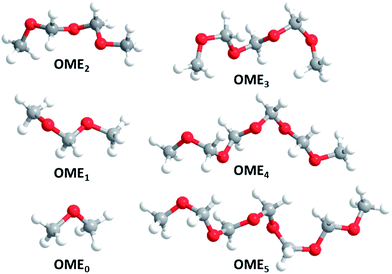 |
| | Fig. 1 Minimum structures of OME0–5 (atom colour coding: red: O, gray: C, white: H). | |
All OMEn with n > 0 form spiral minimum structures with C2 symmetry. In these structures, the so-called anomeric effect, for which OME1 is a popular textbook example,23 is maximized. In general, the anomeric effect stabilizes synclinal (gauche) conformations about the bond C–Y in the system X–C–Y–C where X and Y are heteroatoms having non-bonding electron pairs, commonly at least one of which is nitrogen, oxygen or fluorine.11 Common explanations for this effect involve hyperconjugation of the non-bonding electron pair at X (Y) to the σ* orbital of the adjacent C–Y (X) bond as well as C–X, C–Y dipole minimizations by cancellation of the overall dipole moment. Thus, in OME1, this anomeric effect stabilises the (for steric reasons) unexpected, synclinal conformation by ca. 12 to 20 kJ mol−1. Our exemplary orienting calculations on OME1 and OME2 conformers confirmed this (please refer to the ESI† and specifically Section 5 for details).
To understand the formation and thermodynamic relations of OMEn (n = 0–7) molecules in the gas and homogenous liquid phase, optimisation was performed at various levels of theory and subjected to a CCSD(T)-MP2 compound method, generating energies of almost CCSD(T)/A′VQZ quality. Typically the errors associated with this method were found to be <1 kJ mol−1 for a set of (non-isodesmic) hydrogen bond dissociation energies.24 As for the formation thermodynamics of higher OMEn (n > 1) we use isodesmic dismutation reactions of OME1 into OME0 and the respective OMEn (see eqn (5) and (6) below). We are confident that in these reactions, the error is of the same magnitude or even lower. As a check, the dismutation of OME1 to OME2 and OME0 was calculated with the highly accurate Weizmann-1 (W1) method, which was by about three orders of magnitude more expensive than our compound method. Agreement within 0.15 kJ mol−1 was achieved (see ESI Section 3, S-Table 5† and discussion below for details). Contributions to the enthalpy and entropy at standard conditions (1 bar, 298.15 K) were derived by DFT calculations and further augmented with empiric relations, yielding converged enthalpies of formation ΔfH°(OMEn(g)), standard entropies S°(OMEn(g)) and DFT calculated heat capacity cp(OMEn(g)) values. The calculations were extended to derive associated empirically augmented values also for the liquid phase. Finally, results of the investigation were compared with available experimental data.
Establishing the formation thermodynamics of gaseous OMEn – quantum chemical calculations
Compound method energies of approximately CCSD(T)/A′VQZ quality were performed according to eqn (1):| | | ECCSD(T)/A′VQZ ≈ Ecomp = ECCSD(T)/A′VDZ + EMP2/A′VQZ − EMP2/A′VDZ | (1) |
All individual values contributing to the total energies used to assess Ecomp are compiled in Table S1 in the ESI.†
Corrections to entropy
Due predominantly to low anharmonic C–O–C–O torsional vibrations/hindered rotations and due to the neglect of other conformers, the calculated entropies of OMEn (n = 0–7) are systematically underestimated. To account for this, entropies calculated from BP86-D3(BJ)/def-TZVP harmonic vibrational frequencies were corrected as follows:
• For the C2-chiral OMEn (i.e. where n ≥ 1), R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 was added to account for the enantiomer.
2 was added to account for the enantiomer.
• Further, from experimental gas phase entropies of OME0 (266.4 J mol−1 K−1)25 and OME1 (335.7 J mol−1 K−1)26 and from the calculated entropies (265.0 and 331.8 J mol−1 K−1, including the R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 symmetry correction for OME1), a correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn was added.
2 symmetry correction for OME1), a correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn was added.
The resulting directly calculated as well as corrected entropies are displayed (Table 1).
Table 1 Entropies directly calculated from BP86-D3(BJ)/def-TZVP harmonic vibrational frequencies (S°(freeh)) and their values corrected for enantiomers (+R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) as well as with inclusion of the empirical correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn
2) as well as with inclusion of the empirical correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn
|
n
|
S°(freeh) [J mol−1 K−1] |
S°(corrected) [J mol−1 K−1] |
| FA |
219.1 |
— |
| 0 |
265.0 |
266.4 |
| 1 |
326.1 |
335.7 |
| 2 |
382.3 |
394.5 |
| 3 |
439.2 |
453.8 |
| 4 |
495.6 |
512.7 |
| 5 |
552.2 |
571.8 |
| 6 |
607.2 |
629.3 |
| 7 |
662.9 |
687.4 |
Thermal contributions to reaction energies were calculated with inclusion of BP86-D3(BJ)/def-TZVP calculations at 1 bar, 298.15 K according to eqn (2):
(where
Evrt = sum of translational, rotational, and vibrational energy incl. zero point vibrational energy @BP86-D3(BJ)/def-TZVP).
U° was then corrected to the standard enthalpy H° and Gibbs energy G° by adding RT (eqn (3); cf. RT = 2.48 kJ mol−1 @ 298.15 K) as well as subtracting thereof T·S°, eqn (4), generating H° and corrected G° values (Table 2).
| | | G° = H° − T·S° (T = 298.15 K) | (4) |
Table 2 Assessed standard enthalpy H° and corrected Gibbs energy G° values of all investigated compounds (FA and OMEn, where n = 0–7) in the gas phase at 298.15 K and 1 bar
|
n
|
H°(298.15 K) [kJ mol−1] |
G°(298.15 K) [kJ mol−1] |
| FA |
−300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.4 212.4 |
−300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.7 277.7 |
| 0 |
−406![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304.1 304.1 |
−406![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383.5 383.5 |
| 1 |
−706![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575.4 575.4 |
−706![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675.5 675.5 |
| 2 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844.6 844.6 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962.2 962.2 |
| 3 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 114.2 114.2 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.5 249.5 |
| 4 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607 607![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383.7 383.7 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607 607![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536.6 536.6 |
| 5 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653.3 653.3 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823.7 823.7 |
| 6 |
−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 207 207![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.9 922.9 |
−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110.5 110.5 |
| 7 |
−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.4 192.4 |
−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508 508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397.4 397.4 |
Enthalpies of OMEn formation in the gas phase
With the collected data (Table 2), the standard enthalpies of formation ΔfH°(OMEn) of the gaseous phase OMEn were assessed. Using the general reaction in eqn (5), and the literature data ΔfH°(OME0(g)) = −184.1 kJ mol−1,25 and ΔfH°(OME1(g)) = −348.2 kJ mol−1,27 ΔfH°(OMEn) for n ≥ 1 was calculated viaeqn (6) (Table 3):| | 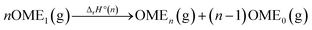 | (5) |
| | | ΔfH°(OMEn) = ΔrH°(n) − (n − 1)ΔfH°(OME0) + nΔfH°(OME1) | (6) |
Table 3 Calculated ΔrH°(n) of eqn (5) and resulting enthalpies of formation ΔfH°(OMEn(g)) in the gas phase (at 298.15 K and 1 bar)
|
n
|
ΔrH°(n) [kJ mol−1] |
ΔfH°(OMEn(g)) [kJ mol−1] |
| 0 |
— |
−184.1 |
| 1 |
0.0 |
−348.2 |
| 2 |
2.1 |
−510.2 |
| 3 |
3.7 |
−672.7 |
| 4 |
5.5 |
−835.0 |
| 5 |
7.2 |
−997.4 |
| 6 |
8.9 |
−1159.8 |
| 7 |
10.6 |
−1322.2 |
Reaction (5) was chosen because it is isodesmic, e.g. the number and types of bonds are the same on both sides of the reaction. Moreover, even the number and types of internal coordinates, like e.g. C–O–C–O torsion angles, are the same on both sides of the reaction resulting in an almost complete error cancellation in quantum chemical calculations. Exemplary calculations with different sized basis sets for OME5 including DFT, HF, MP2, CCSD(T), and CCSD(T)-MP2 composite methods are all within a range of ±2 kJ mol−1 around a reference value that was obtained from a combination of MP2, extrapolated to the complete basis set limit (CBS) with a (CCSD(T) – MP2)/A′VDZ correction (Section 2; S-Table 2 in the ESI†). Comparison of our composite method with more sophisticated – by about three orders of magnitude more expensive – W1 calculations for the OME1 dismutation to OME0 and OME2 gives an agreement within 0.15 kJ mol−1 (S-Table 5, ESI†).
A summary of the final gas phase thermodynamics, including the corrected standard entropies S° and cp directly calculated by DFT that shall be used for further considerations, is collected in Table 4. For completion, the experimental value ΔfH° for FA is included.28
Table 4 Final gas phase thermodynamics, including ΔfH°(OMEn(g)), corrected standard entropies S°(OMEn(g)) and cp(OMEn(g)) directly calculated by DFT
|
n
|
ΔfH°(OMEn(g)) [kJ mol−1] |
S°(OMEn(g)) [J mol−1 K−1] |
c
p(OMEn(g)) [J mol−1 K−1] |
|
Experimental value ΔfH° for formaldehyde (FA).28
|
| FA |
−108.6a |
219.1 |
35.4 |
| 0 |
−184.1 |
266.4 |
63.9 |
| 1 |
−348.2 |
335.7 |
98.1 |
| 2 |
−510.2 |
394.5 |
132.0 |
| 3 |
−672.7 |
453.8 |
166.0 |
| 4 |
−835.0 |
512.7 |
199.9 |
| 5 |
−997.4 |
571.8 |
233.8 |
| 6 |
−1159.8 |
629.3 |
267.8 |
| 7 |
−1322.2 |
687.4 |
301.7 |
Extension of the thermodynamic analysis to OME formation in the liquid phase
In the following, the gas phase thermodynamics were extended to the liquid phase based on the following data, and empirical correction schemes. S°(OME0(l)) of 188.2 J mol−1 K−1 was taken from ref. 29. cp(OME0(l)) was extrapolated from liquid entropies at 220–240 K (ref. 29) via a 2nd order polynomial fitted to these values (eqn (7)):| | | cp(T) = (164.59603 − 0.66123(T/K) + 0.001674(T/K)2) J mol−1 K−1 | (7) |
ΔvapH°(OME0) of 19.2 kJ mol−1 was taken from ref. 25. ΔvapH°(OME1) of 29.6 kJ mol−1, ΔvapS°(OME1) of 93.9 J mol−1 K−1, Δvapcp(OME1) of −31.8 J mol−1 K−1 and ΔvapG°(OME1) of 1.6 kJ mol−1 were calculated from the Antoine parameters.30 For OMEn, where n = 2–5, phase change thermodynamics were calculated from vapour pressure equation parameters.31
ΔvapH°(OMEn) values given in parentheses in Table 5 were calculated from the original data in Table 41 (p. 102) in ref. 32 and compare favourably with our assessment. Table 5 also contains vaporisation thermodynamics that were calculated with COSMO-RS.33–36 Regarding the fact that thousands of possible conformers may exist for the higher OMEn, only the energetically lowest C2 spiral conformer was calculated, which may at least partly explain the increasing deviation of calculated vaporisation energetics with increasing n. Yet, a full conformer treatment for OME1 essentially gave the same vaporisation thermodynamics (difference ca. 0.1 kJ mol−1, see ESI† Section 4 for details). From the phase change thermodynamics (Table 5), the liquid phase thermodynamic data of OMEn (n = 0–5) at standard conditions were calculated and are collected (Table 6).
Table 5 The phase change thermodynamics of OMEn (n = 0–5) at standard conditions
|
n
|
p
vap [bar] |
ΔvapH°(OMEn) [kJ mol−1] |
ΔvapG°(OMEn) [kJ mol−1] |
ΔvapS°(OMEn) [J mol−1 K−1] |
Δvapcp(OMEn) [J mol−1 K−1] |
|
For comparison: values in parentheses represent those calculated from data in Table 41 (p. 102) in ref. 32.
For comparison: values in brackets were calculated with COSMO-RS.33–36 Only the lowest-energy conformer was taken into account.
|
| 0 |
5.9 |
19.2 [20.3]b |
−4.1 [−4.7]b |
78.2 |
−51.9 |
| 1 |
0.53 |
29.6 (29.5)a [29.1]b |
1.6 [−1.3]b |
93.9 |
−31.8 |
| 2 |
0.043 |
39.6 (39.4)a [37.0]b |
7.8 [6.7]b |
106.6 |
−68.6 |
| 3 |
4.0 × 10−3 |
48.5 (47.9)a [44.8]b |
13.7 [11.9]b |
116.7 |
−61.6 |
| 4 |
3.5 × 10−4 |
59.1 (58.0)a [52.6]b |
19.7 [17.1]b |
132.1 |
−81.1 |
| 5 |
3.4 × 10−5 |
68.4 (66.7)a [60.6]b |
25.5 [22.2]b |
143.6 |
−86.5 |
Table 6 Liquid phase thermodynamic data of OMEn (n = 0–5) at standard conditions. The data in parentheses for n = 6, 7 were extrapolated according to the formulae included in Fig. 2
|
n
|
ΔfH°(OMEn(l)) [kJ mol−1] |
ΔfH°(OMEn(l))b [kJ mol−1] |
S°(OMEn(l)) [J mol−1 K−1] |
S°(OMEn(l))b [J mol−1 K−1] |
c
p(OMEn(l))a [J mol−1 K−1] |
|
Note: the heat capacities cp included may be less reliable due to error accumulation (extrapolation/2nd derivative of vapour pressure equation).
Estimated by empirical group contribution methods37 in ref. 6. Less reliable, therefore in parentheses.
|
| 0 |
−203.3 |
— |
188.2 |
— |
115.8 |
| 1 |
−377.8 |
(−380)b |
241.8 |
(244)b |
130.0 |
| 2 |
−549.8 |
(−553)b |
287.9 |
(295)b |
200.6 |
| 3 |
−721.2 |
(−727)b |
337.1 |
(345)b |
227.6 |
| 4 |
−894.1 |
(−901)b |
380.5 |
(396)b |
281.0 |
| 5 |
−1065.7 |
(−1075)b |
428.2 |
(447)b |
320.3 |
| 6 |
(−1238.5) |
(−1248)b |
(477.1) |
(497)b |
— |
| 7 |
(−1410.9) |
— |
(524.7) |
— |
— |
The independently calculated values in Table 6 are in acceptable agreement with those simply estimated through group contribution methods37 in ref. 6 and confirm the trend.
Extrapolation to OME6 and OME7
The good internal consistency of the data is demonstrated by the plots of ΔfH°(OMEn(l)) and S°(OMEn(l)) vs. n (Fig. 2). With correlation coefficients R2 of 1.000 and 0.9992 it appears reasonable to extrapolate also the data for OME6 and OME7 according to the formulae included with the linear regression plot (i.e. as indicated in parentheses in Table 6).
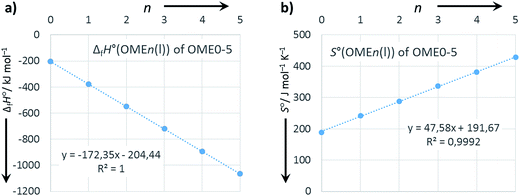 |
| | Fig. 2 Plots of (a) ΔfH°(OMEn(l)) and (b) S°(OMEn(l)) vs. n. Linear regression as dotted lines and regression analysis with formula and R2 included. | |
Comparison to experimental data – establishing data quality
The quality of the combined data was checked against available formation enthalpies calculated from combustion heats,9 and the “FVV Kraftstoffstudie”.38 These data and our combined formation enthalpies of liquid OME3–5 are displayed below (Table 7). The agreement between experimental and combined values based on quantum chemistry with empirical corrections is excellent. It is noted that the internal consistence of the dataset generated in the presented investigation appears to be better than those of the two experimental studies, suggesting that the presented values (emboldened, Table 7) should serve as benchmark values to be used for further investigations.
Table 7 Formation enthalpies from heats of combustion from ref. 9 and “FVV Kraftstoffstudie”38
|
n
|
Combustion heat [kJ mol−1] |
Combustion heat [kJ mol−1] |
ΔfH°(OMEn(l)) [kJ mol−1] |
ΔfH°(OMEn(l)) [kJ mol−1] |
ΔfH°(OMEn(l)) [kJ mol−1] |
|
Formation enthalpies from heats of combustion taken from “FVV Kraftstoffstudie”;38 data originally given in MJ kg−1 (n = 3: 21.71; n = 4: 20.83; n = 5: 20.22).
|
| Ref. |
9
|
38
|
9
|
38
|
This work, Table 6 |
| 3 |
2940.0 |
2955.8 |
−742.3 |
−726.5 |
−721.2
|
| 4 |
3467.1 |
3461.4 |
−894.5 |
−900.2 |
−894.1
|
| 5 |
3975.2 |
3967.1 |
−1065.7 |
−1073.8 |
−1065.7
|
Application for the evaluation of a sustainable route to OMEn
The calculated standard thermodynamic data were used to assess the standard enthalpies of the reaction network necessary for the sustainable production of OMEn from green CO2 and H2. The likely reaction sequences are shown in Fig. 3. Note that the enthalpy values in the grey boxes stem from standard databases,¶ while those with a white background were calculated from the data derived herein (Tables 4 and 6). Part of this data has already been used in the development of the vapour–liquid equilibrium model for OMEn synthesis.8 In this article we have also shown that the thermodynamic baseline for the sustainable production of OME4 from CO2 and H2 over FA and MeOH giving OME1 requires 22% less H2 than in the route via trioxane and OME1, again starting from CO2 and H2 but using the FORMOX process. The current manuscript would suggest that a direct route from CO2 and H2 to DME on the one hand and a dehydrogenation route of methanol to give FA on the other hand could be combined to a water-free process giving access to OME1–5 from DME and FA. Independent experimental work towards these goals is under way in our labs.
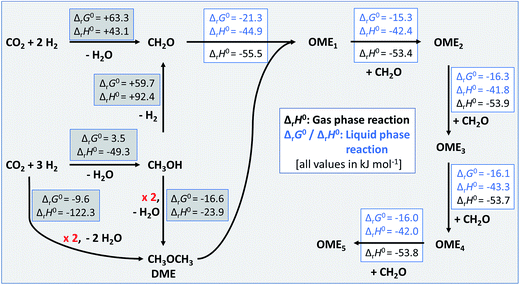 |
| | Fig. 3 Energetics of the reaction network to synthesise sustainable OMEn based on CO2 and H2. Values collected in grey boxes represent available thermodynamic data from standard databases.¶ Those given in boxes with white background were calculated from the data derived herein (Tables 4 and 6). | |
Conclusion
In a systematic investigation we provide converged principal thermodynamic data for the gaseous or liquid OMEn with n = 2–7. The derived datasets (Tables 4 and 6) are internally consistent, bear a minimal error of typically below 1 kJ mol−1 for the gas phase and a somewhat by a factor of 2 or 3 larger error for the condensed phase. They were very positively evaluated against available experimental data, and agree with simple group additivity estimations. Thus, it appears reasonable to suggest the use of this dataset for further investigations regarding this emerging class of OMEn oligomers. One interesting route towards a sustainable synthesis of those liquids appears to be the combination of DME and n FA to give OMEn as described in Fig. 3. Preliminary work towards this goal and performed in our laboratories looks very promising.
Acknowledgements
This work was supported by the Albert-Ludwigs-Universität Freiburg and by the Leistungszentrum Nachhaltigkeit (Sustainability Centre) in the HyCO2 project. RJW is grateful to the Fraunhofer Society and Fraunhofer ISE for providing financial support via the Attract programme.
References
- J. Liu, C. Han, X. Yang, G. Gao, Q. Shi, M. Tong, X. Liang and C. Li, J. Catal., 2016, 333, 162–170 CrossRef CAS.
-
(a) L. Huanjun, G. Tengfei, S. Da, L. Jian and J. Shengfu, Progress in Chemistry, 2016, 28, 942–953 Search PubMed;
(b) K.-a. Thavornprasert, M. Capron, L. Jalowiecki-Duhamel and F. Dumeignil, Catal. Sci. Technol., 2016, 6, 958–970 RSC;
(c) K.-a. Thavornprasert, M. Capron, L. Jalowiecki-Duhamel, O. Gardoll, M. Trentesaux, A.-S. Mamede, G. Fang, J. Faye, N. Touati, H. Vezin, J.-L. Dubois, J.-L. Couturier and F. Dumeignil, Appl. Catal., B, 2014, 145, 126–135 CrossRef CAS;
(d) Z. Fan, H. Guo, K. Fang and Y. Sun, RSC Adv., 2015, 5, 24795–24802 RSC;
(e) S. Chen, Y. Meng, Y. Zhao, X. Ma and J. Gong, AIChE J., 2013, 59, 2587–2593 CrossRef CAS;
(f) J. Gornay, X. Secordel, M. Capron, G. Tesquet, P. Fongarland, E. Payen, J. L. Dubois and F. Dumeignil, Oil & Gas Science and Technology – Revue d'IFP Energies nouvelles, 2010, 65, 751–762 CAS;
(g) N. T. Prado, F. G. E. Nogueria, A. E. Nogueira, C. A. Nunes, R. Diniz and L. C. A. Oliveira, Energy Fuels, 2010, 24, 4793–4796 CrossRef CAS;
(h) F. Yuchuan, S. Qing and S. Jianyi, Chin. J. Catal., 2009, 30, 791–800 Search PubMed;
(i) H. Guo, D. Li, H. Xiao, J. Zhang, W. Li and Y. Sun, Korean J. Chem. Eng., 2009, 26, 902–906 CrossRef CAS;
(j) J. Liu, Q. Sun, Y. Fu, H. Zhao, A. Auroux and J. Shen, Catal. Lett., 2008, 126, 155–163 CrossRef CAS;
(k) Q. Sun, J. Liu, J. Cai, Y. Fu and J. Shen, Catal. Commun., 2009, 11, 47–50 CrossRef CAS;
(l) Q. Zhang, Y. Tan, C. Yang and Y. Han, J. Mol. Catal. A: Chem., 2007, 263, 149–155 CrossRef CAS;
(m) Y. Wang, C. J. Liu and Y. P. Zhang, Plasma Sci. Technol., 2005, 7, 2839–2841 CrossRef CAS;
(n) H. C. Liu and E. Iglesia, J. Phys. Chem. B, 2003, 107, 10840–10847 CrossRef CAS;
(o) N. V. Vlasenko and Y. N. Kochkin, Russ. J. Appl. Chem., 2003, 76, 1615–1619 CrossRef CAS;
(p) J. Liu, Y. Fu, Q. Sun and J. Shen, Microporous Mesoporous Mater., 2008, 116, 614–621 CrossRef CAS;
(q) J. Liu, Q. Sun, Y. Fu and J. Shen, J. Colloid Interface Sci., 2009, 335, 216–221 CrossRef CAS PubMed.
-
(a) S. E. Iannuzzi, C. Barro, K. Boulouchos and J. Burger, Fuel, 2016, 167, 49–59 CrossRef CAS;
(b) M. Haertl, P. Seidenspinner, E. Jacob and G. Wachtmeister, Fuel, 2015, 153, 328–335 CrossRef CAS;
(c) J. Burger and H. Hasse, Chem.
Eng. Sci., 2013, 99, 118–126 CAS;
(d) J. Burger, E. Stroefer and H. Hasse, Chem. Eng. Res. Des., 2013, 91, 2648–2662 CrossRef CAS;
(e) Y. Zheng, Q. Tang, T. Wang, Y. Liao and J. Wang, Chem. Eng. Technol., 2013, 36, 1951–1956 CrossRef CAS;
(f) B. Lumpp, D. Rothe, C. Pastötter, R. Lämmermann and E. Jacob, MTZ Worldwide, 2011, 72(3), 34–38 CrossRef;
(g) J. Burger, M. Siegert, E. Stroefer and H. Hasse, Fuel, 2010, 89, 3315–3319 CrossRef CAS.
-
(a) M. Härtl, K. Gaukel, D. Pélerin, G. Wachtmeister and E. Jacob, MTZ Worldwide, 2017, 52–58 CrossRef;
(b) E. Jacob, W. Maus, M. Härtl, K. Gaukel, D. Pélerin and G. Wachtmeister, MTZ Worldwide, 2017, 52–57 CrossRef.
-
(a) Y. Wu, Z. Li and C. Xia, Ind. Eng. Chem. Res., 2016, 55, 1859–1865 CrossRef CAS;
(b) J. Wu, H. Zhu, Z. Wu, Z. Qin, L. Yan, B. Du, W. Fan and J. Wang, Green Chem., 2015, 17, 2353–2357 RSC;
(c) L. Wang, W.-T. Wu, T. Chen, Q. Chen and M.-Y. He, Chem. Eng. Commun., 2014, 201, 709–717 CrossRef CAS;
(d) H. Li, H. Song, L. Chen and C. Xia, Appl. Catal., B, 2015, 165, 466–476 CrossRef CAS;
(e) X. Fang, J. Chen, L. Ye, H. Lin and Y. Yuan, Sci. China: Chem., 2015, 58, 131–138 CrossRef CAS;
(f) J. Burger, M. Siegert, E. Stroefer and H. Hasse, Fuel, 2010, 89, 3315–3319 CrossRef CAS.
- J. Burger, E. Stroefer and H. Hasse, Chem. Eng. Res. Des., 2013, 91, 2648–2662 CrossRef CAS.
-
(a) J. Burger, E. Stroefer and H. Hasse, Ind. Eng. Chem. Res., 2012, 51, 12751–12761 CrossRef CAS;
(b) N. Schmitz, J. Burger and H. Hasse, Ind. Eng. Chem. Res., 2015, 54, 12553–12560 CrossRef CAS;
(c) N. Schmitz, F. Homberg, J. Berje, J. Burger and H. Hasse, Ind. Eng. Chem. Res., 2015, 54, 6409–6417 CrossRef CAS;
(d) Y. Zhao, Z. Xu, H. Chen, Y. Fu and J. Shen, J. Energy Chem., 2013, 22, 833–836 CrossRef CAS;
(e) Y. Zheng, Q. Tang, T. Wang and J. Wang, Chem. Eng. Sci., 2015, 134, 758–766 CrossRef CAS.
- M. Ouda, G. Yarce, R. J. White, M. Hadrich, D. Himmel, A. Schaadt, H. Klein, E. Jacob and I. Krossing, React. Chem. Eng., 2017 10.1039/c6re00145a.
- L. Lautenschütz, D. Oestreich, P. Seidenspinner, U. Arnold, E. Dinjus and J. Sauer, Fuel, 2016, 173, 129–137 CrossRef.
- L. Yanhua, S. Qing, C. Zhaoxu and S. Jianyi, Acta Chim. Sin., 2009, 67, 767–772 Search PubMed.
-
IUPAC
Compendium of Chemical Terminology, IUPAC, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, Research Triagle Park, NC, 2009 Search PubMed.
-
(a) R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS;
(b) O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef CAS.
-
(a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS;
(b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef;
(c) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
-
(a) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS;
(b) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652–660 CrossRef CAS;
(c) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chim. Acta, 1997, 97, 119–124 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
-
(a) P. Deglmann, F. Furche and R. Ahlrichs, Chem. Phys. Lett., 2002, 362, 511–518 CrossRef CAS;
(b) P. Deglmann and F. Furche, J. Chem. Phys., 2002, 117, 9535 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS.
-
E. Juaristi and G. Cuevas, The Anomeric Effect, CRC Press, Boca Raton, 1995 Search PubMed.
- A. D. Boese, J. M. L. Martin and W. Klopper, J. Phys. Chem. A, 2007, 111, 11122–11133 CrossRef CAS PubMed.
-
CRC Handbook of Chemistry and Physics. A Ready-Reference Book of Chemical and Physical Data, ed. D. R. Lide, CRC Taylor & Francis, Boca Raton, Fla., 87th edn, 2006 Search PubMed.
- D. M. McEachern and J. E. Kilpatrick, J. Chem. Phys., 1964, 41, 3127 CrossRef CAS.
- G. Pilcher and R. A. Fletcher, Trans. Faraday Soc., 1969, 65, 2326–2330 RSC.
- R. A. Fletcher and G. Pilcher, Trans. Faraday Soc., 1970, 66, 794–799 RSC.
- R. M. Kennedy, M. Sagenkahn and J. G. Aston, J. Am. Chem. Soc., 1941, 63, 2267–2272 CrossRef CAS.
- M. Albert, I. Hahnenstein, H. Hasse and G. Maurer, J. Chem. Eng. Data, 2001, 46, 897–903 CrossRef CAS.
- R. H. Boyd, J. Polym. Sci., 1961, 50, 133–141 CrossRef CAS.
-
J. Burger, A Novel Process for the Production of Diesel Fuel Additives by Hierarchical Design, Tech. Univ., Laboratory of Engineering Thermodynamics, Kaiserslautern, 2012, vol. 3 Search PubMed.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369–385 CrossRef CAS.
-
F. Eckert and A. Klamt, COSMOTherm, COSMOtherm, C3.0, release 1501, COSMOlogic GmbH & Co KG, 2015, http://www.cosmologic.de Search PubMed.
- E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1993, 22, 805–1159 CrossRef CAS.
-
U. Albrecht, P. Schmidt, W. Weindorf, R. Wurster and W. Zittel, Zukünftige Kraftstoffe für Verbrennungsmotoren und Zukünftige Kraftstoffe für Verbrennungsmotoren und Gasturbinen, Eine Expertise für die Forschungsvereinigung Verbrennungskraftmaschinen E.V. (FVV), 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7se00053g |
| ‡ Prof. Dr Ing. Jakob Burger, OME Technology made in Germany. Accessed 21.03.2017, available at: http://www.ome-technologies.de/fileadmin/omet/OMETechnologiesGmbH_Jan2017.pdf |
| § By chance, scaling factors for BP86–D3(BJ)/def-TZVP frequencies were found to be very close to unity. Therefore, the contributions to entropy/enthalpy were not scaled. |
| ¶ http://webbook.nist.gov/chemistry/. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a
*a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13-D3(BJ)/def-TZVP14 level with RI-J auxiliary bases15 and D3
13-D3(BJ)/def-TZVP14 level with RI-J auxiliary bases15 and D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 (BJ)17 dispersion correction and with B3LYP-D3(BJ)/def2-TZVPP18 and corresponding RI-J19 auxiliary bases. Vibrational frequencies were calculated analytically at the BP86-D3(BJ)/def-TZVP level with the AOFORCE20 module and all structures represented true minima without imaginary frequencies on the respective hypersurface. Thermal contributions to ab initio reaction energies (see below) were calculated with inclusion of zero point energy, thermal contributions to the enthalpy/entropy (FREEH tool; unscaled§ BP86-D3(BJ)/def-TZVP vibrational frequencies).
16 (BJ)17 dispersion correction and with B3LYP-D3(BJ)/def2-TZVPP18 and corresponding RI-J19 auxiliary bases. Vibrational frequencies were calculated analytically at the BP86-D3(BJ)/def-TZVP level with the AOFORCE20 module and all structures represented true minima without imaginary frequencies on the respective hypersurface. Thermal contributions to ab initio reaction energies (see below) were calculated with inclusion of zero point energy, thermal contributions to the enthalpy/entropy (FREEH tool; unscaled§ BP86-D3(BJ)/def-TZVP vibrational frequencies).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 was added to account for the enantiomer.
2 was added to account for the enantiomer.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 symmetry correction for OME1), a correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn was added.
2 symmetry correction for OME1), a correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn was added.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) as well as with inclusion of the empirical correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn
2) as well as with inclusion of the empirical correction term of (1.4 + n2.49 J mol−1 K−1) for OMEn
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.4
212.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.7
277.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304.1
304.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383.5
383.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 575.4
575.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675.5
675.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006
006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 844.6
844.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006
006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962.2
962.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307
307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 114.2
114.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 307
307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.5
249.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607
607![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383.7
383.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 607
607![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536.6
536.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907
907![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653.3
653.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907
907![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823.7
823.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 207
207![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 922.9
922.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208
208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 110.5
110.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508
508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.4
192.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 508
508![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 397.4
397.4