Kinetics of esterification of 10-undecenoic and ricinoleic acids with near-critical and supercritical methanol
Ram C.
Narayan†
,
Neha
Lamba†
 ,
Ariba
Javed
and
Giridhar
Madras
,
Ariba
Javed
and
Giridhar
Madras
 *
*
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560012, India. E-mail: giridhar@chemeng.iisc.ernet.in; Tel: +91 80 22932321
First published on 26th June 2017
Abstract
Methyl esters of castor oil derived carboxylic acids such as 10-undecenoic acid and ricinoleic acid are useful as biofuels, biolubricants and plasticizers. Esterification of these fatty acids was studied for the first time with near-critical and supercritical methanol without adding any external catalysts. Reaction kinetics were studied for esterification in a wide range of temperatures (523–673 K) and molar ratios (from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 40
1 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at a constant pressure of 20 MPa. Conversions of >90% were obtained for both the carboxylic acids within an hour of reaction time. Different kinetic models were developed and used to correlate the conversions at various temperatures and molar ratios.
1) at a constant pressure of 20 MPa. Conversions of >90% were obtained for both the carboxylic acids within an hour of reaction time. Different kinetic models were developed and used to correlate the conversions at various temperatures and molar ratios.
1. Introduction
The human society today is excessively dependent on crude oil, coal and natural gas as a primary feedstock for synthesizing a plethora of chemicals, ranging from fuels, lubricants, solvents, polymers and fertilizers.1 These feedstocks have proven highly successful over the past century in meeting energy and chemical requirements mainly due to better economics as a consequence of centralized availability, high energy density and easy extractability. Despite these advantages, they are not reliable and sustainable due to their non-renewable and source dependent nature. They also negatively impact the environment due to a positive carbon footprint and global warming.2 In order to offset these shortcomings, there is a need for developing synthesis routes from renewable and locally sourced feedstocks: biomass, such as plants and microbes. More importantly, a green manufacturing process that maximizes environmental protection and sustainability should be the cornerstone of these routes.3 Thus, a manufacturing route utilizing minimal or no solvent or catalyst, consisting of a minimum number of steps and generating lower volumes of waste product streams, without compromising on productivity or quality is as crucial as selecting a renewable source for these chemicals.4,5The past two decades have borne witness to extensive research on supercritical fluids as promising environmentally benign reaction and separation media. These fluids possess gas-like diffusivities and viscosity aiding in better mass transfer and liquid like densities resulting in superior solubility and reaction profiles.6,7 The applications in these frontiers range from extraction to material synthesis. Lipid processing is one of the thrust areas for use of these fluids.8 Supercritical fluids have been used in extraction and reactions to produce both high value–low volume (heat labile) products from minor lipid components and low value–high volume (usually heat tolerant) products from major lipid components.9 In the context of reactions involving major lipid components: oils and fats, esterification and transesterification (to yield fatty acid methyl esters (FAMEs)) with supercritical alcohols have been studied extensively to produce biodiesel.
Different precursors are used for these reactions, like vegetable oils,10,11 animal fats,12 algal oils13 and fatty acids.14 India is the largest producer of castor oil in the world.15 However, there is a dearth of scope for developing second and third generation castor oil derivatives that find multiple applications across various industries. Castor oil based FAMEs are endowed with higher viscosities and polarities due to the presence of a unique hydroxyl group in the fatty acid chain. This makes them unsuitable as diesel fuel and more useful as a base oil of a lubricant. More importantly, the additional hydroxyl group broadens the scope of the possible reactions on the molecular structure of castor oil triglycerides.15 Ricinoleic acid and 10-undecenoic acid are castor oil derived fatty acids, obtained by hydrolysis and pyrolysis of castor oil, respectively. The methyl esters of these fatty acids have been used as precursors in synthesizing a library of lubricant base stocks with varying properties and applications.16–22 These procedures involve multiple catalysts, solvents and very long reaction times. From the standpoint of green chemistry/manufacturing, supercritical reactions compete with conventional counterparts, requiring no catalyst, solvents or elaborate downstream separation procedures. However, the requirement of a high molar excess of alcohol, harsh reaction conditions and high capital expenditures limit the wide scale application of supercritical esterification or transesterification.23
This manuscript reports the synthesis of esters of 10-undecenoic acid and ricinoleic acid with supercritical methanol for the first time. Studies on supercritical esterification or transesterification reactions are usually based on high molar ratios (greater than five times the stoichiometric ratio) justified suitably so as to enhance phase miscibility and consequently the reaction rates.24–27 Reports on low molar ratios (less than five times the stoichiometric amounts) exist,28,29 but are sparse in the literature and require further investigation with regard to kinetics and phase behavior aspects of the reaction. It is, however, essential to integrate the decoupled aspects of the economy and environment that occur with the use of lower molar ratios.
The motivation of the conducted experiments, choice of reaction conditions and kinetic investigations is drawn from addressing the aforementioned limitations of supercritical reactions and developing a deeper understanding of esterification under supercritical conditions of methanol in a wide range of process conditions. On a practical note, the report is expected to aid in sustainable utilization of these second generation castor oil derived fatty acids. In this backdrop, the specific objectives of this manuscript are threefold: firstly, the combined effect of temperature (523–673 K), molar ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–40
1–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and reaction time (0–90 min) on the esterification was studied in detail for both the fatty acid systems. Secondly, an effort was made to understand the variation of phase behavior with progress of esterification using suitable mixing rules. Thirdly, a detailed kinetic analysis was undertaken, using three different kinetic models to delineate the experimental kinetic data across different temperatures and molar ratios.
1) and reaction time (0–90 min) on the esterification was studied in detail for both the fatty acid systems. Secondly, an effort was made to understand the variation of phase behavior with progress of esterification using suitable mixing rules. Thirdly, a detailed kinetic analysis was undertaken, using three different kinetic models to delineate the experimental kinetic data across different temperatures and molar ratios.
2. Materials, methods and analysis
2.1. Materials
10-Undecenoic acid (>98% by GC) and ricinoleic acid (>80% GC) were procured from TCI chemicals (Japan). Methanol (>99.5% by GC) and n-heptane (analytical grade) were purchased from Merck (India). Butyl laurate (>99% by GC) was obtained from Sigma Aldrich (USA). Purified gases for gas chromatography (hydrogen, oxygen, nitrogen and helium) were supplied by Chemix Gases (Bangalore, India). All chemicals were used as such without further purification.2.2. Methods
The esterification reactions were carried out using in-house fabricated SS-316 batch reactors of volume 10 mL (length 0.14 m with an outer diameter of 0.0127 m). One of the ends of the reactor was permanently sealed and the other end was closed by a removable male plug that allows for introduction of reactant fatty acid and methanol and collection of products after the reaction. Compression fittings were used in the fabrication that ensured that the reactors can hold pressures up to 400 bar. An isochoric reaction procedure was used, where the reactants in predetermined amounts were introduced into the reactors and then placed in a furnace that is set to the required temperature (with an uncertainty of ±1 K), after tightly sealing the male plug. The isochoric procedure is reported by many authors and was also used in our previous studies.30–32 Under constant volume (or density) conditions, the reactants sealed in the reactor expand with increasing temperature to achieve the desired pressure at the operating temperature. Typically, the system takes 3 min to reach the operating temperature, after the reactors are loaded into the furnace. Thus, the amount of reactants loaded (referred henceforth to as reactor loading) is critical in determining the phase conditions of the reactor.The reactor loading varies with temperature (T), pressure (P) and initial molar ratio of methanol and fatty acid (henceforth referred to as initial molar ratio (M)). The reactor loading was calculated on the basis of estimated densities using PR-EOS (Peng Robinson equation of state), whose input requires critical properties of components apart from specifications of temperature and pressure. The critical parameters of pure methanol are acquired from the NIST database. The critical parameters of the fatty acids cannot be experimentally determined due to decomposition at higher temperatures. Thus, these were estimated using the Constantinou and Gani group contribution technique.33 At higher molar ratios, methanol is in large excess and thus the mixture critical properties are not very different from the critical properties of methanol. This is, however, not true for lower molar ratios, where the fatty acid contributes significantly to the critical properties. Thus, Lorentz–Berthelot (LB) mixing rules34 were used in conjunction with PR-EOS to estimate the critical properties of the mixture and thus the reaction densities and eventually reactor loading. The reaction mixture under initial conditions (only the reactants) was used to evaluate the reactor loading.
The reactors were taken out of the furnace after the desired reaction time and were immediately plunged in ice, thereby transforming the critical conditions present during the reaction into ambient conditions drastically. As there is no external catalyst added, there is no reaction under ambient conditions. Many experiments were conducted to conclude that the concentration of the reactants or products remains unaltered after the process of quenching. The unreacted fatty acids as well as the formed products were concentrated by evaporating excess methanol and water from the reaction mixture. The conversions of the reactions can be determined from the concentration of these products or reactants in these samples. Gas chromatography (GC) was used to determine the concentrations of these methyl esters. The reaction samples were suitably diluted with n-heptane and spiked with n-butyl laurate as the internal standard (IS).
2.3. GC analysis
The samples prepared as mentioned in Section 2.2 were injected into the GC (Varian CP 3800) equipped with a flame ionization detector (FID), maintained at 573 K that is fueled using UHP (Ultra high pure, >99.999%) hydrogen and oxygen gases with UHP nitrogen being used as make up gas. The injected samples were volatilized in the injector port that is maintained at 573 K. These volatilized samples were carried using UHP helium and separated on a column (VF-5ms, with dimensions 30 m × 0.25 mm with 0.25 μm film thickness of 5% phenyl-methylpolysiloxane). A temperature program (373 K@5 min, 10 K min−1, 573 K@5 min) was maintained in the oven that houses the column. The components of the mixture then pass through the flame ionization detector (FID). The concentration of the analyte esters is determined by comparison with chemically synthesized purified esters by using the slope of the calibration curve. The global experimental error in the conversion data corresponds to about ±3% of the conversion based on triplicate experiments.3. Results and discussion
Esterification is a reversible reaction with lower heats of reaction (about 10–20 kJ mol−1).35–37 Thus, the reaction compositions should be suitably altered to tailor specific conversion/yield requirements. In order to maximize ester concentrations, these reactions are conducted at higher than stoichiometric, initial molar ratios. Typically, supercritical esterification or transesterification reactions are studied at higher initial molar ratios (above 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 12
1 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respectively) to facilitate better solvation (due to decreased dielectric constants of the alcohol) of the triglyceride or fatty acid precursors eventually leading to higher reaction rates. A higher molar excess of alcohol is associated with much higher heating costs (to evaporate methanol) to obtain pure esters affecting the economics of the process. On the other side, the lower molar ratios require lesser energy to evaporate methanol. However, the backward reaction (hydrolysis) would be more prominent at lower ratios because of the reversible nature of esterification reaction, leading to the lower equilibrium conversions. Thus, the study of kinetics across different molar ratios and temperatures is important for a prospective choice of reaction conditions favorable towards both higher conversion and lower energy requirements. The system chosen consists of castor oil derived fatty acids (10-undecenoic acid and ricinoleic acid), that are important precursors towards synthesizing a biodegradable lubricant base stock and methanol, the methylating agent. These fatty acids are in the liquid state under ambient conditions and are sparingly soluble in methanol.
1 respectively) to facilitate better solvation (due to decreased dielectric constants of the alcohol) of the triglyceride or fatty acid precursors eventually leading to higher reaction rates. A higher molar excess of alcohol is associated with much higher heating costs (to evaporate methanol) to obtain pure esters affecting the economics of the process. On the other side, the lower molar ratios require lesser energy to evaporate methanol. However, the backward reaction (hydrolysis) would be more prominent at lower ratios because of the reversible nature of esterification reaction, leading to the lower equilibrium conversions. Thus, the study of kinetics across different molar ratios and temperatures is important for a prospective choice of reaction conditions favorable towards both higher conversion and lower energy requirements. The system chosen consists of castor oil derived fatty acids (10-undecenoic acid and ricinoleic acid), that are important precursors towards synthesizing a biodegradable lubricant base stock and methanol, the methylating agent. These fatty acids are in the liquid state under ambient conditions and are sparingly soluble in methanol.
The molar ratio was varied in the range of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 40
1 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, where 1
1, where 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 represents the stoichiometric composition and 40
1 represents the stoichiometric composition and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 represents systems highly diluted in fatty acid. Molar ratios below 1 were not investigated as the conversion of limiting reactant fatty acid is desired. The temperature is varied in the range of 523–673 K. This temperature range is chosen such that the lower temperature limit is above the critical temperature of pure methanol while the higher limit is chosen based on the susceptibility of side reactions to occur (due to the onset of undesired pyrolysis above 673 K). The pressure was maintained at 20 MPa for all the esterification reactions conducted. This pressure was chosen as it is greater than twice the critical pressure of methanol (about 8.1 MPa). At these high pressures, the variation of density with pressure is very small and thus the pressure effect on the conversion is minimal.38,39
1 represents systems highly diluted in fatty acid. Molar ratios below 1 were not investigated as the conversion of limiting reactant fatty acid is desired. The temperature is varied in the range of 523–673 K. This temperature range is chosen such that the lower temperature limit is above the critical temperature of pure methanol while the higher limit is chosen based on the susceptibility of side reactions to occur (due to the onset of undesired pyrolysis above 673 K). The pressure was maintained at 20 MPa for all the esterification reactions conducted. This pressure was chosen as it is greater than twice the critical pressure of methanol (about 8.1 MPa). At these high pressures, the variation of density with pressure is very small and thus the pressure effect on the conversion is minimal.38,39
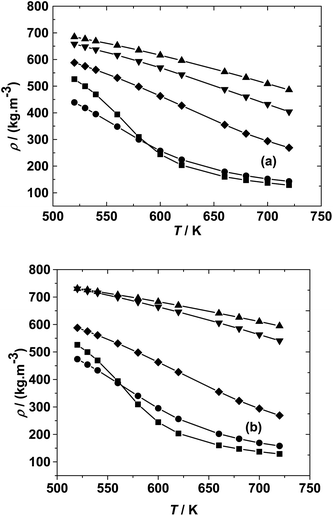
In the isochoric reaction procedure that is followed in this study, the fatty acids and methanol are preloaded into the reactor (based on PR-EOS with LB mixing rule calculations). The global density is defined as the total mass of reactants loaded to the total volume of the reactor. The estimated global densities using these calculations could be different from those of pure methanol reported in the NIST fluid property database. The variation of densities with temperatures and molar ratios is shown in Fig. 1 for both the fatty acid–methanol systems at a constant pressure of 20 MPa. It can be observed that global densities are higher at lower molar ratios and are closer to the NIST data at higher molar ratios.
There is also a profound variation of density with temperature, especially at lower temperatures and higher molar ratios, whereas the variation in density is more gradual at lower molar ratios. This kind of variation can also be observed in triglyceride–methanol systems, albeit at higher molar ratios.40 The variation can be explained on the basis of relative proportions of methanol and the fatty acid. Pure methanol, having a lower critical point as compared to the fatty acid, undergoes a much higher change in density with respect to temperature than fatty acids having much higher critical temperature. The global densities (note the units that are in terms of mass based densities) are higher for the ricinoleic acid–methanol system than those of the 10-undecenoic acid–methanol system at the same temperature and molar ratio. This is due to the higher molecular weight of ricinoleic acid (298 kg kmol−1) as compared to that of 10-undecenoic acid (184 kg kmol−1). Thus, understanding the effect of crucial parameters such as molar ratio and temperature, and the phase behavior of the reaction mixture under these operating conditions is important to design processes like reactive distillation.
3.1. Effect of molar ratio
As discussed earlier, esterification, being a reversible reaction, reaches equilibrium before attaining complete conversion. This is due to the dynamic equilibrium between the amounts of esters formed and hydrolyzed. Thus, the composition of the reaction mixture should be altered. This is realized experimentally by using molar ratios greater than the stoichiometric ratio to enhance esterification over hydrolysis. The application of higher molar ratio leads to higher conversion. However, the amount of methanol to be evaporated after the reaction also increases, increasing the heat load and thus operating costs of the process.Thus, the study of variation of molar ratio is justified to maximize conversions and minimize energy requirements. The molar ratio (alcohol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fatty acid) was varied from the stoichiometric ratio, 1
fatty acid) was varied from the stoichiometric ratio, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at temperatures ranging from 523 K to 673 K for 5 to 90 min for both the reacting systems where methanol was reacted with 10-undecenoic acid and ricinoleic acid, respectively.
1 at temperatures ranging from 523 K to 673 K for 5 to 90 min for both the reacting systems where methanol was reacted with 10-undecenoic acid and ricinoleic acid, respectively.
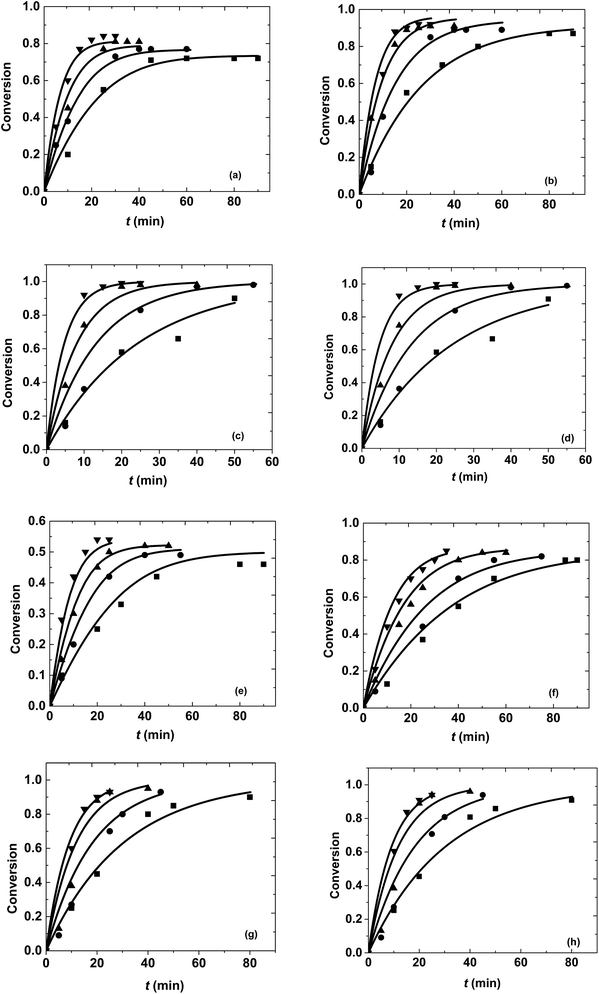
In general, it was observed that ester conversion increased with an increase in molar ratio, time and temperature for both the reactions, as shown in Fig. 2. Under constant reaction conditions, 10-undecenoic acid was more reactive than ricinoleic acid. This can be attributed to the higher molecular weight of ricinoleic acid and the presence of an extra hydroxyl group in the fatty acid chain (in comparison to 10-undecenoic acid). The equilibrium conversions obtained at different molar ratios were 72% to 84% for methanol + 10-undecenoic acid and 46% to 54% for methanol + ricinoleic acid at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 87% to 92% for methanol + 10-undecenoic acid and 80% to 85% for methanol + ricinoleic acid at 2
1, 87% to 92% for methanol + 10-undecenoic acid and 80% to 85% for methanol + ricinoleic acid at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 90% to 99% for methanol + 10-undecenoic acid and 90% to 93% for methanol + ricinoleic acid at 5
1 and 90% to 99% for methanol + 10-undecenoic acid and 90% to 93% for methanol + ricinoleic acid at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The highest equilibrium conversion was obtained at 5
1. The highest equilibrium conversion was obtained at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 followed by 2
1 followed by 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, for both the reactions. The lowest values of equilibrium conversion for 1
1, for both the reactions. The lowest values of equilibrium conversion for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (in the case of stoichiometric amounts) are expected due to the dominance of the backward reaction of hydrolysis. However, the reactions at 2
1 (in the case of stoichiometric amounts) are expected due to the dominance of the backward reaction of hydrolysis. However, the reactions at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios are less prone to hydrolysis because of the excess of methanol. Furthermore, it was observed from Fig. 2(a–c) that the equilibrium conversion was attained at a faster rate for 1
1 molar ratios are less prone to hydrolysis because of the excess of methanol. Furthermore, it was observed from Fig. 2(a–c) that the equilibrium conversion was attained at a faster rate for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in comparison to 2
1 in comparison to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 523 K for methanol + undecenoic acid. However, the equilibrium was attained at similar rates at all the other operating temperatures (573 K, 623 K and 673 K) for all three molar ratios (1
1 at 523 K for methanol + undecenoic acid. However, the equilibrium was attained at similar rates at all the other operating temperatures (573 K, 623 K and 673 K) for all three molar ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for methanol + undecenoic acid.
1) for methanol + undecenoic acid.
In the case of methanol + ricinoleic acid from Fig. 2(e–g), it was found that the equilibrium conversion was always attained at a higher rate for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 than 2
1 than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at all the operating temperatures. This behavior is due to the acid catalytic activity of the carboxylic acids at lower molar ratios. This has also been observed in other studies.32,41,42 Reactions at a molar ratio of 40
1 at all the operating temperatures. This behavior is due to the acid catalytic activity of the carboxylic acids at lower molar ratios. This has also been observed in other studies.32,41,42 Reactions at a molar ratio of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were also performed for both the reactions and the conversions obtained were similar to the conversions obtained at 5
1 were also performed for both the reactions and the conversions obtained were similar to the conversions obtained at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Fig. 2(d) and (h)). The similar experimental conversion profiles at molar ratios 5
1 (Fig. 2(d) and (h)). The similar experimental conversion profiles at molar ratios 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 40
1 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 demonstrate the suitability of pseudo first order kinetics at these molar ratios, making the rate of the reaction and conversion independent of the initial carboxylic acid concentration (thus making it invariant even with molar ratio).
1 demonstrate the suitability of pseudo first order kinetics at these molar ratios, making the rate of the reaction and conversion independent of the initial carboxylic acid concentration (thus making it invariant even with molar ratio).
Thus, the reactions can be performed at lower molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 instead of higher molar ratios such as 40
1 instead of higher molar ratios such as 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and conversions more than 85% and 90% can be obtained for methanol + ricinoleic acid and methanol + 10-undecenoic acid, respectively. Thus the cost of evaporation of excess of methylating agent can be reduced and the process can be made more economical.
1 and conversions more than 85% and 90% can be obtained for methanol + ricinoleic acid and methanol + 10-undecenoic acid, respectively. Thus the cost of evaporation of excess of methylating agent can be reduced and the process can be made more economical.
Properties such as solubility of a solute, dielectric constant and density of the solvent change dramatically around the critical point and thus would alter the product conversions or yields.43,44 Thus, understanding the phase behavior of the reaction mixture around the critical point is important because of these substantial changes in fluid properties around the critical point. The critical properties of the reaction mixture would not only depend on the pure component critical properties but also on the composition of the reaction mixture. The latter is expected to change with the progress of the reaction, which in turn is manipulated by operating temperatures and pressures. The pure component critical properties of the fatty acids used in the present study were obtained using the Constantinou and Gani group contribution technique and the mixture critical properties at different compositions and times were obtained using the LB mixing rules.33,34 The critical properties of the mixture could be obtained from the equation of state. However, the equation of state approach requires the interaction parameters of the reacting species that have to be obtained using the vapor–liquid equilibrium data. These would not be required in the case of LB mixing rules and thus the mixture critical properties could be obtained easily. The LB mixing rules can be applied to a pair of molecules that have different sizes and interaction parameters.45 The critical properties of both the reaction mixtures considered in the present study have been obtained at different temperatures (523 K to 673 K), times (5 to 90 min) and molar ratios (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at a constant pressure of 20 MPa, as represented in Fig. 3.
1) at a constant pressure of 20 MPa, as represented in Fig. 3.
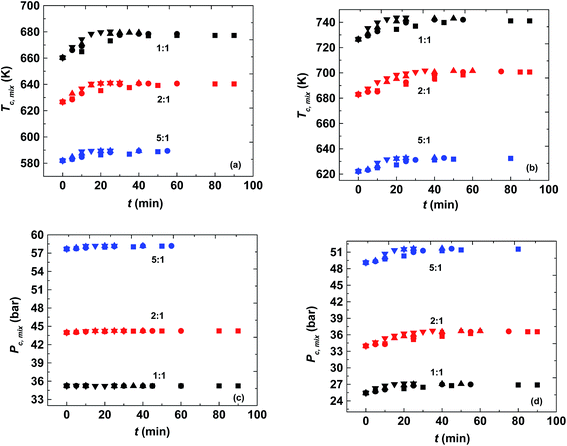
It was found that the critical pressure of the mixture of both the reactions increases with an increase in molar ratio, as shown in Fig. 3(c) and (d). This is because of the difference in the critical pressure of the pure components as can be seen from Table 1. This behavior has also been observed in other reported studies such as, in the case of the transesterification reaction where there is a large difference in the critical properties of pure methanol and the triglycerides, and in the case of esterification of sebacic acid and methanol.40,42,46 However, this observation is contrary to the esterification of sebacic acid with 2-ethyl hexanol where the mixture critical pressure did not change with the molar ratio because of the similar critical pressures of pure sebacic acid and 2-ethylhexanol.47 The critical pressure of the mixture was found to be changing with changing molar ratio for both the reacting systems considered in the present study. However, no appreciable change in mixture critical pressure (only up to 1 bar in the case of methanol + 10-undecenoic acid and 2 to 3 bar in the case of methanol + ricinoleic acid) was observed with the progress of the reaction, as can be seen from Fig. 3(c) and (d). The mixture critical pressures obtained at different operating temperatures and molar ratios were always found to be less than the operating pressure, 200 bar. The mixture critical pressure was found to approach that of the pure component (methanol) at higher molar ratios such as 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 40
1 or 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 because of the excess of methanol at these molar ratios.
1 because of the excess of methanol at these molar ratios.
| Critical properties | Reactants | Products | ||||
|---|---|---|---|---|---|---|
| 10-Undecenoic acida | Ricinoleic acida | Methanolb | Methyl 10-undecenoatea | Methyl ricinoleatea | Waterb | |
| a Calculated using the Constantinou and Gani group contribution technique. b Taken from NIST. | ||||||
| T c (K) | 730.00 | 813.00 | 512.50 | 696.35 | 792.00 | 647.00 |
| P c (atm) | 21.17 | 13.34 | 78.50 | 18.60 | 11.89 | 220.64 |
| V c (L mol−1) | 0.66 | 1.06 | 0.12 | 0.72 | 1.12 | 0.06 |
| Z c | 0.23 | 0.21 | 0.22 | 0.17 | 0.20 | 0.23 |
The critical temperature of the mixture was found to be decreasing with an increase in molar ratio and it approaches the pure methanol critical temperature at higher molar ratios. However, it was found to be increasing with progress of the reaction as shown in Fig. 3(a) and (b). The difference in the mixture critical point at the initial and equilibrium state is most prominent at the lowest molar ratio, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 followed by 2
1 followed by 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It is similar to other reported esterification and transesterification reactions.46,47 The difference was found to be around 17 K (at 1
1. It is similar to other reported esterification and transesterification reactions.46,47 The difference was found to be around 17 K (at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), 14 K (at 2
1), 14 K (at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and 7 K (at 5
1) and 7 K (at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for the reaction with undecenoic acid and around 15 K (at 1
1) for the reaction with undecenoic acid and around 15 K (at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and 9 K to 10 K (at 2
1) and 9 K to 10 K (at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for the reaction with ricinoleic acid, respectively. According to these mixture critical properties obtained using LB mixing rules, the reaction mixtures would be in different phases at different operating temperatures and molar ratios. Thus, both the reaction mixtures at 523 K and 573 K were always in liquid (subcritical region) for all the molar ratios. The reaction mixture of methanol and 10-undecenoic acid was in the liquid or near critical state at all four operating temperatures for 1
1) for the reaction with ricinoleic acid, respectively. According to these mixture critical properties obtained using LB mixing rules, the reaction mixtures would be in different phases at different operating temperatures and molar ratios. Thus, both the reaction mixtures at 523 K and 573 K were always in liquid (subcritical region) for all the molar ratios. The reaction mixture of methanol and 10-undecenoic acid was in the liquid or near critical state at all four operating temperatures for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and, it was found to be in the supercritical state only at 623 K and 673 K for the molar ratio of 5
1 and, it was found to be in the supercritical state only at 623 K and 673 K for the molar ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, the reaction mixture of methanol and ricinoleic acid was in the supercritical phase at only 673 K for 1
1. However, the reaction mixture of methanol and ricinoleic acid was in the supercritical phase at only 673 K for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and, at both 623 and 673 K for 2
1 and, at both 623 and 673 K for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively.
1, respectively.
3.2. Effect of temperature
Reactions were performed at different temperatures ranging from 523 K to 673 K for different reaction times at a constant pressure of 200 bar. The conversions were found to be increasing with increasing temperature and time. Highest conversions were obtained at 673 K after 25 to 30 min of reaction time at all the molar ratios for both the reaction systems as shown in Fig. 2. The equilibrium conversions obtained at different temperatures for a particular molar ratio were found to be similar because of the lower heat of reaction of the esterification reaction.35 However, the attainment of equilibrium required different times at different temperatures and happened quickly at higher temperatures. The kinetics of both the reactions have been explained later in the manuscript. Thermal degradation of fatty acids was observed at different temperatures after a particular interval of time. The reactions shifted to the pyrolytic regime after 30 min at 673 K, 45 min at 623 K, 60 min at 573 K and 90 min at 523 K and would result in undesired products.14,48 Thus, reactions beyond these operating temperatures and times were not performed.3.3. Kinetics of reactions
There are different kinetic models which are used to model the conversion data obtained from the esterification reaction. At higher molar ratios (such as 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the reaction is assumed to be irreversible and the first order kinetic model is used to fit the experimental data as explained below.
1), the reaction is assumed to be irreversible and the first order kinetic model is used to fit the experimental data as explained below.
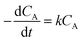 | (1) |
Eqn (1) can be rewritten in terms of conversion as
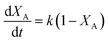 | (2) |
After integration, eqn (2) reduces to
| −ln(1 − XA) = kt | (3) |
However, at lower molar ratios, the reversibility of the reaction cannot be neglected because of the prevalence of hydrolysis at these molar ratios. Thus, different kinetic expressions have been used to account for the reversibility of the reaction.
 , where k′1 and k′2 are the rate coefficients for the forward and backward reactions. Then the rate expression in terms of concentration for the second order reversible reaction can be written as
, where k′1 and k′2 are the rate coefficients for the forward and backward reactions. Then the rate expression in terms of concentration for the second order reversible reaction can be written as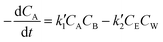 | (4) |
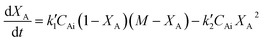 | (5) |
At lower molar ratios, it has been observed in few studies that the rates of the reaction at lower molar ratios are comparatively higher than those at higher molar ratios.32,41,47 The reason for this behavior was found to be the acid catalytic activity of the reactant fatty acid used for the esterification. At lower molar ratios such as stoichiometric ratios or double the stoichiometric ratios, the amount of acid is higher or comparable to the amount of alcohol loaded initially into the reactant. Thus, under the supercritical conditions, the rates would be still faster because of the operating conditions as well as the acid catalytic activity at lower molar ratios. Hence, the expression given below was derived by Saka and Minami41 by modifying the second order reversible kinetic model to account for this acid catalytic behavior.
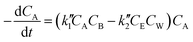 | (6) |
Eqn (6) can be written in terms of conversion as
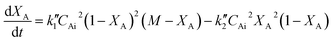 | (7) |
The above mentioned models, eqn (4) and (6), were used to model the conversion data for both the reactions (methanol + 10-undecenoic acid and methanol + ricinoleic acid) performed in the present study. It was found that in the case of lower molar ratios such as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, eqn (4) underestimates the conversions (equilibrium conversions) and eqn (6) overestimates the conversions for higher molar ratios such as 5
1, eqn (4) underestimates the conversions (equilibrium conversions) and eqn (6) overestimates the conversions for higher molar ratios such as 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 40
1 and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as was also observed in the sebacic acid reaction with 2-ethylhexanol.47 To overcome these limitations, a kinetic model was formulated based on a mechanism that includes three elementary reaction steps as propounded below.
1 as was also observed in the sebacic acid reaction with 2-ethylhexanol.47 To overcome these limitations, a kinetic model was formulated based on a mechanism that includes three elementary reaction steps as propounded below.
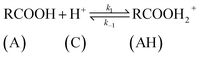 | (8) |
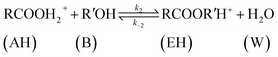 | (9) |
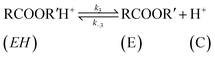 | (10) |
The rate of disappearance of acid (A) can be written as
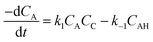 | (11) |
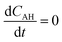 and
and 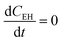 .
.
Thus, eqn (11) becomes
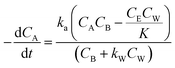 | (12) |
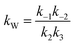 and
and 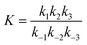 .
.
Eqn (12) can be described in terms of conversion as (eqn (24) of ref. 50 with assumption of Wo = 0)
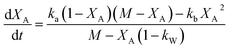 | (13) |
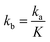 and
and 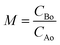 .
.
The analytical solution of eqn (12) obtained after the integration is50
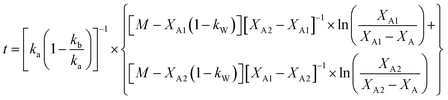 | (14) |
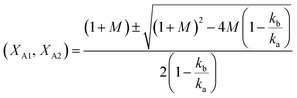
The values of ka, kb, kw and K were obtained from eqn (14) through the non-linear regressions, using the experimental data of time and conversion at different temperatures and molar ratios.
The regression was performed with the following constraints on different parameters: ka, kb, kw > 0 at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; ka, kb > 0 and kw ≪ 1 at 2
1; ka, kb > 0 and kw ≪ 1 at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; ka, kb, kw > 0, kb ≫ ka and kw ≪ 1 at 5
1; ka, kb, kw > 0, kb ≫ ka and kw ≪ 1 at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, for both the reaction systems for the entire range of temperatures considered in this study. It was found from the regression that kw = 0 at 2
1, for both the reaction systems for the entire range of temperatures considered in this study. It was found from the regression that kw = 0 at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and it is non-zero at 1
1 and it is non-zero at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for both the reactions. It was also obtained that kb = 0 at 5
1 for both the reactions. It was also obtained that kb = 0 at 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for different temperatures for both the reactions. All the regression coefficients have been tabulated in Table 2.
1 for different temperatures for both the reactions. All the regression coefficients have been tabulated in Table 2.
| Reaction | Molar ratio | Temperature (K) | k a × 102 (s−1) | k b × 103 (s−1) | k W × 102 | K |
|---|---|---|---|---|---|---|
| Methanol + 10-undecenoic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 3.3 | 4.3 | 5.0 | 7.7 |
| 573 | 5.3 | 4.9 | 7.0 | 10.9 | ||
| 623 | 7.8 | 5.5 | 9.0 | 14.2 | ||
| 673 | 12.0 | 6.4 | 12.0 | 18.8 | ||
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 3.4 | 3.8 | 0.0 | 9.0 | |
| 573 | 6.1 | 4.1 | 0.0 | 14.9 | ||
| 623 | 10.0 | 4.9 | 0.0 | 20.3 | ||
| 673 | 13.8 | 5.9 | 0.0 | 23.4 | ||
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 4.1 | 0.0 | 0.0 | ||
| 573 | 7.5 | 0.0 | 0.0 | |||
| 623 | 12.4 | 0.0 | 0.0 | |||
| 673 | 21.1 | 0.0 | 0.0 | |||
| Methanol + ricinoleic acid | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 1.7 | 16.9 | 5.0 | 1.0 |
| 573 | 2.8 | 25.5 | 10.0 | 1.1 | ||
| 623 | 4.2 | 35.1 | 21.0 | 1.2 | ||
| 673 | 6.3 | 45.0 | 40.0 | 1.4 | ||
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 2.2 | 5.4 | 0.0 | 4.1 | |
| 573 | 3.2 | 7.2 | 0.0 | 4.4 | ||
| 623 | 4.6 | 10.0 | 0.0 | 4.6 | ||
| 673 | 6.7 | 13.9 | 0.0 | 4.9 | ||
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
523 | 3.3 | 0.0 | 0.0 | ||
| 573 | 5.5 | 0.0 | 0.0 | |||
| 623 | 8.5 | 0.0 | 0.0 | |||
| 673 | 11.0 | 0 | 0.0 |
It can be observed from Table 2 that all the rate coefficients and the equilibrium constants for both the reactions increase with the increase in temperature. However, the variation of these coefficients with molar ratio follows a different trend. ka, kw and K were found to be increasing with an increase in molar ratio, whereas kb decreased with increasing molar ratio. Among the two reactions, it was observed that at molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ka and K are higher for the methanol + 10-undecenoic acid reaction and, kb and kw are higher for the methanol + ricinoleic acid reaction. Furthermore, ka and kb are different by an order of magnitude for the methanol + 10-undecenoic acid reaction, and these are similar for the methanol + ricinoleic acid reaction at molar ratios of 1
1, ka and K are higher for the methanol + 10-undecenoic acid reaction and, kb and kw are higher for the methanol + ricinoleic acid reaction. Furthermore, ka and kb are different by an order of magnitude for the methanol + 10-undecenoic acid reaction, and these are similar for the methanol + ricinoleic acid reaction at molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It should also be noted that kw at a molar ratio of 1
1. It should also be noted that kw at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was found to be greater than ka and kb for both the reactions. Thus, a trend of kw > ka > kb was observed at 1
1 was found to be greater than ka and kb for both the reactions. Thus, a trend of kw > ka > kb was observed at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for different operating temperatures. The data were fitted well for both the reactions using eqn (14), as shown in Fig. 2. The new model, eqn (14), reduces to the pseudo-first order irreversible kinetic model (eqn (3)) at a molar ratio of 5
1 for different operating temperatures. The data were fitted well for both the reactions using eqn (14), as shown in Fig. 2. The new model, eqn (14), reduces to the pseudo-first order irreversible kinetic model (eqn (3)) at a molar ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Thus, eqn (3) can be used directly for higher molar ratios of 5
1. Thus, eqn (3) can be used directly for higher molar ratios of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 40
1 or 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
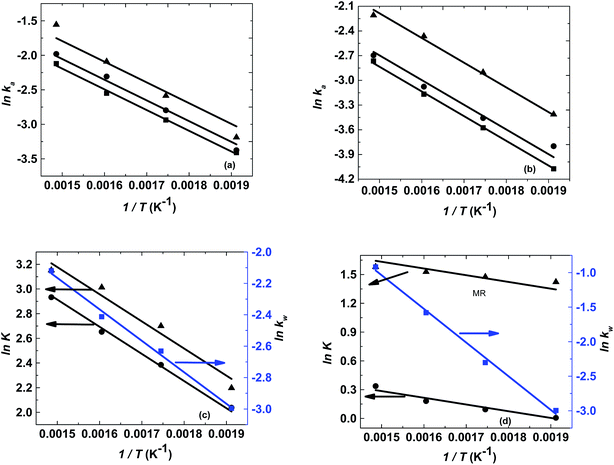
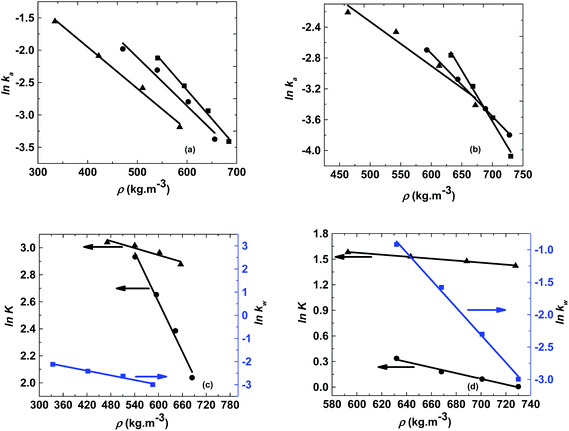
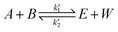
The logarithm of regression coefficients, ka, kw and K, was plotted against the inverse of temperature and the density of the mixture at different molar ratios for both the reactions, as shown in Fig. 4 and 5, respectively. These variations of the regression coefficients with the inverse of temperature as well as with the density of the mixture were found to be linear for both the reactions at all the molar ratios. The density of the mixture at different temperatures and molar ratios (required for the semi logarithmic plots of ka, kw and K with mixture density) was obtained using the LB mixing rule and Peng Robinson equation of state as has been discussed earlier in Section 2.2. The variation of rate coefficients with density has also been reported earlier for many esterification, transesterification and polymer degradation reactions.47,51–53 This variation would provide insights into the experimental data and it suggests that indirectly the density of the reaction mixture (along with temperature and molar ratio) would also affect the ester conversions. Furthermore, a detailed discussion on variation of ka, kw and K with the inverse of temperature has been done in the following paragraph.
The activation energy is a thermodynamic property that is obtained from the slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ka with the inverse of temperature and it should not vary with the molar ratio. Thus, ln
ka with the inverse of temperature and it should not vary with the molar ratio. Thus, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ka was plotted against 1/T and the activation energy obtained for both the reactions was 25 kJ mol−1. However, the intercept of this plot (ln
ka was plotted against 1/T and the activation energy obtained for both the reactions was 25 kJ mol−1. However, the intercept of this plot (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ka with 1/T) provides the frequency factor which is a kinetic parameter and would change with molar ratio. Thus, it was found to be varying from 9.9 to 14.9 for methanol + 10-undecenoic acid, and 5.5 to 9.9 for methanol + ricinoleic acid, at varying molar ratios of 1
ka with 1/T) provides the frequency factor which is a kinetic parameter and would change with molar ratio. Thus, it was found to be varying from 9.9 to 14.9 for methanol + 10-undecenoic acid, and 5.5 to 9.9 for methanol + ricinoleic acid, at varying molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. It was observed that the frequency factor increased with increasing molar ratios because of the increasing interactions between the molecules at higher molar ratios. These Arrhenius plots (ln
1. It was observed that the frequency factor increased with increasing molar ratios because of the increasing interactions between the molecules at higher molar ratios. These Arrhenius plots (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ka with 1/T) for methanol + 10-undecenoic acid and methanol + ricinoleic acid have been shown in Fig. 4(a) and (b), respectively.
ka with 1/T) for methanol + 10-undecenoic acid and methanol + ricinoleic acid have been shown in Fig. 4(a) and (b), respectively.
Furthermore, the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kw with 1/T at a molar ratio of 1
kw with 1/T at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was also found to be linear with a slope and an intercept of −2000 and 0.84 for methanol + 10-undecenoic acid, and −4900 and 6.28 for methanol + ricinoleic acid, respectively as shown in Fig. 4(c) and (d).
1 was also found to be linear with a slope and an intercept of −2000 and 0.84 for methanol + 10-undecenoic acid, and −4900 and 6.28 for methanol + ricinoleic acid, respectively as shown in Fig. 4(c) and (d).
The slope of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K with 1/T (called the enthalpy of reaction, ΔHrxn) was also fixed for different molar ratios and a slope of −2200 for undecenoic acid + methanol and −700 for methanol + ricinoleic acid was obtained for different molar ratios. However, different intercepts of ln
K with 1/T (called the enthalpy of reaction, ΔHrxn) was also fixed for different molar ratios and a slope of −2200 for undecenoic acid + methanol and −700 for methanol + ricinoleic acid was obtained for different molar ratios. However, different intercepts of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K vs. 1/T (called the entropy of reaction, ΔSrxn) were obtained at different molar ratios. ΔHrxn and ΔSrxn of 1.8 kJ mol−1 and 52 to 54 kJ mol−1 for methanol + 10-undecenoic acid, and 5.8 kJ mol−1 and 11 to 22 kJ mol−1 for methanol + ricinoleic acid have been obtained at molar ratios of 1
K vs. 1/T (called the entropy of reaction, ΔSrxn) were obtained at different molar ratios. ΔHrxn and ΔSrxn of 1.8 kJ mol−1 and 52 to 54 kJ mol−1 for methanol + 10-undecenoic acid, and 5.8 kJ mol−1 and 11 to 22 kJ mol−1 for methanol + ricinoleic acid have been obtained at molar ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. ΔHrxn of both the reactions was small and the reactions were slightly endothermic that has also been observed in other reports.35,54,55 Thus, no appreciable change was observed in the equilibrium conversion with temperature as could be seen from Fig. 2. Therefore, it is important to note and conclude that the equilibrium conversion was nearly independent of the temperature and thus the molar ratio is a more dominant factor than the temperature.
1, respectively. ΔHrxn of both the reactions was small and the reactions were slightly endothermic that has also been observed in other reports.35,54,55 Thus, no appreciable change was observed in the equilibrium conversion with temperature as could be seen from Fig. 2. Therefore, it is important to note and conclude that the equilibrium conversion was nearly independent of the temperature and thus the molar ratio is a more dominant factor than the temperature.
4. Conclusions
The effect of variation of temperature, time and molar ratio for methanol + 10-undecenoic acid and methanol + ricinoleic acid was investigated. Conversions of greater than 80% were obtained at molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for both the reactions. Thus, lower molar ratios could be used instead of a higher molar ratio of 40
1 for both the reactions. Thus, lower molar ratios could be used instead of a higher molar ratio of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for obtaining higher conversions, and thus the process would save energy cost and it would be more environmentally benign. The critical pressure of the reaction mixture was found to be a function of only the molar ratio but the critical temperature was a function of both the molar ratio and time. The reaction with 10-undecenoic acid was faster and gave higher conversions than those with ricinoleic acid. The experimental data for both the reactions were well fitted by the three step acid catalyzed mechanistic model. The activation energy of both the reactions (methanol + 10-undecenoic acid and methanol + ricinoleic acid) was found to be 25 kJ mol−1. A lower energy of reaction (1.8 kJ mol−1 to 5.8 kJ mol−1) was obtained for both the reactions. Thus, the reactions are slightly endothermic in nature. The equilibrium conversions are nearly independent of temperature and thus the molar ratio is a more crucial parameter to be controlled.
1 for obtaining higher conversions, and thus the process would save energy cost and it would be more environmentally benign. The critical pressure of the reaction mixture was found to be a function of only the molar ratio but the critical temperature was a function of both the molar ratio and time. The reaction with 10-undecenoic acid was faster and gave higher conversions than those with ricinoleic acid. The experimental data for both the reactions were well fitted by the three step acid catalyzed mechanistic model. The activation energy of both the reactions (methanol + 10-undecenoic acid and methanol + ricinoleic acid) was found to be 25 kJ mol−1. A lower energy of reaction (1.8 kJ mol−1 to 5.8 kJ mol−1) was obtained for both the reactions. Thus, the reactions are slightly endothermic in nature. The equilibrium conversions are nearly independent of temperature and thus the molar ratio is a more crucial parameter to be controlled.
Acknowledgements
The authors thank the Council of Scientific and Industrial Research (CSIR), India for financial support. The corresponding author thanks the Department of Science and Technology (DST), India for the J. C Bose fellowship. The authors also thank Ms. Kaveri Gupta for help in some experiments.References
- S. K. Maity, Renewable Sustainable Energy Rev., 2015, 43, 1427–1445 CrossRef CAS.
- M. J. Groom, E. M. Gray and P. A. Townsend, Conservat. Biol., 2008, 22, 602–609 CrossRef PubMed.
- P. Anastas and N. Eghbali, Chem. Soc. Rev., 2010, 39, 301–312 RSC.
- L. Vaccaro, D. Lanari, A. Marrocchi and G. Strappaveccia, Green Chem., 2014, 16, 3680–3704 RSC.
- F. Cherubini, Energy Convers. Manage., 2010, 51, 1412–1421 CrossRef CAS.
- E. J. Beckman, J. Supercrit. Fluids, 2004, 28, 121–191 CrossRef CAS.
- H. S. Roh, J. Y. Park, S. Y. Park and B. S. Chun, Biotechnol. Bioprocess Eng., 2006, 11, 496–502 CrossRef CAS.
- F. Temelli, J. Supercrit. Fluids, 2009, 47, 583–590 CrossRef CAS.
- O. Guclu-Ustundag and F. Temelli, J. Supercrit. Fluids, 2005, 36, 1–15 CrossRef.
- M. N. Varma, P. A. Deshpande and G. Madras, Fuel, 2010, 89, 1641–1646 CrossRef CAS.
- A. Velez, G. Soto, P. Hegel, G. Mabe and S. Pereda, Fuel, 2012, 97, 703–709 CrossRef CAS.
- V. F. Marulanda, G. Anitescu and L. L. Tavlarides, J. Supercrit. Fluids, 2010, 54, 53–60 CrossRef CAS.
- Y. Nan, J. Liu, R. Lin and L. L. Tavlarides, J. Supercrit. Fluids, 2015, 97, 174–182 CrossRef CAS.
- T. Jin, B. Wang, J. Zeng, C. Yang, Y. Wang and T. Fang, RSC Adv., 2015, 5, 52072–52078 RSC.
- H. Mutlu and M. A. R. Meier, Eur. J. Lipid Sci. Technol., 2010, 112, 10–30 CrossRef CAS.
- V. B. Borugadda and V. V. Goud, Energy Procedia, 2014, 54, 75–84 CrossRef CAS.
- J. A. C. da Silva, V. F. Soares, R. Fernandez-Lafuente, A. C. Habert and D. M. G. Freire, J. Mol. Catal. B: Enzym., 2015, 122, 323–329 CrossRef.
- J. A. C. da Silva, A. C. Habert and D. M. G. Freire, Lubr. Sci., 2013, 25, 53–61 CrossRef.
- G. Geethanjali, K. V. Padmaja and R. B. N. Prasad, Ind. Eng. Chem. Res., 2016, 55, 9109–9117 CrossRef CAS.
- C. S. Madankar, S. Pradhan and S. N. Naik, Ind. Crops Prod., 2013, 43, 283–290 CrossRef CAS.
- S. R. Yasa, S. Cheguru, S. Krishnasamy, P. V. Korlipara, A. K. Rajak and V. Penumarthy, Ind. Crops Prod., 2017, 103, 141–151 CrossRef CAS.
- U. Biermann and J. O. Metzger, Eur. J. Lipid Sci. Technol., 2008, 110, 805–811 CrossRef CAS.
- C. Kiwjaroun, C. Tubtimdee and P. Piumsomboon, J. Cleaner Prod., 2009, 17, 143–153 CrossRef CAS.
- S. Saka and D. Kusdiana, Fuel, 2001, 80, 225–231 CrossRef CAS.
- H. Y. Shin, S. H. Lee, J. H. Ryu and S. Y. Bae, J. Supercrit. Fluids, 2012, 61, 134–138 CAS.
- Y. Sun, S. Ponnusamy, T. Muppaneni, H. K. Reddy, P. D. Patil, C. Li, L. Jiang and S. Deng, Fuel, 2014, 135, 522–529 CrossRef CAS.
- Y. Warabi, D. Kusdiana and S. Saka, Bioresour. Technol., 2004, 91, 283–287 CrossRef CAS PubMed.
- W. Sakdasri, R. Sawangkeaw and S. Ngamprasertsith, Asia-Pac. J. Chem. Eng., 2016, 11, 539–548 CrossRef CAS.
- D. Yujaroen, M. Goto, M. Sasaki and A. Shotipruk, Fuel, 2009, 88, 2011–2016 CrossRef CAS.
- T. Pinnarat and P. E. Savage, J. Supercrit. Fluids, 2010, 53, 53–59 CrossRef CAS.
- A. Velez, S. Pereda and E. A. Brignole, J. Supercrit. Fluids, 2010, 55, 643–647 CrossRef CAS.
- R. C. Narayan and G. Madras, Energy Fuels, 2016, 30, 4104–4111 CrossRef CAS.
- L. Constantinou and R. Gani, AIChE J., 1994, 40, 1697–1710 CrossRef CAS.
- K. Bunyakiat, S. Makmee, R. Sawangkeaw and S. Ngamprasertsith, Energy Fuels, 2006, 20, 812–817 CrossRef CAS.
- A. Alegría and J. Cuellar, Appl. Catal., B, 2015, 179, 530–541 CrossRef.
- A. W. Go, P. L. Tran Nguyen, L. H. Huynh, Y.-T. Liu, S. Sutanto and Y.-H. Ju, Energy, 2014, 70, 393–400 CrossRef CAS.
- A. Chowdhury, R. Chakraborty, D. Mitra and D. Biswas, Ind. Crops Prod., 2014, 52, 783–789 CrossRef CAS.
- J.-J. Jiang and C.-S. Tan, J. Taiwan Inst. Chem. Eng., 2012, 43, 102–107 CrossRef CAS.
- K. White, N. Lorenz, T. Potts, W. R. Penney, R. Babcock, A. Hardison, E. A. Canuel and J. A. Hestekin, Fuel, 2011, 90, 3193–3199 CrossRef CAS.
- A. Velez, P. Hegel, G. Mabe and E. A. Brignole, Ind. Eng. Chem. Res., 2010, 49, 7666–7670 CrossRef CAS.
- E. Minami and S. Saka, Fuel, 2006, 85, 2479–2483 CrossRef CAS.
- R. C. Narayan and G. Madras, Ind. Eng. Chem. Res., 2017, 56, 2641–2649 CrossRef CAS.
- J. Sengers and J. L. Sengers, Annu. Rev. Phys. Chem., 1986, 37, 189–222 CrossRef CAS.
- C. A. Eckert, B. L. Knutson and P. G. Debenedetti, Nature, 1996, 383, 313–318 CrossRef CAS.
- C. McCabe, A. Gil-Villegas and G. Jackson, J. Phys. Chem. B, 1998, 102, 4183–4188 CrossRef CAS.
- P. Hegel, G. Mabe, S. Pereda and E. A. Brignole, Ind. Eng. Chem. Res., 2007, 46, 6360–6365 CrossRef CAS.
- R. C. Narayan and G. Madras, React. Chem. Eng., 2017, 2, 27–35 CAS.
- R. Sawangkeaw, S. Teeravitud, K. Bunyakiat and S. Ngamprasertsith, Bioresour. Technol., 2011, 102, 10704–10710 CrossRef CAS PubMed.
- S. Changi, T. Pinnarat and P. E. Savage, Ind. Eng. Chem. Res., 2011, 50, 12471–12478 CrossRef CAS.
- S. Goto, T. Tagawa and A. Yusoff, Int. J. Chem. Kinet., 1991, 23, 17–26 CrossRef CAS.
- G. Madras, C. Kolluru and R. Kumar, Fuel, 2004, 83, 2029–2033 CrossRef CAS.
- A. Marimuthu and G. Madras, Ind. Eng. Chem. Res., 2007, 46, 15–21 CrossRef CAS.
- J. F. Brennecke and J. E. Chateauneuf, Chem. Rev., 1999, 99, 433–452 CrossRef CAS PubMed.
- A. Chowdhury, D. Sarkar and D. Mitra, Chem. Eng. Technol., 2016, 39, 730–740 CrossRef CAS.
- R. Tesser, M. Di Serio, M. Guida, M. Nastasi and E. Santacesaria, Ind. Eng. Chem. Res., 2005, 44, 7978–7982 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |