Controlling nucleation, growth, and orientation of metal halide perovskite thin films with rationally selected additives†
Benjamin J.
Foley
a,
Justin
Girard
a,
Blaire A.
Sorenson
b,
Alexander Z.
Chen
a,
J.
Scott Niezgoda
a,
Matthew R.
Alpert
a,
Angela F.
Harper
c,
Detlef-M.
Smilgies
d,
Paulette
Clancy
b,
Wissam A.
Saidi
e and
Joshua J.
Choi
*a
aDepartment of Chemical Engineering, University of Virginia, Charlottesville, Virginia 22904, USA. E-mail: jjc6z@virginia.edu
bSchool of Chemical and Biomolecular Engineering, Cornell University, Ithaca, New York 14853, USA
cDepartment of Physics, Wake Forest University, Winston-Salem, North Carolina 27109, USA
dCornell High Energy Synchrotron Source, Cornell University, Ithaca, New York 14853, USA
eDepartment of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, Pennsylvania 15261, USA
First published on 18th October 2016
Abstract
Accelerating the progress toward realizing metal halide perovskite solar cells with improved efficiency, stability and reliability requires a deeper understanding of the thin film formation processes. This paper investigates the impact of rationally selected chemical additives in precursor solutions on the nucleation and growth of metal halide perovskite thin films. Computational screening was performed to guide the selection of tetrahydrothiophene oxide as an additive with stronger solvation efficacy than all other commonly used solvents. In situ grazing incidence X-ray diffraction measurements show that the additives suppress the formation of homogeneous nuclei as well as crystalline intermediate structures. Instead, heterogeneous nucleation on the substrate surface and growth of a thin film with a strongly preferential crystallographic orientation occur directly from the precursor solution. Density functional theory calculations show that the crystallographic orientation of the thin films can be tuned by altering the surface energies with the chemical additives. The crystallographic orientation of the thin films is found to have a significant impact on the open circuit voltage of solar cell devices, highlighting the importance of controlling the metal halide perovskite thin film orientation for improved solar cell efficiency.
Introduction
Metal halide perovskites (MHPs) are garnering great interest from the solar cell research community and have the potential to revolutionize the photovoltaics industry. The record power conversion efficiency of MHP based solar cells has reached 22%,1–11 which rivals that of silicon solar cells. MHP solar cells combine this high efficiency with solution processability, inexpensive and earth-abundant compositions, lightweight, and flexibility, all of which can drastically lower the cost of device fabrication and installation. However, the wide-spread commercial deployment of MHP solar cells is currently limited by a poor understanding of the thin film self-assembly processes that is hindering reliable scaling up of the manufacturing process. A majority of the MHP thin film deposition techniques reported thus far are ad hoc fixes used to obtain pinhole-free films with larger grains. This initial progress has yielded encouraging results in laboratory scale devices,12 but was achieved largely in a trial-and-error fashion. A large variability in the quality of the manufactured MHP films reported throughout the literature13 points to the fact that the research community still does not fully understand the MHP thin film nucleation and growth processes.Broadly speaking, there are two general classes of methods for depositing MHP thin films from solution. The typically referred to as the ‘one step method’ consists of spin-coating a precursor solution on a substrate with subsequent thermal annealing14–17 or orthogonal solvent treatment18–22 to induce nucleation and growth. Various parameters in the precursor solutions such as stoichiometry,10,14,17,23–26 concentration and chemical additives27–44 have been investigated. The other method, often referred to as the ‘two step method’, involves depositing a thin film of PbX2 (X = Br or I) and exposing it to methylammonium iodide (MAI) or formamidinium iodide (FAI).8,45–47 Both of the ‘one step’ and ‘two step’ deposition methods are frequently used for solar cell fabrication, but their thin film growth processes are still poorly understood. To be able to rationally select solution formulation and thin film processing conditions, the first step is to characterize and understand the sub-processes of thin film formation such as types of nucleation, formation of any intermediate structures and growth mechanisms.
In situ studies during the MHP thin film formation can probe the sub-processes of nucleation and growth. Previous studies have employed in situ X-ray diffraction to gain valuable insights into the thin film growth processes of the ‘one step’ and ‘two step’ methods.48–54 For example, methylammonium lead iodide (MAPbI3) thin film growth from the ‘two step’ method was found to proceed via diffusion of the MAI cation into PbI2 crystals, with the final MAPbI3 grain size being highly correlated to that of the already formed PbI2 thin film.48 MAPbI3 formed from the ‘one step, mixed halide’ method was found to nucleate from an ordered intermediate phase, and the crystallographic orientation of the MAPbI3 thin film has been found to be highly dependent on thermal annealing temperature.51 These previous studies highlight the need to perform systematic studies to determine how rationally selected solution formulations, including additives, impact the film formation processes.
Controlling the grain size and crystallographic orientation of thin films is important in MHP solar cells,12 as recently shown, there is a large variation of photovoltaic performance with different crystal facets.55 Homogeneous nucleation and the presence of colloidal species in the solution result in growth and deposition of crystallites with uncontrolled orientation on the substrate.12,56 Crystallization of MHPs from intermediate structures, even though it has been shown to result in pinhole-free films for solar cells,10 relies on complex nucleation and growth processes within or on the intermediate structures.8,9,18,57 Achieving a high degree of control over the growth process and crystallographic orientation of thin films simultaneously is difficult with the homogeneous nucleation as well as crystallization from intermediate structures. In order to induce heterogeneous nucleation and growth of MHP on the substrate surface directly from the solution, the free energy of the precursor solution must be lowered relative to any colloids, homogeneous nuclei, or other intermediate structures. Moreover, changing the free energy of the solution will allow the rate and density of nucleation to be tuned. Using additives in the solution formulation can achieve these goals while enabling control over the crystallographic orientation of thin films via altering the surface energies of different facets through additive binding.
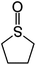
Here we show that such a crystallization scheme can be realized by adding a rationally chosen sulfoxide additive, tetrahydrothiophene oxide (THTO), to the MAPbI3 precursor solution. To date, the choice of solvents and additives for MHP solution formulation has been unjustified from a theoretical standpoint and tends to arise from observed efficacy of solvation, obtained in a trial-and-error fashion. Recently, Stevenson et al.58 opened the door to a systematic solvent selection process by showing that quantitative trends in chemical properties can be used to explain and predict the solvation efficacy. In this work, computational screening was performed to guide the choice of additive with the strongest bond unsaturation. Compared to various common solvents for MHPs such as dimethylsulfoxide (DMSO), dimethylformamide (DMF), gamma-butyrolactone (gBL) as well as other chemicals that have not been previously investigated by the community, THTO was calculated to have the strongest drive for solvation. The strength of the interaction between THTO and MAPbI3 was experimentally confirmed with the extremely high solubility of 60% by weight and release of heat upon dissolution. Addition of THTO in MAPbI3 precursor solution results in a dramatically reduced nucleation density of as few as one per square millimeter, and a smooth film with a strong tetragonal (100) crystallographic orientation. By examining the growth process in situ with grazing incidence X-ray diffraction (GIXD), it was found that the THTO suppresses homogeneous nuclei as well as crystalline intermediate structures. Instead, heterogeneous nucleation at the interface and growth of a highly oriented MAPbI3 thin film occur directly from the precursor solution. Density functional theory (DFT) calculations show that the THTO additives selectively lower the surface energy of a particular facet, which results in the tetragonal (100) crystallographic orientation. The crystallographic orientation of the MAPbI3 thin film was found to significantly impact the open circuit voltage of solar cell devices, which highlights the importance of controlling the thin film orientation.
Experimental section
Materials
Methylammonium iodide was purchased from Dyesol, PbI2 (99.999%), PbCl2 (99.999%), tetrahydrothiophene-1-oxide (THTO) (96%), gamma-butyrolactone (gBL) 99%, dimethylformamide (DMF) anhydrous, 99.8%, titanium diisopropoxide bis(acetylacetonate) 75% wt in isopropanol, isopropanol (IPA) (99%), methanol (99%), nickel acetate tetrahydrate (99%), and diethanolamine (98%) were purchased from Sigma Aldrich and used as received. Dimethylsulfoxide (DMSO) 99.9% was purchased from VWR International. PEDOT:PSS (Clevios HTL solar #1) was purchased from Heraeus and filtered with a 0.45 μm pore size PVDF filter before use. PCBM was purchased from nano-C. ITO substrates (15 ohm cm−2) were purchased from Kintec. Aluminum evaporation material (99.999%) was purchased from Kurt J Lesker company.Thin film formation using THTO additive
1 to 1 molar ratio of MAI and PbI2 were dissolved in gBL at 70 °C with THTO additive at a molar ratio of three THTO to one Pb (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 THTO
1 THTO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pb). The solution was 30% MAPbI3 by weight. This solution was cooled to room temperature and spin-coated on various substrates such as ITO/PEDOT:PSS, ITO, TiO2, NiO and SiO2 at 2000 rpm for 30 seconds. After spin-coating the precursor solution, the samples were annealed at 70 °C for 30 minutes to obtain MAPbI3 thin films.
Pb). The solution was 30% MAPbI3 by weight. This solution was cooled to room temperature and spin-coated on various substrates such as ITO/PEDOT:PSS, ITO, TiO2, NiO and SiO2 at 2000 rpm for 30 seconds. After spin-coating the precursor solution, the samples were annealed at 70 °C for 30 minutes to obtain MAPbI3 thin films.
Formation of substrate thin films
PEDOT:PSS was spin-coated at 1500 rpm for 40 seconds and annealed at 170 °C for 4 minutes. For NiOx, a 0.4 mol L−1 solution of nickel acetate and diethanolamine in methanol was used. This solution was spin-coated at 3000 rpm for 30 seconds and annealed at 400 °C for 10 minutes. For TiO2, titanium diisopropoxide bis(acetylacetonate) in IPA as purchased from Sigma Aldrich was diluted further with IPA until the concentration was 0.3 mol L−1. This solution was spin-coated at 3000 rpm for 30 seconds and annealed at 400 °C for 10 minutes.MAPbI3 thin film fabrication via the mixed halide method
Films were spin-coated on a glass/PEDOT substrate at 2000 rpm for 30 seconds from a precursor solution consisting of 0.8 M PbCl2 and 2.4 M MAI in DMF. The films were annealed at 120 °C for 10 minutes in ambient conditions (relative humidity = 30%).1-D X-ray diffraction measurements
A PANalytical X'Pert X-ray diffraction system with a Cu source operating at 40 kV and 40 mA was used. All measurements were performed ex situ at room temperature.2-D grazing incidence X-ray diffraction measurements
Data were taken at the D-1 beamline at the Cornell High Energy Synchrotron Source using X-rays with a wavelength of 0.1168 Å, a custom precision goniometer, and a Pilatus 200k two dimensional pixel array detector (Dectris). Samples were spin-coated at the beamline (Chemat), using the same protocol as for the ex situ XRD measurements. The temperature of the custom-built sample holder was controlled by a temperature controller (Digi-Sense) and the temperature was monitored during X-ray data collection. The X-ray beam was approximately 0.5 mm wide and 0.1 mm high, and illuminated the entire length (5 mm) of the sample using an incident angle of typically 0.5°. For obtaining depth profiles, the incident angle was varied between 0.1° and 0.5°. For all in situ data collection, the sample was moved to a new position after three GIXD patterns were collected, in order to avoid beam damage.Solar cell fabrication
1 inch by 1 inch patterned ITO substrates were cleaned by sonication with Hellmanex 3 surfactant in deionized water, pure deionized water, then ethanol, and UV-ozone cleaned for 5 minutes. PEDOT:PSS was spin-coated at 1500 rpm for 40 seconds and annealed at 170 °C for 4 minutes. MAPbI3 thin film with preferential crystallographic orientation was deposited from THTO added solution as described previously. A 2% weight solution of PCBM was spin-coated at 1000 rpm. The metal contacts were deposited by evaporating 50 nm of aluminum at a rate of 0.1 nm s−1 in a vacuum of 10−6 Torr. Devices utilizing the same exact architecture were fabricated with a randomly oriented MAPbI3 thin film by using the interdiffusion method.47 Briefly, 1 M PbI2 in DMF was spin-coated at 3000 rpm, followed by 50 mg mL−1 MAI in IPA. The film was annealed at 85 °C for 1 hour.Solar cell testing
The devices were tested with a Keithley source-meter using a scan rate of 1 V s−1 under AM 1.5 illumination from a solar simulator (PV Measurements). The light source was calibrated with a reference silicon solar cell (PV Measurements). The device active area was 0.03 cm2. An optical mask was used to block illuminating the non-device area during testing.Scanning electron microscopy
SEM images were taken with a Quanta 650 SEM operating at 30 kV. All samples were imaged at four or more locations and pictures presented in this work are representative of typical results near the center of the sample. Samples were prepared in the same manner as for solar cells without the PCBM and Al layers on top of the MAPbI3 layer.Calculation of Mayer bond order (MBO) and bond unsaturation of solvent molecules
The MBO value for atom–atom interactions in a (non-periodic) solvent-lead cluster were calculated using an ab initio approach, optimized with the B97-D3 functional59 and the PWPB95 functional60 using the Orca DFT package.61 Electronic structures of the optimized gas phase molecule were used to calculate the MBO of individual atomic interactions between oxygen and the central atom and, subsequently, the “bond unsaturation” value. The bond unsaturation is defined as the formal bond order (two in the case of oxygen) minus the Mayer bond order. Bond unsaturation, rather than the MBO itself is the key quantity, it provides a measure of the driving force for bonding (see the ESI† for more details).Calculation of solvation enthalpy
20 configurations were generated for the coordinated Pb2+ molecule clusters and pure solvent molecule clusters using Packmol,62 each with a different random seed. Adequate sampling is necessary for the variety of configurations that complexes may assume. Subsequently, the systems were subjected to molecular dynamics minimizations, performed in LAMMPS63 using OPLS 2005 parameters. The non-periodic DFT code, Orca61 was used for further geometry optimizations and energy calculations. These optimizations eliminated the congestion on the Pb2+ ion that resulted from the necessity to use a Ba2+ ion (the closest in size to lead) during the MD annealing process, since Pb2+ parameters are not yet available in the OPLS force field.64 Using these relaxed geometries as starting configurations, further geometry optimization using B97-D3 (ref. 59)/def2-TZVP65 obtained more accurate structures and energies. The enthalpy of solvation was then calculated from the energies of the resulting geometries (see the ESI† for more details).Calculation of surface energies
DFT calculations for periodic systems were performed using the Vienna Ab Initio Simulation Package (VASP)66–68 package employing a Perdew–Burke–Ernzerhof (PBE) density functional.69 The ion–electron interactions were described by the projector-augmented wave method using soft potentials. We relaxed all atoms in the system such that the forces were less than 0.01 eV Å−1, and the self-consistent field was terminated when the energy is converged to less than 10−6 eV. The electronic wavefunction was expanded using plane waves with an energy cutoff of 280 eV. We used a supercell approach to model the different slabs with 20 Å of vacuum to mitigate interactions between fictitious images along the non-periodic direction of the slab. The cubic phase was modeled using 2 × 1 surface supercell, while the tetragonal phase was modeled using 2 × 2 surface supercell. The Brillouin zone was sampled using a 2 × 2 × 1 (2 × 3 × 1) k-grid for the tetragonal (cubic) surfaces, and 2 × 2 × 2 (3 × 3 × 3) for the tetragonal (cubic) bulk phases. The THTO molecule was adsorbed on the top and bottom sides of the slab to minimize the dipole of the system along the non-periodic direction. Other computational details are reported in the ESI.†Results and discussion
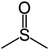
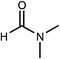
Dimethylsulfoxide (DMSO) strongly interacts with the Pb2+ ion,9,58,70 and this property has been used to influence the crystallization process of MAPbI3 with DMSO acting as a complexing additive8,9,18,71 or a solvent.19,31,72,73 However, it is likely that more optimal additives or solvents exist, and we used computational screening to identify the most promising ones that will lower the free energy of the precursor solution. The Mayer bond order74 (MBO) of the oxygen atom in solvent molecules has been shown to be predictive of the efficacy of the solvent to stabilize Pb2+ ions in a MAPbI3 precursor solution.58 The closely related “bond unsaturation” defined as the formal bond order (two in the case of oxygen) minus the Mayer bond order, is the more useful quantity: generally, the higher the bond unsaturation (given in brackets in Table 1), the better the solvent choice in these systems. The S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functional group was found to be the best for this purpose,58 and the search focused on solvents with this feature. Based on examining the bond unsaturation of several candidates, THTO was predicted to stabilize Pb2+ more strongly than any other candidate molecules and was therefore selected for further study (see Tables 1 and S1 in the ESI†). DFT calculations using a B97-D3 functional predict a significantly more negative enthalpy of solvation of Pb2+ in THTO than values for other commonly used solvents, including DMSO. Solvation enthalpies, Mayer bond orders, and bond unsaturation values of common MHP solvents and THTO are compared in Table 1.
O functional group was found to be the best for this purpose,58 and the search focused on solvents with this feature. Based on examining the bond unsaturation of several candidates, THTO was predicted to stabilize Pb2+ more strongly than any other candidate molecules and was therefore selected for further study (see Tables 1 and S1 in the ESI†). DFT calculations using a B97-D3 functional predict a significantly more negative enthalpy of solvation of Pb2+ in THTO than values for other commonly used solvents, including DMSO. Solvation enthalpies, Mayer bond orders, and bond unsaturation values of common MHP solvents and THTO are compared in Table 1.
The visual appearance of the MAPbI3 crystallization process with THTO additives offers initial evidence of the reduced free energy of the precursor solutions. Thin films deposited from a solution of MAPI3 in pure gBL or DMF appear white and hazy after spin-coating, and crystallize into a brown film after being heated at 70 °C for ∼3 seconds. These observations are consistent with previous studies75,76 that attributed the turbidity to intercalated structure formation.27,72,75,77,78 In contrast, thin films deposited from solutions of MAPbI3 in DMF or gBL with a molar ratio of 3 THTO molecules to one Pb (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 THTO
1 THTO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pb) have no visible turbidity after spin-coating. These thin films take 30 to 40 seconds at 70 °C to turn brown, implying that the presence of THTO significantly delays crystallization of MAPbI3 while suppressing the formation of intermediate structures (see more on this below with in situ X-ray diffraction results). By annealing the thin films in a THTO-rich atmosphere, the nucleation density can be lowered to the extent that individual brown spots can be seen on the substrate. These spots grow together to form a continuous thin film over the course of 4 to 6 minutes, yielding circular structures up to several millimeters in diameter (Fig. S1 and S2 in the ESI†). This slow crystallization is in contrast to most other “one step” deposition mechanisms. Many of the previous methods using orthogonal solvent treatment,21,22 high temperature annealing,79 high pressure gas,76 or flash evaporation of solvent11 were designed to cause rapid and dense nucleation to obtain pinhole-free films. Additives have also been used to increase the nucleation density,44 but, to our knowledge, chemical additives have not been previously used to dramatically slow down the nucleation as shown in our work.
Pb) have no visible turbidity after spin-coating. These thin films take 30 to 40 seconds at 70 °C to turn brown, implying that the presence of THTO significantly delays crystallization of MAPbI3 while suppressing the formation of intermediate structures (see more on this below with in situ X-ray diffraction results). By annealing the thin films in a THTO-rich atmosphere, the nucleation density can be lowered to the extent that individual brown spots can be seen on the substrate. These spots grow together to form a continuous thin film over the course of 4 to 6 minutes, yielding circular structures up to several millimeters in diameter (Fig. S1 and S2 in the ESI†). This slow crystallization is in contrast to most other “one step” deposition mechanisms. Many of the previous methods using orthogonal solvent treatment,21,22 high temperature annealing,79 high pressure gas,76 or flash evaporation of solvent11 were designed to cause rapid and dense nucleation to obtain pinhole-free films. Additives have also been used to increase the nucleation density,44 but, to our knowledge, chemical additives have not been previously used to dramatically slow down the nucleation as shown in our work.
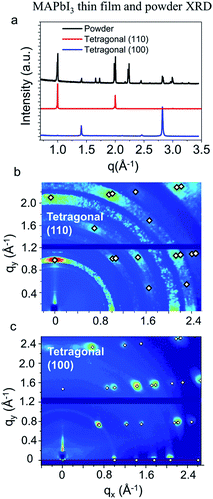
Addition of THTO in solution formulations was found to robustly result in tetragonal (100) oriented MAPbI3 thin films. Fig. 1(a) shows the XRD patterns obtained from a powder MAPbI3 sample with random crystallographic orientation, tetragonal (110), and tetragonal (100) oriented MAPbI3 thin films. The tetragonal (110) and (100) oriented films were obtained from the ‘mixed halide’ and our THTO methods, respectively. Going beyond 1-dimensional XRD patterns, the thin film crystallographic orientation can be unambiguously determined by indexing two-dimensional GIXD patterns with numerous distinctive peaks. The GIXD patterns of tetragonal (110) and tetragonal (100) oriented films are shown in Fig. 1(b) and (c), respectively. The tetragonal (110) orientation is the most commonly observed preferential orientation with MAPbI3 thin films. Several methods,24,26,79–81 most notably the ‘mixed halide’ method,10,17 have been reported to result in a tetragonal (110) orientation. Three methods have yielded tetragonal (100) films,50,72,82 and the vast majority of reported methods yield randomly oriented films.14,18,21,45,56,83 The tetragonal (100) oriented MAPbI3 thin films obtained from precursor solutions with THTO additives, as well as the extremely slow crystallization behavior described above, suggests a different crystallization mechanism from any other previously reported methods.
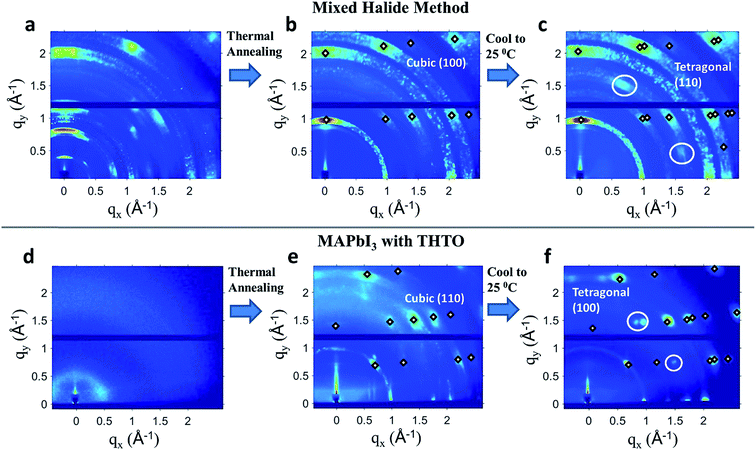
To better understand the thin film growth processes that result in different crystal orientations, we have performed in situ X-ray diffraction studies. When the ‘mixed halide’ method was used, we observed that a highly ordered intermediate structure was formed at room temperature immediately after spin coating, as was observed by others10,50,52 (Fig. 2(a)). Upon thermal annealing at 120 °C, the intermediate structure disappears while a cubic (100) oriented MAPbI3 thin film forms (Fig. 2(b)). The cubic (100) films ultimately converted into a tetragonal (110) film upon cooling to room temperature (Fig. 2(c)). The exact mechanism of nucleation and growth for the mixed halide system is not well understood yet, but the current hypotheses involve a high nucleation density caused by PbCl2 nanoparticles84 and grain coarsening.10,84,85 Our in situ measurements show a coexistence of multiple phases (Fig. 2(a)), some of which have extremely large lattice sizes, indicating a complex transformation from the ordered intermediate phases to the perovskite. Another complication in determining the cause of the orientation in the mixed halide method is that the degree of orientation is highly temperature dependent. It was observed by Saliba et al.,51 as well as by us in this work, that annealing below 110 °C causes the film to be completely random in crystallographic orientation (Fig. S3 in the ESI†).
In contrast to the ‘mixed halide’ method, stoichiometric precursor solutions with molar ratios of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 THTO
1 THTO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pb form a cubic (110) orientation directly from the precursor solution after 45 seconds of thermal annealing at 70 °C (Fig. 2(e)). No crystalline intermediate phase was observed. This orientation was robust with respect to annealing temperature up to 140 °C, although the degree of order gets reduced at higher temperatures (Fig. S4 in the ESI†). Upon cooling to room temperature, the cubic (110) film gets converted to a tetragonal (100) oriented film. As is shown in Fig. 3, both the cubic (110) to tetragonal (100) and cubic (100) to tetragonal (110) consist of only a slight tilting of the lead iodide octahedra. We have experimentally found that the phase transition for both orientations is reversible; the tetragonal (100) and (110) retain their orientation after being heated to 100 °C and cooled back to room temperature (Fig. S6 in the ESI†). Previously, a direct MHP crystallization mechanism has been examined in situ by Moore et al.24 using an ionic liquid which avoided intermediate structures and resulted in the more typically seen tetragonal (110) orientation. Our work is the first in situ examination of a direct crystallization mechanism from a stoichiometric precursor solution with additives that yields the tetragonal (100) orientation.
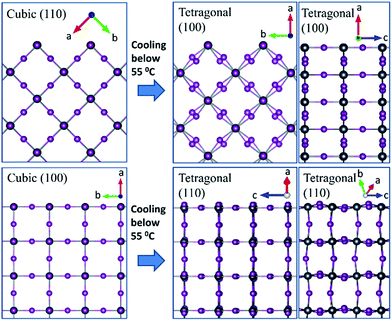
Pb form a cubic (110) orientation directly from the precursor solution after 45 seconds of thermal annealing at 70 °C (Fig. 2(e)). No crystalline intermediate phase was observed. This orientation was robust with respect to annealing temperature up to 140 °C, although the degree of order gets reduced at higher temperatures (Fig. S4 in the ESI†). Upon cooling to room temperature, the cubic (110) film gets converted to a tetragonal (100) oriented film. As is shown in Fig. 3, both the cubic (110) to tetragonal (100) and cubic (100) to tetragonal (110) consist of only a slight tilting of the lead iodide octahedra. We have experimentally found that the phase transition for both orientations is reversible; the tetragonal (100) and (110) retain their orientation after being heated to 100 °C and cooled back to room temperature (Fig. S6 in the ESI†). Previously, a direct MHP crystallization mechanism has been examined in situ by Moore et al.24 using an ionic liquid which avoided intermediate structures and resulted in the more typically seen tetragonal (110) orientation. Our work is the first in situ examination of a direct crystallization mechanism from a stoichiometric precursor solution with additives that yields the tetragonal (100) orientation.
Direct crystallization of highly oriented MAPbI3 thin films from solution suggests that the nucleation is heterogeneous at an interface without additional homogeneous nucleation or formation of colloidal species. The possible locations for the heterogeneous nucleation sites are at the solution/air or substrate/solution interface. We believe that the nucleation occurs at the substrate/solution interface based on our observations that the type of substrate has a major impact on the film formation. We have investigated SiO2, PEDOT:PSS, ITO, TiO2, NiO, and Si as substrates and found that the nucleation, growth rate and final morphology of the films are sensitively dependent on the substrate (see Fig. S7 in the ESI†). This variability with respect to the substrate is consistent with classical nucleation theory, which states that the energy barrier for heterogeneous nucleation on a substrate is a function of the crystal/substrate interfacial energy.12 The location of nucleation can be examined using in situ GIXD by varying the incident angle of the X-ray beam upon the substrate. When the beam is normal to the sample, it travels less distance within the solution to reach the substrate, thus retaining beam integrity and allowing for interrogation of the substrate/solution interface. As the beam angle decreases from 90 degrees relative to the substrate, it becomes absorbed and scattered by more and more solution and therefore is unable to probe deep into the film. Therefore, larger incident angles will sample more of the substrate/solution interface. If nucleation occurs at the substrate/solution interface, the peak intensity relative to background at larger angles is expected to be higher during the initial stages of crystallization, whereas if nucleation occurs at the air/solution interface86 the intensity at smaller angles would be greater. Our analysis of the GIXD data shows the former case is true (see Fig. S8 and S9 in the ESI†). This indicates that heterogeneous nucleation is occurring at the substrate.
Interestingly, despite the large difference in nucleation rate and final film morphology depending on the substrate, the orientation of the MAPbI3 thin film robustly came out to be tetragonal (100) across all substrates (see Fig. S10 in the ESI†). These results suggest that the orientation of MAPbI3 films is determined by interactions at the MAPbI3/solution interface. If growth was limited kinetically by additives binding to a crystal facet and slowing the growth of that surface, low-dimensional structures such as plates or rods with random crystallographic orientation would be expected instead of a highly oriented thin film.87–90 Therefore, the preferential orientation observed in this work seems to be determined by thermodynamics and can be best explained by examining the surface energies of MAPbI3 interacting with THTO. The cubic (100) surface of MAPbI3 is the least polar surface, and it would be expected to be the most stable if contacted by a vacuum. However, other surfaces may be favored in the presence of molecules that interact strongly with MAPbI3. For example, the O atom in DMSO has been shown to interact with Pb atoms,9,58,70 and recently, Zhang et al. showed that the concentration of halide atoms can influence the shape of MAPbX3 (X = I, Br) single crystals by binding with varying affinities to different facets.91 A strong interaction of the THTO with MAPbI3 surface atoms may alter the relative surface energies of the different crystal facets and stabilize the under-coordinated Pb atoms of MAPbI3 on surfaces such as the cubic (110).
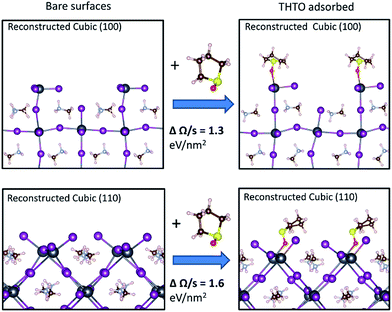
To check for this possibility, DFT66–68 calculations were performed to quantify the effect of adsorbed THTO on the energies of MAPbI3 surfaces. These energies can be calculated using an ab initio thermodynamics approach92 employing a grand canonical ensemble.93,94 In our study, we followed a similar approach to Haruyama et al.95 who investigated the tetragonal phase of MAPbI3. We considered various different surface compositions for each orientation, with and without THTO in the cubic (100), cubic (110), tetragonal (110) and tetragonal (100) surfaces of MAPbI3. Our calculated surface free energies of 1.1 eV nm−2 and 0.89 eV nm−2 for the bare tetragonal (110) and (100) surfaces respectively are in agreement with those calculated by Haruyama et al.95 Since our experimental in situ GIXD results show that the formation of both the tetragonal (100) and (110) orientation is determined by the growth of the corresponding surface in the cubic phase, investigating the interaction of THTO with the cubic surfaces is most relevant for this work. However, the cubic phase with an enlarged primitive cell becomes unstable upon structural relaxation and collapses to a tetragonal structure. This is because the DFT calculations are conducted at T = 0 K and the cubic phase is stable only at high temperatures. We used a larger supercell to model the cubic phase that show distorted bond angles after structural optimization (Fig. 4). Therefore, we will refer to these surfaces as “reconstructed cubic” surfaces. We note that the experimental X-ray diffraction probes the average structure within the bulk of crystals and the exact surface structure, including any reconstruction, during thin film growth is not known. This uncertainty makes sampling several surface configurations all the more important. Nonetheless, our calculation results show that the conclusions are the same when using both the fully tetragonal and reconstructed cubic surfaces (vide infra).
The optimum adsorption configuration for THTO was obtained by sampling different initial configurations obtained by bonding the oxygen atom in THTO to different adsorption sites on the surface. Our results show that THTO adsorbs through interaction between its oxygen atom with the Pb cation on the surface, as shown in Fig. 4. The binding energies are summarized in Table S3,† and these range between −0.78 to −1.5 eV on the cubic (100), and −1.0 to −1.8 eV on the cubic (110) (negative binding energy means that the molecule binding is stable). The surface coverage density of THTO was 1 per 1.1 nm2 for the reconstructed cubic (110) surface and 1 per 0.8 nm2 for the reconstructed cubic (100) surface. We note that, experimentally, MAPbI3 precursors dissolved in pure THTO robustly results in the tetragonal (100) orientated thin films. Therefore, we have not attempted to model the more complex solvent mixture systems and instead focused on understanding the impact of the THTO only. Our calculation results (Fig. 4) show that the reconstructed cubic (110) surface is more stabilized relative to the reconstructed cubic (100) by an additional 0.3 eV nm−2 upon THTO binding. This supports our hypothesis that the tetragonal (100) oriented MAPbI3 films we obtain experimentally (1) is determined by the interactions at the MAPbI3/solution interface during the growth and (2) results from growth of cubic (110) that is greatly stabilized by THTO. The same conclusion can be reached by examining the effect of THTO on the relative stabilities of the tetragonal surfaces (see Fig. S12 in the ESI†).
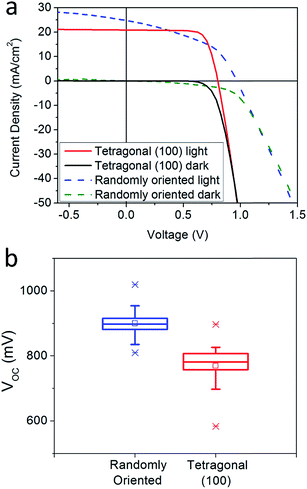
To investigate the impact of different crystallographic orientations on solar cell performance, we have performed solar cell fabrication and characterization. Recently, Leblebici et al.55 employed conductive atomic force microscopy to show that the crystallographic orientation of MHPs is an important variable in solar cell performance; both the short circuit current density (Jsc) and open circuit voltage (Voc) can vary drastically with crystal facet within individual grains.55 In this work, the device architecture employed in our work was ITO/PEDOT:PSS/MAPbI3/PCBM/Al wherein the MAPbI3 thin film was deposited from a THTO-added precursor solution and confirmed with XRD to have pure tetragonal (100) orientation. The film thickness was determined by atomic force microscopy to be 230 nm. Fig. 5 shows the current-density versus voltage curve of the champion device with power conversion efficiency of 12.6%, open circuit voltage of 0.8 V, short circuit current density of 21 mA cm−2 and fill factor of 0.76. With about 60 solar cells, the average open circuit voltage from our devices was 750 mV. In contrast to tetragonal (100) oriented films, solar cells made with the same architecture but with a crystallographically randomly oriented MAPbI3 layer deposited using the interdiffusion method47 (350 nm thick) produced an average Voc of 900 mV. This result is consistent with the literature that shows open circuit voltages as high as 1 V,47 with 900 mV being common79,96–99 using a ITO/PEDOT/MAPbI3/PCBM/Al architecture with randomly oriented MAPbI3 crystals.
A lower Voc with tetragonal (100) oriented MAPbI3 film could have been caused by higher charge recombination or different band alignment across the heterojunction. The high Jsc and fill factor indicate that the MAPbI3 crystals grown using the THTO method are of high quality, as the charges easily diffuse to the contacts. The scanning electron microscopy images show that the randomly oriented films have much small (∼100 nm) grains compared to the tetragonal (100) films (Fig. S14†). However, our photoluminescence lifetime measurements (Fig. S15†) show that the tetragonal (100) oriented film has significantly shorter lifetime (11 ns) compared to randomly oriented films (260 ns). This suggests that the lower Voc from tetragonal (100) film may have been caused by higher recombination on the tetragonal (100) surface. In addition, semiconductors often exhibit changing work functions with different orientations100,101 and it is possible that the tetragonal (100) orientation results in a different band alignment. It is also possible that adsorbed THTO remains on the surface after annealing and alters valence and conduction band energy levels, as observed in colloidal quantum dot systems previously.102 Dissecting which of these mechanisms is responsible for the lower Voc is beyond the scope of this study.
Conclusions
Here we have demonstrated the use of computational screening to rationally select an additive for MAPbI3 precursor solution to alter the nucleation and growth processes. Specifically, we lowered the free energy of the precursor by incorporating a sulfoxide, which strongly interacts with MAPbI3 precursors, allowing an unprecedented degree of control over the nucleation density and growth rate. By altering the relative surface stabilities with chemical additives, the crystallographic orientation of MAPbI3 was tuned. The systematic methodology demonstrated in this work will enable more efficient and robust selection of MHP precursor solution formation, which will lead to more precise degree of control over MHP thin film formation processes. Ultimately, these advances will contribute to accelerating the progress in MHP solar cell efficiency improvement, scale-up of device manufacturing, better stability and reliability.Statement of contributions
B. J. F. and J. J. C. conceived and designed the experiments. B. J. F., J. G., A. Z. C., M. R. A. and D. M. S. performed the GIXD measurements. B. J. F., J. G., A. Z. C. and J. S. N. performed solar cell fabrication and testing. B. A. S., A. F. H. and P. C. performed the computational screening of chemical additives. B. J. F. and W. A. S. performed DFT surface energy calculations. All authors contributed to data analysis and manuscript writing.Acknowledgements
J. J. C. acknowledges support from an Early Career Faculty Award grant from NASA's Space Technology Research Grants Program (NNX15AU43G) and the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0016144. W. A. S. acknowledges a start-up fund from the department of Mechanical Engineering and Materials Science at the University of Pittsburgh and computing time provided, in part, by the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (#NSF OCI-1053575). P. C. acknowledges support from NSF award (CCMI-1536895) and support for AFH through the Cornell Center for Materials Research program with support from the NSF MRSEC program (DMR-1120296) and the REU site program (DMR-1063059). This work is based upon research conducted at the Cornell High Energy Synchrotron Source (CHESS), which is supported by the National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award DMR-1332208.Notes and references
- NREL Chart, http://www.nrel.gov/ncpv/images/efficiency_chart.jpg, 09/05/2016.
- D. Bi, B. Xu, P. Gao, L. Sun, M. Grätzel and A. Hagfeldt, Nano Energy, 2016, 23, 138–144 CrossRef CAS.
- Y. Jo, K. S. Oh, M. Kim, K.-H. Kim, H. Lee, C.-W. Lee and D. S. Kim, Adv. Mater. Interfaces, 2016, 3, 1500768 CrossRef.
- J.-W. Lee, H.-S. Kim and N.-G. Park, Acc. Chem. Res., 2016, 49, 311–319 CrossRef CAS PubMed.
- T. Malinauskas, M. Saliba, T. Matsui, M. Daskeviciene, S. Urnikaite, P. Gratia, R. Send, H. Wonneberger, I. Bruder, M. Graetzel, V. Getautis and M. K. Nazeeruddin, Energy Environ. Sci., 2016, 9, 1681–1686 CAS.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Grätzel, Energy Environ. Sci., 2016, 9, 1989–1997 CAS.
- H. Yoon, S. M. Kang, J.-K. Lee and M. Choi, Energy Environ. Sci., 2016, 9, 2262–2266 CAS.
- W. S. Yang, J. H. Noh, N. J. Jeon, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Science, 2015, 348, 1234–1237 CrossRef CAS PubMed.
- N. Ahn, D. Y. Son, I. H. Jang, S. M. Kang, M. Choi and N. G. Park, J. Am. Chem. Soc., 2015, 137, 8696–8699 CrossRef CAS PubMed.
- H. Zhou, Q. Chen, G. Li, S. Luo, T.-b. Song, H.-S. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546 CrossRef CAS PubMed.
- X. Li, D. Bi, C. Yi, J.-D. Décoppet, J. Luo, S. M. Zakeeruddin, A. Hagfeldt and M. Grätzel, Science, 2016 DOI:10.1126/science.aaf8060.
- Y. Zhou, O. S. Game, S. Pang and N. P. Padture, J. Phys. Chem. Lett., 2015, 6, 4827–4839 CrossRef CAS PubMed.
- A. Sharenko and M. F. Toney, J. Am. Chem. Soc., 2016, 138, 463–470 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- G. E. Eperon, V. M. Burlakov, P. Docampo, A. Goriely and H. J. Snaith, Adv. Funct. Mater., 2014, 24, 151–157 CrossRef CAS.
- L. Etgar, P. Gao, Z. Xue, Q. Peng, A. K. Chandiran, B. Liu, M. K. Nazeeruddin and M. Graetzel, J. Am. Chem. Soc., 2012, 134, 17396–17399 CrossRef CAS PubMed.
- S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344 CrossRef CAS PubMed.
- N. J. Jeon, J. H. Noh, Y. C. Kim, W. S. Yang, S. Ryu and S. I. Seok, Nat. Mater., 2014, 13, 897–903 CrossRef CAS PubMed.
- Y. Rong, Z. Tang, Y. Zhao, X. Zhong, S. Venkatesan, H. Graham, M. Patton, Y. Jing, A. M. Guloy and Y. Yao, Nanoscale, 2015, 7, 10595–10599 RSC.
- S. Ryu, J. Seo, S. S. Shin, Y. C. Kim, N. J. Jeon, J. H. Noh and S. I. Seok, J. Mater. Chem. A, 2015, 3, 3271–3275 CAS.
- M. Xiao, F. Huang, W. Huang, Y. Dkhissi, Y. Zhu, J. Etheridge, A. Gray-Weale, U. Bach, Y. B. Cheng and L. Spiccia, Angew. Chem., Int. Ed. Engl., 2014, 53, 9898–9903 CrossRef CAS PubMed.
- Y. Zhou, M. Yang, W. Wu, A. L. Vasiliev, K. Zhu and N. P. Padture, J. Mater. Chem. A, 2015, 3, 8178–8184 CAS.
- D. T. Moore, H. Sai, K. Wee Tan, L. A. Estroff and U. Wiesner, APL Mater., 2014, 2, 081802 CrossRef.
- D. T. Moore, K. W. Tan, H. Sai, K. P. Barteau, U. Wiesner and L. A. Estroff, Chem. Mater., 2015, 27, 3197–3199 CrossRef CAS.
- C. Roldán-Carmona, P. Gratia, I. Zimmermann, G. Grancini, P. Gao, M. Graetzel and M. K. Nazeeruddin, Energy Environ. Sci., 2015, 8, 3550–3556 Search PubMed.
- W. Zhang, M. Saliba, D. T. Moore, S. K. Pathak, M. T. Horantner, T. Stergiopoulos, S. D. Stranks, G. E. Eperon, J. A. Alexander-Webber, A. Abate, A. Sadhanala, S. Yao, Y. Chen, R. H. Friend, L. A. Estroff, U. Wiesner and H. J. Snaith, Nat. Commun., 2015, 6, 6142 CrossRef CAS PubMed.
- Y. Chen, Y. Zhao and Z. Liang, Chem. Mater., 2015, 27, 1448–1451 CrossRef CAS.
- C.-C. Chueh, C.-Y. Liao, F. Zuo, S. T. Williams, P.-W. Liang and A. K. Y. Jen, J. Mater. Chem. A, 2015, 3, 9058–9062 CAS.
- Q. Dong, Z. Wang, K. Zhang, H. Yu, P. Huang, X. Liu, Y. Zhou, N. Chen and B. Song, Nanoscale, 2016, 8, 5552–5558 RSC.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 CAS.
- J. H. Heo, D. H. Song, H. J. Han, S. Y. Kim, J. H. Kim, D. Kim, H. W. Shin, T. K. Ahn, C. Wolf, T. W. Lee and S. H. Im, Adv. Mater., 2015, 27, 3424–3430 CrossRef CAS PubMed.
- J. H. Heo, D. H. Song and S. H. Im, Adv. Mater., 2014, 26, 8179–8183 CrossRef CAS PubMed.
- H.-L. Hsu, C.-C. Chang, C.-P. Chen, B.-H. Jiang, R.-J. Jeng and C.-H. Cheng, J. Mater. Chem. A, 2015, 3, 9271–9277 CAS.
- J. Huang, M. Wang, L. Ding, Z. Yang and K. Zhang, RSC Adv., 2016, 6, 55720–55725 RSC.
- Y. J. Jeon, S. Lee, R. Kang, J. E. Kim, J. S. Yeo, S. H. Lee, S. S. Kim, J. M. Yun and D. Y. Kim, Sci. Rep., 2014, 4, 6953 CrossRef CAS PubMed.
- G. Li, T. Zhang and Y. Zhao, J. Mater. Chem. A, 2015, 3, 19674–19678 CAS.
- X. Li, M. I. Dar, C. Yi, J. Luo, M. Tschumi, S. M. Zakeeruddin, M. K. Nazeeruddin, H. Han and M. Gratzel, Nat. Chem., 2015, 7, 703–711 CrossRef CAS PubMed.
- P. W. Liang, C. Y. Liao, C. C. Chueh, F. Zuo, S. T. Williams, X. K. Xin, J. Lin and A. K. Jen, Adv. Mater., 2014, 26, 3748–3754 CrossRef CAS PubMed.
- Y. Shi, X. Wang, H. Zhang, B. Li, H. Lu, T. Ma and C. Hao, J. Mater. Chem. A, 2015, 3, 22191–22198 CAS.
- C. Sun, Q. Xue, Z. Hu, Z. Chen, F. Huang, H. L. Yip and Y. Cao, Small, 2015, 11, 3344–3350 CrossRef CAS PubMed.
- Z. Wang, Y. Zhou, S. Pang, Z. Xiao, J. Zhang, W. Chai, H. Xu, Z. Liu, N. P. Padture and G. Cui, Chem. Mater., 2015, 27, 7149–7155 CrossRef CAS.
- Y. Zhao and K. Zhu, J. Phys. Chem. C, 2014, 118, 9412–9418 CAS.
- C. Zuo and L. Ding, Nanoscale, 2014, 6, 9935–9938 RSC.
- C.-C. Chen, Z. Hong, G. Li, Q. Chen, H. Zhou and Y. Yang, J. Photonics Energy, 2015, 5, 057405 CrossRef.
- J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Graetzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- J. H. Im, I. H. Jang, N. Pellet, M. Gratzel and N. G. Park, Nat. Nanotechnol., 2014, 9, 927–932 CrossRef CAS PubMed.
- Z. Xiao, C. Bi, Y. Shao, Q. Dong, Q. Wang, Y. Yuan, C. Wang, Y. Gao and J. Huang, Energy Environ. Sci., 2014, 7, 2619–2623 CAS.
- J. Schlipf, P. Docampo, C. J. Schaffer, V. Korstgens, L. Biessmann, F. Hanusch, N. Giesbrecht, S. Bernstorff, T. Bein and P. Muller-Buschbaum, J. Phys. Chem. Lett., 2015, 6, 1265–1269 CrossRef CAS PubMed.
- T. Miyadera, Y. Shibata, T. Koganezawa, T. N. Murakami, T. Sugita, N. Tanigaki and M. Chikamatsu, Nano Lett., 2015, 15, 5630–5634 CrossRef CAS PubMed.
- Q. Liang, J. Liu, Z. Cheng, Y. Li, L. Chen, R. Zhang, J. Zhang and Y. Han, J. Mater. Chem. A, 2016, 4, 223–232 CAS.
- M. Saliba, K. W. Tan, H. Sai, D. T. Moore, T. Scott, W. Zhang, L. A. Estroff, U. Wiesner and H. J. Snaith, J. Phys. Chem. C, 2014, 118, 17171–17177 CAS.
- K. W. Tan, D. T. Moore, M. Saliba, H. Sai, L. A. Estroff, T. Hanrath, H. J. Snaith and U. Wiesner, ACS Nano, 2014, 8, 4730–4739 CrossRef CAS PubMed.
- P. Pistor, J. Borchert, W. Franzel, R. Csuk and R. Scheer, J. Phys. Chem. Lett., 2014, 5, 3308–3312 CrossRef CAS PubMed.
- L. H. Rossander, T. T. Larsen-Olsen, H. F. Dam, T. M. Schmidt, M. Corazza, K. Norrman, I. Rajkovic, J. W. Andreasen and F. C. Krebs, CrystEngComm, 2016, 18, 5083–5088 RSC.
- S. Y. Leblebici, L. Leppert, Y. Li, S. E. Reyes-Lillo, S. Wickenburg, E. Wong, J. Lee, M. Melli, D. Ziegler, D. K. Angell, D. F. Ogletree, P. D. Ashby, F. M. Toma, J. B. Neaton, I. D. Sharp and A. Weber-Bargioni, Nat. Energy, 2016, 1, 16093 CrossRef.
- K. Yan, M. Long, T. Zhang, Z. Wei, H. Chen, S. Yang and J. Xu, J. Am. Chem. Soc., 2015, 137, 4460–4468 CrossRef CAS PubMed.
- N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Nature, 2015, 517, 476–480 CrossRef CAS PubMed.
- J. M. Stevenson, B. A. Sorenson, V. H. Subramaniam, J. A. Raiford, P. Khylabich, Y. L. Loo and P. Clancy, Chem. Mater., 2016 Search PubMed , submitted.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- F. Nesse, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 73–78 CrossRef.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- S. Plimpton, P. Crozier and A. Thompson, Sandia Natl. Lab., 2007 Search PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- I. Persson, K. Lyczko, D. Lundberg, L. Eriksson and A. Placzek, Inorg. Chem., 2011, 50, 1058–1072 CrossRef CAS PubMed.
- W. Li, J. Fan, J. Li, Y. Mai and L. Wang, J. Am. Chem. Soc., 2015, 137, 10399–10405 CrossRef CAS PubMed.
- S. Bae, S. J. Han, T. J. Shin and W. H. Jo, J. Mater. Chem. A, 2015, 3, 23964–23972 CAS.
- Y. Rong, S. Venkatesan, R. Guo, Y. Wang, J. Bao, W. Li, Z. Fan and Y. Yao, Nanoscale, 2016, 8, 12892–12899 RSC.
- R. S. Mulliken, Chem. Rev., 1931, 9, 347–388 CrossRef CAS.
- F. Hao, C. C. Stoumpos, Z. Liu, R. P. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 16411–16419 CrossRef CAS PubMed.
- F. Huang, Y. Dkhissi, W. Huang, M. Xiao, I. Benesperi, S. Rubanov, Y. Zhu, X. Lin, L. Jiang, Y. Zhou, A. Gray-Weale, J. Etheridge, C. R. McNeill, R. A. Caruso, U. Bach, L. Spiccia and Y.-B. Cheng, Nano Energy, 2014, 10, 10–18 CrossRef CAS.
- X. Guo, C. McCleese, C. Kolodziej, A. C. Samia, Y. Zhao and C. Burda, Dalton Trans., 2016, 45, 3806–3813 RSC.
- H. J. Yen, P. W. Liang, C. C. Chueh, Z. Yang, A. K. Jen and H. L. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 14513–14520 CAS.
- W. Nie, H. Tsai, R. Asadpour, J. C. Blancon, A. J. Neukirch, G. Gupta, J. J. Crochet, M. Chhowalla, S. Tretiak, M. A. Alam, H. L. Wang and A. D. Mohite, Science, 2015, 347, 522–525 CrossRef CAS PubMed.
- Z. Zhou, Z. Wang, Y. Zhou, S. Pang, D. Wang, H. Xu, Z. Liu, N. P. Padture and G. Cui, Angew. Chem., Int. Ed. Engl., 2015, 54, 9705–9709 CrossRef CAS PubMed.
- M. Yang, Y. Zhou, Y. Zeng, C. S. Jiang, N. P. Padture and K. Zhu, Adv. Mater., 2015, 27, 6363–6370 CrossRef CAS PubMed.
- G. Niu, H. Yu, J. Li, D. Wang and L. Wang, Nano Energy, 2016, 27, 87–94 CrossRef CAS.
- M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395–398 CrossRef CAS PubMed.
- Y. Tidhar, E. Edri, H. Weissman, D. Zohar, G. Hodes, D. Cahen, B. Rybtchinski and S. Kirmayer, J. Am. Chem. Soc., 2014, 136, 13249–13256 CrossRef CAS PubMed.
- Q. Dong, Y. Yuan, Y. Shao, Y. Fang, Q. Wang and J. Huang, Energy Environ. Sci., 2015, 8, 2464–2470 CAS.
- J. J. Choi, K. Bian, W. J. Baumgardner, D. M. Smilgies and T. Hanrath, Nano Lett., 2012, 12, 4791–4798 CrossRef CAS PubMed.
- M. Adachi, Y. Murata, J. Takao, J. T. Jiu, M. Sakamoto and F. M. Wang, J. Am. Chem. Soc., 2004, 126, 14943–14949 CrossRef CAS PubMed.
- J. Polleux, N. Pinna, M. Antonietti and M. Niederberger, Adv. Mater., 2004, 16, 436–439 CrossRef CAS.
- C. Schliehe, B. H. Juarez, M. Pelletier, S. Jander, D. Greshnykh, M. Nagel, A. Meyer, S. Foerster, A. Kornowski, C. Klinke and H. Weller, Science, 2010, 329, 550–553 CrossRef CAS PubMed.
- J. Yang, C. Xue, S. H. Yu, J. H. Zeng and Y. T. Qian, Angew. Chem., Int. Ed., 2002, 41, 4697–4700 CrossRef CAS PubMed.
- Y. Zhang, F. Huang and Q. Mi, Chem. Lett., 2016, 45, 1030–1032 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 046103 CrossRef PubMed.
- W. A. Saidi, M. Lee, L. Li, G. Zhou and A. J. H. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 245429 CrossRef.
- W. A. Saidi, J. M. Martirez and A. M. Rappe, Nano Lett., 2014, 14, 6711–6717 CrossRef CAS PubMed.
- J. Haruyama, K. Sodeyama, L. Han and Y. Tateyama, J. Phys. Chem. Lett., 2014, 5, 2903–2909 CrossRef CAS PubMed.
- A. T. Barrows, A. J. Pearson, C. K. Kwak, A. D. F. Dunbar, A. R. Buckley and D. G. Lidzey, Energy Environ. Sci., 2014, 7, 2944 CAS.
- C. Bi, Y. Shao, Y. Yuan, Z. Xiao, C. Wang, Y. Gao and J. Huang, J. Mater. Chem. A, 2014, 2, 18508–18514 CAS.
- H. B. Kim, H. Choi, J. Jeong, S. Kim, B. Walker, S. Song and J. Y. Kim, Nanoscale, 2014, 6, 6679–6683 RSC.
- S. Sun, T. Salim, N. Mathews, M. Duchamp, C. Boothroyd, G. Xing, T. C. Sum and Y. M. Lam, Energy Environ. Sci., 2014, 7, 399–407 CAS.
- L. F. Zagonel, M. Baurer, A. Bailly, O. Renault, M. Hoffmann, S. J. Shih, D. Cockayne and N. Barrett, J. Phys.: Condens. Matter, 2009, 21, 314013 CrossRef CAS PubMed.
- A. Kahn, Mater. Horiz., 2016, 3, 7–10 RSC.
- P. R. Brown, D. Kim, R. R. Lunt, N. Zhao, M. G. Bawendi, J. C. Grossman and V. Bulovic, ACS Nano, 2014, 8, 5863–5872 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ta07671h |
| This journal is © The Royal Society of Chemistry 2017 |