Electronic properties and third-order optical nonlinearities in tetragonal chalcopyrite AgInS₂, AgInS₂/ZnS and cubic spinel AgIn₅S₈, AgIn₅S₈/ZnS quantum dots

Abstract

Comprehensive studies on the electronic properties and spectral dependencies of the third-order nonlinear optical properties of quantum-confined tetragonal chalcopyrite AgInS₂ and its non-stoichiometric cubic spinel AgIn₅S₈ with reference to their corresponding Zn²⁺ alloyed compounds i.e. AgInS₂/ZnS and AgIn₅S₈/ZnS are presented in this work. Nonlinear refraction and nonlinear absorption in the quantum-confined nanocrystals were measured in a wide range of wavelengths (550–1200 nm) using the Z-scan technique. The results revealed the presence of strong two-photon absorption bands in the near-infrared range for both compounds. The impact of Zn²⁺ ion alloying was also investigated for both compounds revealing a significant increase of the cubic nonlinearity for the chalcopyrite quantum dots and a negligible change for the spinel-like quantum dots which was discussed as a consequence of different surface reconstruction mechanisms of the tetragonal and cubic nanocrystals. The cubic nonlinearity of the quantum dots is discussed in terms of electronic properties and linear dielectric function dispersions of both systems obtained within the density functional theory. Kinetics of the two-photon excited state recombination was investigated with the femtosecond time-resolved photoluminescence spectroscopy revealing the complex character of electronic relaxation in both systems. The results indicate that the optical properties of the tetragonal AgInS₂ and cubic AgIn₅S₈ quantum dots are much better suited for the steady-state as well as time-resolved multiphoton fluorescence techniques utilized commonly for bio-sensing applications than their CuIn_xS_y homologues.

---

Introduction

Although luminescence techniques are well recognized for their usability in medical assays and detection of various abnormalities at very low concentration levels, their major limitations will always be related to matching of an appropriate luminescence probe with a particular problem being solved. Steadily evolving diagnostic techniques optimized in their majority for better resolution and higher signal-to-noise (S/N) ratios impose still new requirements for the luminescence markers. This trend is well seen in the field of deep-tissue imaging, where maximization of the S/N ratio may be obtained within the first (NIR-I: 750–850 nm) and second (NIR-II: 1000–1400 nm) optical windows of body tissues. However, while the NIR-I/NIR-II spectral regions seem to be favoured from the technical point of view, scarcity of suitable markers working in those wavelength ranges forced researchers to search for various alternatives for the next generation of red-shifted luminescence markers. Among many candidates, much attention by scientists has been devoted to the ternary quantum dots (QDs) belonging to the A^IB^IIIX^VI group where A = (Cu, Ag), B = (In, Al, Ga) and X = (S, Se, Te).^1–4 This is mainly due to their cadmium-free chemical composition and favourable spectroscopic properties in both the energy and time domains which are well matched with those expected for the next generation probes.

Due to the size effect, the emission band maximum of the A^IB^IIIX^VI nanoparticles can be tuned over the red and the near infra-red (NIR) region allowing for multicolour imaging within the VIS/NIR bands with a single VIS line excitation. Special attention should also be given to the time domain properties of the A^IB^IIIX^VI QDs being characterized by appreciably long (100–250 ns) luminescence lifetimes. This time-scale of luminescence decays is quite unique for the quantum confined systems, and of great importance for any time-resolved techniques such as the fluorescence life-time imaging (FLIM).

It is known that metal-enhanced fluorescence or Förster energy transfers shorten the luminescence lifetime making the analysis very challenging for luminescent agents characterized by lifetimes shorter than 30 ns. On the other hand, long-living markers (micro- and milliseconds) seem to be not well matched to the megahertz range excitation sources typically used in the bio-imaging systems.

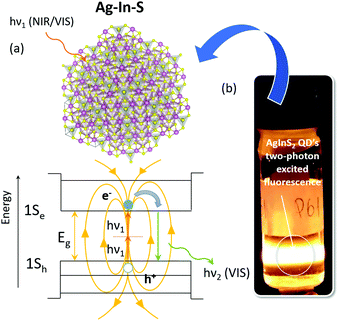
Furthermore, due to significant (e.g. 820 GM for the ca. 2.8 nm CuInS₂ QDs) values of the two-photon absorption cross-section (σ₂) and two-photon action cross-section (σ_TPE = σ₂η, η – quantum efficiency), application of the A^IB^IIIX^VI QDs is not limited to the one-photon operation, but can be easily extended into the regime of nonlinear excitation. This opens the way for efficient NIR-excited/NIR-emitting luminescence probes and their application in ultra-sensitive two-photon microscopy (see the Fig. 1), which has already been discussed in detail in our previous works concerning the CuInS₂ and CuInS₂/ZnS representatives of such probes.^5,6

Fig. 1 (a) Schematic diagram of the virtual states mediated two-photon (TPA) absorption process in the Ag–In–S QDs. (b) Representative image of a colloidal solution of AgInS₂ QDs excited by an 800 nm laser beam (no focusing optics were used).

In general, the whole ternary A^IB^IIIX^VI semiconductor group is characterized by rather rich physicochemistry and defect related properties, which is mainly related to their chemical composition and complex mechanisms of surface charge minimization compared to their binary analogues.⁷ This requires one to give special attention to different homologues of the well-known CuInS₂ like AgInS₂ as well as its non-stoichiometric derivatives.

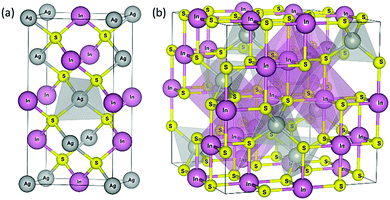
Currently the most studied phase of the AgInS₂ compound is the chalcopyrite AgInS₂ (t-AIS, see Fig. 2) (space group: I4̄2d (No. 122)) crystallizing in the tetragonal system. The chalcopyrite is a direct structural analogue of the II–VI compounds in which each anion is coordinated by two different types of cations, leading to structural changes in the unit cell, formation of uneven chemical bonds and different mechanisms of structural reconstruction at the interface regions. As a result of its chemical composition the A^IB^IIIX^VI compounds are characterized by large tolerance to the off-stoichiometry, being able to exist in a number of non-stoichiometric phases characterized by different structural order, electrical and optical properties and different underlying physics.

Fig. 2 Graphical representation of the unit cell diagram for (a) stoichiometric chalcopyrite AgInS₂ and (b) non-stoichiometric spinel AgIn₅S₈. The indium atoms are coloured purple, and the random location of the indium and silver atoms over the tetrahedral sites is represented as gray spheres and the sulfur atoms are presented in yellow.

Because of its atomic structure implicating relatively dense electronic band location, one of the most interesting non-stoichiometric phases seems to be the AgIn₅S₈ (c-AIS) crystallizing in a cubic spinel-type structure. Several works have already been devoted to the study of AgIn₅S₈ crystals,^8,9 the synthesis of the quantum confined nanocrystals^10–12 as well as their interesting applications in the quantum dot based light emitting diodes¹³ and the role of luminescence markers in bio-imaging and detection.¹⁴ According to the studies performed by Delgado et al.¹⁵ the non-stoichiometric c-AIS crystallizes in a normal spinel structure (space group Fd3̄m (No. 227)) in which 4/5 of the indium (In) atoms occupy the octahedral sites and 1/5 of the In atoms, along with the silver (Ag) atoms that are randomly distributed over the tetrahedral sites as described by the general formula (AgIn)_t(In₄)_oS₈ (see Fig. 2). This change in the structural order has important consequences for the local electronic density, d-electron correlations and finally for the electronic structure of the t-AIS QDs, which is discussed broadly in this paper.

In our previous work we have shown that mechanisms of surface charge state minimization play an important role in the excited state relaxation taking part in the formation of the dark states related to the presence of charged excitons in the QDs followed by effective nonradiative relaxations.¹⁶

It seems that re-localization of the two cations over the tetrahedral and octahedral sites in the spinel-like structure may have important consequences for the mechanisms of surface charge minimization, for the response to the heterogenic ion alloying as well as for the cubic hyperpolarizability of the nanostructures, which are the main subjects of this study.

In this work we report a comprehensive study of the electronic properties and the third-order nonlinear optical response of the stoichiometric tetragonal t-AIS and non-stoichiometric cubic c-AIS quantum confined colloidal nanostructures in comparison with their corresponding Zn²⁺ alloyed QDs. Because of the important impact of the structural order on the optical properties of the QDs, the electronic properties of both systems are discussed widely in terms of the ab initio results i.e. the electronic band structure and the linear dielectric function obtained within the density functional theory (DFT) formalism. The nonlinear absorption and refraction of the QDs were studied in a wide-wavelength range (500–1500 nm) using the femtosecond open- and closed-aperture Z-scan technique. All the results are discussed in terms of the theoretical results obtained by the DFT calculations. Particular attention has also been given to the impact of different mechanisms of surface charge state minimization in the t-AIS and c-AIS QDs, studying the influence of Zn²⁺ ion alloying on the optical properties of corresponding derivatives like the t-AIS/ZnS and c-AIS/ZnS alloys.

Although biomedical applications of multiphoton microscopy are steadily increasing, quantitative information regarding the multi-photon absorption spectra of relevant fluorophores using various excitation and detection wavelengths is still severely lacking. The determination of the relative figures of merit for the t-AIS, t-AIS/ZnS and c-AIS, c-AIS/ZnS QDs in the nonlinear regime should allow one to compare different materials as well as open the way for further optimization and design of more efficient materials.

Experimental

Synthesis procedure

The investigated nanocrystals were prepared using the metathesis reaction between metal thiolates and a sulfur source.¹⁰ The following reagents were used as received and without further purification: indium(III) acetate (In(OAc)₃, 99.99%), silver nitrate (AgNO₃, 99.9%), 1-dodecanethiol (DDT, 98%), zinc stearate (C₃₆H₇₀O₄Zn) and sublimated sulfur (S, 99%). In the standard procedure the AgInS₂ (t-AIS) QDs were synthesized using stoichiometric amounts of In(OAc)₃ (0.4 × 10⁻³ mol) and AgNO₃ (0.4 × 10⁻³ mol) mixed in an excess of DDT (20 cm³) in a three-neck flask. The AgIn₅S₈ (c-AIS) QDs were synthesized with a non-stoichiometric substrate ratio of (0.5 × 10⁻³ mol) In(OAc)₃ and (0.1 × 10⁻³ mol) AgNO₃. The sulfur precursor was prepared separately for each synthesis by dissolving a small excess of sublimated sulfur powder in 3 cm³ of DDT. At first a mixture of AgNO₃, In(OAc)₃ metal salts and DDT was preheated and degassed at 60 °C for 30 minutes and followed by the formation of Ag–In thiolates at 110 °C. After the formation of thiolates, the sulfur source was swiftly injected into the flask, inducing the formation of Ag–In–S QDs. The obtained QDs were washed in a mixture of methanol/chloroform (1 : 1) four times. After that, the washed QDs were precipitated using methanol and finally dispersed in chloroform. The alloyed t-AIS/ZnS and c-AIS/ZnS QDs were formed in a separate step using previously synthesized t-AIS and c-AIS QDs.

Synthesis of the Zn²⁺ alloyed QDs was started using washed and dispersed AIS QDs in chloroform samples. Each sample of pristine t-AIS and c-AIS QDs was divided by half. One half was left as a corresponding AIS reference sample and the second half was mixed in a three-neck flask with (20 cm³) DDT and (0.4 × 10⁻³ mol) zinc stearate. The mixture was preheated at 60 °C and it was followed by AIS/ZnS QDs formation at a moderate temperature of 120 °C for a constant time of 15 min. The obtained product was washed according to the same procedure as used for the AIS QDs and finally dispersed in chloroform.

Measurement details

Structural and morphological properties of the QDs were investigated with an FEI Tecnai G² 20 X-TWIN transmission electron microscope (TEM) and a Renishaw inVia confocal Raman microscope setup. The X-ray diffraction measurements have been performed using a PANalytical X'Pert-Pro diffractometer system working with the Cu K-alpha1 λ = 1.5405980 Å wavelength.

The chemical composition of the samples was analyzed by energy-dispersive X-ray spectroscopy (EDS), performed on a JEOL JSM-6610LVnx scanning electron microscope (SEM) equipped with an Oxford Aztec energy-dispersive X-ray spectroscopy analyser (EDS). The absorption and one-photon excited emission spectra of AIS QDs were obtained with a JASCO V670 spectrophotometer and a Shimadzu UV-3600 spectrofluorometer, respectively.

The Z-scan measurements of the colloidal QDs were performed on their dispersions in chloroform at the concentration of ca. 2% w/w ratio placed in 1 mm glass cells. The laser system used for the Z-scan measurements consisted of a Quantronix Integra-C regenerative amplifier operating as an 800 nm pump and a Quantronix-Palitra-FS BiBO crystal-based optical parametric amplifier. We used the standard open-aperture (OA) and closed-aperture (CA) Z-scan technique introduced by Sheik-Bahae et al.¹⁷ for the determination of the nonlinear optical parameters, the detailed description of the experimental setup can be found in our previous papers.¹⁸

Relaxation of excited states after two-photon excitation of the colloidal nanocrystals was investigated by the femtosecond time-resolved photoluminescence spectroscopy (TRPL).

The laser setup used for the TRPL measurements consisted of a Coherent Libra-S all-in-one ultrafast oscillator, a regenerative amplifier laser system with <100 fs pulse duration and 1 kHz repetition rate, a Coherent OPerA-Solo optical parametric amplifier and a Hamamatsu C5677 streak camera with a time resolution of 14 ps.

Calculations of the ground-state properties and optical response functions of the AgInS₂ and AgIn₅S₈ crystals were performed on the basis of density functional theory (DFT+U) formalism within the projector augmented wave (PAW) method as implemented in the ABINIT software package.¹⁹ More details about the calculations may be found in the ESI.†

The photoluminescence quantum yield measurements of the QDs were performed using an integration sphere setup of the Edinburgh Instruments FLS 980 Spectrometer.

Results and discussion

The microstructural and morphological characterization of the QDs was performed using transmission electron microscopy (TEM). The size of the as prepared bare t-AIS QDs was estimated to be d = 2.80 nm with standard deviation σ = 0.23 nm, while for c-AIS d = 2.51 nm and σ = 0.17 nm. The zinc alloyed counterpart QDs i.e. t-AIS/ZnS and c-AIS/ZnS were found to be slightly larger compared to their reference precursors i.e. d = 2.87 nm σ = 0.34 nm and d = 2.53 nm, σ = 0.18 nm, respectively (for more details on the TEM studies see Fig. 5s and 6s in the ESI†). It seems to be in accordance with the expectations as the relatively short process of cation exchange at the surface of the QDs shall not be responsible for thick shell layer formation. Due to the small size and substantial content of the organic ligands at the QD surface, further identification of the structural properties based on the TEM micrographs was not quite satisfactory.

XRD analysis revealed very weak structural ordering in both of the t-AIS and c-AIS QD samples (see Fig. 2s of the ESI†). It is not surprising if one considers the average size of the nanocrystals. Nevertheless the broadening of XRD reflections, clear shifts and the presence of additional reflections in the low angle range give an important premise about the different structural order between the t-AIS and c-AIS samples. No significant difference between the pristine t-AIS, c-AIS QDs and their zinc (Zn²⁺) alloyed counterparts was observed based on the XRD measurements. Some additional information about the structural properties of the QDs was gained based on their characteristic vibrational properties. As expected, significant broadening of the active Raman modes was observed for all the samples due to the very small size of the QDs, in the range 2.5–2.8 nm (see Fig. 4s, ESI†). Nevertheless, the positions of the Raman peaks obtained for both t-AIS and c-AIS QDs were in agreement with the reference patterns (RRUFF Database). Although exact identification of the modes was effectively hindered by the size-dependent broadening and overlapping of the Raman peaks, some interesting information could be still gathered taking into account the group of the most intensive bands in the spectra. The Raman spectra of the t-AIS QDs were dominated by a maximum at about 280–290 cm⁻¹. The results are consistent with the one already reported in our previous work.¹⁶ This band is typically attributed to the chalcopyrite (space group: I4̄2d (No. 122)) anionic sub-lattice vibrational modes.²⁰ It is worth noting that changes in this band after the Zn²⁺ alloying may be well indicative of the structural changes at the surface of the QDs. However a decrease in the intensity of the 280–290 cm⁻¹ band observed for the t-AIS/ZnS sample shall be rather be associated with the higher content of the organic phase in the sample. The most intensive modes of the c-AIS crystallising in the cubic spinel (space group Fd3̄m (No. 227)) structure were found at about 240 cm⁻¹ and 340 cm⁻¹ being in good relation with the reference spectra obtained from the RRUF database. Nevertheless the EDS analysis confirmed the presence of Zn ions in the samples and no significant changes in the Raman spectra have been found for the c-AIS/ZnS QDs. It is also worth noting that the I–III–VI compounds are characterized by complex reconstruction mechanisms related to minimization of the uncompensated surface charge.¹⁶ These mechanisms may be responsible for significant shifts of the Raman modes, as the surface-to-volume ratio for such nanoparticles reaches quite high values.

The EDS compositional analysis was used to investigate the stoichiometry of the as synthesized t-AIS and c-AIS QDs as well as their zinc alloyed counterparts (see Fig. 3s of the ESI†). The t-AIS QDs have been found as almost stoichiometric compounds where the Ag/In atomic ratio was found as 1.08. The over stoichiometric amount (0.7) of the S/Ag ratio equal to 2.7, has been associated with the excess of the DDT ligand typically found in the prepared solutions.

The chemical composition of the c-AIS QDs revealed silver rich samples characterized by the In/Ag ratio equal to 4.39. It is likely that the indium (In³⁺) deficiency may be assigned to the insufficient fill of the tetrahedral sites normally occupied by the Ag⁺ atoms according to the formula (Ag_1.61In_0.39)_t(In₄)_tS₈. The S : Ag ratio was found as 9.35 being in good agreement with the expectations. Analysis of the zinc alloyed samples generally confirmed the expected presence of the zinc atoms in the synthesized samples; however, a small deficiency (0.1) of the Zn atoms was found for the c-AIS sample.

In this work, the discussion on the electronic properties and optical nonlinearities of both systems i.e. t-AIS and c-AIS is supported by the results obtained from the ab initio DFT+U calculations (see the ESI† for more information).

All the numerical calculations were performed for an ideal infinite crystal. Although quantum confinement effects have been omitted in the calculations, their impact on the electronic structure of the materials may still be well predicted, without harm to the results and further discussion about the underlying physics of the processes observed in those materials. An eight atom primitive cell was used for calculation of the ideal chalcopyrite crystal (Fig. 1s of the ESI†). The 72 valence electrons were considered in the calculations including 11 electrons per silver (Ag), 13 electrons per indium (In, 10 d-electrons) and 6 electrons per each sulfur (S) atom. As expected, the tetragonal AgInS₂ was found to be a direct gap semiconductor with a band gap value of E_g = 1.89 eV. This value is consistent with the experimental values (1.86 eV) reported by other authors, e.g. You et al.²¹ Due to the p–d hybridization and the resulting down-shift of the uppermost valence bands²² significant correction values were needed for the screened Coulomb interaction (9.0 eV) and screened exchange (0.9 eV, 10% of U) to get the E_g close to the values reported experimentally.

The calculated bond lengths for the A^I–S and B^III–S sub-lattices and the tetrahedral distortion parameter u of the tetragonal system were found to be L_AX = 2.517 Å, L_BX = 2.316 Å and u = 0.219, respectively (all values are gathered in Table 1s of the ESI†).

Calculations of the non-stoichiometric c-AIS were more complicated due to the need of taking into account the random distribution of the 1/5 of indium atoms over the tetrahedral sites along with silver atoms. As the random distribution model requires one to use a large super cell (ca. 100 atoms) with a large number of valence electrons and thus large reserves of computational resources, a simplified approach was used in this work. The compound was modelled using a 14 atom primitive cell of the corresponding cubic (Ag₂)_t(In₄)_oS₈ for which both silver (Ag⁺) atoms are located over the tetrahedral sites and all indium (In³⁺) atoms are distributed over the octahedral sites (see Fig. 1s of the ESI†). Distribution of the additional 1/5 of the indium atoms over the tetrahedral sites was modelled by a direct substitution of one Ag⁺ atom in the primitive cell by the In³⁺ resulting in the formation of a compound described by the general formula (AgIn)_t(In₄)_oS₈ (Fig. 1s of the ESI†). Such simplification requires one to deal with the number of valence electrons reduced to 124 electrons and 62 valence bands originating from 1 × Ag (11 el.), 5 × In (65 el.) and 8 × S (48 el.) atoms. Some structural distortions were found in the modelled structure. Both Ag⁺ and In³⁺ ions located over the tetrahedral sites (A^I–S)_t were characterized by different bond lengths.

Characteristic bond lengths for the (Ag–S)_t and (In–S)_t sub-lattices were found to be L_AX = 2.434 Å and L_BX = 2.491 Å, respectively. Significant distortions were also found for all octahedral sites (B^III–S)_o due to partial redistribution of the In³⁺ ions over the tetrahedral sites characterized by different ionic radii and bond lengths. The characteristic (In–S)_o bond length values varied from L_BX = 2.491 Å up to 2.654 Å.

The calculated band gap value for the modelled (AgIn)_t(In₄)_oS₈ compound was E_g = 1.27 eV. This value is much lower than the values reported in the literature by other authors i.e. Gasanly et al. E_g = 1.94 eV,²³ A. Usujima et al. E_g = 1.8 eV at 300 K and E_g = 1.9 eV at 96 K,²⁴ C. Paorici et al. E_g = 1.7 eV²⁵ and M. Isik et al. E_g = 1.84 eV.⁸ For comparison, the energy band gap of the base (Ag₂)_t(In₄)_oS₈ compound was calculated to be E_g = 2.66 eV which shows significant reduction after redistribution of the In³⁺ ions over 1/2 of the tetrahedral sites.

The Kohn–Sham electron energy dispersions in the first Brillouin zone (BZ) of the t-AIS and c-AIS crystals are shown in Fig. 3. Due to the complex character of the band structure the plots have been limited to the band gap region energy. Full dispersions may still be found in the ESI† (Fig. 7s). For both materials the valence band maximum (VBM) and the conduction band minimum (CBM) are located at the centre of the BZ (Γ: 0.0, 0.0, 0.0). Along with the Γ point VBM, the BZ of t-AIS is also characterized by two secondary maxima located at the zone edges and by higher energy transitions. The character of this maxima is well reflected in the absorptive part of the dielectric function Im{ε(ω)} (see Fig. 3c), which is dominated by several maxima corresponding to different resonances located in the energy window between 1.0 and 5.0 eV. It has to be pointed out that the excitonic contribution to the Im{ε(ω)} involving the application of the Bethe–Salpeter formalism was not considered in the current work. The lowest energy maximum of Im{ε(ω)} is well associated with the fundamental transitions of band–band E_g(Γ–Γ) and the split-off bands located at the zone centre. The second maximum may be assigned to the higher energy E(Γ) transitions at the BZ centre. The third maximum is attributed to the BZ edge transitions in all the equivalent 〈100〉 directions.¹⁶

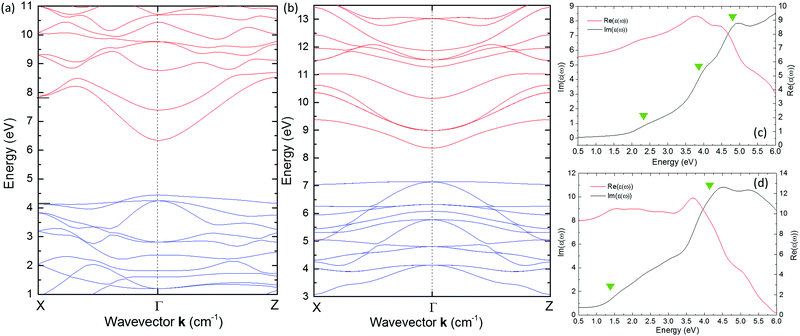Fig. 3 The Kohn–Sham electronic band structure calculated for the (a) tetragonal chalcopyrite AgInS₂ (t-AIS) and the (b) cubic spinel AgIn₅S₈ (c-AIS) crystals. Dispersions of the real (red) and imaginary (black) parts of the dielectric function have been shown in the figure (c) for the t-AIS and (d) for the c-AIS crystals. More details about the calculations may be found in the ESI.†

Dispersion of Im{ε(ω)} for the cubic spinel c-AIS structure is shown in Fig. 3d. As the band structure of the spinel c-AIS is characterized by a single maximum located at the zone centre, the first maximum of Im{ε(ω)} is then assigned to the fundamental E_g(Γ–Γ) transitions and parabolic band filling to the higher energy transitions at the E(Γ) point.

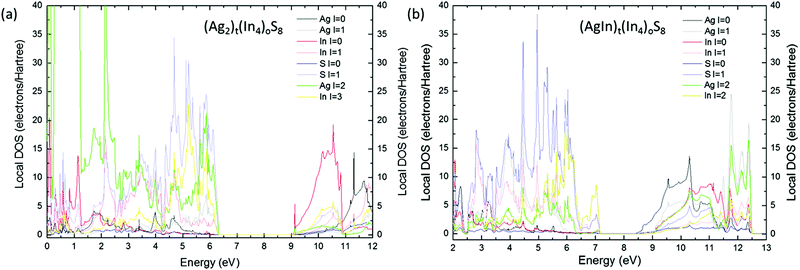
The uppermost valence bands of the t-AIS compound are dominated by the p-electron character (Fig. 4a). It is well seen that the valence band maximum consists mostly of the 3p electrons of sulfur (S). One may see a distinct contribution of the Ag and In d-electrons to the VBM states with the dominating character of the 4d Ag electrons. Typically the contribution of Ag d-electrons to the DOS reaches its maximum at about 4.5 eV deep in the valence band, whereas the In d-electron states form an even deeper maximum located ca. 18 eV below the VBM. The s-electrons of indium atoms are pushed to the conduction band minimum which consists mostly of the In and S s-electron states.

Fig. 4 Local density of states (DOS) calculated for (a) t-AIS and (b) c-AIS as a function of energy in the proximity of the band gap region. The color scheme was used to identify different contributions i.e. colour black for Ag 5s, gray for Ag 4p, red for In 5s, light red for In 5p, dark blue for S 3s and light blue for S 3p electrons. The d-electrons of silver and indium were depicted, respectively, in green and yellow.

A different character of the uppermost valence bands was found for the (AgIn)_t(In₄)_oS₈ model which is shown in Fig. 4b. For this model the valence band maximum consists mostly of the 3p electrons of S atoms with evident dominating character of the 5d states of indium which have been pushed toward the band gap region. The origin of these states may be well explained taking a look at the density of states (DOS) calculated for the base structure i.e. (Ag₂)_t(In₄)_oS₈ containing all the tetrahedral sites filled up by silver atoms (see Fig. 9s of the ESI†). It was found that the presence of these states is directly related to the indium atoms occupying the tetrahedral sites.

This explains the decrease of the effective band gap after redistribution of the In atoms over the tetrahedral sites.

Significant changes have also been observed for the first excited states of the c-AIS. At first a lower contribution from the Ag d-electrons in the c-AIS was observed, which were pushed to the conduction band. The conduction band minimum of the base (Ag₂)_t(In₄)_oS₈ is typically dominated by the In s-electrons with a lower contribution from the In 5d, S 3p and In p-electrons. The Ag s-states are located typically about 3 eV deep in the conduction band. This picture is significantly changed if as-modelled c-AIS is taken into consideration. For (AgIn)_t(In₄)_oS₈ the CBM is dominated by the Ag s-electron states. In such a structure the In s-electron states have been pushed significantly toward higher energies decreasing the contribution of In s-electrons to the minimum of the conduction bands. These results give important physical premise concerning the non-stoichiometric c-AIS compound, showing that the band gap value and the optical properties might be tailored controlling the number of indium atoms located over the tetrahedral sites of the structure. The optical absorbance spectra (Fig. 5, black and red solid lines) obtained experimentally seem to be in agreement with the theoretical results.

Fig. 5 Size-dependent effective two-photon absorption cross section σ₂ [GM/NP] taken per individual nanoparticle: (a) t-AIS QD (black circles) and its corresponding t-AIS/ZnS (red squares) and (b) c-AIS QDs (black circles) and its corresponding c-AIS/ZnS (red squares). One-photon absorption (solid line – right scale) is also replotted here against doubled wavelength values for comparison (dashed lines).

Quantum confinement of the states close to the band edges has been observed as a significant blue-shift (ca. 1.0 eV) of the absorption edge of the samples. A further blue-shift of the absorption edge was also observed after alloying of the t-AIS QDs with zinc ions. The c-AIS QDs were characterized by a much smaller blue-shift effect than that observed for t-AIS. This seems to be consistent with the experimental studies performed by Orlova, showing that alloying of AgIn₅S₈ with different impurities like Zn²⁺ ions has a slight effect on the electro-optical properties of the compound.²⁶

The blue-shift of the absorption edge of the I–III–VI₂ is a well-known effect in the group which stands in contrast to the well-known red-shift, observed typically in the core–shell systems.²⁷ This effect is typically associated with the cation exchange mechanism in which the Ag⁺ and In³⁺ ions are exchanged by Zn²⁺ ions resulting in effectively smaller QDs. These results seem to be in line with the TEM data showing almost no change in the size of the QDs after their alloying with the Zn²⁺ ions. Deep diffusion of the Zn²⁺ ions seems to be not likely due to a moderate synthesis temperature of 120 °C.

A larger blue-shift observed for the t-AIS suggests that the blue-shift effect is strongly related to the crystal structure of both compounds showing that this process may not be thermodynamically favoured for this type of crystal structure.

Special attention should also be given to the surface reconstruction mechanisms having important implications for the optical properties of the 2–3 nm sized QDs. It has been shown in our previous work¹⁶ that t-AIS QDs tend to minimize their surface charge mainly by the formation of S–S bonds and their higher order oligomers with a simultaneous shift of the cation sub-lattices forming a metallic-like sub-layer characterized by a dense spectrum of states. This effect has important consequences for the number of surface states responsible for deep charge trapping and disturbance of the total charge in the QDs. The charge disturbance is further responsible for exciton charging, opening the way for fast non-radiative Auger relaxations being associated with long-lived dark states in the photoluminescence time traces recorded from a single QD.

The experimental data on nonlinear refraction and nonlinear absorption of the colloidal t-AIS, non-stoichiometric c-AIS and their corresponding alloyed structures in the form of t-AIS/ZnS and c-AIS/ZnS were determined in a wide spectral range, from 600 nm up to 1200 nm. It should be noted that a large number of papers describing the nonlinear optical (NLO) studies performed on colloidal solutions quote the macroscopic non-linearity of the solute–solvent system, usually the nonlinear refractive index n₂ and the nonlinear absorption coefficient β. The results presented in that way do not allow one to make any comparisons between different systems since the results depend on the concentration of the active material in the solution as well as on the composition of the nanosystems under investigation. A more useful way is to provide the results taken per single QD, which also allows one to extrapolate the results to a hypothetical pure bulk material or to normalize e.g. by the molecular weight of the particle.

Therefore, in this work the NLO parameters were calculated and presented as values of the real and imaginary parts of the cubic hyperpolarizability γ(−ω; ω, −ω, ω), as well as the effective two-photon absorption cross section σ₂ (see the ESI† for Re(γ) and Im(γ) dispersion).

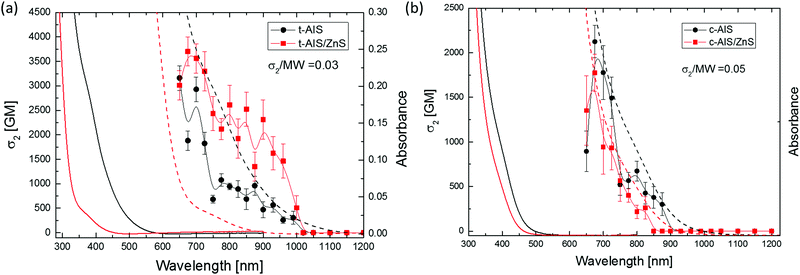
The values of σ₂ calculated for the QDs, as well as those for their corresponding alloyed derivatives, are presented in Fig. 5. The imaginary (absorptive) part of γ shows well-defined peaks in the range of laser wavelengths ca. 650–1000 nm for t-AIS and t-AIS/ZnS and ca. 650–900 nm for c-AIS and c-AIS/ZnS QDs (see Fig. 10s in the ESI† for Im(γ) dispersion), thus indicating the existence of nonlinear absorption processes in those wavelength ranges. The large scatter of the Re(γ) data points is due to the fact that even at the relatively high concentration (ca. 2%) of the QDs in the chloroform solution, the nonlinear refraction response of the samples is still mostly dominated by the solvent and the cell walls.

The strength of the nonlinear absorption of the investigated QDs, plotted as the effective two-photon absorption (TPA) cross-section taken per single QD, is shown in Fig. 5. The t-AIS QDs were characterized by high values of the two-photon absorption cross-section, and σ₂ for the t-AIS QDs was measured to be 3.16 × 10⁻⁴⁶ cm⁴ s per NP or σ₂ = 3160 GM (Goeppert-Mayer units) at 675 nm. The two-photon absorption cross section of the zinc alloyed c-AIS/ZnS QD was found to be slightly lower compared to their unalloyed analogues. The highest value of σ₂ for the c-AIS/ZnS was found to be σ₂ = 1.77 × 10⁻⁴⁸ cm⁴ s per NP or 1770 GM at 675 nm. These results correspond to σ₂/M_W = 0.03 (where M_W is the molecular weight of a single QD) and σ₂/M_W = 0.05 for the t-AIS and c-AIS QDs, respectively, showing that both types of QDs are characterized by comparable values of the TPA strength.

However, when compared to their Cu containing analogues previously investigated by us,⁶ both c- and t-AIS/ZnS QDs showed an increase in the molecular weight scaled two-photon absorption cross-section values.

There are several features of the data presented in Fig. 5 that are worth noting. The nonlinear absorption spectra of the chalcopyrite t-AIS and t-AIS/ZnS QDs do not show any simple relation to the one-photon spectra. In particular, the maxima of the nonlinear absorption of the t-AIS QDs do not match the absorption edge in the one-photon absorption spectra. It was found that the TPA bands correspond to a higher energy transitions rather than the first excitonic band. It was also observed that the effective two-photon absorption cross-section was higher for the t-AIS/ZnS QDs than for the corresponding bare t-AIS QDs. The most significant difference between the t-AIS and t-AIS/ZnS QDs was Δσ₂ = 542 GM (17%).

The major factors responsible for the σ₂ differences involve the localization of the electron and hole wavefunctions in the core region which increases the Coulombic energy of the excitonic bound states E_x,n. The impact of Zn²⁺ alloying is therefore on the increase of the excitonic contribution to the third-order susceptibility. Furthermore, the TPA spectra of the t-AIS and t-AIS/ZnS QDs are characterized by a strong dispersion of σ₂ showing clearly the presence of at least two secondary maxima. The presence of these maxima may be well correlated with the character of the t-AIS electronic band structure shown in Fig. 3. The energy difference between the TPA sub-band maxima (ca. 0.12 eV and ca. 0.22 eV) may be well associated with the higher energy electronic transitions originating from the confined CBM states and the VBM split-off band states at the E(Γ) point in the BZ, as the calculated energy difference between the split-off bands at E(Γ) is 0.197 eV which corresponds well with the experimental value of 0.22 eV. It seems to be reasonable that electronic transitions between the split-off band states should be well pronounced in the σ₂ dispersion, due to the large difference between the effective masses of electrons and holes in the chalcopyrite structure implying rather weak confinement of the valence band states in the QDs. The dispersion of σ₂ for the cubic spinel structure is of different character, showing a rather narrow band in good agreement with the single-photon absorption spectra. The character of these bands may also be well explained looking at the electronic band structure of the cubic spinel (see Fig. 3). The bands may be associated with the excitonic contribution and electronic transitions between the higher energy states formed by the Ag s-electrons which constitute the CBM in the c-AIS crystal. A comparison of the σ₂ normalized by the molar weight between both the t-AIS and the c-AIS systems shows rather comparable values 0.03 and 0.05 respectively. While analysing of the nonlinear properties of these materials one has to consider the type atoms which constitute the material, the number of valence electrons and the character of the chemical bonding. In group I–III–VI compounds there is mixed character of the bonds formed between the A^I–X^VI and the B^III–X^VI atoms. Moreover the ab initio studies performed by the J. E. Jaffe and Alex Zunger²⁸ have already shown that the A^I–X^VI bonds have a large ionic component compared to the highly covalent B^III–X^VI bonds. This has important implications for the nonlinear response as it is expected that the nonlinear susceptibility will increase with the decrease of the bond length for the ionic bonds and will be of opposite character for the covalent bonds. Moreover the d-electrons of the A^I and B^III atoms shall also be considered as valence electrons analysing the nonlinear behaviour of the samples. For the t-AIS compounds L_AX = 2.517 Å and L_BX = 2.316 Å are found almost comparable with a little bit longer A^I–X^VI bond. The c-AIS was found to be more disordered due to the presence of In³⁺ ions in the tetrahedral sites, with large deviations between the B^III–X^VI octahedral bonds ranging from 2.491 Å up to 2.654 Å. It is believed that these sites give the highest contribution to the nonlinear response of the samples. The lower value of σ₂ may then be considered as a result of the Ag rich sample for which the structure is less disordered.

The quantum yields of bare t-AIS and c-AIS QDs were measured as ca. 11.4% and 19.1% respectively. Significantly higher values were noticed for the t-AIS/ZnS alloyed sample QY = 23.5% with almost no effect on c-AIS/ZnS QY = 19.8%, respectively. Based on that one may estimate the two-photon action cross-sections σ_TPE = σ₂η at the level of ca. 360 GM and ca. 338 GM for t-AIS and cubic c-AIS, respectively, and ca. 870 GM and ca. 420 GM, respectively, for the Zn²⁺ alloyed analogues i.e. t-AIS/ZnS and c-AIS/ZnS. Besides the σ_TPE it was found that t-AIS QDs were characterized by much longer PL lifetimes than the cubic spinel c-AIS (Fig. 6). No significant increase in the PL intensity was observed for the alloyed c-AIS/ZnS QDs. This was in clear contrast to their tetragonal analogues (see Fig. 12s, ESI†). Reduction of the luminescence lifetime for the c-AIS QDs may, however, be a result of effective nonradiative relaxation paths in such structures due to the silver rich off-stoichiometry and the presence of a large number of defects in the c-AIS QDs. Nevertheless, one needs to notice that such non-stoichiometric samples may be characterized by significantly different behaviour from sample to sample.

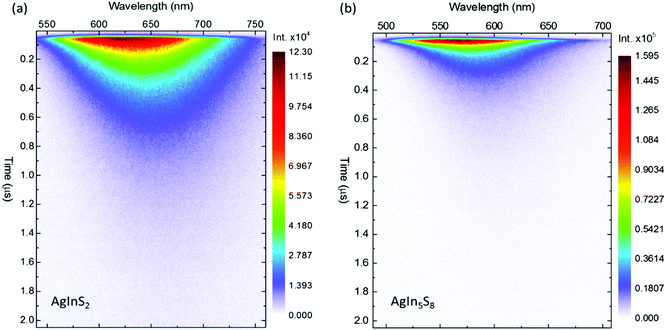Fig. 6 Streak camera images of the time-resolved photoluminescence (TRPL) of two-photon excited (a) AgInS₂ and (b) AgIn₅S₈ quantum dots. The excitation wavelength λ_ex = 800 nm. The TRPL spectra of the corresponding AgInS₂/ZnS and AgIn₅S₈/ZnS quantum dots may be found in Fig. 1s of the ESI.†

A notable common feature of the data is related to a distinct red-shift of the emission maximum as the function of time elapsed from the excitation event. As the red-shift is not clearly dependent on the structural properties it may be somehow associated with the surface effects as discussed in our last work considering AgInS₂ and AgInS₂/ZnS single particle spectroscopy.¹⁶

Conclusions

In summary, a comprehensive study of the electronic properties, and the linear and third-order nonlinear optical response of the chalcopyrite AgInS₂ and non-stoichiometric spinel AgIn₅S₈ QDs has been reported in this work. Both the systems have been widely investigated by comparing them to their analogous nanocrystals that are alloyed with Zn²⁺ ions for additional information about the surface effects i.e. structural reordering after surface cation exchange and their influence on the optical properties of the QDs.

Electronic energy dispersions of both systems were analysed with respect to the experimental results and have been calculated within the density functional theory and local density approximation. According to the theoretical results, both systems were found to be direct-gap semiconductors with the t-AIS E_g = 1.89 eV and c-AIS E_g = 1.27 eV. Although the t-AIS energy gap value was found close to the values reported experimentally, the c-AIS E_g value was significantly lower compared to the literature reports. According to the applied model, it was shown that the decrease of the band gap value for the spinel-like structure results from relocation of the In³⁺ ions over the tetrahedral sites of the (AgIn)_t(In₄)_oS₈ whose electronic states are located in the energy gap region pushing the In 5s states deeper in the conduction band with simultaneous pulling down of the Ag 5s states toward the CBM. According to the results, one may predict that Ag rich (Ag_xIn_1−x)_t(In₄)_oS₈ may have higher values of the energy band gap. The calculated linear optical response of the QDs was qualitatively in good agreement with the results measured experimentally. A more complex character of Im{ε(ω)} was found for the t-AIS crystal showing several maxima associated with the electronic transitions at different locations of the first BZ. The Im{ε(ω)} of the c-AIS compound is dominated mostly by the fundamental and higher energy transitions at the E(Γ) point.

Large nonlinear absorption in the spectral range of 550–1500 nm was observed for all the measured QDs. A two-photon process was identified to be the mechanism responsible for the non-resonant nonlinear absorption in both t-AIS and c-AIS quantum dots. The most significant values of the two-photon absorption cross-section σ₂ = 3.7 × 10⁻⁴⁸ cm⁴ s per NP or 3700 GM (Goeppert-Mayer units) were found for the tetragonal AIS/ZnS QDs at ca. λ_ex = 720 nm where σ₂ of the c-AIS/ZnS QDs was found to be 2.12 × 10⁻⁴⁶ cm⁴ s per NP or 2120 GM at ca. 675 nm. Changes in the σ₂ between the two types of QDs should be related to their electronic properties as the sizes of the QDs may be seen as comparable and size dependent changes of the TPA might be neglected.

The impact of Zn²⁺ ions was observed only for the chalcopyrite AIS QDs and was seen as an increase in the values of σ₂, which should be associated with the localization of the electron and hole wavefunctions in the core region. Small changes of the c-AIS σ₂ after Zn²⁺ alloying are more difficult to explain, however their origin may be found in different mechanisms of structural reconstruction and dangling bond minimization.

The time-resolved measurements revealed similarly complex character of electronic relaxation in both types of QDs. A significant temporal red-shift of the PL maximum with large deviation from the first-order decay law was observed for both types of QDs. Higher values of the two-photon action cross-section were found for the t-AIS QD which is well seen on the TRPL spectra. The t-AIS QDs were also characterized by significantly longer PL lifetimes, and thus they may be considered as better candidates for time-resolved two-photon experiments.

The results indicate that the optical properties of the chalcopyrite AgInS₂/ZnS and AgInS₂ quantum dots make them potentially better candidates for steady-state and time-resolved single/multiphoton fluorescent bio-probes compared to the CuInS₂ based analogues.

Acknowledgements

B. Cichy acknowledges financial support from the National Science Centre Poland (NCN) under the SONATA program (DEC 2013/11/D/ST5/02989). MS thanks NCN for support under the HARMONIA grant (DEC-2012/04/M/ST5/00340). Numerical computations performed in this work were supported by Wrocław Centre for Networking and Supercomputing as well as the INTiBS PAN computing infrastructure.

References

1. S. Liu and X. Su, RSC Adv., 2014, 4, 43415–43428.
2. O. Mashinchian, M. Johari-Ahar, B. Ghaemi, M. Rashidi, J. Barar and Y. Omidi, BioImpacts, 2014, 4, 149–166.
3. D. Deng, Y. Chen, J. Cao, J. Tian, Z. Qian, S. Achilefu and Y. Gu, Chem. Mater., 2012, 24, 3029–3037.
4. K.-T. Yong, I. Roy, R. Hu, H. Ding, H. Cai, J. Zhu, X. Zhang, E. J. Bergey and P. N. Prasad, Integr. Biol., 2010, 2, 121–129.
5. B. Cichy, D. Wawrzynczyk, A. Bednarkiewicz, M. Samoc and W. Strek, Appl. Phys. Lett., 2013, 102, 243702.
6. B. Cichy, D. Wawrzynczyk, A. Bednarkiewicz, M. Samoc and W. Strek, RSC Adv., 2014, 4, 34065–34072.
7. C. De Oliveira, G. F. De Lima, H. A. De Abreu and H. A. Duarte, J. Phys. Chem. C, 2012, 116, 6357–6366.
8. M. Isik and N. Gasanly, Phys. B, 2015, 478, 127–130.
9. A. Usujima, S. Takeuchi, S. Endo and T. Irie, Jpn. J. Appl. Phys., 1981, 20, L505–L507.
10. T. Ogawa, T. Kuzuya, Y. Hamanaka and K. Sumiyama, J. Mater. Chem., 2010, 20, 2226–2231.
11. J. Feng and X. Yang, J. Nanopart. Res., 2012, 14, 1044.
12. S. P. Hong, H. K. Park, J. H. Oh, H. Yang and Y. R. Do, J. Mater. Chem., 2012, 22, 18939–18949.
13. H. C. Yoon, J. H. Oh, M. Ko, H. Yoo and Y. R. Do, ACS Appl. Mater. Interfaces, 2015, 7, 7342–7350.
14. J. Song, T. Jiang, T. Guo, L. Liu, H. Wang, T. Xia, W. Zhang, X. Ye, M. Yang, L. Zhu, R. Xia and X. Xu, Inorg. Chem., 2015, 54, 1627–1633.
15. G. Delgado, A. J. Mora, C. Pineda and T. Tinoco, Mater. Res. Bull., 2001, 36, 2507–2517.
16. B. Cichy, R. M. Rich, A. Olejniczak, Z. Gryczynski and W. Strek, Nanoscale, 2016, 8, 4151–4159.
17. M. Sheik-Bahae, A. A. Said, T. H. Wei, D. J. Hagan and E. W. van Stryland, IEEE J. Quantum Electron., 1990, 26, 760–769.
18. M. Nyk, J. Szeremeta, D. Wawrzynczyk and M. Samoc, J. Phys. Chem. C, 2014, 118, 17914–17921.
19. X. Gonze, B. Amadon, P. M. Anglade, J. M. Beuken, F. Bottin, P. Boulanger, F. Bruneval, D. Caliste, R. Caracas, M. Côté, T. Deutsch, L. Genovese, P. Ghosez, M. Giantomassi, S. Goedecker, D. R. Hamann, P. Hermet, F. Jollet, G. Jomard, S. Leroux, M. Mancini, S. Mazevet, M. J. T. Oliveira, G. Onida, Y. Pouillon, T. Rangel, G. M. Rignanese, D. Sangalli, R. Shaltaf, M. Torrent, M. J. Verstraete, G. Zerah and J. W. Zwanziger, Comput. Phys. Commun., 2009, 180, 2582–2615.
20. L. Borkovska, A. Romanyuk, V. Strelchuk, Y. Polishchuk, V. Kladko, A. Raevskaya, O. Stroyuk and T. Kryshtab, Mater. Sci. Semicond. Process., 2015, 37, 135–142.
21. S. H. You, K. J. Hong, B. J. Lee, T. S. Jeong, C. J. Youn, J. S. Park and S. N. Baek, J. Cryst. Growth, 2002, 245, 261–266.
22. J. L. Shay, B. Tell, H. M. Kasper and L. M. Schiavone, Phys. Rev. B: Solid State, 1972, 5, 5003–5005.
23. N. M. Gasanly, A. Serpengüzel, A. Aydinli, O. Gürlü and I. Yilmaz, J. Appl. Phys., 1999, 85, 3198–3201.
24. A. Usujima, S. Takeuchi, S. Endo and T. Irie, Jpn. J. Appl. Phys., 1981, 20, L505.
25. C. Paorici, L. Zanotti, N. Romeo, G. Sberveglieri and L. Tarricone, Mater. Res. Bull., 1977, 12, 1207–1211.
26. N. S. Orlova, I. V. Bodnar and E. A. Kudritskaya, Cryst. Res. Technol., 1998, 33, 37–42.
27. J. Park and S.-W. Kim, J. Mater. Chem., 2011, 21, 3745–3750.
28. J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 5822–5847.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6tc03854a

---