Solution and gas phase evidence of anion binding through the secondary bonding interactions of a bidentate bis-antimony(III) anion receptor†
Received
30th August 2017
, Accepted 29th November 2017
First published on 30th November 2017
Abstract
The solution and gas phase halide binding to a bis-antimony(III) anion receptor was studied. This new class of anion receptors utilizes the strong Sb-centered secondary bonding interactions (SBIs) that are formed opposite to the polar Sb–O primary bond. 1H NMR titration data were fitted statistically to binding models and solution-phase binding energetics were extracted, while the formation of anion-to-receptor complexes was observed using ESI-MS. Density functional theory calculations suggest that their affinity towards binding halide anions is mitigated by the strong explicit solvation effect in DMSO, which gives insights into future designs that circumvent direct solvent binding and are anticipated to yield tighter and perhaps more selectivity in anion binding.
The secondary bonding interactions (SBIs) of the heavy p-block elements1–3 have seen a surge in their application towards self-assembly. This has particularly been the case for the heavier halogen atoms as they form interactions with electron donors that are structurally analogous to hydrogen bonds. As such, the SBIs of the heavy main group elements are good candidates for anion binding in solution. Reports on 1,2,5-telluradiazole (and 2,1,3-benzotelluradiazole) rings have demonstrated that they could interact with anions in solution and the solid state.4–7 Iodine centred SBIs have also emerged as useful tools for anion binding.8–14 Antimony is also capable of engaging in such interactions;15,16 it can form up to three separate SBIs in its trivalent form and its utility towards crystal engineering has been noted.17,18 Studies have revealed that these interactions are strong and directional, which are driven by a strong electrostatic interaction and complementary orbital overlap.14,19–21 Experimental studies demonstrate that these interactions persist outside of the solid state.22,23 More recently, a stibaindole was reported to be capable of anion binding in the solution phase at the Sb(III) centre.24 Additionally, bidentate systems were designed to bind anions through two chalcogen SBIs.25,26 We previously combined a structural survey with DFT calculations to design a molecule containing two antimony(III) centres that are arranged to bind anions in a complementary manner.19 These gas phase DFT studies suggested that strong binding of high charge density atoms is likely to occur. In fact, the crystal structure of one compound contained SBIs with three separate pyridine molecules. Here we experimentally probe the solution and gas phase binding behaviour of such molecules towards halide anions.
The oxygen-bridged bis-antimony compounds 1 and 2 (Scheme 1) were prepared as previously reported.19 The solubility of 1 was very limited, only dissolving appreciably in warm DMSO. However, it was encouraging that if anions were present the solubility of 1 was drastically improved, even in less polar solvents such as THF. To follow this behaviour, compound 2, which showed enhanced solubility over 1, was studied in the presence of anions in a DMSO solution. This choice of solvent was limited by the need to dissolve 2 in appreciable quantities so that it could be monitored and recorded by NMR spectroscopy.
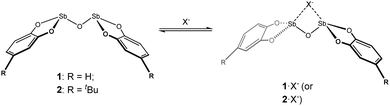 |
| | Scheme 1 Bis-antimony(III) anion receptors and proposed anion binding scheme illustrating potential geometric change induced by binding. | |
During initial investigations, it was noted that the resonances for the aromatic protons on 2 changed in response to added halide anions. Treating 2 with solutions of tetrabutylammonium chloride, bromide, and iodide (TBACl, TBABr, and TBAI, respectively) induced changes in the 1H NMR spectra as a function of the added anion amount. The addition of the strong Lewis acid tris(pentafluorophenyl)borane to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 2 and Cl− in d6-DMSO resulted in the 1H NMR signals shifting back towards free 2. This indicates that the interaction of 2 with Cl− is reversible in solution (Fig. S12, ESI†). As such, 1H NMR titration experiments of 2 and halide anions in d6-DMSO solutions were performed. For TBAI, a change in the chemical shift of 0.025 ppm towards lower frequencies was observed over the course of the titration (0–20 equivalents of I−, Fig. 1 and 2). As the change was very small, we sought to eliminate dilution and/or changes in the ionic strength of the solution as the origin of the change. A titration with pure d6-DMSO demonstrated no measurable change in the chemical shift (Fig. S3, ESI†). A titration of 2 with tetrabutylammonium hexafluorophosphate (TBAPF6), a non-coordinating anion, was performed and again no chemical shift change was observed (Fig. S4, ESI†). This confirmed that the observed change in the chemical shift upon titration with I− was the result of a fast exchange between the two species 2 and 2·I− in solution, where stepwise binding was assumed.27
1 mixture of 2 and Cl− in d6-DMSO resulted in the 1H NMR signals shifting back towards free 2. This indicates that the interaction of 2 with Cl− is reversible in solution (Fig. S12, ESI†). As such, 1H NMR titration experiments of 2 and halide anions in d6-DMSO solutions were performed. For TBAI, a change in the chemical shift of 0.025 ppm towards lower frequencies was observed over the course of the titration (0–20 equivalents of I−, Fig. 1 and 2). As the change was very small, we sought to eliminate dilution and/or changes in the ionic strength of the solution as the origin of the change. A titration with pure d6-DMSO demonstrated no measurable change in the chemical shift (Fig. S3, ESI†). A titration of 2 with tetrabutylammonium hexafluorophosphate (TBAPF6), a non-coordinating anion, was performed and again no chemical shift change was observed (Fig. S4, ESI†). This confirmed that the observed change in the chemical shift upon titration with I− was the result of a fast exchange between the two species 2 and 2·I− in solution, where stepwise binding was assumed.27
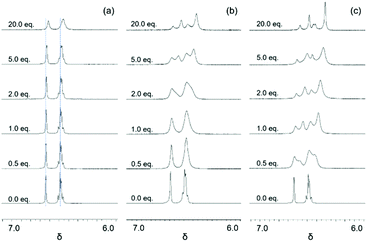 |
| | Fig. 1 Stacked 1H NMR spectra of aromatic regions that show the chemical shift changes as a function of anions (I−, Br−, and Cl−) added (0.0, 0.5, 1.0, 2.0, 5.0, and 20.0 eq. shown). (a) Titration with I− (blue lines drawn to illustrate the changes in chemical shift); (b) titration with Br−; and (c) titration with Cl−. | |
The 1H NMR titration of 2 with TBABr revealed a much more pronounced change compared to that observed with I− (Fig. 1). Here, two significant events were observed. First, upon the addition of Br− (up to approximately 1 eq.) the resonances associated with 2 broadened and shifted to lower frequencies, analogously to what was observed with I−. The observed shifting of peaks would indicate that a set of two species was in fast exchange with a change in their mole fraction. When more Br− was added, a second set of resonances at lower frequencies appeared (at ∼2 equivalents of Br−), and their intensities grew while the intensities of the earlier set of resonances decreased. The new set of resonances suggested that another set of two species in fast exchange was formed. The decreased intensities of the earlier set of resonances accompanied by increased intensities of the later set, however, indicated that slow exchange occurred between these two sets. Finally, as additional equivalents of Br− were added, all observed resonances continued to shift to lower frequencies. This implied that at least four independent species (two sets with two species in each set) in total were in equilibrium. The binding events were assumed to occur in a stepwise fashion, but it could not be immediately determined which one of the following three stepwise equilibria (eqn (1)–(3), (2)–(4) or (3)–(5)) was responsible for the observed changes:
| | 2 + 22·X− ⇌ 23·X− K3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 | (1) |
| | 2 + 2·X− ⇌ 22·X− K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 | (2) |
| | 2 + X− ⇌ 2·X− K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 | (3) |
| | 2·X− + Br− ⇌ 2·[X−]2 K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 | (4) |
| | 2·[X−]2 + Br− ⇌ 2·[X−]3 K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 | (5) |
Titrations of
2 with TBACl revealed
1H NMR spectra (
Fig. 1 and 2) where the changes followed the same patterns observed with TBABr. It was noticed that the second set of resonances appeared much earlier during the titration (0.5 equivalents for Cl
−vs. 2 equivalents for Br
−) and the chemical shift changes were more significant, indicating that tighter binding might occur with Cl
−.
To quantify the iodide binding, the data were fitted with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model (eqn (3)). The binding constant, K11, and the chemical shift of the 1
1 binding model (eqn (3)). The binding constant, K11, and the chemical shift of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (2·I−) were varied to minimize the sum of the square of the differences between the model and the data. The full details of the model as well as the script used for minimization are provided in the ESI.†Fig. 2 shows the fit for with the 1
1 complex (2·I−) were varied to minimize the sum of the square of the differences between the model and the data. The full details of the model as well as the script used for minimization are provided in the ESI.†Fig. 2 shows the fit for with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model and the binding constant is given in Table 1.
1 binding model and the binding constant is given in Table 1.
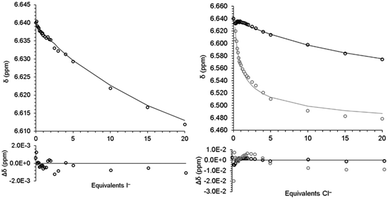 |
| | Fig. 2 Fit of model (line) for eqn (3) to chemical shift (open circles) from titration of 2 with TBAI (left) and eqn (3)–(5) from titration of 2 with TBACl. Black is 2/2·Cl− and grey is 22·Cl−/23·Cl− (right). Differences shown below. | |
Table 1 Stepwise binding constants from titration fitting with standard deviations
| Anion |
K
11 (L mol−1) |
K
21 (L mol−1) |
K
31 (L mol−1) |
| Cl− |
1.4 ± 0.3 |
1900 ± 500 |
8 ± 7 |
| Br− |
0.2 ± 0.1 |
1700 ± 700 |
4 ± 4 |
| I− |
0.16 ± 0.04 |
|
|
The fit for the Cl− and Br− data was based on the assumption that the four species mentioned above were related through stepwise equilibria and that the first (conceptual) step had to be 2 binding with the halide to form the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Following this, either a second equivalent of 2 or halide could bind to the 1
1 complex. Following this, either a second equivalent of 2 or halide could bind to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex and so on. Thus, the equations to represent the equilibrium were eqn (1)–(3), (2)–(4), or (3)–(5). It could not be immediately deduced from the experiment which of these is followed, so each model was independently fitted to the data. A further complication arose as it was not apparent which sets of species were in fast exchange, since fast exchange occurred when the exchange rate is larger than ∼2.2× the difference in the frequency of the resonances in question. This leads to 3 scenarios for each model giving a total of 9 possible models to fit to the data (which are described in the ESI†). Each of these 9 models was fitted and the best fitting model corresponded to eqn (1)–(3), where 2 and 2·X− were in fast exchange (consistent with the iodide titration) and 22·X− and 23·X− were in fast exchange. The binding constants are summarized in Table 1. Greater weighting was assigned to the fitting of the chemical shifts than to the integrated intensities, due to the well-established limitations of extracting highly accurate integrated intensities, particularly in regions of overlap or intermediate-to-slow exchange.
1 complex and so on. Thus, the equations to represent the equilibrium were eqn (1)–(3), (2)–(4), or (3)–(5). It could not be immediately deduced from the experiment which of these is followed, so each model was independently fitted to the data. A further complication arose as it was not apparent which sets of species were in fast exchange, since fast exchange occurred when the exchange rate is larger than ∼2.2× the difference in the frequency of the resonances in question. This leads to 3 scenarios for each model giving a total of 9 possible models to fit to the data (which are described in the ESI†). Each of these 9 models was fitted and the best fitting model corresponded to eqn (1)–(3), where 2 and 2·X− were in fast exchange (consistent with the iodide titration) and 22·X− and 23·X− were in fast exchange. The binding constants are summarized in Table 1. Greater weighting was assigned to the fitting of the chemical shifts than to the integrated intensities, due to the well-established limitations of extracting highly accurate integrated intensities, particularly in regions of overlap or intermediate-to-slow exchange.
Further corroboration of the binding model was sought. Electrospray ionization-mass spectrometry (ESI-MS) was applied to further verify the binding model. DMSO was not used as a solvent for this experiment because of its higher boiling point. Rather, acetonitrile solutions with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios of 2
1 ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X− (X = Cl or Br) in stoichiometry were prepared at the concentration of 0.5 mg mL−1 and the experiments were conducted under the negative mode. For all the three ratios, the isotope patterns of a 1
X− (X = Cl or Br) in stoichiometry were prepared at the concentration of 0.5 mg mL−1 and the experiments were conducted under the negative mode. For all the three ratios, the isotope patterns of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex were observed for both Cl− and Br− and were consistent with theoretical simulations based on the chemical compositions of [C20H24O5Sb2Cl]− and [C20H24O5Sb2Br]−, respectively (Fig. 3a and c). The 2
1 complex were observed for both Cl− and Br− and were consistent with theoretical simulations based on the chemical compositions of [C20H24O5Sb2Cl]− and [C20H24O5Sb2Br]−, respectively (Fig. 3a and c). The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex was only observed with Cl−, which had a stronger binding affinity compared with Br−. The isotopic distribution also agreed well with theoretical simulations based on the chemical composition of [C40H48O10Sb4Cl]−. It was noteworthy that the 3
1 complex was only observed with Cl−, which had a stronger binding affinity compared with Br−. The isotopic distribution also agreed well with theoretical simulations based on the chemical composition of [C40H48O10Sb4Cl]−. It was noteworthy that the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry ratio showed a higher tendency to form the 22·Cl− complex as compared to the 2
1 stoichiometry ratio showed a higher tendency to form the 22·Cl− complex as compared to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios (Fig. S15, ESI†). Two conclusions could be drawn here (1) that the 22·X− complex was formed and experimentally observed and (2) that the speciation was, not unexpectedly, strongly dependent on the solvent.
1 ratios (Fig. S15, ESI†). Two conclusions could be drawn here (1) that the 22·X− complex was formed and experimentally observed and (2) that the speciation was, not unexpectedly, strongly dependent on the solvent.
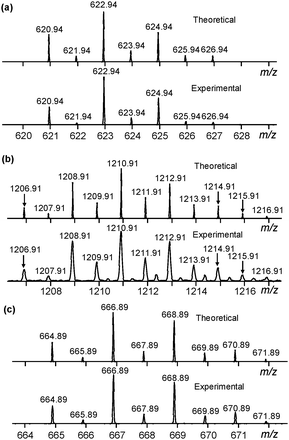 |
| | Fig. 3 (a) Theoretical (upper) and experimental (lower) isotope patterns of 2·Cl− from ESI-MS. (b) Theoretical (upper) and experimental (lower) isotope patterns of 22·Cl− from ESI-MS. (c) Theoretical (upper) and experimental (lower) isotope patterns of 2·Br− from ESI-MS. | |
DFT calculations were performed with ORCA 4.028 to help understand the origin of the rather small binding constant for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes.29 A slightly improved basis set and a functional known to give more accurate results for main-group thermochemistry and noncovalent interactions, B97-D3,7,30 was used as compared to the previous gas-phase study, and largely consistent results were obtained. As in the previous study, 1 was used as a surrogate for the bulkier 2. A variety of different isomers were probed but only the most stable ones are reported in Table 2. Since very large binding constants which over-estimated the binding affinity were predicted in gas-phase calculations, the effect of the solvent dielectric was next probed. Using the conductor-like polarizable continuum model (CPCM)31 the effects of the high dielectric of DMSO could be taken into account. This, as expected, gave a much more reasonable value but it still appeared to slightly over-estimate the 1
1 complexes.29 A slightly improved basis set and a functional known to give more accurate results for main-group thermochemistry and noncovalent interactions, B97-D3,7,30 was used as compared to the previous gas-phase study, and largely consistent results were obtained. As in the previous study, 1 was used as a surrogate for the bulkier 2. A variety of different isomers were probed but only the most stable ones are reported in Table 2. Since very large binding constants which over-estimated the binding affinity were predicted in gas-phase calculations, the effect of the solvent dielectric was next probed. Using the conductor-like polarizable continuum model (CPCM)31 the effects of the high dielectric of DMSO could be taken into account. This, as expected, gave a much more reasonable value but it still appeared to slightly over-estimate the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constant. The explicit solvent effect between the Sb(III) centres and DMSO was next considered. As was suggested by the crystal structure of 1, which showed strong SBIs between the Sb atoms and the nitrogen atoms of two pyridine molecules, a similar DMSO-coordinated molecule (Fig. 4) was taken as the starting point. Depicted by eqn (6) or (7), the DMSO⋯Sb SBI must be broken before the new Sb⋯X− SBI could form in the DMSO solution, and one or both DMSO molecules could be replaced during anion binding. The contribution from dispersion to the energetics is summarized in Table S15 (ESI†). The dispersion energy increases from Cl− to Br− to I−. It should be noted that when implicit solvation in DMSO was modelled, the dispersion contribution of forming 1·Cl− counts only ∼27% of total ΔE, whereas it contributes to ∼50% of total ΔE towards forming 1·I−.
1 binding constant. The explicit solvent effect between the Sb(III) centres and DMSO was next considered. As was suggested by the crystal structure of 1, which showed strong SBIs between the Sb atoms and the nitrogen atoms of two pyridine molecules, a similar DMSO-coordinated molecule (Fig. 4) was taken as the starting point. Depicted by eqn (6) or (7), the DMSO⋯Sb SBI must be broken before the new Sb⋯X− SBI could form in the DMSO solution, and one or both DMSO molecules could be replaced during anion binding. The contribution from dispersion to the energetics is summarized in Table S15 (ESI†). The dispersion energy increases from Cl− to Br− to I−. It should be noted that when implicit solvation in DMSO was modelled, the dispersion contribution of forming 1·Cl− counts only ∼27% of total ΔE, whereas it contributes to ∼50% of total ΔE towards forming 1·I−.
| | | 1·[DMSO]2 + X− ⇌ 1·DMSO·X− + DMSO | (6) |
| | | 1·[DMSO]2 + X− ⇌ 1·X− + 2 DMSO | (7) |
The bonding energies better agree with the experimental values after accounting for this explicit DMSO solvation. The values do not align with the experimental results perfectly, but this may result from the assumptions made in the computational method, or perhaps from the minor influences of the
tert-butyl groups. These calculations suggest that DMSO inhibits binding by both implicit and explicit solvation. Tighter binding to anions would presumably occur in less polar and less nucleophilic solvents. Modelling the formation of the
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
X
− complexes in tetrahydrofuran or chloroform (with the CPCM), where explicit binding was much less likely to occur, revealed that much tighter binding can be anticipated (
Table 2; denoted as Δ
GTHF and Δ
GCHCl3, respectively). Lastly, the geometries of
1 and
1·[DMSO]
2 (
Fig. 4) reveal the presence of intramolecular Sb⋯O SBIs (shown in red) and such intramolecular SBIs must be broken before binding of anions could happen, which also affects the final binding energy. Redesigning of the anion receptor to prevent this should also enhance the affinity for anions.
Table 2 Experimental and DFT calculated Gibbs free energies (kJ mol−1) for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding of 2 with halides
1 binding of 2 with halides
|
|
ΔGexp |
|
ΔGgp |
ΔGCPCMa |
ΔGeqn (6)b |
ΔGeqn (7)b |
| DMSO |
THF |
CHCl3 |
|
ΔGg(as)p(hase) = ΔHgp − TΔSgp; ΔGCPCM = ΔHCPCM − TΔSCPCM; ΔH = ΔE + ΔEthermal + ΔEZPE + ΔEBSSE + ΔEdispersion.
With CPCM(DMSO).
|
|
2·Cl− |
−0.8 |
1·Cl− |
−180.0 |
−4.4 |
−24.3 |
−35.8 |
6.0 |
−13.7 |
|
2·Br− |
4.0 |
1·Br− |
−148.7 |
4.1 |
−13.1 |
−23.0 |
11.5 |
−5.1 |
|
2·I− |
4.5 |
1·I− |
−121.4 |
11.9 |
−2.8 |
−11.5 |
21.6 |
2.7 |
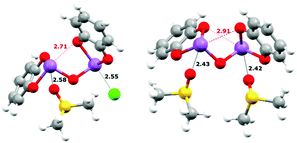 |
| | Fig. 4 Calculated equilibrium structures uisng DFT. Left: 1·DMSO·Cl−; right: 1·[DMSO]2. Intra- (red) and intermolecular (black) SBIs are shown as hashed lines and distances (in Å) are labelled accordingly. A full summary of SBI distances can be found in the ESI.† | |
Strong experimental evidence of solution and gas phase anion binding by bidentate Sb(III) benzodioxastibole oxide derivative is presented. The binding is facilitated by Sb-centred SBIs and is the first example of a bidentate anion receptor with pnictogen bonding. In strong donor solvents, such as DMSO, competition between the solvent and anions exists which limits the magnitude of the binding constant. Furthermore, strong intramolecular SBIs are present in the complex which offset the favourable binding towards anions. DFT calculations suggest that redesigning of the system with increased solubility in less polar and less nucleophilic solvents should lead to a significant enhancement of anion binding. Also, limiting the degrees of rotational freedom around the bridge between the antimony centres could lead to higher binding affinities.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
AFC and JQ are grateful for financial support from the Robert A. Welch Foundation (D-1838, USA), Texas Tech University and the National Science Foundation (NMR instrument grant CHE-1048553). AFC thanks Michael Latham for scientific discussion. XL acknowledges the support from the National Science Foundation (CHE-1506722).
Notes and references
- N. W. Alcock, Adv. Inorg. Chem. Radiochem., 1972, 15, 1–58 CrossRef CAS.
- O. Hassel, Science, 1970, 170(3957), 497–502 CAS.
- The secondary bonding interactions of the heavy p-block elements are often also called noncovalent interactions, charge-transfer interactions, sigma-hole interactions, halogen bonding, chalcogen bonding and pnictogen bonding.
- L. M. Lee, P. J. W. Elder, A. F. Cozzolino, Q. Yang and I. Vargas-Baca, Main Group Chem., 2010, 9, 117–133 CAS.
- N. A. Semenov, A. V. Lonchakov, N. A. Pushkarevsky, E. A. Suturina, V. V. Korolev, E. Lork, V. G. Vasiliev, S. N. Konchenko, J. Beckmann, N. P. Gritsan and A. V. Zibarev, Organometallics, 2014, 33(16), 4302–4314 CrossRef CAS.
- N. A. Semenov, A. V. Lonchakov, N. P. Gritsan and A. V. Zibarev, Russ. Chem. Bull., 2015, 64(3), 499–510 CrossRef CAS.
- G. E. Garrett, G. L. Gibson, R. N. Straus, D. S. Seferos and M. S. Taylor, J. Am. Chem. Soc., 2015, 137(12), 4126–4133 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati, M. Sansotera and G. Terraneo, Chem. Soc. Rev., 2010, 39(10), 3772–3783 RSC.
- S. P. Cornes, C. H. Davies, D. Blyghton, M. R. Sambrook and P. D. Beer, Org. Biomol. Chem., 2015, 13(9), 2582–2587 CAS.
- R. Tepper, B. Schulze, H. Görls, P. Bellstedt, M. Jäger and U. S. Schubert, Org. Lett., 2015, 17(23), 5740–5743 CrossRef CAS PubMed.
- M. S. Taylor, Nat. Chem., 2014, 6(12), 1029–1031 CrossRef CAS PubMed.
- C. J. Massena, N. B. Wageling, D. A. Decato, E. Martin Rodriguez, A. M. Rose and O. B. Berryman, Angew. Chem., Int. Ed., 2016, 55(40), 12398–12402 CrossRef CAS PubMed.
- N. B. Wageling, G. F. Neuhaus, A. M. Rose, D. A. Decato and O. B. Berryman, Supramol. Chem., 2016, 28(7–8), 665–672 CrossRef CAS.
- S. W. Robinson, C. L. Mustoe, N. G. White, A. Brown, A. L. Thompson, P. Kennepohl and P. D. Beer, J. Am. Chem. Soc., 2015, 137(1), 499–507 CrossRef CAS PubMed.
- S. L. Benjamin, W. Levason, G. Reid and R. P. Warr, Organometallics, 2012, 31(3), 1025–1034 CrossRef CAS.
- C. A. Allen, V. M. Cangelosi, L. N. Zakharov and D. W. Johnson, Cryst. Growth Des., 2009, 9(7), 3011–3013 CAS.
- J. Starbuck, N. C. Norman and A. G. Orpen, New J. Chem., 1999, 23, 969–972 RSC.
- S. Moaven, J. Yu, J. Yasin, D. K. Unruh and A. F. Cozzolino, Inorg. Chem., 2017, 56(14), 8372–8380 CrossRef CAS PubMed.
- J. Qiu, D. K. Unruh and A. F. Cozzolino, J. Phys. Chem. A, 2016, 120(46), 9257–9269 CrossRef CAS PubMed.
- A. F. Cozzolino, P. J. W. Elder, L. M. Lee and I. Vargas-Baca, Can. J. Chem., 2013, 91(5), 338–347 CrossRef CAS.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13(2), 291–296 CrossRef CAS PubMed.
- S. H. Jungbauer, S. Schindler, E. Herdtweck, S. Keller and S. M. Huber, Chem. – Eur. J., 2015, 21(39), 13625–13636 CrossRef CAS PubMed.
- A. F. Cozzolino, G. Dimopoulos-Italiano, L. M. Lee and I. Vargas-Baca, Eur. J. Inorg. Chem., 2013,(15), 2751–2756 CrossRef CAS.
- A. M. Christianson and F. P. Gabbaï, Organometallics, 2017, 36(14), 2670–2676 CrossRef CAS.
- G. E. Garrett, E. I. Carrera, D. S. Seferos and M. S. Taylor, Chem. Commun., 2016, 52(64), 9881–9884 RSC.
- S. Benz, M. Macchione, Q. Verolet, J. Mareda, N. Sakai and S. Matile, J. Am. Chem. Soc., 2016, 138(29), 9093–9096 CrossRef CAS PubMed.
- P. Thordarson, Chem. Soc. Rev., 2011, 40(3), 1305–1323 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78 CrossRef CAS.
- A detailed discussion regarding the calculation of different geometries is provided in the ESI† (see Section S1.4).
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13(14), 6670–6688 RSC.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102(11), 1995–2001 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and computational details, NMR titration details, analysis and data fitting methodology, mass spectrometry details, 1H NMR spectra, Cartesian coordinates from DFT calculations. See DOI: 10.1039/c7cp05933g |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
B.
Song
a,
B.
Song
 b,
X.
Li
b,
X.
Li
 b and
A. F.
Cozzolino
b and
A. F.
Cozzolino
 *a
*a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of 2 and Cl− in d6-DMSO resulted in the 1H NMR signals shifting back towards free 2. This indicates that the interaction of 2 with Cl− is reversible in solution (Fig. S12, ESI†). As such, 1H NMR titration experiments of 2 and halide anions in d6-DMSO solutions were performed. For TBAI, a change in the chemical shift of 0.025 ppm towards lower frequencies was observed over the course of the titration (0–20 equivalents of I−, Fig. 1 and 2). As the change was very small, we sought to eliminate dilution and/or changes in the ionic strength of the solution as the origin of the change. A titration with pure d6-DMSO demonstrated no measurable change in the chemical shift (Fig. S3, ESI†). A titration of 2 with tetrabutylammonium hexafluorophosphate (TBAPF6), a non-coordinating anion, was performed and again no chemical shift change was observed (Fig. S4, ESI†). This confirmed that the observed change in the chemical shift upon titration with I− was the result of a fast exchange between the two species 2 and 2·I− in solution, where stepwise binding was assumed.27
1 mixture of 2 and Cl− in d6-DMSO resulted in the 1H NMR signals shifting back towards free 2. This indicates that the interaction of 2 with Cl− is reversible in solution (Fig. S12, ESI†). As such, 1H NMR titration experiments of 2 and halide anions in d6-DMSO solutions were performed. For TBAI, a change in the chemical shift of 0.025 ppm towards lower frequencies was observed over the course of the titration (0–20 equivalents of I−, Fig. 1 and 2). As the change was very small, we sought to eliminate dilution and/or changes in the ionic strength of the solution as the origin of the change. A titration with pure d6-DMSO demonstrated no measurable change in the chemical shift (Fig. S3, ESI†). A titration of 2 with tetrabutylammonium hexafluorophosphate (TBAPF6), a non-coordinating anion, was performed and again no chemical shift change was observed (Fig. S4, ESI†). This confirmed that the observed change in the chemical shift upon titration with I− was the result of a fast exchange between the two species 2 and 2·I− in solution, where stepwise binding was assumed.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model (eqn (3)). The binding constant, K11, and the chemical shift of the 1
1 binding model (eqn (3)). The binding constant, K11, and the chemical shift of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (2·I−) were varied to minimize the sum of the square of the differences between the model and the data. The full details of the model as well as the script used for minimization are provided in the ESI.†Fig. 2 shows the fit for with the 1
1 complex (2·I−) were varied to minimize the sum of the square of the differences between the model and the data. The full details of the model as well as the script used for minimization are provided in the ESI.†Fig. 2 shows the fit for with the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model and the binding constant is given in Table 1.
1 binding model and the binding constant is given in Table 1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Following this, either a second equivalent of 2 or halide could bind to the 1
1 complex. Following this, either a second equivalent of 2 or halide could bind to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex and so on. Thus, the equations to represent the equilibrium were eqn (1)–(3), (2)–(4), or (3)–(5). It could not be immediately deduced from the experiment which of these is followed, so each model was independently fitted to the data. A further complication arose as it was not apparent which sets of species were in fast exchange, since fast exchange occurred when the exchange rate is larger than ∼2.2× the difference in the frequency of the resonances in question. This leads to 3 scenarios for each model giving a total of 9 possible models to fit to the data (which are described in the ESI†). Each of these 9 models was fitted and the best fitting model corresponded to eqn (1)–(3), where 2 and 2·X− were in fast exchange (consistent with the iodide titration) and 22·X− and 23·X− were in fast exchange. The binding constants are summarized in Table 1. Greater weighting was assigned to the fitting of the chemical shifts than to the integrated intensities, due to the well-established limitations of extracting highly accurate integrated intensities, particularly in regions of overlap or intermediate-to-slow exchange.
1 complex and so on. Thus, the equations to represent the equilibrium were eqn (1)–(3), (2)–(4), or (3)–(5). It could not be immediately deduced from the experiment which of these is followed, so each model was independently fitted to the data. A further complication arose as it was not apparent which sets of species were in fast exchange, since fast exchange occurred when the exchange rate is larger than ∼2.2× the difference in the frequency of the resonances in question. This leads to 3 scenarios for each model giving a total of 9 possible models to fit to the data (which are described in the ESI†). Each of these 9 models was fitted and the best fitting model corresponded to eqn (1)–(3), where 2 and 2·X− were in fast exchange (consistent with the iodide titration) and 22·X− and 23·X− were in fast exchange. The binding constants are summarized in Table 1. Greater weighting was assigned to the fitting of the chemical shifts than to the integrated intensities, due to the well-established limitations of extracting highly accurate integrated intensities, particularly in regions of overlap or intermediate-to-slow exchange.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios of 2
1 ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X− (X = Cl or Br) in stoichiometry were prepared at the concentration of 0.5 mg mL−1 and the experiments were conducted under the negative mode. For all the three ratios, the isotope patterns of a 1
X− (X = Cl or Br) in stoichiometry were prepared at the concentration of 0.5 mg mL−1 and the experiments were conducted under the negative mode. For all the three ratios, the isotope patterns of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex were observed for both Cl− and Br− and were consistent with theoretical simulations based on the chemical compositions of [C20H24O5Sb2Cl]− and [C20H24O5Sb2Br]−, respectively (Fig. 3a and c). The 2
1 complex were observed for both Cl− and Br− and were consistent with theoretical simulations based on the chemical compositions of [C20H24O5Sb2Cl]− and [C20H24O5Sb2Br]−, respectively (Fig. 3a and c). The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex was only observed with Cl−, which had a stronger binding affinity compared with Br−. The isotopic distribution also agreed well with theoretical simulations based on the chemical composition of [C40H48O10Sb4Cl]−. It was noteworthy that the 3
1 complex was only observed with Cl−, which had a stronger binding affinity compared with Br−. The isotopic distribution also agreed well with theoretical simulations based on the chemical composition of [C40H48O10Sb4Cl]−. It was noteworthy that the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry ratio showed a higher tendency to form the 22·Cl− complex as compared to the 2
1 stoichiometry ratio showed a higher tendency to form the 22·Cl− complex as compared to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios (Fig. S15, ESI†). Two conclusions could be drawn here (1) that the 22·X− complex was formed and experimentally observed and (2) that the speciation was, not unexpectedly, strongly dependent on the solvent.
1 ratios (Fig. S15, ESI†). Two conclusions could be drawn here (1) that the 22·X− complex was formed and experimentally observed and (2) that the speciation was, not unexpectedly, strongly dependent on the solvent.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes.29 A slightly improved basis set and a functional known to give more accurate results for main-group thermochemistry and noncovalent interactions, B97-D3,7,30 was used as compared to the previous gas-phase study, and largely consistent results were obtained. As in the previous study, 1 was used as a surrogate for the bulkier 2. A variety of different isomers were probed but only the most stable ones are reported in Table 2. Since very large binding constants which over-estimated the binding affinity were predicted in gas-phase calculations, the effect of the solvent dielectric was next probed. Using the conductor-like polarizable continuum model (CPCM)31 the effects of the high dielectric of DMSO could be taken into account. This, as expected, gave a much more reasonable value but it still appeared to slightly over-estimate the 1
1 complexes.29 A slightly improved basis set and a functional known to give more accurate results for main-group thermochemistry and noncovalent interactions, B97-D3,7,30 was used as compared to the previous gas-phase study, and largely consistent results were obtained. As in the previous study, 1 was used as a surrogate for the bulkier 2. A variety of different isomers were probed but only the most stable ones are reported in Table 2. Since very large binding constants which over-estimated the binding affinity were predicted in gas-phase calculations, the effect of the solvent dielectric was next probed. Using the conductor-like polarizable continuum model (CPCM)31 the effects of the high dielectric of DMSO could be taken into account. This, as expected, gave a much more reasonable value but it still appeared to slightly over-estimate the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding constant. The explicit solvent effect between the Sb(III) centres and DMSO was next considered. As was suggested by the crystal structure of 1, which showed strong SBIs between the Sb atoms and the nitrogen atoms of two pyridine molecules, a similar DMSO-coordinated molecule (Fig. 4) was taken as the starting point. Depicted by eqn (6) or (7), the DMSO⋯Sb SBI must be broken before the new Sb⋯X− SBI could form in the DMSO solution, and one or both DMSO molecules could be replaced during anion binding. The contribution from dispersion to the energetics is summarized in Table S15 (ESI†). The dispersion energy increases from Cl− to Br− to I−. It should be noted that when implicit solvation in DMSO was modelled, the dispersion contribution of forming 1·Cl− counts only ∼27% of total ΔE, whereas it contributes to ∼50% of total ΔE towards forming 1·I−.
1 binding constant. The explicit solvent effect between the Sb(III) centres and DMSO was next considered. As was suggested by the crystal structure of 1, which showed strong SBIs between the Sb atoms and the nitrogen atoms of two pyridine molecules, a similar DMSO-coordinated molecule (Fig. 4) was taken as the starting point. Depicted by eqn (6) or (7), the DMSO⋯Sb SBI must be broken before the new Sb⋯X− SBI could form in the DMSO solution, and one or both DMSO molecules could be replaced during anion binding. The contribution from dispersion to the energetics is summarized in Table S15 (ESI†). The dispersion energy increases from Cl− to Br− to I−. It should be noted that when implicit solvation in DMSO was modelled, the dispersion contribution of forming 1·Cl− counts only ∼27% of total ΔE, whereas it contributes to ∼50% of total ΔE towards forming 1·I−.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X− complexes in tetrahydrofuran or chloroform (with the CPCM), where explicit binding was much less likely to occur, revealed that much tighter binding can be anticipated (Table 2; denoted as ΔGTHF and ΔGCHCl3, respectively). Lastly, the geometries of 1 and 1·[DMSO]2 (Fig. 4) reveal the presence of intramolecular Sb⋯O SBIs (shown in red) and such intramolecular SBIs must be broken before binding of anions could happen, which also affects the final binding energy. Redesigning of the anion receptor to prevent this should also enhance the affinity for anions.
X− complexes in tetrahydrofuran or chloroform (with the CPCM), where explicit binding was much less likely to occur, revealed that much tighter binding can be anticipated (Table 2; denoted as ΔGTHF and ΔGCHCl3, respectively). Lastly, the geometries of 1 and 1·[DMSO]2 (Fig. 4) reveal the presence of intramolecular Sb⋯O SBIs (shown in red) and such intramolecular SBIs must be broken before binding of anions could happen, which also affects the final binding energy. Redesigning of the anion receptor to prevent this should also enhance the affinity for anions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding of 2 with halides
1 binding of 2 with halides



