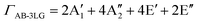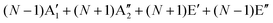Open Access Article
Open Access ArticleRaman spectroscopy of graphene-based materials and its applications in related devices
Jiang-Bin
Wu
ab,
Miao-Ling
Lin
ab,
Xin
Cong
ab,
He-Nan
Liu
a and
Ping-Heng
Tan
 *ab
*ab
aState Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China
bCAS Center of Excellence in Topological Quantum Computation, and College of Materials Science and Opto-Electronic Technology, University of Chinese Academy of Science, Beijing 100049, China. E-mail: phtan@semi.ac.cn
First published on 25th January 2018
Abstract
Graphene-based materials exhibit remarkable electronic, optical, and mechanical properties, which has resulted in both high scientific interest and huge potential for a variety of applications. Furthermore, the family of graphene-based materials is growing because of developments in preparation methods. Raman spectroscopy is a versatile tool to identify and characterize the chemical and physical properties of these materials, both at the laboratory and mass-production scale. This technique is so important that most of the papers published concerning these materials contain at least one Raman spectrum. Thus, here, we systematically review the developments in Raman spectroscopy of graphene-based materials from both fundamental research and practical (i.e., device applications) perspectives. We describe the essential Raman scattering processes of the entire first- and second-order modes in intrinsic graphene. Furthermore, the shear, layer-breathing, G and 2D modes of multilayer graphene with different stacking orders are discussed. Techniques to determine the number of graphene layers, to probe resonance Raman spectra of monolayer and multilayer graphenes and to obtain Raman images of graphene-based materials are also presented. The extensive capabilities of Raman spectroscopy for the investigation of the fundamental properties of graphene under external perturbations are described, which have also been extended to other graphene-based materials, such as graphene quantum dots, carbon dots, graphene oxide, nanoribbons, chemical vapor deposition-grown and SiC epitaxially grown graphene flakes, composites, and graphene-based van der Waals heterostructures. These fundamental properties have been used to probe the states, effects, and mechanisms of graphene materials present in the related heterostructures and devices. We hope that this review will be beneficial in all the aspects of graphene investigations, from basic research to material synthesis and device applications.
1 Introduction
Graphene is a truly two-dimensional (2d) system, consisting of sp2 carbon hexagonal networks with strong covalent bonds.1 Multilayer graphene (MLG) can be stacked layer by layer in a Bernal (AB) or rhombohedral (ABC) way through van der Waals (vdW) coupling.2–6 High-quality monolayer graphene (1LG) and MLG can be produced by several methods, such as micromechanical exfoliation (ME), chemical vapor deposition (CVD), and epitaxial growth from the SiC surface.1,7–10 Other artificial fabrication routes for production, such as the reduction of a graphene oxide (GO) solution and organic synthesis, tend to introduce defects into the graphene,11–13 such as vacancies and dislocations, as well as exposing the graphene to oxidation, hydrogenation, fluorination, and other chemical functionalizations.14–16 Graphene can also be decomposed into one-dimensional (1d) and zero-dimensional (0d) forms, such as graphene nanoribbons (GNR) and nanographene.17–21 All these materials with various dimensions are derived from 1LG and can be termed graphene-based materials. The remarkable properties of graphene-based materials, including their high carrier mobility (near-ballistic transport), high thermal conductivity, unique optical and mechanical properties, and high specific surface area, make them promising materials for high-frequency nanoelectronics, micro- and nanomechanical systems, thin-film transistors, transparent and conductive composites and electrodes, batteries and supercapacitors with high charging speeds, highly sensitive chemical sensors, flexible and printable optoelectronics, and photonics.1,22–27 On the other hand, recent research studies have advanced to investigate vertical van der Waals heterostructures (vdWHs) because they can be formed by vertically stacking various 2d materials (2DMs) by van der Waals forces but without any constraints of lattice matching and fabrication compatibility, offering huge opportunities for the design of new functionalities.28–30 In particular, hybrid systems consisting of transition metal dichalcogenides (TMD) and graphene (TMD/graphene vdWHs) have been used for various high-performance devices by taking advantage of the high mobility of graphene and the natural band gap of TMDs.31–35 1LG and MLG are the essential building blocks for vdWHs36 as electrodes in various high-performance devices, such as field-effect tunneling transistors, logic transistors, photovoltaics, and memory devices.37–42 Therefore, a versatile technique to identify and characterize graphene-based materials both at the laboratory and the mass-production scale and to probe the state, effects, and functionalization mechanism of these materials in the heterostructures and devices is essential for material synthesis, basic research, and device applications.Raman spectroscopy is a fast, nondestructive, and high-resolution tool for the characterization of the lattice structure and the electronic, optical, and phonon properties of carbon materials, including three-dimensional (3d) diamond and graphite, 2d graphene, 1d carbon nanotubes, and 0d fullerenes, as shown in Fig. 1(a).43–54 Raman spectra of all graphene-based materials show few prominent features regardless of the final structure.55 However, the positions, line shapes, and intensities of these peaks give abundant useful information for the investigation of the structures and electronic properties of graphene-based materials.55–57 For example, for the G mode of graphene excited by an excitation energy (εL, EL or Eex), the peak position (Pos(G)) or frequency (ω(G), or ωG), line shapes (Lorentzian or Fano), full width at half maximum (FWHM(G) or ΓG), peak intensities (I(G) or IG), and peak area (A(G) or AG), i.e., integrated intensity, are closely related to its doping level.58–65 In Fig. 1(b), the Raman spectra of various graphene-based materials showing the D, G and 2D spectral regions are shown, demonstrating their similarity. The intrinsic properties of samples from monolayer to few-layer graphene, as well as bulk graphite, can be distinguished from the spectral profile of the 2D modes. In addition, the D peak can be used to characterize graphene-based materials with defects, such as disordered graphene, graphene oxide, and nanographene.66–68 On the other hand, the Raman features of graphene-based materials depend not only on the phonon properties but also on the corresponding electronic properties, e.g., the unique linear band structure in 1LG and distinct band structures in MLG.44 In 1LG, the origin of the overtone and combination modes, such as the 2D and D + D′′ modes, is the triple resonance (TR) or double resonance (DR) process, which is related to the linear dispersion of its electronic bands.66,69 For N-layer graphenes (NLGs), the stacking order has an important influence on the band and interlayer phonon properties, leading to N- and stacking-orientation-dependent Raman spectra.5,6,53,55,57,70,71 In addition, quantum interference effects play a key role in determining the Raman intensity of graphene.58,72,73 Moreover, in the presence of external perturbations, such as defects,15,16,74–80 doping,58–65 strain, stress,81–87 magnetic fields,88–98 and temperature,99–103 the electronic and lattice vibration properties change significantly, which can be determined using Raman spectroscopy. Based on the Raman spectra of intrinsic 1LG and MLG and their responses to external perturbations, Raman spectroscopy has been widely utilized to investigate the properties of graphene materials and their effects on the performance of related devices.
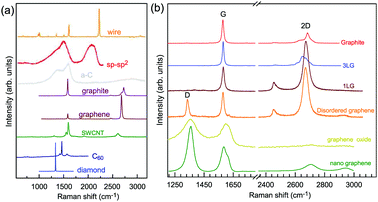 | ||
| Fig. 1 (a) Raman spectra of carbon solids and nanostructures, including 1d carbon wires, sp–sp2 carbon, amorphous carbon (a-C), graphite, graphene, single-walled carbon nanotubes (SWNT), C60, and diamond. Raman spectra of carbon wire, sp–sp2 carbon, a-C are reproduced with permission from ref. 43. Copyright 2015, Beilstein-Institut. (b) Raman spectra of graphene-based materials, including graphite, 1LG, 3LG, disordered graphene, graphene oxide and nanographene. | ||
Here, we present a systemic review of the Raman spectroscopy of graphene materials both in terms of the fundamental properties and device applications. First, we give a basic picture of the Raman spectroscopy of intrinsic 1LG, which is directly related to the electronic band structures and phonon dispersion curves. Secondly, the effect of the stacking (AB, ABC, and twist) and number of layers on the phonon modes is discussed. The resonant Raman scattering in 1LG and NLG is also presented. Then, the Raman spectra of 1LG under perturbation, including doping, strain, stress, temperature, and magnetic fields, are demonstrated. We discuss, in depth, the defects in graphene and their characterization using Raman spectroscopy, and demonstrate how to use the spectral features of Raman spectra to identify the number of layers of graphene materials. In the last three sections, we present some examples of the applications of Raman spectroscopy to graphene-related materials and devices, including GO, nanographene, epitaxial graphene grown from SiC, CVD-grown graphene, graphene-based heterostructures, field effect transistors (FETs), ion batteries, and solar cells. The application of Raman imaging is also presented in detail. We hope that this review will act as a guide for anyone who has an interest in the use of Raman spectroscopy with graphene-related systems and would like to employ Raman spectroscopy to characterize graphene-related materials and related devices.
2 Raman spectroscopy of monolayer graphene
2.1 Electronic band structure of monolayer and multilayer graphene
1LG is a single layer of carbon atoms with each atom bound to three neighbors in a honeycomb structure. The unit cell of its crystal lattice contains two carbon atoms, A and B, each forming a triangular in-plane network. The displacement of the A and B atoms, i.e., the length of carbon–carbon covalent bond (aC–C), is 0.142 nm, which results in a lattice constant of a = 0.246 nm, as shown in Fig. 2(a). NLG is a layered stacking structure prepared from 1LG in the out-of-plane direction (c-axis). The most common and stable stacking type is AB stacking, in which two adjacent graphene layers are stacked, oriented by a 60° rotation. From the top view, the empty centers of the hexagons on one layer are occupied by the carbon atoms at the hexagonal corner sites of the adjacent layers. Fig. 2(b) shows the atomic structure of the AB-stacked 2LG (AB-2LG). The typical value of the interlayer space is 0.35 nm. For AB-3LG, the atoms of the top layer are in the same positions as those of the second nearest layer from the top view, continuing in this manner for MLG with more layers. Thus, AB-3LG can be represented as ABA graphene and AB-4LG is ABAB graphene. Moreover, the unit cell of graphite can also be shown as in Fig. 2(b), having lattice constants of a = 0.246 nm and c = 0.67 nm. In reciprocal space, 1LG also has a honeycomb structure, as shown in Fig. 2(c). There are some high symmetry points within the first Brillouin zone (BZ) of 1LG: the Γ point at the zone center, the M points in the middle of the hexagonal sides, and the K and K′ points at the corners of the hexagons, which are all inequivalent.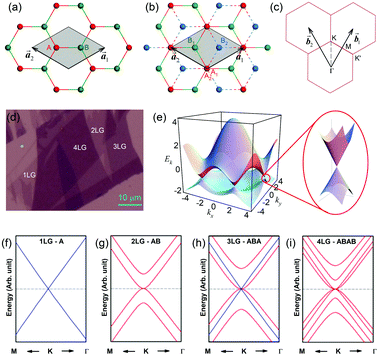 | ||
Fig. 2 (a) The top view of the unit cell of 1LG showing the inequivalent atoms A and B and unit vectors 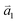 and and 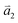 . (b) A top view of AB-stacked 2LG. (c) The unit cell of the reciprocal space of 1LG, showing the first Brillouin zone with its high symmetry points and axes. The primitive vectors . (b) A top view of AB-stacked 2LG. (c) The unit cell of the reciprocal space of 1LG, showing the first Brillouin zone with its high symmetry points and axes. The primitive vectors 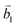 and and 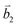 and high symmetry points are shown. (d) Optical image of NLG mechanically exfoliated on a SiO2/Si substrate. (e) Band structure of 1LG. Reproduced with permission from ref. 104. Copyright 2009, American Physical Society. (f–i) Band structures of 1LG (f), AB-stacked 2LG (g), 3LG (h), and 4LG (i) in the vicinity of the K point near the Fermi level (shown by the horizontal gray dashed line). and high symmetry points are shown. (d) Optical image of NLG mechanically exfoliated on a SiO2/Si substrate. (e) Band structure of 1LG. Reproduced with permission from ref. 104. Copyright 2009, American Physical Society. (f–i) Band structures of 1LG (f), AB-stacked 2LG (g), 3LG (h), and 4LG (i) in the vicinity of the K point near the Fermi level (shown by the horizontal gray dashed line). | ||
Mechanical exfoliation is an important method to produce NLG and can yield clean and extremely high-quality graphene.1,105–107Fig. 2(d) shows an optical image of an NLG flake on a SiO2/Si substrate. Spreading graphene flakes on the SiO2/Si substrate with a specific thickness (90 or 300 nm) of SiO2 layer can make the graphene flake visible and enhance its Raman signal, an effect originating from optical interference effects in the air/NLG/SiO2/Si multilayers.108,109
Graphene is a zero-gap semi-metal with a linear electronic band dispersion, which leads to its high mobility.1,110 This band structure also gives rise to its unique optical properties.23,111Fig. 2(f–i) show the band structure of 1LG, AB-2LG, -3LG, and -4LG, respectively. The band structure of AB-2LG shows a parabolic line near the Fermi level, whereas that of AB-3LG is a composite of 1LG and AB-2LG band structures. The band structures from 1LG to 4LG (AB-stacked) are different because of the interlayer vdW coupling and changes in symmetry.112,113 The band structure of NLG modifies the 2D mode profile of the corresponding Raman spectra by double resonant Raman scattering.44,49 Thus, Raman spectroscopy can be used to probe the band structure of 1LG and 2LG,44,114 as well as to identify the number of layers of NLG,44,115 as will be discussed later.
2.2 Phonon dispersion and Raman spectrum of graphene
The phonon modes (lattice vibrations) of a crystal at the Γ point correspond to the irreducible representation of its symmetry group, which is essential for the interpretation of the Raman spectra. There are two and four atoms in the unit cell of 1LG and graphite, respectively, resulting in six and twelve phonon modes at the Γ point, respectively. The point group symmetries of 1LG and graphite are both D6h. The lattice vibrations of 1LG and graphite at the Γ point can be expressed as: Γ1LG = A2u + B2g + E1u + E2g and Γbulk = 2(A2u + B2g + E1u + E2g), respectively.56,118,119 The three acoustic modes in both 1LG and the bulk correspond to one A2u mode and one E1u (doubly degenerate) mode.49,56 There are three optical phonon modes in 1LG, containing a doubly degenerate in-plane mode, E2g, and one out-of-plane mode, B2g, as shown in Fig. 3(a). In graphite, because the neighboring layers are inequivalent, Davydov splitting of the optical modes occurs.49,56 The E2g mode in 1LG generates an infrared-active E1u mode and a Raman-active E2g mode in graphite, and the B2g mode in 1LG divides into an infrared-active A2u mode and a silent B2g mode. The remnant E2g mode and one B2g mode are the shear and layer-breathing (LB) modes, which correspond to the in-plane and out-of-plane interlayer vibrations of the rigid atomic layers, respectively.118,120,121 The shear mode is referred to as the C mode in MLG because it provides a direct measurement of the interlayer Coupling and was first observed in MLG.70 For some multilayer 2d materials, other notations of the shear modes, such as S and SM, have been introduced by various research groups.54 The normal mode displacements and measured frequencies of the phonon modes of 1LG and graphite are shown in Fig. 3(a). The Raman active mode has been observed in 1LG and graphite at ∼1582 cm−1, the so-called G mode. The G band is associated with the doubly degenerate (longitudinal optical (LO) and in-plane transverse optical (TO)) phonon mode (E2g symmetry) at the BZ center and is a characteristic peak of graphene-related materials. The peak position of the G mode is sensitive to external perturbations, such as defects, doping, strain, and temperature and, thus, is widely used to probe the responses of graphene-based materials and related devices to external perturbations. However, owing to the weak interlayer vdW couplings, Pos(C) and Pos(LB), are very low (less than 130 cm−1) and exhibit significant layer-number dependence in MLG, as discussed later.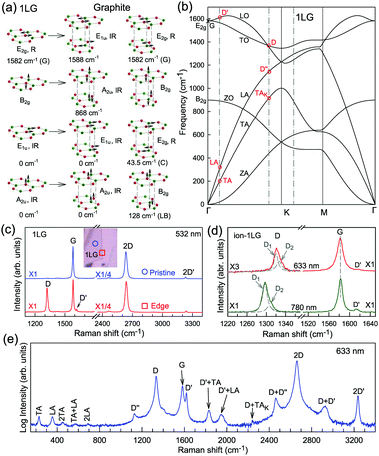 | ||
| Fig. 3 (a) Normal mode displacements of phonon modes at the Γ points of 1LG and graphite, which show how each phonon mode in 1LG gives rise to two phonon modes of graphite. Red and green dots represent inequivalent carbon atoms. Black arrows show atom displacements for each mode. The Raman-active (R) and infrared-active (IR) modes are identified. (b) Phonon dispersion curves of 1LG calculated by density functional perturbation theory. Reproduced with permission from ref. 116. Copyright 2008, American Physical Society. The assignments of each phonon branch are labeled. (c) First- and second-order Raman spectra of pristine 1LG and at its edge (square), whose measured spots in the flake are labeled by circles and squares in the inset, respectively. (d) Comparison of Raman spectra with D, G, and D′ bands of ion-1LG for 633 and 780 nm excitation. The two components (D1 and D2) of the D mode are shown with Lorentzian fitting. The dashed lines are guides to the eye. (e) The expected Raman modes observed in graphite whiskers in the spectral region from 150 to 3400 cm−1 excited at 632.8 nm. Reproduced with permission from ref. 117. Copyright 2001, American Physical Society. All the first- and second-order Raman modes are assigned. | ||
Fig. 3(b) shows the phonon dispersion of 1LG calculated by density functional perturbation theory (DFPT) within the local density approximation,116 which provides information about the atomic vibrations out of the BZ center. The phonon dispersion of 1LG has three acoustic and three optical branches inherited from the six vibrational modes at the Γ point. The three acoustic branches are the in-plane longitudinal acoustic (LA), transverse acoustic (TA), and out-of-plane acoustic (ZA) modes. The LA and TA branches have linear dispersion and higher frequencies than the ZA branch near the Γ point. The large slopes of the LA (21.36 km s−1) and TA (13.79 km s−1) branches result in the high in-plane sound velocity of graphene,122,123 which is also responsible for the ultrahigh thermal conductivity of graphene.124 The three optical branches are the LO, TO, and out-of-plane optical (ZO) branches, with the corresponding optical modes at the Γ point: E2g (LO and TO) and B2g (ZO) modes, as shown in Fig. 3(a and b). The LO and TO branches split when the phonon wave vector 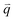 is far from the Γ point, and the frequency of the TO branch monotonically decreases along the Γ–K axis. Inelastic X-ray and neutron scattering are the most common techniques used to detect the phonon dispersion of solid materials,125,126 but they are not suitable for 2DMs because of the size limit. Raman spectroscopy can usually be used to probe the phonon modes at the BZ center. However, for graphene-based materials, the phonon modes far from Γ can also be probed by Raman spectroscopy via the double resonant Raman process.69,127,128
is far from the Γ point, and the frequency of the TO branch monotonically decreases along the Γ–K axis. Inelastic X-ray and neutron scattering are the most common techniques used to detect the phonon dispersion of solid materials,125,126 but they are not suitable for 2DMs because of the size limit. Raman spectroscopy can usually be used to probe the phonon modes at the BZ center. However, for graphene-based materials, the phonon modes far from Γ can also be probed by Raman spectroscopy via the double resonant Raman process.69,127,128
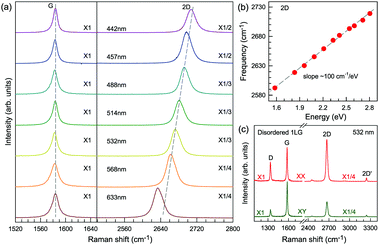
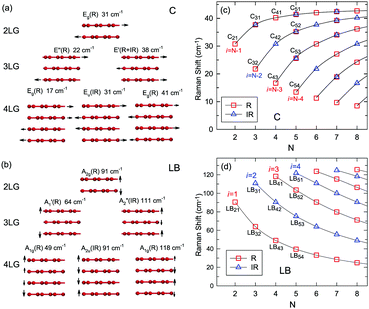
Fig. 3(c) shows two typical Raman spectra of pristine 1LG (at the sample center) and 1LG at its edge. The Raman spectrum of pristine 1LG consists of a set of distinct peaks in the spectral region from 1500–3400 cm−1. Except for the G mode at around 1580 cm−1, the 2D and 2D′ peaks appear around 2700 and 3240 cm−1, respectively. The 2D peak arises from the overtone of TO phonons around the K point and is activated by triple resonance Raman scattering (TRRS); moreover, it is strongly dispersive with excitation energy because of a Kohn anomaly at the K point.129 The 2D′ peak arises from the overtone of LO phonons around the Γ point, which is also activated by TRRS. The corresponding fundamental modes of the 2D and 2D′ peaks, i.e., the D and D′ peaks, require a defect for their activation in the double resonance Raman scattering (DRRS), and, thus, they are absent in the Raman spectrum of pristine 1LG. Edges naturally exist in every graphene sample and are a kind of defect because the translational symmetry is broken. Thus, the D and D′ peaks are observed in the Raman spectrum of 1LG at its edge, as shown in Fig. 3(c). Defects can be introduced into 1LG by some techniques, such as ion-implantation, so that the D and D′ peaks can also be observed in ion-implanted 1LG (ion-1LG) and other kinds of disordered 1LG,15,130,131 as shown in Fig. 3(d).
Besides the distinct D, G, D′, G, 2D, and 2D′ modes, other weak Raman modes can also be observed in 1LG. All of the expected Raman modes in 1LG have been observed in graphite whiskers.117 The spiral structure and cone tip suggest the existence of a twist angle between adjacent layers in the whisker, leading to weaker interlayer coupling compared to graphite, similar to the case of twisted 2LG with small twist angle.57 Therefore, the graphite whisker exhibits a typical Raman spectral feature identical to that of graphene, such as a single Lorentzian 2D peak and much stronger intensity of the 2D mode relative to the G mode (I(2D) ⋍ 13I(G) in Fig. 3(e)). Therefore, graphite whiskers are considered to be a prototype to show the abundant Raman modes that should be observed in 1LG. Indeed, many weak first- and second-order Raman modes have been revealed in its Raman spectrum, as indicated in Fig. 3(e), which can be well understood by DRRS or TRRS based on the phonon dispersion of 1LG, as discussed later.
2.3 The principle of double and triple resonance Raman scattering in graphene
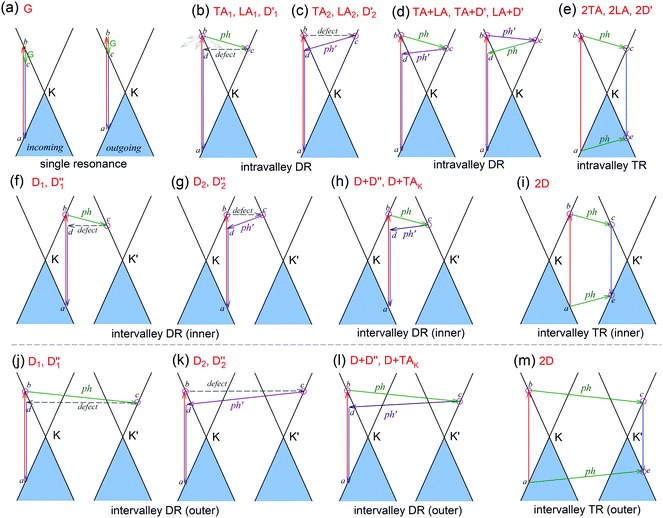
The peculiar band structures of graphene and other materials result in the corresponding Raman modes being involved in the resonant Raman process, e.g., the case of graphene depicted in Fig. 4. In principle, according to the fundamental Raman selection rule of momentum conservation,132 a one-phonon mode of an intrinsic crystal at the Γ point can be Raman active if it is symmetry allowed. In fact, the G-band is the only band originating from a normal first-order Raman scattering process in graphene systems. When the excitation energy is chosen to match or be near to an optical transition bandgap of the crystal, the Raman intensity can be enhanced by orders of 2 to 6, so-called resonant Raman spectroscopy. Because two linear electronic bands of intrinsic 1LG cross at the Fermi energy, an incoming photon with energy εL can always excite a resonant transition from state a in the valence band to state b in the conduction band with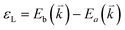 , where
, where 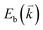 and
and 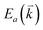 are the energies of the electrons in the conduction and valence bands with momentum
are the energies of the electrons in the conduction and valence bands with momentum 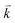 , respectively. The excited electron can be scattered by the E2g phonons to recombine with a hole, satisfying the incoming single resonance process. The outgoing single resonance process can also be satisfied for the G mode of 1LG. Both resonance processes are shown in Fig. 4(a).
, respectively. The excited electron can be scattered by the E2g phonons to recombine with a hole, satisfying the incoming single resonance process. The outgoing single resonance process can also be satisfied for the G mode of 1LG. Both resonance processes are shown in Fig. 4(a).
The excited electron 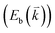 can also be scattered by phonons of an arbitrary wave vector,
can also be scattered by phonons of an arbitrary wave vector, 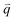 , as shown in Fig. 4(b) by the dashed arrows. The scattering probability, however, will be particularly high if the phonon scatters the electron from the real electronic state b into another real state c. If the electronic transition b → c is allowed, for a given phonon and electron dispersion, the scattering process is only fulfilled by one pair of phonon energies, ħωph, and phonon wave vector,
, as shown in Fig. 4(b) by the dashed arrows. The scattering probability, however, will be particularly high if the phonon scatters the electron from the real electronic state b into another real state c. If the electronic transition b → c is allowed, for a given phonon and electron dispersion, the scattering process is only fulfilled by one pair of phonon energies, ħωph, and phonon wave vector, 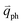 ; thus, the electron energy at state c is
; thus, the electron energy at state c is 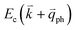 and
and 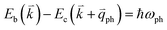 to maintain energy conservation. Such one-phonon first-order Raman scattering is forbidden by selection rules. However, the electron at state c can be scattered back to the state d with wave vector
to maintain energy conservation. Such one-phonon first-order Raman scattering is forbidden by selection rules. However, the electron at state c can be scattered back to the state d with wave vector 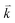 by crystal defects, which then emits a photon by recombining with a hole at state a, as depicted in Fig. 4(b). The above resonant process is one-phonon second-order Raman scattering, where the two scattering processes consist of one inelastic scattering event by emitting a phonon and one elastic scattering event by crystal defects. This scattering process yields the double resonance condition where
by crystal defects, which then emits a photon by recombining with a hole at state a, as depicted in Fig. 4(b). The above resonant process is one-phonon second-order Raman scattering, where the two scattering processes consist of one inelastic scattering event by emitting a phonon and one elastic scattering event by crystal defects. This scattering process yields the double resonance condition where 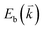 is always one of the resonant electronic states and
is always one of the resonant electronic states and 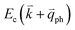 is the second resonant state. The two scattering processes can also start from an elastic scattering event followed by an inelastic scattering event (Fig. 4(c)).
is the second resonant state. The two scattering processes can also start from an elastic scattering event followed by an inelastic scattering event (Fig. 4(c)).
If the elastic scattering of defects, such as the electron from 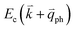 to a virtual state d in Fig. 4(b) or from
to a virtual state d in Fig. 4(b) or from 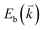 to
to 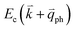 in Fig. 4(c), is displaced by another inelastic phonon scattering, the process becomes two-phonon second-order Raman scattering, as illustrated in Fig. 4(d). Further, if the valence and conduction bands are almost mirror bands, a TR Raman process can occur. For example, for the special case of 1LG, as shown in Fig. 4(e), the photo-excited electron can be scattered by a phonon (ωph) with
in Fig. 4(c), is displaced by another inelastic phonon scattering, the process becomes two-phonon second-order Raman scattering, as illustrated in Fig. 4(d). Further, if the valence and conduction bands are almost mirror bands, a TR Raman process can occur. For example, for the special case of 1LG, as shown in Fig. 4(e), the photo-excited electron can be scattered by a phonon (ωph) with 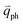 ; meanwhile, the photo-excited hole can be scattered by a phonon (ωph) with
; meanwhile, the photo-excited hole can be scattered by a phonon (ωph) with 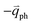 . In this case, the electron–hole generation is a resonant process, and both electron and hole scattering will be resonant. Finally, the electron–hole recombination will also be resonant. Therefore, for the TR Raman process, all steps in the normal double resonance process become resonant.
. In this case, the electron–hole generation is a resonant process, and both electron and hole scattering will be resonant. Finally, the electron–hole recombination will also be resonant. Therefore, for the TR Raman process, all steps in the normal double resonance process become resonant.
The resonance processes in Fig. 4(b–e) are intravalley double resonance processes because two resonant electronic states are connected within the same Dirac cones at the K point (or the K′ point) of 1LG. Instead, if the resonance process connects two associated resonant electronic states within the two inequivalent Dirac cones at the K and K′ points of 1LG, the corresponding double resonance mechanism is called an intervalley process. By analogy to the intravalley DR and TR processes in Fig. 4(b–e), the intervalley DR and TR processes also occur, as shown in Fig. 4(f–i). The double resonance processes in Fig. 4 only depict the incoming resonance process. The outgoing resonance process can also occur; thus, there are four possible resonant processes of fundamental and combination Raman modes because the order of the two scattered phonons leads to phonons with various wave vectors, 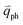 . However, the selected wave vector of the phonon produced by the outgoing resonance process is equal to that of the corresponding incoming resonance process. Finally, there are two inequivalent double resonant processes for the fundamental and combination Raman modes mediated by the scattering of electrons. Two inequivalent processes for combination Raman modes are degenerate for the overtone, so there is only one double resonant process for the overtone mediated by the scattering of electrons. It should be pointed out that the inelastic scattering of the hole by phonon emission/absorption and elastic scattering of the hole mediated by the defect can also be involved in the DR Raman process.56
. However, the selected wave vector of the phonon produced by the outgoing resonance process is equal to that of the corresponding incoming resonance process. Finally, there are two inequivalent double resonant processes for the fundamental and combination Raman modes mediated by the scattering of electrons. Two inequivalent processes for combination Raman modes are degenerate for the overtone, so there is only one double resonant process for the overtone mediated by the scattering of electrons. It should be pointed out that the inelastic scattering of the hole by phonon emission/absorption and elastic scattering of the hole mediated by the defect can also be involved in the DR Raman process.56
In principle, many different initial electronic states around the Dirac point and phonons with different symmetries and wave vectors can satisfy the DR conditions. However, considering (1) the existence of singularities in the density of phonon states that satisfy the DR condition, (2) the angular dependence of the electron–phonon scattering matrix elements, and (3) destructive interference effects when the Raman transition probability is calculated, only a few specific DR processes contribute to the observed Raman modes. Because there are two inequivalent DR Raman processes for both intravalley and intervalley DR Raman processes, each εL can select two phonon wave vectors of 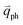 and
and 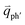 for the fundamental and combination modes and one phonon wave vector of
for the fundamental and combination modes and one phonon wave vector of 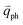 for the overtones near the Γ and K points, respectively. Because the phonon energy in 1LG is much smaller than εL,
for the overtones near the Γ and K points, respectively. Because the phonon energy in 1LG is much smaller than εL, 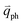 is almost equal to
is almost equal to 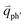 . Thus, in principle, for each εL, the phonons with almost equal
. Thus, in principle, for each εL, the phonons with almost equal 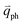 at different branches of the phonon dispersion curves can be probed by the DR Raman process. These are linked by the vertical dotted-dashed lines close to the Γ and K points, respectively, for the intravalley and intervalley DR Raman processes in Fig. 3(b).
at different branches of the phonon dispersion curves can be probed by the DR Raman process. These are linked by the vertical dotted-dashed lines close to the Γ and K points, respectively, for the intravalley and intervalley DR Raman processes in Fig. 3(b).
2.4 Understanding the Raman spectrum of graphene based on resonance Raman scattering
In 1LG, only the G mode is Raman active at the Γ point. The other observed Raman modes in Fig. 3(c and e) originate from the DR or TR Raman scattering in which one phonon or two phonons are involved. These Raman modes can be assigned based on the electronic band structures and phonon dispersion curves of 1LG, as labeled in Fig. 3(c–e). The Raman modes associated with one-phonon DR Raman process can only be observed in the presence of defects because defects are necessary to activate such Raman processes. However, the combination modes and overtones can be observed in the defect-free 1LG. The possible DR Raman process for each mode is depicted in Fig. 4(b–i). Because ħωph ≪ εL, once a phonon with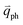 in one branch satisfies the requirement of the DR Raman process, the other phonons with
in one branch satisfies the requirement of the DR Raman process, the other phonons with 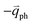 should also satisfy the requirement. Therefore, for each εL, the phonons in the different branches (linked by three vertical lines in Fig. 3(b)) can satisfy the requirements of the intravalley or intervalley DR Raman processes. However, because of different electron–phonon coupling for different phonon branches, not all the phonons excited by εL can be observed in the Raman spectra.
should also satisfy the requirement. Therefore, for each εL, the phonons in the different branches (linked by three vertical lines in Fig. 3(b)) can satisfy the requirements of the intravalley or intervalley DR Raman processes. However, because of different electron–phonon coupling for different phonon branches, not all the phonons excited by εL can be observed in the Raman spectra.
The well-known D and 2D bands originate from intervalley one-phonon and two-phonon DR Raman scattering between two nonequivalent Dirac cones (K and K′), respectively, involving one TO phonon near the K(K′) point and one defect in the case of the D band and two TO phonons for the 2D band.69,133 The two inequivalent one-phonon DR processes separately activate one TO phonon near the K point so that the observed D mode actually has an asymmetrical profile that can be fitted by two Lorentzian subpeaks, as shown in Fig. 3(d) for the experimental result and in Fig. 4(f and g) for their resonance processes. The intervalley TR resonance process of the 2D mode is depicted in Fig. 4(i). For the intervalley DR process, Fig. 4(f–i) only depict the inner intervalley DR or TR processes, which activate the phonons along K–Γ. Although the outer DR (or TR) processes (Fig. 4(j–m)) can also satisfy the DR (or TR) conditions and activate the phonons along the K–M axis, the main contribution to both the D and 2D modes is from the phonons along the Γ–K axis according to the numerical calculations.80
The phonon at the LA branch near the K point can also be activated by a defect in the intervalley DR process, which has been observed at ∼1150 cm−1 in graphite whiskers and is assigned to the D′′ peak.117,128,134–136 In 1LG, an asymmetrical Raman peak is observed at ∼2450 cm−1, whose intensity is comparable to that of the 2D′ mode. The assignment of this mode has puzzled scientists for a long time because it also appears in graphite.117,128,135,136 This mode is also observed in graphite whiskers and has been assigned to the D + D′′ peak,117 and was confirmed by later theoretical work, see ref. 80 and 137. A very weak peak at ∼2250 cm−1 has been observed in graphene whiskers and other carbon materials. It can be assigned to the D + TAK mode, which is a combination of a D phonon and a phonon belonging to the TA branch near the K point.80 It should be noted that the fundamental TAK mode has not been observed in carbon materials. All these modes result from the intervalley DR processes of the fundamental and combination modes, as depicted in Fig. 4(f–h).
The well-known D′ (∼1620 cm−1) and 2D′ (∼3240 cm−1) bands originate from intravalley one-phonon and two-phonon DR Raman processes, respectively, involving one LO phonon near the Γ point and one defect in the case of the D′ band and two LO phonons for the 2D′ band.138 The asymmetrical profile of the D mode cannot be revealed for the D′ mode because of its weak intensity and the small dispersion of the corresponding LO phonon near the Γ point. The TA and LA phonons near the Γ point can also be activated by defects in the one-phonon DR intravalley Raman process. There have been few reports on the corresponding Raman modes in 1LG, but they have been observed in graphite whiskers and are assigned as TA and LA modes (Fig. 3(e)), which also exhibit asymmetrical spectral profiles. Their combination modes (TA + LA) and overtones (2TA, 2LA) are also observed in graphite whiskers (Fig. 3(e)). The typical intravalley combination modes are the D′ + TA and D′ + LA modes, which can be clearly observed in 1LG. The two modes are, respectively, a combination of a D′ phonon with the TA and LA phonons, which have opposite 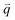 with respect to the D′ phonon.80,122,123 The intravalley DR processes of the fundamental and combination modes are depicted in Fig. 4(b–d), and the intravalley TR process of the overtone is depicted in Fig. 4(e).
with respect to the D′ phonon.80,122,123 The intravalley DR processes of the fundamental and combination modes are depicted in Fig. 4(b–d), and the intravalley TR process of the overtone is depicted in Fig. 4(e).
Obviously, the frequency of Raman modes is usually independent of εL because these Raman modes usually arise from optical phonons at the Γ point and the quasi-momentum of a photon is usually much smaller than the phonon wave vector at the zone edge. However, for DR or TR Raman processes, as depicted in Fig. 5, the wave vector (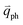 ) of the involved phonons is determined by εL.122,123,129,133,139 Thus, the peak position of the corresponding Raman mode is dependent on εL. For example, as shown in Fig. 5(a and b), Pos(2D) of graphene is dispersive with a slope of ∼100 cm−1 eV−1, which is twice that of the D mode. Similar behavior has been observed in various graphite materials. It is also well known that the frequencies of the Stokes and anti-Stokes components of a Raman mode should be equal to each other. However, the wave vectors of phonons involved in the Stokes and anti-Stokes DR and TR Raman processes are different from each other. Therefore, there exists a frequency discrepancy between the Stokes and anti-Stokes components of the dispersive Raman modes. Such a frequency discrepancy had been observed in other graphene-based materials, such as bulk graphite,135 graphite whiskers,117 and multi-walled carbon nanotubes.128
) of the involved phonons is determined by εL.122,123,129,133,139 Thus, the peak position of the corresponding Raman mode is dependent on εL. For example, as shown in Fig. 5(a and b), Pos(2D) of graphene is dispersive with a slope of ∼100 cm−1 eV−1, which is twice that of the D mode. Similar behavior has been observed in various graphite materials. It is also well known that the frequencies of the Stokes and anti-Stokes components of a Raman mode should be equal to each other. However, the wave vectors of phonons involved in the Stokes and anti-Stokes DR and TR Raman processes are different from each other. Therefore, there exists a frequency discrepancy between the Stokes and anti-Stokes components of the dispersive Raman modes. Such a frequency discrepancy had been observed in other graphene-based materials, such as bulk graphite,135 graphite whiskers,117 and multi-walled carbon nanotubes.128
In contrast to the unpolarized G mode, the intensities of the D, D′, 2D, and 2D′ peaks of disordered graphene are dependent on the polarization configuration of Raman scattering, as shown in Fig. 5(c), because of the selective optical absorption and emission mediated by electron–phonon coupling.80,117,140,141
Besides graphene, the DR Raman process is also present in other graphene-based materials, such as graphite, carbon nanotubes, and mutlilayer graphenes, although they do not have linear band structures.
3 Raman spectroscopy of multilayer graphene
3.1 Group theory of AB-stacked multilayer graphene
Lattice vibrations can be classified based on the irreducible representation of the symmetry groups of the crystal. Table 1 presents the space groups for 1LG, AB-NLG, and graphite and the corresponding point groups at the high symmetry points.49 Because the phonon along the Γ–K (T) axis mainly contributes to the DR Raman process in graphene,80 the symmetry information along the Γ–K direction is also shown. Both 1LG and graphite have D6h symmetry, and even NLG (ENLG) has D3d symmetry, whereas odd NLG (ONLG) (N ≥ 3) has D3h symmetry.| Space group | Point group | ||||
|---|---|---|---|---|---|
| Γ | K(K′) | M | T(Γ–K) | ||
| 1LG | P6/mmm | D 6h | D 3h | D 2h | C 2v |
| NLG even |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 m1 |
D 3d | D 3 | C 2h | C 2 |
| NLG odd |
P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 m2 |
D 3h | C 3h | C 2v | C 1h |
| Graphite | P63/mmc | D 6h | D 3h | D 2h | C 2v |
The first-order Raman process usually occurs at the Γ point because of momentum conservation. The Raman-active modes can be revealed by looking at the quadratic form of the basis function corresponding to the representation. The irreducible representations of 1LG and NLG for the lattice vibrations (Γvib) at the Γ point and along the Γ–K direction in the first BZ are listed in Table 2. The notations of both Bethe and Mulliken are adopted here. A more complete group theory analysis for every high symmetry point inside the first BZ and its dependence on the number of layers can be found in ref. 142. The irreducible representations of the lattice vibrations (Γvib) at Γ are summarized for 1LG, AB-2LG, and AB-3LG with Mulliken notation as follows:
| Γ1LG = A2u + B2g + E1u + E2g, |
| ΓAB-2LG = 2(A1g + Eg + A2u + Eu), |
We take AB-2LG as an example to show the different lattice vibrations in MLG with respect to 1LG. There are nine optical modes at Γ in AB-2LG. The G band in AB-2LG belongs to the Eg irreducible representation, which is doubly degenerate. The Eg mode represents the atomic motion of the nearest neighbor carbon atoms moving against each other within the plane and in phase between the two layers, denoted as the symmetric G mode.49 The Eu representation is not Raman active in AB-2LG because of the lack of inversion symmetry in the D3h point group. This mode represents the atomic motion of the nearest neighbor carbon atoms moving against each other within the plane but out-of-phase between the two layers, denoted as the antisymmetric G band.49 This Eu mode can become active if this inversion symmetry operation is broken by the presence of twisted stacking,57,143,144 doping,145,146 and strain.147 There also exists an ultralow-frequency (ULF) Eg mode at ∼31 cm−1, which corresponds to the interlayer rigid shear vibration.70 The other two A1g irreducible representations give rise to phonon modes at ∼90 cm−1 and ∼867 cm−1.71,148,149 The mode at ∼90 cm−1 corresponds to the interlayer breathing vibration normal to the basal plane, which is denoted as the LB mode.
With increasing N, the atomic displacements of each phonon vibration in AB-NLG become more complicated. In AB-3LG, the corresponding G and C modes are assigned to be E′ and E′′ representations, and the out-of-plane vibrational modes are assigned to  and
and  representations, respectively.
representations, respectively.
3.2 High-frequency Raman spectra of AB-stacked multilayer graphene
The Raman spectra of MLG consist of two fundamentally different sets of peaks. Those, such as D, G, 2D, etc., also present in 1LG and arise from in-plane vibrations and others, such as the C and LB modes, arise from the relative motions of the planes themselves, either perpendicular or parallel to the normal direction. In NLG, all vibrational modes split due to the confinement in the direction perpendicular to the basal plane. In the high-frequency region, because of the weak interlayer coupling in MLG, the peak position of the G mode, Pos(G), in the intrinsic NLG is almost ∼1582 cm−1 and is not sensitive to N. However, because NLGs with fewer than ten layers show distinctive band structures, the peak parameters of the Raman modes activated by the DR Raman process (e.g., the 2D mode) in NLG are significantly dependent on N.Fig. 6(a–c) shows the Raman spectra of 1LG and AB-stacked 2–5LGs excited by a 633 nm laser and AB-stacked 4–5LGs excited by a 532 nm laser. Indeed, all the G peaks are at around 1582 cm−1 and can be fitted with a single Lorentzian line shape.44 1LG has a single 2D peak at 2629.7 cm−1. The 2D band of AB-2LG can be well fitted with four Lorentzian peaks.44,115,142 Under 633 nm excitation, five and six 2D components can be identified in the Raman spectra of AB-stacked 3–4LG, as shown in Fig. 6(a and b) by arrows, crosses, and stars. These spectral features can be used to clearly identify N of NLG up to four if a Raman system with a high resolution (better than 1.0 cm−1) is used. Because the different components of the 2D bands may exhibit different resonant behaviors with laser excitation,114 it is very important to choose an appropriate laser wavelength (longer than 630 nm) to identify the number of layers of graphene flakes by Raman spectroscopy.115 For example, the 2D band of AB-4LG excited by 633 nm laser light shows more distinct spectral features than that by 532 nm excitation. The D mode of disordered NLG also exhibits similar spectral features to the corresponding 2D mode.
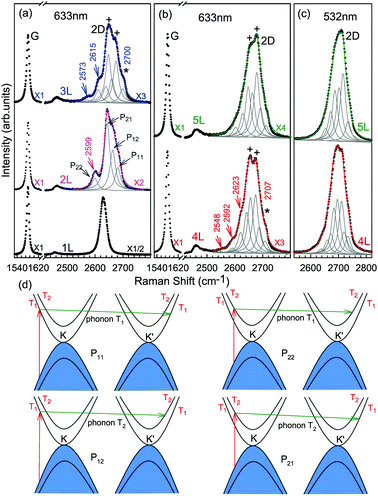 | ||
| Fig. 6 Raman spectra (dotted curves) of G and 2D peaks for AB-stacked 1–3LGs measured using a 633 nm laser (a) and those of AB-stacked 4–5LGs excited by both 633 (b) and 532 nm lasers (c). The 2D peaks are fitted by Lorentzian line shapes (gray peaks). The solid lines with colors are the sum of fitted Lorentzian curves. The arrows, crosses, and stars indicate the weak shoulders at the low energy side of the 2D peaks for AB-stacked 2–4LGs, the strongest components of the 2D peaks for AB-stacked 3–5LGs, and the high energy side of the 2D peaks for AB-stacked 3–4LGs, respectively. Reproduced with permission from ref. 115. Copyright 2010, American Physical Society. (d) The four allowed DR processes in AB-2LG. According to the scattering order of the phonon, the four DR processes are denoted as P11, P22, P12, and P21, respectively, and the corresponding 2D components are marked in (a). | ||
Because of the existence of several electronic bands in MLG and several possible DR Raman processes, many 2D components may be expected in MLG. How many 2D components actually exist in NLG is determined by the selection rules of the electron–photon and electron–phonon couplings in the DR Raman process. The symmetries of the electrons and phonons can be obtained from space group analysis. Taking AB-2LG as an example, the number of allowed DR processes will be larger than 1LG because both electronic and phonon branches are doubled. Along the T direction in the BZ, the transitions of T1 ⇌ T2 are allowed in AB-2LG, as shown in Fig. 6(d).80,110,142 The TO phonons for AB-2LG have T1 and T2 symmetries. For the electron scattering by a T1 phonon, the allowed process should occur between K and K′ electronic bands with the same symmetry T1 → T1 or T2 → T2. This also happens for the electron scattering by a T2 phonon but it connects conduction bands of different symmetries, i.e., T1 ⇌ T2. This gives rise to four possible DR processes, as shown in Fig. 6(a). The 2D components associated with the four DR processes have been clearly observed in the Raman spectra of AB-2LG, as shown in Fig. 6(a). The case for AB stacked 3–5LG is more complex according to point group analysis.142 However, because of the possible degeneracy and overlapping of these peak components, the number of observed components is much lower than the theoretical one. To obtain good fits, six and eight components are, respectively, required for the 2D bands of AB-3LG and AB-4LG if the peak widths of all components are kept as a fixed constant of 24 cm−1 in the fitting process.115
Besides the D and 2D modes, other Raman modes in NLG activated by DR Raman process also show N-dependent spectral features, such as the LA + D′, TA + D′, and D + D′′ modes.
3.3 Ultralow-frequency Raman spectra of AB-stacked multilayer graphene
The Raman modes of AB-MLG in the ultralow-frequency region are mainly related to the interlayer C and LB vibrations.53,54,70 There are N − 1 degenerate pairs of C modes and N − 1 LB modes for AB-NLG, which are denoted as CNN−i and LBNN−i (i = 1, 2,…,N − 1), respectively, where CN1 (LBN1) (i.e., i = N − 1) has the highest frequency and CNN−1 (LBNN−1) (i.e., i = 1) has the lowest frequency. The C and LB modes can be Raman active (R), infrared active (IR) or both, depending on the symmetry of NLG and the number of layers (N).53,54,57,71,150 The symmetry can be divided into D3d for ENLG and D3h for ONLG, as discussed above.53,142,150 The N − 1 C modes in ENLG and ONLG can be represented by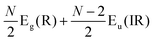 and
and 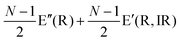 , respectively, where Eg and E′′ are Raman active, Eu is IR active, and E′ is both Raman and IR active. According to their Raman tensors, only Eg and E′ can be observed in the backscattering configuration. N − 1 LB modes in ENLG and ONLG are represented by
, respectively, where Eg and E′′ are Raman active, Eu is IR active, and E′ is both Raman and IR active. According to their Raman tensors, only Eg and E′ can be observed in the backscattering configuration. N − 1 LB modes in ENLG and ONLG are represented by 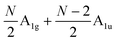 and
and 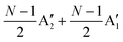 , respectively, in which A1g and
, respectively, in which A1g and 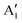 are Raman active and A1u and
are Raman active and A1u and 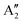 are IR active.
are IR active.
Because the C and LB modes are rigid layer lattice vibrations, ω(C) and ω(LB) can be identified by regarding each graphene layer in AB-MLG as a single ball so that AB-NLG can be simplified as a linear chain with N balls in which only nearest-neighbor interlayer interaction is considered. This is known as the linear chain model (LCM).70,151 By assuming that the force constant of the interlayer coupling per unit area is α‖0 (α⊥0) for the C (LB) modes, the frequencies ω (in cm−1) of the N − 1 C and LB modes can be calculated by solving the corresponding N × N (tridiagonal) dynamical matrix as follows:70,71
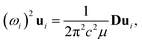 | (1) |
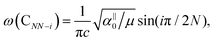 | (2) |
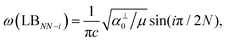 | (3) |
| v(i)j = cos[i(2j − 1)π/2N] | (4) |
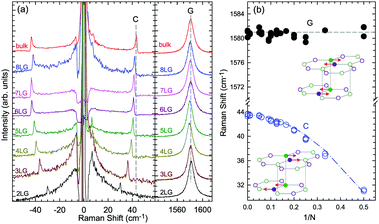
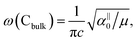 and
and  , which are
, which are 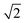 times of ω(C21) and ω(LB21), respectively. ω(Cbulk) was measured as 43.5 cm−1,152 while ω(LBbulk) was estimated as ∼125.3 cm−1 based on the Pos(LB) measurements in tMLGs,57,71 and, thus, α‖0 = 12.8 × 1018 N m−3 and α⊥0 = 106.5 × 1018 N m−3. Therefore, eqn (2) can be simplified as follows:
times of ω(C21) and ω(LB21), respectively. ω(Cbulk) was measured as 43.5 cm−1,152 while ω(LBbulk) was estimated as ∼125.3 cm−1 based on the Pos(LB) measurements in tMLGs,57,71 and, thus, α‖0 = 12.8 × 1018 N m−3 and α⊥0 = 106.5 × 1018 N m−3. Therefore, eqn (2) can be simplified as follows:| ω(CNN−i) = ω(Cbulk)sin(iπ/2N), | (5) |
| ω(LBNN−i) = ω(LBbulk)sin(iπ/2N), | (6) |
Once the normal mode displacements corresponding to ω(C) and ω(LB) have been obtained, the symmetry and Raman activity of the C and LB modes can be deduced.53,54,57,70,71 As examples, Fig. 7(a and b) depict the frequencies and the corresponding normal mode displacements for N − 1 C and LB modes in AB-stacked 2–4LG, respectively. Fig. 7(c and d) plot all the C and LB modes as a function of N, respectively, in which the Raman-active and infrared-active modes are also identified. The C modes in Fig. 7(c) are plotted with the branches of i = N − 1, N − 2,…, because only the CN1 modes are observed in the intrinsic MLG at room temperature.70 The LB modes in Fig. 7(d) are plotted with the branches of i = 1, 2, 3,…, because all the LB modes in the branches of i = 2n − 1 (n = 1, 2, 3,…) are Raman active.
 | ||
| Fig. 7 Symmetry, frequency, Raman activity, and normal mode displacement for each C mode (a) and LB mode (b) of AB-(2–4)LG. The frequencies of C (c) and LB (d) modes as a function of number of layers calculated by LCM and 2LCM, respectively. The rectangles and triangles indicate the Raman and infrared active modes, respectively. Reproduced with permission from ref. 150. Copyright 2016, Elsevier. | ||
Based on the LCM, if α‖0 and α⊥0 are independent of N in AB-MLG, ω(C) and ω(LB) in AB-MLG are determined by ω(Cbulk) and ω(LBbulk). In the intrinsic AB-MLG, whether the C or LB modes can be experimentally observed relies on their Raman activity, the strength of the electron–phonon coupling (EPC), and the appropriate polarization configuration. Fig. 8(a) plots the C mode, as well as the G mode, of AB-stacked 2–8LG and bulk graphite,70 whereas Fig. 8(b) shows the positions of these two modes as a function of 1/N. In contrast to the G peak, which remains constant at ∼1582 cm−1, ω(C) decreases monotonically with decreasing N. The N-dependent ω(C) can be well fitted by ω(CN1) = ω(Cbulk)cos(π/2N) based on the LCM,70 which suggests that α‖0 remains constant at 12.8 × 1018 N m−3 in AB-NLG. Concerning the line shape, the G peaks maintain Lorentzian line shapes, while the C modes display a unique profile asymmetry and can be well fitted by the Breit–Wigner–Fano (simplified as Fano) line shape. Details about the line shapes of the C modes will be discussed later. Unlike the C modes, the LB modes of AB-NLG cannot be observed directly at room temperature because of the weak EPC.70 However, these modes have been observed either indirectly (via overtones and combination modes)153 or by increasing the laser power (heating).154
 | ||
| Fig. 8 (a) Stokes Raman spectra of the C peak (left) and G peak (right) for AB-stacked 2–8LG and bulk graphite. (b) The position of the G peak (filled black circles) and C peak (open blue circles) as a function of inverse number of layers. The red dashed-dotted line was calculated by LCM. The insets show the atomic displacements of the C and G modes. The vertical dashed lines in (a) and the horizontal line in (b) are eye guides. Reproduced with permission from ref. 70. Copyright 2012, Nature Publishing Group. | ||
Overall, the LCM can predict the N-dependence of ω(C) in NLG and the constant interlayer interaction of α‖0 from AB-2LG to bulk graphite. The LCM discussed above could be applied to the C and LB modes of all 2D materials, such as MoS2, WSe2, black phosphorus (BP), ReS2, ReSe2, and even 2D heterostructures.151,155–167 Because ω(C) and ω(LB) are significantly dependent on the number of layers, N, the C and LB modes can be used to identify the thickness or number of layers of two-dimensional material flakes.151,155,167,168
3.4 Raman spectra of ABC-stacked multilayer graphene
Stacking order has a strong impact on the electrical and optical properties of MLG. Apart from the AB stacking, ABC (rhombohedral) stacking is also common in NLG. Lui et al.169 found that ∼85% of the area in graphene flakes corresponds to ABA stacking and the remaining ∼15% corresponds to ABC stacking, which is in agreement with the X-ray diffraction study on bulk graphite.170 The spectral profiles of the 2D mode are quite different for AB- and ABC-stacked NLG,5,6,150,171 which reflects their different electronic structures. Taking 3LG as an example, Fig. 9(a) plots the G and 2D modes of ABC- and AB-stacked 3LG. Similar to the DR Raman process in AB-2LG discussed above, the three degenerate TO phonons in 3LG can couple to all electron bands, in theory generating fifteen sub-peaks for AB-stacked 3LG; however, the profiles can be well-fitted using six sub-peaks, as shown by dashed-dotted lines in Fig. 9(a).142 In ABC-3LG, the 2D mode is more asymmetrical. Additionally, the G mode of ABC-stacked 3LG (∼1581 cm−1) is 1 cm−1 red shifted compared to that of AB-stacked 3LG (∼1582 cm−1). Detailed characterization of the 2D mode profile in ABC-stacked and AB-stacked 4–6LG can be found in ref. 5, 150 and 171. However, the differences in the 2D mode profile between AB- and ABC-stacked NLG are εL-dependent and become more complicated with increasing N.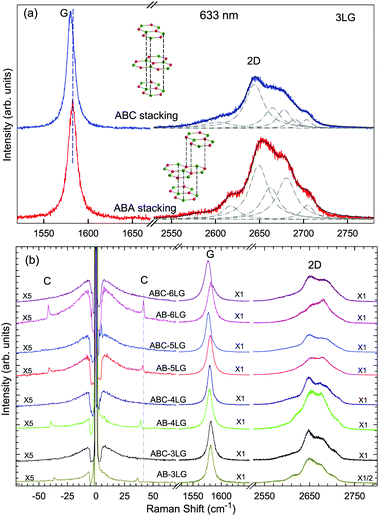 | ||
| Fig. 9 (a) Raman spectra of 3LG measured in the ABA and ABC zones in the G and 2D mode regions under excitation at 633 nm. A schematic diagram of ABA and ABC structures is shown. The 2D peaks of ABA- and ABC-3LGs are fitted by Lorentzian line shapes (dashed-dotted lines). (b) Raman spectra of 3–6LG with AB and ABC stacking in the C, G, and 2D peak spectral regions. The C modes are observed in AB-NLG (N = 3, 4, 5, 6) but not in ABC-NLG. Reproduced with permission from ref. 150. Copyright 2016, Elsevier. | ||
Later, Lui et al.169 and Zhang et al.150 demonstrated that the interlayer vibrations such as the C modes can be used to reveal the stacking order of NLG based on their different symmetries. Lui et al. observed a noticeable Raman peak at ∼33 cm−1, assigned to C31 in AB-3LG, whereas a pronounced peak at ∼19 cm−1, attributed to C32, was observed in ABC-3LG at a high temperature (800 K) induced by laser heating when the samples were suspended on a quartz substrate. The vanishing of C31 in ABC-3LG is due to its Raman inactivity, whereas the absence of C32 in AB-NLG is ascribed to the unsuitable polarization configuration.169 Zhang et al. carried out further investigation on the ULF Raman spectra of both AB- and ABC-NLG deposited on Si/SiO2 substrates at room temperature and found that CN1 can only be observed in AB-stacked but not ABC-stacked NLG, as shown in Fig. 9(b). ABC-NLG belongs to the D3d point group where the C modes are represented by 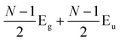 for ONLG and
for ONLG and 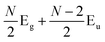 for ENLG.150 According to the irreducible representation of CN1 in ABC-NLG, CN1 was assigned to IR-active Eu in ONLG, whereas it was Raman-active Eg in ENLG. Thus, it was concluded that the absence of the CN1 mode in ABC-stacked ONLG is due to symmetry limitations, whereas the disappearance in ABC-stacked ENLG is probably due to the small EPC. It is also noted that CNN−i could not be observed on SiO2 even when the laser power was as high as 10 mW because it merges with the substrate background, unlike the sample on a quartz substrate.150,169 Thus, this can be utilized as a new method to distinguish AB- and ABC-stacking in NLG.
for ENLG.150 According to the irreducible representation of CN1 in ABC-NLG, CN1 was assigned to IR-active Eu in ONLG, whereas it was Raman-active Eg in ENLG. Thus, it was concluded that the absence of the CN1 mode in ABC-stacked ONLG is due to symmetry limitations, whereas the disappearance in ABC-stacked ENLG is probably due to the small EPC. It is also noted that CNN−i could not be observed on SiO2 even when the laser power was as high as 10 mW because it merges with the substrate background, unlike the sample on a quartz substrate.150,169 Thus, this can be utilized as a new method to distinguish AB- and ABC-stacking in NLG.
3.5 Raman spectra of twisted multilayer graphene
Besides the AB and ABC stacking configurations, NLG can also be formed by assembling mLG (AB-mLG if m > 1) and nLG (AB-nLG if n > 1) flakes together with a twist angle (θt) at the twisted interface, which is denoted as tNLG or t(m+n)LG. More constituents and twisted interfaces in tNLG are also possible. The twist angle in tNLG can be determined by the positions of the so-called R and R′ Raman bands.57,172,173 The R and R′ modes originate from the non-center LO and TO phonons of the constituents, which are folded back to the Γ point by the presence of Moiré superlattices in t(m+n)LG.57,172,173 In twisted 2LG (t2LG or t(1+1)LG), novel physical properties arise because of the periodically modulated interactions between the two Dirac electron gases with a large Moiré supercell, as shown in Fig. 10(a).174–186t2LG has a Dirac-like linear dispersion with a Fermi velocity lower than that of 1LG.177,181,182,187 In principle, the band structure of t(m+n)LG can be considered as the overlapping of the band structures of the mLG and nLG constituents after considering the effects of zone folding resulting from the Moiré superlattices. By changing θt, it is possible to tune the optical absorption of tNLG.178,183,185,186 Because of the θt-dependent energy of van Hove singularities (VHS) in tNLG178,183,185 and different stacking sequences, tNLG exhibits rich electronic and optical properties.57,71,143,144,188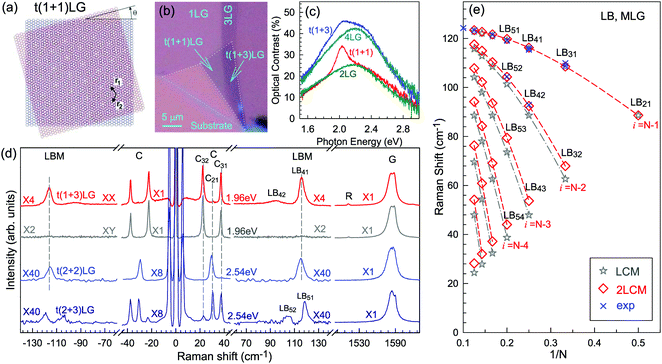 | ||
| Fig. 10 (a) Moiré pattern of t(1+1)LG. (b) Schematic diagram of t(1+3)LG. (c) Optical image of a flake comprising a t(1+1)LG and a t(1+3)LG. Reproduced with permission from ref. 57. Copyright 2014, Nature Publishing Group. (d) Stokes/anti-Stokes Raman spectra in the C and LB spectral range, and Stokes Raman spectra in the G peak region for t(1+3)LG, t(2+2)LG and t(2+3)LG. Polarized Raman spectra of t(1+3)LG are also shown. Reproduced with permission from ref. 71. Copyright 2015, American Chemical Society. (e) The theoretical wavenumber of the LB modes as a function of N calculated from LCM and 2LCM. The gray dashed-dotted and red dashed lines are eye guides for LCM and 2LCM, respectively. Blue crosses show the experimental (exp) data. | ||
tNLG can be formed by the accidental folding of graphene flakes during the exfoliation process or by the transfer of graphene flakes onto other graphene flakes.57,144,189 Most MLG flakes grown by CVD also exhibit twisted stacking.190–192Fig. 10(b) shows the optical image of the t(1+1)LG and t(1+3)LG formed by mechanical exfoliation, and their optical contrasts are shown in Fig. 10(c). In comparison to AB-stacked 2LG and 4LG, optical contrasts of both t(1+1)LG and t(1+3)LG exhibit additional resonant spectral features around 2.0 eV. These features correspond to the energies of VHSs in the joint density of states (JDOSs) of all optically allowed transitions (JDOSOAT) in t(1+1)LG and t(1+3)LG. Once εL matches the energies of the VHSs, the C and LB modes are resonantly observed in the Raman spectra.
The twist in t(m+n)LG significantly modifies the symmetry and Raman activity of the C and LB modes with respect to AB-MLG. t(m+n)LG (m ≠ n) has C3 symmetry, and the corresponding irreducible representation is Γvib = A + E, and both A and E modes are Raman active. In t(m+n)LG with m ≠ n, all nondegenerate LB modes have A symmetry, and all doubly degenerate C modes have E symmetry. t(n+n)LG (n ≥ 2) has D3 symmetry, and the corresponding irreducible representation is Γvib = A1 + A2 + E. The A1 and E modes are Raman active, whereas the A2 mode is Raman inactive. In t(2+2)LG, LB41, and LB43 have A1 symmetry, whereas LB42 has A2 symmetry, and all the C modes are E symmetry. The changes of the symmetry and Raman activity and the presence of VHS energies of JDOSOAT in tNLGs make the C and LB modes observable when εL matches the corresponding VHS energies.
Fig. 10(d) shows the Stokes/anti-Stokes Raman spectra in the C and LB spectral range and the Stokes Raman spectra in the G peak region for t(1+3)LG, t(2+2)LG and t(2+3)LG in the backscattering configuration. In t(1+3)LG, the C modes of 3LG and the LB modes of 4LG are observed. The absence of the LB modes in the cross (XY) polarization configuration confirms the nature of the LB vibrations. This indicates that the twisted interface obstructs the interlayer shear coupling so that only the C modes of the AB-stacked constituents can be measured.57 The shear coupling at the twisted interface (α‖t) is found to be 20% of the bulk case (α‖0).57 However, the twisted interface will not affect the interlayer breathing coupling, so the LB modes of all layers are observed.71 For the LB modes, based on LCM and experimental ω(LBN1) in tNLGs, the fitted α⊥0 is ∼106 × 1018 Nm−3, and the silent LB mode (B2g) in graphite is determined to be ∼125.3 cm−1, slightly smaller than ∼128 cm−1 determined by neutron spectrometry. However, the simulated ω(LB42) and ω(LB52) based on LCM are 3–4 cm−1 lower than those observed in t(1+3)LG and t(2+3)LG, suggesting that the θt-independent second-nearest-neighbor breathing interactions (β⊥0) is necessary to fit the experimental values of ω(LB42) and ω(LB52). The new model is denoted as 2LCM and β⊥0 of ∼9.3 × 1018 N m−3 can be used to fit well the experimental data. Because the relative motions of the second-nearest-neighbor layers are always out-of-phase for the LBN2 modes, α⊥0 with additional β⊥0 is crucial to reproduce their frequencies, as indicated by Fig. 10(e). However, the second-nearest-neighbor layers are always in-phase for the LBN1 modes; thus, ω(LBN1) is insensitive to β⊥0, and it can be well estimated by the LCM.
Because of the softened α‖t and identical α⊥0 to the bulk case at the twist interface in tNLGs, ω(C) is mainly determined by the number of layers of each AB-stacked constituents, whereas ω(LB) is mainly determined by the number of layers (N) of tNLGs, as shown in Fig. 10(d) for t(1+3)LG, t(2+2)LG and t(2+3)LG. Therefore, the number of layers of AB-stacked constituents and tNLG itself can be identified by the observed ω(C) and ω(LB), respectively, under resonant conditions.
4 Resonance Raman spectroscopy of monolayer and multilayer graphenes
Raman scattering is a process related to photo-excited electron–hole pairs, phonon scattering by electrons or holes, and electron–hole recombination. Thus, the Raman intensities and profiles of Raman modes are determined by the EPC and band structures of the materials. The intensity of the Raman modes of graphene can be calculated by second-order perturbation theory.80,172 Because of the unique band structure, most of the Raman modes in graphene are involved in resonance processes. As discussed before, the combination modes and first-order Raman modes activated by defects, e.g., 2D, D + D′′, and D, originate from the TR or DR process.56 The intensity of the G mode in 1LG is also dominated by quantum interference effects. In AB-NLG, the Fano profile of C modes arises from the quantum interference between the C mode and a continuum of electronic transitions near the K point, as shown in Fig. 8(c and d). In tNLG, the first-order modes (C, LB and G modes) can be enhanced by the singularities in JDOSOAT. Because the DR and TR Raman processes in graphene and MLG have been discussed above in detail, we will address the latter three cases of resonance in the following subsections.4.1 Quantum interference of the G mode in graphene
The peculiar linear band structure of graphene means that the G mode always satisfies the incoming and outgoing resonant conditions, as demonstrated in Fig. 4(a). Besides the two resonant intermediate excited states (pathway I in Fig. 11(a)), there are many nonresonant intermediate excited states (pathway II in Fig. 11(a)), which also contribute to the Raman scattering of the G mode. The Raman intensity of the G mode, I(G), is a result of total quantum interference between different Raman pathways in graphene. For an intrinsic graphene sample with EF = 0, it is not easy to reveal the effects of quantum interference between different Raman pathways because it requires the modification of intermediate excited states with transition energies close to the laser excitation energy Eex. When graphene is doped to EF, an optical transition can be blocked by hole doping when the initial state has an energy higher than the Fermi level and is not occupied, as shown in Fig. 11(b). In this case, one can modify intermediate excited states with transition energies close to Eex.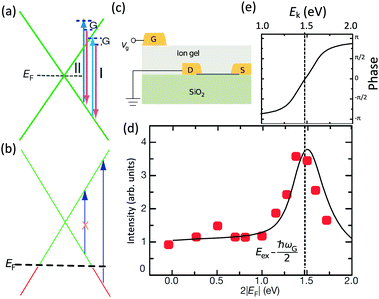 | ||
| Fig. 11 (a) Illustration of two representative G-mode Raman pathways (I and II) through two different intermediate excited states in graphene with EF = 0. (b) Hole doping results in electronic transitions from zero energy to 2|EF| being blocked because of empty initial states. (c) An ion-gel-gated graphene device on a SiO2 substrate can make graphene p-doped. (d) I(G) as a function of 2|EF| (symbols). Black line: theoretical prediction. (e) Quantum phase of Raman pathway amplitude illustrated as a function of intermediate excitation energy. Reproduced with permission from ref. 58. Copyright 2011, Nature Publishing Group. | ||
Chen et al. tuned the hole doping by electrostatic doping58 in an ion-gel-gated graphene device on a SiO2 substrate, as illustrated in Fig. 11(c). They found that, when near-infrared laser excitation (Eex = 1.58 eV) is used and some of the pathways are blocked, I(G) does not diminish as expected but increases dramatically,58 as depicted in Fig. 11(d). The observation cannot be interpreted well by the general assumption that the pathway for G mode Raman scattering is due to resonance alone (I in Fig. 11(a)).
To further understand the phenomenon, the pathways close to resonance (II in Fig. 11(a) and off-resonance are expanded. Under these conditions, all pathways interfering with each other have different quantum mechanical amplitudes, including phase and magnitude. For any specific one-phonon and one-photon state, I(G) can be described by
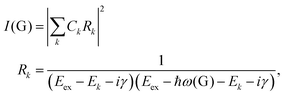 | (7) |
The above results show that the simple picture of G-mode graphene Raman scattering, in which only the on-resonance pathways are considered, is invalid. This unexpected phenomenon presents evidence for a new understanding of resonance Raman scattering in graphene.
4.2 Fano resonance in multilayer graphenes
A Raman peak usually exhibits a symmetric Lorentzian line shape, such as the G peak in 3LG and graphite, as shown in Fig. 12(a). However, the C modes in AB-NLG and graphite show Fano line shapes, as shown in Fig. 12(b) for 3LG and graphite. The Fano resonance effect describes a quantum interference effect between a discrete state (in this case phonon states) and a continuum transition, in which the excited eigenstates are a mixture of the discrete and continuum states.193 Historically, the Fano line shape was observed in heavily doped silicon systems,194 metallic carbon nanotubes,195 nanowires,196 and topological insulators.197 The Fano resonance is highly asymmetric, in which the asymmetry of the line shape depends on the coupling coefficient between discrete and continuum states. The Fano lineshape can be expressed by70,198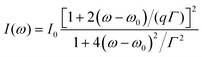 | (8) |
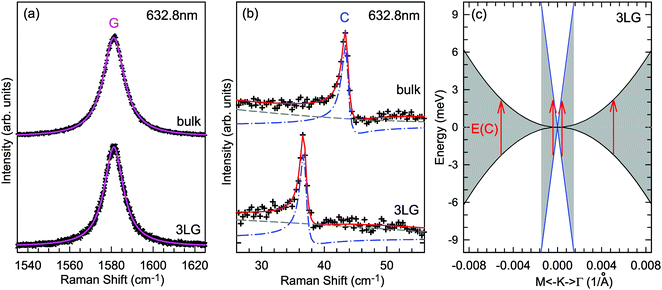 | ||
| Fig. 12 (a) Lorentzian line shape of the G peak in 3LG and bulk graphite. (b) The C peak of 3LG and bulk graphite fitted by a Breit–Wigner–Fano line shape. The solid red lines, dashed lines, and dashed-dotted lines are the fitted curves, background, and Fano components, respectively. Spectra in (a and b) were excited at 1.96 eV. (c) Schematic band structure of 3LG close to K. The gray regions highlight transitions near K that could resonate with the C mode. Red arrows indicate transitions with the same energy as the C mode, E(C). Reproduced with permission from ref. 70. Copyright 2012, Nature Publishing Group. | ||
In principle, the G mode in graphene and NLG should also exhibit the Fano line shape. Indeed, the G band of 1LG exhibits an asymmetric line shape near the charge neutrality point as a manifestation of Fano resonance, whereas the line shape is symmetric when the graphene sample is electron or hole doped.199 The observed Fano resonance can be interpreted as an interference between the phonon and excitonic many-body spectra in graphene.199 However, the line shape of the G mode in neutral 1LG shows only a very slight asymmetry because of the small 1/|q|, ∼0.07, which is much smaller than that of the C modes (∼0.370), leading to an almost imperceptibly asymmetric peak. The G band of AB-2LG does not exhibit any Fano resonance, regardless of doping.199 The Fano resonance can also be observed in the infrared spectra of phonons in NLG because of the strong coupling between phonons and interband electronic transitions.200,201
4.3 Resonant Raman spectroscopy of twisted multilayer graphene
In comparison to AB-NLG, the band structures of tNLG are significantly affected by the presence of a twisted interface and Moiré pattern, introducing several θt-dependent VHSs to the density of states (DOSs).57,71,182,185,186 The relationship between the energies of the VHSs of parallel bands near K and θt can be estimated,186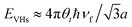 , where a is the lattice constant of graphene (2.46 Å), ℏ is the reduced Planck's constant, and νf is the Fermi velocity of 1LG (∼106 m s−1). For a fixed laser excitation energy εL, the Raman signal of t(1+1)LG is enhanced around a specific θt when εL matches the VHS energy of the corresponding t(1+1)LG.185,186 Similar results had been observed in t(m+n)LG.202
, where a is the lattice constant of graphene (2.46 Å), ℏ is the reduced Planck's constant, and νf is the Fermi velocity of 1LG (∼106 m s−1). For a fixed laser excitation energy εL, the Raman signal of t(1+1)LG is enhanced around a specific θt when εL matches the VHS energy of the corresponding t(1+1)LG.185,186 Similar results had been observed in t(m+n)LG.202
To probe the intrinsic resonant Raman behavior of t(m+n)LG, it is necessary to study a t(m+n)LG with specific θt using tunable excitation energies. Indeed, as shown in Fig. 13(a), I(G) of a t(1+1)LG can be enhanced by a factor of more than 30 at a specific εL. In the quantum mechanical picture of Raman scattering, incident photons first excite a set of intermediate electronic states, which are then scattered by phonons and radiate energy-shifted photons. However, only the optically allowed electronic transitions are involved in the resonant Raman process. Therefore, the VHS energies of JDOSOAT should be considered for Raman resonance in t(m+n)LG. JDOSOAT can be calculated using the following equation:57
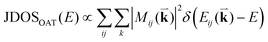 | (9) |
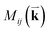 is the optical matrix element between the ith conduction and jth valence bands, and
is the optical matrix element between the ith conduction and jth valence bands, and 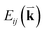 gives the transition energy of a i → j band pair at the wave vector
gives the transition energy of a i → j band pair at the wave vector 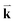 . The band structure of t(1+1)LG with 10.6° ((p,q) = (1,9)) is calculated and shown in Fig. 13(b), and the optically allowed transitions are marked by dashed arrows. The squared optical matrix elements of the corresponding transitions are shown in Fig. 13(c). Indeed, the transitions with energy ∼1.15 eV between parallel bands along K–M are forbidden, as indicated by solid arrows with crosses. The JDOSOAT of t(1+1)LG is shown in Fig. 13(d). There is one distinctive VHS in the JDOSOAT of t(1+1)LG, which is labeled by an arrow. When εL matches the VHS energies of JDOSOAT of the t(1+1)LG, the Raman resonance of the G mode occurs. The experimental εL-dependent peak area of the G mode (A(G)) in t(1+1)LG can be well fitted using the calculated VHS energy of 1.95 eV.
. The band structure of t(1+1)LG with 10.6° ((p,q) = (1,9)) is calculated and shown in Fig. 13(b), and the optically allowed transitions are marked by dashed arrows. The squared optical matrix elements of the corresponding transitions are shown in Fig. 13(c). Indeed, the transitions with energy ∼1.15 eV between parallel bands along K–M are forbidden, as indicated by solid arrows with crosses. The JDOSOAT of t(1+1)LG is shown in Fig. 13(d). There is one distinctive VHS in the JDOSOAT of t(1+1)LG, which is labeled by an arrow. When εL matches the VHS energies of JDOSOAT of the t(1+1)LG, the Raman resonance of the G mode occurs. The experimental εL-dependent peak area of the G mode (A(G)) in t(1+1)LG can be well fitted using the calculated VHS energy of 1.95 eV.
 | ||
| Fig. 13 (a) G mode of t(1+1)LG excited by seven εL. The R and R′ modes are indicated by arrows. The spectra are scaled and offset for clarity. (b) The band structure of (1,9) t(1+1)LG. The optically allowed transitions are marked by dashed arrows. The transitions between parallel bands along the K–M direction are forbidden, as indicated by the solid arrows with crosses. (c) Squared optical matrix elements of the corresponding band pairs in (b). (d) JDOSOAT in t(1+1)LG along Γ–K–M–Γ. (e) A(G) of t(1+1)LG as a function of εL. Filled circles: experimental data. Solid lines: simulations. Reproduced with permission from ref. 57. Copyright 2014, Nature Publishing Group. | ||
The DR process in t(1+1)LG is more complicated than that in 1LG because of the zone-folding effect of the band structures. Similar to 1LG, the 2D peak of t(1+1)LG usually shows a single Lorentzian peak; however, the FWHM and frequency of the 2D peak in t(1+1)LG also depend on θt.186,203,204
The resonance Raman behavior of t(m+n)LG (m > 1, n > 1) becomes complicated because of its novel band structures and EPC. Because there may exist multiple VHS energies of JDOSOAT in t(m+n)LG, the resonant profiles of A(C), A(LB), and A(G) are usually composed of several subpeaks corresponding to each VHS energy.57 The strong resonance Raman effect makes the C and LB modes observable in t(m+n)LG, paving the way to probe interface coupling and stacking orders of tNLG, especially for CVD-grown tNLG.57,71,144,202,205
5 Disordered monolayer and multilayer graphenes
One generally refers to defects in graphene as anything that breaks the symmetry of the infinite carbon honeycomb lattice.206 The amount and nature of the defects strongly depend on the production method and may change from sample to sample. Both the amount and the nature of defects can have a strong influence on the properties of graphene samples.208 For example, atomic-sized defects can introduce midgap states close to the Dirac point and have been identified as the major limiter of electron mobility for graphene deposited on substrates.209,210 Extended line defects could be used to guide charge, as well as spin, atoms, and molecules.211,212 Defects also have a strong influence on chemical reactivity, which makes defective graphene a prospective catalyst.213 It is crucial to understand how the defects in graphene affect its Raman spectrum and how to use Raman spectroscopy to identify these defects.5.1 Raman spectra of defect-containing graphene flakes
It is well-known that, with respect to pristine graphite and graphene, additional Raman modes can be observed in disordered graphite and graphene, e.g., the so-called D and D′ modes. These modes cannot be attributed to the vibration mode from defects themselves, but correspond to phonons with momentum q ≠ 0 because of the presence of defects in the sample. This defect induced process is not allowed in a purely crystalline sample (without defects) because of momentum conservation. The intensity, peak position, and linewidth of the Raman modes in pristine graphite and graphene can significantly change with the increasing number of defects.Fig. 14(a) shows an example of the Raman spectra of 1LG samples subjected to different ion implantation conditions.15 By increasing the ion dose, I(D) increases from the zero value of pristine 1LG. Above 1013 Ar+ per cm2 the Raman peaks start to broaden significantly. Above 1015 Ar+ per cm2 the spectra show a decreased intensity, indicating the full amorphization or partial sputtering of the graphene layer.15Fig. 14(b and c) show the peak intensity and peak area (integrated intensity) of the D, G, D′, and 2D modes in oxidized graphenes with increasing plasma exposure.206 Note that the units are arbitrary, that is, we can compare the trend of the different peaks with exposure time, but we cannot compare the absolute numbers for a fixed time. The number of defects increases with increasing plasma exposure time. I(D) and I(D′) show similar trends to that of Ar+-implanted 1LG, as shown in Fig. 14(a). The evolution of I(D) with respect to the number of defects can be divided into two stages. In stage 1, the low defect stage, I(D) increases with respect to the number of defects. In stage 2, as the number of defects further increases, I(D) decreases, as shown in Fig. 14(b and c). Interestingly, I(2D) decreases sharply in stage 2. Because the 2D mode can be easily observed only when the crystallinity of graphene is high (pristine or with a few defects), it can be employed as an indicator of relatively high-quality graphene. I(G) in Fig. 14(b) slightly decreases with increasing plasma exposure time, and A(G) shows the opposite behavior because of the width broadening. I(G) and A(G) at low defect concentrations are insensitive to the number of defects because they arise from the in-plane C–C bond stretching of all pairs of sp2 atoms in both rings and chains.214 This makes I(G) or A(G) an intensity reference for the defect-induced Raman modes in defect-containing graphene flakes, as discussed later.
 | ||
| Fig. 14 (a) Evolution of the D, G, and D′ modes of 1LG samples implanted by different ion doses in units of Ar+ per cm2. Reproduced with permission from ref. 15. Copyright 2010, Elsevier. Raman intensity as (b) amplitude and (c) integrated area of oxidized graphene under increasing plasma exposure. Reproduced with permission from ref. 206. Copyright 2012, American Chemical Society. (d) Raman spectra of nLG (n = 1, 2, 3 and 4) implanted with 90 keV carbon (12C) ions at a fluence of 5 × 1013 C+ per cm2 by an LC-4 type system. Reproduced with permission from ref. 207. Copyright 2015, Elsevier. | ||
The Raman intensity of the defect-induced modes (e.g., D and D′) is proportional to the average number of defects in the unit cell, nd, at a low defect concentration. Based on the double resonance theory,215 the intensity of a Raman mode in graphene is closely related to the finite lifetime (τ) of the electronic states involved in the Raman process, which corresponds to a line broadening energy γ = ℏ/τ because the electronic states interact, e.g., with phonons and defects. The total broadening energies (γtot) should consider the sum of the broadening of the corresponding electronic states. γtot can be considered as the sum of two contributions, γep and γD, where γep is the intrinsic broadening (present in perfectly crystalline samples) arising from electron–phonon scattering and γD is extrinsic (induced by the presence of defects and dependent on the sample quality), arising from electron-defect elastic scattering. For a simplified case, γtot depends only on the excitation energy, εL, of the type of defect and its concentration, nd, through γtot = γep(εL) + γD(εL, nd). The D mode depends on nd through two distinct mechanisms. First, it is proportional to nd (I(D) ∝ nd). Secondly, it depends on nd through electron/hole broadening energies (γtot = γep + γD). With increasing nd, γD increases, thus leading to a decrease in the intensity of the resonant phonon modes. At low defect concentrations (γtot ≫ γD), the first mechanism is dominant and, thus, I(D) increases as nd increases. With further increasing nd, the second mechanism becomes dominant, leading to a decrease in I(D). However, I(2D) is sensitive to γtot and the electronic structure of the defect-containing graphene. Therefore, I(2D) decreases with γtot broadening when the band structure changes slightly.215 The process can also be divided into two steps: (1) γep ≫ γD and γtot ∼ γep, where I(2D) remains constant, and (2) γD ≫ γep and γtot ∼ γD, where I(2D) reduces continuously. Thus, the decreasing slope of I(2D) depends on how heavily the various types of defects influence the graphene, in particular, the band structure. Some special laser lines should be chosen to enhance the 2D band when the bandgap is open to the visible and even ultraviolet range, similar to that in carbon nanotubes.216,217 Furthermore, for defect-containing graphene in stage 2, I(2D) gradually becomes weaker. I(2D) can even become invisible for heavily disordered graphene. In this case, the graphene sheet starts to be dominated by the fully-disordered areas. The above analysis can be extended to different types of defects, allowing the characterization of the defects in graphene.
Raman spectra of ion-implanted MLGs show similar spectral features to that of 1LG, as discussed above.207,218 As depicted in Fig. 14(d), the D band of ion-implanted 1LG exhibits an asymmetrical lineshape and can be fitted by two Lorentzian subpeaks, i.e., the D1 and D2 peaks, which result from two DR Raman processes, as demonstrated in Fig. 4(f and g), respectively. I(D1) = 3I(D2). If we assume that one of the two D subpeaks corresponding to each 2D component in the MLGs is dominant, as in 1LG, the D band profiles should be very similar to the corresponding 2D band. Indeed, similar profiles of the D and 2D bands have been observed for ion-implanted NLG, as indicated by the arrows in Fig. 14(b). When NLGs are implanted by the same ion dose, I(D) becomes weaker with increasing N because the average number of defects in ion-implanted NLG decreases with increasing N.
5.2 A general model for point defects and line defects
Point and line defects are two typical sets of defects in graphene, whose schematic diagrams are shown in Fig. 15(a and b), respectively. Point defects are characterized by the average distance between nearest defects (LD) or by the defect density (σ = 1/LD2). The typical point defects in graphene and MLG can be introduced by ion implantation or ion-bombardment.15,16,66,207 These techniques have been used for other two-dimensional materials to create point defects.220–222 Line defects are characterized by their average crystallite size (La) or by the crystallite area (La2). A highly crystalline turbostratic graphitic structure from amorphous carbon under a high heat treatment temperature is formed by graphene layers with line defects.223,224 Most graphene samples are likely to exhibit both types of defects, as illustrated in Fig. 15(c). Raman spectroscopy is an ideal tool to identify the number of defects.15,77,219 Thus, we will address a phenomenological theory to identify the concentrations of point and line defects using I(D)/I(G) or A(D)/A(G) in the following paragraphs. | ||
| Fig. 15 Illustrations of graphene samples with point defects (a) and line defects (b). (c) Illustrations of a graphene sample containing both point and line defects. The red regions in (a–c) define the structurally damaged area (S-region), and the green circles and lines in (a–c) are the activated area (A-regions) where the D band is active. (d) ΓG as a function of La or LD. The solid and dashed lines are the plots of eqn (10) as a function of La (ξ = La) and LD (ξ = 10LD), respectively. (e) (AD/AG)EL4 as a function of La or LD. The solid and dashed lines are the plots of eqn (11) and (12) as a function of La and LD, respectively. (f) (AD/AG)EL4 as a function of ΓG. The solid and dashed lines are obtained by simultaneously solving eqn (10)vs.eqn (11) and eqn (10)vs.eqn (12), respectively. (g and h) Theoretical calculation for (AD/AG)EL4 as a function of the G band spectral linewidth ΓG. The symbols were obtained from numerical simulations. In (g), equal symbols connected by lines represent samples with a given La value (indicated in the legend), with decreasing LD distances from smaller to larger ΓG values. (h) The opposite: equal symbols connected by lines represent samples with a given LD value (indicated in the legend) with decreasing La distances from smaller to larger ΓG values. Reproduced with permission from ref. 219. Copyright 2017, IOP Publishing. | ||
Because of the quantum confinement effect, the FWHM of the G peak (ΓG) increases with increasing defect density. Fig. 15(d) shows ΓG as a function of La or LD. ΓG increases exponentially as the phonon localization length ξ decreases with respect to the phonon coherence length lph, as proposed by Ribeiro-Soares et al.:224
ΓG(La,LD) = 15 + 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp (−ξ/lph). exp (−ξ/lph). | (10) |
The other protocol is based on the intensity ratio between the disorder-induced D band and the G band, i.e., I(D)/I(G). To avoid the influence of peak broadening and the wavelength dependence of the peak intensity, the integrated intensity (peak area) ratio, (AD/AG)EL4, is considered here. (AD/AG)EL4 as a function of La and LD is shown in Fig. 15(e). There are two stages for the evolution of (AD/AG)EL4 with increasing defect density. In the low defect density stage, (AD/AG)EL4 increases, because the intensity of the D peak increases with increasing number of defects. At a high defect density stage, (AD/AG)EL4 decreases because the disordered lattice structure reduces AD. The evolution of AD/AG can be understood quantitatively using a phenomenological model.15 For point defects, a single point defect on the graphene sheet causes modifications on two length scales, here denoted as rA and rS (with rA > rS), which are the radii of two circular areas measured from the impact point. Within the shorter radius rS, structural disorder from the impact occurs, labeled as the structurally damaged region (S-region) and marked in green in Fig. 15(a and c). For distances larger than rS but shorter than rA, the lattice structure is preserved, but the proximity to a defect causes a breaking of selection rules, and leads to an enhancement of the D band, labeled as the activated region (A-region) and marked by red in Fig. 15(a and c). Similarly, the S-region and A-region of line defects are shown in Fig. 15(b and c). Thus, the emergence of the D mode requires both A- and S-regions. (AD/AG)EL4 is dominated by the competition between the S- and A-regions. At a low defect density, there is no competition between the S-region and A-region, leading to an increase in (AD/AG)EL4. At a high defect density, the A-region is occupied by the S-region, leading to a decrease in (AD/AG)EL4. Based on this phenomenological model, (AD/AG)EL4 as a function of La or LD can be given by solving the approximate rate equations for the evolution of S- and A-regions:
 | (11) |
 | (12) |
As shown in Fig. 15(d and e), the defect-density-dependent behavior of ΓG is different between the point and line defects. This is also true for (AD/AG)EL4. Thus, by combining the experimental ΓG and (AD/AG)EL4, the defect types can be identified, as shown in Fig. 15(f).
For the situation where the line and point defects coexist, (AD/AG)EL4 as a function of La and LD can also be given by solving the approximate rate equations for the evolution of the S- and A-regions:
 | (13) |
Fig. 15(g and h) show the theoretical calculation of (AD/AG)EL4 as a function of the G band spectral linewidth, ΓG, for the coexistence of point and line defects. Because both crystallite size and point defects contribute to phonon localization, the localization length ξ is chosen as the minimum value between La and αLD for the calculation of ΓG. The plots in Fig. 15(g and h) provide a user-friendly diagram for the quantification of defects by varying La and LD, respectively. The dashed lines in Fig. 15(g and h) are the same plot of ΓG-dependent (AD/AG)EL4 obtained from eqn (13) and (10) by varying LD and considering a fixed value of La = 500 nm (La → ∞, which reproduces pure point defects). Similarly, the solid lines in Fig. 15(g and h) correlate the ΓG-dependent (AD/AG)EL4 obtained from eqn (13) and (10) for different La with LD fixed at 500 nm (LD → ∞, which reproduces pure line defects). These two curves delimit a phase space that embraces samples with point and line defects. One can obtain the density of line and point defects by locating the positions in Fig. 15(g and h) according to the experimental (AD/AG)EL4 and ΓG.
Fig. 15(g and h) and the related equations contain clear specifications for the quantification of defects, establishing a protocol for disentangling the contributions of point-like and line-like defects in the Raman spectra of graphene-based materials. La and LD are important structural parameters to identify the transition between perfect graphene and amorphous carbon. The evaluation of the values from Fig. 15(g and h) is useful for understanding and optimizing the synthetic, purification, and functionalization processes of graphene-based materials, such as graphitic nanocarbon made for inks225 and conductive coatings.226
5.3 Edges
Edges naturally exist in graphene samples and also appear when graphene layers are etched into nanoribbons and quantum dots.227,228 The properties of graphene strongly depend on the edge orientation in different crystallographic directions.229–231 Edge is a special kind of defect because the translational symmetry is broken here. An immediate consequence of symmetry breaking is the Raman activation of the defect-related modes, such as the D and D′ modes. The edges of 1LG have two basic orientation configurations, i.e., armchair edge and zigzag edge, whose wave vectors involved in the elastic scattering event of the DR Raman process are nA and nZ, respectively, as demonstrated in Fig. 16(a). Electrons or holes in the DR Raman process cannot be scattered between the K and K′ valleys by nZ. Therefore, a perfect zigzag edge cannot produce a D peak.56,77,232 This does not apply to an intervalley scattering mode (i.e., D′), which can be activated both by armchair and zigzag edges.56 Because the atomic structures of perfect zigzag and armchair edges in a graphene layer are only constructed from the two outermost atoms at the edge, the edge of the graphene layer is quite different from line defects, as discussed in Section 5.2. | ||
| Fig. 16 (a) Left panel: Ideal zigzag and armchair edges. Right panel: Equi-energy contours for electronic states involved in the D peak. nZ and nA indicate directions normal to the zigzag and armchair edges, respectively. (b) Real-space Raman processes take place at a given point in space. Photon-excited electrons (e) and holes (h) move along classical trajectories. After emitting phonons or scattering at edges, the D mode is activated (left panel) when e and h must meet with opposite momenta at the same point in space to recombine radiatively and produce the scattered photon. Otherwise, the D mode cannot be activated (right panel). The length scale (x) in the vicinity of an edge contributing to the D mode is determined by the traveling distance (∼4 nm) of e and h over the lifetime of the virtual electron–hole pair. Reproduced with permission from ref. 56. Copyright 2013, Nature Publishing Group. (c) Raman spectra at a graphene edge measured for different incident polarization measured at 633 nm (left panel), and I(D)/I(G) as a function of laser polarization direction (right panel). Reproduced with permission from ref. 77. Copyright 2009, American Chemical Society. | ||
To understand the Raman spectrum at graphene edges, the Raman process in real space should be considered. In real space, phonons, defects, electrons, and holes can be viewed as quasi-particles. A complete Raman process is limited by the momenta (spatial extent and direction) of electrons and holes. Therefore, first, a perfect armchair edge requires that the electronic momentum is perpendicular to the edge so that electron and hole can meet and recombine radiatively to activate the D mode. Moreover, the spatial extent of electron and hole involved in the DR Raman process to meet and recombine radiatively is estimated to be ∼4 nm,77 which means that only the zone ∼4 nm from the edge contributes to the D mode, as shown in Fig. 16(b).56 The D mode at perfect armchair edges shows polarization dependence because of the requirements of the DR Raman process. When the polarization of the incident laser is along the K–M direction, the D mode presents the strongest intensity. For a linearly polarized light oriented at an angle θ with respect to the perfect armchair edge, the θ-dependent I(D) is: I(D) ∝ cos2(θ),77 as shown in Fig. 16(c). For the D′ peak, its real-space Raman process is analogous to that of the D peak. For both zigzag and armchair edges, this leads to the same I(D′) ∝ cos2(θ) dependence.56,75–77,232 For ideal edges, the D peak is zero for zigzag orientations and large for armchair orientations. However, for real samples, I(D)/I(G) does not always show a significant dependence on the edge orientation. For exfoliated samples, even though edges can appear macroscopically smooth and oriented at well-defined angles, they are not necessarily microscopically ordered.77 In this case, the polarization dependence for a disordered edge is determined by contributions from armchair and zigzag segments with different orientations.
In the case of MLG edges, each graphene layer in MLG will contribute its own edge to the overall edges. Ideal MLG edges should exhibit good alignment of all the edges of the graphene layers, as shown in Fig. 17(a and b) for 2LG and 3LG cases, respectively. In reality, each graphene layer in MLG is misaligned with adjacent layers to a significant extent, from micrometers (see Fig. 17(c)) to nearly zero. This is also true of CVD-grown NLG samples.202 The well-aligned nLG edge can be denoted as nLGnE, where the subscript E refers to ‘edge’. In the general case, a specific alignment configuration at the nLG edge is the well-aligned edge of mLG (including m = 1) lying on (n–m)LG, denoted as nLGmE (n > m). The edge of a graphene layer lying on (n−1)LG, denoted as nLG1E, is a building block for MLG edges, and, thus, the edges of each graphene layer in Fig. 17(d) can be denoted as 1LG1E, 2LG1E, 3LG1E, and 4LG1E.
 | ||
| Fig. 17 Optical microscope images of (a) 2LG and (b) 3LG with well-aligned edges, and (c) a graphene flake containing 1LG, 2LG, 3LG, and 4LG. (d) Schematic diagram of side-view alignment configuration at the edges of the graphene flake in (c). hi (i = 1, 2, 3) refer to the misalignment distances between the edges of two adjacent misaligned graphene layers. (e) Raman spectra at the edges of nLG1E (n = 1, 2, 3, 4) as indicated by the circles in (c). The dashed lines show the 2D bands of 1LG and 2LG (2LG and 3LG) used to fit that at 2LG1E (3LG1E). Reproduced with permission from ref. 207. Copyright 2015, Elsevier. | ||
Raman spectroscopy is a rapid and nondestructive technique to identify MLG edges.207,218Fig. 17(e) depicts the Raman spectra of a graphene flake at nLG1E edges (n = 1, 2, 3, 4), which can be clearly identified in the optical image. The D-band profile at nLG1E resembles that of ion-implanted nLG. Because only one graphene layer contributes to the D band at nLG1E (n > 1), its intensity is weaker than that at the corresponding nLGnE. The 2D bands at nLG1E (n > 1) are composed of the 2D bands from nLG and (n−1)LG, as shown by the dashed lines in Fig. 17(e). Moreover, based on the spectral features of the D and 2D bands, the alignment configurations of the edges in NLG can be identified.207 It is possible to identify the misalignment distance between 2LG1E and 1LG1E of 2LG down to the nanometer scale.218
5.4 Probing the nature of defects in graphene by Raman spectroscopy
According to their nature and origin, defects in graphene can be defined such as edges, implanted atoms, vacancies, grain boundaries, and defects associated with a change in carbon hybridization, for example, from sp2 to sp3.206 One, two, or more kinds of defects can exist in a graphene sample. The general models for point defects introduced by implanted atoms, line defects, and edges have been discussed above. Vacancies (see Fig. 18(a)) can be viewed as point defects15,16,237 that are slightly different from common point defects66,219 induced by the ion-implantation technique. The grain boundaries are the interfaces between two graphene domains with different crystallographic orientations and can be defined by the misorientation angle between two crystalline domains,238e.g., the misorientation angle for grain boundary in Fig. 18(b) is 27°. This type of defect can behave as a line defect.208 However, it is difficult to define a similar parameter for the vacancy and grain boundary defects in the same way as the LD and La parameters in common point or line defects.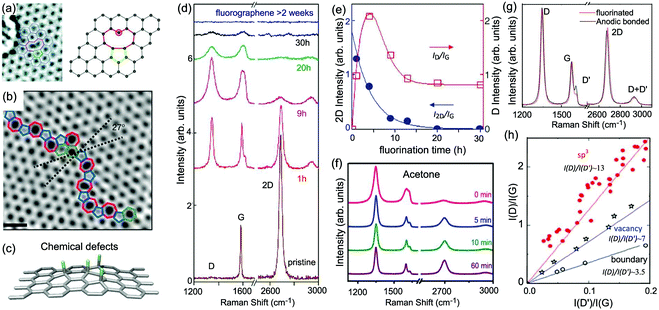 | ||
| Fig. 18 Representative schematics of (a) vacancies, (b) grain boundaries, and (c) chemical defects (sp3-type defects). Reproduced with permission from ref. 208, copyright 2011, American Chemical Society, ref. 233, copyright 2011, Nature Publishing Group, and ref. 234, copyright 2017, American Chemical Society. (d) Raman spectra of as-prepared fluorinated graphene exposed to XeF2 for different fluorination times. The Raman spectra are offset for clarity. (e) I(D)/I(G) and I(2D)/I(G) as a function of fluorination time. Reproduced with permission from ref. 130. Copyright 2010, Wiley Online Library. (f) Raman spectra of as-prepared fluorinated graphene (SF6, 25 W, 2 min) and fluorinated graphene after different treatment times in different solvents, such as acetone. Reproduced with permission from ref. 235. Copyright 2017, Wiley Online Library. (g) Raman spectrum of fluorinated (red) and defective graphene produced by anodic bonding (black), showing the same D, G, and 2D intensities but different D intensities. (h) I(D)/I(G) vs. ratio I(D′)/I(G), showing the linear dependence between the two parameters at low defect concentration, giving different I(D)/I(D′) for different types of defects. Data are from ion-bombarded graphene,16,66 oxidized graphene,131 and graphite with different grain sizes.236 The solid lines are eye guides. Reproduced with permission from ref. 206. Copyright 2012, American Chemical Society. | ||
The sp3-type defects are usually induced by chemical decoration, such as mild oxidation, hydrogenation, or fluorination.130,239–242 Thus, they are also known as chemical defects. By attaching exotic atoms to each site of graphene, as illustrated in Fig. 18(c), the optical, electronic, and magnetic properties can be modified. For example, the change of the hybridization of carbon atoms from sp2 to sp3 can remove the conducting π band and open the energy gap240,242,243 or form local magnetic moments.244,245 Therefore, the quantitative characterization of such defects in graphene-based systems via Raman spectroscopy is of intense research interest.
Here, we take fluorinated graphene as an example to elucidate the Raman fingerprint of sp3-type defects (chemical derivatives),130,246 which can be prepared by the mechanical cleavage of graphite fluoride or by exposing the graphene to atomic fluorine compounds such as XeF2 and CF4 plasma. Fig. 18(d) shows the Raman spectra of fluorinated graphene after repeated exposure to XeF2 plasma. As shown in the figure, prominent defect-induced D and D′ peaks have emerged. Fig. 18(e) summarizes I(D)/I(G) and I(2D)/I(G). The I(D)/I(G) ratio suddenly increases after the initial fluorination and then gradually decreases to saturation upon increasing the fluorination time. However, the I(2D)/I(G) ratio monotonically decreases. Both the G and 2D modes broaden and the D′ peak overlaps with the G modes after continuous fluorination. I(G) changes only slightly for fluorination times of less than 9 h. Although it is difficult to characterize the sp3-type defect concentration quantitatively in this case, I(D)/I(G) and I(2D)/I(G) follow a two-stage evolution, as depicted in Fig. 14(b and c).
Compared with the other types of defects, one characteristic feature of sp3-type defects is that such defects can be partially recovered under specific conditions.235,240,246 In the case of fluorinated graphene, it is reported that the initial fluorine desorption occurs at around 300 °C, leading to the recovery of the graphene lattice.246–249 The solvent used in the transfer process can also be used for defluorination.235Fig. 18(f) plots the Raman spectra of as-prepared fluorinated graphene after fluorination (25 W, 1 min) using SF6 as the source gas and those after different treatment times in acetone. The recovery of the 2D peak and weakening of I(D′), as well as the reduction in the FWHM of all peaks, can be clearly observed, implying that the sample undergoes defluorination. After defluorination, although the I(2D)/I(G) ratio increases, I(D)/I(G) is still so large that the full recovery of defects cannot occur. The sharp D peak after the defluorination process is attributed to the presence of vacancies in the fluorinated graphene, which cannot be recovered again after treatment in acetone.235 The defluorination is more likely to occur in a more polar solvent, such as acetone, isopropanol, and deionized water, because a polar solvent is more likely to interact with the F atoms attached to the graphene.
Until now, significant work has been performed to investigate the nature of defects in graphene-based systems, usually using the D and D′ modes.206 Generally, both the D and D′ modes show similar trends in peak intensities and widths at low defect concentrations. In this case, I(D) and I(D′) increase with increasing ion dose and fluorination time, as shown in Fig. 14(a) and 18(d), respectively. When investigating the intensities, different types of defects can induce different features in the D and D′ modes. Two representative Raman spectra (with low defect concentrations) of fluorinated graphene and defective graphene obtained by anodic bonding in graphene are shown in Fig. 18(g), where the D, G, and 2D modes exhibit similar intensities but those of I(D′) are quite different. Fluorinated graphene has a higher I(D)/I(D′) than defective graphene formed by anodic bonding. Considering both D and D′ modes are defect-induced modes, I(D) and I(D′) are linearly proportional to the defect concentration. Consequently, I(D)/I(D′) only depends on the physical origin of the defect but is independent of the defect concentration. This suggests that I(D)/I(D′) can be used to identify the nature of the defects.206 Using a systematic analysis of their relationship of all types of defects, such as sp3-type defects, vacancies, and boundaries, the I(D)/I(D′) values are revealed to reach maximum (∼13) for sp3-type defects and decrease to ∼7 for vacancies and ∼3.5 for boundaries. Interestingly, I(D)/I(D′) of the pristine defects introduced by anodic bonding is the same as that of ion-implanted graphene, which is an indicator of vacancy-like defects. Therefore, I(D)/I(D′) can be used experimentally to obtain information on the nature of defects in graphene. This makes Raman spectroscopy a powerful tool to fully characterize the disorder in graphene.
6 Identifying number of layers of graphene flakes by Raman spectroscopy for standardization
There are several hundred companies worldwide producing or using graphene-based materials. Many issues concern the large-scale production, processing, and application of graphene-based materials outside of the laboratory. For industry to have confidence in the graphene materials that are produced commercially, the properties of these materials must be accurately, reliably, and reproducibly measured. For example, the properties of graphene flakes are strongly related to their thickness, i.e., number of layers (N), and, thus, the determination of N of graphene flakes is critical for quality appraisal in graphene industrial products. According to the N-dependent band lattice vibrations and band structures, the value of N of graphene flakes can be identified by several parameters (position, profile, and intensity) of the corresponding Raman bands. Thus, Raman spectroscopy can be expected to serve as a robust, fast, accurate, nondestructive, and even substrate-free approach for the N counting or thickness identification of graphene flakes168 produced by micromechanical exfoliation, CVD growth, or transfer processes on various substrates, bridging the gap between the characterization and international standardization of the thickness determination of graphene flakes and the gap between academia and industry.6.1 Identification of monolayer graphene
The I(G) of NLG deposited on a SiO2/Si substrate increases monotonically until reaching ten or more layers and decreases for thicker graphene flakes.168,250 To identify N of NLG by I(G), the crucial step is to distinguish 1LG in the graphene flake. For exfoliated flakes on a SiO2/Si substrate, the 2D band exhibits a single Lorentzian peak, while AB-nLG (n > 1) and ABC-nLG (n > 2) exhibit broad bands, which can be fitted by several Lorentzian peaks.115,168 Therefore, the profile of the 2D band can be used to identify 1LG in the exfoliated flakes, as shown in Fig. 19(a). This method is a substrate-free approach to identify the exfoliated 1LG on any substrate.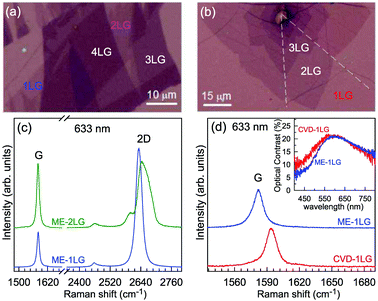 | ||
| Fig. 19 Optical images of (a) ME-NLG and (b) CVD-NLG flakes. The scale bars are shown. (c) Raman spectra of ME-1LG and ME-2LG. (d) Raman spectra of CVD-1LG and ME-1LG both deposited onto 90 nm-SiO2-thick SiO2/Si substrates. Inset: optical contrast spectra of ME-1LG and CVD-1LG. The excitation wavelength for Raman spectra is 633 nm. Reproduced with permission from ref. 205. Copyright 2017, Wiley Online Library. | ||
It is challenging to identify 1LG produced by CVD and other methods. For example, CVD-2LG tends to be t(1+1)LG, in which the 2D-band profile is mostly likely to be a single Lorentzian peak with a blueshift in peak position because of its small Fermi velocity.187 Therefore, a single Lorentzian peak of the 2D band is no longer a reliable index to identify 1LG in CVD-grown flakes. The I(G) of 1LG on a multilayer dielectric substrate is mainly modified by the multiple reflections at the interfaces and optical interference within the medium. If the CVD-grown flake contains 1LG, its I(G) should be approximately equal to that of ME-1LG when they are deposited on the same substrate. Thus, ME-1LG can be considered as a standard sample when it is transferred onto the same substrate as the CVD-grown flake to be characterized. By comparing the I(G) of the CVD-grown flake with that of the standard ME-1LG, CVD-1LG can be easily identified. Indeed, as shown in Fig. 19(b), the I(G) values of CVD-1LG and ME-1LG on SiO2/Si are identical, although ω(G) of CVD-1LG is blueshifted to 1590 cm−1 because it is slightly doped. Meanwhile, ME-1LG and CVD-1LG deposited on the same substrate should have similar optical contrast, almost identical amplitudes, and similar profiles, as demonstrated in the inset to Fig. 19(b), which is helpful to further confirm the identity of CVD-1LG.
This approach can be extended to identify 1LG produced by other methods, such as epitaxial growth on SiC. The 2D band of NLG epitaxially-grown on SiC also exhibits a single Lorentzian peak.251 Thus, it is necessary to transfer ME-1LG onto SiC for use as a standard sample to identify 1LG epitaxially grown on SiC.
6.2 Intensity of the G and Si peaks
Once 1LG has been determined, the experimental I(G) of NLG, i.e., INLG(G), normalized by I1LG(G) must be compared with the theoretical one to precisely identify N of the graphene flakes. If NLG is exfoliated on the SiO2/Si substrate, INLG(G) is modified by multiple reflections at the interfaces and optical interference within the four-layer structure, which contains air(ñ0), NLG(ñ1, d1), SiO2(ñ2, d2), and Si(ñ3, d3), where ñi and di (i = 0, 1, 2, 3) are the complex refractive index and the thickness of each medium, respectively, as shown in Fig. 20(a). The thickness of the SiO2 layer is denoted as hSiO2. The transfer-matrix method can quantify the Raman intensities of NLG on multilayer structures,73,252 in which excitation wavelength, objective NA, and Raman tensor must be considered, and the s- and p-polarization components should be treated separately.73,252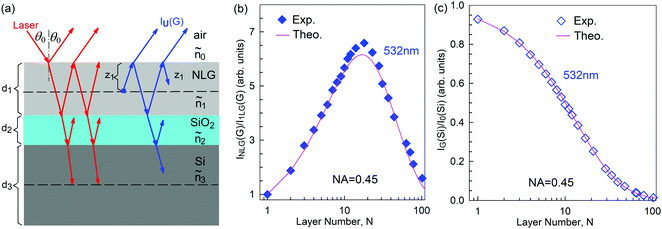 | ||
| Fig. 20 (a) Schematic diagrams of multiple reflections and optical interference in the multilayer structures containing air, NLG, SiO2, and Si for the incident laser and outgoing Raman signals (the G peak from NLG). The experimental (Exp.) and theoretical (Theo.) (b) INLG(G)/I1LG(G) and (c) IG(Si)/I0(Si) (d) as a function of N of NLG flakes. The objective numerical aperture (NA) is 0.45. The excitation wavelength is 532 nm. Reproduced with permission from ref. 252. Copyright 2015, Royal Society of Chemistry. | ||
Fig. 20(b) shows the experimental and theoretical INLG(G)/I1LG(G) for NLG transferred onto a Si(110) substrate covered with 89 nm SiO2. INLG(G)/I1LG(G) is not monotonically dependent on N. However, the case of the Si Raman signal from the SiO2/Si substrate beneath the NLG (denoted as IG(Si)) is different. IG(Si) decreases monotonically with increasing N because both the laser excitation and the Raman signal from the Si substrate are absorbed by the NLG flake. If I(Si) from the bare SiO2/Si substrate is denoted as I0(Si), IG(Si)/I0(Si) can be used to identify graphene flakes with N up to 100 because of the strong Si Raman signal and high signal-to-noise ratio of IG(Si)/I0(Si), as shown in Fig. 20(c). In general, this technique can be utilized to identify N of mechanically exfoliated NLG or epitaxially-grown NLG on SiC, whose complex refractive index is not sensitive to the N of NLG. This technique is not suitable for CVD-grown tNLG because its I(G) exhibits N-dependent resonant behavior.
It should be noted that both INLG(G)/I1LG(G) and IG(Si)/I0(Si) are very sensitive to hSiO2, objective NA, and laser wavelength (λlas). To get reliable theoretical values of INLG(G)/I1LG(G) and IG(Si)/I0(Si) to precisely identify the N of graphene flakes, hSiO2 must be confirmed by initial measurement by a spectroscopic ellipsometer or another technique, and it is better to use an objective with an NA smaller than 0.55. Considering that IG(Si)/I0(Si) < 0.45 when N > 10, one can identify N (N < 10) of NLG by INLG(G)/I1LG(G) with a constraint condition of IG(Si)/I0(Si) > 0.45. In principle, it is sufficient to determine N up to 10 because the electronic structure of NLG rapidly evolves with N, approaching the three-dimensional limit of graphite at 10 layers.22
6.3 Peak profile of the 2D mode
As discussed above, the peak profile of NLG also shows N-dependent spectral features. Because the 2D band originates from a two-phonon DR Raman process, it is closely related to the band structure of the graphene layers. 1LG has a single and sharp 2D band, but the 2D band of NLG can be fitted by multiple Lorentzian peaks because of the multiple resonance Raman processes related to its electronic band structures. Ferrari et al.44 clearly explained the changes of the 2D bands of monolayer and bilayer graphenes based on their line shape and peak positions. Zhao et al.115 have demonstrated that the 2D-band profiles of 1LG and AB-stacked NLG (N < 5) excited at 633 nm clearly exhibit distinct subpeaks, which can be used to identify 1LG and AB-stacked 2–4LG with AB stacking, as shown in Fig. 5, while the 2D bands excited by blue or green lasers do not exhibit these distinct features even for 3LG. However, for more than five graphene layers, the difference between their Raman spectra is insufficient to distinguish them accurately. Because the different components of the 2D band may exhibit different resonant behaviors with different laser excitations, it is very important to choose an appropriate laser wavelength to identify N of NLG.115The peak profile of the 2D band can also be used to determine whether mechanically-exfoliated NLG is ABC-stacked.5,6,150
6.4 Peak positions of the C and LB modes
According to the LCM, ω(C) and ω(LB) of AB- and ABC-NLG are directly determined by N. However, at room temperature, only the CN1 modes can be observed in AB-NLG,70 and both the C and LB modes are absent in ABC-NLG.150 Based on ω(CN1) = ω(Cbulk)cos(π/2N), one can determine N of AB-NLGs up to an N of 5.70 However, the weak I(CN1) limits its application in the determination of N for AB-NLG.For the tNLG, because of the formation of a Moiré superlattice, the band structure of tNLG is quite different from its constituents. A series of VHSs appear in the JDOSOAT of tNLG, as revealed from its optical contrast.57I(C) and I(LB) are significantly enhanced in tNLG once the excitation energy is in resonance with the energies of the VHSs in the JDOSOAT, as shown in Fig. 10. Because the interface shear coupling in tNLG is only ∼20% of the corresponding value in graphite, whereas the interface layer-breathing coupling in tNLG is almost identical to the bulk case, the observed C modes in tNLG are related to the shear vibrations of its constituents and the LB modes are revealed to be dependent on the total N of tNLG but not on its constituents. Therefore, The LB modes can be used to identify the number of layers of tNLG, while the C modes provide a convenient method to determine the number of layers of its constituents. For example, in t(2+3)LG, under the resonant condition, one can observe the C21 mode of the AB-2LG constituent, the C31 and C32 modes of the AB-3LG constituent, and the LB51 and (or) LB52 modes corresponding to AB-5LG. Because twisted stacking commonly occurs in CVD-MLG, this technique has been developed to distinguish the stacking orders of CVD-grown tNLG.202,205
In short, this approach, based on the interlayer vibrational modes, is a robust, nondestructive, and substrate-free way to identify N of AB-NLG and CVD-grown tNLG and the number of layers of the constituents in tNLG. The method can be extended to the determination of N of ultrathin flakes of other two-dimensional materials, such as semimetals (NiTe2 and VSe2),253 semiconductors (WS2, WSe2, MoS2, MoSe2, MoTe2, TaS2, RhTe2, and PdTe2),151,155,156,254–259 insulators (HfS2),260 superconductors (NbS2, NbSe2, NbTe2, and TaSe2),261–263 and topological insulators (Bi2Se3 and Bi2Te3).160,264,265
7 Raman spectra of monolayer and multilayer graphenes under external perturbation
Graphene and MLG under external perturbation have attracted considerable attention because external perturbations can modify the electric, phonon, thermal, and mechanical properties of NLG. This facilitates various applications such as in tunable photonic devices, flexible electronics, FETs, and catalysts for hydrogen evolution.110,266 For example, the band gap of AB-2LG can be widened under an asymmetric electric field.267,268 Under the magnetic field, the quantum Hall effect and Berry phase in 1LG can be observed.98,269,270 Negative thermal expansion coefficients have also been observed.271,272 In addition, high-performance elastic properties and intrinsic strengths have been observed under stress.273,274Raman spectroscopy is an ideal technique to probe the influence of external environmental conditions on material systems by spectral-feature analysis with high spectral resolution.56 This makes Raman spectroscopy useful in fundamental research and device characterization. Indeed, the phonon spectra of graphene are significantly affected by external perturbations, and their responses to external perturbations can be precisely probed by Raman spectroscopy.56,98,275 In the following sections, we will discuss how external perturbations, such as doping induced by an electric field58–60,62–65 and charge transfer,61 strain,81–87 and temperature,99–103,276 modify the Raman spectra of graphene and MLG and how to use Raman spectroscopy to probe those external perturbations.
7.1 Doping
The Fermi level of graphene can be tuned by doping, which makes it a candidate for use in electronic and photoelectric devices.266,277–279 The carrier density in graphene layers can reach a high level via electronic doping and chemical doping. By means of electronic doping, a gate voltage is used to tune the Fermi level, in which the doping level of graphene can reach up to 5 × 1013 cm−2. Furthermore, A strong perpendicular electric field can open up a band gap of ∼0.3 eV in 2LG.Doped graphene at various top-gated voltages has been characterized by Raman spectroscopy, as shown in Fig. 21(a).60,63 The G peak stiffens and sharpens for both electron and hole doping (see Fig. 21(a and b)), implying the breakdown of the adiabatic Born–Oppenheimer (ABO) approximation.63 The 2D peak will blueshift monotonically when it is p-doped, but redshift when it is n-doped (see Fig. 21(c)).60,63 The doping level can be determined by I(2D)/I(G), as shown in Fig. 21(d), and will be discussed in detail later. Moreover, two splitting G modes (a symmetric, in-phase Raman-active mode and an antisymmetric, out-of-phase Raman inactive mode) in 2LG, arising from the interlayer coupling, can be observed upon applying a perpendicular electric field, which can be created, for example, by top and bottom gates of opposite bias in field-effect devices. This is because the electrical field reduces the symmetry of graphene bilayer by removing the inversion center, resulting in new eigenstates, G+ and G−, that are linear combinations of the in-phase and out-of-phase modes.62,145 In addition, the ubiquitous substrate-mediated mechanical strain in 2DMs can also lead to the Raman shifts. This effect should be carefully distinguished from the charge doping effects based on the Raman spectroscopic analysis.280
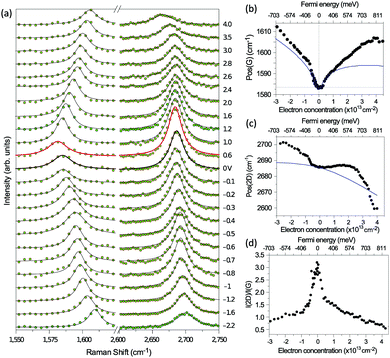 | ||
| Fig. 21 (a) Raman spectra at gate voltages between −2.2 and 4.0 V. The dots are the experimental data, the black lines are fitted Lorentzian peaks, and the red line corresponds to the Dirac point. Pos(G) (b), FWHM(G) (c), and I(2D)/I(G) (d) as a function of electron and hole doping. Reproduced with permission from ref. 60. Copyright 2008, Nature Publishing Group. | ||
Besides electrostatic doping, NLG can also be doped chemically by depositing or adsorbing atoms/molecules on one or both sides, and a charge carrier density is introduced by charge transfer between the chemical impurity and graphene layers.281–285 When 1–4LG flakes were dipped into sulfuric acid, H2SO4 molecules were found to be only physically adsorbed on the surface layers of the graphene flakes as an electron–acceptor dopant without intercalation.115 For example, 18 M H2SO4 can be used to fully dope NLG, whose Raman spectra are almost identical to those of stage-N graphite intercalation compounds (GIC), as shown in Fig. 22(a). Here, the stage-N GIC means a NLG sandwiched by two intercalant layers.121 The G peak of H2SO4-doped 1LG blueshifts to 1624 cm−1 from that (1582 cm−1) of pristine flakes. The doped 2LG has a single G peak at 1613 cm−1, which indicates symmetric doping on both sides, and there is no net electric field between the layers.115 Two G peaks (G+ and G−) have been observed in H2SO4-doped 3LG and 4LG. The G peak splitting shows that doping is primarily in the surface graphene layers, creating perpendicular electric fields that point inward. The interior layers have lower hole densities. This situation could also be created by top and bottom gates of the same voltage in a device configuration. With further increasing N, the electric field no longer penetrates the innermost layers, and, thus, the outermost two graphene layers on each surface have non-negligible doping, but the interior layers are undoped and experience no electric field. Thus, the I(G−) of the interior layers increases with increasing N.
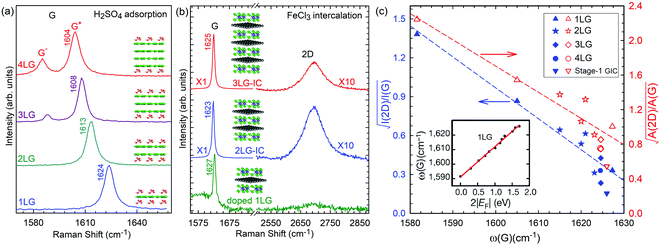 | ||
Fig. 22 (a) Raman spectra of 1–4LG when sulfuric acid molecules are adsorbed on both sides. Adapted with permission from ref. 115. (b) Raman spectra of doped 1LG and stage-1 2–3LG intercalation compounds with FeCl3, excited by 532 nm. (c) Variation of 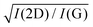 and and 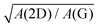 as a function of ω(G) for doped 1LG, stage-1 2–4LG intercalation compounds, and stage-1 graphite intercalation compounds. Inset: ω(G) as a function of |EF|. Reproduced with permission from ref. 61. Copyright 2011, American Chemical Society. The inset in panel (c) was reproduced with permission from ref. 58. Copyright 2011, Nature Publishing Group. as a function of ω(G) for doped 1LG, stage-1 2–4LG intercalation compounds, and stage-1 graphite intercalation compounds. Inset: ω(G) as a function of |EF|. Reproduced with permission from ref. 61. Copyright 2011, American Chemical Society. The inset in panel (c) was reproduced with permission from ref. 58. Copyright 2011, Nature Publishing Group. | ||
Chemical doping of NLG (N > 1) can also be realized by intercalating molecules or atoms into the graphene layers, resulting in stage-n GIC with n ≤ N. In fact, stage-n GIC can be considered as n graphene layers sandwiched by two intercalant layers,121 where two adjacent n-graphene-layers are decoupled from each other. The charge transfer between intercalants and graphene layers in stage-n GIC makes the n graphene layers heavily doped.61,286 This can also occur for NLG, and the NLG IC is formed.61,286NLG flakes can be intercalated by FeCl3 by a two-zone vapor transport method to form stage-1 NLG ICs (see Fig. 22(b)). Fig. 22(b) also shows that ω(G) of pristine 2LG and 3LG is significantly blueshifted to ∼1624 cm−1 after the intercalation, and their 2D bands exhibit a single Lorentzian profile, resulting in electronic decoupling of each layer in 2LG and 3LG ICs. The EF of stage-1 NLG ICs can be as large as 0.9 eV, which can be confirmed by multi-wavelength Raman spectroscopy.61
To determine the doping level of 1LG by Raman scattering, in addition to multi-wavelength Raman spectroscopy,61 the EF of p-doped 1LG or stage-1 NLG ICs can also be determined from ω(G) and 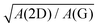 . Wang and co-workers found that58 the relationship between the Fermi level shift and ω(G) peak position is linear if the Fermi level shift is larger than ∼0.1 eV, as shown in the inset of Fig. 22(c). One can use the following relationship to determine the doping level,
. Wang and co-workers found that58 the relationship between the Fermi level shift and ω(G) peak position is linear if the Fermi level shift is larger than ∼0.1 eV, as shown in the inset of Fig. 22(c). One can use the following relationship to determine the doping level,
| |EF| = Δω(G)/21, | (14) |
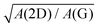 can be written as follows:61
can be written as follows:61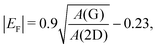 | (15) |
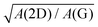 is linear with ω(G). Indeed, the data collected from different doping levels of doped 1LG and NLG ICs show a linear relationship between
is linear with ω(G). Indeed, the data collected from different doping levels of doped 1LG and NLG ICs show a linear relationship between 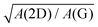 (also
(also 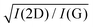 ) and ω(G). In stage-1 FeCl3-GIC, eqn (15) gives |EF| ∼ 0.85 eV, similar to that determined by the multi-wavelength Raman method.61
) and ω(G). In stage-1 FeCl3-GIC, eqn (15) gives |EF| ∼ 0.85 eV, similar to that determined by the multi-wavelength Raman method.61
7.2 Magnetic fields
When graphite is exposed to a perpendicular magnetic field (B), the carriers precess around the zone edge in two-dimensional circular orbits, resulting in its electronic spectrum quenching into discrete Landau levels (LLs).287 This is also the case for 1LG. 1LG under B exhibits discrete fourfold (spin and valley) degenerate LLs with energies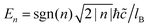 , where n = …, −2, −1, 0, 1, 2,… is the index of LLs in the conduction (n > 0) and valence (n < 0) bands,
, where n = …, −2, −1, 0, 1, 2,… is the index of LLs in the conduction (n > 0) and valence (n < 0) bands, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) and
and 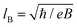 are the electron velocity of the Dirac cone at zero B, and the magnetic length, respectively,104 as shown in Fig. 23(a). The LL occupancy is characterized by the filling factor, v = 2πlB2ρs, where ρs is the carrier density. Fully filled LLs with n = 0, 1,… have v = 2, 6,…104 Electron excitations between LLs can be described in terms of magneto-excitons. If the energy of an optical phonon matches that of the inter-Landau-level (LL) transitions, the effects of electron–phonon interactions will be enhanced, so-called magnetophonon resonances (MPRs).88,94,95,98,288 According to the matrix structure of the interaction terms between different LLs, the following selection rules are optically active in 1LG:289 (i) n− → n+; (ii) (n ∓ 1)− → (n ∓ 1)+; and (iii) n− → (n + 1)+, (n + 1)− → n+, which belong to the symmetry representations A2, A1, and E2, respectively, originating from the prescribed hexagonal symmetry (C6v) of the band structures in 1LG.89,289 Thus, in 1LG, the doubly degenerate E2g phonon at Γ (the so-called G mode) can interact strongly with the LL transitions (iii) with E2 symmetry. This strong interaction results in the renormalization of the phonon frequencies and the line broadening of the G mode,60,62–64,290,291 which can be tuned by electric and magnetic fields through Fermi energy shifts and Landau quantization. Furthermore, the selection rules of circular polarization for various LL transitions (originating from the angular momentum transfer), e.g., σ+ for −n → n + 1 and σ− for −n−1 → n valence-to-conduction band transitions (σ+ and σ− represent right- and left-hand circular polarization, respectively), make the MPRs distinguishable for lattice vibrations under different circular polarizations.
are the electron velocity of the Dirac cone at zero B, and the magnetic length, respectively,104 as shown in Fig. 23(a). The LL occupancy is characterized by the filling factor, v = 2πlB2ρs, where ρs is the carrier density. Fully filled LLs with n = 0, 1,… have v = 2, 6,…104 Electron excitations between LLs can be described in terms of magneto-excitons. If the energy of an optical phonon matches that of the inter-Landau-level (LL) transitions, the effects of electron–phonon interactions will be enhanced, so-called magnetophonon resonances (MPRs).88,94,95,98,288 According to the matrix structure of the interaction terms between different LLs, the following selection rules are optically active in 1LG:289 (i) n− → n+; (ii) (n ∓ 1)− → (n ∓ 1)+; and (iii) n− → (n + 1)+, (n + 1)− → n+, which belong to the symmetry representations A2, A1, and E2, respectively, originating from the prescribed hexagonal symmetry (C6v) of the band structures in 1LG.89,289 Thus, in 1LG, the doubly degenerate E2g phonon at Γ (the so-called G mode) can interact strongly with the LL transitions (iii) with E2 symmetry. This strong interaction results in the renormalization of the phonon frequencies and the line broadening of the G mode,60,62–64,290,291 which can be tuned by electric and magnetic fields through Fermi energy shifts and Landau quantization. Furthermore, the selection rules of circular polarization for various LL transitions (originating from the angular momentum transfer), e.g., σ+ for −n → n + 1 and σ− for −n−1 → n valence-to-conduction band transitions (σ+ and σ− represent right- and left-hand circular polarization, respectively), make the MPRs distinguishable for lattice vibrations under different circular polarizations.
 | ||
| Fig. 23 (a) 1LG band structure at B = 0. Mode splitting ensues in the vicinity of the MPR between 0 → 1 electron–hole excitations and the E2g phonon. (b) Calculated mode splitting gσ as a function of the filling factor, ν. Open circles indicate the filling factors probed by experiment. (c) Peak position of the G peak Lorentzian components as a function of B for the (left) low and (right) intermediate carrier densities. Open black circles represent the central E2g phonon line component. Filled red (σ+) and gray (σ−) circles are the electron–phonon coupled modes. Dashed lines plot the calculated frequencies of the G modes interacting with the magneto-exciton based on the Dyson equation.88 Blue squares show additional components observed close to resonance. Circular-polarized magneto-Raman spectra at (d) 2 < ν < 6 and (e) ν < 2. The pink spectrum shows the component corresponding to σ+, and the gray spectrum shows the component corresponding to σ−. Reproduced with permission from ref. 95. Copyright 2013, American Physical Society. | ||
Indeed, the MPR effect can be described as a resonant mixing of electronic and lattice excitations into a combination mode, leading to splitting and, thus, EPC-dependent anticrossings.88 Because the σ+ and σ− magnetoexcitons are based on different LL transitions, changing the carrier density and, thus, the LL occupancy in 1LG would affect the splitting of the phonon fine structure differently.88,94,95 For example, filling (depleting) the final states with electrons or depleting (filling) the initial states would block the corresponding LL transitions, thus suppressing (promoting) coupling between magnetoexcitons and phonons. This progress can be expressed by the so-called splitting, g, introduced in ref. 88, as depicted in Fig. 23(b). If v = 0, corresponding exactly to a half-filled n = 0 LL, the coupling strengths of σ+ and σ−-polarized modes are equal, causing the G peak to split equally for σ+ and σ− phonon polarizations.88 For 0 < v < 2, in which n = 0 LL is more than half-filled, the −1 → 0 (σ−) transition becomes partly blocked, while the 0 → +1 (σ+) transition is promoted, giving rise to different splittings in the fine structure of the σ+- and σ−-polarized modes. When 2 < v < 6, the n = 0 LL is fully occupied, leaving no space for MPRs with the σ− phonon, whereas the n = +1 LL is only partly filled, resulting in a MPR-induced fine structure in the σ+ phonon line shape (with maximum splitting at v = 2). Finally, if v > 6, both −1 → 0 and 0 → 1 transitions are blocked, completely suppressing the MPR-induced fine structure of both modes. Therefore, the σ∓ can be resolved by MPR effects using various excitation/detection configurations.88,89 Furthermore, the splitting of G peaks induced by the MPR effects can be grouped into three categories as a function of v.88,95 Based on the Dyson equation under the resonance approximation,88,95 the frequencies of the G peak at v < 2 (0.4 × 1012 cm−2) and 2 < v < 6 (2.0 × 1012 cm−2) after coupling with magneto-excitons can be calculated, as depicted in Fig. 23(c) (dashed lines). The strongest anticrossing corresponding to 0 → 1 (σ+) and −1 → 0 (σ−) is shown under a magnetic field of 20–25 T.
Fig. 23(d and e) show the polarization and B dependence of the G peak at different carrier densities in terms of experiments. At a high carrier density (v > 6), there is no significant change in the G peak.95 When the carrier density is ∼2 × 1012 cm−2, the G peak exhibits a strong, anticrossing like splitting, reaching ∼150 cm−1 (∼20 meV) for B = 25 T, as shown in Fig. 23(d). The electron–phonon coupled modes appear only in the σ+ geometry, implying MPRs at 2 < v < 6. As the carrier density further decreases so that v < 2, the G peak splitting changes (Fig. 23(e)). In contrast to the 2 < v < 6 case, the coupled modes now appear in both σ+ and σ− polarizations. The spectra at B > 30 T reveal that the coupled mode consists of two peaks (pink and gray peaks), which can be assigned to the σ± polarized modes originating from the coupling of E2g phonons with 0 → 1 and −1 → 0 magnetoexcitons. All the experimental data are in agreement with those calculated, as shown in Fig. 23(c). It should be noted here that the additional component at an intermediate carrier density inside the anticrossing gap (Fig. 23(d)) results from the overall effect of inhomogeneous strain.
A similar MPR effect has been observed in 1LG on the surface of graphite,91,92,96 non-Bernal stacked MLG on SiC,90 ABA- and ABC-stacked 3LG,97 and bulk graphite.93 In addition, a simultaneous redshift and line broadening of the 2D mode in a magnetic field have also been revealed, which are attributed to the modified momenta of the optical phonons emitted during the double resonance Raman scattering process.292 A knowledge of the Raman spectra of graphene flakes under a magnetic field can be helpful in uncovering the subtleties of the magnetophonon resonance. The mode splitting can be further utilized to estimate the strength of electron–phonon coupling and to distinguish various circular-polarized lattice vibrations.
7.3 Strain and stress
The application of an external stress on a crystal results in a lattice strain, i.e., a change in the interatomic distances and consequent redistribution of the electronic charge. In graphene, strain can even open the band gap.85,293 Isotropic compression (hydrostatic pressure) generally results in an increase in the frequency of the vibrational modes (phonon hardening), while isotropic tension results in a decrease in the vibrational frequency (phonon softening).294 The Grüneisen parameter gives the rate of change of a given phonon frequency with strain in a crystal. In metrology applications, accurate values of Grüneisen parameters are crucial for quantifying the amount of strain in the system, which can be estimated by probing the phonon frequency change from its value in the absence of strain.Graphene bubbles and balloons can be used to study the Raman spectrum of graphene under biaxial strain.147,295 Graphene bubbles are formed during the deposition of large graphene flakes on an oxidized silicon substrate. Bilayer graphene balloons are produced by pressurizing a specially made metallic container covered with large bilayer graphene membranes with nitrogen gas, as shown in Fig. 24(a). The Raman shifts of the G and 2D modes in the graphene bubbles are shown in Fig. 24(b and c), respectively. All the Raman modes redshift under the tensile strain. The Grüneisen parameters (γ) of the G (1.8), 2D (2.6), D (2.52), and 2D′ (1.66) peaks have been measured, and they are in excellent agreement with calculated parameters.84,147 Because the initial doping or strain caused by the interaction between graphene and the substrate can strongly affect the measured Grüneisen parameters, graphene bubbles are a better system to observe the pure strain effect on the Raman modes.147 For the Raman spectrum of bilayer graphene balloons, the strain does not alter the AB-stacking configuration when the strain is less than 1.2%, as shown in Fig. 24(d).
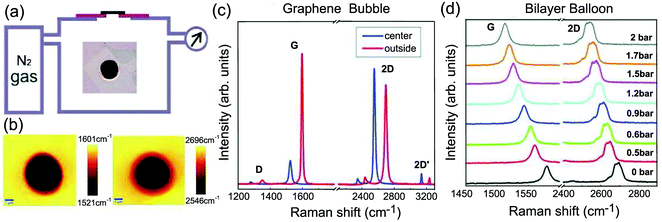 | ||
| Fig. 24 (a) Schematic showing the experimental setup used to make the graphene balloons. The inset shows an optical micrograph of a large bilayer covering a 50 μm aperture in a copper scaffold. (b) Raman map of the G and 2D peak positions for a graphene bubble. The 2D and G peak positions decrease significantly when moving from the substrate to the center of the bubble. (c) Raman spectra measured at the center of a single-layer bubble and on the flat area on the substrate at 488 nm. (d) Raman spectra of a bilayer graphene balloon measured at different differential pressures at 514.5 nm. Reproduced with permission from ref. 147. Copyright 2012, American Chemical Society. | ||
The application of anisotropic stress, e.g., uniaxial strain, has more complex effects. The uniaxial strain can break the symmetry, resulting in the lifting of the degeneracy of phonon frequencies.84,294 The G mode, which arises from the doubly degenerate E2g mode in the intrinsic 1LG, will split into two peaks, G+ and G− (E+2g and E−2g). The eigenvectors of the G+ and G− are orthogonal.81,84,87,147,294,296 When the uniaxial tension strain is applied, sp2 bonds along the direction parallel to the applied strain are lengthened and softened, yielding the G− peak, while those perpendicular to it are only slightly affected, giving the G+ peak. Thus, under uniaxial strain, only the peak of the G− mode is significantly shifted relative to the G peak of unstrained 1LG (by as much as 30 cm−1 for 1.3% strain), while the peak G+ mode is only moderately shifted (up to 15 cm−1). Because this effect is purely mechanical,84,294 the FWHM of G− and G+ remain constant. For the 2D band, the FWHM is also unchanged but the peak can redshift and split because of the softening of the TO phonon and the changing band structure.81–83,85 Moreover, according to the Raman tensor, the E+2g and E−2g modes are polarized.297 The polarized directions of those modes are orthogonal, which results in E2g showing a depolarization behavior in the intrinsic 1LG. The intensities of the two peaks G− and G+ vary with the polarization of the scattered light along the direction of the strain, allowing the crystallographic orientation with respect to the strain to be probed.87,294,298 A good understanding of the Raman spectrum in graphene under strain can help us to characterize the wrinkles in CVD-grown graphene,299,300 understand the strain transfer in supported graphene,301 and investigate the properties of the graphene engine.302
7.4 Temperature
Phonon anharmonicity in a solid is a fundamental topic in solid state physics. Temperature-dependent Raman spectroscopy is a powerful technique to probe the phonon anharmonicity. In the first-order approximation, the frequency of a Raman mode is linear with temperature, i.e., Δω = χΔT, where χ is the first-order temperature coefficient. The frequency shift of the Raman mode with temperature can be represented as follows:303 | (16) |
The pure temperature coefficient for pristine graphite was found to be χT = −0.011 cm−1 K−1 while χV can be ignored in the measured temperature range.303 In most experiments, both contributions are reflected in the extracted values of the temperature coefficient and it must be interpreted as the sum of both contributions,303,304i.e., χ = χT + χV.
Temperature-dependent Raman spectra of 1LG and MLG have been measured by several groups.99,101,103,304 The extracted values of the 1LG and AB-2LG temperature coefficient of the G mode are −(1.6 ± 0.2) × 10−2 cm−1 K−1 and −(1.5 ± 0.06) × 10−2 cm−1 K−1, respectively.99,101,103,304 The temperature coefficient of the 2D mode is −(3.4 ± 0.4) × 10−2 cm−1 K−1 for 1LG, which means the 2D peak is more sensitive to the temperature than the G mode.305 The uncertainty may result from factors such as the cleanliness of the sample, influence of the substrate, doping, and disorder. Once the χ values of 1LG and MLG have been determined, the temperature of the graphene flakes can be obtained in situ. This temperature measurement method can be utilized to determine the thermal conductivity102,103,276,306 and thermal expansion coefficient271 of 1LG and the thermal transport of graphene FETs307 by in situ Raman spectroscopy.
8 Raman images of graphene flakes
Confocal Raman spectroscopy gives spatially resolved information about the vibrational spectrum, so-called Raman images. A state of the art Raman imaging system can achieve a spatial resolution of ∼300 nm if we do not use some special techniques, such as near-field Raman technique, tip enhanced Raman scattering (TERS),311 or microspheres (or lens). With the development of high-performance charge-coupled devices (CCDs) and also the optimization of optical items, the integration time required for obtaining a smooth Raman spectrum can be as short as milliseconds, which greatly minimizes the time to acquire Raman imaging. Raman images can be generated based on different parameters of Raman peaks, e.g., peak intensity, peak area (or integrated intensity), position, width, and also the ratios or differences between two peaks. As mentioned above, the Raman spectra of graphene are sensitive to its morphology and external perturbations. Thus, Raman images of graphene can yield information concerning the spatial distribution of the number of layers, stacking order, defects, doping, strain, and temperature, which is important for device applications.5,77,109,307,309,312–315 In this section, we show several examples of Raman images of graphene with different morphologies and external perturbations, including the number of layers, stacking order, edge, strain, and temperature. Raman images can also be used to reveal the growth mechanism of graphene flakes.8.1 Number of layers, crystal domain, and stacking order
As discussed above, the I(G) of a graphene flake depends on its number of layers, N.252,308,312 Thus, Raman intensity images can offer an identification to N of graphene flakes with high spatial resolution. Indeed, using the Raman intensity image in Fig. 25(a), one can identify 1–4LG. | ||
| Fig. 25 (a) Optical image and Raman image of I(G) of graphene flakes with one, two, three, and four layers. Reproduced with permission from ref. 308. Copyright 2007, American Chemical Society. (b) DF-TEM of a t2LG flake (θt is labeled for each domain in the TEM image) and Raman image of I(G) of the same t2LG sample. Reproduced with permission from ref. 185. Copyright 2012, American Chemical Society. (c) Optical images and spatial maps of FWHM(2D) for 3LG samples under 514 nm excitation, where the red and yellow regions correspond to ABA and ABC 3LG domains, respectively. The scale bars are 10 μm in length. Reproduced with permission from ref. 5. Copyright 2010, American Chemical Society. (d) Raman maps of I(G) and I(D) in the proximity of the graphene edge. Reproduced with permission from ref. 77. Copyright 2009, American Chemical Society. (e) Raman imaging of I(D) and I(G) at edges with angles of 90° (zigzag and armchair) and of 60° (armchair). The images of I(G) show the positions and shapes of the 1LG sheets. Green arrows: the laser polarization. The superimposed frameworks are eye guides indicating the edge chirality. Reproduced with permission from ref. 75. Copyright 2008, AIP Publishing. (f) Raman images of (f1) unstrained graphene, (f2–f5) strained graphene, and (f6) relaxed graphene by extracting ω(2D) and (f7) mean of ω(2D) of the entire graphene as a function of strain. The inset shows the area of interest subjected to statistical analysis. The bending/strain is in the horizontal direction. Reproduced with permission from ref. 309. Copyright 2008, American Chemical Society. (g) Optical micrographs of the isotope-labeled graphene grown under isothermal conditions with different PMe, (g1) 160 and (g2) 285 mTorr, and the corresponding Raman images of ω(G), (g3) 160 mTorr, and (g4) 285 mTorr, which schematically show the isotope distributions of 12C and 13C. The colors are decoded in the color bar with methane dosing sequences and times. Scale bars are 5 μm. Reproduced with permission from ref. 310. Copyright 2010, American Chemical Society. | ||
A significant proportion of CVD-grown 2LG is twisted 2LG. There are several single crystal domains in each t2LG flake. Polygonal domains in CVD-grown t2LG flakes evoke the orientation θt-dependent grain structure, as shown in Fig. 25(b), where the dark field (DF)-TEM image is a false color composite of the domains mapped individually by diffraction-filtered imaging.185 Each t2LG exhibits a θt-dependent band structure and optical properties, resulting in θt-dependent I(G), as discussed in Section 4.3. The right panel of Fig. 25(b) clearly demonstrates that the variations in Raman intensity are strongly correlated with θt; furthermore, I(G) is nearly constant within a domain. In particular, there is a strong enhancement of the G band integrated area for a few specific domains, such as the 12.4° domain excited at 2.33 eV. Thus, the single crystal domains can be distinguished by Raman images of I(G) with an appropriate excitation energy.
The stacking order of MLG affects the band structure, and the band structure can be revealed by the profile of its 2D band. For example, ME-NLG exhibits different stacking orders, i.e., AB and ABC, in the same flake.5 The different DR resonant processes result in different FWFM(2D) for AB- and ABC-stacked MLG. Therefore, FWHM images of the 2D band can yield a stacking distribution in the ME-NLG, especially ME-3LG and -4LG, as shown in Fig. 25(c).
8.2 Edges and strain
The edge is a special defect59 that can also activate the D peak. Based on the DR Raman process, the D peak cannot be activated at a perfect zigzag edge, although it is observable at the armchair edge. I(D) at the armchair edge shows polarization dependence.59 Thus, by fixing the laser polarization at a particular angle, the Raman mapping of I(D) can be used to identify the chirality of the graphene edge.75 As shown in the left panel of Fig. 25(e), the two edges with angles of 90° in the same flake can be determined as armchair and zigzag edges based on the absence and appearance of the D peak, respectively. The two edges with angles of 60° in the same flake are armchair edges, which can also be confirmed from the right panel of Fig. 25(e). However, one cannot exclude the existence of some zigzag fragments in the armchair edges only by using Raman images.Strain has a large influence on the frequency shift of the G and 2D bands.84 If graphene is mechanically exfoliated on a polyethylene terephthalate (PET) film, tensile strain is introduced into the graphene layer on the top surface of the PET film by bending, as shown in Fig. 25(f). The amount of strain is determined by dividing the increase in length of the strained top surface by the unstrained length. Fig. 25(f) shows an image of ω(2D) of the graphene layer on PET under strain.309 The strain distribution is not perfectly uniform because of the contact between graphene and PET. Consequently, the van der Waals force between the graphene and substrate differs from region to region, which is revealed in the Raman image of ω(2D). Fig. 25(f7) shows the mean of ω(2D) from the entire graphene sample as a function of strain, which can be applied to analyze the strain status of graphene in related devices.
8.3 Growth mechanism
CVD growth on Ni and Cu provides large area graphene that can be transferred to other substrates after the removal of the metal by wet chemical etching. However, the temperature, methane-to-hydrogen ratio, growth pressure, and substrates are also critical parameters affecting the structural perfection of the CVD-grown graphene.310,316–318 A technique based on isotope labeling has been widely used to reveal the growth mechanism of low-dimensional materials, such as single-walled carbon nanotubes and graphene.318 The same materials grown with different isotopes exhibit different physical and chemical properties because of the different masses of the isotopes. In particular, the frequencies and linewidths of Raman modes in materials labeled by isotopes will be significantly different between different isotopes. For example, ω(G) of 13C graphene is located at ∼1520 cm−1, while that of 12C graphene is located at 1582 cm−1.318 Thus, Raman mapping of ω(G) in the graphene labeled with 13C and 12C during the growth sequence and with time allows the mechanism of graphene growth by CVD to be determined.Large area graphene can be grown by the CVD of methane on Cu foils. The growth parameters such as temperature (T), methane flow rate (JMe), and methane partial pressure (PMe) could affect the domain size and crystal quality of the grown graphene film. The effect of PMe on graphene growth kinetics has been studied under isothermal conditions with a fixed T of 1035 °C and JMe of 7 standard cubic centimeters per minute (sccm). To grow graphene using the C isotope labeling technique, the Cu surface was exposed to 13CH4 and 12CH4 (normal methane) sequentially. Because graphene growth on Cu occurs by surface adsorption, the isotope distribution in the local graphene regions will reflect the dosing sequence and can be mapped according to their different ω(G). Fig. 25(g1 and g2) show optical micrographs of graphene grown under PMe of 160 and 285 mTorr, and the corresponding Raman images of ω(G) are shown in Fig. 25(g3 and g4), respectively, where the isotope distributions of the two cases using the A(G) of 13C graphene at 1490–1550 cm−1 and that of 12C graphene at 1550–1610 cm−1 are indicated in the color bar with methane dosing sequences and time. Under the condition of PMe = 160 mTorr (Fig. 25(g3)), graphene growth terminated after the sixth dose (3 min) and achieved a maximum coverage of ∼90%. Afterward, there was no change, even though the Cu surface was further exposed to CH4. However, graphene growth terminated after the fourth dose (1.5 min) and achieved a full coverage in the case of PMe = 285 mTorr, as shown in Fig. 25(g4). Additionally, the growth rate of graphene sharply reduced with increasing coverage at both pressures because of C species formed by the Cu-catalyzed decomposition of CH4, as shown Fig. 25(g3 and g4). When the Cu surface is undersaturated, there is no nucleation for graphene even though CxHy converts to the vapor phase. However, graphene starts to nucleate, grow, and becomes an island under saturation conditions, stopping because the lack of CxHy means that C cannot be absorbed on the island edges. That is, partial coverage on the Cu surface is achieved by the formation of graphene islands. Furthermore, when the Cu surface is supersaturated, graphene islands continue to grow to form graphene domains, fully covering the Cu surface because of sufficient CxHy.
This Raman imaging technique based on isotope labeling can also be utilized to monitor the other parameters of graphene growth, such as T and JMe. Moreover, the growth mechanism of other 2DMs can also be optimized by this method.
9 Raman spectroscopy in graphene-based materials
9.1 Graphene quantum dots and carbon dots
Graphene quantum dots (GQDs) and carbon dots (C-dots) are typical graphene materials with a lateral size down to the nanometer scale.322,323 GQDs and C-dots have attracted a great deal of attention in recent years because of their promise in bioimaging,324 optoelectronic devices,325 pollutant detection,326 and catalysis.327GQD is also referred to as nanographene. GQDs are originally defined as the products obtained by cutting graphene into small pieces with dimensions of a few nanometers (2–20 nm).328 GQDs are crystalline and mainly composed of sp2-hybridized carbon.329 With time, small disks with dimensions of a few nanometers cut from MLGs have also become known as GQDs. Quantum confinement and edge effects in GQDs with sizes of less than 100 nm become pronounced as the sheets become smaller, particularly once their dimensions fall below 10 nm.329 This results in nonzero band gaps, leading to strong photoluminescence once the GQD size is sufficiently small. The band gaps of GQDs can be tuned by changing their size, shape, and geometry, as well as the nature of their edges.68,328,330–334 The correlation between size and band gap has been demonstrated by scanning tunneling spectroscopy experiments.333
Atomic force microscopy (AFM) images of as-grown GQDs on SiO2 substrates with different growth durations are shown in Fig. 26(a–c).68,335 In the early growth stages, GQDs are nucleated everywhere on the SiO2 surface (Fig. 26(a)). The larger graphene islands are ∼1.2–1.5 nm thick, which is equivalent to four or five layers, as confirmed by the AFM measurements shown in Fig. 26(d). Continued growth yields more nucleation sites on the surface of SiO2, resulting in the whole surface being covered with a continuous and uniform GQD film. Further growth results in thicker GQDs (Fig. 26(c)) with 6–7 layers. Fig. 26(e) shows the Raman spectra of the samples shown in Fig. 26(a–c). The D, G, and 2D peaks show characteristic spectral features of disordered graphene structures.49,56 A high I(D) originates from either small crystallite sizes or an abundance of edges, as discussed in Section 5.56,77 The I(D)/I(G) ratio decreases and I(2D) increases as the growth time increases, which means that a higher quality nanographene film is obtained over time, consistent with the AFM images.15 The XPS spectrum of the as-grown GQD film on SiO2 with a dominant sp2 peak shown in Fig. 26(f) confirms its graphene structure.68
 | ||
| Fig. 26 AFM images of graphene grown on SiO2 with growth durations of 2 (a), 3 (b), and 4 h (c). Topography height profile (d) along the line shown in image (a). (e) Raman spectra of the graphene shown in (a–c), measured at 633 nm excitation with a ∼1 μm beam spot. (f) X-ray photoelectron spectroscopy (XPS) characteristics of the as-grown graphene, with binding energies ranging from 280 to 292 eV. Reproduced with permission from ref. 68. Copyright 2011, Tsinghua University Press and Springer-Verlag, Berlin, Heidelberg. (g) Selected area electron diffraction (SAED) pattern and high-resolution (HR)-TEM images of C-dots with different diameters. Reproduced with permission from ref. 319. Copyright 2012, Royal Society of Chemistry. Aqueous solution of the polyethylene glycol (PEG1500N)-attached carbon dots (h) excited at 400 nm and photographed through band-pass filters of different wavelengths, as indicated, and (i) excited at the indicated wavelengths and photographed directly. Reproduced with permission from ref. 320. Copyright 2006, American Chemical Society. (j) XPS spectra of graphite and C-dots. (k) Raman spectra (λ = 633 nm) of graphite and C-dots. Reproduced with permission from ref. 321. Copyright 2012, Royal Society of Chemistry. | ||
C-Dots are quasi-spherical carbon nanoparticles with diameters of 2–10 nm that have a high oxygen content and consist of combinations of graphitic and turbostratic carbon in various volumetric ratios (see Fig. 26(g)).320,328,336 The graphitic structure of C-dots is also apparent in the XPS spectra,321 which contain a strong peak corresponding to sp2 carbon atoms, as shown in Fig. 26(j). Therefore, C-dots can be considered as a kind of graphene-based material. In particular, compared with conventional inorganic quantum dots, C-dots have many advantages, including low toxicity, chemical inertness, and biocompatibility.319,328,337 Typical C-dots have excellent water solubility and are suitable for subsequent functionalization with various organic, polymeric, inorganic, or biological species.338 C-dots with well-defined dimensions and tunable surface functionalities can be used as building blocks for advanced functional architectures.319,328 The most characteristic and significant property of C-dots is their relatively strong photoluminescence, which depends on their size, the excitation wavelength, and the surface functionalization, as shown in Fig. 26(h and i).320,339 The Raman spectra of C-dots contain characteristic D and G bands at about 1350 and 1600 cm−1, respectively, as shown in Fig. 26(k). The high I(D)/I(G) ratio indicates its small size, the presence of turbostratic carbon, and disordered surface structures.
9.2 Nanoribbons
Graphene nanoribbons (GNR) are a special graphene material with two edges. Both the edge effects and quantum confinement effect must be considered to understand their Raman spectra. Therefore, the Raman spectrum of a GNR is similar to that of graphene edges and is also dependent on its width.19–21,79,227,340,341 The edges are in a perfect position to add functional groups, and the type of functional group affects the properties of the GNRs and the corresponding Raman spectra.19,21Fig. 27(a) shows four GNRs, which are functionalized with long alkyl chains (–C12H25) to increase solubility.342 The structures in Fig. 27(a(i–iii)) represent a series of ‘cove-shaped’ GNRs with the same edge pattern and increasing width, where a benzo ring periodically decorates the zigzag (ZZ) edge. These structures are labeled nCNRs, where n indicates the width of the ZZ GNR core (here, n = 4, 6, 8).343 In addition to those samples, Fig. 27(a(iv)) also shows a GNR based on the chiral-edged (4,1)-GNR with periodically fused benzo rings; this is called m-ANR in ref. 343. The m-ANR has the same width as the 8CNR, but its ‘chirality’ leads to slightly different edge patterns.
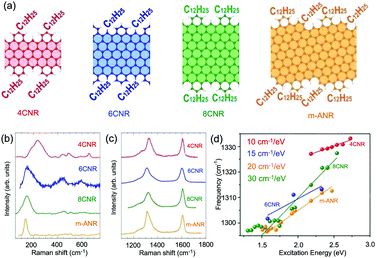 | ||
| Fig. 27 (a) Structural models of the GNRs. Ball-and-stick representation of the atomic structure of the cove-shaped GNRs investigated, i.e., 4CNR, 6CNR, 8CNR, and m-ANR. The schematics show the characteristic variable width of these GNRs and the location of the alkyl side chains in each case. The shaded areas indicate the corresponding zigzag/chiral GNRs. (b) Low- and (c) high-frequency regions of the Raman spectrum for the cove-shaped GNRs in (a). The 4CNR and 6CNR were excited at ∼2.4 eV, while 8CNR and m-ANR were excited at ∼1.9 eV. (d) Peak dispersion of GNRs as a function of excitation energy for the D peaks. Reproduced with permission from ref. 21. Copyright 2016, American Chemical Society. | ||
In the ultralow frequency region, there is a new Raman peak corresponding to radial-like breathing mode (RLBM),344 which is the relative in-plane vibration between the atoms close to the edges. The frequency of the RLBMs is between 120 and 250 cm−1, as shown in Fig. 27(b). The RLBM is especially sensitive not just to the width but also to the edge modulation and functionalization, making it very different from the ideal cases studied to date, where the RLBM does not show a significant dependence on edge type.
The G peaks of all the GNRs in Fig. 27(a) are upshifted (∼1605 cm−1) and broader (FWHM ∼ 25 cm−1) than that (FWHM ∼ 15 cm−1) of pristine graphene, as shown in Fig. 27(c). Similar results were observed in small graphite domains50 and polycyclic aromatic hydrocarbons (PAH)345 because of the relaxation of the momentum conservation induced by the finite size.
Fig. 27(c) also shows a prominent D peak that is characterized by a dominant component at about 1310–1330 cm−1 with an intensity comparable to that of the G peak and one or more shoulders at its lower energy side. In graphene, the D peak activated by the intervalley DR process69 is strongly dispersive with an excitation energy arising from a Kohn anomaly at K,129 where the typical phonon dispersion of graphene is ∼50 cm−1 eV−1.44,77 In the case of GNRs, smaller D-peak dispersions of 10–30 cm−1 eV−1 have been measured for the different GNRs, as shown in Fig. 27(d). The observed dispersion is expected to be related to some disorder-induced scattering, for example, edge functionalization, defects formed during the GNR production, or length distribution. Thus, the small dispersion of the D peak can be used to fingerprint the presence of GNRs and differentiate them from other sp2 carbon nanostructures.
9.3 Graphene layers grown on SiC
Graphene can be epitaxially grown on Si terminated SiC (Si-SiC) and C terminated SiC (C-SiC) substrates,346–348 which is suitable for large area fabrication and is more compatible with current Si processing techniques for future applications. Epitaxial graphene (EG) may interact with the SiC substrate, which could modify its optical and electronic properties. A bandgap of ∼0.26 eV was observed by angle-resolved photoemission spectroscopy, which can be attributed to the interaction of EG with the SiC substrate. Fig. 28(a) shows the top view and side view of a graphene on the SiC(0001) surface. A 13 × 13 graphene lattice lies above the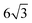 reconstructed SiC surface. The small and the large black circles represent
reconstructed SiC surface. The small and the large black circles represent 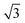 and
and 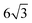 lattices, respectively.
lattices, respectively.
 | ||
| Fig. 28 (a) Top and side views of a graphene on the SiC(0001) surface. The green, yellow, and gray spheres represent C in graphene and Si and C in SiC, respectively. (b) Raman spectra of 1LG on SiC (1LG/SiC), SiC, graphene (by subtracting the SiC spectrum from that of 1LG/SiC), and exfoliated 1LG (1LG/SiC-1LG) in the SiC, G and 2D mode spectral region. (c) Raman spectra of epitaxial graphene layers (EGs) on the C-SiC substrate with different thicknesses. Panels (a and c) were reproduced with permission from ref. 251. Copyright 2008, American Physical Society. | ||
Fig. 28(b) shows the intrinsic Raman spectrum of the EG sample on SiC. The G and 2D peaks show different blueshifts in peak position with respect to ME-1LG.251,349 The blueshift varies by up to 18 cm−1 for the G peak and 35 cm−1 for the 2D peak,251 and the G mode on SiC is broadened. The blueshift of the G and 2D peaks cannot be attributed to charge transfer60 from defects and the substrate but, instead, is due to the presence of compressive strain in the graphene layer.349,350 The small difference between the lattice constant of the reconstructed 13 × 13 graphene layer supercell (εG = 31.923 Å) and the reconstructed SiC  supercell (εSiC = 31.935 Å) cannot account for the significant amount of strain measured. However, compressive strain at room temperature in the graphene layer can be ascribed to the large difference in the coefficients of thermal expansion between graphene (ρG)351 and SiC (ρSiC)352 during the cooling process from the synthesis temperature.349,350 If the epitaxial film is in mechanical equilibrium with the SiC surface, as a stress-free monolayer commensurate with the
supercell (εSiC = 31.935 Å) cannot account for the significant amount of strain measured. However, compressive strain at room temperature in the graphene layer can be ascribed to the large difference in the coefficients of thermal expansion between graphene (ρG)351 and SiC (ρSiC)352 during the cooling process from the synthesis temperature.349,350 If the epitaxial film is in mechanical equilibrium with the SiC surface, as a stress-free monolayer commensurate with the  -reconstructed SiC surface at Ts, a large compressive strain would develop in the film during the cooling process because SiC contracts on cooling whereas graphene expands.350
-reconstructed SiC surface at Ts, a large compressive strain would develop in the film during the cooling process because SiC contracts on cooling whereas graphene expands.350
Fig. 28(c) shows the thickness-dependent Raman spectra of the EG samples on a C-SiC substrate.251 The 2D mode of EG samples on C-SiC (also Si-SiC) substrates exhibits a single Lorentzian profile no matter how many layers exist in the EG samples. It has been experimentally shown that MLG grown on the carbon terminated face of 4H-SiC does not grow as simple AB stacked layers.353 Instead, MLG grows with a high density of rotational faults where adjacent sheets are rotated about 2° relative to each other. First principles calculations demonstrate that the small twist angle between adjacent graphene layers produces an epitaxially-grown MLG on SiC with an electronic structure that is indistinguishable from an isolated single graphene sheet in the vicinity of the Dirac point.353 This explains its single-layer electronic properties, even though the film is composed of tens of graphene layers. Therefore, the 2D mode of epitaxial MLGs on C-SiC and Si-SiC substrates exhibits similar lineshapes to that of graphene. As the thicknesses of epitaxial MLG increase, the Raman peaks (D, G, and 2D) of epitaxial MLG shift to lower frequencies, i.e., toward that of bulk graphite. This can be easily understood because, when the thickness of epitaxial MLG increases, the effect of the substrate on epitaxial MLG becomes weaker and the lattice of epitaxial MLG relaxes.
9.4 CVD-grown multilayer graphene
CVD can grow graphene films of high quality.7,317 Given the many possible applications of high-quality graphene, routes toward industrial-scale synthesis are of great importance. For most industrial-level devices (and other) applications, large single-crystal graphene films are ideal for top-down processing. In the past ten years, the island size of single-crystal graphene has increased by more than four orders of magnitude, from micrometers to inches. Raman spectroscopy has been widely used to characterize the quality, disorder, domain boundaries, and doping of CVD-grown graphene films. However, we do not address the Raman spectra of CVD-grown graphene films because they are almost identical to those of mechanically-exfoliated 1LG.When the growth conditions are optimized, MLG flakes can also be grown by CVD. CVD-grown NLG (CVD-NLG) with transparency, high electrical conductivity, and flexibility is considered to be a candidate for transparent and conducting electrodes, which could be used in touchscreen panels, organic light-emitting diodes, and solar cells.356–359 By changing the growth conditions, NLG with different stacking orders, including AB and twisted stacking, can be obtained. Here, we will review Raman features of CVD-2LG, -3LG, and thicker flakes.172,173,185,186,202,205,354,355,360,361
2LG islands can be observed in the CVD-1LG film with appropriate growth conditions.185,186 These islands sitting on 1LG have in general a multilobe star morphology. The lobes constitute the second layer and, in the center, three or more stacked layers can be identified by optical contrast when using an optical microscope, as shown in Fig. 29(a).185 In particular, it has been shown that a significant proportion of CVD-2LG is twisted 2LG (t2LG), where the two layers are rotated by a relative angle of θt (Fig. 29(a), inset). DF-TEM studies have demonstrated that polygonal domains in CVD-2LG evoke the orientation θt-dependent grain structure (Fig. 29(b)), where the DF-TEM image is a false color composite of the domains mapped individually by diffraction-filtered imaging.185,186I(G) images clearly demonstrate that the variations in Raman intensity are strongly correlated with θt; furthermore, I(G) is nearly constant within a domain (Fig. 29(c)). In particular, there is a strong enhancement of the G band integrated area (AG) for a few specific domains, such as the 12.4° domain in Fig. 29(d).185 This enhancement results from the singularity in the JDOSOAT of t2LG,57 whose energy is exclusively a function of θt and whose optical transition strength is governed by interlayer interactions, as discussed in Section 4.3.
 | ||
| Fig. 29 (a) Optical image of CVD-NLG flakes. (b) Dark-field TEM of a t2LG, where θt is labeled for each domain in the TEM image. (c) G band Raman image of the same t2LG sample in (b). (d) A plot of G band integrated intensity vs. θt across many t2LG samples. Panels (a–d) are reproduced with permission from ref. 185. Copyright 2012, American Chemical Society. (e) Raman spectra of t2LG with different θt values. * Indicates the new Raman peaks observed in t2LG. Reproduced with permission from ref. 354. Copyright 2013, Tsinghua University Press and Springer-Verlag, Berlin, Heidelberg. (f) Optical micrographs of as-grown 3LG grains after transfer onto SiO2 (90 nm)/Si substrates. Four different types of stacking arrangements are shown. Scale bar: 20 μm. (g) The 2D peaks in the trilayer regions correspond to four types of stacking arrangements in (f), respectively. Panels (f and g) are reproduced with permission from ref. 355. Copyright 2014, American Chemical Society. (h) Optical image of a CVD-MLG flake and the corresponding I(G) Raman image under 633 nm excitation. The zones with different I(G) are indicated by white dashed lines. (i) Raman spectra of different tNLG in a zone in (g) in the C, LB, R, and G spectral regions excited at 488 nm. The spectra are scaled and offset for clarity. Panels (h and i) were adapted with permission from ref. 202. Copyright 2016, Elsevier. | ||
Besides the G mode, the so-called R and R′ modes have been observed at the low and high energy sides of the G mode.172,173,354,360 The R and R′ band frequency is related to a Raman process that involves the scattering of a photo-excited electron by a phonon with wave vector q, and momentum conservation is achieved by the electron being elastically scattered by a superlattice wave vector −q determined by θt.354,360 The R and R′ modes come from the in-plane TO and LO phonon branches, and their frequencies are directly determined by θt. In principle, the phonons in other phonon branches can also be involved in such a Raman process and become Raman active. Indeed, several Raman modes can be observed in the range of 100–900 cm−1, which can be assigned to the phonons of the ZO′, TA, LA, and ZO branches.360 Because the q of the observed phonons in the 1LG BZ is determined by θt, phonons with wave vectors q in the interior of the BZ of 1LG can be spanned by changing the θt of t2LG.
Regular stacked NLG can also be grown by CVD. Mechanical exfoliation of graphite offers a simple way to obtain high-quality 3LG with ABA or ABC stacking. Crystallographically, 3LG can be viewed as two 2LGs with two separate stacking orientations, i.e., top and bottom 2LG. Atmospheric pressure CVD-grown 3LG can form some special stacking configurations. If the angle θt between adjacent layers is used to denote the stacking orientation, ABA, 30–30, 30-AB, and AB-30 have been found to be major stacking orientations in the CVD-grown 3LG under specific growth conditions, and the optical micrographs of each stacking orientation are shown in Fig. 29(f). If we define the possible twist angle between bottom two layers as θt1 and that between top two layers as θt2, the 30–30 stacking orientation can be denoted as t(1+1+1)LG with θt1 = θt2 = 30°, 30-AB as t(1+2)LG with θt1 = 30°, and AB-30 as t(2+1)LG with θt2 = 30°.
The profile of the 2D peak in ABA CVD-3LG (top left corner of Fig. 29(g)) is almost identical to that of natural AB-3LG prepared by exfoliation, which can be fitted by six Lorentzian peaks. The t(1+1+1)LG (30–30) and t(1+1)LG (30) show a linear band structure similar to 1LG, leading to the single Lorentzian peak of the 2D mode,186 as shown in the top right corner of Fig. 29(g). The 30-AB and AB-30 3LG are the t(1+2)LGs with θt1 or θt2 of 30°. The band structure of t(n+m)LG can be considered as the overlapping of the band structure of the nLG and mLG constituents. Thus, the 2D mode profile of t(1+2)LG can be viewed as the superposition of the 2D mode profile of 1LG and AB-2LG. The 2D mode profile of AB-2LG can be fitted by four Lorentzian peaks, and that of 1LG shows a single Lorentzian peak. Therefore, the 2D mode profiles of 30-AB and AB-30 3LG can be fitted by five Lorentzian peaks, as shown in the lower panel of Fig. 29(g).
Once one twisted interface exists in NLG, the NLG is tNLG. In principle, there may exist up to N − 1 twisted interfaces in tNLG. CVD-grown NLG (N > 1) tends to be tNLG, which opens the possibility of studying various tNLG with different stacking sequences and twist angles. The stacking sequence of tNLG becomes more and more complicated with increasing N. When an additional layer is incorporated into a tNLG, AB-stacked or twisted interface can be formed relative to its adjacent layer. Continuing this trend, if N > 2, the number of stacking sequences of tNLG can reach 2N−1−1. For example, t3LG can be t(2+1)LG, t(1+2)LG, or t(1+1+1)LG. Adding one twisted interface can result in significant changes to its band structures and result in new singularities in the JDOSOAT of the twisted system. The number of twisted interfaces in tNLG can be probed by the corresponding R modes; for example, three R modes have been observed in CVD-t(1+1+1+1)LG.205 Meanwhile, in comparison to CVD-1LG and CVD-t2LG, CVD-tNLG (N > 2) exhibits abundant spectral features in the ULF range, which are related to the interlayer vibration modes once the excitation energy matches the energies of the singularities in the JDOSOAT of the twisted system, and the enhanced C and LB modes can be resonantly observed.57,71,202,205 The peculiar interlayer coupling in tNLG makes ω(C) sensitive to the number of layers of the constituents and ω(LB) to the total number of layers N.57,71,202,205 This offers a convenient and reliable way to identify the stacking order of CVD-MLG by probing its C, LB, and R modes.205
Fig. 29(h) shows an optical image of a CVD-NLG flake (left panel), in which 1–6LG can be clearly identified, and an I(G) Raman image under 633 nm excitation (right panel).202 The zones with different I(G) are indicated by white dashed lines and marked as Z1, Z2, Z3, and Z4, respectively. The images have the same scale. Fig. 29(i) shows typical Raman spectra of tNLG from N = 2 to N = 6 at the same zone in the ULF region.202 Only one R mode with the same frequency is observed in this zone, indicating that all the NLGs (N > 1) in the same zone have only one twisted interface. This may indicate that all the NLGs share one twisted interface between the top two graphene layers according to the growth mechanism of CVD-MLG. The LB mode contributions in the tNLG originate from all graphene layers;71 thus, we can determine N according to the observed ω(LB) and mark them as tNLG in the corresponding spectra in Fig. 29(i). Because the twisted interface would obstruct the interlayer shear coupling,57,71 the C modes in tNLGs are localized in the AB-stacked constituents. With increasing total number of layers (N), it is found that the C modes in the tNLG (N > 2) always follow those of AB-(N−1)LG and all the (N−2) C modes are observed. This indicates that tNLG contains an AB-(N−1)LG constituent. Therefore, the stacking sequence of the tNLG flakes is t(1+n)LG (N = n + 1). Moreover, t(1+n)LG in different zones exhibits similar spectral features (e.g., the number and frequency of the C and LB modes) independent of θt. This offers a reliable way to identify the stacking orders (number of layers and stacking sequence) and interlayer coupling strength of CVD-MLGs, and one can determine whether a MLG sample exhibits a fully non-stacked arrangement or if some of these layers are stacked in the AB-stacking with respect to the non-stacked layers.205
9.5 Graphene-based van der Waals heterostructures
Graphene-based vdWHs formed by vertically stacking other types of 2DMs (e.g., TMDs) with graphene flakes have attracted significant interest.28 The wide range of assemblies with 2DMs pave a way to modulate the fascinating physical properties with promising potential in nanoelectronics and optoelectronic devices. In these heterostructures, interfacial interactions between two atomic layers can dramatically influence the properties of the systems and induce remarkable phenomena that are absent in individual layers.28,362–366 Normally, graphene and TMD flakes are two types of essential building blocks for vdWHs. Because graphene materials exhibit high mobilities, whereas TMD flakes have finite band gaps, TMD/graphene vdWHs have been used for various high-performance devices, such as field-effect tunneling transistors,31 logic transistors, photovoltaics, and memory devices,32–35,367 taking advantage of the properties of these two materials. In general, graphene flakes have been widely used as electrodes in vdWH-based devices to achieve higher performance because they have fewer defects compared with devices directly deposited on metal contacts.31,35 An atomically sharp and non-damaged interface and a modified interfacial coupling are essential to the performance of TMD/graphene vdWHs. Therefore, it is very important to investigate the interfacial coupling in TMD/graphene vdWHs for their future application in high-performance devices.Taking MoS2 as an example, the graphene-MoS2 vdWHs can be usually prepared by transferring one m-layer MoS2 (mLM) flake onto an nLG or the nLG onto the mLM, denoted as mLM/nLG and nLG/mLM, respectively. Fig. 30(a) shows the optical images of 2L MoS2(2LM)/2LG, and the corresponding atomic structure is represented in Fig. 30(b). In general, an annealing process is necessary after transfer to form good interfacial coupling because the two as-transferred 2DM flakes may not couple with each other. For MoS2/graphene vdWHs, it is revealed that 30 min of annealing in an Ar atmosphere at 300° is the best condition to remove moisture and impurities. A slight redshift of E12g and a blueshift of A1g have been observed after annealing, originating from the multiple effects of doping, strain, and changes to the interface coupling.36 Thus, it is difficult to evaluate the interface quality of mLM/nLG vdWHs by these high-frequency Raman modes. However, the C and LB modes, which are sensitive to the interlayer coupling, are a good choice to estimate the interface quality, as depicted by the ULF Raman signals of 2LM/nLG (n = 1, 2,…, 6, 8) in Fig. 30(c). Several LB branches can be detected in 2LM/nLGs, whose frequencies redshift with increasing n of nLG, as indicated by the dashed lines. This implies that the LB interfacial coupling between 2LM and nLG constituents is significant and both constituents contribute to the observed LB modes. Therefore, the vdWHs must be considered as an overall system with N (N = n + 2) layers to model the LB vibration in 2LM/nLG vdWHs, similar to the case of twisted multilayer graphenes.71 The LB modes can be analyzed by the LCM, in which each MoS2 and graphene layer is treated as a ball with corresponding mass per unit area, as shown in Fig. 30(d) using 2LM/3LG as an example. There are n + 1 LB modes in 2LM/nLG. In the LCM of 2LM/nLG vdWHs, the previously determined LB force constants in MoS2 and MLG are used,71,151 that is, α⊥0(M) = 84 × 1018 N m−3, α⊥0(G) = 106.5 × 1018 N m−3, and β⊥0(G) = 9.5 × 1018 N m−3 for the nearest LB force constants in MoS2 and MLG flakes and the second nearest LB force constant of MLG flakes, respectively. If we denote the interfacial LB force constant between 2LM and nLG constituents as α⊥0(I), all the LB modes in different 2LM/nLG vdWHs (crosses in Fig. 30(e)) can be well reproduced with only one parameter, α⊥0(I) = 60 × 1018 N m−3, as depicted by triangles and solid lines in Fig. 30(e). For comparison, the n-dependent Pos(LB) of the (n−1) LB modes in nLG are also plotted in Fig. 30(e) as gray circles linked by gray dashed lines. The n-dependent Pos(LB) evolution of the LB modes in 2LM/nLG vdWHs are quite different from that in nLG, which clearly demonstrates how the interfacial LB coupling can modify the interlayer lattice dynamics of vdWHs from their constituents. Further investigation of nLG/mLM vdWHs has revealed that Pos(LB) in nLG/mLM are almost identical to those of mLM/nLG, which implies that the interface coupling in graphene–MoS2 vdWHs is not sensitive to the stacking order or twist angles. Polarized Raman spectra show that one C mode was also observed in 2LM/nLG vdWHs. However, the observed Pos(C) of the 2LM/nLG vdWHs are almost identical to Pos(C21) of pristine 2LM, which indicates the weak interfacial shear coupling between graphene and MoS2 layers in the vdWHs, similar to the case in twisted multilayer graphene.71
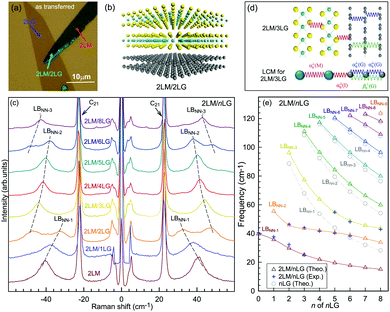 | ||
| Fig. 30 (a) Optical image of 2LM/2LG vdWHs formed by transferring a 2LM flake on a 2LG flake. (b) Schematic illustration of 2LM/2LG vdWHs. (c) Stokes/anti-Stokes Raman spectra in the region of C and LB modes of pristine 2LM and 2LM/nLG vdWHs annealed for 30 min. The black dashed lines are eye guides. (d) Schematic diagram of an LCM for the LB modes in 2LM/3LG, in which the next nearest LB coupling in the 3LG constituents is considered. (e) Pos(LB) of nLG and 2LM/nLG as a function of n of nLG based on the LCM model. The crosses show the experimental Pos(LB) in 2LM/nLG. Reproduced with permission from ref. 36. Copyright 2017, American Chemical Society. | ||
In short, in comparison to the C modes, the LB modes can provide significant information about the interface quality and also the interlayer lattice dynamics of vdWHs, whereas the shear modes tend to localize in the constituents because of the much weaker shear coupling in the graphene-based vdWHs. Such ULF Raman studies on semimetal–semiconductor vdWH prototypes36 can be extended to measure the interfacial interactions in various vdWHs368 and would be beneficial to fundamentally understand their properties for further engineering of vdWH-based electronic and photonic devices.
9.6 Graphene oxide and reduced graphene oxide
Graphite oxide (GO) is a compound of carbon, oxygen, and hydrogen in variable ratios, obtained by treating graphite with strong oxidizers and subsequent exfoliation in water. GOs have a broad range of properties depending on the degree of oxidation and synthesis and have been recognized as promising precursors for the bulk production of graphene-based materials and devices.12,371–373 However, there exist abundant oxygen-containing groups (e.g., epoxy, hydroxyl, and carboxyl) on the GO sheet, which makes it insulating and significantly restricts its applications in electronics.374 Reducing GO to produce reduced graphene oxide (rGO) has been used in the mass production of graphene. To date, significant research efforts have been dedicated to the reduction of GO, as evidenced by the vast body of related publications.374–377 In the beginning, methods for GO reduction could be simply categorized into two types, one being chemical reduction and the other thermal treatments.378–380 Later, laser annealing and electrochemical reduction were introduced to produce rGO.381–383 The reduction of GO to rGO is a vital process because it has a significant impact on the quality of the rGO produced, and, thus, determines how similar rGO will be, in terms of structure, to pristine graphene. Raman spectroscopy has shown its ability to characterize GOs and rGOs.67,370,384Under suitable conditions,239,385,386 GO can undergo complete exfoliation in water, yielding colloidal suspensions of almost entirely individual graphene oxide sheets. Such sheets can be chemically functionalized, dispersed in polymer matrices, and deoxygenated to yield novel composites.239 Moreover, GO sheets can be assembled into a paper-like material under a directional flow. Vacuum filtration of colloidal dispersions of graphene oxide sheets yielded, after drying, free-standing GO papers with thicknesses ranging from 1 to 30 μm, as shown in Fig. 31(a).369 Scanning electron microscopy (SEM) images (see Fig. 31(b)) revealed well-packed layers through almost the entire cross-section of the paper samples. The peak in the X-ray diffraction (XRD) pattern of a typical GO paper specimen (see Fig. 31(c)) corresponds to a layer-to-layer distance (d-spacing) of about 0.83 nm, which is much larger than that of graphite because of the molecules between two adjacent GO sheets. Fig. 31(d) shows the micro-Raman spectra of a typical GO paper. The G peak and 2D peak are characteristic of sp2 hybridized carbon–carbon bonds in graphene.55,56 The strong and broad D band and high I(D)/I(G) ratio in GO confirm its lattice distortions and a large amount of sp3-like defects caused by the oxidation process. This is also confirmed by the blueshift of the G peak, which is overlapped by the redshifted D′ peak to form a single band at ∼1595 cm−1 because of the phonon quantum confinement effect induced by the small domain size in GO. The 2D band is more sensitive to the defects of graphene-based materials, as discussed in Section 5. The absence of the 2D band in GO also indicates that GO is dominated by the fully-disordered sp2 bonding network.
 | ||
| Fig. 31 (a) Low- and (b) high-resolution SEM side-view images of a 10 μm-thick GO paper. (c) X-ray diffraction pattern of the GO paper sample. Reproduced with permission from ref. 369. Copyright 2007, Nature Publishing Group. (d) Raman spectrum of a typical GO paper. (e) Cross-section TEM images of a stack of rGO platelets. (f) Powder XRD patterns of graphite, GO, and rGO. (g) XPS characterization of rGO platelets. (h) Raman spectra of rGO (blue) and the GO reference sample (red). Reproduced with permission from ref. 370. Copyright 2010, Nature Publishing Group. | ||
There are a number of ways to create rGO from GO, although all methods are based on chemical, thermal, or electrochemical means. Some of these techniques are able to produce very high quality rGO, similar to pristine graphene, but can be complex or time consuming to carry out. Moon et al. reported a novel reducing agent system (hydroiodic acid with acetic acid (HI-AcOH)) that allows for the efficient, one-pot reduction of a solution-phased rGO powder.370 The clusters in the powders are not fully restored into the hexagonal graphene framework, and the rGO platelets have inclusions containing aperiodically decorated functional groups. Furthermore, the graphitic laminar structure of stacks of rGO platelets could be resolved in the ‘ordered’ region. Fig. 31(e) shows a cross-section of one such stack, and the average interlayer distance of the stack is 3.64 Å. Fig. 31(f) shows powder XRD patterns of graphite, GO, and rRG. The 2θ angles of the XRD peaks (d-spacing) of rGO shifted from 10.27° (d-spacing ∼8.60 Å) of GO to 24.57° (d-spacing ∼3.62 Å) after reduction, which is similar to the SEM measurements. The XPS peaks of rGO at 285 eV in Fig. 31(g) assigned to C are one main C–C and four small C–O components.387 The peak intensities and atomic ratios (O1s/C1s) of rGO in the C1s peaks are decreased significantly in comparison with those of GO. Fig. 31(h) shows the Raman spectra of rGO and a GO reference. The G-band of rGO occurs at 1581 cm−1, which corresponds to the recovery of the hexagonal network of carbon atoms with defects. The I(D)/I(G) ratio of rGO increases notably, indicating that the reduction process may alter the structure of GO, resulting in a high number of structural defects. However, if we note the G peak at 1581 cm−1 and the appearance of the D′ peak, the defect status of rGO should be at stage 1 while that of GO should be at stage 2. Therefore, the higher I(D)/I(G) ratio of rGO actually indicates fewer defects with respect to GO after the reduction process. The 2D peak (∼2680 cm−1) becomes significant in rGO and the D + G band is present at ∼2910 cm−1, demonstrating the restoration of graphite structures. Analogously, by combining the XPS and Raman spectra, rGO produced by other methods can also be analyzed.67,382
9.7 Graphene–polymer composites
Because of the excellent mechanical, thermal, and electrical properties, graphene–polymer composites are expected to have a variety of applications in the automotive, aerospace, construction, and electronics industries.226,388–390 A classic example of such a system is the birefringence measurements made on poly(methyl methacrylate) (PMMA) and polystyrene (PS) structures. There are already commercially available photoelasticity-based sensors, such as the Photostress gray-field polariscope from Stress Photonics.Raman spectroscopy is the ideal tool to probe the status of graphene in this system.226 The exfoliated and CVD-grown graphene composite coatings are prepared by the dry-transfer method. Fig. 32(a) shows a schematic of the sample preparation. The in situ Raman measurements were carried out on the graphene and the graphene/polymer composite coating. Well-defined Raman spectra with a characteristic 2D band (around 2640 cm−1) and G band (around 1580 cm−1) are obtained from both the exfoliated and CVD-grown graphene. The top panel of Fig. 32(b) shows the example flakes found in the composite system with increasing number of layers, where the I(2D)/I(G) is greater than three for monolayer graphene. The absence of the D band for the exfoliated graphene reveals its high-quality.44 The bottom panel of Fig. 32(b) shows the Raman spectra of as-grown CVD graphene on Cu foil and in the coatings. I(2D)/I(G) is greater than 2 and the FWHM of 2D mode ∼25 cm−1. The G peak of different graphene layers in exfoliated composite coatings does not change with increasing number of layers and ω(G) is close to that of intrinsic 1LG, while ω(G) in CVD-graphene composite coatings blueshifts about ∼20 cm−1 from the CVD-graphene on the copper foil. This difference is due to the strain induced in the transfer process. The dry-transfer mechanically exfoliated sample has no residual stresses, whereas the CVD sample is in compression following the solvent evaporation during its transfer.226
 | ||
| Fig. 32 (a) A schematic representation of the preparation of model composite coatings. (b) Top: Raman spectra of different layers of graphene in exfoliated composite coatings. Absence of the D band at ∼1350 cm−1 indicates the high crystallinity of the sample. Bottom: Raman spectra of the as produced CVD-grown graphene on Cu foil and in the composite coating. The spectra from poly(methyl methacrylate) (PMMA) top coat and SU-8 is shown as a reference in both cases. Spectra are offset for clarity. Reproduced with permission from ref. 226. Copyright 2014, Wiley Online Library. | ||
10 Applications of Raman spectroscopy in graphene-based devices
When graphene materials are incorporated into some functional devices, their intrinsic properties are modified by the environment and even the device itself. During device fabrication, the graphene materials undergo several processes. For example, to realize the specific functions of the device, graphene materials might be decorated with functional groups or be in a certain state so that their peculiar properties can be used. In all cases, on-line, real-time, and nondestructive characterization techniques are crucial for the monitoring of the properties (and their modification) of graphene materials during the fabrication process and to probe the functions of graphene materials in the device. Some conventional methods show limitations concerning characterization, especially as device dimensions continue to shrink. Raman spectroscopy is a powerful scientific tool that allows researchers to identify important physical and chemical parameters of graphene materials in devices, such as number of layers, chemical identity, stacking geometry, doped charge, defects, contaminants, edge chirality, strain, stability, chemically attached functional groups, and energy gaps. For 1LG and MLG, which are only angstrom-scale in the z-direction, the electronic band structure of graphene is easily modified by changing any of the above mentioned physical and chemical parameters. In the following subsections, we show the advantages and efficiencies of Raman spectroscopy in effectively characterizing some typical graphene-based devices, which is expected to be an important examination tool in the industrialization of graphene applications in the future.10.1 Graphene-based field-effect transistors
The graphene FET is a device with source and drain electrodes, and the Si/SiO2 substrate can be adopted as a back gate.24,60,63 A graphene FET is not only the basic device of analog and digital circuits391 but also the basic structure of other devices, e.g., photodetectors392,393 and sensors.394,395 One of the most important variables in a graphene FET is its doping level, which can be identified by Raman spectroscopy, as discussed above.60,61,63 Another important issue concerning graphene FETs is the heat generation and dissipation when a large current drive is necessary to address several other FETs or when high switching speeds for radio frequency applications are desired.307,396 The dissipated electric power can increase the operating temperature of the device so that thermal management of the device becomes critical. Therefore, it is important to understand the heat generation and dissipation in the graphene FET.Freitag et al. fabricated a graphene FET307 whose SEM image is shown in Fig. 33(a) as an inset. The graphene FET is 2.65 μm long and 1.45 μm wide. The SiO2 gate oxide thickness is 300 nm. The FET can support electrical power densities up to at least 210 kW cm−2. Fig. 33(a) shows the 2D-band of the graphene FET while a current flows through it. ω(2D) decreases sharply with increasing electric power and the peak broadens. As Fig. 33(b) shows, the decrease in energy is proportional to the dissipated electric power, which suggests that Joule heating is responsible for the phonon softening. It is known that ω(2D) decreases linearly with temperature.304 Using the proportionality factor of −29.4 K cm−1,304 one can calibrate a temperature scale for the electronic measurements and, thus, it was shown that the center of the graphene FET heats up at a rate of 3.3 K kW−1 cm−2. At the highest power density, 210 kW cm−2, the graphene 2D-derived temperature reaches 1050 K. The intensity mapping of ω(2D) can give the temperature distribution in the graphene.307 As shown in Fig. 33(c), ω(2D) in the graphene FET shows a unified distribution in the absence of an applied voltage. When a voltage is applied, because of the different energy dissipation pathways, the center of the FET has a higher temperature than the edges. The temperature distribution in the graphene FET at different electrical powers is shown in Fig. 33(d). The yellow bars are the electrodes. The temperature distribution can be explained by a model that considers the thermal resistance between the graphene and electron and also the thermal resistance between the graphene and SiO2 substrate, as shown in Fig. 33(e). The simulation shows that the lateral heat flow in the thin graphene sheet is five times larger than the lateral flow in SiO2 (despite being 1000 times thinner than the SiO2 film).307 This helps spread the hot spot in the graphene sheet, which would otherwise be even hotter in the middle, and it also spreads some of the heat power to the contacts. Nevertheless, 77% of the power is dissipated through the SiO2 directly below the FET, while the remaining 23% is dissipated through the contacts and the neighboring sites. Thus, the main heat dissipation channel is the silicon under the graphene FET, as shown in Fig. 33(f).
 | ||
| Fig. 33 (a) The 2D band spectra measured in the middle of the FET device at various drain voltages. The gate voltage is 0 V, εL = 2.41 eV. Inset: SEM image of the device. (b) ω(2D) and temperature as a function of applied electrical power. Inset: Corresponding I–V curve. (c) Spatially resolved images of ω(2D) at four different drain voltages. The graphene flake extends beyond the left and right contacts (indicated in yellow). (d) Experimental temperature along the graphene sheet (parallel to the current flow) at 59.3 (black), 125.7 (green), and 161.3 kW cm−2 (red) dissipated electronic power. The blue line corresponds to the zero-power case, defined as room temperature. Electrodes are depicted in yellow. (e) The corresponding modeled temperature profile along the graphene device for the same bias conditions. (f) Cross section of the temperature distribution in the gate stack for 161.3 kW cm−2 of dissipated electronic power. Reproduced with permission from ref. 307. Copyright 2009, American Chemical Society. | ||
Notably, the doping level changes slightly with a drain voltage but without a gate voltage.307 At low doping, ω(2D) depends simply on the temperature.60ω(G) is sensitive to both doping level and temperature change.60,304 Thus, ω(G) cannot be used to identify the thermal distribution in a graphene FET under a drain voltage.
The above result shows the ability of Raman spectroscopy to probe the in situ temperature of graphene in electronic devices. This technique can be extended to other graphene-based FETs, such as the graphene/BN FET.397
10.2 Graphene-based energy storage devices
Technologies for efficient energy storage are urgently required because of environmental pollution, limited fossil resources, and the huge demand for energy. Therefore, interest in energy storage devices, such as ion batteries and electrochemical capacitors (ECs), has increased enormously.399,400 The main reactions of ion batteries are reversible ion intercalation/de-intercalation cycles between two layered compounds, corresponding to the charge–discharge process, with electrochemical reactions.401 For ECs, the interface between the electrodes and electrolyte can be treated as a capacitor.400 According to the electrochemical activity or inactivity of electrode materials, the ECs are divided into electric double-layer capacitors (EDLCs) and pseudocapacitors, respectively. Thus, the electrode material is important for energy storage. The 2DMs, such as TMDs,402 MXenes,403 and graphene-based materials,27,404 have many fantastic properties, e.g., high surface area and possible redox reactions, and are widely used as electrodes in ion batteries and ECs. In situ spectroelectrochemical measurements can be used to characterize electrode materials during ion (lithium,405 sodium,406 and potassium398) battery or EC processes.382,405,407 Here, we take potassium ion (K-ion) batteries with NLG electrodes as an example to show how Raman spectroscopy can help us to understand the mechanisms of energy storage and the distortion of the electrode material in the charge–discharge process of energy storage devices.398To ensure equilibrium conditions between subsequent Raman scans, an extremely slow scan rate (0.05 mV s−1) is used in the linear sweep voltammetry (LSV) measurements. Selective Raman spectra are shown in Fig. 34(a) for different states of charge. Fig. 34(b) displays all Raman spectra taken from 0.37 to 0.01 V in a waterfall plot. The top of Fig. 34(c) shows the LSV measured during the in situ Raman experiment. The G peak positions and intensities are shown in the bottom and middle of Fig. 34(c), respectively. Together these plots help visualize and quantify the distinct peak shifts and intensity changes of the Raman spectra. Notably, the D peak (∼1330 cm−1) was not observed throughout the in situ measurements, indicating that no significant degradation of the sp2 hybridized carbon in the NLG takes place.398,406 An initial scan taken at 2.0 V reveals a similar spectrum to that of NLG, containing 2D and G peaks with the G peak at 1582 cm−1. At 0.37 V, the G peak blue shifts to 1589 cm−1 because of the formation of a low-defect-concentration stage GIC. From 0.37 to 0.25 V, minimal changes are observed in both the electrochemical and Raman data, which are attributed to the sparse ion composition of the low-defect-concentration stage compound. Near 0.24 V, the first reduction peak occurs in the LSV as ordered staging begins, indicated by a higher frequency shoulder in the G peak and a decrease in the 2D intensity. Initially, the charge is equally distributed between all layers, and only a single uncharged G peak (Guc) is present. When cations start to intercalate into graphite, the charge density increases on layers adjacent to the intercalants, forming an upshifted Gc (G charged) peak.146,406,407 The graphene layers not adjacent to the ions continue to show the Guc peak leading to a doublet in the Raman spectra at stages above stage 2.408,409 At 0.24 V, the Gc/Guc intensity ratio is indicative of stage 6 KC72.410 From 0.24 to 0.15 V, the Gc peak increases in intensity, the Guc and 2D peaks decrease, and all peaks red shift. The opposite behavior of the Gc and Guc intensities is due to continued staging where more graphene layers become charged and fewer uncharged layers remain. Both the Guc peak and 2D peak have vanished by 0.15 V. This is because stage 2 no longer involves any uncharged graphene layers, correlating with the disappearance of the Guc peak because of the emergence of a stage 2 compound. At this stage, the doping level (|EF|, EF is the Fermi level) is sufficiently high to invalidate the transitions of the DR process for the 2D peak.58,60,61 From 0.15 to 0.01 V, the Raman spectra evolve from a symmetrical G peak to an asymmetric Fano resonance shape because of interference between the metallic like behavior of stage 1 GICs.410 Optical microscope images of the NLG at an open circuit voltage of 0.01 V also support the formation of stage 1 KC8, as shown by the change in color from gray to bright orange (inset of Fig. 34(c)).
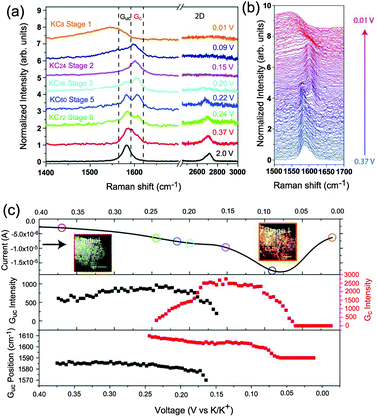 | ||
| Fig. 34 (a) Selective Raman spectra taken at different states of charge, as indicated in the linear sweep voltammograms. (b) Waterfall plot of all Raman spectra taken between 0.37 and 0.01 V. (c) Top, LSV measured during the in situ Raman experiment. The colored circles indicate the state of charge for the Raman spectra in (a). Middle: Peak intensities for the Guc and Gc peaks. Bottom: Peak positions for the Guc and Gc peaks. Inset: Optical microscope image of the NLG coated foam initially and fully potassiated. Scale bar: 20 μm. Reproduced with permission from ref. 398. Copyright 2016, Royal Society of Chemistry. | ||
The above results demonstrate that Raman spectroscopy is useful in electrode material preparation and redox reactions, as well as to increase the cycle life of energy storage devices. This method can be extended to identify ion batteries and ECs containing other 2D materials as electrodes.411
10.3 Graphene-based solar cells and organic light emitting diodes
Having unique properties, i.e., high optical transparence, high electrical conduction, and excellent mechanical flexibility, graphene and its derivatives have been investigated extensively in the field of solar cells and organic light emitting diodes (OLEDs). Many impressive results have been reported, where graphene-based materials (GO film and CVD-grown graphene) have been used as the electrodes, i.e., transparent anodes,357,413,414 non-transparent anodes,415 transparent cathodes,416 and catalytic counter electrodes,417 as well as where graphene has been used as the active layer, i.e., light harvesting materials,418 Schottky junctions,419 electron transport layers,420 hole transport layers, both hole and electron transport layers,421 and interfacial layers in the tandem configuration.422Usually, CVD-grown graphene has a higher electrical conductivity than the GO film because of the higher crystal quality. Here, we present an example of the layer-by-layer (LBL) transferred CVD-grown graphene as the solar cell anode,412 as shown in Fig. 35(a). A single layer of graphene does not have sufficiently high sheet conductivity. Stacking multilayer graphene together, followed by doping, is required to achieve higher extrinsic conductivity. A direct LBL interface coupling route for fabricating multilayer graphene films is shown in Fig. 35(b). In this LBL stacked graphene, the overall electrical conductivity is determined by the crystal quality and also the interlayer coupling. Raman spectroscopy is an ideal tool to identify the interlayer coupling and also the number of layers in this LBL transferred system.
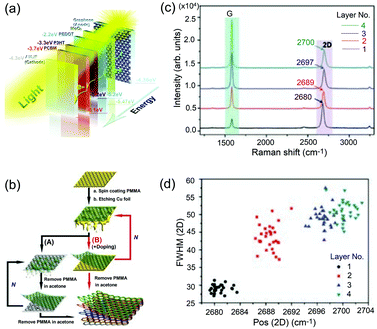 | ||
| Fig. 35 (a) Schematic diagram of a photovoltaic (solar cell) device structure. (b) Schematic drawing of NLG films made by normal wet transfer (A) and direct coupling LBL assembly (B) (N = 0, 1, 2, 3…). (c) Raman spectra of graphene films with 1 to 4 layers. (d) A statistical result of FWHM(2D) and peak Pos(2D) from 1 to 4 layers. Reproduced with permission from ref. 412. Copyright 2011, Wiley Online Library. | ||
As shown in Fig. 35(c), I(G) increases with the number of layers because of the increased signal from the graphene flake. In the AB- and ABC-stacked NLG, the interlayer coupling affects the electronic band and results in a complicated 2D band profile. Here, the LBL transferred graphene is the tNLG with randomly stacked orientations at each interface, denoted as complete tNLG. This complete tNLG has a linear electronic band dispersion similar to 1LG.182 Thus, the 2D band of the complete tNLG also shows a single Lorentzian peak. However, the Fermi velocity of the tNLG is reduced because of the interlayer coupling. The lower Fermi velocity would lead to the blueshift of the 2D peak, as shown in Fig. 35(c and d). Moreover, the FWHM of the 2D peak in the complete tNLG would be broadened with respect to the number of layers. Therefore, according to the behavior of the 2D peak, the interlayer coupling and the number of layers of the LBL transferred graphene can be identified.
Graphene can also be adopted as the electrode of an OLED.423 In these OLEDs, the transparent conducting top electrode can be formed of a large-area multilayer graphene/bonding layer/polyethylene terephthalate structure. In this structure, the strain is induced in the NLG. As a means of probing the uniaxial strain on the NLG, polarized Raman spectroscopy is usually performed.423 The splitting of the G mode (denoted as the G+ and G− bands) can be observed under uniaxial strain. The upshift and downshift of the G mode indicate compression and tension, respectively. The local stress can be estimated from the expression, Δω = ωG0 − ωG± = −ωG0γε, where ωG0 is the G-band peak of unstrained graphene, γ = 2 is the Grüneisen parameter of G mode,87,424 and ε is the stress.
10.4 Graphene-based nanoelectromechanical systems
The outstanding mechanical,273 electrical,1,426 and optical427 properties of graphene make it an ideal material for flexible, conductive, and semitransparent films. Multilayer graphene with several tens of graphene layers is sufficiently stiff428 to produce freestanding cantilevers with very high aspect ratios that can be used to make suspended mirrors with masses from tens to hundreds of femtograms. Moreover, the optical cavities formed by suspending the cantilevers over a silica surface can be electrostatically actuated, making them well suited for the development of nanoelectromechanical systems (NEMS).429 NEMS can be operated as ultrasensitive mass sensors430,431 and ultrahigh-frequency resonators432 and can also be used to explore fundamental physical phenomena such as nonlinear damping273 and quantum effects in macroscopic objects.433 Various dissipation mechanisms are known to limit the mechanical quality factors of NEMS and to induce aging because of material degradation; thus, there is a need for methods that can probe the motion of these systems and the stresses within them at the nanoscale.425 Raman spectroscopy has been used to probe the local stress within such a multilayer graphene cantilever.425Fig. 36(a) depicts a NEMS prepared from micrometer-sized multilayer graphene planar flakes, which are clamped on one side by a gold film with overhanging silicon oxide. The typical samples have a thickness of 100 graphene layers (30 nm) to prevent collapse, as shown in Fig. 36(b). ω(G) (or ωG) of the graphene flake follows a quadratic dependence with small voltage variations. The G peak shift is indeed synchronized with the interferometric response intensity of G mode, as shown in Fig. 36(c), and exhibits softening of 1.9 cm−1 at the maximum cantilever deflection. This peak softening is interpreted as a stress/strain effect and, by analogy with measurements of strained graphene,87,434,435 one can extract a corresponding strain value of 0.06% at the maximum deviation resulting from a quasi-static stress of 600 MPa.
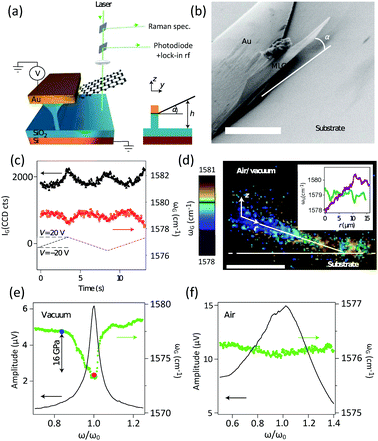 | ||
| Fig. 36 (a) Schematic view of a nanoelectromechanical device. The cantilever can be actuated with an external voltage while its optical properties are analyzed with a high-sensitivity Raman spectrometer and a fast photodiode. (b) SEM images showing a typical multilayer graphene cantilever clamped to a gold film on an oxidized silicon substrate. (c) The intensity IG (black symbols, left axis) and shift ωG (red symbols, right axis) of the Raman G peak of a multilayer graphene cantilever vs. time during electrostatic actuation (dashed line). Peak softening can be seen. (d) False color plot showing the value of ωG measured during a confocal (x, z) scan of the cantilever cross-section. The inset shows how ωG varies along the cantilever before (purple) and after (green) the collapse of the cantilever onto the silica substrate. Black marks indicate the hinge position. Scale bar: 5 μm. (e and f) Amplitude of cantilever oscillations (black line: left axis) and Raman shift (green symbols: right axis) vs. drive frequency in a vacuum (e) and in air (f). Reproduced with permission from ref. 425. Copyright 2012, Nature Publishing Group. | ||
The Raman signature of graphene flakes in NEMS depends on the position along the flake, which reflects the stress distribution in the cantilever. A micro-Raman confocal depth scan (x, z) (Fig. 36(d)) reveals a linear increase of ω(G) along the cantilever axis, from the free end of the cantilever to the hinge. This is not observed when the multilayer graphene is collapsed (Fig. 36(d), inset). This linear shift could be interpreted as a continuously increasing electrostatic field effect60,64 owing to charge within the substrate, which also influences ω(G).296 In Fig. 36(e and f), the fundamental mechanical resonance of this multilayer graphene cantilever is detected using the Raman signal under different experimental conditions. A large softening behavior (green curve, ∼6 cm−1) is observed when mechanical excitation coincides with the mechanical resonance width, which is in agreement with Fizeau interferometry measurements (black curve). In contrast to the vacuum case (Fig. 36(e), the quality factor Qvac ∼ 26.1), the same sample in air (Fig. 36(f)) presents a reduced quality factor (Qair ∼ 2.3), as well as a reduced Raman G-peak softening, which illustrates that the dynamical stress in air is less intense. The value of Qair agrees with a typical viscous damping model436 for this particular geometry and represents the predominant damping mechanism limiting the quality factor in air. However, this mechanism is no longer dominant under vacuum, where dissipation may be governed by clamping losses.
10.5 Graphene-based vdW two-dimensional heterostructure devices
Recently, vdW heterostructures formed by vertically stacked various 2DMs, such as graphene and TMDs, have offered more promising properties and functionalities for many electronic and optoelectronic applications than the constituent materials.367,438–443Fig. 37(a–c) show a cross-sectional view, optical microscope image, and topographical sketch of a representative graphene-coated MoS2 (graphene/MoS2 heterostructure),437 respectively. Charge transfer between graphene and TMDs in the graphene/TMD heterostructures occurs, forming a Schottky junction.437 A technique is necessary to in situ probe the charge transfer within the heterostructures. The doping carrier density (n) and the Fermi level relative to the Dirac point (EDirac − EF) of graphene can be calculated based on ω(G) and ω(2D).60,61 In particular, ω(G) upshifts monotonically upon increasing the doping level for p and moderate n doping in graphene, while ω(2D) upshifts in the case of p-doping (EF < EDirac) and downshifts in the case of n-doping (EF > EDirac).60 Therefore, following the discussion in Section 7.1, the doping level and the carrier density (ne or nh) of graphene can be easily quantified by the spectral parameters of Raman spectroscopy. The spectral parameters of graphene are more sensitive to its doping level than those of TMDs; thus, the charge transfer between graphene and MoS2 in the heterostructures can be determined by the spectral features of the graphene constituent.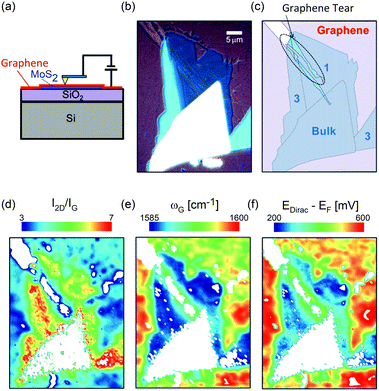 | ||
| Fig. 37 (a) Schematic diagram of a graphene/MoS2 system. Optical microscope image (b) and topographical diagram (c) of a CVD grown graphene single crystal on MoS2. Spatial Raman maps for I(2D)/I(G) (d), ωG (e), and the calculated EDirac − EF (f) for the graphene/MoS2 heterostructure. Reproduced with permission from ref. 437. Copyright 2014, American Chemical Society. | ||
Fig. 37(d–f) show the spatial Raman maps of I(2D)/I(G), ωG, and the calculated EDirac − EF of the graphene constituent in the heterostructures, respectively. According to eqn (15), I(2D)/I(G) under 514 nm excitation can be used to identify the doping level of graphene. The average positions of the G and 2D peaks for the graphene on SiO2 (ωG = 1593 cm−1 and ω2D = 2648 cm−1), as well as their intensity ratio (I(2D)/I(G) = 4), indicate that graphene is heavily p-doped with a carrier density n = –2 × 1013 cm−2 and EF − EDirac = −550 mV. On the other hand, the corresponding parameters for graphene in contact with MoS2 (ωG ∼ 1586 cm−1, ω2D = 2644 cm−1, and I(2D)/I(G) = 6) suggest that graphene is p-doped with n = −1 × 1013 cm−2 and EF − EDirac = −250 mV. This suggests that additional electrons are transferred from MoS2 to graphene so that graphene is ‘counter doped’ by the underlying MoS2 flake or, in other words, MoS2 is hole doped by graphene.
11 Conclusions
Graphene has extraordinary electronic, optoelectronic, and mechanical properties, and a variety of device applications. We have reviewed the origin of all Raman modes in intrinsic graphene, including the first-order G mode and DR-activated first-order and second-order Raman modes. The C, LB, and 2D modes in NLGs have also been discussed in detail, which are significantly sensitive to the number of layers N and stacking order (AB, ABC, and twist stacking). The resonance Raman spectroscopy of NLG has also been presented. The external perturbations to graphene flakes could affect their lattice vibrations and also band structures, which can be revealed by Raman spectroscopy. The effects of point defects, line defects, and edges on the D, G, and 2D modes have been discussed in detail, and it has been clearly demonstrated how to probe the nature of defects in graphene by Raman spectroscopy. The Raman spectral features, such as the lineshape and peak positions of the C, LB, and 2D modes, the intensity of the G mode of NLG, and that of the Si mode of the substrate, have been utilized to identify the value of N of graphene flakes. Raman spectroscopy has also been applied to characterize graphene-based materials, such as nanographene, carbon dots, graphene oxide, epitaxial graphene on SiC, NLG grown by CVD, and graphene-based van der Waals heterostructures. Raman imaging has also been shown to provide spatially distributed information concerning the number of layers, stacking order, edges, strain, and growth mechanism of graphene flakes. Finally, Raman spectroscopy has been shown to be an on-line, real-time, and nondestructive characterization technique to monitor the property modification or designed function on demand of graphene materials in related devices, such as FETs, energy storage devices, solar cells, OLEDs, NEMS, and graphene-based vdW heterostructures. We hope that this review will be an essential guide to the Raman spectroscopy of graphene-based materials for scientists in the field of material synthesis, basic research, and device and industrial applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the National Key Research and Development Program of China (Grant No. 2016YFA0301204), the National Natural Science Foundation of China (Grant No. 11474277 and 11434010), the Key Research Program of the Chinese Academy of Sciences (Grant No. XDPB06-02, XDPB08-2), and Beijing Municipal Science and Technology Commission.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- T. Ohta, A. Bostwick, J. L. McChesney, T. Seyller, K. Horn and E. Rotenberg, Phys. Rev. Lett., 2007, 98, 206802 CrossRef PubMed.
- K. F. Mak, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 104, 176404 CrossRef PubMed.
- J. H. Warner, M. Mukai and A. I. Kirkland, ACS Nano, 2012, 6, 5680–5686 CrossRef CAS PubMed.
- C. H. Lui, Z. Li, Z. Chen, P. V. Klimov, L. E. Brus and T. F. Heinz, Nano Lett., 2010, 11, 164–169 CrossRef PubMed.
- C. Cong, T. Yu, K. Sato, J. Shang, R. Saito, G. F. Dresselhaus and M. S. Dresselhaus, ACS Nano, 2011, 5, 8760–8768 CrossRef CAS PubMed.
- X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung and E. Tutuc, et al. , Science, 2009, 324, 1312–1314 CrossRef CAS PubMed.
- A. Reina, X. Jia, J. Ho, D. Nezich, H. Son, V. Bulovic, M. S. Dresselhaus and J. Kong, Nano Lett., 2008, 9, 30–35 CrossRef PubMed.
- C. Virojanadara, M. Syväjarvi, R. Yakimova, L. Johansson, A. Zakharov and T. Balasubramanian, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245403 CrossRef.
- M. Sprinkle, M. Ruan, Y. Hu, J. Hankinson, M. Rubio-Roy, B. Zhang, X. Wu, C. Berger and W. A. De Heer, Nat. Nanotechnol., 2010, 5, 727–731 CrossRef CAS PubMed.
- H. A. Becerril, J. Mao, Z. Liu, R. M. Stoltenberg, Z. Bao and Y. Chen, ACS Nano, 2008, 2, 463–470 CrossRef CAS PubMed.
- G. Eda, G. Fanchini and M. Chhowalla, Nat. Nanotechnol., 2008, 3, 270–274 CrossRef CAS PubMed.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873 CrossRef CAS PubMed.
- M. M. Lucchese, F. Stavale, E. M. Ferreira, C. Vilani, M. Moutinho, R. B. Capaz, C. Achete and A. Jorio, Carbon, 2010, 48, 1592–1597 CrossRef CAS.
- L. G. Cançado, A. Jorio, E. M. Ferreira, F. Stavale, C. Achete, R. Capaz, M. Moutinho, A. Lombardo, T. Kulmala and A. Ferrari, Nano Lett., 2011, 11, 3190–3196 CrossRef PubMed.
- G. Lu, L. E. Ocola and J. Chen, Nanotechnology, 2009, 20, 445502 CrossRef PubMed.
- Z.-S. Wu, G. Zhou, L.-C. Yin, W. Ren, F. Li and H.-M. Cheng, Nano Energy, 2012, 1, 107–131 CrossRef CAS.
- X. Jia, J. Campos-Delgado, M. Terrones, V. Meunier and M. S. Dresselhaus, Nanoscale, 2011, 3, 86–95 RSC.
- R. Yang, Z. Shi, L. Zhang, D. Shi and G. Zhang, Nano Lett., 2011, 11, 4083–4088 CrossRef CAS PubMed.
- I. A. Verzhbitskiy, M. D. Corato, A. Ruini, E. Molinari, A. Narita, Y. Hu, M. G. Schwab, M. Bruna, D. Yoon and S. Milana, et al. , Nano Lett., 2016, 16, 3442–3447 CrossRef CAS PubMed.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- F. Bonaccorso, Z. Sun, T. Hasan and A. Ferrari, Nat. Photonics, 2010, 4, 611–622 CrossRef CAS.
- Y.-M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Farmer, H.-Y. Chiu, A. Grill and P. Avouris, Science, 2010, 327, 662 CrossRef CAS PubMed.
- F. Torrisi, T. Hasan, W. Wu, Z. Sun, A. Lombardo, T. S. Kulmala, G.-W. Hsieh, S. Jung, F. Bonaccorso and P. J. Paul, et al. , ACS Nano, 2012, 6, 2992–3006 CrossRef CAS PubMed.
- Z. Sun, T. Hasan, F. Torrisi, D. Popa, G. Privitera, F. Wang, F. Bonaccorso, D. M. Basko and A. C. Ferrari, ACS Nano, 2010, 4, 803–810 CrossRef CAS PubMed.
- L. Miao, J. Wu, J. Jiang and P. Liang, J. Phys. Chem. C, 2012, 117, 23–27 Search PubMed.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. C. Neto, Science, 2016, 353, 6298 CrossRef PubMed.
- D. Bischoff, M. Eich, A. Varlet, P. Simonet, H. C. Overweg, K. Ensslin and T. Ihn, Mater. Today, 2016, 19, 375–381 CrossRef CAS.
- L. Britnell, R. V. Gorbachev, B. D. Jalil, R. Belle, F. Schedin, A. Mishchenko, T. Georgiou, M. I. Katsnelson, L. Eaves, S. V. Morozov, N. M. Peres, J. Leist, A. K. Geim, K. S. Novoselov and L. A. Ponomarenko, Science, 2012, 335, 947–950 CrossRef CAS PubMed.
- L. Britnell, R. M. Ribeiro, A. Eckmann, R. Jalil, B. D. Belle, A. Mishchenko, Y.-J. Kim, R. V. Gorbachev, T. Georgiou, S. V. Morozov, A. N. Grigorenko, A. K. Geim, C. Casiraghi, A. H. C. Neto and K. S. Novoselov, Science, 2013, 340, 1311–1314 CrossRef CAS PubMed.
- W. J. Yu, Z. Li, H. Zhou, Y. Chen, Y. Wang, Y. Huang and X. Duan, Nat. Mater., 2013, 12, 246–252 CrossRef CAS PubMed.
- T. Georgiou, R. Jalil, B. D. Belle, L. Britnell, R. V. Gorbachev, S. V. Morozov, Y.-J. Kim, A. Gholinia, S. J. Haigh, O. Makarovsky, L. Eaves, L. A. Ponomarenko, A. K. Geim, K. S. Novoselov and A. Mishchenko, Nat. Nanotechnol., 2013, 8, 100–103 CrossRef CAS PubMed.
- F. Withers, O. Del Pozo-Zamudio, A. Mishchenko, A. P. Rooney, A. Gholinia, K. Watanabe, T. Taniguchi, S. J. Haigh, A. K. Geim, A. I. Tartakovskii and K. S. Novoselov, Nat. Mater., 2015, 14, 301–306 CrossRef CAS PubMed.
- H. Li, J.-B. Wu, F. Ran, M.-L. Lin, X.-L. Liu, Y. Zhao, X. Lu, Q. Xiong, J. Zhang, W. Huang, H. Zhang and P.-H. Tan, ACS Nano, 2017, 11, 11714–11723 CrossRef CAS PubMed.
- A. Azizi, S. M. Eichfeld, G. Geschwind, K. Zhang, B. Jiang, D. Mukherjee, L. Hossain, A. F. Piasecki, B. Kabius and J. A. Robinson, et al. , ACS Nano, 2015, 9, 4882–4890 CrossRef CAS PubMed.
- Y. Lin, J. Li, S. C. D. La Barrera, S. M. Eichfeld, Y. Nie, R. Addou, P. Mende, R. M. Wallace, K. Cho and R. M. Feenstra, et al. , Nanoscale, 2016, 8, 8947–8954 RSC.
- M. M. Furchi, A. Pospischil, F. Libisch, J. Burgdorfer and T. Mueller, Nano Lett., 2014, 14, 4785–4791 CrossRef CAS PubMed.
- F. Withers, O. D. Pozozamudio, A. Mishchenko, A. P. Rooney, A. Gholinia, K. Watanabe, T. Taniguchi, S. J. Haigh, A. K. Geim and A. I. Tartakovskii, et al. , Nat. Mater., 2015, 14, 301–306 CrossRef CAS PubMed.
- G. Lee, Y. Yu, X. Cui, N. Petrone, C. Lee, M. S. Choi, D. Lee, C. Lee, W. J. Yoo and K. Watanabe, et al. , ACS Nano, 2013, 7, 7931–7936 CrossRef CAS PubMed.
- M. S. Choi, G. Lee, Y. Yu, D. Lee, S. H. Lee, P. Kim, J. Hone and W. J. Yoo, Nat. Commun., 2013, 4, 1624 CrossRef PubMed.
- A. Milani, M. Tommasini, V. Russo, A. L. Bassi, A. Lucotti, F. Cataldo and C. S. Casari, Beilstein J. Nanotechnol., 2015, 6, 480–491 CrossRef PubMed.
- A. Ferrari, J. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. Novoselov and S. Roth, et al. , Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- F. Tuinstra and J. L. Koenig, J. Chem. Phys., 1970, 53, 1126–1130 CrossRef CAS.
- J. W. Ager III, D. K. Veirs and G. M. Rosenblatt, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6491 CrossRef.
- M. S. Dresselhaus, A. Jorio, M. Hofmann, G. Dresselhaus and R. Saito, Nano Lett., 2010, 10, 751–758 CrossRef CAS PubMed.
- F. Innocenti, A. Milani and C. Castiglioni, J. Raman Spectrosc., 2010, 41, 226–236 CAS.
- L. Malard, M. Pimenta, G. Dresselhaus and M. Dresselhaus, Phys. Rep., 2009, 473, 51–87 CrossRef CAS.
- A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095 CrossRef CAS.
- M. S. Dresselhaus, G. Dresselhaus, R. Saito and A. Jorio, Phys. Rep., 2005, 409, 47–99 CrossRef.
- D. S. Bethune, G. Meijer, W. C. Tang, H. J. Rosen, W. G. Golden, H. Seki, C. A. Brown and M. S. de Vries, Chem. Phys. Lett., 1991, 179, 181–186 CrossRef CAS.
- M.-L. Lin, J.-B. Wu, X.-L. Liu and P.-H. Tan, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5224.
- L. Liang, J. Zhang, B. G. Sumpter, Q. Tan, P.-H. Tan and V. Meunier, ACS Nano, 2017, 11, 11777–11802 CrossRef CAS PubMed.
- A. C. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef CAS.
- A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- J.-B. Wu, X. Zhang, M. Ijäs, W.-P. Han, X.-F. Qiao, X.-L. Li, D.-S. Jiang, A. C. Ferrari and P.-H. Tan, Nat. Commun., 2014, 5, 5309 CrossRef CAS PubMed.
- C.-F. Chen, C.-H. Park, B. W. Boudouris, J. Horng, B. Geng, C. Girit, A. Zettl, M. F. Crommie, R. A. Segalman and S. G. Louie, et al. , Nature, 2011, 471, 617–620 CrossRef CAS PubMed.
- C. Casiraghi, S. Pisana, K. Novoselov, A. Geim and A. Ferrari, Appl. Phys. Lett., 2007, 91, 233108 CrossRef.
- A. Das, S. Pisana, B. Chakraborty, S. Piscanec, S. Saha, U. Waghmare, K. Novoselov, H. Krishnamurthy, A. Geim and A. Ferrari, et al. , Nat. Nanotechnol., 2008, 3, 210–215 CrossRef CAS PubMed.
- W.-J. Zhao, P.-H. Tan, J. Liu and A. C. Ferrari, J. Am. Chem. Soc., 2011, 133, 5941–5946 CrossRef CAS PubMed.
- A. Das, B. Chakraborty, S. Piscanec, S. Pisana, A. Sood and A. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155417 CrossRef.
- S. Pisana, M. Lazzeri, C. Casiraghi, K. S. Novoselov, A. K. Geim, A. C. Ferrari and F. Mauri, Nat. Mater., 2007, 6, 198–201 CrossRef CAS PubMed.
- J. Yan, Y. Zhang, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2007, 98, 166802 CrossRef PubMed.
- J. Yan, E. A. Henriksen, P. Kim and A. Pinczuk, Phys. Rev. Lett., 2008, 101, 136804 CrossRef PubMed.
- E. M. Ferreira, M. V. Moutinho, F. Stavale, M. Lucchese, R. B. Capaz, C. Achete and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125429 CrossRef.
- D. Yang, A. Velamakanni, G. Bozoklu, S. Park, M. Stoller, R. D. Piner, S. Stankovich, I. Jung, D. A. Field and C. A. Ventrice, et al. , Carbon, 2009, 47, 145–152 CrossRef CAS.
- L. Zhang, Z. Shi, Y. Wang, R. Yang, D. Shi and G. Zhang, Nano Res., 2011, 4, 315–321 CrossRef CAS.
- C. Thomsen and S. Reich, Phys. Rev. Lett., 2000, 85, 5214 CrossRef CAS PubMed.
- P.-H. Tan, W.-P. Han, W.-J. Zhao, Z.-H. Wu, K. Chang, H. Wang, Y.-F. Wang, N. Bonini, N. Marzari and N. Pugno, et al. , Nat. Mater., 2012, 11, 294–300 CrossRef CAS PubMed.
- J.-B. Wu, Z.-X. Hu, X. Zhang, W.-P. Han, Y. Lu, W. Shi, X.-F. Qiao, M. Ijiäs, S. Milana and W. Ji, et al. , ACS Nano, 2015, 9, 7440–7449 CrossRef CAS PubMed.
- D. Basko, New J. Phys., 2009, 11, 095011 CrossRef.
- D. Yoon, H. Moon, Y.-W. Son, J. S. Choi, B. H. Park, Y. H. Cha, Y. D. Kim and H. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125422 CrossRef.
- D. Basko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205428 CrossRef.
- Y. You, Z. Ni, T. Yu and Z. Shen, Appl. Phys. Lett., 2008, 93, 3112 Search PubMed.
- A. K. Gupta, T. J. Russin, H. R. Gutiérrez and P. C. Eklund, ACS Nano, 2008, 3, 45–52 CrossRef PubMed.
- C. Casiraghi, A. Hartschuh, H. Qian, S. Piscanec, C. Georgi, A. Fasoli, K. Novoselov, D. Basko and A. Ferrari, Nano Lett., 2009, 9, 1433–1441 CrossRef CAS PubMed.
- C. Cong, T. Yu and H. Wang, ACS Nano, 2010, 4, 3175–3180 CrossRef CAS PubMed.
- S. Ryu, J. Maultzsch, M. Y. Han, P. Kim and L. E. Brus, ACS Nano, 2011, 5, 4123–4130 CrossRef CAS PubMed.
- P. Venezuela, M. Lazzeri and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035433 CrossRef.
- M. Huang, H. Yan, T. F. Heinz and J. Hone, Nano Lett., 2010, 10, 4074–4079 CrossRef CAS PubMed.
- M. Mohr, J. Maultzsch and C. Thomsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 201409 CrossRef.
- D. Yoon, Y.-W. Son and H. Cheong, Phys. Rev. Lett., 2011, 106, 155502 CrossRef PubMed.
- T. Mohiuddin, A. Lombardo, R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. Basko, C. Galiotis and N. Marzari, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205433 CrossRef.
- Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang, Y. P. Feng and Z. X. Shen, ACS Nano, 2008, 2, 2301–2305 CrossRef CAS PubMed.
- J. E. Proctor, E. Gregoryanz, K. S. Novoselov, M. Lotya, J. N. Coleman and M. P. Halsall, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 073408 CrossRef.
- M. Huang, H. Yan, C. Chen, D. Song, T. F. Heinz and J. Hone, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 7304–7308 CrossRef CAS PubMed.
- M. Goerbig, J.-N. Fuchs, K. Kechedzhi and V. I. Falko, Phys. Rev. Lett., 2007, 99, 087402 CrossRef CAS PubMed.
- O. Kashuba and V. I. Falko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 241404 CrossRef.
- C. Faugeras, M. Amado, P. Kossacki, M. Orlita, M. Sprinkle, C. Berger, W. De Heer and M. Potemski, Phys. Rev. Lett., 2009, 103, 186803 CrossRef CAS PubMed.
- J. Yan, S. Goler, T. D. Rhone, M. Han, R. He, P. Kim, V. Pellegrini and A. Pinczuk, Phys. Rev. Lett., 2010, 105, 227401 CrossRef PubMed.
- C. Faugeras, M. Amado, P. Kossacki, M. Orlita, M. Kühne, A. Nicolet, Y. I. Latyshev and M. Potemski, Phys. Rev. Lett., 2011, 107, 036807 CrossRef CAS PubMed.
- Y. Kim, Y. Ma, A. Imambekov, N. Kalugin, A. Lombardo, A. Ferrari, J. Kono and D. Smirnov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 121403 CrossRef.
- P. Kossacki, C. Faugeras, M. Kühne, M. Orlita, A. Mahmood, E. Dujardin, R. Nair, A. Geim and M. Potemski, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205431 CrossRef.
- Y. Kim, J. Poumirol, A. Lombardo, N. Kalugin, T. Georgiou, Y. Kim, K. Novoselov, A. Ferrari, J. Kono and O. Kashuba, et al. , Phys. Rev. Lett., 2013, 110, 227402 CrossRef CAS PubMed.
- C. Qiu, X. Shen, B. Cao, C. Cong, R. Saito, J. Yu, M. S. Dresselhaus and T. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165407 CrossRef.
- C. Cong, J. Jung, B. Cao, C. Qiu, X. Shen, A. Ferreira, S. Adam and T. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235403 CrossRef.
- C. Faugeras, M. Orlita and M. Potemski, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5213.
- A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907 CrossRef CAS PubMed.
- N. Bonini, M. Lazzeri, N. Marzari and F. Mauri, Phys. Rev. Lett., 2007, 99, 176802 CrossRef PubMed.
- J.-U. Lee, D. Yoon, H. Kim, S. W. Lee and H. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 081419 CrossRef.
- S. Chen, Q. Wu, C. Mishra, J. Kang, H. Zhang, K. Cho, W. Cai, A. A. Balandin and R. S. Ruoff, Nat. Mater., 2012, 11, 203–207 CrossRef CAS PubMed.
- W. Cai, A. L. Moore, Y. Zhu, X. Li, S. Chen, L. Shi and R. S. Ruoff, Nano Lett., 2010, 10, 1645–1651 CrossRef CAS PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- Y. M. Chang, H. Kim, J. H. Lee and Y.-W. Song, Appl. Phys. Lett., 2010, 97, 211102 CrossRef.
- A. Martinez, K. Fuse and S. Yamashita, Appl. Phys. Lett., 2011, 99, 121107 CrossRef.
- M. Yi and Z. Shen, J. Mater. Chem. A, 2015, 3, 11700–11715 CAS.
- P. Blake, E. Hill, A. C. Neto, K. Novoselov, D. Jiang, R. Yang, T. Booth and A. Geim, Appl. Phys. Lett., 2007, 91, 063124 CrossRef.
- C. Casiraghi, A. Hartschuh, E. Lidorikis, H. Qian, H. Harutyunyan, T. Gokus, K. Novoselov and A. Ferrari, Nano Lett., 2007, 7, 2711–2717 CrossRef CAS PubMed.
- M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2009, 110, 132–145 CrossRef PubMed.
- J. M. Dawlaty, S. Shivaraman, J. Strait, P. George, M. Chandrashekhar, F. Rana, M. G. Spencer, D. Veksler and Y. Chen, Appl. Phys. Lett., 2008, 93, 131905 CrossRef.
- S. Latil and L. Henrard, Phys. Rev. Lett., 2006, 97, 036803 CrossRef PubMed.
- M. Aoki and H. Amawashi, Solid State Commun., 2007, 142, 123–127 CrossRef CAS.
- L. Malard, J. Nilsson, D. Elias, J. Brant, F. Plentz, E. Alves, A. C. Neto and M. Pimenta, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 201401 CrossRef.
- W.-J. Zhao, P.-H. Tan, J. Zhang and J. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 245423 CrossRef.
- M. Lazzeri, C. Attaccalite, L. Wirtz and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 081406 CrossRef.
- P.-H. Tan, C.-Y. Hu, J. Dong, W.-C. Shen and B.-F. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 214301 CrossRef.
- S. Reich and C. Thomsen, Philos. Trans. R. Soc., A, 2004, 362, 2271–2288 CrossRef CAS PubMed.
- K. Mani and R. Ramani, Phys. Status Solidi B, 1974, 61, 659–668 CrossRef CAS.
- R. J. Nemanich, G. Lucovsky and S. A. Solin, Proceedings of the International Conference on Lattice Dynamics, Flammarion, 1975.
- M. Dresselhaus and G. Dresselhaus, Adv. Phys., 1981, 30, 139–326 CrossRef CAS.
- C. Cong, T. Yu, R. Saito, G. F. Dresselhaus and M. S. Dresselhaus, ACS Nano, 2011, 5, 1600–1605 CrossRef CAS PubMed.
- R. Rao, R. Podila, R. Tsuchikawa, J. Katoch, D. Tishler, A. M. Rao and M. Ishigami, ACS Nano, 2011, 5, 1594–1599 CrossRef CAS PubMed.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Oxford University Press, 1998 Search PubMed.
- M. Mohr, J. Maultzsch, E. Dobardžić, S. Reich, I. Milošević, M. Damnjanović, A. Bosak, M. Krisch and C. Thomsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035439 CrossRef.
- S. Siebentritt, R. Pues, K.-H. Rieder and A. M. Shikin, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 7927 CrossRef CAS.
- R. Saito, A. Jorio, A. Souza Filho, G. Dresselhaus, M. Dresselhaus and M. Pimenta, Phys. Rev. Lett., 2001, 88, 027401 CrossRef PubMed.
- P.-H. Tan, L. An, L. Liu, Z. Guo, R. Czerw, D. L. Carroll, P. M. Ajayan, N. Zhang and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 245410 CrossRef.
- S. Piscanec, M. Lazzeri, F. Mauri, A. Ferrari and J. Robertson, Phys. Rev. Lett., 2004, 93, 185503 CrossRef CAS PubMed.
- R. R. Nair, W. Ren, R. Jalil, I. Riaz, V. G. Kravets, L. Britnell, P. Blake, F. Schedin, A. S. Mayorov, S. Yuan, M. I. Katsnelson, H.-M. Cheng, W. Strupinski, L. G. Bulusheva, A. V. Okotrub, I. V. Grigorieva, A. N. Grigorenko, K. S. Novoselov and A. K. Geim, Small, 2010, 6, 2877–2884 CrossRef CAS PubMed.
- I. Childres, L. A. Jauregui, J. Tian and Y. P. Chen, New J. Phys., 2011, 13, 025008 CrossRef.
- Y. Peter and M. Cardona, Fundamentals of semiconductors: physics and materials properties, Springer Science & Business Media, 2010 Search PubMed.
- I. Pócsik, M. Hundhausen, M. Koós and L. Ley, J. Non-Cryst. Solids, 1998, 227, 1083–1086 CrossRef.
- P. May, M. Lazzeri, P. Venezuela, F. Herziger, G. Callsen, J. S. Reparaz, A. Hoffmann, F. Mauri and J. Maultzsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075402 CrossRef.
- P.-H. Tan, Y. Deng and Q. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 5435 CrossRef CAS.
- Y. Kawashima and G. Katagiri, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 10053 CrossRef CAS.
- J. Jiang, R. Saito, G. G. Samsonidze, S. G. Chou, A. Jorio, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 235408 CrossRef.
- D. Basko, S. Piscanec and A. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165413 CrossRef.
- R. Vidano, D. Fischbach, L. Willis and T. Loehr, Solid State Commun., 1981, 39, 341–344 CrossRef CAS.
- D. Yoon, H. Moon, Y.-W. Son, G. Samsonidze, B. H. Park, J. B. Kim, Y. Lee and H. Cheong, Nano Lett., 2008, 8, 4270–4274 CrossRef CAS PubMed.
- S. Sahoo, R. Palai and R. Katiyar, J. Appl. Phys., 2011, 110, 044320 CrossRef.
- L. Malard, M. Guimaraes, D. Mafra and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125426 CrossRef.
- C. Cong and T. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235430 CrossRef.
- C. Cong and T. Yu, Nat. Commun., 2014, 5, 4709 CAS.
- M. Bruna and S. Borini, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125421 CrossRef.
- L. Malard, D. Elias, E. Alves and M. Pimenta, Phys. Rev. Lett., 2008, 101, 257401 CrossRef CAS PubMed.
- J. Zabel, R. R. Nair, A. Ott, T. Georgiou, A. K. Geim, K. S. Novoselov and C. Casiraghi, Nano Lett., 2012, 12, 617–621 CrossRef CAS PubMed.
- S. K. Saha, U. Waghmare, H. Krishnamurthy and A. Sood, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 165421 CrossRef.
- J.-W. Jiang, H. Tang, B.-S. Wang and Z.-B. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235421 CrossRef.
- X. Zhang, W.-P. Han, X.-F. Qiao, Q.-H. Tan, Y.-F. Wang, J. Zhang and P.-H. Tan, Carbon, 2016, 99, 118–122 CrossRef CAS.
- X. Zhang, W.-P. Han, J.-B. Wu, S. Milana, Y. Lu, Q.-Q. Li, A. Ferrari and P.-H. Tan, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115413 CrossRef.
- P.-H. Tan, J.-B. Wu, W.-P. Han, W.-J. Zhao, X. Zhang, H. Wang and Y.-F. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235404 CrossRef.
- C. H. Lui, L. M. Malard, S. Kim, G. Lantz, F. E. Laverge, R. Saito and T. F. Heinz, Nano Lett., 2012, 12, 5539–5544 CrossRef CAS PubMed.
- C. H. Lui, Z. Ye, C. Keiser, X. Xiao and R. He, Nano Lett., 2014, 14, 4615–4621 CrossRef CAS PubMed.
- X. Zhang, X.-F. Qiao, W. Shi, J.-B. Wu, D.-S. Jiang and P.-H. Tan, Chem. Soc. Rev., 2015, 44, 2757–2785 RSC.
- Y. Zhao, X. Luo, H. Li, J. Zhang, P. T. Araujo, C. K. Gan, J. Wu, H. Zhang, S. Y. Quek and M. S. Dresselhaus, et al. , Nano Lett., 2013, 13, 1007–1015 CrossRef CAS PubMed.
- X. Ling, L. Liang, S. Huang, A. A. Puretzky, D. B. Geohegan, B. G. Sumpter, J. Kong, V. Meunier and M. S. Dresselhaus, Nano Lett., 2015, 15, 4080–4088 CrossRef CAS PubMed.
- C. H. Lui, Z. Ye, C. Ji, K.-C. Chiu, C.-T. Chou, T. I. Andersen, C. Means-Shively, H. Anderson, J.-M. Wu and T. Kidd, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165403 CrossRef.
- H. Zhao, J. Wu, H. Zhong, Q. Guo, X. Wang, F. Xia, L. Yang, P.-H. Tan and H. Wang, Nano Res., 2015, 8, 3651–3661 CrossRef CAS.
- Y. Zhao, X. Luo, J. Zhang, J. Wu, X. Bai, M. Wang, J. Jia, H. Peng, Z. Liu and S. Y. Quek, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245428 CrossRef.
- X.-F. Qiao, J.-B. Wu, L. Zhou, J. Qiao, W. Shi, T. Chen, X. Zhang, J. Zhang, W. Ji and P.-H. Tan, Nanoscale, 2016, 8, 8324–8332 RSC.
- A. A. Puretzky, L. Liang, X. Li, K. Xiao, B. G. Sumpter, V. Meunier and D. B. Geohegan, ACS Nano, 2016, 10, 2736–2744 CrossRef CAS PubMed.
- E. Lorchat, G. Froehlicher and S. Berciaud, ACS Nano, 2016, 10, 2752–2760 CrossRef CAS PubMed.
- J.-W. Jiang, B.-S. Wang and H. S. Park, J. Phys.: Condens. Matter, 2016, 28, 165401 CrossRef PubMed.
- S. Huang, L. Liang, X. Ling, A. A. Puretzky, D. B. Geohegan, B. G. Sumpter, J. Kong, V. Meunier and M. S. Dresselhaus, Nano Lett., 2016, 16, 1435–1444 CrossRef CAS PubMed.
- S. Dong, A. Zhang, K. Liu, J. Ji, Y. Ye, X. Luo, X. Chen, X. Ma, Y. Jie and C. Chen, et al. , Phys. Rev. Lett., 2016, 116, 087401 CrossRef PubMed.
- X.-F. Qiao, X.-L. Li, X. Zhang, W. Shi, J.-B. Wu, T. Chen and P.-H. Tan, Appl. Phys. Lett., 2015, 106, 223102 CrossRef.
- X.-L. Li, W.-P. Han, J.-B. Wu, X.-F. Qiao, J. Zhang and P.-H. Tan, Adv. Funct. Mater., 2017, 27, 1604468 CrossRef.
- C. H. Lui, Z. Ye, C. Keiser, E. B. Barros and R. He, Appl. Phys. Lett., 2015, 106, 041904 CrossRef.
- H. Wilhelm, B. Croset and G. Medjahdi, Carbon, 2007, 45, 2356–2364 CrossRef CAS.
- T. Nguyen, J. Lee, D. Yoon and H. Cheong, Sci. Rep., 2014, 4, 4630 CrossRef PubMed.
- V. Carozo, C. Almeida, B. Fragneaud, P. Bedê, M. Moutinho, J. Ribeiro-Soares, N. Andrade, A. Souza Filho, M. Matos and B. Wang, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085401 CrossRef.
- V. Carozo, C. M. Almeida, E. H. Ferreira, L. G. Cançado, C. A. Achete and A. Jorio, Nano Lett., 2011, 11, 4527–4534 CrossRef CAS PubMed.
- E. J. Mele, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161405 CrossRef.
- R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237 CrossRef CAS PubMed.
- D. S. Lee, C. Riedl, T. Beringer, A. C. Neto, K. von Klitzing, U. Starke and J. H. Smet, Phys. Rev. Lett., 2011, 107, 216602 CrossRef PubMed.
- E. S. Morell, J. Correa, P. Vargas, M. Pacheco and Z. Barticevic, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121407 CrossRef.
- P. Moon and M. Koshino, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205404 CrossRef.
- R. Bistritzer and A. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035440 CrossRef.
- A. Luican, G. Li, A. Reina, J. Kong, R. Nair, K. S. Novoselov, A. K. Geim and E. Andrei, Phys. Rev. Lett., 2011, 106, 126802 CrossRef CAS PubMed.
- G. Trambly de Laissardière, D. Mayou and L. Magaud, Nano Lett., 2010, 10, 804–808 CrossRef PubMed.
- J. L. Dos Santos, N. Peres and A. C. Neto, Phys. Rev. Lett., 2007, 99, 256802 CrossRef PubMed.
- G. Li, A. Luican, J. L. Dos Santos, A. C. Neto, A. Reina, J. Kong and E. Andrei, Nat. Phys., 2010, 6, 109–113 CrossRef CAS.
- J. D. Sanchez-Yamagishi, T. Taychatanapat, K. Watanabe, T. Taniguchi, A. Yacoby and P. Jarillo-Herrero, Phys. Rev. Lett., 2012, 108, 076601 CrossRef PubMed.
- R. W. Havener, H. Zhuang, L. Brown, R. G. Hennig and J. Park, Nano Lett., 2012, 12, 3162–3167 CrossRef CAS PubMed.
- K. Kim, S. Coh, L. Z. Tan, W. Regan, J. M. Yuk, E. Chatterjee, M. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Phys. Rev. Lett., 2012, 108, 246103 CrossRef PubMed.
- Z. Ni, Y. Wang, T. Yu, Y. You and Z. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235403 CrossRef.
- E. S. Morell, M. Pacheco, L. Chico and L. Brey, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 125414 CrossRef.
- A. K. Gupta, Y. Tang, V. H. Crespi and P. C. Eklund, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 241406 CrossRef.
- J. T. Robinson, S. W. Schmucker, C. B. Diaconescu, J. P. Long, J. C. Culbertson, T. Ohta, A. L. Friedman and T. E. Beechem, ACS Nano, 2012, 7, 637–644 CrossRef PubMed.
- J. Campos-Delgado, G. Algara-Siller, C. Santos, U. Kaiser and J.-P. Raskin, Small, 2013, 9, 3247–3251 CAS.
- J. Coraux, T. N. Plasa, C. Busse and T. Michely, New J. Phys., 2008, 10, 043033 CrossRef.
- U. Fano, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- F. Cerdeira, T. Fjeldly and M. Cardona, Phys. Rev. B: Solid State, 1973, 8, 4734 CrossRef CAS.
- H. Lin, L. A. Wray, Y. Xia, S. Xu, S. Jia, R. J. Cava, A. Bansil and M. Z. Hasan, Nat. Mater., 2010, 9, 546–549 CrossRef CAS PubMed.
- R. Gupta, Q. Xiong, C. Adu, U. Kim and P. Eklund, Nano Lett., 2003, 3, 627–631 CrossRef CAS.
- J. Zhang, Z. Peng, A. Soni, Y. Zhao, Y. Xiong, B. Peng, J. Wang, M. S. Dresselhaus and Q. Xiong, Nano Lett., 2011, 11, 2407–2414 CrossRef CAS PubMed.
- M. Klein and M. Cardona, Top. Appl. Phys., 1975, 8, 148 CrossRef.
- D. Yoon, D. Jeong, H.-J. Lee, R. Saito, Y.-W. Son, H. C. Lee and H. Cheong, Carbon, 2013, 61, 373–378 CrossRef CAS.
- Z. Li, C. H. Lui, E. Cappelluti, L. Benfatto, K. F. Mak, G. L. Carr, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2012, 108, 156801 CrossRef PubMed.
- T.-T. Tang, Y. Zhang, C.-H. Park, B. Geng, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie and S. G. Louie, et al. , Nat. Nanotechnol., 2010, 5, 32–36 CrossRef CAS PubMed.
- J.-B. Wu, H. Wang, X.-L. Li, H. Peng and P.-H. Tan, Carbon, 2016, 110, 225–231 CrossRef CAS.
- R. He, T.-F. Chung, C. Delaney, C. Keiser, L. A. Jauregui, P. M. Shand, C. Chancey, Y. Wang, J. Bao and Y. P. Chen, Nano Lett., 2013, 13, 3594–3601 CrossRef CAS PubMed.
- Y. Y. Wang, J. Jiang, C. W. Gao, H. Y. Nan, Z. H. Ni, D. Wang, B. Zhong and G. W. Wen, J. Raman Spectrosc., 2016, 47, 668–673 CrossRef CAS.
- M.-L. Lin, T. Chen, W. Lu, Q.-H. Tan, P. Zhao, H.-T. Wang, Y. Xu and P.-H. Tan, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5219.
- A. Eckmann, A. Felten, A. Mishchenko, L. Britnell, R. Krupke, K. S. Novoselov and C. Casiraghi, Nano Lett., 2012, 12, 3925–3930 CrossRef CAS PubMed.
- Q.-Q. Li, X. Zhang, W.-P. Han, Y. Lu, W. Shi, J.-B. Wu and P.-H. Tan, Carbon, 2015, 85, 221–224 CrossRef CAS.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41 CrossRef CAS PubMed.
- Z. H. Ni, L. A. Ponomarenko, R. R. Nair, R. Yang, S. Anissimova, I. V. Grigorieva, F. Schedin, P. Blake, Z. X. Shen, E. H. Hill, K. S. Novoselov and A. K. Geim, Nano Lett., 2010, 10, 3868–3872 CrossRef CAS PubMed.
- J. Chen, W. G. Cullen, C. Jang, M. S. Fuhrer and E. D. Williams, Phys. Rev. Lett., 2009, 102, 236805 CrossRef PubMed.
- J. Lahiri, Y. Lin, P. Bozkurt, I. I. Oleynik and M. Batzill, Nat. Nanotechnol., 2010, 5, 326–329 CrossRef CAS PubMed.
- L. D. Carr and M. T. Lusk, Nat. Nanotechnol., 2010, 5, 316–317 CrossRef CAS PubMed.
- D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373–4379 CrossRef CAS PubMed.
- C. Casiraghi, A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085401 CrossRef.
- P. Venezuela, M. Lazzeri and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035433 CrossRef.
- A. Jorio, M. S. Dresselhaus, R. Saito and G. F. Dresselhaus, Raman spectrocopy in graphene-related systems, Wiley-VCH, Weinheim, Germany, 2011 Search PubMed.
- Y. Stubrov, A. Nikolenko, V. Gubanov and V. Strelchuk, Nanoscale Res. Lett., 2016, 11, 2 CrossRef PubMed.
- X. Zhang, Q.-Q. Li, W.-P. Han, Y. Lu, W. Shi, J.-B. Wu, A. S. Mikhaylushkin and P.-H. Tan, Nanoscale, 2014, 6, 7519–7525 RSC.
- L. G. Cançado, M. G. da Silva, E. H. M. Ferreira, F. Hof, K. Kampioti, K. Huang, A. Pénicaud, C. A. Achete, R. B. Capaz and A. Jorio, 2D Mater., 2017, 4, 025039 CrossRef.
- S. Mignuzzi, A. J. Pollard, N. Bonini, B. Brennan, I. S. Gilmore, M. A. Pimenta, D. Richards and D. Roy, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195411 CrossRef.
- W. Shi, X. Zhang, X.-L. Li, X.-F. Qiao, J.-B. Wu, J. Zhang and P.-H. Tan, Chin. Phys. Lett., 2016, 33, 057801 CrossRef.
- W. Shi, M.-L. Lin, Q.-H. Tan, X.-F. Qiao, J. Zhang and P.-H. Tan, 2D Mater., 2016, 3, 025016 CrossRef.
- L. Cançado, K. Takai, T. Enoki, M. Endo, Y. Kim, H. Mizusaki, A. Jorio, L. Coelho, R. Magalhaes-Paniago and M. Pimenta, Appl. Phys. Lett., 2006, 88, 163106 CrossRef.
- J. Ribeiro-Soares, M. Oliveros, C. Garin, M. David, L. Martins, C. Almeida, E. Martins-Ferreira, K. Takai, T. Enoki and R. Magalhaes-Paniago, et al. , Carbon, 2015, 95, 646–652 CrossRef CAS.
- L. Huang, Y. Huang, J. Liang, X. Wan and Y. Chen, Nano Res., 2011, 4, 675–684 CrossRef CAS.
- A. P. A. Raju, A. Lewis, B. Derby, R. J. Young, I. A. Kinloch, R. Zan and K. S. Novoselov, Adv. Funct. Mater., 2014, 24, 2865–2874 CrossRef CAS.
- M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805 CrossRef PubMed.
- P. Silvestrov and K. Efetov, Phys. Rev. Lett., 2007, 98, 016802 CrossRef CAS PubMed.
- Ç. Ö. Girit, J. C. Meyer, R. Erni, M. D. Rossell, C. Kisielowski, L. Yang, C.-H. Park, M. Crommie, M. L. Cohen and S. G. Louie, et al. , Science, 2009, 323, 1705–1708 CrossRef PubMed.
- K. A. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235–242 CrossRef CAS PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- L. Cançado, M. Pimenta, B. Neves, M. Dantas and A. Jorio, Phys. Rev. Lett., 2004, 93, 247401 CrossRef PubMed.
- P. Y. Huang, C. S. Ruiz-Vargas, A. M. van der Zande, W. S. Whitney, M. P. Levendorf, J. W. Kevek, S. Garg, J. S. Alden, C. J. Hustedt, Y. Zhu, J. Park, P. L. McEuen and D. A. Muller, Nature, 2011, 469, 389–392 CrossRef CAS PubMed.
- J. T. Robinson, M. K. Zalalutdinov, C. D. Cress, J. C. Culbertson, A. L. Friedman, A. Merrill and B. J. Landi, ACS Nano, 2017, 11, 4745–4752 CrossRef CAS PubMed.
- Y. Xu, A. Ali, K. Shehzad, N. Meng, M. Xu, Y. Zhang, X. Wang, C. Jin, H. Wang, Y. Guo, Z. Yang, B. Yu, Y. Liu, Q. He, X. Duan, X. Wang, P.-H. Tan, W. Hu, H. Lu and T. Hasan, Adv. Mater. Technol., 2017, 2, 1600241 CrossRef.
- P. Lespade, A. Marchand, M. Couzi and F. Cruege, Carbon, 1984, 22, 375–385 CrossRef CAS.
- J.-H. Zhong, J. Zhang, X. Jin, J.-Y. Liu, Q. Li, M.-H. Li, W. Cai, D.-Y. Wu, D. Zhan and B. Ren, J. Am. Chem. Soc., 2014, 136, 16609–16617 CrossRef CAS PubMed.
- O. V. Yazyev and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195420 CrossRef.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- C. Shen, G. Huang, Y. Cheng, R. Cao, F. Ding, U. Schwingenschlögl and Y. Mei, Nanoscale Res. Lett., 2012, 7, 268 CrossRef PubMed.
- A. Felten, A. Eckmann, J.-J. Pireaux, R. Krupke and C. Casiraghi, Nanotechnology, 2013, 24, 355705 CrossRef CAS PubMed.
- X. Dong, Y. Shi, Y. Zhao, D. Chen, J. Ye, Y. Yao, F. Gao, Z. Ni, T. Yu, Z. Shen, Y. Huang, P. Chen and L.-J. Li, Phys. Rev. Lett., 2009, 102, 135501 CrossRef PubMed.
- X. Hong, K. Zou, B. Wang, S.-H. Cheng and J. Zhu, Phys. Rev. Lett., 2012, 108, 226602 CrossRef CAS PubMed.
- N. Soin, S. C. Ray, S. Sarma, D. Mazumder, S. Sharma, Y.-F. Wang, W.-F. Pong, S. S. Roy and A. M. Strydom, J. Phys. Chem. C, 2017, 121, 14073–14082 CAS.
- L. Cheng, S. Jandhyala, G. Mordi, A. T. Lucero, J. Huang, A. Azcatl, R. Addou, R. M. Wallace, L. Colombo and J. Kim, ACS Appl. Mater. Interfaces, 2016, 8, 5002–5008 CAS.
- J. T. Robinson, J. S. Burgess, C. E. Junkermeier, S. C. Badescu, T. L. Reinecke, F. K. Perkins, M. K. Zalalutdniov, J. W. Baldwin, J. C. Culbertson, P. E. Sheehan and E. S. Snow, Nano Lett., 2010, 10, 3001–3005 CrossRef CAS PubMed.
- S.-H. Cheng, K. Zou, F. Okino, H. R. Gutierrez, A. Gupta, N. Shen, P. C. Eklund, J. O. Sofo and J. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205435 CrossRef.
- H. Yang, M. Chen, H. Zhou, C. Qiu, L. Hu, F. Yu, W. Chu, S. Sun and L. Sun, J. Phys. Chem. C, 2011, 115, 16844–16848 CAS.
- Y. Wang, Z. Ni, Z. Shena, H. Wang and Y. Wu, Appl. Phys. Lett., 2008, 92, 043121 CrossRef.
- Z. Ni, W. Chen, X. Fan, J. Kuo, T. Yu, A. Wee and Z. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115416 CrossRef.
- X.-L. Li, X.-F. Qiao, W.-P. Han, Y. Lu, Q.-H. Tan, X.-L. Liu and P.-H. Tan, Nanoscale, 2015, 7, 8135–8141 RSC.
- H. Starnberg, H. Brauer, L. Holleboom and H. Hughes, Phys. Rev. Lett., 1993, 70, 3111 CrossRef CAS PubMed.
- H. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. Rao, Angew. Chem., Int. Ed., 2010, 122, 4153–4156 CrossRef.
- H. Fang, S. Chuang, T. C. Chang, K. Takei, T. Takahashi and A. Javey, Nano Lett., 2012, 12, 3788–3792 CrossRef CAS PubMed.
- D. Kong, H. Wang, J. J. Cha, M. Pasta, K. J. Koski, J. Yao and Y. Cui, Nano Lett., 2013, 13, 1341–1347 CrossRef CAS PubMed.
- Q.-J. Song, Q.-H. Tan, X. Zhang, J.-B. Wu, B.-W. Sheng, Y. Wan, X.-Q. Wang, L. Dai and P.-H. Tan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 115409 CrossRef.
- B. Sipos, A. F. Kusmartseva, A. Akrap, H. Berger, L. Forró and E. Tutiš, Nat. Mater., 2008, 7, 960–965 CrossRef CAS PubMed.
- M. Ghorbani-Asl, A. Kuc, P. Miró and T. Heine, Adv. Mater., 2016, 28, 853–856 CrossRef CAS PubMed.
- K. Xu, Z. Wang, F. Wang, Y. Huang, F. Wang, L. Yin, C. Jiang and J. He, Adv. Mater., 2015, 27, 7881–7887 CrossRef CAS PubMed.
- Y. Zhou, Z. Wang, P. Yang, X. Zu, L. Yang, X. Sun and F. Gao, ACS Nano, 2012, 6, 9727–9736 CrossRef CAS PubMed.
- M. M. Ugeda, A. J. Bradley, Y. Zhang, S. Onishi, Y. Chen, W. Ruan, C. Ojeda-Aristizabal, H. Ryu, M. T. Edmonds and H.-Z. Tsai, et al. , Nat. Phys., 2016, 12, 92–97 CrossRef CAS.
- H. Li, G. Lu, Y. Wang, Z. Yin, C. Cong, Q. He, L. Wang, F. Ding, T. Yu and H. Zhang, Small, 2013, 9, 1974–1981 CrossRef CAS PubMed.
- C. Li, O. van t Erve, J. Robinson, Y. Liu, L. Li and B. Jonker, Nat. Nanotechnol., 2014, 9, 218–224 CrossRef CAS PubMed.
- Y. Min, J. W. Roh, H. Yang, M. Park, S. I. Kim, S. Hwang, S. M. Lee, K. H. Lee and U. Jeong, Adv. Mater., 2013, 25, 1425–1429 CrossRef CAS PubMed.
- A. C. Ferrari, F. Bonaccorso, V. Fal'Ko, K. S. Novoselov, S. Roche, P. Bøggild, S. Borini, F. H. Koppens, V. Palermo and N. Pugno, et al. , Nanoscale, 2015, 7, 4598–4810 RSC.
- Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen and F. Wang, Nature, 2009, 459, 820–823 CrossRef CAS PubMed.
- K. F. Mak, C. H. Lui, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2009, 102, 256405 CrossRef PubMed.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- K. Novoselov, E. McCann, S. Morozov, V. I. Fal ko, M. Katsnelson, U. Zeitler, D. Jiang, F. Schedin and A. Geim, Nat. Phys., 2006, 2, 177–180 CrossRef.
- D. Yoon, Y.-W. Son and H. Cheong, Nano Lett., 2011, 11, 3227–3231 CrossRef CAS PubMed.
- Y. Su, H. Wei, R. Gao, Z. Yang, J. Zhang, Z. Zhong and Y. Zhang, Carbon, 2012, 50, 2804–2809 CrossRef CAS.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- J. W. Suk, R. D. Piner, J. An and R. S. Ruoff, ACS Nano, 2010, 4, 6557–6564 CrossRef CAS PubMed.
- N. Bendiab, J. Renard, C. Schwarz, L. Djevahirdjian, V. Bouchiat, J. Coraux and L. Marty, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5267.
- H. Malekpour and A. Balandin, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5230.
- X. Wang, X. Li, L. Zhang, Y. Yoon, P. K. Weber, H. Wang, J. Guo and H. Dai, Science, 2009, 324, 768–771 CrossRef CAS PubMed.
- B. Guo, L. Fang, B. Zhang and J. R. Gong, Insci. J., 2011, 1, 80–89 CrossRef CAS.
- H. Liu, Y. Liu and D. Zhu, J. Mater. Chem., 2011, 21, 3335–3345 RSC.
- J. E. Lee, G. Ahn, J. Shim, Y. S. Lee and S. Ryu, Nat. Commun., 2012, 3, 1024 CrossRef PubMed.
- N. Jung, B. Kim, A. C. Crowther, N. Kim, C. Nuckolls and L. Brus, ACS Nano, 2011, 5, 5708–5716 CrossRef CAS PubMed.
- N. Jung, N. Kim, S. Jockusch, N. J. Turro, P. Kim and L. Brus, Nano Lett., 2009, 9, 4133–4137 CrossRef CAS PubMed.
- B. Das, R. Voggu, C. S. Rout and C. Rao, Chem. Commun., 2008, 5155–5157 RSC.
- R. Voggu, B. Das, C. S. Rout and C. N. R. Rao, J. Phys.: Condens. Matter, 2008, 20, 472204 CrossRef.
- A. C. Crowther, A. Ghassaei, N. Jung and L. E. Brus, ACS Nano, 2012, 6, 1865–1875 CrossRef CAS PubMed.
- D. Zhan, L. Sun, Z. H. Ni, L. Liu, X. F. Fan, Y. Wang, T. Yu, Y. M. Lam, W. Huang and Z. X. Shen, Adv. Funct. Mater., 2010, 20, 3504–3509 CrossRef CAS.
- J. W. McClure, Phys. Rev., 1956, 104, 666–671 CrossRef CAS.
- A. A. Bykov, A. Kalagin and A. K. Bakarov, JETP Lett., 2005, 81, 523–526 CrossRef CAS.
- O. Kashuba and V. I. Fal'ko, New J. Phys., 2012, 14, 105016 CrossRef.
- J. Yan, T. Villarson, E. A. Henriksen, P. Kim and A. Pinczuk, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 241417 CrossRef.
- M. Lazzeri, S. Piscanec, F. Mauri, A. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155426 CrossRef.
- C. Faugeras, P. Kossacki, D. M. Basko, M. Amado, M. Sprinkle, C. Berger, W. A. de Heer and M. Potemski, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155436 CrossRef.
- F. Guinea, M. Katsnelson and A. Geim, Nat. Phys., 2010, 6, 30–33 CrossRef CAS.
- N. Ferralis, J. Mater. Sci., 2010, 45, 5135–5149 CrossRef CAS.
- J.-U. Lee, D. Yoon and H. Cheong, Nano Lett., 2012, 12, 4444–4448 CrossRef CAS PubMed.
- S. Berciaud, S. Ryu, L. E. Brus and T. F. Heinz, Nano Lett., 2009, 9, 346–352 CrossRef CAS PubMed.
- R. Loudon, Adv. Phys., 1964, 13, 423–482 CrossRef CAS.
- S.-M. Choi, S.-H. Jhi and Y.-W. Son, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 081407 CrossRef.
- M. S. Bronsgeest, N. Bendiab, S. Mathur, A. Kimouche, H. T. Johnson, J. Coraux and P. Pochet, Nano Lett., 2015, 15, 5098–5104 CrossRef CAS PubMed.
- S. R. Na, X. Wang, R. D. Piner, R. Huang, C. G. Willson and K. M. Liechti, ACS Nano, 2016, 10, 9616–9625 CrossRef CAS PubMed.
- C. Bousige, F. Balima, D. Machon, G. S. Pinheiro, A. Torres-Dias, J. Nicolle, D. Kalita, N. Bendiab, L. Marty, V. Bouchiat, G. Montagnac, A. G. Souza Filho, P. Poncharal and A. San-Miguel, Nano Lett., 2017, 17, 21–27 CrossRef CAS PubMed.
- J. H. Lee, J. Y. Tan, C.-T. Toh, S. P. Koenig, V. Fedorov, A. H. Castro Neto and B. Özyilmaz, Nano Lett., 2014, 14, 2677–2680 CrossRef CAS PubMed.
- P.-H. Tan, Y. Deng, Q. Zhao and W. Cheng, Appl. Phys. Lett., 1999, 74, 1818 CrossRef CAS.
- I. Calizo, A. Balandin, W. Bao, F. Miao and C. Lau, Nano Lett., 2007, 7, 2645–2649 CrossRef CAS PubMed.
- I. Calizo, F. Miao, W. Bao, C. Lau and A. Balandin, Appl. Phys. Lett., 2007, 91, 071913 CrossRef.
- C. Faugeras, B. Faugeras, M. Orlita, M. Potemski, R. R. Nair and A. Geim, ACS Nano, 2010, 4, 1889–1892 CrossRef CAS PubMed.
- M. Freitag, M. Steiner, Y. Martin, V. Perebeinos, Z. Chen, J. C. Tsang and P. Avouris, Nano Lett., 2009, 9, 1883–1888 CrossRef CAS PubMed.
- Z. Ni, H. Wang, J. Kasim, H. Fan, T. Yu, Y. Wu, Y. Feng and Z. Shen, Nano Lett., 2007, 7, 2758–2763 CrossRef CAS PubMed.
- T. Yu, Z. Ni, C. Du, Y. You, Y. Wang and Z. Shen, J. Phys. Chem. C, 2008, 112, 12602–12605 CAS.
- X. Li, C. W. Magnuson, A. Venugopal, J. An, J. W. Suk, B. Han, M. D. Borysiak, W. Cai, A. Velamakanni and Y. Zhu, et al. , Nano Lett., 2010, 10, 4328–4334 CrossRef CAS PubMed.
- K.-D. Park, M. B. Raschke, J. M. Atkin, Y. H. Lee and M. S. Jeong, Adv. Mater., 2017, 29, 1603601 CrossRef PubMed.
- D. Graf, F. Molitor, K. Ensslin, C. Stampfer, A. Jungen, C. Hierold and L. Wirtz, Solid State Commun., 2007, 143, 44–46 CrossRef CAS.
- S. Chen, Q. Li, Q. Zhang, Y. Qu, H. Ji, R. S. Ruoff and W. Cai, Nanotechnology, 2012, 23, 365701 CrossRef PubMed.
- C. Stampfer, F. Molitor, D. Graf, K. Ensslin, A. Jungen, C. Hierold and L. Wirtz, Appl. Phys. Lett., 2007, 91, 241907 CrossRef.
- J. Campos, H. Miranda, C. Rabelo, E. Sandoz-Rosado, S. Pandley, J. Riikonen, A. Cano-Marquez and A. Jorio, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5225.
- Q. Li, H. Chou, J. Zhong, J. Liu, A. Dolocan, J. Zhang, Y. Zhou, R. S. Ruoff, S. Chen and W. Cai, et al. , Nano Lett., 2013, 13, 486–490 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- X. Li, W. Cai, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4268–4272 CrossRef CAS PubMed.
- H. Li, Z. Kang, Y. Liu and S. Lee, J. Mater. Chem., 2012, 22, 24230–24253 RSC.
- Y. Sun, B. Zhou, Y. Lin, W. Wang, K. A. S. Fernando, P. Pathak, M. J. Meziani, B. A. Harruff, X. Wang and H. Wang, et al. , J. Am. Chem. Soc., 2006, 128, 7756–7757 CrossRef CAS PubMed.
- H. Ming, Z. Ma, Y. Liu, K. Pan, H. Yu, F. Wang and Z. Kang, Dalton Trans., 2012, 41, 9526–9531 RSC.
- Y. Dong, N. Zhou, X. Lin, L. Jianpeng, Y. Chi and G. Chen, Chem. Mater., 2010, 22, 5895–5899 CrossRef CAS.
- L. Zheng, Y. Chi, Y. Dong, J. Lin and B. Wang, J. Am. Chem. Soc., 2009, 131, 4564–4565 CrossRef CAS PubMed.
- L. Cao, X. Wang, M. J. Meziani, F. Lu, H. Wang, P. G. Luo, Y. Lin, A. H. Barbara, L. M. Veca and D. Murray, et al. , J. Am. Chem. Soc., 2007, 129, 11318–11319 CrossRef CAS PubMed.
- Y. Li, Y. Hu, Y. Zhao, G. Shi, L. Deng, Y. Hou and L. Qu, Adv. Mater., 2011, 23, 776–780 CrossRef CAS PubMed.
- H. X. Zhao, L. Q. Liu, Z. De Liu, Y. Wang, X. J. Zhao and C. Z. Huang, Chem. Commun., 2011, 47, 2604–2606 RSC.
- L. Cao, S. Sahu, P. Anilkumar, C. E. Bunker, J. Xu, K. A. S. Fernando, P. Wang, E. A. Guliants, K. N. Tackett and Y. Sun, J. Am. Chem. Soc., 2011, 133, 4754–4757 CrossRef CAS PubMed.
- V. Georgakilas, J. A. Perman, J. Tucek and R. Zboril, Chem. Rev., 2015, 115, 4744–4822 CrossRef CAS PubMed.
- L. A. Ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. Hill, K. S. Novoselov and A. K. Geim, Science, 2008, 320, 356–358 CrossRef CAS PubMed.
- X. Yan, X. Cui, B. Li and L. Li, Nano Lett., 2010, 10, 1869–1873 CrossRef CAS PubMed.
- S. Neubeck, L. A. Ponomarenko, F. Freitag, A. J. M. Giesbers, U. Zeitler, S. V. Morozov, P. Blake, A. K. Geim and K. S. Novoselov, Small, 2010, 6, 1469–1473 CrossRef CAS PubMed.
- L. Li and X. Yan, J. Phys. Chem. Lett., 2010, 1, 2572–2576 CrossRef CAS.
- K. Ritter and J. W. Lyding, Nat. Mater., 2009, 8, 235–242 CrossRef CAS PubMed.
- J. Peng, W. Gao, B. K. Gupta, Z. Liu, R. Romero-Aburto, L. Ge, L. Song, L. B. Alemany, X. Zhan, G. Gao, S. A. Vithayathil, B. A. Kaipparettu, A. A. Marti, T. Hayashi, J.-J. Zhu and P. M. Ajayan, Nano Lett., 2012, 12, 844–849 CrossRef CAS PubMed.
- H. Li, X. He, Z. Kang, H. Huang, Y. Liu, J. Liu, S. Lian, C. H. A. Tsang, X. Yang and S. Lee, Angew. Chem., Int. Ed., 2010, 49, 4430–4434 CrossRef CAS PubMed.
- S. Hu, K. Niu, J. Sun, J. Yang, N. Zhao and X. Du, J. Mater. Chem., 2009, 19, 484–488 RSC.
- Z. Yang, M. Xu, Y. Liu, F. He, F. Gao, Y. Su, H. Wei and Y. Zhang, Nanoscale, 2014, 6, 1890–1895 RSC.
- Y. Fan, H. Cheng, C. Zhou, X. Xie, Y. Liu, L. Dai, J. Zhang and L. Qu, Nanoscale, 2012, 4, 1776–1781 RSC.
- Y. Wang and A. Hu, J. Mater. Chem. C, 2014, 2, 6921–6939 RSC.
- F. Cervantes-Sodi, G. Csanyi, S. Piscanec and A. Ferrari, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165427 CrossRef.
- J. Campos-Delgado, J. M. Romo-Herrera, X. Jia, D. A. Cullen, H. Muramatsu, Y. A. Kim, T. Hayashi, Z. Ren, D. J. Smith and Y. Okuno, et al. , Nano Lett., 2008, 8, 2773–2778 CrossRef CAS PubMed.
- A. Narita, I. A. Verzhbitskiy, W. Frederickx, K. S. Mali, S. A. Jensen, M. R. Hansen, M. Bonn, S. De Feyter, C. Casiraghi and X. Feng, et al. , ACS Nano, 2014, 8, 11622–11630 CrossRef CAS PubMed.
- S. Osella, A. Narita, M. G. Schwab, Y. Hernandez, X. Feng, K. Müllen and D. Beljonne, ACS Nano, 2012, 6, 5539–5548 CrossRef CAS PubMed.
- R. Saito, M. Furukawa, G. Dresselhaus and M. Dresselhaus, J. Phys.: Condens. Matter, 2010, 22, 334203 CrossRef CAS PubMed.
- C. Castiglioni, M. Tommasini and G. Zerbi, Philos. Trans. R. Soc., A, 2004, 362, 2425–2459 CrossRef CAS PubMed.
- F. Varchon, R. Feng, J. Hass, X. Li, B. N. Nguyen, C. Naud, P. Mallet, J.-Y. Veuillen, C. Berger and E. H. Conrad, et al. , Phys. Rev. Lett., 2007, 99, 126805 CrossRef CAS PubMed.
- S. Zhou, G.-H. Gweon, A. Fedorov, P. First, W. De Heer, D.-H. Lee, F. Guinea, A. C. Neto and A. Lanzara, Nat. Mater., 2007, 6, 770–775 CrossRef CAS PubMed.
- J. Robinson, X. Weng, K. Trumbull, R. Cavalero, M. Wetherington, E. Frantz, M. LaBella, Z. Hughes, M. Fanton and D. Snyder, ACS Nano, 2009, 4, 153–158 CrossRef PubMed.
- J. Röhrl, M. Hundhausen, K. Emtsev, T. Seyller, R. Graupner and L. Ley, Appl. Phys. Lett., 2008, 92, 201918 CrossRef.
- N. Ferralis, R. Maboudian and C. Carraro, Phys. Rev. Lett., 2008, 101, 156801 CrossRef PubMed.
- N. Mounet and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205214 CrossRef.
- G. A. Slack and S. Bartram, J. Appl. Phys., 1975, 46, 89–98 CrossRef CAS.
- J. Hass, F. Varchon, J. E. Millán-Otoya, M. Sprinkle, N. Sharma, W. A. de Heer, C. Berger, P. N. First, L. Magaud and E. H. Conrad, Phys. Rev. Lett., 2008, 100, 125504 CrossRef CAS PubMed.
- J. Campos-Delgado, L. G. Cançado, C. A. Achete, A. Jorio and J.-P. Raskin, Nano Res., 2013, 6, 269–274 CrossRef CAS.
- H. Zhao, Y.-C. Lin, C.-H. Yeh, H. Tian, Y.-C. Chen, D. Xie, Y. Yang, K. Suenaga, T.-L. Ren and P.-W. Chiu, ACS Nano, 2014, 8, 10766–10773 CrossRef CAS PubMed.
- L. Gomez De Arco, Y. Zhang, C. W. Schlenker, K. Ryu, M. E. Thompson and C. Zhou, ACS Nano, 2010, 4, 2865–2873 CrossRef CAS PubMed.
- S. Bae, H. Kim, Y. Lee, X. Xu, J.-S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim and Y. I. Song, et al. , Nat. Nanotechnol., 2010, 5, 574–578 CrossRef CAS PubMed.
- J. Xue, J. Sanchez-Yamagishi, D. Bulmash, P. Jacquod, A. Deshpande, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero and B. J. LeRoy, Nat. Mater., 2011, 10, 282–285 CrossRef CAS PubMed.
- G. Wang, Y. Kim, M. Choe, T.-W. Kim and T. Lee, Adv. Mater., 2011, 23, 755–760 CrossRef CAS PubMed.
- A. Jorio and L. G. Cançado, Solid State Commun., 2013, 175, 3–12 CrossRef.
- V. Popov, J. Raman Spectrosc., 2017 DOI:10.1002/jrs.5189.
- M. P. Levendorf, C.-J. Kim, L. Brown, P. Y. Huang, R. W. Havener, D. A. Muller and J. Park, Nature, 2012, 488, 627–632 CrossRef CAS PubMed.
- Z. Liu, L. Ma, G. Shi, W. Zhou, Y. Gong, S. Lei, X. Yang, J. Zhang, J. Yu, K. P. Hackenberg, A. Babakhani, J.-C. Idrobo, R. Vajtai, R. Vajtai and P. M. Ajayan, Nat. Nanotechnol., 2013, 8, 119–124 CrossRef CAS PubMed.
- H. Fang, C. Battaglia, C. Carraro, S. Nemsak, B. Ozdol, J. S. Kang, H. A. Bechtel, S. B. Desai, F. Kronast, A. A. Unal, G. Conti, C. Conlon, G. K. Palsson, M. C. Martin, A. M. Minor, C. S. Fadley, E. Yablonovitch, R. Maboudian and A. Javey, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6198–6202 CrossRef CAS PubMed.
- Y. Gong, S. Lei, G. Ye, B. Li, Y. He, K. Keyshar, X. Zhang, Q. Wang, J. Lou, Z. Liu, R. Vajtai, W. Zhou and P. M. Ajayan, Nano Lett., 2015, 15, 6135–6141 CrossRef CAS PubMed.
- S. Latini, K. T. Winther, T. Olsen and K. S. Thygesen, Nano Lett., 2017, 17, 938–945 CrossRef CAS PubMed.
- S. Bertolazzi, D. Krasnozhon and A. Kis, ACS Nano, 2013, 7, 3246–3252 CrossRef CAS PubMed.
- C. H. Lui, Z. Ye, C. Ji, K.-C. Chiu, C.-T. Chou, T. I. Andersen, C. Means-Shively, H. Anderson, J.-M. Wu, T. Kidd, Y.-H. Lee and R. He, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165403 CrossRef.
- D. A. Dikin, S. Stankovich, E. J. Zimney, R. D. Piner, G. H. B. Dommett, G. Evmenenko, S. T. Nguyen and R. S. Ruoff, Nature, 2007, 448, 457–460 CrossRef CAS PubMed.
- I. K. Moon, J. Lee, R. S. Ruoff and H. Lee, Nat. Commun., 2010, 1, 73 Search PubMed.
- X. Huang, S. Li, Y. Huang, S. Wu, X. Zhou, S. Li, C. L. Gan, F. Boey, C. A. Mirkin and H. Zhang, Nat. Commun., 2011, 2, 292 CrossRef PubMed.
- X. Huang, S. Li, S. Wu, Y. Huang, F. Boey, C. L. Gan and H. Zhang, Adv. Mater., 2012, 24, 979–983 CrossRef CAS PubMed.
- D. R. Dreyer, S. Park, C. W. Bielawski and R. S. Ruoff, Chem. Soc. Rev., 2010, 39, 228–240 RSC.
- Y. Zhang, L. Guo, H. Xia, Q. Chen, J. Feng and H. Sun, Adv. Opt. Mater., 2014, 2, 10–28 CrossRef.
- S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565 CrossRef CAS.
- Y. Zhu, S. Murali, M. D. Stoller, A. Velamakanni, R. D. Piner and R. S. Ruoff, Carbon, 2010, 48, 2118–2122 CrossRef CAS.
- S. Pei and H. Cheng, Carbon, 2012, 50, 3210–3228 CrossRef CAS.
- S. Eigler, S. Grimm, M. Enzelbergerheim, P. Muller and A. Hirsch, Chem. Commun., 2013, 49, 7391–7393 RSC.
- R. Larciprete, S. Fabris, T. Sun, P. Lacovig, A. Baraldi and S. Lizzit, J. Am. Chem. Soc., 2011, 133, 17315–17321 CrossRef CAS PubMed.
- I. K. Moon, J. Lee and H. Lee, Chem. Commun., 2011, 47, 9681–9683 RSC.
- R. Trusovas, K. Ratautas, G. Račiukaitis, J. Barkauskas, I. Stankevičiené, G. Niaura and R. Mažeikiené, Carbon, 2013, 52, 574–582 CrossRef CAS.
- G. K. Ramesha and S. Sampath, J. Phys. Chem. C, 2009, 113, 7985–7989 CAS.
- S. J. An, Y. Zhu, S. H. Lee, M. D. Stoller, T. Emilsson, S. Park, A. Velamakanni, J. An and R. S. Ruoff, J. Phys. Chem. Lett., 2010, 1, 1259–1263 CrossRef CAS.
- T. V. Cuong, V. H. Pham, Q. T. Tran, S. H. Hahn, J. S. Chung, E. W. Shin and E. J. Kim, Mater. Lett., 2010, 64, 399–401 CrossRef CAS.
- S. Stankovich, R. D. Piner, X. Chen, N. Wu, S. T. Nguyen and R. S. Ruoff, J. Mater. Chem., 2006, 16, 155–158 RSC.
- P. Cui, J. Lee, E. Hwang and H. Lee, Chem. Commun., 2011, 47, 12370–12372 RSC.
- J. Shen, Y. Hu, M. Shi, X. Lu, C. Qin, C. Li and M. Ye, Chem. Mater., 2009, 21, 3514–3520 CrossRef CAS.
- T. Kuilla, S. Bhadra, D. Yao, N. H. Kim, S. Bose and J. H. Lee, Prog. Polym. Sci., 2010, 35, 1350–1375 CrossRef CAS.
- W.-L. Song, M.-S. Cao, M.-M. Lu, S. Bi, C.-Y. Wang, J. Liu, J. Yuan and L.-Z. Fan, Carbon, 2014, 66, 67–76 CrossRef CAS.
- Y.-B. Luo, J.-S. Cheng, Q. Ma, Y.-Q. Feng and J.-H. Li, Anal. Methods, 2011, 3, 92–98 RSC.
- Y.-M. Lin, A. Valdes-Garcia, S.-J. Han, D. B. Farmer, I. Meric, Y. Sun, Y. Wu, C. Dimitrakopoulos, A. Grill and P. Avouris, et al. , Science, 2011, 332, 1294–1297 CrossRef CAS PubMed.
- F. Xia, T. Mueller, Y.-M. Lin, A. Valdes-Garcia and P. Avouris, Nat. Nanotechnol., 2009, 4, 839–843 CrossRef CAS PubMed.
- T. Mueller, F. Xia and P. Avouris, Nat. Photonics, 2010, 4, 297–301 CrossRef CAS.
- H. Choi, J. S. Choi, J.-S. Kim, J.-H. Choe, K. H. Chung, J.-W. Shin, J. T. Kim, D.-H. Youn, K.-C. Kim and J.-I. Lee, et al. , Small, 2014, 10, 3685–3691 CrossRef CAS PubMed.
- W. Li, X. Geng, Y. Guo, J. Rong, Y. Gong, L. Wu, X. Zhang, P. Li, J. Xu and G. Cheng, et al. , ACS Nano, 2011, 5, 6955–6961 CrossRef CAS PubMed.
- Y.-M. Lin, K. A. Jenkins, A. Valdes-Garcia, J. P. Small, D. B. Farmer and P. Avouris, Nano Lett., 2009, 9, 422–426 CrossRef CAS PubMed.
- H. Wang, T. Taychatanapat, A. Hsu, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero and T. Palacios, IEEE Electron Device Lett., 2011, 32, 1209–1211 CrossRef CAS.
- K. Share, A. P. Cohn, R. E. Carter and C. L. Pint, Nanoscale, 2016, 8, 16435–16439 RSC.
- D. P. Dubal, O. Ayyad, V. Ruiz and P. Gomez-Romero, Chem. Soc. Rev., 2015, 44, 1777–1790 RSC.
- Y. Wang, Y. Song and Y. Xia, Chem. Soc. Rev., 2016, 45, 5925–5950 RSC.
- M.-S. Balogun, Y. Luo, W. Qiu, P. Liu and Y. Tong, Carbon, 2016, 98, 162–178 CrossRef CAS.
- X. Cong, C. Cheng, Y. Liao, Y. Ye, C. Dong, H. Sun, X. Ji, W. Zhang, P. Fang and L. Miao, et al. , J. Phys. Chem. C, 2015, 119, 20864–20870 CAS.
- W. Zhang, C. Cheng, P. Fang, B. Tang, J. Zhang, G. Huang, X. Cong, B. Zhang, X. Ji and L. Miao, Phys. Chem. Chem. Phys., 2016, 18, 4376–4384 RSC.
- H. Wan, J. Liu, Y. Ruan, L. Lv, L. Peng, X. Ji, L. Miao and J. Jiang, ACS Appl. Mater. Interfaces, 2015, 7, 15840–15847 CAS.
- L. J. Hardwick, P. W. Ruch, M. Hahn, W. Scheifele, R. Kötz and P. Novák, J. Phys. Chem. Solids, 2008, 69, 1232–1237 CrossRef CAS.
- A. P. Cohn, K. Share, R. Carter, L. Oakes and C. L. Pint, Nano Lett., 2015, 16, 543–548 CrossRef PubMed.
- R. Baddour-Hadjean and J.-P. Pereira-Ramos, Chem. Rev., 2009, 110, 1278–1319 CrossRef PubMed.
- M. Inaba, H. Yoshida, Z. Ogumi, T. Abe, Y. Mizutani and M. Asano, J. Electrochem. Soc., 1995, 142, 20–26 CrossRef CAS.
- Q. Shi, K. Dokko and D. A. Scherson, J. Phys. Chem. B, 2004, 108, 4789–4793 CrossRef CAS.
- J. C. Chacon-Torres, L. Wirtz and T. Pichler, ACS Nano, 2013, 7, 9249–9259 CrossRef CAS PubMed.
- F. Xiong, H. Wang, X. Liu, J. Sun, M. Brongersma, E. Pop and Y. Cui, Nano Lett., 2015, 15, 6777–6784 CrossRef CAS PubMed.
- Y. Wang, S. W. Tong, X. F. Xu, B. Özyilmaz and K. P. Loh, Adv. Mater., 2011, 23, 1514–1518 CrossRef CAS PubMed.
- Z. Yin, S. Sun, T. Salim, S. Wu, X. Huang, Q. He, Y. M. Lam and H. Zhang, ACS Nano, 2010, 4, 5263–5268 CrossRef CAS PubMed.
- S. Li, Y. Luo, W. Lv, W. Yu, S. Wu, P. Hou, Q. Yang, Q. Meng, C. Liu and H.-M. Cheng, Adv. Energy Mater., 2011, 1, 486–490 CrossRef CAS.
- J. Liang, H. Bi, D. Wan and F. Huang, Adv. Funct. Mater., 2012, 22, 1267–1271 CrossRef CAS.
- D. Zhang, F. Xie, P. Lin and W. C. Choy, ACS Nano, 2013, 7, 1740–1747 CrossRef CAS PubMed.
- Z. Wen, S. Cui, H. Pu, S. Mao, K. Yu, X. Feng and J. Chen, Adv. Mater., 2011, 23, 5445–5450 CrossRef CAS PubMed.
- V. Gupta, N. Chaudhary, R. Srivastava, G. D. Sharma, R. Bhardwaj and S. Chand, J. Am. Chem. Soc., 2011, 133, 9960–9963 CrossRef CAS PubMed.
- Y. Lin, X. Li, D. Xie, T. Feng, Y. Chen, R. Song, H. Tian, T. Ren, M. Zhong and K. Wang, et al. , Energy Environ. Sci., 2013, 6, 108–115 CAS.
- W. Zhou, J. Zhu, C. Cheng, J. Liu, H. Yang, C. Cong, C. Guan, X. Jia, H. J. Fan and Q. Yan, et al. , Energy Environ. Sci., 2011, 4, 4954–4961 CAS.
- J. Liu, Y. Xue, Y. Gao, D. Yu, M. Durstock and L. Dai, Adv. Mater., 2012, 24, 2228–2233 CrossRef CAS PubMed.
- Z. Yin, J. Zhu, Q. He, X. Cao, C. Tan, H. Chen, Q. Yan and H. Zhang, Adv. Energy Mater., 2014, 4, 1–19 Search PubMed.
- J. T. Lim, H. Lee, H. Cho, B.-H. Kwon, N. S. Cho, B. K. Lee, J. Park, J. Kim, J.-H. Han and J.-H. Yang, et al. , Sci. Rep., 2015, 5, 17748 CrossRef PubMed.
- S. S.-Y. Juang, C.-Y. Liu, C.-W. Huang, J. H.-H. Liao, T. Wang, Y. Yu and H.-C. Chui, Appl. Surf. Sci., 2015, 331, 472–476 CrossRef CAS.
- A. Reserbat-Plantey, L. Marty, O. Arcizet, N. Bendiab and V. Bouchiat, Nat. Nanotechnol., 2012, 7, 151–155 CrossRef CAS PubMed.
- A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef.
- R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. Peres and A. K. Geim, Science, 2008, 320, 1308 CrossRef CAS PubMed.
- T. J. Booth, P. Blake, R. R. Nair, D. Jiang, E. W. Hill, U. Bangert, A. Bleloch, M. Gass, K. S. Novoselov and M. I. Katsnelson, et al. , Nano Lett., 2008, 8, 2442–2446 CrossRef CAS PubMed.
- J. S. Bunch, A. M. Van Der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craighead and P. L. McEuen, Science, 2007, 315, 490–493 CrossRef CAS PubMed.
- B. Lassagne, D. Garcia-Sanchez, A. Aguasca and A. Bachtold, Nano Lett., 2008, 8, 3735–3738 CrossRef CAS PubMed.
- K. Jensen, K. Kim and A. Zettl, Nat. Nanotechnol., 2008, 3, 533–537 CrossRef CAS PubMed.
- H. Peng, C. Chang, S. Aloni, T. Yuzvinsky and A. Zettl, Phys. Rev. Lett., 2006, 97, 087203 CrossRef CAS PubMed.
- A. D. O. Connell, M. Hofheinz, M. Ansmann, R. C. Bialczak, M. Lenander, E. Lucero, M. Neeley, D. Sank, H. Wang and M. Weides, et al. , Nature, 2010, 464, 697–703 CrossRef PubMed.
- O. Frank, G. Tsoukleri, J. Parthenios, K. Papagelis, I. Riaz, R. Jalil, K. S. Novoselov and C. Galiotis, ACS Nano, 2010, 4, 3131–3138 CrossRef CAS PubMed.
- O. Frank, G. Tsoukleri, I. Riaz, K. Papagelis, J. Parthenios, A. C. Ferrari, A. K. Geim, K. S. Novoselov and C. Galiotis, Nat. Commun., 2011, 2, 255 CrossRef.
- H. Hosaka, K. Itao and S. Kuroda, Sens. Actuators, A, 1995, 49, 87–95 CrossRef CAS.
- C.-J. Shih, Q. H. Wang, Y. Son, Z. Jin, D. Blankschtein and M. S. Strano, ACS Nano, 2014, 8, 5790–5798 CrossRef CAS PubMed.
- K. Roy, M. Padmanabhan, S. Goswami, T. P. Sai, G. Ramalingam, S. Raghavan and A. Ghosh, Nat. Nanotechnol., 2013, 8, 826–830 CrossRef CAS PubMed.
- G. W. Shim, K. Yoo, S.-B. Seo, J. Shin, D. Y. Jung, I.-S. Kang, C. W. Ahn, B. J. Cho and S.-Y. Choi, ACS Nano, 2014, 8, 6655–6662 CrossRef CAS PubMed.
- P. T. K. Loan, W. Zhang, C.-T. Lin, K.-H. Wei, L.-J. Li and C.-H. Chen, Adv. Mater., 2014, 26, 4838–4844 CrossRef CAS PubMed.
- L. Ju, J. Velasco Jr, E. Huang, S. Kahn, C. Nosiglia, H.-Z. Tsai, W. Yang, T. Taniguchi, K. Watanabe and Y. Zhang, et al. , Nat. Nanotechnol., 2014, 9, 348–352 CrossRef CAS PubMed.
- Y. Liu, N. O. Weiss, X. Duan, H. C. Cheng, Y. Huang and X. Duan, Nat. Rev. Mater., 2016, 1, 16042 CrossRef CAS.
- H. Cheng, G. Wang, D. Li, Q. He, A. Yin, Y. Liu, H. Wu, M. Ding, Y. Huang and X. Duan, Nano Lett., 2015, 16, 367–373 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2018 |