First-principles study of a MXene terahertz detector†
Y. I.
Jhon
,
M.
Seo
and
Y. M.
Jhon
 *
*
Sensor System Research Center, Korea Institute of Science and Technology, Seoul, 02792, Republic of Korea. E-mail: ymjhon@kist.re.kr
First published on 20th November 2017
Abstract
2D transition metal carbides, nitrides, and carbonitrides called MXenes have attracted increasing attention due to their outstanding properties in many fields. By performing systematic density functional theory calculations, here we show that MXenes can serve as excellent terahertz detecting materials. Giant optical absorption and extinction coefficients are observed in the terahertz range in the most popular MXene, namely, Ti3C2, which is regardless of the stacking degree. Various other optical properties have been investigated as well in the terahertz range for in-depth understanding of its optical response. We find that the thermoelectric figure of merit (ZT) of stacked Ti3C2 flakes is comparable to that of carbon nanotube films. Based on excellent terahertz absorption and decent thermoelectric efficiency in MXenes, we finally suggest the promise of MXenes in terahertz detection applications, which includes terahertz bolometers and photothermoelectric detectors. Possible ZT improvements are discussed in large-scale MXene flake films and/or MXene–polymer composite films.
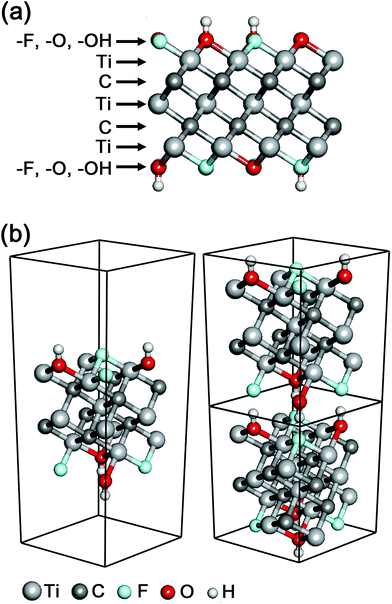
A new class of 2D materials called MXenes, which are transition metal carbides, carbonitrides, and nitrides,1,2 have attracted increasing attention due to their promising potential in many fields including electrochemical capacitors,3,4 electromagnetic interference shielding,5 composite reinforcement,6 water purification,7 chemical catalysts,8 biosensors,9 photothermal therapy,10 and so on.11 The chemical formula of MXenes is Mn+1Xn (n = 1–3), where M is an early transition metal (Sc, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, etc.) and X is carbon and/or nitrogen.12 The M layers and/or the X layers can also be mixed with multiple M and/or X elements, respectively, and the mixing includes both forms of a mix of M1 (or X1) layers and M2 (or X2) layers as well as [M1, M2] (or [X1, X2]) mixed layers. In the typical structure of MXenes, n + 1 layers of M cover n layers of X in the form of [MX]nM, and the surfaces of MXenes are usually terminated with a mix among hydroxyl, oxygen and fluorine functional groups (Fig. 1a).
Meanwhile, in recent years, terahertz (THz) technology has drawn great research interest for non-destructive evaluation and spectroscopy in the fields ranging from security scanning to chemical and/or medical diagnosis.13 THz waves can penetrate most non-metallic materials, like microwaves, as well as offering much finer spatial resolution compared to microwaves, which makes them ideally suitable for imaging and point measurements. THz technology can also provide an excellent spectroscopic method because many organic molecules have unique absorption features that are in the THz range as demonstrated in our previous study of the highly selective THz detection of various sugars.14 Despite its great potential, however, THz detection is not an easy task and persistent efforts have been made to develop new THz detecting materials.
Most MXenes have metallic properties, while certain ordered, double transition metal MXenes (e.g., Mo2TiC2) have very narrow band gaps in the electronic structure.15 Recently, we have shown the promise of MXenes in the broadband application of saturable absorbers to generate femtosecond mode-locked pulse lasers due to their unique metallic characteristics.16 It was also reported that MXenes possess an outstanding internal light-to-heat conversion efficiency.17 Based on these facts, we inferred that MXenes have great potential in THz detection applications including THz bolometers and photothermoelectric detectors. In the present study, to validate this, we have performed systematic density functional theory (DFT) calculations18,19 of the electronic band structures, THz optical properties, and the thermoelectric figure of merit (ZT) of monolayer and/or stacked Ti3C2Tx (Tx: –F, –O or –OH), which is the most popular MXene.
In the calculations of electronic structures and optical properties, we considered the mixed surface termination of –F and –OH in Ti3C2 (Fig. 1), which is one of the most likely models for the surface termination combination.20 It should be noted that previous Ti3C2 MXene computational studies have assumed only a single species of surface termination,21 which is much less probable and severely artificial.
Using DFT calculations, we first confirmed that both monolayer and stacked Ti3C2 flakes possess metallic electronic band structures (Fig. S1, ESI†) in good agreement with experimental observations. Then, we performed systematic optical DFT calculations of the Ti3C2 flakes in the THz range (0.3–3 THz, that is, 0.0012–0.012 eV) which has never been investigated until now. Note that the energy resolution in previous MXene DFT studies has always been equal to and/or larger than ∼0.01 eV (which is close to the upper limit of the THz range) and thus reasonable analysis of optical absorption and its detailed picture in the THz range have not been presented for MXenes so far.22
In order to investigate the optical properties of Ti3C2 flakes, we used the Kubo–Greenwood formulism (eqn (1)) and the following relations:23,24
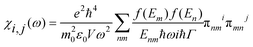 | (1) |
| ε(ω) = 1 + χ(ω) | (2) |
 | (3) |
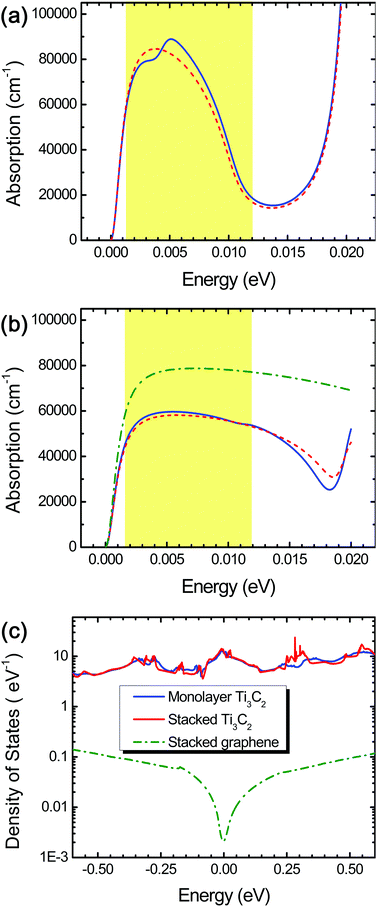
We observed excellent light extinction and optical absorption in both monolayer and stacked Ti3C2 flakes in the THz range (0.0012–0.012 eV) as shown in Fig. 2 and 5 and Fig. S2 in the ESI.† We found that spin–orbit coupling, which can change low-lying electronic states, negligibly affects the optical properties of Ti3C2 in the THz range as seen as the red short-dashed lines in Fig. 2a and b. Stacked Ti3C2 flakes have the optical absorption coefficient as high as 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–60
000–60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 throughout the THz range (Fig. 2b), while the optical absorption coefficient increases further to 70
000 cm−1 throughout the THz range (Fig. 2b), while the optical absorption coefficient increases further to 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–90
000–90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in the case of the monolayer Ti3C2 in the range of 0.0012–0.008 eV, but drastically decreases down to 20
000 cm−1 in the case of the monolayer Ti3C2 in the range of 0.0012–0.008 eV, but drastically decreases down to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 as the THz energy increases from 0.008 to 0.012 eV (Fig. 2a).
000 cm−1 as the THz energy increases from 0.008 to 0.012 eV (Fig. 2a).
Despite the lower optical absorption coefficient in the range of 0.0012–0.008 eV, we suppose that the stacked Ti3C2 film has many superb advantages over the monolayer Ti3C2 with respect to feasible fabrication (e.g., via drop-casting) as well as sufficient absorption capacity (the large thickness), while conserving the 2D characteristics fairly well due to its unique hydrogen-bond-based stacking of the layers.16 Hereafter, hence we will focus on stacked Ti3C2 flakes and/or films for THz detection materials.
For comparison, we also calculated the optical absorption coefficient of stacked graphene flakes, and found that it was larger (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–80
000–80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) compared to that of stacked Ti3C2 flakes throughout the THz range (the green dashed-dotted line in Fig. 2b). Despite this, we suppose that stacked Ti3C2 flakes exhibit superior THz absorption than stacked graphene flakes because the stacked Ti3C2 flakes possess several-order higher electronic density of states around the Fermi energy level, leading to a larger THz absorption density, as shown in Fig. 2c. In contrast, the stacked graphene flakes as well as monolayer graphene possess a very small amount of the electronic density of states around the Fermi energy level, resulting in a significantly lowered THz absorption density.
000 cm−1) compared to that of stacked Ti3C2 flakes throughout the THz range (the green dashed-dotted line in Fig. 2b). Despite this, we suppose that stacked Ti3C2 flakes exhibit superior THz absorption than stacked graphene flakes because the stacked Ti3C2 flakes possess several-order higher electronic density of states around the Fermi energy level, leading to a larger THz absorption density, as shown in Fig. 2c. In contrast, the stacked graphene flakes as well as monolayer graphene possess a very small amount of the electronic density of states around the Fermi energy level, resulting in a significantly lowered THz absorption density.
Optical absorption in the range other than a THz region (e.g., an infrared (IR) region) is also important in applications for light harvesting, bio-sensing, and so on.25,26 Regarding this issue, we have shown excellent absorption in Ti3CN MXene in the near-to-far-IR region both experimentally and theoretically in our previous study.16 Herein, to confirm this clearly for Ti3C2 MXene, we further performed DFT calculations of optical absorption in Ti3C2 in the visible-to-IR region (Fig. S3, ESI†), which indicated a promising potential of Ti3C2 in broadband opto-electronic applications.
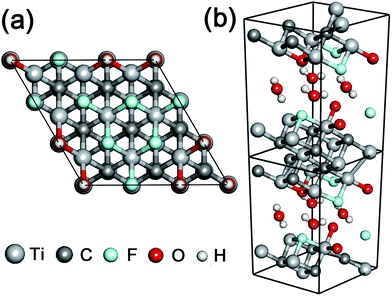
In order to investigate the cell size effect, we further performed DFT calculations of a larger simulation cell in which the layer surface of stacked Ti3C2 was almost doubled as shown in Fig. 3a. We observed a three-fold increase of the THz absorption maximally compared to that in the initial cell size (Fig. 4a). We supposed that it is attributed to significant clustering of the same kind of surface termination (not just due to the cell-size enlargement), and it was inferred that the THz absorption of actual systems should lie between the values shown in Fig. 2b and 4a.
The combination of surface termination examined above corresponds to the case of direct interlayer hydrogen bonding in stacked Ti3C2. We also performed DFT calculations assuming the other combination of surface termination in which O- and F-terminations as well as interlayer water molecules contribute to the interlayer interaction in stacked Ti3C2 (Fig. 3b),27 and the result showed that considerable THz absorption still occurred in stacked Ti3C2 (Fig. 4b). The stacked Ti3C2 exhibited a metallic behavior even in the presence of interlayer water molecules as shown in its electronic density of states around the Fermi energy level (Fig. S4†).
A variety of other optical properties of stacked Ti3C2 flakes, which include the spectra of the refractive index, reflectivity, complex dielectric constants, and complex optical conductivity, have also been investigated in the THz range (Fig. 5) for in-depth understanding of their optical response as well as providing a reference data set for the corresponding experiments that can be used for a cross-checking of the above THz absorption behavior since these optical properties are intimately related to one another.24 From this, we were able to obtain useful information specific to diverse relevant THz applications. We observed that the reflectivity in stacked Ti3C2 is rather independent of the frequency in the THz region. It should be noted that the refractive index and a real part of the dielectric constant showed a similar frequency dependence, while the extinction coefficient and an imaginary part of the dielectric constant showed a similar frequency dependence to each other. The large optical absorption in the higher THz range in stacked Ti3C2, which is different from the behavior of the extinction coefficient, is due to the fact that a multiplication of the frequency should be considered in the estimation of the optical absorption when compared to the extinction coefficient.
An interaction via hydrogen bonds is stronger than the van der Waals interaction although they are all non-bonded interactions. Consequently, it has been widely accepted that the interlayer interaction via hydrogen bonds in MXene should be stronger than that of van der Waals stacking in graphene but the stability of stacked MXenes has not been proved explicitly so far, particularly in the presence of interlayer water molecules. To make this issue clear, we performed the DFT calculations for the stacking energy of Ti3C2 with –O and –F terminations and interlayer water molecules by subtracting the energies of constituent “individual Ti3C2 layers” and “water molecule layers” from the energy of “stacked Ti3C2 with interlayer water molecules”. We also calculated the stacking energy of Ti3C2 with –OH and –F terminations (without water molecules) in a similar manner.
The results showed that the stacking energies are ∼1.305 and ∼1.731 eV for stacked Ti3C2 with and/or without interlayer water molecules, respectively, for the system size shown in Fig. 1 and 3. Considering that four hydrogen bonds are involved in these systems, the average hydrogen-bond energy was calculated to be 31.50 and 41.78 kJ mol−1, respectively, which are within the reasonable range as they lie between the hydrogen-bond energies of O–H⋯O (21 kJ mol−1) and F–H⋯F (161.5 kJ mol−1) that is the strongest case,28 validating our computational approach employed in this study. Meanwhile, it was reported that the stacking energy of bilayer graphene is 11.59 and 17.79 meV per atom for AA and AB stacking, respectively.29 Assuming that one carbon atom corresponds to one van der Waals bond, the van der Waals bond energy in bilayer graphene should be 1.112 and 1.717 kJ mol−1 for AA and AB stacking, respectively.
By evaluating the interlayer area, the stacking energy density that is closely concerned with the interlayer structural stability was eventually obtained to be 37.855, 50.213, and 6.782 meV Å−2, for stacked Ti3C2 MXenes with and/or without interlayer water molecules and bilayer graphene, respectively. From this, we see that the stacking energy density of Ti3C2 with –O and –F terminations and interlayer molecules is slightly smaller than that of Ti3C2 with –OH and –F terminations but they are all one order higher than that of graphene, indicating a good structural stability of stacked Ti3C2 MXene regardless of the presence of interlayer water molecules.
Finally, we investigated the thermoelectric performance of stacked Ti3C2 with –O and –OH surface terminations (we considered –O instead of –F in order to utilize the parameter sets currently available in the reactive force fields and/or the Slater–Koster approach) by constructing a device system composed of a channel and electrode regions and then examining the phonon and electronic transport properties within the nonequilibrium Green's function formulism30 rather than simply evaluating the transport properties by applying the Boltzmann transport equation31 to Ti3C2 with a small unit-cell size.21 To the best of our knowledge, the thermoelectric properties of stacked Ti3C2 flakes have not been examined so far.
The thermoelectric figure of merit (ZT) is defined as shown below:
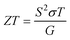 | (4) |
In order to avoid a heavy computational cost required in our device system (Fig. 6a), we employed molecular mechanics based on the reactive force field32 for the phonon transmission spectrum while a density-function tight-binding approach based on the Slater–Koster method33 was adopted to calculate the electron transmission spectrum (see the computational details in the ESI†). The phonon (as well as thermal electron) and electron transmission spectra account for G and σ, respectively, in ZT.
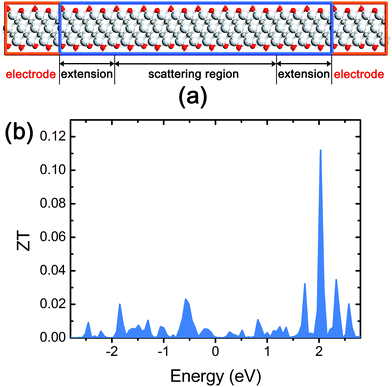 | ||
| Fig. 6 (a) The side view of the device for thermoelectric characterization of stacked Ti3C2 flakes; (b) the ZT spectra of the stacked Ti3C2 flakes. | ||
We found that the stacked Ti3C2 flakes have a ZT of 4.56 × 10−4 at the Fermi energy level (Fig. 6b). This ZT value is significantly lower than the value of commercial thermoelectric materials, but large enough to be used in THz detection applications considering that the ZT of carbon nanotube (CNT) films in well-functioning CNT-based THz detectors was reported to be in the range 1.0 × 10−5–1.8 × 10−4 as achieving a good noise equivalent power.34 The maximum ZT of the stacked Ti3C2 flakes is calculated to be 0.112 which can be obtained by a Fermi energy shift via n-type doping.
In summary, for the first time, we investigated the potential of MXenes as THz detecting materials by systematically performing DFT calculations on the most popular MXene, namely, Ti3C2, and discovered that excellent THz optical absorption occurs in this 2D material regardless of stacking. Considering the feasible production and the great optical absorption capacity, stacked MXene flakes and/or films (but also being thin enough to achieve a reasonable sensitivity) were suggested to be superior THz adsorption materials when compared to monolayer Ti3C2.
Despite the larger THz absorption coefficient of stacked graphene flakes than that of stacked Ti3C2 flakes, we inferred that stacked Ti3C2 flakes and/or films exhibit better THz absorption performance than stacked graphene flakes benefiting from their sufficient electronic density of states around the Fermi energy level in contrast to the faint degree of electronic states in stacked graphene flakes.
Thermoelectric calculations showed that stacked Ti3C2 flakes have a decent ZT value, enough to be used in THz detectors. Based on the above findings in MXenes, we finally suggest that MXenes can serve as excellent THz detecting materials such as in THz bolometric sensors, photothermoelectric detectors (with p–n junctions or asymmetric electrodes, etc.), and MXene-integrated pyroelectric sensors as well as THz antennas.34–37 We examined titanium carbide MXene here but suppose that other MXene members may also have promising potential in this application.
Compared to individual monolayer and/or stacked MXene, we infer that ZT can be significantly improved in MXene–polymer composite films3 and/or large-scale MXene films, which are packed with MXene flakes and can be formed by spin casting, due to the structural breaking between MXene flakes hindering phonon transport, thus leading to improvements in photothermoelectric THz detection.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Development Program funded by the Ministry of Trade, Industry & Energy, Republic of Korea (no. 10048690), the KIST Institutional Program (no. 2E27270), the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (2016R1A2B2010858), and the National Institute of Supercomputing and Network/Korea Institute of Science and Technology Information with supercomputing resources including technical support (KSC-2017-C2-0004).Notes and references
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. Barsoum, Adv. Mater., 2011, 23, 4248 CrossRef CAS PubMed.
- M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322 CrossRef CAS PubMed.
- O. Mashtalir, M. Lukatskaya, M. Zhao, M. Barsoum and Y. Gogotsi, Adv. Mater., 2015, 27, 3501 CrossRef CAS PubMed.
- M. Zhu, Y. Huang, Q. Deng, J. Zhou, Z. Pei, Q. Xue, Y. Huang, Z. Wang, H. Li, Q. Huang and C. Zhi, Adv. Energy Mater., 2016, 6, 1600969 CrossRef.
- F. Shahzad, M. Alhabeb, C. Hatter, B. Anasori, S. Hong, C. Koo and Y. Gogotsi, Science, 2016, 353, 1137 CrossRef CAS PubMed.
- Z. Ling, C. Ren, M. Zhao, J. Yang, J. Giammarco, J. Qiuc, M. Barsoum and Y. Gogotsi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16676 CrossRef CAS PubMed.
- Q. Peng, J. Guo, Q. Zhang, J. Xiang, B. Liu, A. Zhou, R. Liu and Y. Tian, J. Am. Chem. Soc., 2014, 136, 4113 CrossRef CAS PubMed.
- X. Xie, Y. Xue, L. Li, S. Chen, Y. Nie, W. Ding and Z. Wei, Nanoscale, 2014, 6, 11035 RSC.
- H. Liu, C. Duan, C. Yang, W. Shen, F. Wang and Z. Zhu, Sens. Actuators, B, 2015, 218, 60 CrossRef CAS.
- J. Xuan, Z. Wang, Y. Chen, D. Liang, L. Cheng, X. Yang, Z. Liu, R. Ma, T. Sasaki and F. Geng, Angew. Chem., Int. Ed., 2016, 55, 14569 CrossRef CAS PubMed.
- M. Naguib, V. Mochalin, M. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992 CrossRef CAS PubMed.
- B. Anasori, M. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098 CrossRef CAS.
- A. Sanchez, N. Laman, B. Schulkin and T. Tongue, J. Infrared, Millimeter, Terahertz Waves, 2013, 34, 500 CrossRef.
- D. Lee, J. Kang, J. Lee, H. Kim, C. Kim, J. Kim, T. Lee, J. Son, Q. Park and M. Seo, Sci. Rep., 2015, 5, 15459 CrossRef CAS PubMed.
- F. Romer, U. Wiedwald, T. Strusch, J. Halim, E. Mayerberger, M. Barsoumb and M. Farle, RSC Adv., 2017, 7, 13097 RSC.
- Y. Jhon, J. Koo, B. Anasori, M. Seo, J. Lee, Y. Gogotsi and Y. Jhon, Adv. Mater., 2017, 29, 1702496 CrossRef PubMed.
- R. Li, L. Zhang, L. Shi and P. Wang, ACS Nano, 2017, 11, 3752 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Atomistix Toolkit version 2015.3, Quantum Wise A/S, Copenhagen, Denmark Search PubMed.
- K. Harris, M. Bugnet, M. Naguib, M. Barsoum and G. Goward, J. Phys. Chem. C, 2015, 119, 13713 CAS.
- A. Gandi, H. Alshareef and U. Schwingenschlögl, Chem. Mater., 2016, 28, 1647 CrossRef CAS.
- G. Berdiyorov, AIP Adv., 2016, 6, 055105 CrossRef.
- W. Harrison, Solid State Theory, McGraw-Hill press, New York, USA, 1970 Search PubMed.
- R. Martin, Electronic structure: Basic theory and practical methods, Cambridge University Press, New York, 2004 Search PubMed.
- K. Manthiram and A. Alivisatos, J. Am. Chem. Soc., 2012, 134, 3995 CrossRef CAS PubMed.
- Y. Wang, J. Ou, A. Chrimes, B. Carey, T. Daeneke, M. Alsaif, M. Mortazavi, S. Zhuiykov, N. Medhekar, M. Bhaskaran, J. Friend, M. Strano and K. Kalantar-Zadeh, Nano Lett., 2015, 15, 883 CrossRef CAS PubMed.
- M. Hope, A. Forse, K. Griffith, M. Lukatskay, M. Ghidiu and Y. Gogotsi, Phys. Chem. Chem. Phys., 2016, 18, 5099 RSC.
- J. Emsley, Chem. Soc. Rev., 1980, 9, 91 RSC.
- E. Mostaani and N. Drummond, Phys. Rev. Lett., 2015, 115, 115501 CrossRef CAS PubMed.
- M. Brandbyge, J. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- W. Li, J. Carrete, N. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747 CrossRef CAS.
- A. Jaramillo-Botero, Q. An, M. Cheng, W. Goddard III, L. Beegle and R. Hodyss, Phys. Rev. Lett., 2012, 109, 213201 CrossRef PubMed.
- R. Luschtinetz, J. Frenzel, T. Milek and G. Seifert, J. Phys. Chem. C, 2009, 113, 5730 CAS.
- K. Erikson, X. He, A. Talin, B. Mills, R. Hauge, T. Iguchi, N. Fujimura, Y. Kawano, J. Kono and F. Léonard, ACS Nano, 2015, 9, 11618 CrossRef CAS PubMed.
- X. Cai, A. Sushkov, R. Suess, M. Jadidi, G. Jenkins, L. Nyakiti, R. Myers-Ward, S. Li, J. Yan, D. Gaskill, T. Murphy, H. Drew and M. Fuhrer, Nat. Nanotechnol., 2014, 9, 814 CrossRef CAS PubMed.
- I. Akyildiz, J. Jornet and C. Han, IEEE Wirel. Commun., 2014, 21, 130 CrossRef.
- S. Kuznetsov, A. Paulish, M. Navarro-Cia and A. Arzhannikov, Sci. Rep., 2016, 6, 21079 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr05351g |
| This journal is © The Royal Society of Chemistry 2018 |