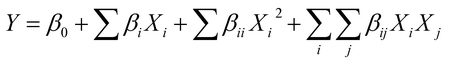Treatment of real benzene dye intermediates wastewater by the Fenton method: characteristics and multi-response optimization

Abstract

Benzene dye intermediates (BDI) wastewater has caused major environmental concern due to its potential carcinogenic, teratogenic, and mutagenic effects. Treatability reports dealing with the advanced chemical oxidation of BDI are limited. In this work, the Fenton method was applied to treat the real BDI wastewater to provide a deep insight into single as well as combinative effects of the main process variables influencing the treatment performance. First, we evaluated the effects of the reaction time, initial pH, initial [H₂O₂] concentration, and initial [Fe²⁺] concentration on the Fenton oxidation efficiency of real BDI wastewater. Furthermore, based on the Box–Behnken response surface methodology (RSM), an empirical mathematical model between response values, namely the chemical oxygen demand (COD), total organic carbon (TOC), color removal efficiency, sludge iron mass ration (SIMR), and influence factors were established to evaluate the interaction effects and optimize the experimental conditions. All of the proposed models were adequate with an R² range from 0.9561 to 0.9880. In addition, three of these factors had different effects on four studied response values. By overlaying the responses, the optimum conditions were obtained at an initial pH of 4.13, an initial [H₂O₂] concentration of 1.0 M, and an initial [Fe²⁺] concentration of 0.36 M. Verification experiments were conducted at the optimum conditions, which led to a COD removal efficiency of 85.29%, a TOC removal efficiency of 75.23%, a color removal efficiency of 99.99%, and a SIMR response of 0.39, respectively, and the results were in good agreement with the values predicted by the model. In addition, the BOD₅/COD ratio was observed to increase from 0.08 to 0.49, indicating an improvement in biodegradability.

---

1. Introduction

Dye intermediates are important products of the chemical industry and are used extensively in the dyestuff and pharmaceutical industries.^1–3 The common characteristics of real dye intermediate wastewater are high toxicity and a high concentration of chemical oxygen demand (COD), as well as a low ratio of BOD₅/COD (<0.1), which have potential carcinogenic, teratogenic, and mutagenic effects.^4–6 Due to the wide application of the dyestuff industry in the world, large amounts of wastewater are discharged without proper treatment, bringing irreversible pollution damage to the surface water, groundwater and soil, causing serious public environmental safety problems.

Various techniques have been used to treat dye intermediate wastewater, such as evaporation, solvent extraction,⁷ absorption,^8,9 and biodegradation.^4,6 However, these technologies have some disadvantages. For example, evaporation often produces volatile organic compounds (VOCs), resulting in secondary environmental pollution.¹⁰ Moreover, extraction agents are relatively costly, and the technological stability is not good enough. Adsorption is troubled with poor regeneration of adsorbent and is greatly affected by the nature of adsorbent on the amount of adsorption.¹¹ Biological treatment processes are usually very slow, and require a significant period of time to commence due to acclimation.¹²

Due to the complexity of dye intermediate wastewaters and the recalcitrance to biological treatment,¹³ advanced oxidation processes (AOPs) are considered suitable and promising treatment technologies based on their strong oxidation performance and a wide range of applications.¹⁴ For AOPs, photocatalysis,¹⁵ ozonation⁷ and Fenton oxidation¹¹ have been attempted and have proven effective in the treatment of various dye intermediate wastewaters.

Among them, the Fenton method plays an important role in AOPs¹⁶ because it is cost effective, easy to apply, and no energy input is required to activate hydrogen peroxide.¹⁴ Therefore, in the past few decades, researchers have been paying increasing attention to the Fenton method and diverse Fenton processes to treat dye intermediate wastewater. Gu et al. reported that enhanced Fenton process,¹¹ Fenton-like method combined with adsorption,¹⁷ and enhanced Fenton processes combined with humic acid adsorption¹⁴ were very effective and suitable for dealing with naphthalene dye intermediate wastewater. Arslan-Alaton et al.¹⁸ also indicated that photo-Fenton-like oxidation of naphthalene dye intermediate H-acid is highly efficient.

Dye intermediates mainly include four types: benzene, naphthalene, anthraquinone and heterocycle. Previously reported studies were focused on the treatment of naphthalene dye intermediate wastewater by Fenton methods. It is reported that benzene dye intermediates (BDI) are the most widely used dye intermediates around the world.^19,20 However, studies aiming at the treatment of real BDI wastewater by Fenton methods have been very limited. Hence, it is important to understand the process and the characteristics of real BDI degradation by Fenton oxidation.

During the Fenton process, several process variables including initial pH, initial [H₂O₂] and [Fe²⁺] dosages will affect the Fenton oxidation efficiency and may also interact with each other.¹⁸ Response surface methodology (RSM), a powerful mathematical and statistical design tool, can be used to evaluate and optimize the performance of complex systems by considering the relative significance of several affecting factors even in the presence of complicated, multi-dimensional interactions.¹⁸ A further benefit of using the RSM design is the reduction of the number of experiments needed compared to a full experimental design at the same level. In addition, the eventual objective of RSM is to determine the optimum operating conditions for the system, or to determine the region, which satisfies the operating specifications.²¹ In the last few years, RSM has been used to evaluate and optimize the interactive effects of independent factors in Fenton processes for wastewater treatment such as landfill leachate,²² pharmaceutical²³ and dye wastewater.²⁴ However, using RSM, estimation of the effect of the interaction between various operating conditions on the BDI wastewater especially under multi-response conditions by Fenton process has rarely been reported.

In this study, Fenton treatment was employed to deal with real BDI wastewater. RSM with multiple response values was used to optimize the process parameters. First, single factor experiments were carried out to study the effects of reaction time, initial pH, initial [H₂O₂] and [Fe²⁺] dosages to provide a suitable influence factor range for the following response surface analysis. Then, based on the Box–Behnken RSM, the effects of various factors, specifically the COD, TOC, color removal efficiencies, and the sludge to iron mass ratio (SIMR) were analyzed to seek the optimal conditions according to an overlay plot. Finally, the accuracy of the optimal reaction conditions by the model was verified. This study provides insight into individual factors as well as interaction effects of independent variables that influence the treatment performance in BDI wastewater treatment, which is helpful for understanding the degradation characteristics of BDI and the optimization of influencing factors by Fenton method.

2. Materials and methods

2.1 Wastewater sources and characteristics

The contaminated water samples were obtained from the benzene dye production plant at the Tengger desert, which is located in the northwest of China in the Ningxia Hui Autonomous Region. The wastewater that was acquired had a COD concentration between 3900–4500 mg L⁻¹, a BOD₅ concentration between 280–350 mg L⁻¹, a BOD₅/COD ratio between 0.06–0.08, and a color of about 12 000 multiple. The specific component is shown in Table S1.†

2.2 Chemicals

Hydrogen peroxide (30%), ferrous sulfate, sodium hydrate and sulphuric acid (98%) were purchased from Sinopharm Chemical Reagent Beijing Co., Ltd. All chemicals were analytical grade and were prepared using ultra-pure water from a millipore system with a resistivity of 18.2 MΩ cm.

2.3 Experimental methods

The wastewater sample (100 mL) was put in a beaker (250 mL) with a magnetic stirrer. The initial solution pH was adjusted to the desired value by using 0.5 M H₂SO₄ or 1 M NaOH solution. A measured amount of catalytic ferrous sulfate was added, followed by the addition of H₂O₂ to the solution to start the reaction. At selected time intervals, 5 mL aliquots of the reaction mixture were taken and immediately injected with 10 M NaOH to terminate the reaction.²⁵ The mixed solution was centrifuged for 10 min at 12 000 rpm and the supernatant was withdrawn for the subsequent analysis. All measurements were performed in triplicate, and the results displayed in tables were the average value of at least three measurements with an accuracy of ±5%.

A Box–Behnken design with three independent variables (initial pH, initial [H₂O₂] concentration (M), and initial [Fe²⁺] concentration (M)) at three levels was performed to explore the effect of independent process variables on four responses (COD removal, TOC removal, color removal and SIMR). The independent variables and their ranges were chosen based on single factor experiment results. The whole design consisted of 17 experimental runs carried out in random order. Table 1 shows the coded and level of the independent variables at which the experiments were conducted to estimate the response variables. Empirical models were developed based on four responses correlated to the three process variables.

Table 1 Level and code based on Box–Behnken response surface methodology

Variables	Unit	Code and level
		−1	0	+1
Initial pH	—	3.0	4.0	5.0
Initial [H2O2] concentration	M	0.5	0.75	1.0
Initial [Fe^2+] concentration	M	0.05	0.25	0.45

---

Experimental data were analyzed by the RSM procedure of the statistical analysis system and were fit to a second-order polynomial model.^26,27 The quadratic equation for the variables was as follows:^28,29

where Y is the predicted response, β₀ is a constant; β_i is the first-order model coefficient; β_ii is the squared coefficient for the factor i; β_ij is the linear model coefficient for the interaction between factors i and j, and X_i is the coded value of the main effect.^30–32

2.4 Analytical methods

The COD, BOD₅, pH and color of the wastewater were measured using standard methods. The TOC values of samples were measured with a TOC analyzer (Shimadzu, Japan). The main pollutants in the influent of real benzene dye intermediate wastewater were detected by gas chromatograph-mass spectrometer (GC-MS). SIMR was calculated using the following equation:

SIMR = (sludge mass (g))/(ferrous sulfate dosage (g))

The Design Expert Software (version 8.0.6, Stat-Ease, Inc., Minneapolis, MN) was used for the statistical design of experiments and data analysis. Analysis of variances (ANOVA) was used for graphical analyses to obtain the interaction between the process variables and the responses.³³ The quality of the fit polynomial model was expressed by the coefficient of determination R² and R_adj². Model terms were selected or rejected based on the P value (probability) with 95% confidence level. Three-dimensional (3D) plots and their respective contour plots were obtained based on the effects of the two factors at three levels. Moreover, a perturbation plot was created to compare the effect of all the factors at a particular point in the design space the optimum region was identified based on the main parameters in the overlay plot. The adequacy of the regression equations was checked by comparing the experimental data with predicted values obtained from the equations.²²

3. Results and discussion

3.1 Single factor experiment

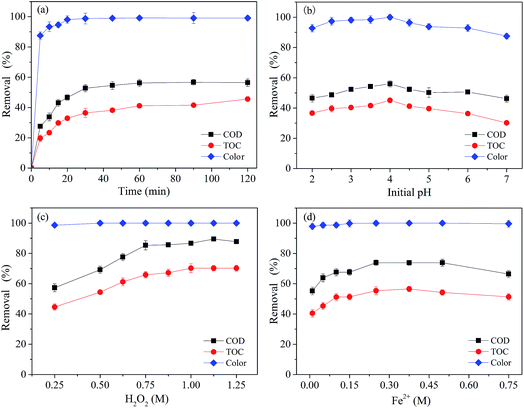
The main factors that affect the Fenton method are reaction time, initial pH, initial [H₂O₂] concentration, and initial [Fe²⁺] concentration.^18,22,34,35 It is necessary to study the extent of their influence and determine the most suitable process parameters to optimize treatment.

Effect of reaction time. In order to determine the most appropriate reaction time of the Fenton method for practical application, a series of tests were performed within the time interval range of 0–120 min. The initial pH of 4.0, initial [H₂O₂] of 0.25 M, and initial [Fe²⁺] of 0.05 were chosen based on initial COD of 4000 mg L⁻¹. The removal of COD, TOC, and color were evaluated to determine the best reaction time. The results are illustrated in Fig. 1(a), which clearly demonstrate that the BDI contaminant was rapidly degraded by the Fenton method. During the initial 20 min, the removal efficiencies of COD, TOC and color increased rapidly, as 46.65%, 32.93% and 98.08% of the total removal was observed, respectively. As the reaction continued, the removal efficiency increased slowly and 56.25%, 41.18% and 99.17% of the total removal was observed between 20–60 min. The reaction reached equilibrium after 60 min. At this time, a lot of bubbles were generated which inferred that some organic pollutants might be finally oxidized into carbon dioxide.

Fig. 1 Effect of (a) reaction time (initial pH = 4.0, [H₂O₂] = 0.25 mol L⁻¹, [Fe²⁺] = 0.05 mol L⁻¹) (b) initial pH (reaction time 60 min, [H₂O₂] = 0.25 mol L⁻¹, [Fe²⁺] = 0.05 mol L⁻¹) (c) initial [H₂O₂] concentration (reaction time 60 min, initial pH 4.0, [Fe²⁺] = 0.05 mol L⁻¹) (d) initial [Fe²⁺] concentration (reaction time 60 min, initial pH 4.0, initial [H₂O₂] = 0.75 M) on removal.

To explain the results above, it is hypothesized that at the beginning of the reaction, the system produced a sufficient amount of hydroxyl radical (˙OH) that degraded organic compounds quickly. As the reaction proceeds, catalyst deactivation and hydrogen peroxide decomposition occur, and the system no longer produces active substances (˙OH), effectively stopping further degradation of pollutants. It was also observed that the removal efficiency of TOC was about 10% lower than that of COD, indicating that partial organic matters were not mineralized. This is probably because the Fenton reaction consumed the produced radicals faster than organic compounds at a certain oxidation stage, which is in agreement with a previous report.³⁶

Based on these results, a reaction time of 60 min was used for further experiments.

Effect of initial pH. In order to find the optimal pH conditions for the degradation of BDI wastewater by Fenton oxidation, experiments were performed at initial pH values ranging from 2.0 to 7.0, the results of which are shown in Fig. 1(b).

It was observed that with the increase of pH from 2.0 to 4.0, the removal efficiency of COD, TOC and color increased initially from 46.11%, 36.67% and 92.79% to 56.02%, 45.11% and 99.99% respectively, and then decreased to 46.21%, 30.22% and 87.50% with the increase of pH from 4.0 to 7.0. The TOC removal efficiency was lower than the COD removal efficiency under the same conditions. In the range of pH in this study, the differences between the best COD, TOC, color removal and the worst were 9.91%, 14.89% and 12.94%., respectively. The best removal efficiency overall was obtained at a pH of 4.0. At lower pH values, the formation of the complex species [Fe(H₂O)₆]²⁺ slows down the oxidation reaction due to its slower reaction with H₂O₂ compared to that of [Fe(OH)(H₂O)₅]⁺.^37,38 The formation of the stable oxonium ion [H₃O₂]⁺ in the presence of high concentrations of H⁺ also makes the peroxide electrophilic enhancing its stability and presumably hindering the reaction activity between H₂O₂ and Fe²⁺. On the contrary, under the conditions of higher pH, the production of ˙OH is inhibited by ferric hydroxo complexes. Moreover, Fe²⁺ or Fe³⁺ tends to generate a variety of amorphous complex precipitation even further forming Fe(OH)₄⁻ when the pH value is higher,^39,40 which significantly decreases the oxidation capability of the system. Hydrogen peroxide is also unstable in basic solution and may decompose to give oxygen and water and lose its oxidation ability. Thus, H₂O₂ and Fe²⁺ have a difficulty in establishing an effective redox system and their degradation is also less effective. Hence, pH = 4.0 was selected as the optimum pH for further experiments.

Effect of initial [H₂O₂] concentration. Generally, it has been accepted that the degradation efficiency of an organic contaminant increases with an increase in the concentration of [H₂O₂].⁴¹ However, in the actual wastewater treatment process, large initial [H₂O₂] dosage may affect the treatment efficiency, due to the formation of large amounts of oxygen bubbles, thereby wasting a large number of ˙OH. Therefore, it is very important to study the most suitable dosage of [H₂O₂]. Experiments were carried out as the initial [H₂O₂] concentrations ranged from 0.25 to 1.25 M. As shown in Fig. 1(c), increasing the initial [H₂O₂] concentration enhanced the COD, TOC, and color removal efficiencies significantly. With the increase of initial [H₂O₂] concentration from 0.25 to 0.75 M, the removal efficiency of COD, TOC and color increased from 57.30%, 44.63% and 98.63% to 85.36%, 65.88% and 99.99% respectively. This is presumably because the increased [H₂O₂] concentration could promote the production of HO˙, as illustrated in eqn (1).

Fe²⁺ + H₂O₂ → Fe³⁺ + ˙OH + OH⁻ (1)

However, further increase of the initial [H₂O₂] concentration was not observed to enhance the removal efficiency. The removal efficiency of COD, TOC and color just increased from 85.36%, 65.88% and 99.99% to 87.75%, 70.20 and 100% respectively with futher increasing the initial [H₂O₂] concentration from 0.25 to 0.75 M. It was probably due to the competition between intermediates and organics for the consumption of ˙OH. The larger initial [H₂O₂] dosage might lead to more side reactions and react with ˙OH to form hydroperoxyl radicals (HO₂˙), as shown in eqn (2), the rate constant of which was found to be about (1.2–4.5) × 10⁷ M⁻¹ s⁻¹.⁴²

H₂O₂ + ˙OH → HO₂˙/O₂˙⁻ + H₂O (2)

Therefore, based on the above experimental results, the most appropriate initial [H₂O₂] concentration was selected as 0.75 M in the actual treatment process.

Effect of initial [Fe²⁺] concentration. In the Fenton process, the Fe²⁺ and H₂O₂ are two major chemicals that determine the operation cost as well as the removal efficiency. Experiments were performed as the initial [Fe²⁺] concentration ranged from 0.01 to 0.75 M. The results are shown in Fig. 1(d).

The removal efficiency of COD and TOC increased from 55.20% and 40.50% to the maximum values 73.86% and 55.36%, respectively, with the initial [Fe²⁺] concentration increasing from 0.01 M to 0.25 M. Further increasing the initial [Fe²⁺] concentration to 0.75 M, the removal efficiency of COD and TOC slightly decreased to 66.40% and 51.30%. However, the color removal efficiency was almost unchanged at different initial [Fe²⁺] concentrations (0.01 to 075 M), which was around 99.86%.

When the initial [Fe²⁺] concentration was lower than 0.25 M, the oxidation removal of COD and TOC decreased with the decrease of initial [Fe²⁺] concentration. This was probably due to the lower amount of catalyst [Fe²⁺], thereby decreasing the reaction rate of the decomposition of H₂O₂ and decreasing the oxidation capacity of the Fenton system.⁴³ At the same time, due to excessive decomposition of H₂O₂, a lot of ˙OH was generated, which could react with other ˙OH, as shown in eqn (3), leading to an insufficient quantity of ˙OH to react with target contaminants, resulting in a decrease in oxidative degradation ability of the Fenton method.⁴⁴

˙OH + ˙OH → H₂O₂ (3)

Moreover, the generation of HO₂˙ occurred in the presence of a relative excess of H₂O₂ (eqn (4)) with an oxidation potential much lower than that of ˙OH.¹⁶

Fe³⁺ + HO₂˙ → Fe²⁺ + H⁺ + O₂ (4)

However, oxidation efficiency decreased when the initial [Fe²⁺] concentration was higher than 0.25 M, which is mainly due to the increase of scavenging effects of [Fe²⁺] on ˙OH. The relative surplus of [Fe²⁺] reacted with the available ˙OH (eqn (5)), which resulted in the consumption of ˙OH that had been generated in the system.⁴⁴

˙OH + organics → products + H₂O (5)

These results indicated clearly that the initial [Fe²⁺] concentration of 0.25 M was the optimal concentration for further experimental conditions.

3.2 Modeling of Fenton method for treatment of BDI wastewater using RSM

Model establishment and regression analysis. According to the results of single factor tests and the costs of the initial investment and disposal, the influence factors of the Box–Behnken response surface method are shown in Table 1. After the influencing factors were selected, selection of suitable response values was also required. After selecting the removal efficiencies of COD, TOC color, and SIMR as response values, a total of 17 groups of experiments were conducted. Table 2 shows the detailed test scheme and results.

Table 2 Experimental design and results

Run	Variables			Responses
	Initial pH	H2O2 (M)	Fe^2+ (M)	COD removal (%)	TOC removal (%)	Color removal (%)	SIMR
1	4.0 (0)	0.75 (0)	0.25 (0)	83.63	71.63	99.73	0.41
2	3.0 (−1)	0.75 (0)	0.45 (+1)	60.86	54.84	98.23	0.30
3	5.0 (+1)	1.0 (+1)	0.25 (0)	80.38	71.00	98.37	0.48
4	3.0 (−1)	0.5 (−1)	0.25 (0)	75.50	66.69	97.41	0.44
5	5.0 (+1)	0.75 (0)	0.45 (+1)	78.75	69.25	97.96	0.31
6	4.0 (0)	0.5 (−1)	0.05 (−1)	82.00	71.66	99.73	1.97
7	5.0 (+1)	0.5 (−1)	0.25 (0)	75.50	66.69	97.82	0.50
8	3.0 (−1)	1.0 (+1)	0.25 (0)	80.38	71.00	98.37	0.40
9	4.0 (0)	1.0 (+1)	0.45 (+1)	85.25	72.99	99.86	0.30
10	4.0 (0)	0.75 (0)	0.25 (0)	83.63	72.49	99.73	0.46
11	4.0 (0)	1.0 (+1)	0.05 (−1)	75.50	66.69	99.32	1.62
12	4.0 (0)	0.75 (0)	0.25 (0)	82.00	70.22	99.73	0.45
13	5.0 (+1)	0.75 (0)	0.05 (−1)	62.49	55.20	98.37	1.42
14	4.0 (0)	0.5 (−1)	0.45 (+1)	75.50	66.69	99.05	0.28
15	3.0 (−1)	0.75 (0)	0.05 (−1)	75.50	66.69	98.91	1.73
16	4.0 (0)	0.75 (0)	0.25 (0)	85.25	71.70	99.59	0.48
17	4.0 (0)	0.75 (0)	0.25 (0)	85.25	72.49	99.73	0.48

---

As shown in Table 2, the whole design consisted of 17 experimental runs carried out in random order, which included 12 factorial points, 1 center point and 4 parallelism control points. The design principle is that three factors and three levels constitute a 3 × 3 cube, and there are three points on the edge of each test point. We selected 12 groups at the center point on each edge, 1 group of cube center, and additional 4 parallel groups to control the whole test parallelism. After the 17 groups of experiments were finished, the results were put into the form in turn. Using design expert (8.0.6), experimental data in Table 2 were analyzed by polynomial regression. Variance analysis and significant test results for the quadratic regression equations were shown in Table 3.

Table 3 Analysis of variance for response surface quadratic model

Source	Sum of squares	Df	Mean square	F value	P value
COD removal
Model	814.59	9	90.51	39.60	<0.0001	Significant
A-initial pH	2.97	1	2.97	1.30	0.2914
B-H2O2	21.15	1	21.15	9.26	0.0188
C-Fe^2+	2.97	1	2.97	1.30	0.2914
AB	0.000	1	0.000	0.000	1.0000
AC	238.64	1	238.64	104.42	<0.0001
BC	66.11	1	66.11	28.93	0.0010
A^2	275.56	1	275.56	120.58	<0.0001
B^2	18.10	1	18.10	7.92	0.0260
C^2	175.92	1	175.92	76.98	<0.0001
Residual	16.00	7	2.29
Lack of fit	8.59	3	2.86	1.55	0.3329	Not significant
Pure error	7.40	4	1.85
Cor total	830.59	16
TOC removal
Model	464.01	9	51.56	32.11	<0.0001	Significant
A-initial pH	1.06	1	1.06	0.66	0.4427
B-H2O2	12.37	1	12.37	7.70	0.0275
C-Fe^2+	1.56	1	1.56	0.97	0.3573
AB	0.000	1	0.000	0.000	1.0000
AC	167.68	1	167.68	104.43	<0.0001
BC	31.72	1	31.72	19.76	0.0030
A^2	124.42	1	124.42	77.49	<0.0001
B^2	27.92	1	27.92	17.39	0.0042
C^2	95.98	1	95.98	59.78	0.0001
Residual	11.24	7	1.61
Lack of fit	7.80	3	2.60	3.03	0.1564	Not significant
Pure error	3.44	4	0.86
Cor total	475.25	16
Color removal
Model	308.93	9	34.33	17.77	0.0005	Significant
A-initial pH	2.92	1	2.92	1.51	0.2589
B-H2O2	19.44	1	19.44	10.06	0.0157
C-Fe^2+	2.44	1	2.44	1.26	0.2980
AB	0.000	1	0.000	0.000	1.0000
AC	28.04	1	28.04	14.51	0.0066
BC	61.54	1	61.54	31.86	0.0008
A^2	119.91	1	119.91	62.07	0.0001
B^2	0.60	1	0.60	0.31	0.5956
C^2	61.73	1	61.73	31.95	0.0008
Residual	13.52	7	1.93
Lack of fit	8.96	3	2.99	2.62	0.1876	Not significant
Pure error	4.56	4	1.14
Cor total	322.45	16
SIMR
Model	3.05	9	0.34	1842.69	<0.0001	Significant
A-initial pH	0.000358	1	0.00043587	1.95	0.2052
B-H2O2	0.002100	1	0.0021	11.42	0.0118
C-Fe^2+	2.25	1	2.25	12 209.85	<0.0001
AB	0.0004	1	0.0004	2.17	0.1838
AC	0.0001389	1	0.0001389	0.76	0.4137
BC	0.077	1	0.077	418.69	<0.0001
A^2	0.0005109	1	0.0005109	2.78	0.1395
B^2	0.000866	1	0.000866	4.71	0.0666
C^2	0.72	1	0.72	3912.75	<0.0001
Residual	0.001287	7	0.0001839
Lack of fit	0.001068	3	0.000356	6.49	0.0513	Not significant
Pure error	0.0002196	4	0.00005489
Cor total	3.05	16

---

Table 3 presents the details of variance analysis and status of significant parameters for four responses. The model was significant with P values less than 0.05 at 95% confidence level showing statistical significance of the model. It also suggested that the quadratic model was well described the data and could be efficiently applied to the studied system. The quadratic polynomial model was established between three factors including initial pH (X₁), initial [H₂O₂] concentration (X₂), and initial [Fe²⁺] concentration, plus four response values, which were COD removal efficiency (Y₁), TOC removal efficiency (Y₂), color removal efficiency (Y₃) and SIMR (Y₄). The fitted quadratic regression equation is shown in Table 4.

Table 4 Statistical results of the proposed models in terms of the coded factors^a

Response	Proposed quadratic model	R^2	Radj^2
a All the responses (Y) are as defined in text; R^2: determination coefficient; Radj^2: adjusted R^2.
Y1	83.95 + 0.61X1 + 1.63X2 + 0.61X3 + 7.72X1X3 + 4.07X2X3 − 8.09X1^2 + 2.07X2^2 − 6.46X3^2	0.9807	0.9560
Y2	71.71 + 0.36X1 + 1.24X2 + 0.44X3 + 6.47X1X3 + 2.82X2X3 − 5.44X1^2 + 2.57X2^2 − 4.77X3^2	0.9764	0.9459
Y3	99.70 − 0.051X1 + 0.24X2 − 0.15X3 − 0.10X1X2 + 0.068X1X3 + 0.31X2X3 − 1.41X1^2 − 0.29X2^2 + 0.082X3^2	0.9561	0.8996
Y4	0.45 − 0.02X1 − 0.047X2 − 0.69X3 + (5.086 × 10^−0.003)X1X2 + 0.08X1X3 + 0.093X2X3 − 0.052X1^2 + 0.052X2^2 + 0.53X3^2	0.9880	0.9726

---

The variance analysis results of four parameters (Y₁–Y₄) showed that the significant (P < 0.05) response surface models with high R² value varying from 0.9561 to 0.9880 were obtained as shown in Table 4. These high R² coefficients ensured a satisfactory adjustment of the quadratic models to the experimental data. The adjusted R² values of 0.9560, 0.9459, 0.8996 and 0.9726 respectively for four models Y₁–Y₄ were high, which advocated high significance of the models. Therefore, the response surface models were accurately employed for predicting variation percentage of these four parameters.

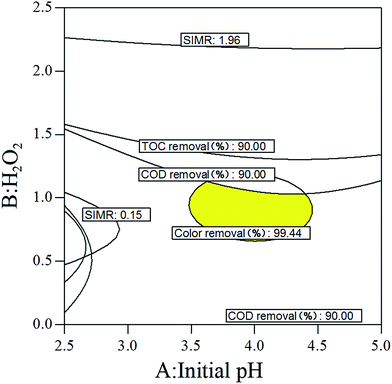
Of the three factors, the initial [H₂O₂] concentration had the most significant effect on three of the four response values, specifically COD, TOC and color removal efficiency. The order of the significance of three factors was as follows: initial [H₂O₂] concentration (F = 9.26, 7.70 and 6.85) > initial [Fe²⁺] concentration (F = 1.30, 0.97 and 2.83) > initial pH (F = 1.30, 0.66 and 0.31). In contrast, the initial [Fe²⁺] concentration had the most significant effect on the remaining response value, the SIMR. The order of the significance of the three factors was as follows: initial [Fe²⁺] concentration (F = 429.78) > initial [H₂O₂] concentration (F = 1.98) > initial pH (F = 0.36). Thus, in the process of Fenton oxidation treatment of BDI wastewater, it was necessary to strictly control the initial [H₂O₂] concentration of the reaction system, which was the key factor to ensure efficient Fenton oxidation. At the same time, in the case of sufficient amount of the catalyst, the amount of iron should also be properly controlled to reduce sludge production. In addition, the initial pH usually affected the catalytic activity of iron oxide, as well as the oxidation-reduction potential of ˙OH. However, in our experiments, the effect of pH on the four response values was not significant, indicating that Fenton oxidation degradation of BDI wastewater can be achieved at a wide range of pH. In addition, there were observed relationships between the three factors. The most significant interaction was observed between the initial pH and initial [Fe²⁺] concentration for the response values of COD and TOC removal efficiency. However, for the color removal efficiency and SIMR, the most significant interaction occurred between the initial [H₂O₂] concentration and [Fe²⁺] concentration.

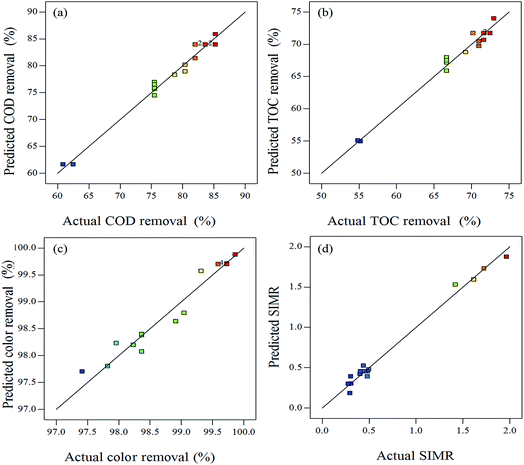
Moreover, plots comparing the actual and predicted values for COD, TOC, color removal efficiencies and SIMR indicated a good agreement between real data and the ones obtained from the model (Fig. 2). Therefore, this model could be used to predict the optimization experimental conditions of the BDI wastewater by the Fenton method.

Fig. 2 Predicted vs. actual value plots for (a) COD removal (b) TOC removal (c) color removal (d) SIMR.

Multiple responses surface analysis. The effect of all the factors is illustrated in the perturbation plot (Fig. 3). It was apparent that the initial pH (X₁) and the initial [Fe²⁺] concentration (X₃) had a significant negative effect on COD (Y₁) and TOC (Y₂) removal, while the initial [H₂O₂] concentration (X₂) had a positive effect on them. In contrast, the initial [Fe²⁺] concentration (X₃) had a significant positive effect on color removal (Y₃) and SIMR (Y₄) while the initial pH (X₁) and the initial [H₂O₂] concentration (X₂) had a negative effect on them. In this instance, the positive effect means the corresponding response value (Y) increases with an increase of the effect factor (X) level. In contrast, the negative effect means the Y decreases with an increase of X level.

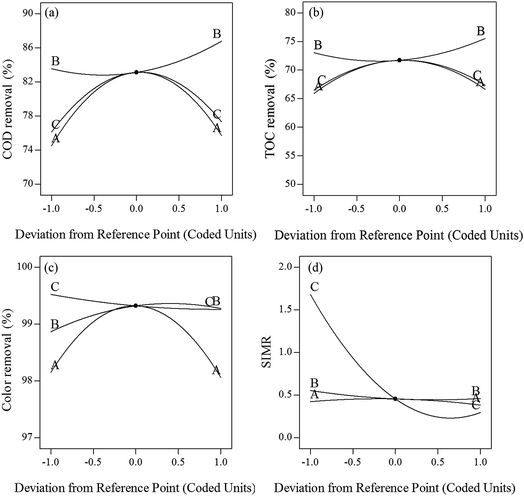Fig. 3 Perturbation graphs for (a) COD removal (b) TOC removal (c) color removal (d) SIMR (A-initial pH, B-initial [H₂O₂] concentration, C-initial [Fe²⁺] concentration).

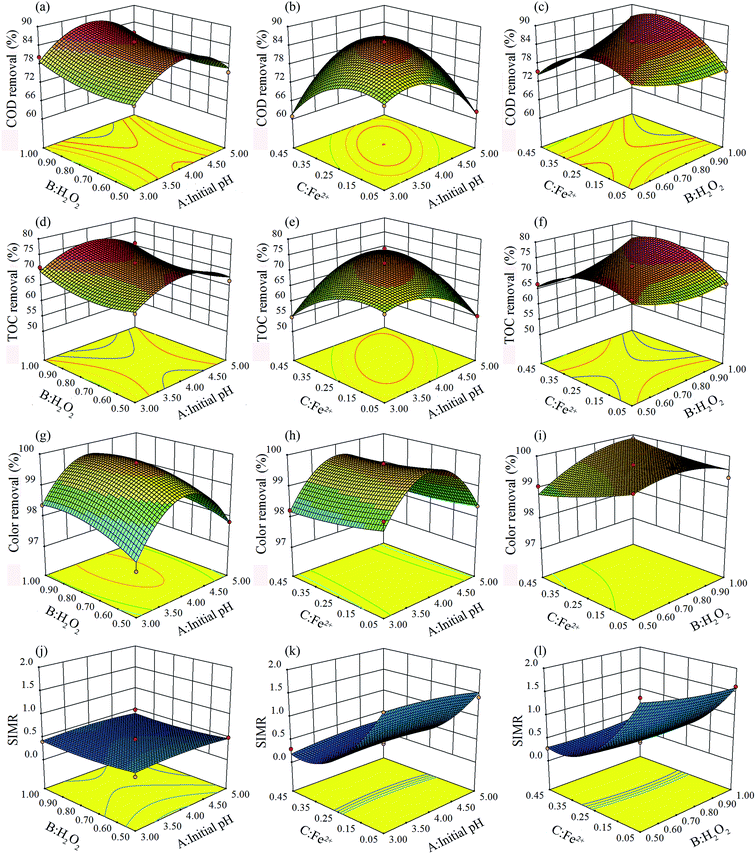
Three-dimensional response surfaces of the quadratic model were used to evaluate the interactions among independent variables and responses, as two variables were kept constant and the others varied within the experimental ranges.^5,45 The three-dimensional response surface of COD, TOC, color removal efficiencies, and SIMR plotted against the variables are shown in Fig. 4.

Fig. 4 Three-dimensional response surface plots of COD removal about (a) initial pH and H₂O₂ (b) initial pH and Fe²⁺ (c) H₂O₂ and Fe²⁺; of TOC removal about (d) initial pH and H₂O₂ (e) initial pH and Fe²⁺ (f) H₂O₂ and Fe²⁺; of color removal about (g) initial pH and H₂O₂ (h) initial pH and Fe²⁺ (i) H₂O₂ and Fe²⁺; of SIMR about (j) initial pH and H₂O₂ (k) initial pH and Fe²⁺ (l) H₂O₂ and Fe²⁺.

In the three-dimensional plots, deeper color indicates a greater value. The degree of curvature of a surface represents the degree that various responses have been affected. The more circular contour curvature represents a weaker interaction.

Considering the COD and TOC removal shown in Fig. 4(a)–(f), there was no significant interaction effect between initial pH and initial [H₂O₂] concentration especially in Fig. 4(a) and (d). At any specific pH value, with the change of initial [H₂O₂] concentration, the change regulations of the COD and TOC removal efficiencies were basically the same. At the same time, at any initial [H₂O₂] concentration, with the change of initial pH from 3.0 to 5.0, the change regulations of the COD and TOC removal efficiencies increased first and then decreased. In addition, there was no significant interaction effect between initial pH and initial [Fe²⁺] concentration as shown in Fig. 4(b) and (e). COD and TOC removal efficiencies both increased first and then decreased at any initial pH or initial [Fe²⁺] concentration. Only a weak interaction occurred between initial [H₂O₂] concentration and initial [Fe²⁺] concentration (Fig. 4(c) and (f)). When initial [Fe²⁺] concentration was lower, the COD and TOC removal efficiencies decreased gradually with the increase of initial [H₂O₂] concentration. In contrast, COD and TOC removal efficiencies increased gradually with the increase of initial [H₂O₂] concentration at higher initial [Fe²⁺] concentration.

For color removal efficiency (Fig. 4(g)–(i)), there was no significant interaction effect between initial pH and initial [Fe²⁺] concentration. In contrast, a weak interaction occurred between initial pH and initial [H₂O₂] concentration (Fig. 4(g)). When the initial [H₂O₂] concentration was lower, the change trend of color removal efficiency (increased first and then decreased) was more significant. However, the degree of change became weaker with the increase of initial [H₂O₂] concentration.

The interaction between initial [H₂O₂] concentration and initial [Fe²⁺] concentration was relatively significant. As shown in Fig. 4(j)–(l), there was no obvious interaction among the three factors. SIMR was only affected by the initial [Fe²⁺] concentration.

Analysis of optimization and model validation. The main objective of the optimization is to determine the optimum values of variables for BDI wastewater treatment with Fenton process from the models obtained using experimental data. In order to obtain the optimal reaction conditions, the optimization function of expert design (8.0.6) software was used to set up the constraint conditions of each influencing factor, namely the maximum COD, TOC and color removal efficiencies and the minimum SIMR. With multiple responses, the optimal condition where all parameters simultaneously meet the desirable criteria can be visually searched by superimposing or overlaying critical response contours on a contour plot (Fig. 5). Graphical optimization displays the area of feasible response values in the factor space, in which the regions that do fit the optimization criteria are shaded. According to the response surface model, the maximum COD, TOC, and color removal efficiencies and minimum SIMR under constraint conditions were calculated, and the results are shown in Table 5.

Fig. 5 Overlay plot for optimal region.

Table 5 The optimization solutions for chosen responses

Number	Initial pH	H2O2	Fe^2+	Removal (%)			SIMR	Desirability
				COD	TOC	Color
1	4.13	1.00	0.36	88.75	76.28	99.72	0.29	0.726
2	4.13	1.00	0.36	88.77	76.30	99.71	0.29	0.726
3	4.14	1.00	0.36	88.77	76.30	99.72	0.29	0.726
4	4.11	1.00	0.36	88.72	76.25	99.72	0.29	0.726
5	4.13	1.00	0.37	88.72	76.25	99.72	0.29	0.726
6	4.10	1.00	0.36	88.69	76.23	99.73	0.29	0.726
7	4.13	1.00	0.35	88.80	76.32	99.71	0.30	0.726
8	4.14	1.00	0.37	88.67	76.21	99.73	0.30	0.725
9	4.18	1.00	0.37	88.83	76.36	99.70	0.30	0.725
10	4.07	1.00	0.36	88.59	76.14	99.74	0.29	0.725
11	4.10	1.00	0.37	88.54	76.10	99.75	0.30	0.725

---

In order to verify the aforementioned results achieved from models and experiments, triplicate experiments were carried out under above optimal conditions number 1 (initial pH 4.13, 1.0 M [H₂O₂] and 0.36 M [Fe²⁺] dosage).

As shown in Table 6, the result obtained from experiments for all response parameters was in good agreement with that from the model prediction. Low errors and standard deviations showed the model could accurately reflect the influence of various factors on the four responses of BDI wastewater. In the actual operation process, the water samples before and after optimization of Fenton treatment were detected respectively by GC-MS. The results are shown in Fig. S2 and S3.† The peaks in Fig. S2† corresponded to the 11 kinds of benzene dye intermediate compounds shown in Table S1.† After the Fenton treatment of wastewater, these peaks almost disappeared. Therefore, the benzene compounds in the original wastewater bad been removed, and the newly formed organic compounds were mainly a small amount of formic acid, acetic acid and others. Therefore, we believe that the toxicity of wastewater was presumably reduced greatly. In the case of an improved biodegradability, the ratio of BOD₅/COD was increased from 0.08 to 0.49, suggesting an appropriate state for subsequent biological treatment.

Table 6 Verification experiments at optimum conditions

Conditions	Removal (%)			SIMR
	COD	TOC	Color
Experimental average value	85.29	75.23	99.99	0.39
Prediction value	88.75	76.28	99.73	0.41
Error	−3.46	−1.05	0.26	−0.02
STDVE	±1.71	±2.45	±0.18	±0.0041

---

4. Conclusion

The Fenton method was selected as an effective method to treat real BDIs. As evaluation indexes, the removal efficiencies of COD, TOC, and color were evaluated. Through single factor tests, the effect of the reaction time, initial pH, initial [H₂O₂] concentration and initial [Fe²⁺] concentration on Fenton oxidation efficiency was investigated. The best results of single factor tests were as follows: the reaction time is 60 min, the initial pH is 4.0, the initial [H₂O₂] concentration is 0.75 M, and the initial [Fe²⁺] concentration is 0.25 M.

Based on the Box–Behnken RSM, the COD, TOC, color removal efficiencies and SIMR were selected as response values. The separate action and interaction of the initial pH, the initial [H₂O₂] concentration, and the initial [Fe²⁺] concentration were analyzed. For the four response values, among the three factors, the initial [H₂O₂] concentration had the most significant effect on COD, TOC and color removal efficiencies. In contrast, the initial [Fe²⁺] concentration had the most significant effect on SIMR. However, in our current study, the effect of pH on the four response values was not significant, indicating effective Fenton oxidation of BDI wastewater can be achieved at a wide range of pH.

The results obtained from experiment were in good agreement with those achieved from the model prediction. By overlaying the responses, the overall optimum conditions were obtained at an initial pH of 4.13, an initial [H₂O₂] concentration of 1.0 M, and an initial [Fe²⁺] concentration of 0.36 M. To verify the model validity, extra experiments were conducted under optimal conditions, which led to a COD removal efficiency of 85.29%, a TOC removal efficiency of 75.23%, a color removal efficiency of 99.99% and a SIMR response of 0.39, respectively, and the results were in good agreement with the values predicted by the model. According to the GC-MS results the Fenton-treated wastewater is presumably not toxic. In addition, the ratio of BOD₅/COD increased from 0.08 to 0.49, indicating an improved biodegradability. These results are very helpful in understanding the degradation characteristics of BDI by Fenton method and the optimization of influenced factors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the financial of water quality control principles for safe storage of reclaimed groundwater (Project No. 51238001), the Natural Science Foundation of China (Grant 41672239), the Research Fund of China Geological Survey (DD20160300, 1212011121166), and the National Water Pollution Control and Treatment Science and Technology Major Project (2015ZX07406005-001).

References

1. P. Gregory, Kirk-Othmer Encycl. Chem. Technol., 2000, 1–66.
2. R. I. Steiner and J. D. Miskie, Riegel's Handb Ind Chem, 1992, pp. 809–861.
3. I. Arslan-Alaton, G. Basar and T. Olmez-Hanci, Color. Technol., 2012, 128, 387–394.
4. H. Lu, J. Zhou, J. Wang, H. Ai, C. Zheng and Y. Yang, Biodegradation, 2008, 19, 643–650.
5. I. Arslan-Alaton, G. Tureli and T. Olmez-Hanci, J. Photochem. Photobiol., A, 2009, 202, 142–153.
6. C. C. Hsueh, L. P. You, J. Y. Li, C. T. Chen, C. C. Wu and B. Y. Chen, J. Taiwan Inst. Chem. Eng., 2016, 64, 180–188.
7. K. Swaminathan, K. Pachhade and S. Sandhya, Desalination, 2005, 186, 155–164.
8. G. Xiao and L. Long, Appl. Surf. Sci., 2012, 258, 6465–6471.
9. L. Gu, H. Guo, P. Zhou, N. Zhu, D. Zhang, H. Yuan and Z. Lou, Environ. Sci. Pollut. Res., 2014, 21, 2043–2053.
10. N. Zhu, L. Gu, H. Yuan, Z. Lou, L. Wang and X. Zhang, Water Res., 2012, 46, 3859–3867.
11. C. Minero, M. Lucchiari, V. Maurino and D. Vione, RSC Adv., 2013, 3, 26443–26450.
12. J. Shen, C. Ou, Z. Zhou, J. Chen, K. Fang, X. Sun, J. Li, L. Zhou and L. Wang, J. Hazard. Mater., 2013, 260, 993–1000.
13. A. Ahmad, S. H. Mohd-Setapar, C. S. Chuong, A. Khatoon, W. A. Wani, R. Kumar and M. Rafatullah, RSC Adv., 2015, 5, 30801–30818.
14. L. Gu, N. Zhu, L. Wang, X. Bing and X. Chen, J. Hazard. Mater., 2011, 198, 232–240.
15. A. Ajmal, I. Majeed, R. N. Malik, H. Idriss and M. A. Nadeem, RSC Adv., 2014, 4, 37003–37026.
16. E. Neyens and J. Baeyens, J. Hazard. Mater., 2003, 98, 33–50.
17. L. Gu, N. Zhu, H. Guo, S. Huang, Z. Lou and H. Yuan, J. Hazard. Mater., 2013, 246–247, 145–153.
18. I. Arslan-Alaton, N. Ayten and T. Olmez-Hanci, Appl. Catal., B, 2010, 96, 208–217.
19. D. H. Ahn, W. S. Chang and T. I. Yoon, Process Biochem., 1999, 34, 429–439.
20. N. Koprivanac, G. Bosanac, Z. Grabaric and S. Papic, Environ. Technol., 2008, 14, 37–41.
21. R. L. Mason, R. F. Gunst and J. L. Hess, Technometrics, 2003, 225, 783–786.
22. Y. Wu, S. Zhou, F. Qin, X. Ye and K. Zheng, J. Hazard. Mater., 2010, 180, 456–465.
23. Y. Xie, L. Chen and R. Liu, Chemosphere, 2016, 155, 217–224.
24. J. H. Shen, J. J. Horng, Y. S. Wang and Y. R. Zeng, Chemosphere, 2017, 182, 364–372.
25. N. Masomboon, C. Ratanatamskul and M. C. Lu, J. Hazard. Mater., 2010, 176, 92–98.
26. M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. A. Escaleira, Talanta, 2008, 76, 965–977.
27. L. R. Rad, M. Irani, F. Divsar, H. Pourahmad, M. S. Sayyafan and I. Haririan, J. Taiwan Inst. Chem. Eng., 2015, 47, 190–196.
28. M. B. Kasiri, H. Aleboyeh and A. Aleboyeh, Environ. Sci. Technol., 2008, 42, 7970–7975.
29. M. Moradi and F. Ghanbari, Journal of Water Process Engineering, 2014, 4, 67–73.
30. A. Amiri and M. R. Sabour, Waste Manag., 2014, 34, 2528–2536.
31. B. Bianco, I. D. Michelis and F. Vegliò, J. Hazard. Mater., 2011, 186, 1733–1738.
32. R. Colombo, T. C. R. Ferreira, S. A. Alves, R. L. Carneiro and M. R. V. Lanza, J. Environ. Manage., 2013, 118, 32–39.
33. Sukriti, J. Sharma, A. S. Chadha, V. Pruthi, P. Anand, J. Bhatia and B. S. Kaith, J. Environ. Manage., 2017, 190, 176–187.
34. N. Masomboon, C. Ratanatamskul and M. C. Lu, J. Hazard. Mater., 2010, 176, 92.
35. J. Shi, T. Long, R. Ying, L. Wang, X. Zhu and Y. Lin, Chemosphere, 2017, 180, 117–124.
36. L. Lunar, D. Sicilia, S. Rubio, D. Pérez-Bendito and U. Nickel, Water Res., 2000, 34, 1791–1802.
37. Y. Wu, S. Zhou, X. Ye, R. Zhao and D. Chen, Colloids Surf., A, 2011, 379, 151–156.
38. Y. W. Kang and K. Y. Hwang, Water Res., 2000, 34, 2786–2790.
39. H. Zhang, H. J. Choi, P. Canazo and C. Huang, J. Hazard. Mater., 2009, 161, 1306–1312.
40. A. D. Bokare and W. Choi, J. Hazard. Mater., 2014, 275, 121–135.
41. M. D. G. D. Luna, M. L. Veciana, J. I. Colades, C. C. Su and M. C. Lu, J. Taiwan Inst. Chem. Eng., 2014, 45, 565–570.
42. C. K. Duesterberg and T. D. Waite, Environ. Sci. Technol., 2006, 40, 4189–4195.
43. H. S. El-Desoky, M. M. Ghoneim and N. M. Zidan, Desalination, 2010, 264, 143–150.
44. R. Saini, M. K. Mondal and P. Kumar, Environ. Prog. Sustainable Energy, 2017, 36, 420–427.
45. Y. Akhi, M. Irani and M. E. Olya, J. Taiwan Inst. Chem. Eng., 2016, 63, 327–335.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09404c

---