Open Access Article
Open Access ArticleEffect of R-site element on crystalline phase and thermal stability of Fe substituted Mn mullite-type oxides: R2(Mn1−xFex)4O10−δ (R = Y, Sm or Bi; x = 0, 0.5, 1)†
Sampreetha Thampy‡
a,
Nickolas Ashburn‡a,
Thomas J. Martinb,
Chenzhe Lic,
Yongping Zhenga,
Julia Y. Chan b,
Kyeongjae Cho
b,
Kyeongjae Cho a and
Julia W. P. Hsu
a and
Julia W. P. Hsu *a
*a
aDepartment of Materials Science and Engineering, University of Texas at Dallas, Richardson, TX 75080, USA. E-mail: jwhsu@utdallas.edu
bDepartment of Chemistry and Biochemistry, University of Texas at Dallas, Richardson, TX 75080, USA
cSchool of Mechanical and Aerospace Engineering, Seoul National University, Seoul 151-742, Republic of Korea
First published on 19th December 2017
Abstract
Combining experimental and theoretical studies, we investigate the role of R-site (R = Y, Sm, Bi) element on the phase formation and thermal stability of R2(Mn1−xFex)4O10−δ (x = 0, 0.5, 1) mullite-type oxides. Our results show a distinct R-site dependent phase behavior for mullite-type oxides as Fe is substituted for Mn: 100% mullite-type phase was formed in (Y, Sm, Bi)2Mn4O10; 55% and 18% of (Y, Sm)2Mn2Fe2O10−δ was found when R = Y and Sm, respectively, for equal Fe and Mn molar concentrations in the reactants, whereas Bi formed 54% O10- and 42% O9-mixed mullite-type phases. Furthermore, when the reactants contain 100% Fe, no mullite-type phase was formed for R = Y and Sm, but a sub-group transition to Bi2Fe4O9 O9-phase was found for R = Bi. Thermogravimetric analysis and density functional theory (DFT) calculation results show a decreasing thermal stability in O10-type structure with increasing Fe incorporation; for example, the decomposition temperature is 1142 K for Bi2Mn2Fe2O10−δ vs. 1217 K for Bi2Mn4O10. On the other hand, Bi2Fe4O9 O9-type structure is found to be thermally stable up to 1227 K. These findings are explained by electronic structure calculations: (1) as Fe concentration increases, Jahn–Teller distortion results in mid band-gap empty states from unstable Fe4+ occupied octahedra, which is responsible for the decrease in O10 structure stability; (2) the directional sp orbital hybridization unique to Bi effectively stabilizes the mullite-type structure as Fe replaces Mn.
1. Introduction
Functional materials based on transition metal oxides with mullite-type crystalline structure, R2M4O10−δ (R = Y, rare-earth or Bi; M = transition metal), have gained much attention due to their interesting magnetic and multiferroic properties.1,2 Recently, these compounds show great promise in energy applications, e.g. in solid oxide fuel cells,3 as photocatalysts,4 and NOx oxidation catalysts,5–7 and are considered as a potential alternative to platinum group metals. R2M4O10−δ adopts the orthorhombic crystal structure of space group Pbam and consists of infinite chains of edge-sharing MO6 octahedra along the c-direction (Fig. S1, ESI†). The structure can be classified according to two sub-groups depending on the oxygen concentration: R2Mn4O10 (O10) and R2M4O9 (O9). The two sub-groups differ in the MOx (4h Wyckoff site) units that link the MO6 (4f Wyckoff site) octahedral chains: edge-shared distorted MO5 square pyramid in the O10-type (Fig. S1b, ESI†) or vertex-sharing MO4 tetrahedra along the ab-direction in the O9-type (Fig. S1c, ESI†). The R atoms, which are in 3+ oxidation state, are located in the structural channels running parallel along the c-axis (Fig. S1a, ESI†).8–12 It is clear that the transition metal (M) atoms, which occupy both the 4f- and 4h-Wyckoff sites, will strongly affect the structure formation and stability;10,12 however, the role of R-site elements is less obvious.Mn–Fe mullite-type oxides have been studied owing to their interesting magnetic behavior. As the ionic radii of Fe3+ and Mn3+ are similar, substituting Mn with Fe should not cause much lattice distortion.12–19 However, because Fe4+ exhibits strong Jahn–Teller distortion and causes structure instability, sub-group transition from R2Mn4O10 O10-type to R2Fe4O9 O9-type is expected. Curiously, experimental studies reported such a sub-group transition in R = Bi Mn–Fe compounds,12,19 but only the O10-type structure has been observed when R = Y or rare earth elements.13–18 In addition, except for Bi, no pure R2Mn2Fe2O10 mullite-type phase has been successfully synthesized with other R-site elements; impurity phases corresponding to perovskite or binary oxides or both are found in these compounds upon calcination at high temperatures and under high oxygen pressure.13–17 Moreover, there are significant differences and conflicting reports on the maximum Fe concentration that supports the structure stability in Fe–Mn mullites.12,19 Published literature reported the experimental observation, but lacked the fundamental understanding on the role of R-site elements on mullite-type phase formation and stability or why Bi compounds forms the stable mullite-type structure for all Mn–Fe compositions.
While R-site elements are trivalent, their electronic structure can differ significantly. Here, we carry out combined experimental and theoretical studies to understand the role of R-site elements on phase formation and thermal stability of R2(Mn1−xFex)4O10−δ (R = Y, Sm, and Bi; x = 0, 0.5, 1) compounds. The three R-site elements are chosen because Y3+ has a closed shell, Sm3+ representing a lanthanide analogue with unpaired electrons, and Bi3+ with sp3 hybridization. These compounds were synthesized by co-precipitation-calcination method. The crystalline phases were characterized using X-ray diffraction (XRD) and structure refinement was carried out by Rietveld method. The oxidation states of R, Mn, and Fe were determined by X-ray photoelectron spectroscopy (XPS). The thermal stability and phase transformation during decomposition was studied by thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC). To explain the differences observed experimentally, we performed density functional theory (DFT) calculations with energy correction methodology previously employed to calculate the thermal stability of different R2Mn4O10 compounds.20 In addition, electronic structures were investigated to explain the R-site dependence as a function of Fe substitution. The insight gained through such combined experimental and theoretical studies will advance the design of mullite-type oxides with desired properties.
2. Experimental methods
2.1. Synthesis and characterization
R2Mn4O10 (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn = 1
Mn = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), R2Mn2Fe2O10−δ (R
2), R2Mn2Fe2O10−δ (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn
Mn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1
Fe = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and R2Fe4O9 (R
1), and R2Fe4O9 (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 1
Fe = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) were synthesized using analytical grade R(NO3)3·6H2O, Mn(CH3CO2)2·4H2O, and Fe(NO3)3·9H2O precursors by co-precipitation method.21 The precipitate obtained was then filtered and dried at 378 K overnight. The dried samples were ground and calcined at 773 K for 8 h in air to eliminate organic materials, followed by a second calcination step at high temperatures. For 100% Mn compounds, the calcination was carried out at 1373 K, 1273 K, and 1073 K for Y, Sm, and Bi, respectively, in air to obtain single-phase materials. For 50% Fe/50% Mn and 100% Fe samples, the calcination was carried out at 1073 K in air. This temperature was chosen to obtain mullite-type phase in all three R-site compounds. For Bi compounds, temperatures higher than 1073 K are too close to their decomposition temperatures; for Y or Sm compounds, the mullite-type phase cannot form below 1073 K. Thus, to get a meaningful comparison, synthesis conditions were kept constant.
2) were synthesized using analytical grade R(NO3)3·6H2O, Mn(CH3CO2)2·4H2O, and Fe(NO3)3·9H2O precursors by co-precipitation method.21 The precipitate obtained was then filtered and dried at 378 K overnight. The dried samples were ground and calcined at 773 K for 8 h in air to eliminate organic materials, followed by a second calcination step at high temperatures. For 100% Mn compounds, the calcination was carried out at 1373 K, 1273 K, and 1073 K for Y, Sm, and Bi, respectively, in air to obtain single-phase materials. For 50% Fe/50% Mn and 100% Fe samples, the calcination was carried out at 1073 K in air. This temperature was chosen to obtain mullite-type phase in all three R-site compounds. For Bi compounds, temperatures higher than 1073 K are too close to their decomposition temperatures; for Y or Sm compounds, the mullite-type phase cannot form below 1073 K. Thus, to get a meaningful comparison, synthesis conditions were kept constant.
X-ray diffraction data were collected two ways. First, the crystalline phases of the reaction products were characterized using powder Rigaku Ultima III X-ray diffractometer equipped with Ni-filtered Cu Kα1,2 radiations (λKα1 = 0.15406 nm, λKα2 = 0.15444 nm).22 The patterns were collected over a 2θ range from 20° to 60° with a step size of 0.02° and a scan speed of 0.2° per min. The measured diffraction patterns were compared to the powder diffraction files to identify the crystalline phases. To obtain accurate phase compositions and lattice parameters, X-ray powder diffraction data were also collected with a Bruker D8 Advance powder diffractometer operating at 40 kV/30 mA equipped with a LYNXEYE XE detector and a Cu Kα source (λKα1 = 0.15406 nm, λKα2 = 0.15444 nm) with a 0.06 mm incident beam and a 5.0 mm receiving slit with a Ni filter. Ground polycrystalline powders were placed on a low-background holder. X-ray diffraction data were collected over a 2θ range from 10° to 80° with a step size of 0.02° and an exposure time of 2 s rotating at five rotations per minute. The crystalline phases were first identified by comparing with reported crystal structure. Multi-phase Rietveld refinement was performed using DIFFRAC PLUS TOPAS 4.2 (Bruker AXS, Karlsruhe, Germany). For the Rietveld model, λKα1 = 0.15406 nm wavelength was used.
X-ray photoelectron spectra were measured using a PHI5000 Versa Probe II (Physical Electronics Inc.) using a monochromatic Al Kα X-ray source (1486.6 eV). Peak fitting was performed using Multipak software as reported in our previous work.21 The estimated error in binding energy measurements is ± 0.01 eV.
To measure the decomposition temperature, TGA and DSC measurements were carried out at a heating rate of 2 K min−1 from room temperature to 1273–1473 K in air (Q600, TA Instruments). To study the phase changes observed in the TGA-DSC measurements and to identify the crystalline phases of the decomposed products, we simulated the reactions by heating a different aliquot of the same sample in a muffle furnace (KSL-1100X, MTI Corporation) to obtain enough decomposed material for XRD measurements.
3. Theoretical methodology
Density functional theory (DFT) with the spin-polarized generalized gradient approximation (GGA) embedded in Vienna ab initio simulation package (VASP) was employed.23–26 The plane-wave basis based projector augmented-wave pseudopotentials were used in the calculation. The valence-electron configurations used in the pseudopotentials are as follows: 4s24p64d15s2 for Y, 5s25p64f16s2 for Sm, 5d106s26p3 for Bi, 3p63d54s2 for Mn, 3d64s2 for Fe, and 2s22p4 for O. To achieve a better description of the systems' total energy and electronic structures, GGA + U method23,24 and hybrid DFT with Heyd–Scuseria–Ernzerhof approach (HSE06)27 were applied. All structures in our calculations were relaxed until a force convergence criterion of 0.001 eV nm−1 was fulfilled. High 450 eV energy cut-off and a Monkhorst–pack k-space sampling mesh with a density of 0.003 nm−1 (GGA + U) or 0.01 nm−1 (HSE06) for each direction was used to assure an accurate total energy for all the simulated systems. Furthermore, to determine the most likely magnetic state, the structures were relaxed with consideration of all possible spin states. The mullite structure was found to be most stable in a high-spin ferromagnetic state after relaxation. All results shown below are performed in this spin state.Formation enthalpy calculated by the GGA or GGA + U method still includes significant errors.28 Therefore, we used corrections on the total energies to improve the accuracy of the ternary compounds' formation enthalpies. Eqn (1) has been used to make the corrections in our calculations.
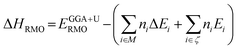 | (1) |
4. Results and discussion
4.1. Mullite-type phase formation with Fe substitution
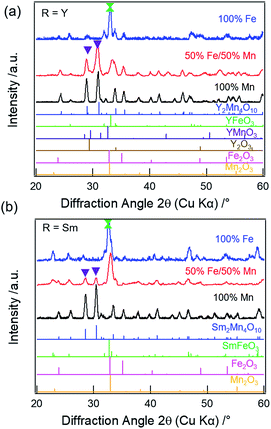
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 (21%), Mn2O3 (16%), and YMnO3
31 (21%), Mn2O3 (16%), and YMnO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 (7%) impure phases, respectively. For R = Sm, the XRD pattern (Fig. 1b, red) does show weak reflections corresponding to the mullite-type phase (purple inverted triangles), however, the phase purity is only 18%. The primary phases are found to be SmFeO3 (47%) and Mn2O3 (35%), respectively (Fig. S2c & Table S2, ESI†). Munoz et al. reported the presence of perovskite impurity phase in their Y2Mn2Fe2O10 compound, but found that the mullite phase purity can be increased by annealing at 1173 K for 12 h under high oxygen pressure of 200 bar.14 Thus, one possibility for the presence of the non-mullite-type phases in our samples is the low oxygen partial pressure in the annealing atmosphere. However, as previously reported, complete elimination of the non-mullite-type phase in R2Mn2Fe2O10 compounds is not possible for R = Y, Sm, Er, Yb, and Tb, even when the thermal treatments are carried out at high oxygen pressure or when synthesized under mechanical milling.13–17 The lattice parameters obtained from the refinements for the mullite-type phase are listed in Table S3 (ESI†).
32 (7%) impure phases, respectively. For R = Sm, the XRD pattern (Fig. 1b, red) does show weak reflections corresponding to the mullite-type phase (purple inverted triangles), however, the phase purity is only 18%. The primary phases are found to be SmFeO3 (47%) and Mn2O3 (35%), respectively (Fig. S2c & Table S2, ESI†). Munoz et al. reported the presence of perovskite impurity phase in their Y2Mn2Fe2O10 compound, but found that the mullite phase purity can be increased by annealing at 1173 K for 12 h under high oxygen pressure of 200 bar.14 Thus, one possibility for the presence of the non-mullite-type phases in our samples is the low oxygen partial pressure in the annealing atmosphere. However, as previously reported, complete elimination of the non-mullite-type phase in R2Mn2Fe2O10 compounds is not possible for R = Y, Sm, Er, Yb, and Tb, even when the thermal treatments are carried out at high oxygen pressure or when synthesized under mechanical milling.13–17 The lattice parameters obtained from the refinements for the mullite-type phase are listed in Table S3 (ESI†).
On full replacement of Mn with Fe (100% Fe), XRD patterns of both Y (Fig. 1a, blue) and Sm (Fig. 1b, blue) compounds show no reflections corresponding to mullite phase. The perovskite (YFeO3 (57%) or SmFeO3 (72%)) is found to be the primary phase, along with Y2O3 or Sm2O3, respectively, and Fe2O3 secondary phases. The refined patterns for Y (Fig. S2b†) and Sm (Fig. S2d†) are shown in the ESI.† Thus, mullite-type phase formation is found to be unfavorable when R = Y or Sm at higher Fe concentration.
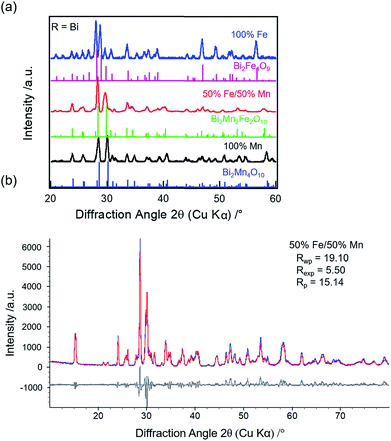
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 (4%) and BiFeO3
33 (4%) and BiFeO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 (1%). Thus, a sub-group transition from O10- to O9-type structure is observed for R = Bi when Fe concentration increases from 50% to 100% unlike R = Y or Sm.
34 (1%). Thus, a sub-group transition from O10- to O9-type structure is observed for R = Bi when Fe concentration increases from 50% to 100% unlike R = Y or Sm.
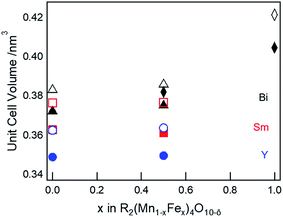
The refined lattice parameters for the mullite-type compounds are listed in Table S3 (ESI†). The unit cell volume as a function of Fe concentration for R = Y (blue solid circles), Sm (red solid squares), and Bi (black solid triangles) compounds are depicted in Fig. 3. In general, the unit cell volume systematically decreases with the substitution of a smaller R ions (Y3+ < Sm3+ < Bi3+) in the O10-type phase, consistent with Vegard's law. Up to 50% Fe in the mullite-type structure, only a small change in the unit cell volume is observed. This observation is consistent with that Fe primarily substitutes for Mn3+ in the square pyramidal (4h) sites and given similar ionic radii of Fe3+ (0.058 nm) and Mn3+ (0.058 nm),35 cell dimensions do not change significantly upon full substitution in these sites. As Fe concentration exceeds 50% and all Mn3+ have been replaced, Fe must substitute on the octahedral (4f) sites. We then observed a significant increase in unit cell volume for Bi2Fe4O9 (∼9%, black solid diamond), which is attributed to the replacement of smaller Mn4+ (0.053 nm)35 by larger Fe3+ ions (0.065 nm)35 in the octahedral sites. These results show a distinct R-site dependent phase behaviour of mullite-type oxides: only Bi is found to form a stable mullite-type structure at all Mn–Fe compositions. In order to understand this unique behaviour of Bi compared to Y or Sm, we study formation enthalpy and electronic structure using DFT (see Section 4.4 below). Since neither Y nor Sm could form stable Fe substituted mullite-type structures, we carried out the XPS and decomposition studies focusing on Bi O10 and O9-type compounds.
4.2. XPS of Bi2(Mn1−xFex)4O10−δ compounds
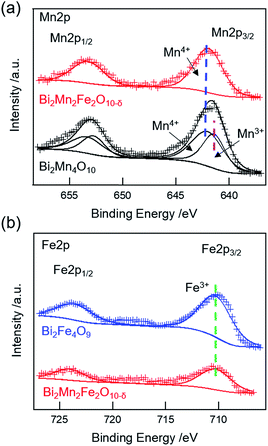
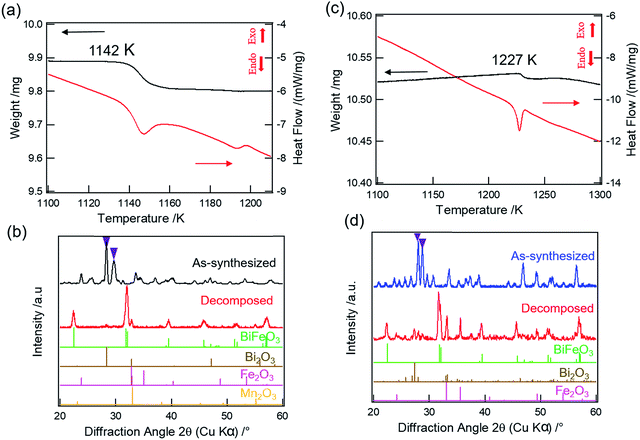
XPS studies were carried out on Bi2Mn4O10, Bi2Mn2Fe2O10−δ, and Bi2Fe4O9 stable structures to probe whether there are changes in the oxidation states of Mn and Fe. The measured and fitted XPS spectra of Mn 2p and Fe 2p core-levels are shown in Fig. 4. The Mn 2p spectrum of Bi2Mn4O10 (Fig. 4a, black) can be deconvoluted into two peaks at 641.2 eV and 641.8 eV, corresponding to the binding energies of 2p3/2 Mn3+ (pink dashed line) and Mn4+ (blue dashed line), respectively, in good agreement with the literature.36 On the other hand, the Mn 2p spectrum of Bi2Mn2Fe2O10−δ (Fig. 4a, red) exhibits only a single peak at 641.9 eV, corresponding to the binding energy of 2p3/2 Mn4+.36 No peak corresponding to Mn3+ is found, indicating that 4h square pyramidal sites are fully replaced by Fe. The Fe 2p spectra for Bi2Mn2Fe2O10−δ (Fig. 4b, red) and Bi2Fe4O9 (Fig. 4b, blue) is fitted to a single peak. The binding energy of Fe 2p3/2 at 710.3 eV (Fig. 4b, green dashed line) corresponds to 3+ oxidation state.36 No peaks corresponding to Fe4+ (712.5 eV)37 are found in either structure. The XPS results are consistent with Rietveld refinement of the XRD results for this sample, which shows the co-existence of Bi2Mn2Fe2O10 and Bi2Fe4O9. Mn ions in Bi2Mn2Fe2O10 are exclusively in the 4f sites, i.e. 4+, and Fe ions occupy the 4h sites, i.e. 3+, while Fe in both sites of Bi2Fe4O9 have 3+ oxidation state. We further calculated the Fe/Mn and (Mn + Fe)/Bi ratios of the Bi2Mn2Fe2O10−δ sample following Gesing et al. in order to understand which metal is enriched on the surface layers.38 The surface Fe/Mn ratio is found to be 0.73 ± 0.13, indicating that the surface is enriched with Mn, while (Mn + Fe)/Bi is found to be 1.61 ± 0.11 compared to the formula ratio of 2. These results indicate that the Fe composition is intrinsic to the bulk phase rather than only on the surface. Combined XRD and XPS results show that Fe3+ ions preferentially occupy 4h square-pyramidal and Mn4+ occupy 4f octahedral sites in Bi2Mn2Fe2O10−δ. While in Bi2Fe4O9, Fe3+ ions are distributed in tetrahedral and octahedral sites, respectively.4.3. Thermal stability and decomposition reaction of Bi2(Mn1−xFex)4O10−δ
We further carried out TGA-DSC measurements of Bi2(Mn1−xFex)4O10−δ compounds to study their thermal stability. 100% Mn compound, i.e. Bi2Mn4O10, is found to be thermally stable until 1217 K as reported in our previous work.20 Fig. 5a shows the TGA-DSC data of calcined Bi2Mn2Fe2O10−δ sample heated from room temperature to 1273 K in air. We observe a clear weight loss in TGA (Fig. 5a, black) and a corresponding endothermic peak in DSC (Fig. 5a, red), which may be attributed to the thermal decomposition of the sample. The temperature associated with the thermal event is 1142 K, determined from the onset of weight loss. In order to establish that the observed weight loss corresponds to thermal decomposition in the sample and to determine the decomposed product(s) using XRD, we mimicked the TGA experiment by heating the calcined Bi2Mn2Fe2O10−δ sample in a furnace from room temperature to 1173 K in air without dwell time at the final temperature. Note that a different aliquot of the same sample used in the TGA-DSC experiment was used here. The XRD pattern of the sample heated above the decomposition temperature (Fig. 5b, red) shows no diffraction peak corresponding to the mullite-type phase (Fig. 5b, purple inverted triangles) when compared to the XRD pattern of the as-synthesized sample (Fig. 5b, black). On further examining the diffraction pattern (Fig. 5b, red), we find that the mullite-type phase decomposes primarily to BiFeO3 perovskite along with Bi2O3, Fe2O3, and Mn2O3 secondary phases; no reflections corresponding to the BiMnO3 perovskite phase are found. Based on the decomposed products, we propose the decomposition reaction for Bi2Mn2Fe2O10−δ compound in eqn (2):
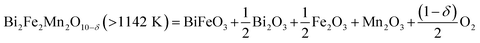 | (2) |
Attributing the weight loss in TGA at 1142 K (Fig. 5a, black) to the oxygen loss upon decomposition, we find δ = 0.6. When compared to the decomposition temperature of Bi2Mn4O10, incorporation of 50% Fe in the mullite-type structure lowers the thermal stability by ∼75 K. Moreover, in contrast to Bi2Mn4O10, where only binary oxides were found upon decomposition,20 the formation of BiFeO3 perovskite is found in Bi2Mn2Fe2O10−δ decomposition. Note that this sample exhibits a second thermal event at ∼1190 K, which has no associated weight loss. Having two decomposition temperatures are consistent with the sample having two phases: the mixed Fe–Mn O10 phase decomposes at lower temperature and the Fe O9 phase decomposes at higher temperature (see below).
Heating the already calcined Bi2Fe4O9 sample from room temperature to 1273 K in the TGA-DSC experiment results in a small weight loss (Fig. 5c, black) along with an endothermic peak (Fig. 5c, red), which may correspond to the thermal decomposition of Bi2Fe4O9 phase. The weight loss at this temperature (Fig. 5c, black) is small compared to Bi2Mn2Fe2O10−δ sample, 0.05% vs. 0.8% (Fig. 5a, black). To investigate this transition, we heated the calcined Bi2Fe4O9 sample from room temperature to 1273 K in air without dwell time at the final temperature. The XRD pattern (Fig. 5d, red) confirms the thermal decomposition of the Bi2Fe4O9 as no characteristic reflections of mullite-type phase (Fig. 5d, purple inverted triangles) are found when compared to the diffraction pattern of the as-synthesized sample (Fig. 5d, blue). The decomposition results primarily in the formation of the BiFeO3 perovskite phase along with Bi2O3 and Fe2O3 secondary phases. We therefore propose the decomposition reaction for Bi2Fe4O9 as given in eqn (3):
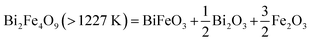 | (3) |
As eqn (3) shows, this decomposition reaction does not release oxygen, consistent with very small weight loss observed in TGA. One possibility is that the decomposition may be caused by the vaporization of Bi2O3 which is reported to occur above 1100 K, thus resulting in a small weight loss during decomposition.39,40 The second possibility is the creation of oxygen vacancies in the decomposed Bi2O3 and Fe2O3 as shown in the DFT calculations (Section 4.4.3); the small amount of oxygen loss (0.03 oxygen atom) during decomposition can be attributed to the creation of oxygen vacancies in the decomposition products. These results show that Bi2Mn4O10 and B2iFe4O9 are thermally more stable than Bi2Mn2Fe2O10−δ. To explain the experimentally observed differences, we present DFT calculation results below.
4.4. DFT calculations
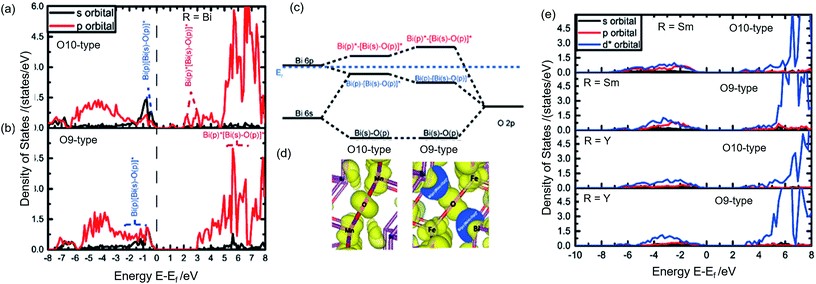
To answer the first question, we show the Fe and Mn density of states (DOS) in both 4f octahedral and 4h tetrahedral sites for O9 and O10-type structure in Fig. S4 & S5 (ESI†). We found that Fe4+ in the 4f octahedral sites of O10-type structure causes large Jahn–Teller distortion, which results in mid band-gap empty states, thus violating Hund's rule through the exchange interaction. This does not occur in the O9-type structure. Therefore, the Bi2Fe4O10 O10-type structure becomes unstable.
Although Y, Sm, and Bi are all in 3+ oxidation states, mullite-type structure is found only for R = Bi compounds at high Fe concentrations, indicating Bi mullite-type compounds have lower structural destabilization with increasing Fe substitution compared to other R-site compounds. In order to understand this phenomenon, we considered the R-site contribution to the electronic structure. In Fig. 7a & b, the projected-DOS of Bi in stable O10 and O9-type structures, respectively are illustrated. Significant sp orbital hybridization for Bi is observed in O9-type (Fig. 7b) near the Fermi level. Bi–O sp-antibonding states near the Fermi surface hybridizing with Bi p-electrons help stabilize the crystal structure.41 Such hybridization is only limited to near the Fermi level in the O10-type structures (Fig. 7a) due to the high oxidation state of Bi in the local crystal fields. In contrast, due to the shift of p and s orbitals towards the Fermi level in the DOS, more p-electron contribution is found in the hybridization below the Fermi surface in the O9-type structure (Fig. 7b). This is shown by the almost identical and overlapping s and p orbitals right below the Fermi level. As shown in Fig. 7c, we find that excessive p-electrons promote sp hybridization, which further stabilize Bi orbital energy. The outcome of the enhanced sp hybridization is shown to be the directional polarization of Bi electrons (Fig. 7d). In this case, a repulsive force between the Bi atoms could be introduced, thus maintaining the structure's framework along the ab-plane. The polarization resulted in elongation of the crystal lattice in a–b direction (Bi–Bi length was prolonged from 0.37 nm to 0.42 nm) further facilitate Fe forming MO4 tetrahedral polyhedral without any distortion.
Unlike Bi, electronic structures of Sm and Y compounds (Fig. 7e) show that the extra charge from the O10 to O9-type transition would fill up 4d orbital in Y and the 4f orbital in Sm. These orbitals are compact and do not hybridize, thus failing to form the necessary directional polarization that is required to maintain a stable structure. Hence, Y and Sm cannot form stable O9-type phase while Bi can. Since O10-type is unstable due to the Jahn–Teller distortion of Fe4+ at high Fe content and no sp hybridization exists to stabilize the O9-type structure, compounds with R = Y or rare earth elements do not form mullite-type structures at these temperatures.
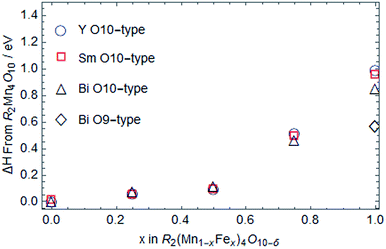
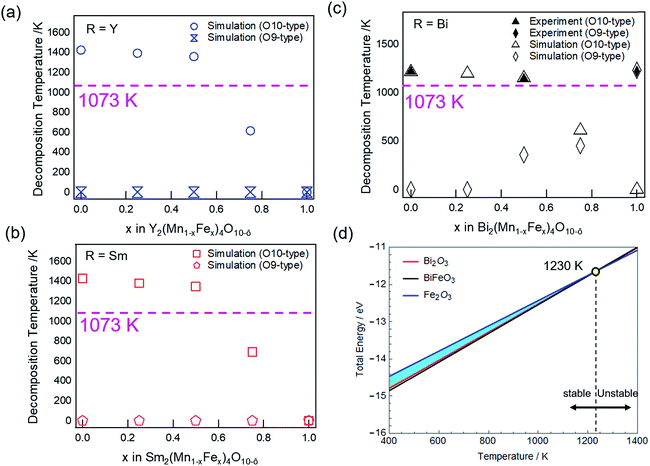
As we further increase the Fe concentration (x ≥ 0.6), the decomposition temperature of O10-type structure falls below the calcination temperature (Fig. 8a–c, pink dashed line). Consequently, the O10-type structure cannot be formed for all R-site elements studied in this report. Thus, combined experimental and theoretical results show that the thermal stability of O10-type structures decreases with increasing Fe concentration. With respect to the calcination temperature used in this report (1073 K), the substitution limit for Fe in R = Y and Sm O10-type compounds are predicted to be x ≤ 0.6. However, simulation predicts O10 structures, if formed, to have higher thermal stability for Y and Sm than Bi compound.
Considering the thermal stability of O9-type structures, Y (Fig. 8a, blue open dumbbells) and Sm (Fig. 8b, red open pentagons) are found to be thermodynamically unstable for all Fe/Mn ratios. On the other hand, Bi O9-type is calculated to have a distinct decomposition temperature in Fe rich structures (Fig. 8c, black open diamonds). The decomposition temperature is found to increase with Fe concentration, but for x < 1, the decomposition temperature is below the calcination temperature (Fig. 8c, pink line), hence unable to form O9-type structure. The decomposition temperature for Bi2Fe4O9 (at x = 1) is calculated to be 1230 K, which is higher than Bi2Mn2Fe2O10−δ (1150 K) and in good agreement with the experimental result.
Fig. 8d shows the change in total energy as a function of temperature for Bi2Fe4O9. The solid lines define the boundaries where precipitation of the compound begins under the simulated Bi2Fe4O9 calcination conditions. The blue shaded region (Fig. 8d) represents the phase space where Bi2Fe4O9 is stable in the system. The upper limit of the stable region is confined by Fe2O3 (Fig. 8d, blue line) while the lower limit is governed by Bi2O3 (Fig. 8d, red line) and BiFeO3 (Fig. 8d, black line) phases. The temperature at which BiFeO3, Bi2O3, and Fe2O3 converge defines the limit of the Bi2Fe4O9 stable region, predicted to be 1230 K (Fig. 8d, yellow circle), in agreement with the experimental value of 1227 K. Further increasing the temperature will result in decomposition to BiFeO3, Bi2O3, and Fe2O3 phases, as in the experimental decomposition products (Fig. 5d, red).
Since the formation enthalpy of Bi2Fe4O9 is ∼0.6 eV higher than that of Bi2Mn4O10 (Fig. 6), one would expect the decomposition temperature of Bi2Fe4O9 to be much lower than that of Bi2Mn4O10. Examining the stereochemical activity of Bi lone electron pair also lead to the same conclusion.42 In contrast, experimentally we observed the reverse, 1227 K for Bi2Fe4O9 vs. 1217 K for Bi2Mn4O10. The reason is that the decomposition products of Bi2Fe4O9 are also less stable than those for Bi2Mn4O10, with 0.8 eV per formula unit higher energy. In addition, examining the stability of oxygen vacancies in Fe2O3, Bi2O3, and BiFeO3, we find that these oxygen deficient phases are more stable than their stoichiometric oxides. More oxygen vacancies are expected in Bi2O3 because its formation enthalpy only increases by 0.58 eV per unit cell for one oxygen vacancy, vs. 2.78 eV and 2.97 eV increase in the formation enthalpy for one oxygen vacancy in Fe2O3 and BiFeO3, respectively. Oxygen vacancy formation in the decomposition products could explain the observed non-zero weight loss during the decomposition of Bi2Fe4O9 (Fig. 5c, black), although we cannot rule out the vaporization of Bi2O3. In Fig. 8d, both Fe2O3 and Bi2O3 were plotted with small vacancy amounts as required to cause decomposition. After taking into account everything discussed above, we calculated Bi2Fe4O9 to have a higher decomposition temperature than Bi2Mn4O10 (1230 K vs. 1213 K), as borne out by experiments.
5. Conclusions
In summary, we investigated R-site dependent phase formation and thermal stability of R2(Mn1−xFex)4O10−δ compounds. For the Mn compounds, Y, Sm, and Bi analogues are found to form pure O10 mullite-type phase with an orthorhombic unit cell. However, with 50% Fe and 50% Mn in the reactants, only 55% and 18% of the products when R = Y and Sm consists of (Y, Sm)2Mn2Fe2O10−δ mullite-type phase, respectively, whereas Bi forms a mixed phase of O10-(Bi2Mn2Fe2O10−δ, 54%) and O9-(Bi2Fe4O9, 42%) type structures. Furthermore, when the reactants contain 100% Fe, the mullite-type structure completely destabilizes for Y and Sm, but a sub-group transition to Bi2Fe4O9 (O9) phase is found for R = Bi. From XPS, we determine that the Mn and Fe exists in 4+ and 3+ oxidation states in Bi2Mn2Fe2O10−δ, respectively, indicating Mn4+ and Fe3+ are ordered in 4f octahedra and 4h square pyramids. While in Bi2Fe4O9, only Fe3+ is found, consistent with Fe4+ destabilizing O10-type structure. The thermal stability shows a decreasing decomposition temperature with increasing Fe concentration in O10-type structures (1142 K for Bi2Mn2Fe2O10−δ vs. 1217 K for Bi2Mn4O10) while Bi2Fe4O9 is found to decompose at the highest temperature (1227 K). Our DFT simulation confirms distinctly different phase behaviors among R = Y, Sm, and Bi compounds as observed experimentally and predicts Fe substitution limits for R = Y and Sm for the formation of mullite-type structure to be x < 0.6. The R-site dependent phase behaviors arise from the combination of unstable Fe4+ Jahn–Teller distortion in MO6 octahedra and orbital hybridization of R-site element. While Fe inevitably destabilizes the O10-type structure with increasing Fe concentration, we find that the directional sp orbital hybridization in Bi effectively stabilizes the O9 mullite-type structure. Y and rare earth elements do not have sp hybridization, and hence are unable to form O9-type structure. Our work provides a fundamental understanding for the unique phase behavior of Bi Mn–Fe mullite-type compounds previously reported in the literature without explanation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank J. M. Kweun, M. Cho, Y. Y. Kim for helpful discussions at the initial stage of this research. This work was funded in part by a grant (AT-1843) from the Welch Foundation and a funding from International Energy Joint R & D Program (No. 20168510011350) of the Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Ministry of Knowledge Economy. J. Y. C acknowledges NSF-DMR #1700030 for partial support. J. W. P. H acknowledges the Texas Instruments Distinguished Chair in Nanoelectronics.Notes and references
- L. M. Volkova and D. V. Marinin, J. Phys.: Condens. Matter, 2009, 21(015903), 1–14 Search PubMed.
- J. A. Alonso, M. T. Casais, M. J. Martínez-Lope, J. L. Martínez and M. T. Fernández-Díaz, J. Phys.: Condens. Matter, 1997, 9, 8515–8526 CrossRef CAS.
- I. Abrahams, A. J. Bush, G. E. Hawkes and T. Nunes, J. Solid State Chem., 1999, 147, 631–636 CrossRef CAS.
- Q. Ruan and W. Zhang, J. Phys. Chem. C, 2009, 113, 4168–4173 CAS.
- W. Wang, G. McCool, N. Kapur, G. Yuan, B. Shan, M. Nguyen, U. M. Graham, B. H. Davis, G. Jacobs, K. Cho and X. Hao, Science, 2012, 337, 832–835 CrossRef CAS PubMed.
- Z. Feng, J. Wang, X. Liu, Y. Wen, R. Chen, H. Yin, M. Shen and B. Shan, Catal. Sci. Technol., 2016, 6, 5580–5589 CAS.
- S. Thampy, Y. Zheng, S. Dillon, C. Liu, Y. Jangjou, Y. J. Lee, W. S. Epling, K. Xiong, Y. J. Chabal, K. Cho and J. W. P. Hsu, Catal. Today, 2017 DOI:10.1016/j.cattod.2017.05.008.
- R. X. Fischer and H. Schneider, Mullite, in The mullite-type family of crystal structures, ed. H. Schneider and S. Komarneni, John Wiley & Sons, 2006, pp. 16–18 Search PubMed.
- N. Niizeki and M. Wachi, Z. Kristallogr., 1968, 127, 173–187 CrossRef CAS.
- M. Burianek, T. F. Krenzel, M. Schmittner, J. Schreuer, R. X. Fischer, M. Muhlberg, G. Nenert, H. Schneider and T. M. Gesing, Int. J. Mater. Res., 2012, 103, 449–455 CrossRef CAS.
- M. M. Murshed, G. Nenert, M. Burianek, L. Robben, M. Muhlberg, H. Schneider, R. X. Fischer and T. M. Gesing, J. Solid State Chem., 2013, 197, 370–378 CrossRef CAS.
- H. Schneider, R. X. Fischer, T. M. Gesing, J. Schreuer and M. Muhlberg, Int. J. Mater. Res., 2012, 103, 422–429 CrossRef CAS.
- J. A. Alonso, M. J. Martínez-Lope and J. L. Martínez, Phys. Rev. B, 2005, 72(184402), 1–8 Search PubMed.
- A. Munoz, J. A. Alonso, M. J. Martínez-Lope and J. L. Martínez, Chem. Mater., 2004, 16, 4087–4094 CrossRef CAS.
- K. S. Kumar, N. Aparnadevi, A. Muthukumaran and C. Venkateswaran, Trans. Indian Inst. Met., 2015, 68, 693–698 CrossRef.
- M. J. Martínez-Lope, M. Retuerto, J. A. Alonso, M. García-Hernández, K. Krezhov, I. Spirov, T. Ruskov and M. T. Fernández-Díaz, Solid State Commun., 2009, 149, 540–545 CrossRef.
- M. Retuerto, M. J. Martínez-Lope, A. Muñoz, T. Ruskov, I. Spirov, K. Krezhov, M. T. Fernández-Díaz, M. García-Hernández and J. A. Alonso, Solid State Commun., 2010, 150, 1831–1836 CrossRef CAS.
- K. S. Kumar and C. Venkateswaran, J. Phys. D: Appl. Phys., 2011, 44(325001), 1–6 Search PubMed.
- Z. R. Kann, J. T. Auletta, E. W. Hearn, S. U. Weber, K. D. Becker, H. Schneider and M. W. Lufaso, J. Solid State Chem., 2012, 185, 62–71 CrossRef CAS.
- C. Li, S. Thampy, Y. Zheng, M. Kweun, Y. Ren, J. Y. Chan, H. Kim, M. Cho, Y. Y. Kim, J. W. P. Hsu and K. Cho, J. Phys.: Condens. Matter, 2016, 28(125602), 1–10 Search PubMed.
- S. Thampy, V. Ibarra, Y. Lee, G. McCool, K. Cho and J. W. P. Hsu, Appl. Surf. Sci., 2016, 385, 490–497 CrossRef CAS.
- M. H. Mendenhall, A. Henins, L. T. Hudson, C. I. Szabo, D. Windover and J. P. Cline, J. Phys. B: At., Mol. Opt. Phys., 2017, 50(115004), 1–18 Search PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- D. C. Langreth and M. J. Mehl, Phys. Rev. B, 1983, 28, 1809–1834 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B, 2011, 84(045115), 1–10 Search PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125(234109), 1–9 Search PubMed.
- G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Model., 1983, 23(2), 66–69 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Chem. Mater., 2007, 19, 543–552 CrossRef CAS.
- S. Lany, Phys. Rev. B, 2008, 78(245207), 1–8 Search PubMed.
- P. Coppens and M. Eibschutz, Acta Crystallogr., 1965, 19, 524–531 CrossRef CAS.
- K. Lukaszewicz and K. Kalicinska, Ferroelectrics, 1974, 7, 81–82 CrossRef CAS.
- E. M. Levin and R. S. Roth, J. Res. Natl. Bur. Stand., Sect. A, 1963, 68, 189–195 Search PubMed.
- S. A. Fedulov, Y. N. Venevtsev, G. S. Zhdanov, E. G. Smazhevskaya and I. S. Rez, Kristallografiya, 1962, 7, 77 CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–769 CrossRef.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- M. Ghaffari, M. Shannon, H. Hui, O. Tan and A. Irannejad, Surf. Sci., 2012, 606, 670–677 CrossRef CAS.
- T. M. Gesing, M. Schowalter, C. Weidenthaler, M. M. Murshed, G. Nenert, C. B. Mendive, M. Curti, A. Rosenauer, J.-C. Buhl, H. Schneider and R. X. Fischer, J. Mater. Chem., 2012, 22, 18814–18823 RSC.
- S.-U. Weber, T. M. Gesing, G. Eckold, R. X. Fischer, F.-J. Litterst and K.-D. Becker, J. Phys. Chem. Solids, 2014, 75, 416–426 CrossRef CAS.
- A. Maitre, M. Francois and J. C. Gachon, J. Phase Equilib. Diffus., 2004, 25, 59–67 CrossRef CAS.
- K. E. Kweon and G. S. Hwang, Phys. Rev. B, 2012, 8(165209), 1–8 Search PubMed.
- M. Curti, T. M. Gesing, M. M. Murshed, T. Bredow and C. B. Mendive, Z. Kristallogr., 2013, 228, 629–634 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Crystal structure of mullite-type oxides, U value table, Rietveld refinement plots, mullite phase purity table, experimental and simulated lattice parameters, density of states Bi2Fe4O10 (O10) and Bi2Fe4O9 (O9), density of states Bi2Mn4O9 (O9) and Bi2Mn4O10 (O10), TGA-DSC and XRD pattern of Y2Mn2Fe2O10−δ. See DOI: 10.1039/c7ra09699b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2018 |