Coexistence of Co doping and strain on arsenene and antimonene: tunable magnetism and half-metallic behavior

Abstract

Effectively modulating the magnetism of two-dimensional (2D) systems is critical for the application of magnetic nanostructures in quantum information devices. In this work, by employing density functional theory calculations, we found the coexistence of Co doping and strain can effectively control the spin states of arsenene and antimonene structures. Unstrained Co-doped arsenene (arsenene–Co) and Co-doped antimonene (antimonene–Co) structures are nonmagnetic while under a strain, the magnetic moments of both cases were abruptly increased to about 2 μ_B. The emergence of magnetism can be reflected by the reduction of the interactions between Co and its neighboring atoms by the strain, which leads to the spin-splitting of Co-3d states. More importantly, we found that the transition of magnetism accompanies the modifications of the electronic properties of arsenene and antimonene so that under strain both structures can exhibit a novel half-metallic behavior. These results provide an effective pathway for the development of arsenene- and antimonene-based electronic devices by applying Co doping and strain.

---

Introduction

2D materials with atomic thickness have recently attracted tremendous attention because of their charming properties and potential applications.^1–4 Graphene, a 2D counterpart of graphite, was firstly fabricated by Geim et al. They showed that graphene can possess an ultrahigh carrier mobility at room temperature.^5,6 Then, Singla et al. obtained 2D boron nitride that shares a similar structure to graphene, and reported that such a layered structure can be applied in the field of methyl orange dyes.⁷ Subsequently, an MoS₂ sheet was also realized by Radisavljevic et al. They showed that 2D MoS₂ is an ideal effective field-effect transistor owing to its suitable bandgap and band structure.⁸ Recently, Li et al. also realized phosphorene, and revealed that phosphorene is expected to be used for optoelectronic applications due to its high mobility and on/off ratio.⁹ In addition, various 2D structures, such as silicene, stanene, graphitic carbon nitride, and transition metal oxide sheets, with novel electronic properties have also been reported by Kara et al.,¹⁰ Zhu et al.,¹¹ Zhang et al.¹² and Sun et al.,¹³ respectively. Effective obtainment of 2D structures opens a pathway for the development of next-generation nanoscale electronic devices.

In order to meet the increasing demand for superior devices, different schemes have been proposed to modulate the properties of 2D materials.^14–24 Among these, doping and strain are considered as two of the most popular schemes. Note that most previous studies have focused on doping-function or strain-function alone.^17,19–24 Interestingly, some recent research has shown that, in contrast to the effect of only doping or only strain, the synergistic effect of doping and strain seems more interesting for the operation of the electronic properties, especially for the magnetic property, of 2D materials. For example, under the coexistence of transition metal (TM)-doping and strain in graphene, Huang et al. observed a sudden transition of the magnetism in the graphene,²⁵ which cannot be found in only TM-doped graphene²⁶ or only strain-interacted graphene.²⁷ For the coexistence of TM-doping and strain in phosphorene, Zhai et al. predicted a transition from a state with a low magnetic moment to a state with high magnetic moment²⁸ and Cai et al. revealed that phosphorene can undergo a transition from an antiferromagnetic order to a ferromagnetic order or to a different antiferromagnetic ordering.²⁹ In addition, our previous work also showed that the strain can effectively modulate the magnetism of TM-embedded MoS₂ sheets.³⁰ Thus, exploring the effects of the coexistence of doping and strain is significant for tuning the properties of 2D structures.

Recently, two new 2D semiconductors with high stability, named arsenene and antimonene, were identified theoretically and proposed for various applications by Zhang et al.³¹ In particular, on the basis of the epitaxial method, antimonene has been successfully fabricated by Wu et al.³² Previous studies of arsenene and antimonene mainly focused on the effect of strain or doping. For example, Zhang et al., Cao et al. and Wang et al. studied effects of tension and compressive strains on arsenene,^33–35 and Lu et al., Zhang et al. and Zhao et al. studied the effects of tension and compressive strains on antimonene.^36–38 Meanwhile, Iordanidou et al., Sun et al., Liu et al., Du et al., Luo et al., Li et al. and Li et al. investigated the influences of adsorption- and substitution-doping on arsenene,^39–45 and Akturk et al. and Yang et al. investigated the influences of adsorption- and substitution-doping on antimonene.^46,47 In this paper, we explored the influence of the coexistence of doping and strain on arsenene and antimonene. Although great efforts have been made to investigate the effects of doping and strain on arsenene and antimonene, as mentioned above, this is the first work to systematically explore the synergistic effects of doping and strain on arsenene and antimonene. Here we take Co substitution as an example for the doping. The paper is organized as follows: (1) to ensure the veracity of our calculation, we firstly compare the results of the structural and electronic properties of pristine arsenene and antimonene with those of previous reports. (2) Secondly, we studied the stabilities of arsenene and antimonene under the coexistence of Co doping and strain. (3) We then analyzed the magnetic transitions of arsenene and antimonene under the coexistence of Co doping and strain, and explored the origin of the interesting magnetic transitions. (4) Finally, we studied the effect of the coexistence of Co doping and strain on the electronic properties of arsenene and antimonene. On the basis of these studies, we can clearly determine the influence of the coexistence of Co doping and strain on arsenene and antimonene, which is important for the development of paper-like spintronic devices.

Calculation details and models

Our calculations were performed using density functional theory, as implemented in the Vienna ab initio Simulation Package (VASP). The electronic exchange–correlation interaction is treated using the Perdew–Burke–Ernzerhof functional (PBE) within the generalized gradient approximation (GGA). A 4 × 4 supercell was used during the calculations. The electronic wave functions were expanded using a plane-wave basis set with a cutoff energy of 500 eV. For the structure optimization, the k-point sampling in the reciprocal space was represented with 8 × 8 × 1 grid meshes, and, for the electronic structure calculations, the k-point sampling in the reciprocal space was represented with 10 × 10 × 1 grid meshes. A vacuum space of about 15 Å was used to avoid the interaction between neighboring layers. All results are obtained based on the spin-polarized calculations. The positions of all atoms in the layer are fully relaxed during the optimization. The criterion of convergence was selected when the residual forces on all atoms were smaller than 0.01 eV Å⁻¹.

Results and discussion

A. Pristine arsenene and antimonene

In order to ensure the veracity of our calculations, we firstly compared the structural parameters and electronic properties of pristine arsenene and antimonene with those of previous works. Fig. 1a gives the optimized geometric structures of pristine arsenene and antimonene. From the top view, we can see that the lattices of arsenene and antimonene are similar to that of graphene where each As atom in arsenene is covalently bonded to three neighboring As atoms and each Sb atom in antimonene is covalently bonded to three neighboring Sb atoms. From the side view, the lattices of arsenene and antimonene are somewhat different from that of graphene in that arsenene and antimonene are buckled structures while in graphene each C atom occupies the same atom layer. The optimized lattice constant, bond length, bond angle and thickness of pristine arsenene are about 3.61 Å, 2.51 Å, 91.9° and 1.40 Å, respectively, and optimized lattice constant, bond length, bond angle and thickness of pristine antimonene are 4.12 Å, 2.89 Å, 90.8° and 1.65 Å, respectively. These results are in close agreement with those of previous studies.^47–49 The calculated band structures of arsenene and antimonene are shown in Fig. 1b. Clearly, arsenene and antimonene are indirect semiconductors, in which the valence band maximum is located at the Γ point while the conduction band minimum lies between Γ and M points. Calculated bandgaps are about 1.60 and 1.26 eV for arsenene and antimonene, respectively, which are also in good agreement with previous theoretical reports at the same level.^50–53

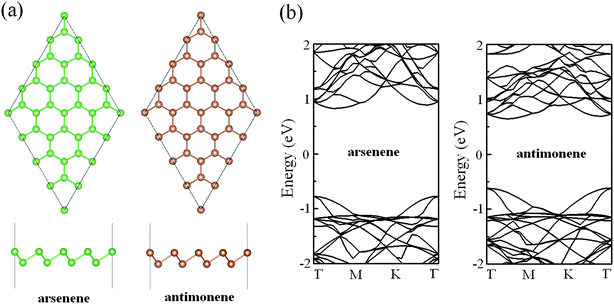Fig. 1 (a) Optimized geometric structures of pristine arsenene and antimonene. (b) Band structures of pristine arsenene and antimonene.

B. Stability of arsenene and antimonene under the coexistence of Co doping and strain

Considering possible structure breakage or phase transition, we then investigated the stabilities of arsenene and antimonene under the coexistence of Co doping and strain. Schematic views for the coexistence of Co doping and strain on arsenene and antimonene are shown in Fig. 2a. Here the arsenene–Co structure was constructed by replacing an As atom of arsenene by a Co atom and the antimonene–Co structure was created by replacing a Sb atom of antimonene with a Co atom. The strain was defined as ε% = Δc/c₀, where c₀ is the lattice parameter of the unstrained system and Δc is the variation of the lattice parameter. Positive ε and negative ε mean tension strain and compression strain, respectively. Fig. 2b shows the changes of the total energies of arsenene–Co and antimonene–Co systems with the strain. When the tension (or compression) strain was applied, the total energies of both structures approximately present a monotonously increased tendency. It indicates a relatively large elastic range for the arsenene and antimonene. In this range, the structure breakage or phase transition will not occur, providing a large space to modulate the electronic and magnetic properties on them.

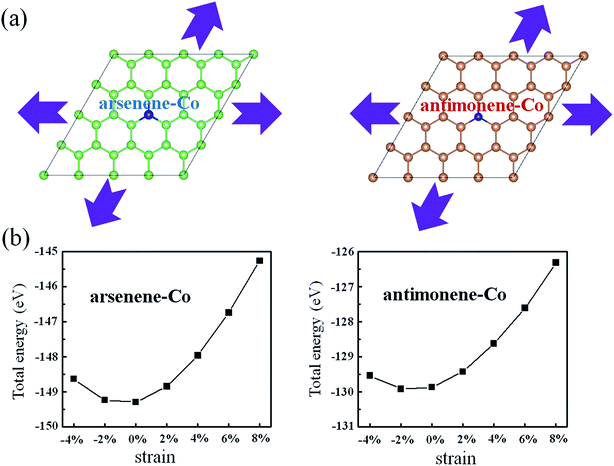Fig. 2 (a) Schematic illustration of the interaction of strain on arsenene–Co and antimonene–Co structures. (b) Total energies of arsenene–Co and antimonene–Co structures under different strains.

C. Magnetic properties of arsenene and antimonene under the coexistence of Co doping and strain

Subsequently, we turned to study the effect of coexistence of Co doping and strain on the magnetic properties of arsenene and antimonene. Fig. 3 depicts the strain effect on the evolutions of the magnetism and the energy difference between the nonspin and spin states for arsenene–Co and antimonene–Co structures. A positive value of the energy difference between the nonspin and spin states indicates that the magnetic state is stable in energy. We found that the arsenene–Co structure under −4%, −2%, 0%, 2% and 4% strains and antimonene–Co structure under −4%, −2%, 0% and 2% strains relax to the nonmagnetic ones. Thus, unstrained arsenene–Co and antimonene–Co structures and the arsenene–Co and antimonene–Co structures under small compressive and tension strains are nonmagnetic. Interestingly, the situations are different at high strains. Under 6% and 8% strains, the magnetic arsenene–Co structure is more stable than the nonmagnetic one with energy differences of 59 and 190 meV, respectively, and under 4%, 6% and 8% strains, the magnetic antimonene–Co structure is more stable than the nonmagnetic one with energy differences of 15, 130 and 250 meV, respectively. The calculated magnetic moments of the arsenene–Co structure are about 2.0 and 2.1 μ_B for 6% and 8% strains, respectively, and the calculated magnetic moments of the antimonene–Co structure are about 2.0, 2.0 and 2.3 μ_B for 4%, 6% and 8% strains, respectively. Corresponding spatial spin density distributions of arsenene–Co and antimonene–Co structures under 0% and 6% strains are shown in the insets of Fig. 3, which clearly shows that the spin polarization derives from the doped Co atom for both structures. As a result, the coexistence of Co doping and strain can effectively modulate the spin of the system, which is significant for practical electromechanical nanodevice applications. For example, the ultrathin arsenene and antimonene structures can be designed as a logic state of “0” with the nonspin state or “1” with the spin state, achieving a desired spin switch.

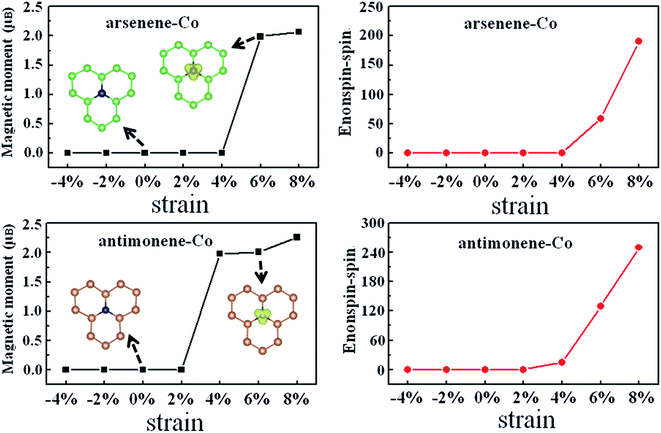Fig. 3 Magnetic moment and energy difference between nonspin state and spin state, E_{nonspin–spin}, for arsenene–Co and antimonene–Co structures under different strains.

D. Explanation of the origin of the transition of spin polarization

Explanation of the interesting transition of the spin polarization with the strain can firstly be attributed to the changes of the geometric structures. As shown in Fig. 4, under 0% strain, the average Co–As bond length is about 2.28 Å, which is smaller than the value of 2.51 Å found for the As–As bond length in pristine arsenene, and the average Co–Sb bond length is about 2.47 Å, which is smaller than the value of 2.89 Å found for the Sb–Sb bond length in pristine antimonene. These results indicate that the interaction between Co and As atoms in arsenene–Co system and the interaction between Co and Sb atoms in antimonene–Co system are strong. As a result, it suppresses the magnetism of the Co atom. Under −4% and −2% strains, the calculated average Co–As bond lengths in the arsenene–Co system are about 2.25 and 2.26 Å, respectively, and under −4% and −2% strains the calculated average Co–Sb bond lengths in the antimonene–Co system are about 2.43 and 2.45 Å, respectively. Naturally, under compressive strain, the interaction between the Co and the host material is strengthened. Thus, no magnetism was found in these cases. Consequently, a reduction of the interaction between the Co and the host is expected for the introduction of magnetism. Note that, although the Co–As bond lengths in the arsenene–Co system under 2% and 4% strains and the Co–Sb bond length in antimonene–Co system under 2% strain were slightly increased, these cases remained nonmagnetic. With further increase of strain, drastic changes in the bond length between Co and As atoms in the arsenene–Co structure and the bond length between Co and Sb atoms in the antimonene–Co structure take place. Under 6% and 8% strains, the Co–As bond lengths in the arsenene–Co structure become about 2.39 and 2.41 Å, respectively, and under 4%, 6% and 8% strains the Co–Sb bond lengths in the antimonene–Co structure become about 2.57, 2.60 and 2.62 Å, respectively. Strain effects on the distribution of charge density for the local arsenene–Co and antimonene–Co structures are shown in Fig. 5. It clearly shows that, owing to the increase of bond length, the accumulation of electrons between the Co atom and its neighboring atoms was decreased gradually. Thus, at large strain, the interaction between Co and As atoms in the arsenene–Co structure and the interaction between Co and Sb atoms in the antimonene–Co structure are small, which makes them exhibit substantial magnetism.

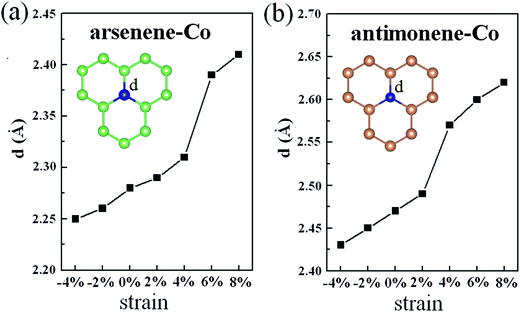Fig. 4 (a) Average Co–As bond length in arsenene–Co structure under different strains. (b) Average Co–Sb bond length in antimonene–Co structure under different strains.

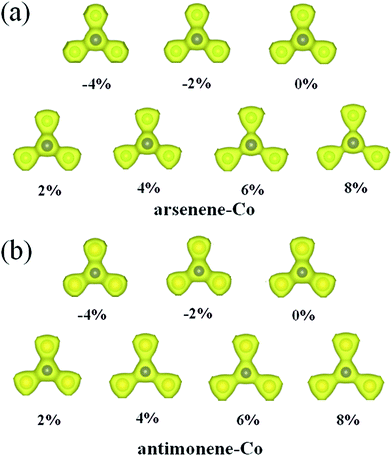Fig. 5 Charge densities for local (a) arsenene–Co and (b) antimonene–Co structures under different strains.

To gain a further insight into the evolution of magnetism, we studied the strain effect on the electronic structures of Co atoms for arsenene–Co and antimonene–Co structures. Fig. 6 shows the strain dependence of the spin-polarized partial density of states (PDOS). Here, −4%, 0% and 8% strains were considered. Under 0% and −4% strains, we clearly observed that spin-up states match spin-down states very well for the Co atoms of the arsenene–Co and antimonene–Co structures. Thus, arsenene–Co and antimonene–Co structures without strain or under compression strain are nonmagnetic. In contrast, the states of the Co atom are redistributed under the large strain. Under 8% strain, spin splitting was found for the Co atoms of arsenene–Co and antimonene–Co structures. Detailed examination shows that the spin states derive mainly from Co-3d states. For both structures, the spin-up Co-3d states are mainly located in the energy range from −3.0 to −1.5 eV while the spin-down Co-3d states are mainly located in the energy range from −1.5 to 0.7 eV. Thus, under the large strain, the arsenene–Co and antimonene–Co systems exhibit substantial magnetism.

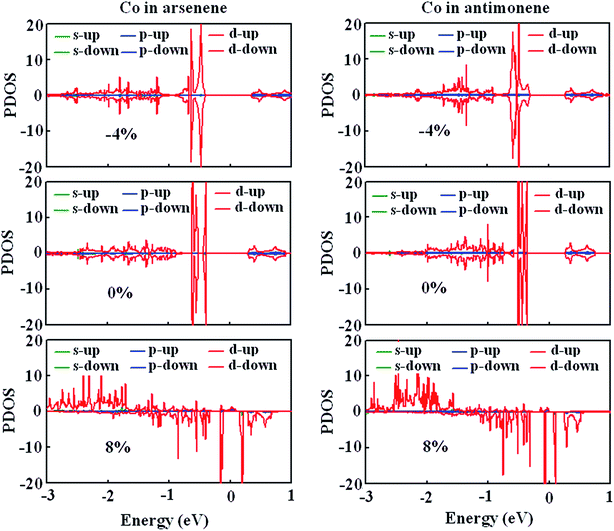Fig. 6 PDOS of Co atom in (a) arsenene–Co and (b) antimonene–Co structures under −4%, 0% and 8% strains.

E. Electronic properties of arsenene and antimonene under the coexistence of Co doping and strain

Finally, we studied the electronic properties of arsenene and antimonene structures under the coexistence of Co doping and strain. The evolutions of the spin-polarized band structure and density of states (DOS) of the arsenene–Co and antimonene–Co systems under different strains are shown in Fig. 7 and 8, respectively. The red line stands for the up-spin and the black line stands for the down-spin. The particular change of the electronic structure suggests that an interesting transition occurred under the strain, i.e., nonmagnetic semiconductor → magnetic half-metal transition, for both cases. Under small strains, the arsenene–Co and antimonene–Co structures are nonmagnetic semiconductors. The calculated bandgaps of arsenene–Co structure are about 0.74, 0.76, 0.68, 0.58 and 0.48 eV for −4%, −2%, 0%, 2% and 4% strains, respectively, and the calculated bandgaps of the antimonene–Co structure are about 0.57, 0.64, 0.62 and 0.53 eV for −4%, −2%, 0% and 2% strains, respectively. In sharp contrast to the nonmagnetic semiconducting characteristic, the arsenene–Co structure under 6% and 8% strains and the antimonene–Co structure under 4%, 6% and 8% strains exhibit a magnetic half-metallic behavior. In these cases, the structure has a metallic nature for the up-spin state and a semiconducting nature for the down-spin state, providing an ability to achieve completely spin-resolved electric current. Detailed examination shows that the states at the Fermi level are mainly contributed by the arsenene and antimonene for the arsenene–Co and antimonene–Co structures, respectively. The role of the doped Co atom is small.

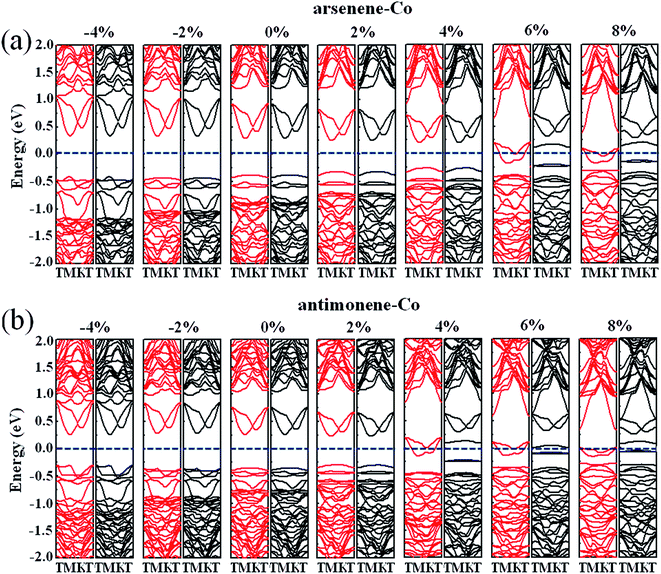Fig. 7 Band structures for (a) arsenene–Co and (b) antimonene–Co structures under different strains.

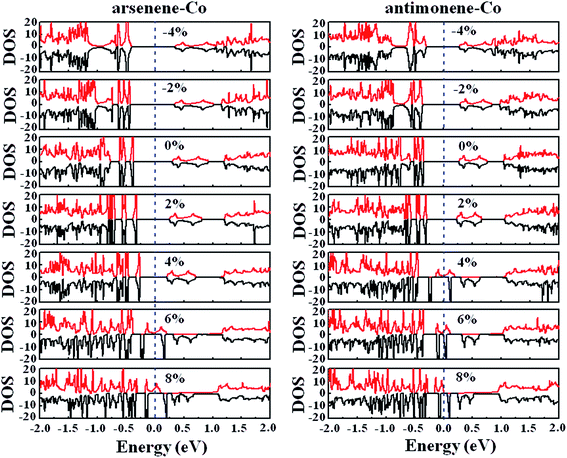Fig. 8 DOS for (a) arsenene–Co and (b) antimonene–Co structures under different strains.

Conclusion

First-principles calculations based on DFT were carried out to investigate the effect of coexistence of Co doping and strain on arsenene and antimonene. The ground states of unstrained arsenene–Co and antimonene–Co structures are nonmagnetic owing to the formation of strong bonds between Co and its nearby atoms. Interestingly, as the tension strain increases, the interactions between Co and its nearby atoms decrease gradually. As a result, under large strain, substantial magnetism was found in arsenene–Co and antimonene–Co structures owing to the splitting of Co-3d states. This result indicates the possibility of controlling the spin states of arsenene and antimonene structures from nonmagnetism to magnetism. Furthermore, under strain, arsenene–Co and antimonene–Co structures can exhibit half-metallic property. Detailed examination shows that arsenene and antimonene contribute the states at the Fermi level for arsenene–Co and antimonene–Co structures, respectively. These results provide an effective pathway for the development of arsenene- and antimonene-based electronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by the National Natural Science Foundation of China (No. 11504044) and the New Academic Researcher Award (No. Y03111023901014002).

References

1. X. D. Duan, C. Wang, A. L. Pan, R. Q. Yu and X. F. Duan, Chem. Soc. Rev., 2015, 44, 8859–8876.
2. C. L. Tan, X. H. Cao, X. J. Wu, Q. Y. He, J. Yang, X. Zhang, J. Z. Chen, W. Zhao, S. K. Han and G. H. Nam, Chem. Rev., 2017, 117, 6225–6331.
3. L. L. Peng, Y. Zhu, D. H. Chen, R. S. Ruoff and G. H. Yu, Adv. Energy Mater., 2016, 6, 1600025.
4. K. Kalantar-zadeh, J. Z. Ou, T. Daeneke, M. S. Strano, M. Pumera and S. L. Gras, Adv. Funct. Mater., 2015, 25, 5086–5099.
5. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
6. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
7. P. Singla, N. Goel, V. Kumar and S. Singhal, Ceram. Int., 2015, 41, 10565–10577.
8. B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150.
9. L. K. Li, Y. J. Yu, G. J. Ye, Q. Q. Ge, X. D. Ou, H. Wu, D. L. Feng, X. H. Chen and Y. B. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
10. A. Kara, H. Enriquez, A. P. Seitsonen, L. C. L. Y. Voon, S. Vizzini, B. Aufray and H. Oughaddou, Surf. Sci. Rep., 2012, 67, 1–18.
11. F. F. Zhu, W. J. Chen, Y. Xu, C. L. Gao, D. D. Guan, C. H. Liu, D. Qian, S. C. Zhang and J. F. Jia, Nat. Mater., 2015, 14, 1020–1025.
12. J. S. Zhang, Y. Chen and X. C. Wang, Energy Environ. Sci., 2015, 8, 3092–3108.
13. Z. Q. Sun, T. Liao, Y. H. Dou, S. M. Hwang, M. Park, L. Jiang, J. H. Kim and S. X. Dou, Nat. Commun., 2014, 5, 3813.
14. M. Houssa, K. Iordanidou, G. Pourtois, V. V. Afanas'ev and A. Stesmans, Appl. Surf. Sci., 2017, 416, 853–857.
15. J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870.
16. H. P. Komsa, J. Kotakoski, S. Kurasch, O. Lehtinen, U. Kaiser and A. V. Krasheninnikov, Phys. Rev. Lett., 2012, 109, 035503.
17. Y. D. Ma, Y. Dai, M. Guo, C. W. Niu, Y. T. Zhu and B. B. Huang, ACS Nano, 2012, 6, 1695–1701.
18. S. Nakaharai, T. Iijima, S. Ogawa, S. Suzuki, S. L. Li, K. Tsukagoshi, S. Sato and N. Yokoyama, ACS Nano, 2013, 7, 5694–5700.
19. H. Rostami, A. G. Moghaddam and R. Asgari, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085440.
20. X. X. Li, X. J. Wu and J. L. Yang, J. Am. Chem. Soc., 2014, 136, 11065–11069.
21. S. L. Zhang, M. Q. Xie, B. Cai, H. J. Zhang, Y. D. Ma, Z. F. Chen, Z. Zhu, Z. Y. Hu and H. B. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 245303.
22. S. L. Zhang, N. Wang, S. G. Liu, S. P. Huang, W. H. Zhou, B. Cai, M. Q. Xie, Q. Yang, X. P. Chen and H. B. Zeng, Nanotechnology, 2016, 27, 274001.
23. Y. Wang, S. S. Wang, Y. H. Lu, J. Z. Jiang and S. Y. A. Yang, Nano Lett., 2016, 16, 4576–4582.
24. S. W. Kim, H. Jung, H. J. Kim, J. H. Choi, S. H. Wei and J. H. Cho, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96, 075416.
25. B. Huang, J. Yu and S. H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075415.
26. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
27. G. Gui, J. Li and J. X. Zhong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075435.
28. C. Y. Zhai, X. Q. Dai, W. Li, Y. Q. Ma, T. X. Wang and Y. N. Tang, Superlattices Microstruct., 2017, 101, 49–56.
29. X. L. Cai, C. Y. Niu, J. J. Wang, W. Y. Yu, X. Y. Ren and Z. L. Zhu, Phys. Lett. A, 2017, 381, 1236–1240.
30. Y. G. Zhou, Q. L. Su, Z. G. Wang, H. Q. Deng and X. T. Zu, Phys. Chem. Chem. Phys., 2013, 15, 18464–18470.
31. S. L. Zhang, Z. Yan, Y. F. Li, Z. F. Chen and H. B. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115.
32. X. Wu, Y. Shao, H. Liu, Z. L. Feng, Y. L. Wang, J. T. Sun, C. Liu, J. O. Wang, Z. L. Liu, S. Y. Zhu, Y. Q. Wang, S. X. Du, Y. G. Shi, K. Ibrahim and H. J. Gao, Adv. Mater., 2017, 29, 1605407.
33. H. J. Zhang, Y. D. Ma and Z. F. Chen, Nanoscale, 2015, 7, 19152.
34. H. W. Cao, Z. Y. Yu and P. F. Lu, Superlattices Microstruct., 2015, 86, 501–507.
35. Y. P. Wang, C. W. Zhang, W. X. Ji, R. W. Zhang, P. Li, P. J. Wang, M. J. Ren, X. L. Chen and M. Yuan, J. Phys. D: Appl. Phys., 2016, 49, 055305.
36. H. Lu, J. F. Gao, Z. Y. Hu and X. H. Shao, RSC Adv., 2016, 6, 102724.
37. A. X. Zhang, J. T. Liu, S. D. Guo and H. C. Li, Phys. Chem. Chem. Phys., 2017, 19, 14520.
38. M. W. Zhao, X. M. Zhang and L. Y. Li, Sci. Rep., 2015, 5, 16108.
39. K. Iordanidou, J. Kioseoglou, V. V. Afanas'ev, A. Stesmans and M. Houssa, Phys. Chem. Chem. Phys., 2017, 19, 9862–9871.
40. M. L. Sun, S. K. Wang, Y. H. Du, J. Yu and W. C. Tang, Appl. Surf. Sci., 2016, 389, 594–600.
41. M. Y. Liu, Q. Y. Chen, Y. Huang, C. Cao and Y. He, Superlattices Microstruct., 2016, 100, 131–141.
42. J. Du, C. X. Xia, Y. P. An, T. X. Wang and Y. Jia, J. Mater. Sci., 2016, 51, 9504–9513.
43. M. Luo, Y. H. Shen and T. L. Yin, Jpn. J. Appl. Phys., 2017, 56, 015201.
44. G. Li, Y. C. Zhao, S. M. Zeng and J. Ni, Appl. Surf. Sci., 2016, 390, 60–67.
45. Z. J. Li, W. Xu, Y. Q. Yu, H. Y. Du, K. Zhen, J. Wang, L. B. Luo, H. L. Qiu and X. B. Yang, J. Mater. Chem. C, 2016, 4, 362.
46. O. U. Akturk, E. Akturk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035450.
47. L. F. Yang, Y. Song, W. B. Mi and X. C. Wang, Appl. Phys. Lett., 2016, 109, 022103.
48. L. Z. Kou, Y. D. Ma, X. Tan, T. Frauenheim, A. J. Du and S. Smith, J. Phys. Chem. C, 2015, 119, 6918–6922.
49. M. Y. Liu, Y. Huang, Q. Y. Chen, C. Cao and Y. He, Sci. Rep., 2016, 6, 29114.
50. C. Kamal and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085423.
51. C. X. Xia, B. Xue, T. X. Wang, Y. T. Peng and Y. Jia, Appl. Phys. Lett., 2015, 107, 193107.
52. X. P. Chen, Q. Yang, R. S. Meng, J. K. Jiang, Q. H. Liang, C. J. Tan and X. Sun, J. Mater. Chem. C, 2016, 4, 5434.
53. H. Lu, J. F. Gao, Z. Y. Hu and X. H. Shao, RSC Adv., 2016, 6, 102724.

---