Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing and looking for novel cage compounds based on bicyclo-HMX as high energy density compounds
Yong Panab and
Weihua Zhu *a
*a
aInstitute for Computation in Molecular and Materials Science, Department of Chemistry, Nanjing University of Science and Technology, Nanjing 210094, China. E-mail: zhuwh@njust.edu.cn; Fax: +86 25 84303919
bSchool of Chemical Engineering and Materials Science, Nanjing Polytechnic Institute, Nanjing 210048, China
First published on 19th December 2017
Abstract
We designed four novel cage compounds 2,4,6,8,9-pentanitro-2,4,6,8,9-pentaazatricyclo[3.3.1.03,7]nonane (PATN), 2,4,6,8,9,9-hexanitro-2,4,6,8-tetraazatricyclo[3.3.1.03,7]nonane (HNTATN), 2,4,6,8,9-pentanitro-2,4,6,8-tetraazatricyclo[3.3.1.03,7]nonane (PNTATN), and 2,4,6,8-tetranitro-2,4,6,8-tetraaza-9-oxatricyclo[3.3.1.03,7]nonane (TAOTN) by introducing the intramolecular –N(NO2)–, –C(NO2)2–, –CH(NO2)–, or –O– linkage into the bicyclo-HMX framework. Then, their molecular and electronic structures, energetic properties, thermal stability, and impact sensitivity were investigated using density functional theory. We discussed the effects of molecular geometry and electronic structure on their detonation properties. Their thermal stability was discussed based on bond dissociation energies and strain energies. We evaluated their impact sensitivity compared with known energetic compounds. Because of their detonation performance, thermal stability, and impact sensitivity, the potential candidates for high energy density compounds were selected. Our design strategy, constructing the novel cage skeleton by introducing a intramolecular linkage, may offer another way to obtain potential energetic compounds with outstanding energetic performance and low sensitivity.
1 Introduction
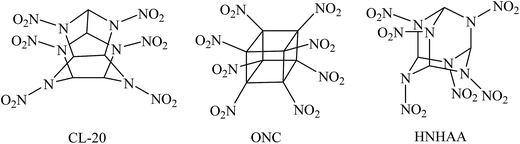
Energetic materials such as explosives, propellants, and pyrotechnics are widely used for innumerable military and industrial applications. During the last several decades, the search for novel high energy density compounds (HEDCs) has become a hot spot in this field and seems to be never-ending to meet with the requirements of the rapid development of military and modern industry. As an important class of HEDCs, highly nitrated cage compounds have attracted considerable interests due to their high strain energies, compact structures, and self-contained oxidizability.1–6 Generally, cage compounds with highly compact structure have higher densities than their acyclic or monocyclic analogues. Moreover, the cage strain inherent in the systems can led to high positive heat of formation (HOF) over traditional explosives such as 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (HMX) or hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX). Therefore, highly nitrated cage compounds usually exhibit high positive HOF, high density, excellent detonation performance, and acceptable thermal stability. Among them, 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20), octanitrocubane (ONC), and 2,4,6,8,9,10-hexanitrohexaazaadamantane (HNHAA, see Fig. 1) represent the most prominent cage explosives.1,7–9 And many new energetic compounds were developed based on the three cage skeletons of isowurtzitane, cubane, and adamantane.10–19 Although the cage HEDCs have excellent energetic properties and lower sensitivity, these new energetic cage compounds, which usually had a complex structure and contained seven or more nitro groups, made them difficult to be synthesized. In addition, too many nitro groups made them very sensitive toward outer stimuli and further increases the difficulty and cost of the synthesis. To date, there are few impressive candidates of HEDCs with novel cage skeleton containing fewer substituents than CL-20 but exhibiting excellent energetic performance comparable with CL-20 or ONC. Thus, ingenious strategy is needed to design and develop new energetic materials with novel cage skeletons.cis-2,4,6,8-Tetranitro-1H,5H-2,4,6,8-tetraazabicyclo[3.3.0]octane, commonly called “bicyclo-HMX” because of its structural analogy with HMX, is an important bicyclic nitramine explosive and can be used in solid propellants.20,21 Bicyclo-HMX has four nitramine moieties in the structure and exhibits outstanding detonation properties comparable with HMX.22,23 Thus, it is reasonable to assume that its bicyclic framework is a good parent structure for developing novel polynitro cage compounds with improved energetic properties and induced sensitivity.
Now, theoretical studies based on quantum chemical treatment have gained acceptance as a useful research tool to screen the candidates of HEDCs, thereby avoiding expensive and dangerous experimental tests.24,25 Furthermore, the molecular structures, HOFs, energetic properties, strain energy, thermal stability, and impact sensitivity for the title compounds were investigated by using density functional theory (DFT). The structure–property relationships were explored for the title compounds to understand the roles of different linkages in the designed cage skeleton.
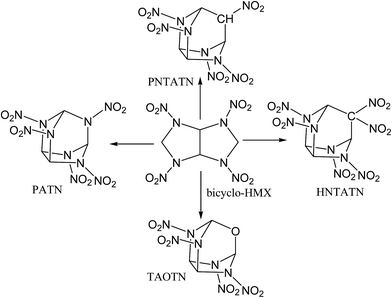
In this work, based on the bicyclic framework of bicyclo-HMX, four novel cage energetic compounds were designed by employing a new strategy: first, novel compact cages were formed by introducing –NH–, –CH2–, or –O– linkages to link the C1 and C5 in the bicyclo-HMX skeleton. Then, a kind of novel compact cage skeleton, azatricyclo[3.3.1.03,7]nonane, was constructed. Furthermore, the hydrogen atoms in the intramolecular –NH– and –CH2– linkages were substituted by nitro groups. Finally, four novel cage compounds 2,4,6,8,9-pentanitro-2,4,6,8,9-pentaazatricyclo[3.3.1.03,7]nonane (PATN), 2,4,6,8,9-pentanitro-2,4,6,8-tetraazatricyclo[3.3.1.03,7]nonane (PNTATN), 2,4,6,8,9,9-hexanitro-2,4,6,8-tetraazatricyclo[3.3.1.03,7]nonane (HNTATN), and 2,4,6,8-tetranitro-2,4,6,8-tetraaza-9-oxatricyclo[3.3.1.03,7]nonane (TAOTN) were generated (see Fig. 2). The introduction of the nitro groups or oxygen atom can significantly enhance the relatively low oxygen balance of bicyclo-HMX (−16.32%). In addition, except for HNTATN, these cage compounds contain only four or five nitro groups, less than the number of the nitro groups for CL-20 or HNHAA. Considering the more compact cage structure and better oxygen balance than the parent compound bicyclo-HMX, all of the designed cage compounds may have good energetic performance. Our main purpose is to screen novel energetic cage compounds with high HOF, high density, and excellent detonation properties, good thermal stability, and low sensitivity by using DFT.
The remainder of this paper is organized as follows. A description of our computational method is given in Section 2. The results and discussion are presented in Section 3, followed by a summary of our conclusions in Section 4.
2 Computational methods
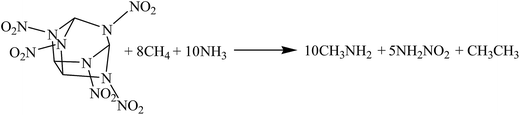
The hybrid DFT-B3LYP methods with the 6-311G(d,p) basis set were adopted for the optimizations of the molecular structures and the predictions of HOFs. Previous studies have shown that the basis set 6-311G(d,p) is able to precisely predict the molecular structures and energies of energetic organic compounds.22,24,26,27The gas-phase HOFs were calculated by the isodesmic reactions based on total energies (E0), zero-point energies (ZPE), and thermal correction (HT) obtained from the DFT-B3LYP/6-311G(d,p) calculations. The isodesmic reactions in which the numbers of all kinds of bonds can keep invariable are widely used to decrease the calculation errors of HOFs.24,25,28,29 The corresponding isodesmic reactions used to obtain the gas-phase HOFs of the title compounds at 298 K are as follows:
 | (1) |
 | (2) |
For the isodesmic reaction, the heat of reaction ΔH298 K at 298 K can be calculated from the following equation:
| ΔH298 K = ∑ΔHf,P − ∑ΔHf,R | (3) |
| ΔH298 K = ΔE298 K + Δ(PV) = ΔE0 + ΔZPE + ΔHT + ΔnRT | (4) |
As most energetic compounds are usually solid, the calculation of detonation properties requires solid-phase HOF (ΔHf,solid).30 According to Hess's law of constant heat summation,31 the gas-phase HOF (ΔHf,gas) and heat of sublimation (ΔHsub) can be used to evaluate their solid-phase HOF:
| ΔHf,solid = ΔHf,gas − ΔHsub | (5) |
The ΔHsub can be calculated by the empirical expression suggested by Politzer et al.:30,32
| ΔHsub = aA2 + b(νσtot2)0.5 + c | (6) |
The detonation velocity and28 pressure were estimated by the Kamlet-Jacobs equations37 as
D = 1.01(N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 1/2Q1/2)1/2(1 + 1.30ρ) 1/2Q1/2)1/2(1 + 1.30ρ)
| (7) |
P = 1.558ρ2N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 1/2Q1/2 1/2Q1/2
| (8) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) , the average molecular weight of these gases; Q, the heat of detonation (cal g−1), which can be evaluated by the HOF difference between products and explosives according to the principle of exothermic reactions; and ρ, the crystal density of explosives (g cm−3).
, the average molecular weight of these gases; Q, the heat of detonation (cal g−1), which can be evaluated by the HOF difference between products and explosives according to the principle of exothermic reactions; and ρ, the crystal density of explosives (g cm−3).
The crystal density was obtained based on an improved approach proposed by Politzer et al.,38 in which the interaction index νσtot2 was introduced.
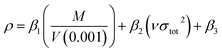 | (9) |
Strain energy (SE)40 is an important index to correlate the structure with the stability and reactivity of the cage compounds. In this work, the strain energy of the azatricyclo[3.3.1.03,7]nonane cage skeleton were calculated from the change of total energies (E0) with zero-point energies (ZPE) in the homodesmotic reaction:40–43
| SE = ∑Eproduct − ∑Ereactant + ΔZPE | (10) |
The strength of bonding, which could be evaluated by bond dissociation energy (BDE), is fundamental to understand chemical processes.44 The energy required for bond homolysis at 298 K and 1 atm corresponds to the enthalpy of reaction A–B(g) → A˙(g) + B˙(g), which is the bond dissociation enthalpy of the molecule A–B by definition.45 For many organic molecules, the terms “bond dissociation energy” (BDE) and “bond dissociation enthalpy” often appear interchangeably in the literature.46 Therefore, at 0 K, the homolytic bond dissociation energy can be given in terms of eqn (11).
| BDE0(A–B) → E0(A˙) + E0(B˙) − E0(A–B) | (11) |
The bond dissociation energy with zero-point energy (ZPE) correction can be calculated by eqn (12).
| BDE(A–B)ZPE = BDE0(A–B) + ΔEZPE | (12) |
Impact sensitivity is generally characterized through a drop weight test and reported as the height in cm, designated as h50. For the title compound, impact sensitivity was predicted by a simple method suggested by Pospíšil et al.47,48
| h50 = ασ+2 + βν + γ | (13) |
The calculations were performed with the Gaussian 09 package.51 The optimizations were performed without any symmetry restrictions using the default convergence criteria in the program. All of the optimized structures were characterized to be true local energy minima on the potential energy surfaces without imaginary frequencies.
3 Results and discussion
3.1 Molecular geometry and electronic structure
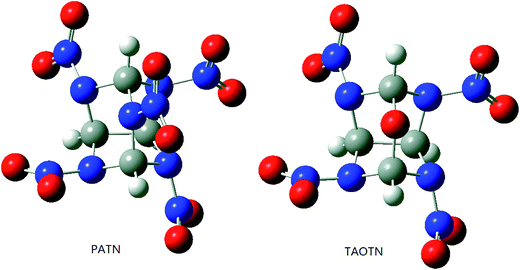
It is necessary to examine the geometric structure of the title compounds before studying their various properties. The optimized structures of PATN and TAOTN are displayed in Fig. 3. And Table 1 lists some selected bond parameters of the title compounds and bicyclo-HMX.| Compd. | C–N | C–C | EHOMO | ELUMO | ΔE |
|---|---|---|---|---|---|
| a The values in parentheses are the average one. | |||||
| PATN | 1.460–1.482(1.472)a | 1.595 | −9.180 | −3.215 | 5.965 |
| TAOTN | 1.461–1.478(1.469)a | 1.600 | −8.991 | −2.994 | 5.997 |
| HNTATN | 1.451–1.481(1.467)a | 1.594 | −9.195 | −4.009 | 5.186 |
| PNTATN | 1.454–1.487(1.470)a | 1.591 | −9.084 | −3.267 | 5.817 |
| bicyclo-HMX | 1.455–1.468 (1.461)a | 1.567 | −8.923 | −2.750 | 6.173 |
Seen from Fig. 3, the molecule of PATN or TAOTN has a highly compact structure and may be considered to have two six-membered rings and two five-membered rings. The cage skeleton of HNTATN or PNTATN is basically the same with PATN or TAOTN.
As shown in Table 1, the C–C bond, connecting two five-membered rings in the cage skeleton, is elongated due to the cage or ring strain in the system and its length is much longer than the normal C–C single bond length (1.54 Å). Furthermore, every cage compound has larger C–C bond length and average C–N bond length than their parent compound bicyclo-HMX, indicating that there is a larger inherent strain in the cage skeleton compared to the bicyclic skeleton of bicyclo-HMX. Among these compounds, TAOTN has the longest C–C bond length and PATN has the longest average C–N bond length.
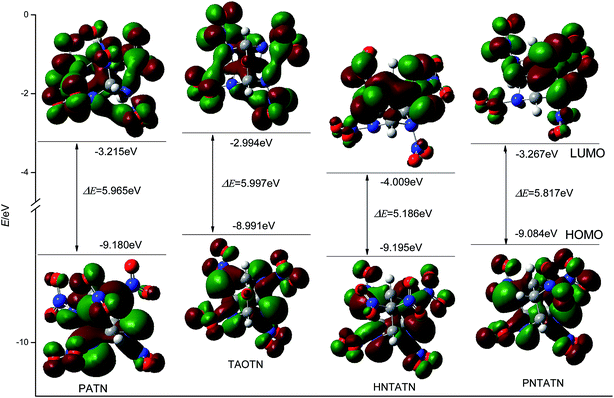
Table 1 also lists the energies of HOMO, LUMO, and their energy gap (ΔE) of the title compounds and bicyclo-HMX. All of the title compounds have a smaller ΔE than bicyclo-HMX. Among them, TAOTN has the largest energy gap, whereas HNTATN has the smallest energy gap. It is known that the energy gap (ΔE) is an important stability index of the molecules and the molecule with a larger energy gap often has high stability and low chemical reactivity.8,52 Thus, TAOTN may be less active and more stable than other three compounds in chemical processes with electron transfers or leaps, while HNTATN may exhibit a higher reactivity and lower stability in the chemical processes. The 3D plots of HOMO and LUMO for the title compounds were illustrated in Fig. 4, in which the positive phase is shown in red while the negative one is shown in green. It can be seen from Fig. 4 that all of the C–N orbits participate in both HOMO and LUMO levels. This shows that the removal of an electron from HOMO or addition of an electron to LUMO could weaken their cage skeleton.
The molecular electrostatic potentials (MEPs) for the title compounds were shown in Fig. 5. The MEPs for the 0.001 electron per bohr3 isosurface of electron density were evaluated at the B3LYP/6-311G(d,p) level. The colors range from −0.02 to 0.02 hartree, with red denoting electron-rich regions (negative potential) and blue denoting electron-deficient (positive potential) regions.
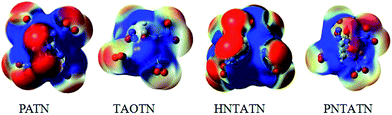 | ||
| Fig. 5 Electrostatic potentials of the title compounds, color coding for MEPs are from red (negative) to blue (positive). | ||
Electrostatic potentials can be used to analyzing the impact sensitivity of energetic compounds. According to previous studies,53 the cage compounds with a larger electron deficiency at the center of the cage skeleton are often more sensitive to outer impact than those with a lower electron deficiency. Seen from the MEPs of these cage compounds, the positive potentials locates at the center of the cage skeleton, while the negative potentials appears to be distributed mostly on the N–NO2 or C–NO2 moiety. Clearly, PATN and HNTATN have stronger positive potential focused in the region than other two cage compounds. This indicates that they might have relatively high impact sensitivity. In addition, the positive potential within the inner structure for TAOTN is dispersed around the oxygen atoms in the cage skeleton, which might decrease the sensitivity.
3.2 Gas-phase and solid-phase heats of formation
The solid-phase HOF, ΔHf,solid, is an important property for energetic materials. Table 2 lists the total energies, ZPEs, thermal corrections, and gas-phase HOFs for reference compounds in the isodesmic reactions. The gas-phase HOFs of CH4, NH3, CH3NH2, CH3NO2, and CH3OCH3 were taken from experimental results.54 The HOF value of NH2NO2 was calculated from the atomization reaction at the G3 level.| Compd. | E0 | ZPE | HT | HOF |
|---|---|---|---|---|
| a The scaling factor is 0.98 for ZPE.24b The experimental values were from ref. 54.c The value was calculated at the G3 level from the atomization reaction.d The calculated value was taken from ref. 12. | ||||
| NH3 | −56.5760 | 0.0343 | 10.00 | −45.94b |
| CH4 | −40.5337 | 0.0446 | 10.03 | −74.60b |
| CH3NH2 | −95.8884 | 0.0638 | 11.56 | −22.50b |
| CH3OCH3 | −155.0719 | 0.0793 | 13.99 | −184.10b |
| CH3CH3 | −79.8563 | 0.0744 | 11.76 | −84.00b |
| CH3NO2 | −245.0817 | 0.0497 | 14.04 | −80.80c |
| NH2NO2 | −261.1138 | 0.0394 | 12.28 | 8.16c (8.00d) |
Table 3 presents the total energies, ZPEs, thermal corrections, ΔHf,gas, and ΔHf,solid of the title compounds and bicyclo-HMX. It is found that the calculated ΔHf,solid value of bicyclo-HMX is in agreement with the previous report,22 indicating that the predicted HOF method chosen for the title compounds is credible. As shown in Table 2, all the cage compounds exhibit high positive ΔHf,gas (357.13–619.01 kJ mol−1) and ΔHf,solid (251.58–500.74 kJ mol−1). Except for TAOTN, the title compounds have much larger ΔHf,gas and ΔHf,solid values than bicyclo-HMX, which shows that properly constructing a cage framework based on a bicyclic unit can remarkably increase energy extent of the parent compound. Especially, PATN has the highest ΔHf,gas and ΔHf,solid values among these cage compound. Although PATN possesses five nitramine moieties, which has only more one N–NO2 group than bicyclo-HMX, its HOF value increases 200 kJ mol−1 compared to bicyclo-HMX. Previous research suggested that energetic cage compounds derive most of their energies from substantial cage strain.1,18 This indicates that PATN may possess much higher cage strain in the structure than parent bicyclo-HMX and other cage compounds.
| Compd. | E0 | ZPE | HT | ΔHf,gas | A | ν | σtot2 | ΔHsub | ΔHf,solid |
|---|---|---|---|---|---|---|---|---|---|
| a σtot2 is in kcal mol−1 and A is in Å2. The scaling factor is 0.98 for ZPE.24b The calculated value in parentheses was from ref. 22. | |||||||||
| PATN | −1454.3188 | 0.1638 | 53.00 | 619.01 | 269.09 | 0.08 | 163.84 | 118.27 | 500.74 |
| TAOTN | −1269.6635 | 0.1500 | 45.15 | 357.13 | 242.50 | 0.10 | 162.33 | 105.55 | 251.58 |
| HNTATN | −1642.8235 | 0.1768 | 61.27 | 534.80 | 287.24 | 0.06 | 186.65 | 127.91 | 406.89 |
| PNTATN | −1438.3027 | 0.1763 | 53.41 | 477.88 | 269.17 | 0.09 | 195.31 | 122.20 | 355.68 |
| bicyclo-HMX | −1195.6600 | 0.1675 | 47.20 | 402.43 | 112.69 | 0.10 | 215.00 | 112.71 | 289.72 (286.73b) |
3.3 Detonation properties
Detonation velocity (D) and detonation pressure (P) are two important performance parameters for energetic materials. Table 4 presents the calculated ρ, Q, D, P, and oxygen balance (OB) of the title compounds and bicyclo-HMX. For the purpose of comparison, the energetic properties of HNHAA are calculated, as HNHAA is only one more N–NO2 group than the compound PATN in the structure. And the experimental detonation properties of two known explosives CL-20 and HMX are also listed in this table. The semi-empirical Kamlet-Jacobs formula has been proved to be reliable for predicting the explosive properties of energetic high-nitrogen compounds.28,55 The calculated ρ, D, and P values of bicyclo-HMX (1.860 g cm−3, 9.14 km s−1, and 37.82 GPa) agree well with the previous research results.22,23 This shows that our predictions for the title compounds are reliable.| Compd. | Q (cal g−1) | OB | ρ (g cm−3) | D (km s−1) | P (GPa) |
|---|---|---|---|---|---|
| a Oxygen balance (%) for CaHbOcNd: 1600 × (c − 2a − b/2)/Mw; Mw: molecular weight of the title compounds.b Calculated values from ref. 22.c Calculated values from ref. 23.d Experimental values from ref. 4. | |||||
| PATN | 1736.84 | 0.00 | 1.981 | 9.80 | 45.03 |
| TAOTN | 1639.00 | −5.19 | 1.968 | 9.53 | 42.46 |
| HNTATN | 1724.72 | 0.00 | 1.998 | 9.77 | 44.96 |
| PNTATN | 1658.35 | −11.39 | 1.949 | 9.42 | 41.24 |
| bicyclo-HMX | 1624.66 | −16.32 | 1.860 (1.87b, 1.86c) | 9.14 (9.19b, 9.05c) | 37.82 (38.40b, 37.00c) |
| HNHAA | 1522.47 | 7.77 | 2.021 | 9.64 | 44.10 |
| CL-20 | 2.040d | 9.40d | 42.00d | ||
| HMX | 1.910d | 9.10d | 39.00d | ||
As shown in Table 4, all the title compounds exhibit outstandingly high density with the predicted density ranging from 1.949 to 1.998 g cm−3, which are significantly higher than that of bicyclo-HMX (1.860 g cm−3). Moreover, all the designed cage compounds exhibit excellent detonation properties, which is to a great extent due to their unique cage structures. Their D and P values remarkably exceed those of bicyclo-HMX or HMX, showing that they can be regarded as promising candidates of HEDCs. Especially, PATN and HNTATN present extraordinary high detonation properties: D > 9.76 km s−1 and P > 44.95 GPa, which are even superior to those of famous explosive CL-20 (9.40 km s−1 and 42.00 GPa) or HNHAA (9.64 km s−1 and 44.10 GPa). TAOTN and PNTATN also exhibit remarkably high D and P values, which are superior to or comparable with those of CL-20.
In addition, all the title compounds possess higher heat of detonation (Q) and better oxygen balance compared to their parent compound bicyclo-HMX. PATN has the highest Q value (1736.84 cal g−1) among them, while the TAOTN has the lowest one. Previous studies showed that the impact sensitivity of energetic compound roughly increases with Q.56 Thus, it may be inferred that TAOTN or PNTATN has a relatively low sensitivity, while PATN or HNTATN may exhibit a relatively high sensitivity to external impact. In addition, it's worth noting that oxygen balance of PATN and HNTATN are equal to zero, making them combust completely to avoid releasing some toxic gases such as carbon monoxide during their decomposition.
Hence, constructing a cage skeleton based on the bicyclic framework by introducing –N(NO2)–, –C(NO2)2–, –CH(NO2)–, or –O– can substantially increase heat of detonation, density, and oxygen balance of the parent compound, which further dramatically increase detonation properties for the title cage compounds.
3.4 Strain energies
Table 5 lists the energies of the cage strain for the title compounds at the B3LYP/6-311G(d,p) level via homodesmotic reactions. It is found that when the structure converts from a bicyclic framework into a cage skeleton, the strain energy remarkably increases in the cage molecule. Especially, the strain energy of the cage compound PATN is the highest value among them, almost double the strain energy of bicyclo-HMX. The high strain energy in the cage system will be released during the explosion and result in producing an additional energy for the title compounds.| Compd. | SE | BDE of N–NO2 | BDE of C–N in the cage | BDE of C–C in the cage | BDE of C–O in the cage | BDE of C–NO2 |
|---|---|---|---|---|---|---|
| a Calculated values from ref. 9. | ||||||
| PATN | 344.56 | 141.40 | 299.54 | 182.91 | ||
| TAOTN | 288.52 | 150.67 | 251.94 | 181.34 | 233.01 | |
| HNTATN | 331.59 | 142.98 | 235.55 | 178.72 | 122.90 | |
| PNTATN | 274.42 | 144.62 | 235.48 | 188.11 | 181.29 | |
| Bicyclo-HMX | 177.21 | |||||
| HNHAA | 143.85 (142.65a) | 246.52 (252.07a) | ||||
In addition, although PATN, TAOTN, HNTATN, and PNTATN have similar cage skeleton, their strain energies differ quite a bit. For example, when the N–NO2 group in the structure of PATN is replaced by oxygen atom or the –CH–NO2 group, the strain energy of the cage skeleton decreases more than 56 kJ mol−1. It indicates that TAOTN and PNTATN have better thermal stability than PATN.
3.5 Thermal stability
BDE can provide useful information for understanding the stability of the investigated molecules. Generally, the smaller the BDE of a bond is, the weaker the bond is, and the easier the bond becomes a trigger bond. To investigate thermal stability of the title compounds, four possible bond dissociations have been considered: (1) the N–NO2 bond linked to the cage; (2) the C–NO2 bond linked to the cage; (3) the C–N bond in the cage; (4) the C–O bond in the cage only for the compound TAOTN.Table 5 also presents the BDEs of the relatively weaker bonds of the title compounds. For the purpose of comparison, the BDEs of the relatively weaker bonds of HNHAA are given. Seen from Table 5, the N–NO2 bonds linked to the cage have the lowest BDE values in the molecule of PATN, TAOTN, and PNTATN, respectively, which means that the N–NO2 bonds are the weakest one and easier to rupture than other bonds in thermal decomposition for the three compounds. However, the weakest C–NO2 bond of HNTATN have lower BDE value (122.90 kJ mol−1) than other bonds in the molecule, showing the rupture of C–NO2 bonds appear to be the initial step in thermal decomposition or detonation.
Among them, TAOTN has the highest BDE value (150.67 kJ mol−1) of the relatively weaker bond and possesses better thermal stability than other cage compounds. Also, the BDEs of the relatively weaker N–NO2, C–N, and C–C bond of HNTATN are lower than those of other three cage compounds. It manifests that HNTATN may be less stable compared to other three compounds. This is because containing gem-dinitro groups on the bridge carbon atom decreases thermal stability of the cage compound. Generally, these conclusions are consistent with molecular structure analysis or cage strain analysis as mentioned above.
On the whole, all the title compounds possess good thermal stability and meet the thermal stability requirement as HEDMs.
3.6 Impact sensitivity
Impact sensitivity, generally reported as the height in cm and designated h50, is often used to judge whether energetic compounds are sensitive or insensitive to external impact.57 The higher h50 is, the more sensitive is the explosive. Table 6 lists the estimated impact sensitivity (h50) of the title compounds. For the purpose of comparison, the h50 values of HNHAA, CL-20, and HMX are calculated. The evaluated h50 value of CL-20 or HMX is very close to the experimental results,53 indicating that our predicted results are reliable.Seen from Table 6, the title compounds exhibit higher h50 values than HNHAA or CL-20, except that compound HNTATN has a slightly lower h50 value than CL-20. According to the estimated h50 values, PATN, TAOTN, and PNTATN are anticipated to be more insensitive to external impact than HNHAA or CL-20 but more sensitive than HMX. In addition, TAOTN has the highest h50 value of 19.14 cm among the title cage compounds, showing that the introduction of the intramolecular oxy-bridge can effectively decrease the sensitivity of the cage compound. However, HNTATN has the lowest estimated h50 values among these compounds and exhibit relatively high impact sensitivity, which also indicates that containing gem-dinitro groups on the bridge carbon atom increases impact sensitivity for the cage compounds.
Overall, PATN, TAOTN, or PNTATN exhibits high positive HOF, high density, excellent detonation properties superior to or comparative with CL-20, and lower impact sensitivity than CL-20 or HNHAA. As it is only five or four nitramine moieties in the relatively simple structure, the three cage compounds may be regards as very attractive potential HEDCs. In addition, although the thermal stability and impact sensitivity of HNTATN is a bit poor compared to other three cage compounds, it possesses ideal oxygen balance, good thermal stability, and excellent detonation properties superior to CL-20 or HNHAA. Thus, HNTATN is also regarded as promising candidates for HEDCs.
3.7 Design of synthetic route
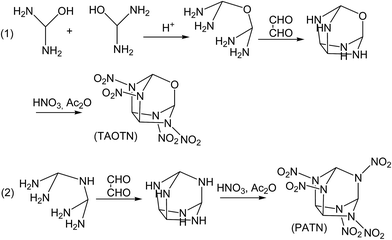
Although the title compounds have not been synthesized so far, the synthesis of some compounds with similar cage skeletons such as trioxatricyclo[3.3.1.03,7]nonane and triphosphatricyclo[3.3.1.03,7]nonane were reported.58–60 Thus, it may be expected that the synthesis of the title compounds can be realized successfully in the future. Here we designed the synthetic routes for the two compounds TAOTN and PATN. Considering that there are only four or five nitro groups in the molecules, the main difficulty of the synthesis may be how to synthesize 2,4,6,8-tetraazaoxatricyclo[3.3.1.03,7]nonane and 2,4,6,8,9-pentaazatricyclo[3.3.1.03,7]nonane. Furthermore, they can be converted smoothly into the final compounds by nitration. As shown in Fig. 6, TAOTN can be prepared in three steps from diaminomethanol. Firstly, the intermediate oxydi(methanediamine) can be synthesized by the dehydration reaction between two diaminomethanol molecules in the acid condition. Then the intermediate reacts with oxalaldehyde as condensation reaction to get the cage skeleton, 2,4,6,8-tetraazaoxatricyclo[3.3.1.03,7]nonane. The last step is the nitration that the mixing of nitric acid and acetic anhydride is used to react with tetraazaoxatricyclo[3.3.1.03,7]nonane step by step till to obtain the target product TAOTN with four nitro groups. Similarly, PATN is also obtained after condensation and nitration.4 Conclusions
In this work, the structures, HOFs, energetic properties, strain energy, thermal stability, and impact sensitivity of the four novel cage compounds based on the bicyclo-HMX framework were systematically studied using the DFT-B3LYP method and compared with the parent compound or some famous energetic compounds.It is found that all the title compounds have much higher density, heat of detonation, and detonation properties and better oxygen balance than the parent compound bicyclo-HMX. Compared to famous explosives CL-20 or HNHAA, all the title compounds possess relatively simple structures, good thermal stability, superior or comparative detonation properties, and much lower impact sensitivity, except that HNTATN has slightly higher impact sensitivity than CL-20. Especially, PATN and TAOTN exhibit a best combination of high density, good thermal stability, better detonation properties, and lower impact sensitivity than CL-20. Furthermore, designed feasible synthetic routes of PATN and TAOTN shows that they can be synthesized successfully in the future. Thus, all of the four cage compounds are promising candidates for HEDCs.
In addition, these results indicate that our design strategy of constructing new cage skeleton by introducing the intramolecular –N(NO2)–, –C(NO2)2–, –CH(NO2)–, or –O– linkage based on the bicyclic nitramine is proven to be very useful and gives more options for designing novel cage compounds with excellent energetic performance and induced sensitivity. The new approach may be applied to design and develop energetic compounds with high denotation properties, good thermal stability, and low sensitivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21773119), the University of Natural Science Foundation in Jiangsu Province (Grant No. 17KJB320001), and the Qing Lan Project of Jiangsu Province in China.References
- A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–15 CrossRef CAS PubMed.
- L. E. Fried, M. R. Manaa, P. F. Pagoria and R. L. Simpson, Annu. Rev. Mater. Res., 2001, 31, 291–321 CrossRef CAS.
- Q. Wu, W. H. Zhu and H. M. Xiao, RSC Adv., 2014, 4, 3789–3797 RSC.
- M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and A. S. Rao, J. Hazard. Mater., 2009, 161, 589–607 CrossRef CAS PubMed.
- Y. Pan and W. H. Zhu, J. Phys. Chem. A, 2017, 121, 9163–9171 CrossRef CAS PubMed.
- L. A. Paquette, J. W. Fischer and P. Engel, J. Org. Chem., 1985, 50, 2524–2527 CrossRef CAS.
- A. T. Nielsen, R. A. Nissan, D. J. Vanderah, C. L. Coon, R. D. Gilardi, C. F. George and J. Flippen-Anderson, J. Org. Chem., 1990, 55, 1459–1466 CrossRef CAS.
- F. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115, 11788–11795 CrossRef CAS PubMed.
- X. J. Xu, H. M. Xiao, X. H. Ju, X. D. Gong and W. H. Zhu, J. Phys. Chem. A, 2006, 110, 5929–5933 CrossRef CAS PubMed.
- X. J. Xu, W. H. Zhu and H. M. Xiao, J. Mol. Struct.: THEOCHEM, 2008, 853, 1–6 CrossRef CAS.
- Y. Pan, W. H. Zhu and H. M. Xiao, Comput. Theor. Chem., 2017, 1114, 77–86 CrossRef CAS.
- V. Ghule, P. Jadhav, R. Patil, S. Radhakrishnan and T. Soman, J. Phys. Chem. A, 2010, 114, 498–503 CrossRef CAS PubMed.
- Q. Wu, W. H. Zhu and H. M. Xiao, J. Mol. Model., 2014, 20, 2483 CrossRef PubMed.
- Y. Pan, W. H. Zhu and H. M. Xiao, Can. J. Chem., 2013, 91, 1243–1251 CrossRef CAS.
- J. Y. Zhang, H. C. Du, F. Wang, X. D. Gong and Y. S. Huang, J. Mol. Model., 2012, 18, 165–170 CrossRef CAS PubMed.
- J. Y. Zhang, F. Wang and X. D. Gong, Struct. Chem., 2013, 24, 1339–1346 CrossRef CAS.
- Y. F. Ling, X. L. Ren, W. P. Lai and J. Luo, Eur. J. Org. Chem., 2015, 2015, 1541–1547 CrossRef CAS.
- J. Y. Zhang, H. C. Du, F. Wang, X. D. Gong and Y. S. Huang, J. Phys. Chem. A, 2011, 115, 6617–6621 CrossRef CAS PubMed.
- Y. Wang, C. Qi, J. W. Song, X. Q. Zhao, C. H. Sun and S. P. Pang, J. Mol. Model., 2013, 19, 1079–1087 CrossRef CAS PubMed.
- L. Qiu, W. H. Zhu, J. J. Xiao and H. M. Xiao, J. Phys. Chem. B, 2008, 112, 3882–3893 CrossRef CAS PubMed.
- W. M. Koppes, M. H. Chaykovsky, G. Adolph, R. Gilardi and C. J. George, J. Org. Chem., 1987, 52, 1113–1119 CrossRef CAS.
- F. Wang, G. X. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115, 13858–13864 CrossRef CAS PubMed.
- D. Klasovitý, S. Zeman, A. Růzicka, M. Jungová and M. Rohác, J. Hazard. Mater., 2009, 164, 954–961 CrossRef PubMed.
- T. Wei, W. H. Zhu, X. W. Zhang, Y. F. Li and H. M. Xiao, J. Phys. Chem. A, 2009, 113, 9404–9412 CrossRef CAS PubMed.
- Y. Pan, W. H. Zhu and H. M. Xiao, J. Mol. Model., 2012, 18, 3125–3138 CrossRef CAS PubMed.
- Y. Pan, J. S. Li, B. B. Cheng, W. H. Zhu and H. M. Xiao, Comput. Theor. Chem., 2012, 992, 110–119 CrossRef CAS.
- X. W. Fan and X. H. Ju, J. Comput. Chem., 2008, 29, 505–513 CrossRef CAS PubMed.
- T. Wei, W. H. Zhu, J. J. Zhang and H. M. Xiao, J. Hazard. Mater., 2010, 179, 581–590 CrossRef CAS PubMed.
- Y. Pan, W. H. Zhu and H. M. Xiao, Struct. Chem., 2013, 24, 1071–1087 CrossRef CAS.
- P. Politzer and J. S. Murray, Cent. Eur. J. Energ. Mater., 2011, 8, 209–220 CAS.
- P. W. Atkins, Physical chemistry, Oxford University Press, Oxford, 1982 Search PubMed.
- P. Politzer, P. Lane and J. S. Murray, Cent. Eur. J. Energ. Mater., 2011, 8, 39–52 CAS.
- E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005–1013 CrossRef CAS PubMed.
- F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691 CrossRef CAS PubMed.
- M. Jaidann, S. Roy, H. Abou-Rachid and L. S. Lussier, J. Hazard. Mater., 2010, 176, 165–173 CrossRef CAS PubMed.
- F. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115, 11852–11860 CrossRef CAS PubMed.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48, 23–35 CrossRef CAS.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro-Labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
- B. M. Rice and E. F. C. Byrd, J. Comput. Chem., 2013, 34, 2146–2151 CrossRef CAS PubMed.
- M. Zhao and B. M. Gimarc, J. Phys. Chem., 1993, 97, 4023–4030 CrossRef CAS.
- D. H. Magers and S. R. Davis, J. Mol. Struct.: THEOCHEM, 1999, 487, 205–210 CrossRef CAS.
- X. W. Fan, X. H. Ju, Q. Y. Xia and H. M. Xiao, J. Hazard. Mater., 2008, 151, 255–260 CrossRef CAS PubMed.
- X. W. Fan, L. Qiu and X. H. Ju, Struct. Chem., 2009, 20, 1039–1042 CrossRef CAS.
- S. W. Benson, Thermochemical Kinetics, Wiley-Interscience, New York, 2nd edn, 1976 Search PubMed.
- I. Mills, T. Cvitas, K. Homann, N. Kallay and K. Kuchitsu, Quantities, Units, and Symbols in Physical Chemistry, Blackwell Scientific Publications, Oxford, 1988 Search PubMed.
- S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed.
- M. Pospíšil, P. Vávra, M. C. Concha, J. S. Murray and P. Politzer, J. Mol. Model., 2011, 17, 2569–2574 CrossRef PubMed.
- M. Pospíšil, P. Vávra, M. C. Concha, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 895–901 CrossRef PubMed.
- M. H. Keshavarz, Propellants, Explos., Pyrotech., 2010, 35, 175–181 CrossRef CAS.
- J. S. Li, J. Hazard. Mater., 2010, 174, 728–733 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- P. Ravi, G. M. Gore, A. K. Sikder and S. P. Tewari, Int. J. Quantum Chem., 2012, 112, 1667–1677 CrossRef CAS.
- B. M. Rice and J. J. Hare, J. Phys. Chem. A, 2002, 106, 1770–1783 CrossRef CAS.
- J. A. Dean, LANGE'S Handbook of Chemistry, McGraw-Hill Book Co., New York, 15th edn, 1999 Search PubMed.
- L. Qiu, H. M. Xiao, X. D. Gong, X. H. Ju and W. H. Zhu, J. Phys. Chem. A, 2006, 110, 3797–3807 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, J. Mol. Model., 2015, 21, 262–272 CrossRef PubMed.
- J. S. Li, J. Phys. Chem. B, 2010, 114, 2198–2202 CrossRef CAS PubMed.
- Y. Yokomori and M. Yoshioka, Anal. Sci., 1197, 13, 701–702 CrossRef.
- J. Ellermann, E. Köck, H. Zimmermann and M. Gomm, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 443–445 CrossRef.
- H. Zimmermann, M. Gomm, J. Ellermann and E. Köck, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 2410–2412 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |