Open Access Article
Open Access ArticleHydration of the methanesulfonate–ammonia/amine complex and its atmospheric implications†
Shou-Kui Miaoab,
Shuai Jiangb,
Xiu-Qiu Pengab,
Yi-Rong Liub,
Ya-Juan Fengb,
Yan-Bing Wangab,
Feng Zhaoab,
Teng Huanga and
Wei Huang *abc
*abc
aLaboratory of Atmospheric Physico-Chemistry, Anhui Institute of Optics & Fine Mechanics, Chinese Academy of Sciences, Hefei, Anhui 230031, China
bSchool of Information Science and Technology, University of Science and Technology of China, Hefei, Anhui 230026, China. E-mail: huangwei6@ustc.edu.cn
cCenter for Excellent in Urban Atmospheric Environment, Institute of Urban Environment, Chinese Academy of Sciences, Xiamen, Fujian 361021, China
First published on 16th January 2018
Abstract
Methanesulfonate (MSA−), found in substantial concentrations in the atmosphere, is expected to enhance aerosol nucleation and the growth of nanoparticles, but the details of methanesulfonate clusters are poorly understood. In this study, MSA− was chosen along with ammonia (NH3) or three common amines and water (H2O) to discuss the roles of ternary homogeneous nucleation and ion-induced nucleation in aerosol formation. We studied the structural characteristics and thermodynamics of the clusters using density functional theory at the PW91PW91/6-311++G(3df,3pd) level. The analysis of noncovalent interactions predicts that the amines can form more stable clusters with MSA− than NH3, in agreement with the results from structures and thermodynamics; however, the enhancement in stability for amines is not large enough to overcome the difference in the concentrations of NH3 and amines under typical atmospheric conditions. In addition, the favorable free energies of formation for the (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters at 298.15 K show that MSA− could contribute to the aerosol nucleation process with binding NH3/amines and H2O up to n = 3. There are strong temperature and humidity dependences for the formation of complexes; higher humidity and temperature promote the formation of larger hydrates. Finally, for the (MSA−)(NH3/amines)(H2O)n clusters, the evaporation rates were determined to further investigate the atmospheric implications.
1. Introduction
Atmospheric aerosols have significant impact in several areas including earth climate, air quality and public health.1–5 Direct atmospheric nucleation via the formation of solid or liquid aerosols from gas-phase species is an important source of aerosol particles.6–10 Although the nucleation mechanism has been studied continuously, there are still many uncertainties in the compositions and the actual species that contribute to the nucleation and growth of nanoparticles in the atmosphere, especially at the molecular cluster level.5,10–13Both experimental and theoretical results have indicated that sulfuric acid (H2SO4) plays a critical role in atmospheric nucleation, and it has been widely identified as one of the major atmospheric nucleating species.11,14,15 The main source of H2SO4 in the atmosphere is the emitted SO2 from fossil fuel and biomass burning, which readily reacts with hydroxyl radicals (˙OH) and water vapor.16,17 Gas-phase H2SO4 has low vapor pressure and can easily supersaturate;15,18,19 therefore, it has been found that the H2SO4 undergoes a quick gas-condensed phase transition and serves as an effective nucleating species for water vapor, the key nucleating species in the atmosphere.11,14,15,20,21 However, the binary homogeneous nucleation of H2SO4 and water (H2O) is not enough to understand the observed nucleation events in the atmosphere, implying that some other compounds are involved in the nucleation phenomena.6,11,13
The importance of ammonia (NH3) in atmospheric nucleation has been extensively discussed.22–25 According to previous studies, NH3 has an enhancing effect on H2SO4 nucleation, responsible for the formation of NH4HSO4 and (NH4)2SO4 clusters.20,26 These species represent the three major forms of sulfur-containing aerosols, along with particulate sulfuric acid. Apart from NH3, amines are among the few basic compounds present in the actual atmosphere, and as such can be expected to bind strongly to H2SO4 or other nucleation precursors. All the field, laboratory, and modelling studies have suggested that the amines might play a significant role in the formation and subsequent growth of aerosol particles;10,27,28 some amines may even be more effective than NH3 at enhancing the particle formation. In the recent quantum chemical study involving several amines possibly existing in the atmosphere, it was pointed out that they could form more strongly bound structures with H2SO4 than NH3.27,29,30 Proton transfer of some amine-acid clusters is easier than NH3-acid clusters, leading to stronger binding.31,32 It is possible that amines, instead of NH3, are the major enhancers of H2SO4–H2O nucleation, or may significantly contribute to particle formation in the atmosphere. The smog chamber experiments and field measurements demonstrate that the acid–base reaction may play a significant role in particle formation, and it is viewed as an important nucleation mechanism, for example, the particle formation involving H2SO4 with NH3 and amines.27,33 Quantum calculations also explain the important role of acid–base reactions, which enhance neutral and ion-induced H2SO4–H2O nucleation.32,34,35
Methanesulfonic acid (MSA) and H2SO4 are viewed as the two main oxidation products of ocean-released dimethyl sulfide in the atmosphere.36–39 MSA is widely detected in particles, and its typical gas-phase concentration is roughly 10–100% of that of H2SO4 in the coastal marine boundary layer.39–42 Based on previous work, it has been shown that MSA is a less potent clustering agent in comparison with H2SO4, but its role is far from negligible in the atmosphere.43,44 The results of experiments and quantum chemical calculations indicate that the reactions of MSA with NH3 and amines including methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA) can contribute to the new particle formation under normal conditions.39,45,46 Although the concentration of amines is 1–3 orders of magnitude lower than that of NH3 in the actual atmosphere, they still play a key role in new particle formation (NPF) with MSA.46 MSA also enhances the formation of molecular clusters containing H2SO4 and DMA, and its effect is related to the temperature and concentrations of MSA and DMA.43 The research on the contribution of MSA to NPF with the common nucleation precursors such as MSA, methanol, formic acid, acetone, dimethylether, formaldehyde and methyl formate has emphasized the importance of MSA in NPF.44
In addition, the role of ions in atmospheric nucleation processes has been intensively debated.47–52 The mechanism of ion-mediated nucleation has been proposed to explain nucleation events in the earth's atmosphere. Previous studies at the Cosmics Leaving OUtdoor Droplets (CLOUD) facility at CERN indicate that ions surely enhance the formation of particles to a certain extent.53 In the ambient atmosphere, the clusters containing HSO4− are frequently observed. The results of experimental thermodynamics on some (HSO4−)(H2SO4) clusters suggest that these clusters have a high H2SO4 affinity and are able to promote cluster growth by H2SO4 uptake. The atmospheric ions as the nucleation catalysts could attract H2SO4, H2O and most of the common organic pollutants, providing an evident increase in nanoparticle formation.54 For MSA, it binds one or two water molecules with several hydrogen bonds to form the relatively stable clusters; however, the addition of more water would result in the proton transfer from MSA to the neighboring water molecules.55,56 Upon reaching a critical cluster size, the separation of methanesulfonate (MSA−) and the hydrated proton occurs.55,56 Proton transfer from MSA to NH3 or amines might be another source of MSA−.57 In this work, MSA− is selected for further research.
The ion-mediated nucleation of MSA− is expected to enhance the nucleation and growth of nanoparticles, but the details about the methanesulfonate clusters are poorly understood. In this study, MSA− is chosen along with NH3 or three other common amines possibly present in the atmosphere, and water to discuss the roles of ternary homogeneous nucleation and ion-induced nucleation in the aerosol nucleation. The three common amines discussed here are MA, DMA, and TMA. The hydration of (MSA−)(NH3/amines) is investigated with density functional theory (DFT) at the PW91PW91/6-311++G(3df,3pd) level. We have searched for the energy minima of structures of (MSA−)(NH3/amines)(H2O)n (n = 0–3) and determined their thermodynamic properties. The results were then used to gain further insight into the ternary nucleation of MSA−, NH3/amines and H2O, as well as the weak attraction analysis at the molecular level. The effects of humidity and temperature on the formation of (MSA−)(NH3/amines)(H2O)n (n = 0–3) and its atmospheric relevance are studied. Besides, the evaporation rates of these clusters are investigated for the first time. This work is a continuation of longstanding efforts to investigate ion–molecule interactions, hydrogen-bonded interactions, water cluster formation and atmospheric processes.49
2. Theoretical methods
The initial geometries of the various monomers and (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters have been obtained using the Basin Hopping (BH) algorithm58–60 coupled with DFT, and the generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) functional, and the double numerical plus d-functions (DND) basis set implemented in the DMol3 software package61 are applied in the procedure. This BH method was highly efficient at exploring atomic and molecular systems based on our previous studies.62–69 In this work, the number of BH searches range from 10 to 20 according to the cluster sizes, and each BH search consists of 1000 sampling steps at 3000 K with randomly generated molecular structures.The initial geometries of (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters were optimized at the PW91PW91/6-31+G* level by DFT. The stable isomers from the first optimization were selected to be further optimized by the PW91PW91/6-311++G(3df,3pd) level of theory as a higher level of theory to get the final configurations. The PW91PW91/6-311++G(3df,3pd) level implemented in the Gaussian 09 software package70 was used for the second optimization and frequency calculation. This methodology was adopted because it would take much less time to get the final structures with two-step optimizations than that through once direct optimization with the PW91PW91/6-311++G(3df,3pd) level of theory. The PW91PW91 functional showed great performance on a large number of atmospheric clusters containing sulfuric acid, water and the common organic acids, including predictions of structural characteristics, the thermodynamics of cluster formation and satisfactory similarity compared with experimental results.71–74 In order to make sure the results are consistent, the other three methods (CAM-B3LYP, M06-2X and ωB97x-D) were utilized for the smallest clusters, including different monomers and dimers. The density functional rather than wave function theory method (i.e. MP2) has been used in the systems for comparison with each other, as in the work of Elm et al.75 Due to the absence of wave function theory, the computational costs could be reduced. Besides, the recent benchmark studies proposed the pool of potential density functional methods, which are applied in our benchmark work,75,76 and thus the accuracy of our benchmark is maintained. The benchmark results with four functionals are displayed in Table 1 for the (MSA−)(NH3), (MSA−)(MA), (MSA−)(DMA) and (MSA−)(H2O). The Gibbs free energy calculated by PW91PW91 is close to that calculated by CAM-B3LYP, M06-2X and ωB97x-D, and the deviation is very low with the values less than 1 kcal mol−1. In the (MSA−)(TMA) cluster, the free energy change calculated by PW91PW91 is closer to that by CAM-B3LYP and ωB97x-D, where the deviation is also less than 1 kcal mol−1, rather than M06-2X; it could be acceptable in that the differences among the results of different functionals are considered to increase with the increasing clusters size. Thus, the PW91PW91 was chosen as the specific DFT method in our systems. In addition, the energy differences caused by various functionals do not change the order of stability for different dimers, that is, (MSA−)(DMA) > (MSA−)(MA) > (MSA−)(NH3) > (MSA−)(TMA).
| Isomer | Functional | G (Hartree) | ΔG (kcal mol−1) |
|---|---|---|---|
| MSA− | CAM-B3LYP | −663.87 | |
| M06-2X | −663.82 | ||
| ωB97x-D | −663.86 | ||
| PW91PW91 | −663.87 | ||
| NH3 | CAM-B3LYP | −56.54 | |
| M06-2X | −56.54 | ||
| ωB97x-D | −56.55 | ||
| PW91PW91 | −56.54 | ||
| MA | CAM-B3LYP | −95.80 | |
| M06-2X | −95.80 | ||
| ωB97x-D | −95.82 | ||
| PW91PW91 | −95.81 | ||
| DMA | CAM-B3LYP | −135.07 | |
| M06-2X | −135.07 | ||
| ωB97x-D | −135.10 | ||
| PW91PW91 | −135.09 | ||
| TMA | CAM-B3LYP | −174.34 | |
| M06-2X | −174.35 | ||
| ωB97x-D | −174.39 | ||
| PW91PW91 | −174.36 | ||
| H2O | CAM-B3LYP | −76.43 | |
| M06-2X | −76.42 | ||
| ωB97x-D | −76.43 | ||
| PW91PW91 | −76.43 | ||
| (MSA−)(NH3) | CAM-B3LYP | −720.41 | 0.88 |
| M06-2X | −720.35 | 0.96 | |
| ωB97x-D | −720.41 | 1.29 | |
| PW91PW91 | −720.41 | 1.02 | |
| (MSA−)(MA) | CAM-B3LYP | −759.67 | 0.24 |
| M06-2X | −759.62 | −0.32 | |
| ωB97x-D | −759.68 | 0.28 | |
| PW91PW91 | −759.68 | −0.66 | |
| (MSA−)(DMA) | CAM-B3LYP | −798.94 | 0.24 |
| M06-2X | −798.90 | −0.64 | |
| ωB97x-D | −798.96 | −0.15 | |
| PW91PW91 | −798.96 | −0.74 | |
| (MSA−)(TMA) | CAM-B3LYP | −838.21 | 3.03 |
| M06-2X | −838.16 | 5.03 | |
| ωB97x-D | −838.24 | 2.58 | |
| PW91PW91 | −838.23 | 2.18 | |
| (MSA−)(H2O) | CAM-B3LYP | −740.31 | −5.48 |
| M06-2X | −740.25 | −6.39 | |
| ωB97x-D | −740.30 | −5.43 | |
| PW91PW91 | −740.31 | −5.88 |
Finally, the optimized geometries were used for single point energy calculations with the DF-LMP2-F12/VDZ-F12 (second-order Møller–Plesset perturbation theory-explicitly correlated methods with density fitting) method implemented in Molpro 2010.1 (ref. 77) to get more accurate structure parameters. This level of theory is accurate for single-point energy calculations according to the previous work.52 The PW91PW91/6-311++G(3df,3pd) thermodynamic corrections were combined with DF-LMP2-F12/VDZ-F12 single-point energies to evaluate the zero-point corrected energies [E(0 K)], energies including atmospheric temperature enthalpies [H(T)] and Gibbs free energies [G(T)]. Compared with the PW91PW91/6-311++G(3df,3pd) binding energies (ΔE), the energies obtained by the DF-LMP2-F12/VDZ-F12 single-point energies with the PW91PW91/6-311++G(3df,3pd) thermodynamic corrections are closer to the results of CCSD(T)-F12a/VDZ-F12, as shown in Table 2.
| Isomer | Method | E (Hartree) | ΔE (kcal mol−1) |
|---|---|---|---|
| MSA− | PW91PW91 | −663.15 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −663.10 | ||
| CCSD(T)-F12a/VDZ-F12 | −663.14 | ||
| NH3 | PW91PW91 | −56.48 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −56.45 | ||
| CCSD(T)-F12a/VDZ-F12 | −56.49 | ||
| MA | PW91PW91 | −95.71 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −95.64 | ||
| CCSD(T)-F12a/VDZ-F12 | −95.72 | ||
| DMA | PW91PW91 | −134.93 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −134.84 | ||
| CCSD(T)-F12a/VDZ-F12 | −134.96 | ||
| TMA | PW91PW91 | −174.17 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −174.05 | ||
| CCSD(T)-F12a/VDZ-F12 | −174.21 | ||
| H2O | PW91PW91 | −76.36 | |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −76.34 | ||
| CCSD(T)-F12a/VDZ-F12 | −76.36 | ||
| (MSA−)(NH3) | PW91PW91 | −719.65 | −7.32 |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −719.56 | −7.67 | |
| CCSD(T)-F12a/VDZ-F12 | −719.64 | −8.91 | |
| (MSA−)(MA) | PW91PW91 | −758.76 | −8.56 |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −758.80 | −9.04 | |
| CCSD(T)-F12a/VDZ-F12 | −758.88 | −9.87 | |
| (MSA−)(DMA) | PW91PW91 | −798.10 | −9.31 |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −797.96 | −10.26 | |
| CCSD(T)-F12a/VDZ-F12 | −798.12 | −10.82 | |
| (MSA−)(TMA) | PW91PW91 | −837.33 | −6.10 |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −837.17 | −6.39 | |
| CCSD(T)-F12a/VDZ-F12 | −837.36 | −6.85 | |
| (MSA−)(H2O) | PW91PW91 | −739.53 | −13.70 |
| DF-LMP2-F12/VDZ-F12//PW91PW91 | −739.46 | −13.72 | |
| CCSD(T)-F12a/VDZ-F12 | −739.52 | −15.79 |
3. Results and discussion
3.1 Structures
Fig. 1 displays the optimized global minimum clusters at the PW91PW91/6-311++G(3df,3pd) level of theory for the (MSA−)(NH3)(H2O)n (n = 0–3), (MSA−)(MA)(H2O)n (n = 0–3), (MSA−)(DMA)(H2O)n (n = 0–3), and (MSA−)(TMA)(H2O)n (n = 0–3) systems, that will be discussed in this section. The “n” (n = 0–3) represents the number of water molecules up to three. The sulfur atoms are depicted in yellow, oxygen atoms in red, nitrogen atoms in blue, carbon atoms in dark gray and the hydrogen atoms in light gray. The hydrogen bonds are indicated with dotted lines. The Cartesian coordinates for the optimized global minimum clusters are shown in the ESI.†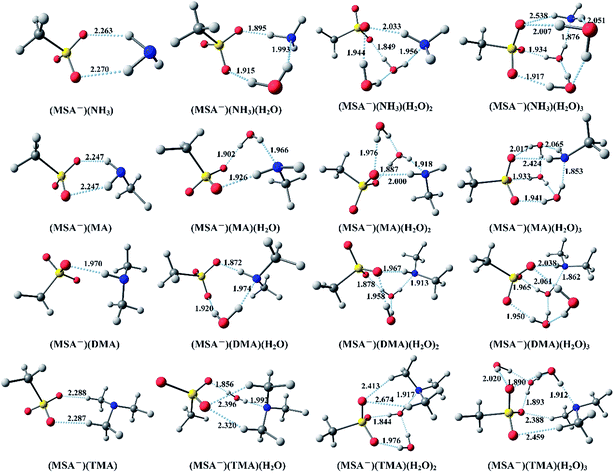 | ||
| Fig. 1 The global minima for (MSA−)(NH3/amines)(H2O)n (n = 0–3) optimized at the PW91PW91/6-311++G(3df,3pd) level. | ||
In Fig. 1, for the (MSA−)(NH3) dimer, the SO3 group of MSA− serves as the hydrogen bond acceptor from the NH3, forming two O–H hydrogen bonds with the lengths of 2.263 Å and 2.270 Å, respectively. For the (MSA−)(NH3)(H2O) cluster, the added H2O builds a ring structure with the MSA− and NH3. In this configuration, the NH3–H2O dimer is bound to MSA− with shorter hydrogen bond lengths than those in the MSA−–NH3 dimer, the hydrogen bond between the NH3 and water is also less than 2 Å. In (MSA−)(NH3)(H2O)2, the (H2O)2 dimer binds the SO3 group of MSA− with two strong hydrogen bonds, while the NH3 forms a weak hydrogen bond to the MSA− as a donor and a relatively strong hydrogen bond with the (H2O)2 dimer as an acceptor. The (H2O)3 trimer and NH3 are combined with the SO3 group in the (MSA−)(NH3)(H2O)3 cluster to form an approximate cubic structure, in which six oxygens, one sulfur and one nitrogen atom are viewed as the vertices of the cube. Eight hydrogen bonds found in this geometry make the structure stable, and the SO3 group of MSA− is the hydrogen bond acceptor from the NH3 and several waters.
For the (MSA−)(MA) dimer, the NH2 group of MA is bound to the MSA−, forming two hydrogen bonds with the same length of 2.247 Å, which are stronger than the those in (MSA−)(NH3). The one added water breaks the conformation of (MSA−)(MA) and allows the formation of a ring structure with three strong hydrogen bonds less than 2 Å in the (MSA−)(MA)(H2O) cluster. The structure of (MSA−)(MA)(H2O)2 is the same as that of (MSA−)(NH3)(H2O)2, and it can be seen that the NH3 is replaced by the MA. Just like the (MSA−)(NH3)(H2O)3, an approximate cubic structure is formed in the (MSA−)(MA)(H2O)3. The amino group of MA serves as a single acceptor–two donors bridge the MSA and water. Besides, the amino group, regardless of being from the NH3 or the MA, plays a key role in the establishment of the structure, in which the other part, just like the nitrogen atom and methyl group, can be ignored. Therefore, the structures of the (MSA−)(MA)(H2O)n system are highly similar to those of the (MSA−)(NH3)(H2O)n system for up to three water molecules.
In (MSA−)(DMA), the oxygen atom of the SO3 group as the hydrogen bond acceptor forms a strong hydrogen bond (1.970 Å) with the NH group of DMA. For the (MSA−)(DMA)(H2O) cluster in the ring structure built by the MSA−, DMA and H2O, the NH group of DMA acts as a single donor and a single acceptor, where the hydrogen bond between MSA− and DMA is stronger than that in (MSA−)(NH3)(H2O) and (MSA−)(MA)(H2O) clusters. The (MSA−)(DMA)(H2O)2 cluster has a similar structure to the (MSA−)(NH3)(H2O)2 and (MSA−)(MA)(H2O)2. DMA can form a stronger N–H hydrogen bond with the (H2O)2 dimer, with the length of 1.913 Å, compared to that in (MSA−)(NH3)(H2O)2 (1.956 Å) and (MSA−)(MA)(H2O)2 (1.918 Å), and another O–H hydrogen bond with length 1.967 Å, which is stronger than those in (MSA−)(NH3)(H2O)2 (2.033 Å) and (MSA−)(MA)(H2O)2 (2.000 Å). It can be expected that the DMA can form a more stable structure than NH3 or MA with MSA− in the presence of water. In (MSA−)(DMA)(H2O)3, the (H2O)3 trimer bridges the MSA− with DMA to form a similar cubic structure. The added water molecules promote the formation of multi-bridging hydrogen bonds. Moreover, the two methyl groups of DMA are still free and rarely participate in the formation of structures.
Two weak hydrogen bonds with lengths of 2.288 Å and 2.287 Å, respectively, are found between the MSA− and TMA in the (MSA−)(TMA) dimer, where the hydrogen bonds are weaker than those in the dimer of (MSA−)(NH3), (MSA−)(MA), and (MSA−)(DMA). Because of the existence of three methyl groups in TMA, the one added water cannot form a ring structure with the other molecules, and an oxygen atom of MSA− forms two hydrogen bonds (2.320 Å and 2.396 Å, respectively) with the two methyl groups of TMA. For the (MSA−)(TMA)(H2O)2, the (H2O)2 dimer binds with the two oxygen atoms in MSA−, and the TMA forms two hydrogen bonds with the remaining oxygen atom of the CH3O group. In this structure, the three oxygen atoms accept four hydrogen bonds without free oxygen atoms, in comparison with the other (MSA−)(NH3/amines)(H2O)2 clusters. The (MSA−)(TMA)(H2O)3 cluster is based on the (MSA−)(TMA)(H2O)2 with the third water bound to the (H2O)2 dimer and MSA−, forming two hydrogen bonds.
From the analysis above, it can be seen that the MSA− is combined with NH3 or different amines through one or more hydrogen bonds. It is obvious that the hydrogen bond with the length less than 2 Å in the (MSA−)(DMA) cluster is stronger than those in the other dimers. With the addition of water molecules, more hydrogen bonds are formed in the (MSA−)(NH3/amines)(H2O)n clusters, which might promote cluster formation in the actual atmosphere. For all the hydrates in Fig. 1, the water is always viewed as the hydrogen bond donor, and the MSA− is the hydrogen bond acceptor. Additionally, the possible evolution routes are found in the hydrates of (MSA−)(NH3/amines): for the monohydrate, the added water breaks the conformation of the (MSA−)(NH3/amines) dimer to allow the formation of a ring structure. The (H2O)2 dimer in the dihydrate connects the MSA− and the NH3/amines. The ammonia/amines and the (H2O)2 dimer form several hydrogen bonds with the SO3 group of MSA−. However, the CH3 group of MSA− could be ignored in the cluster conformation. For the trihydrate of (MSA−)(NH3/amines), the (H2O)3 trimer, the SO3 group and ammonia/amines are combined with about eight hydrogen bonds to form an approximate cubic stable structure.
3.2 Analysis of noncovalent interactions
In the (MSA−)(NH3/amines) dimers, the NH3 or amine binds to the MSA− with one or more hydrogen bonds. According to the structural results, the DMA can possibly form more stable clusters than the other NH3/amines with MSA−, but the details are lacking and need further investigation. “Atoms in Molecules (AIM)” has been regarded as one of the most efficient tools to explore the intermolecular interactions, such as hydrogen bonds.78–82 In this study, the topological analysis of electron density at bond critical points (BCPs), which provides evidence for the existence of the hydrogen bonds and deepens the nature of the intermolecular hydrogen bond in the compounds, is analyzed with the AIM methodology to discuss the interactions between the MSA− and NH3 or different amines. For the investigation of the topological characteristics at the bond critical point, the electron density (ρ), its Laplacian (∇2ρ), the electronic energy density (H), the electronic kinetic energy density (G), and the electronic potential energy density (V) are presented in Table 3.| Parameter | (MSA−)(NH3) | (MSA−)(MA) | (MSA−)(DMA) | (MSA−)(TMA) |
|---|---|---|---|---|
| ρ/a.u. | 0.0134/0.0141 | 0.0148/0.0148 | 0.0254 | 0.0132/0.0132 |
| ∇2ρ/a.u. | 0.0451/0.0457 | 0.0477/0.0477 | 0.0804 | 0.0423/0.0423 |
| H/a.u. | 0.0014/0.0014 | 0.0014/0.0014 | 0.0008 | 0.0014/0.0014 |
| G/a.u. | 0.0099/0.0100 | 0.0105/0.0105 | 0.0193 | 0.0091/0.0091 |
| V/a.u. | −0.0086/−0.0087 | −0.0091/−0.0091 | −0.0185 | −0.0077/−0.0077 |
| −G/V | 1.1511/1.1494 | 1.1538/1.1538 | 1.0432 | 1.1818/1.1818 |
As shown in Table 3, the electronic densities in intermolecular hydrogen bonds are from 0.0132 to 0.0254 a.u. for the (MSA−)(NH3/amines) dimers, which are in the accepted range for a hydrogen bond of (0.0070 to 0.0302) a.u. The value of electronic density indicates the strength of the hydrogen bond.83,84 The larger the value of ρ, the stronger the hydrogen bond is. From Table 3, we found that the order of the ρ value for the dimers is (MSA−)(DMA) > (MSA−)(MA) > (MSA−)(NH3) > (MSA−)(TMA), indicating the bond strength. Their corresponding positive ∇2ρ values imply the closed-shell system interactions in all dimers, which are hydrogen bonding, ionic interactions or van der Waals forces, rather than a covalent bond. Their values of ∇2ρ are also in the general range of 0.024 to 0.139 a.u. for a hydrogen bond.85,86 The strongest and weakest hydrogen bonds are found in the (MSA−)(DMA) and (MSA−)(TMA) dimers, respectively, in view of their ∇2ρ values. Furthermore, the electronic energy density (H) is viewed as an important index to explore the non-covalent interaction. The positive H values show that these (MSA−)(NH3/amines) dimers are basically electrostatic in closed-shell system interactions, while the interaction is predominantly covalent in the case of H < 0. The value of −G/V is used to determine whether the regions correspond to covalent or noncovalent interactions. The −G/V values are larger than 1 in Table 3, showing that the interaction for all the dimers are noncovalent. On the other hand, the smaller the value of −G/V, the stronger the hydrogen bond is. Thus, the intermolecular hydrogen bond interaction between MSA− and DMA is the strongest.
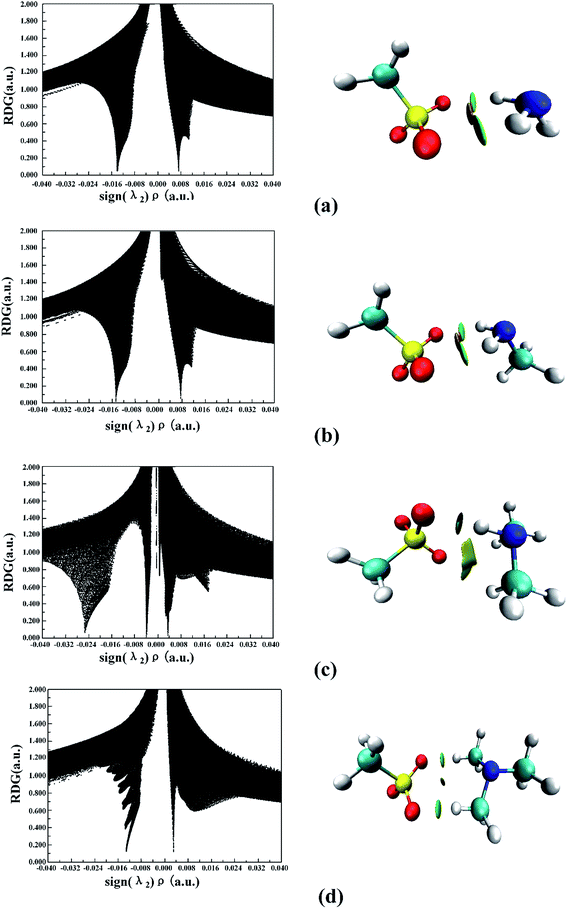
The noncovalent interaction (NCI) index, which is based on the relationship between the electron density and the reduced density gradient, has been mentioned as an extension of AIM by Yang and coworkers.79 The reduced density gradient (RDG), s, in DFT as a fundamental dimensionless quantity was calculated to reveal the deviation from a homogeneous electron distribution:
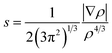 | (1) |
Plots of the RDG (s) vs. the electron density (ρ) multiplied by the sign of the second Hessian eigenvalue (λ2) for the (MSA−)(NH3), (MSA−)(MA), (MSA−)(DMA), and (MSA−)(TMA) dimers is shown in Fig. 2 using the Multiwfn program. The reduced gradient spikes in the low densities indicate the existence of the stabilizing interactions of noncovalent bonding. For the (MSA−)(DMA) dimer, there is only one low-reduced gradient spike at low density of the sign(λ2)ρ value of −0.0254 a.u., showing a stable hydrogen bond interaction. From (MSA−)(NH3) to (MSA−)(MA), and to (MSA−)(TMA), the characteristic peaks directed toward the sign(λ2)ρ values are very near zero, which are −0.0134/−0.0141, −0.0148/−0.0148 and −0.0132/−0.0132, respectively, indicative of the relatively weak hydrogen bond interactions between the MSA− and the NH3 or the corresponding amines. In the case of (MSA−)(MA), (MSA−)(NH3) and (MSA−)(TMA), although the number of peaks is more than one, their locations are so close that only one spike is seen for each dimer in Fig. 2. The characteristic peaks directed toward sign(λ2)ρ values larger than the hydrogen bond interaction is weaker, therefore, the hydrogen bond interactions become weaker from (MSA−)(MA) to (MSA−)(NH3), and to (MSA−)(TMA).
 | ||
| Fig. 2 Noncovalent interactions (NCI) analysis among the global minima for (MSA−)(NH3) (a), (MSA−)(MA) (b), (MSA−)(DMA) (c), (MSA−)(TMA) (d). | ||
Fig. 2 also shows that there exists a bonding isosurface between the middle region of the MSA− and NH3/amines. From the (MSA−)(TMA) to (MSA−)(NH3), to (MSA−)(MA), and to (MSA−)(DMA), the color coding of these bonding isosurfaces is from green to blue, which demonstrates that the stability order of the hydrogen bonding interactions for different dimers is (MSA−)(DMA) > (MSA−)(MA) > (MSA−)(NH3) > (MSA−)(TMA). The reduced gradient isosurface (s = 0.05 au) obtained by the VMD program87 agrees well with the analysis of the scatter plots above.
3.3 Thermodynamics of the cluster formation
Thermodynamic analysis provides a significant method to investigate the possibility of cluster formation. Gibbs free energy changes are effective for evaluating the strength of the intermolecular interaction and the spontaneity of the process of the cluster formation,28 and are therefore used to understand the interaction of methanesulfonate with NH3 or amine and their hydration. The relative single-point energies, ΔE (0 K), of the (MSA−)(NH3)(H2O)n (n = 0–3) clusters are calculated using the following eqn (2) and (3). The intermolecular enthalpy, ΔH (298.15 K), and the Gibbs free energy, ΔG (298.15 K), are obtained in the same way for all the systems:| ΔE = E(MSA−)(NH3) − EMSA− − ENH3 | (2) |
| ΔE = E(MSA−)(NH3)(H2O)n − E(MSA−)(NH3)(H2O)n−1 − EH2O | (3) |
| Reaction | ΔE (0 K) | ΔH (298.15 K) | ΔG (298.15 K) |
|---|---|---|---|
| MSA− + NH3 ↔ (MSA−)(NH3) | −7.67 | −7.51 | −0.45 |
| (MSA−)(NH3) + H2O ↔ (MSA−)(NH3)(H2O) | −12.24 | −13.31 | −2.56 |
| (MSA−)(NH3)(H2O) + H2O ↔ (MSA−)(NH3)(H2O)2 | −12.39 | −13.29 | −3.27 |
| (MSA−)(NH3)(H2O)2 + H2O ↔ (MSA−)(NH3)(H2O)3 | −11.78 | −12.96 | −1.51 |
| MSA− + MA ↔ (MSA−)(MA) | −9.04 | −8.51 | −1.14 |
| (MSA−)(MA) + H2O ↔ (MSA−)(MA)(H2O) | −12.86 | −13.88 | −3.16 |
| (MSA−)(MA)(H2O) + H2O ↔ (MSA−)(MA)(H2O)2 | −12.36 | −13.25 | −2.63 |
| (MSA−)(MA)(H2O)2 + H2O ↔ (MSA−)(MA)(H2O)3 | −11.41 | −12.46 | −1.85 |
| MSA− + DMA ↔ (MSA−)(DMA) | −10.26 | −9.68 | −1.68 |
| (MSA−)(DMA) + H2O ↔ (MSA−)(DMA)(H2O) | −13.07 | −13.99 | −3.49 |
| (MSA−)(DMA)(H2O) + H2O ↔ (MSA−)(DMA)(H2O)2 | −12.47 | −13.32 | −3.30 |
| (MSA−)(DMA)(H2O)2 + H2O ↔ (MSA−)(DMA)(H2O)3 | −11.21 | −12.14 | −1.16 |
| MSA− + TMA ↔ (MSA−)(TMA) | −6.39 | −5.71 | 1.90 |
| (MSA−)(TMA) + H2O ↔ (MSA−)(TMA)(H2O) | −14.23 | −15.08 | −4.43 |
| (MSA−)(TMA)(H2O) + H2O ↔ (MSA−)(TMA)(H2O)2 | −12.68 | −13.54 | −3.19 |
| (MSA−)(TMA)(H2O)2 + H2O ↔ (MSA−)(TMA)(H2O)3 | −11.53 | −12.41 | −2.04 |
The relative single-point energy at 0 K of MSA− with NH3 (−7.67 kcal mol−1) is much weaker than that with MA (−9.04 kcal mol−1) and DMA (−10.26 kcal mol−1), while a little stronger than that with TMA (−6.39 kcal mol−1), shown in Table 4. The temperature effect is taken into account to acquire the thermochemical properties of the clusters under atmospheric conditions. At 298.15 K, the interaction of MSA− with NH3/amines and their hydrates contain the contributions from the translational, rotational and vibrational energies, and the thermodynamics of clusters are with regard to enthalpies and entropies. Even if the enthalpies or the entropies are considered, the interaction of MSA− with DMA is still the strongest, followed by MA, NH3 and TMA. The enthalpy changes of the reactions are −9.68, −8.51, −7.51 and −5.71 kcal mol−1, and the Gibbs free energy changes are −1.68, −1.14, −0.45 and 1.90 kcal mol−1 for (MSA−)(DMA), (MSA−)(MA), (MSA−)(NH3) and (MSA−)(TMA), respectively.
The thermodynamic properties of hydrates are also shown in Table 4. For the (MSA−)(NH3)(H2O)n (n = 1–3) system, the formation of (MSA−)(NH3) hydrates by the stepwise addition of water is exothermic by 11.78–12.39 kcal mol−1. For the clusters formed by the (MSA−)(MA) dimer and one to three waters, 11.41–12.86 kcal mol−1 is released. The formation of the clusters containing the (MSA−)(DMA) dimer and one to three waters is exothermic by 11.21–13.07 kcal mol−1, and 11.53–14.23 kcal mol−1 is released during the formation of the (MSA−)(TMA)(H2O)n (n = 1–3) clusters. The Gibbs free energies of the formation of hydrates are in the range of about −1 to −4 kcal mol−1. The favorable free energies of formation for the (MSA−)(NH3/amines)(H2O)n (n = 1–3) clusters at 298.15 K predicted that MSA− can contribute to the aerosol nucleation process by binding to NH3/amines and water until n = 3. From the ΔG values, we also find that the initial formation of (MSA−)(NH3/amines)(H2O) monohydrate is highly favorable. However, entropic effects may limit the stepwise addition of more water, and the subsequent addition of water molecules to an existing monohydrate is less thermodynamically favorable.
Moreover, the ΔG values of the global minima for the (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters increase with increasing the temperature from 260 K to 300 K in Table 5, which shows that the stability of the clusters decreases with the increasing temperature. In other words, the clusters discussed in this study might be more favorable in the conditions of lower temperatures.
| Reaction | ΔG (260 K) | ΔG (280 K) | ΔG (300 K) |
|---|---|---|---|
| MSA− + NH3 ↔ (MSA−)(NH3) | −1.35 | −0.87 | −0.40 |
| (MSA−)(NH3) + H2O ↔ (MSA−)(NH3)(H2O) | −3.93 | −3.21 | −2.49 |
| (MSA−)(NH3)(H2O) + H2O ↔ (MSA−)(NH3)(H2O)2 | −4.54 | −3.87 | −3.20 |
| (MSA−)(NH3)(H2O)2 + H2O ↔ (MSA−)(NH3)(H2O)3 | −2.97 | −2.20 | −1.43 |
| MSA− + MA ↔ (MSA−)(MA) | −2.09 | −1.59 | −1.09 |
| (MSA−)(MA) + H2O ↔ (MSA−)(MA)(H2O) | −4.53 | −3.81 | −3.09 |
| (MSA−)(MA)(H2O) + H2O ↔ (MSA−)(MA)(H2O)2 | −3.99 | −3.27 | −2.56 |
| (MSA−)(MA)(H2O)2 + H2O ↔ (MSA−)(MA)(H2O)3 | −3.20 | −2.49 | −1.78 |
| MSA− + DMA ↔ (MSA−)(DMA) | −2.71 | −2.16 | −1.62 |
| (MSA−)(DMA) + H2O ↔ (MSA−)(DMA)(H2O) | −4.83 | −4.12 | −3.42 |
| (MSA−)(DMA)(H2O) + H2O ↔ (MSA−)(DMA)(H2O)2 | −4.58 | −3.91 | −3.23 |
| (MSA−)(DMA)(H2O)2 + H2O ↔ (MSA−)(DMA)(H2O)3 | −2.56 | −1.82 | −1.09 |
| MSA− + TMA ↔ (MSA−)(TMA) | 0.92 | 1.44 | 1.95 |
| (MSA−)(TMA) + H2O ↔ (MSA−)(TMA)(H2O) | −5.79 | −5.07 | −4.36 |
| (MSA−)(TMA)(H2O) + H2O ↔ (MSA−)(TMA)(H2O)2 | −4.51 | −3.81 | −3.12 |
| (MSA−)(TMA)(H2O)2 + H2O ↔ (MSA−)(TMA)(H2O)3 | −3.36 | −2.66 | −1.97 |
3.4 Atmospheric relevance
In view of the results and analysis of geometry, noncovalent interactions and thermodynamics discussed above, it has been found that the MSA− could form more stable clusters with amines (especially DMA and MA) than NH3. However, this does not imply that the amines are more important for the atmospheric nucleation, compared with NH3, and their difference in concentrations should be included. Whether the enhancement in stability due to amines could be large enough to overcome the difference in typical atmospheric concentrations of NH3 and amines is poorly understood and needs to be further researched. The exact values depend on the initial concentrations of NH3 and amines.The earlier studies show that the amines are more easily oxidized by OH than NH3, resulting in a much higher concentration of NH3 than that of amine by at least two orders of magnitude.88 The typical concentrations of NH3 are in the range of 0.1–10 ppb in the continental air, meaning that the amine concentrations are about 1–100 ppt. Sellegri et al.89 concluded that the trimethylamine concentrations are from 34 to 80 ppt during a spring measurement campaign in Hyytiälä, Finland, which is close to the estimation above. However, higher amine concentrations have been reported at a number of sites in the boundary layer recently, i.e., the concentrations for some amines are more than 100 ppb in the vicinity of a dairy farm in California, based on the investigation by Rabaud et al.90 Nevertheless, the concentration of NH3 should be obviously higher than the amines in most cases.
From the law of mass balance, the ratio of the concentrations of NH3-containing to DMA-containing clusters is defined by the following:
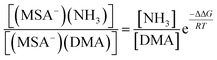 | (4) |
According to the eqn (4) and the free energies, we have calculated the ratio of the concentrations of (MSA−)(NH3) to (MSA−)(DMA) dimer as a function of the gas-phase concentration ratio of NH3 to DMA. The results are given in Table 6. We found that the ratio of NH3 and DMA concentrations is only 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and the concentration of (MSA−)(NH3) is equal to that of the (MSA−)(DMA) dimer. When the ratio is increased to 100
1, and the concentration of (MSA−)(NH3) is equal to that of the (MSA−)(DMA) dimer. When the ratio is increased to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1000
1 and 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, correspondingly, (MSA−)(NH3) concentrations are at one and two orders of magnitude higher than those of (MSA−)(DMA). Chen et al.45,46 have indicated that the neutral MSA contributes to NPF with the reaction of amines/NH3 and water. MSA tends to form particles with amines rather than NH3, and the particle formation rates of amines with MSA are 2–3 orders of magnitude higher than that of NH3, but the concentrations of amines are 1–3 orders of magnitude lower compared to those of ammonia. Therefore, although the amines have relatively low concentrations in the actual atmosphere, it is considered as a significant role in NPF. Kurtén et al.27 investigated the structure and thermodynamics of the dimers of H2SO4 or HSO4− with NH3 and amines, and found that the (H2SO4)(NH3/amine) complexes are more stable than the (HSO4−)(NH3/amine). Moreover, the (H2SO4)(amine) cluster is remarkably stronger than that of (H2SO4)(NH3), while the (HSO4−)(amine) is a little stronger than (HSO4−)(NH3). The greater stability of the (H2SO4)(amine) or (HSO4−)(amine) cluster compared to those with NH3 does overcome the difference in concentration. However, for MSA−, the advantage of amines in ΔG contributes to ten times stronger stabilizing effects than NH3 with MSA−. The stabilizing effect could be determined by two factors, which are the stepwise Gibbs free energy changes and the concentration ratios of amines with respect to NH3. If the NH3 concentrations are more than one order of magnitude higher than that of DMA, the enhancement in stability due to amines appears not to be large enough to overcome the difference in the concentrations of NH3 and amines.
1, correspondingly, (MSA−)(NH3) concentrations are at one and two orders of magnitude higher than those of (MSA−)(DMA). Chen et al.45,46 have indicated that the neutral MSA contributes to NPF with the reaction of amines/NH3 and water. MSA tends to form particles with amines rather than NH3, and the particle formation rates of amines with MSA are 2–3 orders of magnitude higher than that of NH3, but the concentrations of amines are 1–3 orders of magnitude lower compared to those of ammonia. Therefore, although the amines have relatively low concentrations in the actual atmosphere, it is considered as a significant role in NPF. Kurtén et al.27 investigated the structure and thermodynamics of the dimers of H2SO4 or HSO4− with NH3 and amines, and found that the (H2SO4)(NH3/amine) complexes are more stable than the (HSO4−)(NH3/amine). Moreover, the (H2SO4)(amine) cluster is remarkably stronger than that of (H2SO4)(NH3), while the (HSO4−)(amine) is a little stronger than (HSO4−)(NH3). The greater stability of the (H2SO4)(amine) or (HSO4−)(amine) cluster compared to those with NH3 does overcome the difference in concentration. However, for MSA−, the advantage of amines in ΔG contributes to ten times stronger stabilizing effects than NH3 with MSA−. The stabilizing effect could be determined by two factors, which are the stepwise Gibbs free energy changes and the concentration ratios of amines with respect to NH3. If the NH3 concentrations are more than one order of magnitude higher than that of DMA, the enhancement in stability due to amines appears not to be large enough to overcome the difference in the concentrations of NH3 and amines.
| [NH3]/[DMA] ratio | [(MSA−)(NH3)]/[(MSA−)(DMA)] ratio |
|---|---|
| 10 | 1.243 |
| 100 | 12.43 |
| 1000 | 124.3 |
In this work, the method for calculating the concentration of clusters is only a limited and simplistic approximation; the situation in the atmosphere is actually much more complicated. Eqn (4) presumes a pseudo-steady-state situation, in which the formation of clusters does not significantly exhaust the gas-phase reservoir of reactant molecules. Unfortunately, in the actual condition, the formation of MSA−-amine clusters depletes the amine reservoir quickly, and then the steady-state conditions in eqn (4) will not apply. However, it could be a valid way to get a qualitative assessment of how important the various clusters are in their formations, and compare their different contributions to the aerosol nucleation. A quantitatively precise result of the relative importance of amine-containing and NH3 – containing clusters in the atmosphere would not only rely on much more accurate concentration data of NH3 and amines, but also the reliable kinetic nucleation simulations, which should be acquired in further studies.
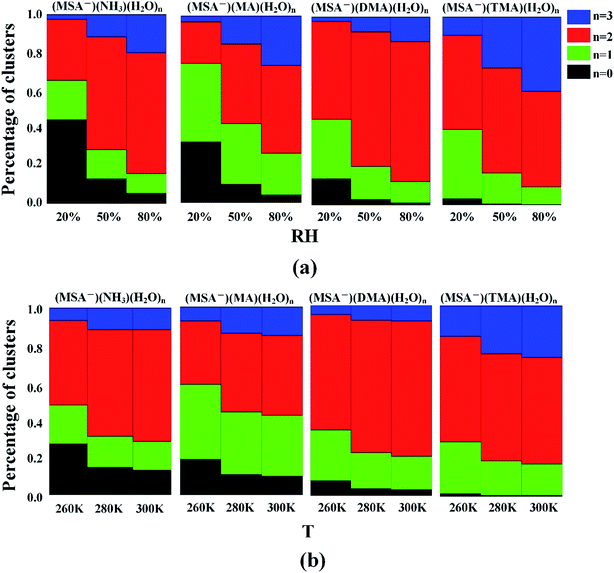
3.5 Influences of humidity and temperature on hydrate distributions
For the hydrates, the water molecules could easily bind to the (MSA−)(NH3/amines) core based on the favorable stepwise free energies of formation of the (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters except for the (MSA−)(TMA) dimer in Table 4, to promote the aerosol formation process. However, the binding number of water molecules in the clusters could be affected by the various relative humidities (RHs). To get further results, the hydrate distributions of non-aqueous “cores” ((MSA−)(NH3/amines) heterodimer) were estimated at various RHs in Fig. 3(a).32,91For the (MSA−)(NH3)(H2O)n (n = 0–3) system, 44% of (MSA−)(NH3) is non-hydrated at 20% RH, but that number decreases to 13% and 5% at 50% RH and 80% RH, respectively. The most common hydrated cluster is always the dihydrate, and its population increases from 32% to 60% and to 64% throughout the RH range from 20% to 80%, but the second hydrated cluster is changed with the various RH, which is the monohydrate at the RH = 20% and 50%, and the trihydrate at the RH = 80%. For (MSA−)(MA)(H2O)n (n = 0–3), the number of hydrates gets to 96% at the RH of 80%. The most abundant cluster in this system is the monohydrate at RH = 20%, which is replaced by the dihydrate if the RH is more than 50%. The peak of the cluster distribution moves from the monohydrate cluster to the dihydrate. The most common cluster is the dihydrate for the DMA-containing and TMA-containing systems. In (MSA−)(DMA)(H2O)n, the content of (MSA−)(DMA)(H2O)2 is the largest and increases with the increasing RH. When the RH gets to 80%, the (MSA−)(DMA)(H2O)2 accounts for 74% of the total amount. For (MSA−)(TMA)(H2O)n, the total concentration of (MSA−)(TMA) was mainly dispersed into the (MSA−)(TMA)(H2O)2 and (MSA−)(TMA)(H2O)3 clusters, and these two clusters occupy 83% of all the (MSA−)(TMA)(H2O)n clusters at RH = 50%, which is 90% at RH = 80%. In this case, the trihydrate content increases, and the number reaches 40% at the RH of 80%, although a little less than the dihydrate.
The obvious sensitivity of hydrate distributions to relative humidity can be seen through the results in Fig. 3(a) as we previously determined,35 where the degree of change for hydrate distributions varies according to the different systems. The unhydrated cluster dominates only when the relative humidity is very low. Once the RH reaches 50%, more than 87% of clusters are hydrated in all the cases, and the population is nearly 100% for the (MSA−)(DMA) and (MSA−)(TMA). With the increasing humidities, the number of monohydrates is lower, which contributes to the enhanced content of dihydrate and trihydrate. This denotes that the increasing RH not only promotes the formation of hydrates, but also the larger hydrates, such as the dihydrate and the trihydrate in our study.
According to the earlier studies, the variation of temperature is another factor impacting the hydrate distributions.35 As shown in Table 5, there is a strong temperature dependence of the Gibbs free energies of stepwise hydration, which affects the formation of (MSA−)(NH3/amines)(H2O)n hydrates. The study in Fig. 3(b) suggests that the higher temperature favors the formation of dihydrate and trihydrate, compared with nonhydrate and monohydrate. For the temperature range of 260 K to 280 K, the obvious variation of hydration distribution is seen from Fig. 3(b), and the change is relatively slow from T = 280 K to 300 K. The general trend is that the dihydrate and trihydrate contents increase, while the number of nonhydrates and monohydrates decrease with higher temperature in the systems. The effect of temperature mainly results from the change of ΔG and the saturation vapor pressure of water vapor from the temperature of 260 K to 300 K.
3.6 Evaporation rates
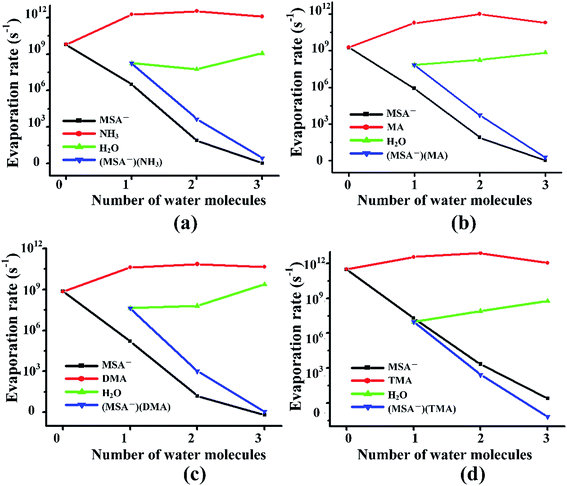
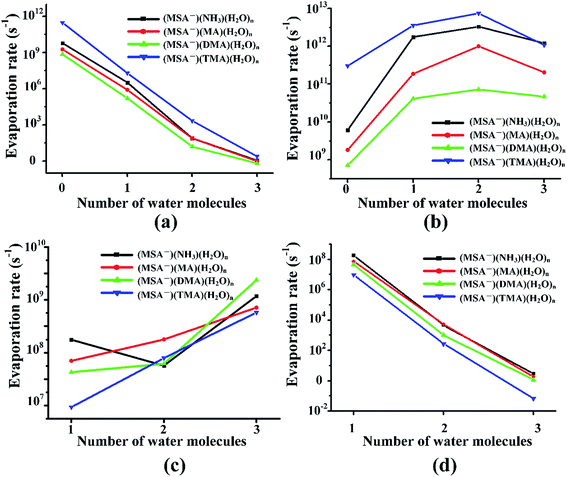
Previous studies revealed that the cluster evaporation rates based on the formation free energy obtained by quantum chemical calculation is a significant parameter for understanding the very early stages of particle formation.30,92 As shown in Fig. 4, for all the unhydrated clusters, the evaporation rates of MSA− are as large as 109–1011 s−1 for (MSA−)(NH3/amines)(H2O)n. When one water molecule is added to the dimers, the evaporation of MSA− is significantly reduced by about three orders of magnitude. The MSA− evaporation continues dropping from 10–103 s−1 to nearly zero with the increasing water molecules from n = 2 to 3. The evaporation of NH3/amines in Fig. 4 changes in a different way compared to MSA− with the various water molecules. Once the clusters are hydrated, the evaporation has an obvious increase from 109–1011 s−1 to about 1011–1012 s−1. The change in evaporation rate for water is different for the different systems. In the (MSA−)(MA)(H2O)n, (MSA−)(DMA)(H2O)n and (MSA−)(TMA)(H2O)n clusters, they increase monotonically with the added water; in particular, its evaporation rate is close to the DMA evaporation for the (MSA−)(DMA)(H2O)n clusters at n = 3. There is a little difference in the (MSA−)(NH3)(H2O)n clusters where the change is non-monotonic, however, the water evaporation increases more or less with the addition of more water in general. The evaporation of (MSA−)(NH3/amines) decreases rapidly with the addition of one to three water molecules in the (MSA−)(NH3/amines) hydrates. In the (MSA−)(NH3)(H2O)n, (MSA−)(MA)(H2O)n and (MSA−)(DMA)(H2O)n clusters, the order of evaporation rate is NH3/amines > H2O > (MSA−)(NH3/amines) > MSA−. However, the order is changed in (MSA−)(TMA)(H2O)n where the evaporation of (MSA−)(TMA) is even less than MSA−, and the gap is enhanced with more water.In the different systems containing MSA−, NH3/amines and several waters, the MSA− in Fig. 5(a) gets a marked drop in the evaporation rate from 109–1012 s−1 at n = 0 to nearly zero at n = 3. The evaporation rate order of MSA− is the sequence of (MSA−)(TMA) > (MSA−)(NH3) > (MSA−)(MA) > (MSA−)(DMA). For the larger hydrates containing three waters, the MSA− evaporation rate for the different systems is close to zero, which indicates that the evaporation of MSA− could be ignored with the addition of more water. The order of evaporation of NH3/amines in Fig. 5(b) is also (MSA−)(TMA) > (MSA−)(NH3) > (MSA−)(MA) > (MSA−)(DMA), consistent with the results of MSA−. The evaporation number increases as the water molecules increase until n = 2 as the turning point. In Fig. 5(c), except for the (MSA−)(NH3)(H2O)n (n = 0–3), the water evaporation increases from n = 1 to 3. In the (MSA−)(NH3)(H2O)n clusters, the evaporation rate of n = 2 is the lowest point. The results could be proved by the analysis of ΔG, shown in Table 4, in which the stability order of hydrates is (MSA−)(NH3)(H2O)2 > (MSA−)(NH3)(H2O) > (MSA−)(NH3)(H2O)3, and (MSA−)(NH3)(H2O)2 is the most stable cluster in this system. In addition to the evaporation of monomers, we also investigated the cluster fission, as shown in Fig. 5(d). Our results showed that the value of (MSA−)(NH3/amines)(H2O)n (n = 0–3) ⇔ (MSA−)(NH3/amines) + (H2O)n (n = 0–3) fission rate is close to the MSA− evaporation rate with respect to the number of water molecules. The (MSA−)(TMA) dimer is unfavorable compared to the (MSA−)(NH3), (MSA−)(MA) and (MSA−)(DMA) dimer, but it could easily bind to water to form the stable (MSA−)(TMA)(H2O)n hydrates based on the thermodynamic values in Table 4, contributing to the relatively low evaporation of the (MSA−)(TMA) cluster.
Comparing the evaporation rates, we can see that the evaporation reactions of NH3/amines are more important than the evaporation reactions of the acid ions and water molecules. The presence of water markedly changes the effect of MSA− and NH3/amines on the evaporation rates. The base molecules and water evaporations increase more or less with the increasing waters, while the MSA− and (MSA−)(NH3/amines) evaporations decrease due to the formation of the stable MSA−-containing hydrates. The lifetime of a cluster will be determined by the evaporation rate of the base molecules rather than the others.
4. Conclusions
For the (MSA−)(NH3/amines)(H2O)n (n = 0–3) clusters, the global minimum was obtained for each sized cluster. We investigated the thermodynamics of hydration of (MSA−)(NH3/amines) using high-level DFT calculations, and discussed its implication on atmospheric nucleation.Multiple strong hydrogen bonds are formed in the (MSA−)(NH3/amines)(H2O)n (n = 0–3) complexes to promote the cluster formation. Due to the acid–base reactions that are expected to give birth to neutral or charged clusters that have relevance for NPF, MSA− probably forms clusters with NH3 or amines in the atmosphere. The favorable stepwise free energies of formation for the hydrates at 298.15 K suggest that MSA−, acting as a stabilizer of small clusters, can contribute to the nucleation process by binding with NH3 or different amines and water until n = 3.
The stability order for the MSA− – base dimers is (MSA−)(DMA) > (MSA−)(MA) > (MSA−)(NH3) > (MSA−)(TMA), according to the analysis of weak attraction, which is in agreement with the results of structures and thermodynamics. Although MSA− could form more stable clusters with amines, compared to NH3, the enhancement in stability for amines cannot be large enough to overcome the difference in the concentrations between NH3 and amines under typical atmospheric conditions. It implies that (MSA−)(NH3) clusters are more abundant and important in the atmospheric nucleation, compared with (MSA−)(amines).
There are strong humidity and temperature dependences for the (MSA−)(NH3/amines)(H2O)n complexes: the higher humidity and temperature promote the formation of hydrates. The populations of larger hydrates, including the dihydrate and trihydrate, are enhanced with the increasing RH and temperature, rather than the monohydrate. From the analysis of evaporation rates, we found that the evaporation reactions of NH3/amines are more important than the evaporation reactions of the ionic acid and water molecules, which determine the lifetime of (MSA−)(NH3/amines)(H2O)n (n = 0–3). In addition, the presence of water changes the effects of MSA− and NH3/amines on the evaporation rates markedly.
Based on the study of (MSA−)(NH3/amines)(H2O)n, this work tentatively provides a reference for the further investigation of NPF. Further theoretical, experimental and field research are required to investigate the synergy of MSA− and NH3 or amines on the nucleation system involving H2SO4, MSA−, NH3, amines and H2O, which is beyond the scope of the present paper.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21403244, 41775122, 21573241, 41605099, 41705097, 41705111, 41775112 and 41527808), the National Science Fund for Distinguished Young Scholars (Grant No. 41725019), the Key Research Program of Frontier Science, CAS (Grant No. QYZDB-SSW-DQC031), the Key Research Program of the Chinese Academy of Sciences (Grant No. ZDRW-ZS-2016-4-3-6) and the National Key Research and Development Program (Grant No. 2016YFC0202203 and 2016YFC0203703).References
- R. J. Charlson, J. H. Seinfeld, A. Nenes, M. Kulmala, A. Laaksonen and M. C. Facchini, Science, 2001, 292, 2025–2026 CrossRef CAS PubMed.
- G. Oberdörster and M. J. Utell, Environ. Health Perspect., 2002, 110, A440 CrossRef.
- A. Saxon and D. Diaz-Sanchez, Nat. Immunol., 2005, 6, 223–226 CrossRef CAS PubMed.
- S. Guo, M. Hu, M. L. Zamora, J. Peng, D. Shang, J. Zheng, Z. Du, Z. Wu, M. Shao and L. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17373–17378 CrossRef CAS PubMed.
- M. R. Heal, P. Kumar and R. M. Harrison, Chem. Soc. Rev., 2012, 41, 6606–6630 RSC.
- M. Kulmala, Science, 2003, 302, 1000–1001 CrossRef CAS PubMed.
- D. V. Spracklen, K. S. Carslaw, M. Kulmala, V. M. Kerminen, S. L. Sihto, I. Riipinen, J. Merikanto, G. W. Mann, M. P. Chipperfield and A. Wiedensohler, Geophys. Res. Lett., 2008, 35, L06808 Search PubMed.
- C. Kuang, P. McMurry and A. McCormick, Geophys. Res. Lett., 2009, 36, L09822 CrossRef.
- J. Merikanto, D. Spracklen, G. Mann, S. Pickering and K. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes and A. Kürten, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2011, 112, 1957–2011 CrossRef PubMed.
- B. R. Bzdek, M. R. Pennington and M. V. Johnston, J. Aerosol Sci., 2012, 52, 109–120 CrossRef CAS.
- R. Zhang, G. Wang, S. Guo, M. L. Zamora, Q. Ying, Y. Lin, W. Wang, M. Hu and Y. Wang, Chem. Rev., 2015, 115, 3803–3855 CrossRef CAS PubMed.
- B. Temelso, T. E. Morrell, R. M. Shields, M. A. Allodi, E. K. Wood, K. N. Kirschner, T. C. Castonguay, K. A. Archer and G. C. Shields, J. Phys. Chem. A, 2012, 116, 2209–2224 CrossRef CAS PubMed.
- M. Kulmala, H. Vehkamäki, T. Petäjä, M. Dal Maso, A. Lauri, V.-M. Kerminen, W. Birmili and P. H. McMurry, J. Aerosol Sci., 2004, 35, 143–176 CrossRef CAS.
- B. Temelso, T. N. Phan and G. C. Shields, J. Phys. Chem. A, 2012, 116, 9745–9758 CrossRef CAS PubMed.
- B. R. Bzdek, C. A. Zordan, M. R. Pennington, G. W. Luther III and M. V. Johnston, Environ. Sci. Technol., 2012, 46, 4365–4373 CrossRef CAS PubMed.
- M. Kulmala, K. Lehtinen and A. Laaksonen, Atmos. Chem. Phys., 2006, 6, 787–793 CrossRef CAS.
- M. Kulmala, I. Riipinen, M. Sipilä, H. E. Manninen, T. Petäjä, H. Junninen, M. Dal Maso, G. Mordas, A. Mirme and M. Vana, Science, 2007, 318, 89–92 CrossRef CAS PubMed.
- S. Ball, D. Hanson, F. Eisele and P. McMurry, J. Geophys. Res., 1999, 104, 23709–23718 CrossRef CAS.
- J. H. Seinfeld and S. N. Pandis, Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, 2012 Search PubMed.
- J. J. Marti, A. Jefferson, X. P. Cai, C. Richert, P. H. McMurry and F. Eisele, J. Geophys. Res., 1997, 102, 3725–3735 CrossRef CAS.
- J. Zollner, W. Glasoe, B. Panta, K. Carlson, P. McMurry and D. Hanson, Atmos. Chem. Phys., 2012, 12, 4399–4411 CrossRef CAS.
- T. Kurtén, L. Torpo, M. Sundberg, V.-M. Kerminen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2007, 7, 2765–2773 CrossRef.
- T. Kurtén, L. Torpo, C. G. Ding, H. Vehkamäki, M. R. Sundberg, K. Laasonen and M. Kulmala, J. Geophys. Res., 2007, 112, D04210 CrossRef.
- P. Korhonen, M. Kulmala, A. Laaksonen, Y. Viisanen, R. McGraw and J. Seinfeld, J. Geophys. Res., 1999, 104, 26349–26353 CrossRef CAS.
- T. Kurtén, V. Loukonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef.
- X.-Q. Peng, Y.-R. Liu, T. Huang, S. Jiang and W. Huang, Phys. Chem. Chem. Phys., 2015, 17, 9552–9563 RSC.
- A. B. Nadykto, F. Yu, M. V. Jakovleva, J. Herb and Y. Xu, Entropy, 2011, 13, 554–569 CrossRef CAS.
- I. K. Ortega, O. Kupiainen, T. Kurten, T. Olenius, O. Wilkman, M. J. McGrath, V. Loukonen and H. Vehkamaki, Atmos. Chem. Phys., 2013, 13, 3321–3327 CrossRef CAS.
- Y. Chai, S. Shen, G. Weng and Y. Pan, Chem. Commun., 2014, 50, 11668–11671 RSC.
- D. J. Bustos, B. Temelso and G. C. Shields, J. Phys. Chem. A, 2014, 118, 7430–7441 CrossRef CAS PubMed.
- W. A. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. R. Hanson, P. H. McMurry and C. Jen, J. Geophys. Res., 2015, 120, 1933–1950 CAS.
- J. Chen, S. Jiang, Y.-R. Liu, T. Huang, C.-Y. Wang, S.-K. Miao, Z.-Q. Wang, Y. Zhang and W. Huang, RSC Adv., 2017, 7, 6374–6388 RSC.
- C.-Y. Wang, Y. Ma, J. Chen, S. Jiang, Y.-R. Liu, H. Wen, Y.-J. Feng, Y. Hong, T. Huang and W. Huang, J. Phys. Chem. A, 2016, 120, 2357–2371 CrossRef CAS PubMed.
- A. Ravishankara, Y. Rudich, R. Talukdar and S. B. Barone, Philos. Trans. R. Soc., B, 1997, 352, 171–182 CrossRef CAS.
- G. Ayers, J. Cainey, R. Gillett and J. Ivey, Philos. Trans. R. Soc., B, 1997, 352, 203–211 CrossRef CAS.
- D. R. Hanson, J. Phys. Chem. A, 2005, 109, 6919–6927 CrossRef CAS PubMed.
- M. L. Dawson, M. E. Varner, V. Perraud, M. J. Ezell, R. B. Gerber and B. J. Finlayson-Pitts, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18719–18724 CrossRef CAS PubMed.
- H. Berresheim, T. Elste, H. G. Tremmel, A. G. Allen, H. C. Hansson, K. Rosman, M. Dal Maso, J. M. Makela, M. Kulmala and C. D. O'Dowd, J. Geophys. Res., 2002, 107, 8100 CrossRef.
- B. J. Huebert, L. Z. Zhuang, S. Howell, K. Noone and B. Noone, J. Geophys. Res., 1996, 101, 4413–4423 CrossRef CAS.
- V. M. Kerminen, M. Aurela, R. E. Hillamo and A. Virkkula, Tellus B, 1997, 49, 159–171 CrossRef.
- N. Bork, J. Elm, T. Olenius and H. Vehkamaki, Atmos. Chem. Phys., 2014, 14, 12023–12030 CrossRef.
- H. Zhao, X. Jiang and L. Du, Chemosphere, 2017, 174, 689–699 CrossRef CAS PubMed.
- H. Chen, M. E. Varner, R. B. Gerber and B. J. Finlayson-Pitts, J. Phys. Chem. B, 2016, 120, 1526–1536 CrossRef CAS PubMed.
- H. Chen, M. J. Ezell, K. D. Arquero, M. E. Varner, M. L. Dawson, R. B. Gerber and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2015, 17, 13699–13709 RSC.
- S.-T. Pei, S. Jiang, Y.-R. Liu, T. Huang, K.-M. Xu, H. Wen, Y.-P. Zhu and W. Huang, J. Phys. Chem. A, 2015, 119, 3035–3047 CrossRef CAS PubMed.
- T. Kurten, V. Loukonen, H. Vehkamaki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103 CrossRef CAS.
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- E. G. Goken and A. W. Castleman Jr, J. Geophys. Res., 2010, 115, D16203 CrossRef.
- A. Sorokin, F. Arnold and D. Wiedner, Atmos. Environ., 2006, 40, 2030–2045 CrossRef CAS.
- Y.-P. Zhu, Y.-R. Liu, T. Huang, S. Jiang, K.-M. Xu, H. Wen, W.-J. Zhang and W. Huang, J. Phys. Chem. A, 2014, 118, 7959–7974 CrossRef CAS PubMed.
- N. T. Tsona, H. Henschel, N. Bork, V. Loukonen and H. Vehkamaki, J. Phys. Chem. A, 2015, 119, 9670–9679 CrossRef CAS PubMed.
- J. Herb, Y. Xu, F. Yu and A. B. Nadykto, J. Phys. Chem. A, 2013, 117, 133–152 CrossRef CAS PubMed.
- H. Hernandez-Soto, E. Jaffer, S. Chen and M. J. Pesch, Comput. Theor. Chem., 2015, 1065, 7–11 CrossRef CAS.
- L. Wang, J. Phys. Chem. A, 2007, 111, 3642–3651 CrossRef CAS PubMed.
- B. R. Bzdek, D. P. Ridge and M. V. Johnston, J. Geophys. Res., 2011, 116, D03301 CrossRef.
- J.-W. Yoon, J.-H. Park, C.-C. Shur and S.-B. Jung, Microelectron. Eng., 2007, 84, 2552–2557 CrossRef CAS.
- D. J. Wales and J. P. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- W. Huang, R. Pal, L.-M. Wang, X. C. Zeng and L.-S. Wang, J. Chem. Phys., 2010, 132, 054305 CrossRef PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS.
- W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 897–904 CrossRef CAS PubMed.
- W. Huang, A. P. Sergeeva, H.-J. Zhai, B. B. Averkiev, L.-S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206 CrossRef CAS PubMed.
- L.-L. Yan, Y.-R. Liu, T. Huang, S. Jiang, H. Wen, Y.-B. Gai, W.-J. Zhang and W. Huang, J. Chem. Phys., 2013, 139, 244312 CrossRef PubMed.
- S. Jiang, Y. R. Liu, T. Huang, H. Wen, K. M. Xu, W. X. Zhao, W. J. Zhang and W. Huang, J. Comput. Chem., 2014, 35, 159–165 CrossRef CAS PubMed.
- K.-M. Xu, T. Huang, H. Wen, Y.-R. Liu, Y.-B. Gai, W.-J. Zhang and W. Huang, RSC Adv., 2013, 3, 24492–24502 RSC.
- Y.-R. Liu, H. Wen, T. Huang, X.-X. Lin, Y.-B. Gai, C.-J. Hu, W.-J. Zhang and W. Huang, J. Phys. Chem. A, 2014, 118, 508–516 CrossRef CAS PubMed.
- S.-K. Miao, S. Jiang, J. Chen, Y. Ma, Y.-P. Zhu, Y. Wen, M.-M. Zhang and W. Huang, RSC Adv., 2015, 5, 48638–48646 RSC.
- J. Chen, S. Jiang, S.-K. Miao, X.-Q. Peng, Y. Ma, C.-Y. Wang, M.-M. Zhang, Y.-R. Liu and W. Huang, RSC Adv., 2015, 5, 91500–91515 RSC.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A. 02, Wallingford, CT, 2009, vol. 270, p. 271 Search PubMed.
- J. Herb, A. B. Nadykto and F. Yu, Chem. Phys. Lett., 2011, 518, 7–14 CrossRef CAS.
- Y. Xu, A. B. Nadykto, F. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2009, 114, 387–396 CrossRef PubMed.
- Y. Xu, A. B. Nadykto, F. Yu, L. Jiang and W. Wang, J. Mol. Struct.: THEOCHEM, 2010, 951, 28–33 CrossRef CAS.
- W. Xu and R. Zhang, J. Phys. Chem. A, 2012, 116, 4539–4550 CrossRef CAS PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445 RSC.
- J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS PubMed.
- H.-J. Werner, P. Knowles, G. Knizia, F. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov and G. Rauhut, See http://www.molpro.net, 2010.
- N. J. Martinez Amezaga, S. C. Pamies, N. M. Peruchena and G. L. Sosa, J. Phys. Chem. A, 2010, 114, 552–562 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. Huang, R. Du, G. Liu, X. Zhao, S. Ye and G. Wu, J. Chem. Thermodyn., 2012, 55, 60–66 CrossRef CAS.
- Y. Zeng, X. Zhang, X. Li, S. Zheng and L. Meng, Int. J. Quantum Chem., 2011, 111, 3725–3740 CAS.
- D. J. R. Duarte, G. L. Sosa and N. M. Peruchena, J. Mol. Model., 2013, 19, 2035–2041 CrossRef CAS PubMed.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757 RSC.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628 CrossRef.
- R. G. A. Bone and R. F. W. Bader, J. Phys. Chem., 1996, 100, 10892–10911 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph. Model., 1996, 14, 33–38 CrossRef CAS.
- D. V. Spracklen, K. S. Carslaw, M. Kulmala, V. M. Kerminen, G. W. Mann and S. L. Sihto, Atmos. Chem. Phys., 2006, 6, 5631–5648 CrossRef CAS.
- K. Sellegri, M. Hanke, B. Umann, F. Arnold and M. Kulmala, Atmos. Chem. Phys., 2005, 5, 373–384 CrossRef CAS.
- N. E. Rabaud, S. E. Ebeler, L. L. Ashbaugh and R. G. Flocchini, Atmos. Environ., 2003, 37, 933–940 CrossRef CAS.
- M. Noppel, H. Vehkamaki and M. Kulmala, J. Chem. Phys., 2002, 116, 218–228 CrossRef CAS.
- M. J. McGrath, T. Olenius, I. K. Ortega, V. Loukonen, P. Paasonen, T. Kurten, M. Kulmala and H. Vehkamaki, Atmos. Chem. Phys., 2012, 12, 2345–2355 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra12064h |
| This journal is © The Royal Society of Chemistry 2018 |