Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Prediction of microRNA–disease associations with a Kronecker kernel matrix dimension reduction model†
Guanghui Li *a,
Jiawei Luo*b,
Qiu Xiaob,
Cheng Liangc and
Pingjian Dingb
*a,
Jiawei Luo*b,
Qiu Xiaob,
Cheng Liangc and
Pingjian Dingb
aSchool of Information Engineering, East China Jiaotong University, Nanchang, 330013, China. E-mail: ghli16@hnu.edu.cn
bCollege of Computer Science and Electronic Engineering, Hunan University, Changsha, 410082, China. E-mail: luojiawei@hnu.edu.cn; alcs417@hnu.edu.cn
cCollege of Information Science and Engineering, Shandong Normal University, Jinan, 250000, China
First published on 23rd January 2018
Abstract
Identifying the associations between human diseases and microRNAs is key to understanding pathogenicity mechanisms and important for uncovering novel prognostic markers. To date, a series of computational approaches have been developed for the prediction of disease–microRNA associations. However, these methods remain difficult to perform satisfactorily for diseases with a few known associated microRNAs. This study introduces a novel computational model, namely, the Kronecker kernel matrix dimension reduction (KMDR) model, for identifying potential microRNA–disease associations. This model combines microRNA space and disease space in a larger microRNA–disease space by using the Kronecker product or the Kronecker sum. The predictive performance of our proposed approach was evaluated and validated based on known association datasets. The experimental results show that KMDR achieves reliable prediction with an average AUC of 0.8320 for 22 complex diseases, which indeed outperforms other competitive methods. Moreover, case studies on kidney cancer, breast cancer, and esophageal cancer further demonstrate the applicability of our method in the identification of new disease–microRNA pairs. The source code of KMDR is freely available at https://github.com/ghli16/KMDR.
Introduction
MicroRNAs (miRNAs), which are ∼22 nucleotides in length, are a special class of small non-coding RNAs that repress translation or cause degradation of their target mRNAs during post-transcriptional regulation.1 According to the literature, miRNAs are involved in multiple biological or cellular processes, such as cell development,2 differentiation,3 metabolism,1 and apoptosis.4 In addition, emerging evidence has indicated that functional disruption of miRNA is associated with diverse complex human diseases, including cancer.5–8 Therefore, predicting disease-associated miRNAs is crucial for elucidating mechanisms of pathogenicity and discovering novel drug targets. However, validating miRNA–disease association by biomedical experiments is costly and time-consuming. Given that a large number of miRNA association datasets have become available, it is necessary to design computational methods to reveal new types of disease-related miRNAs with high accuracy.Based on the principle that functionally related miRNA molecules are likely to be regulated in phenotypically similar diseases, a number of computational tools have been put forward to uncover latent links between diseases and miRNAs.9–13 For instance, Jiang et al.14 predicted disease–miRNA interactions using hypergeometric distribution on an integrated human phenome-microRNAome network. However, the efficacy of this method is limited in that it relies on predicted miRNA–target interactions, which may be inaccurate and incomplete. Xuan et al.15 established a miRNA functional similarity network derived from known disease–miRNA relationships, disease similarity, miRNA clusters and family data. Then, they predicted potential miRNAs related to a given disease based on weighted k-most similar neighbors. Considering that the aforementioned methods only utilize local network association information for ranking the potential links, Chen et al.16 developed a global network similarity model by implementing the random walk algorithm on a constructed miRNA–miRNA functional similarity network. Shi et al.17 also modeled the disease–miRNA relationship prediction process as a random walk on a protein–protein interaction network, which calculated functional associations between disease-related genes and miRNA-targeted genes. Similarly, MIDP18 extrapolated new disease–miRNA interactions based on random walk on the miRNA functional similarity network. This model assigned different transition matrices to known and unknown miRNAs in order to use the prior information known about these miRNAs. To implement prediction for new diseases, random walk was applied to a disease–miRNA bilayer network, namely, MIDPE. Furthermore, researchers have recently integrated multiple similarities, including semantic similarities between diseases, functional similarities between miRNAs, and Gaussian interaction profile kernel similarities of miRNAs and diseases, to achieve better prediction performance. For example, Chen et al.19 introduced a similarity search method named WBSMDA, based on the within-score and between-score of each candidate disease–miRNA pair, to predict novel disease–miRNA interactions. Subsequently, You et al.20 presented the approach of path-based miRNA–disease association prediction (PBMDA) to mine latent links between disease and miRNAs on the same types of biological datasets. In addition, machine learning methods have proved efficient in this field. Xu et al.21 extracted four topological features from a constructed miRNA target-dysregulated network and imported these features into a support vector machine (SVM) to identify positive miRNAs associated with prostate cancer from negative ones. However, the performance of this approach is far from satisfactory because it is currently rather difficult, or even impossible, to select negative miRNA–disease association samples. To overcome this limitation, a semi-supervised model called RLSMDA, which did not need negative samples, was proposed by Chen et al.22 This method is especially useful when applied to diseases with no known associations to any miRNA. By integrating known disease–miRNA interactions and the similarities of miRNAs and diseases, Luo et al.23 proposed a novel computational model named KRLSM, which performed predictions on the entire disease–miRNA space by using Kronecker product algebraic properties. Recently, the method of RKNNMDA24 used K-Nearest Neighbors algorithm to search for k-nearest-neighbors both for each miRNA and disease from the similarity scores of miRNAs and diseases, and finally obtained the candidate associations according to SVM Ranking model. However, the performance of the above models remains unsatisfactory for sparse miRNA–disease association datasets.
Considering that known miRNA–disease pairs are rare in current datasets, we address the problem of association prediction on sparse known miRNA–disease interaction networks. In this study, we propose a Kronecker kernel matrix dimension reduction model, which combines the cosine similarity matrices of miRNAs and diseases into one miRNA–disease similarity matrix by using Kronecker product or Kronecker sum to identify latent relationships between diseases and miRNAs. We tested the predictive performance of this method on HMDD datasets. The experiments show that, in terms of AUC, reliable results were achieved for 22 diseases associated with at least 60 miRNAs. Additionally, we have carried out the case studies on kidney cancer, breast cancer, and esophageal cancer to further make evaluation. Among these three important cancers, more than 90 percent of the top 50 miRNA candidates were verified by the published biological literature and by three public databases.
Materials and methods
Data preparation
The known disease–miRNA interactions were obtained from the HMDD database (January 2014 Version).25 After filtering out duplicate records, 5424 distinct, experimentally confirmed interactions were obtained, containing 378 diseases and 495 miRNAs. In addition, three other public databases (i.e., dbDEMC,26 miRCancer,27 and PhenomiR2.0 (ref. 28)) were used to confirm prediction results with case studies.Problem formalization
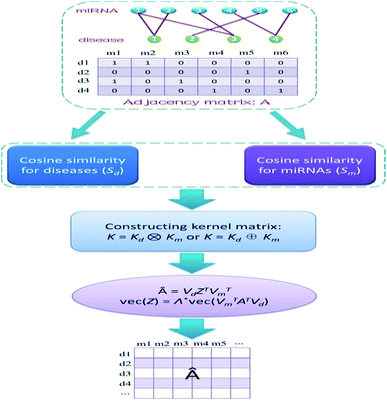
We address the issue of identifying novel associations in a miRNA–disease bipartite network. Formally, Xm = {m1, m2, …, mnm} and Xd = {d1, d2, …, dnd} denote the sets of all miRNAs and all diseases in the network, respectively. The edge set of the network represents the known miRNA–disease pairs. We can store this network in a nd × nm adjacency matrix A, where [A]ij is equal to 1 if disease di interacts with miRNA mj, and is 0 otherwise. Therefore, the i-th row of A is a binary vector that represents the correlation between disease di and each miRNA, whereas the j-th column of A stands for the association between miRNA mj and each disease. We need to calculate relevance likelihood of each non-interacting miRNA–disease pair and then infer novel associations among these pairs.Calculation of cosine similarities for diseases and miRNAs
Cosine similarities for diseases were computed assuming that diseases showing similar patterns of interaction and non-interaction with the miRNAs of a disease–miRNA association network tend to interact in a similar way with new miRNAs; a similar assumption was made for miRNAs. Binary vector IP(di) represents the interaction pattern of disease di, which encodes the presence or absence of interaction with each miRNA (i.e., the i-th row of the adjacency matrix A). Therefore, the cosine similarity between disease di and dj can be computed as follows:
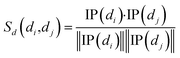 | (1) |
After calculating the cosine value for each disease–disease pair, the disease similarity matrix Sd was established.
Similarly, the miRNA cosine similarity matrix Sm can be calculated as follows:
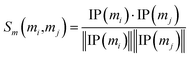 | (2) |
In this equation, IP(mi) is the interaction pattern of miRNA mi, which encodes the presence or absence of interaction with each disease (i.e., the i-th column of the adjacency matrix A).
There are other methods to calculate a similarity matrix from interaction profiles. For instance, Chen et al.29,30 proposed using the Gaussian interaction profile (GIP) kernel. We have conducted brief experiments with GIP kernel, which indicate that cosine similarity method consistently outperform the method based on GIP kernel in terms of AUC for 22 selected diseases. The detailed results are presented in ESI Fig. S1.†
Constructing kernel matrices
We constructed kernel matrices based on cosine similarity matrices Sd or Sm. These similarity matrices are symmetric, but they may not always be positive semi-definite. To satisfy the positive semi-definite property, we applied a simple transformation by adding a small multiple of the identity matrix to their diagonals. We denote the resulting kernel matrices for diseases and miRNAs by Kd and Km, respectively. These two base kernels, Kd and Km, are independent of each other, therefore, combining the kernels into a whole kernel that directly correlates with disease–miRNA pairs is a better alternative. We can construct such whole kernels via the Kronecker product kernel or Kronecker sum kernel, namely, K = Kd ⊗ Km or K = Kd ⊕ Km.Kernel matrix dimension reduction model
Based on the assumption that two similar node pairs tend to have the same connection strength, the prediction score matrix  could be written as follows:| vec(Â) = S·vec(A) | (3) |
Assume that kernel matrix K is an n × n matrix. The eigen decomposition of K is expressed as K = VΛVT, where V = [v1, v2, …, vn]; vi is an eigenvector of K. Λ is a diagonal matrix whose elements are [Λ]ii = λi, where λi is an associated eigenvalue of vi. Therefore, according to linear algebra theory, we can obtain the eigen decomposition of K:
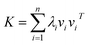 | (4) |
For further simplification, we assume that the eigenvalues of K are sorted in a non-increasing order (i.e., λ1 ≥ λ2 ≥ … ≥ λn). Generally, larger eigenvalues are more important than smaller ones. Therefore, we only consider the larger eigenvalues of top p, and construct a link similarity matrix S as follows:
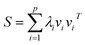 | (5) |
Note that if p is not very large, λp is always greater than 0; thus, the rank of the link similarity matrix S is p, and the rank of the kernel matrix K is always not less than p. Hence, we call this method the kernel matrix dimension reduction method (KMDR). Finally, substituting eqn (5) into eqn (3), we obtained the general formula of KMDR as follows:
| vec(Â) = VΛ*VT·vec(A) | (6) |
Obviously, if we use a different kernel matrix, the final prediction score matrix by KMDR will also be different. Hence, based on the Kronecker product kernel and Kronecker sum kernel, KMDR could result in two independent sub-algorithms: KMDR-KP and KMDR-KS; KP and KS are short for Kronecker product and Kronecker sum, respectively. Fig. 1 illustrates the overall flowchart of the KMDR method.
Note that there is a slight difference between this model and the method described by Kuang et al.31 We use the larger eigenvalues of top p to combine the symmetric matrix viviT (i ∈ {1, 2, …, p}), while the method described by Kuang et al. uniformly uses a single constant, and therefore, may not be able to distinguish between the importance of different eigenvalues.
KMDR-KP
In KMDR-KP, the Kronecker product Kd ⊗ Km of the disease and miRNA kernels is| K((di,mj),(dk,ml)) = Kd(di,dk)Km(mj,ml) | (7) |
Hence, the size of the kernel matrix K is ndnm × ndnm, which would require a large memory overhead even for a moderate number of diseases and miRNAs. To reduce computational cost, a more efficient improvement has been made on the basis of eigen decompositions, as performed in.32 Let Kd = VdΛdVdT and Km = VmΛmVmT be the eigen decompositions of the kernel matrices Kd and Km. As the vectors (eigenvalues) of a Kronecker product are the Kronecker product of vectors (eigenvalues), we can rewrite the Kronecker product kernel as K = Kd ⊗ Km = VΛVT, where V = Vd ⊗ Vm and Λ = Λd ⊗ Λm. To efficiently multiply this kernel matrix with vec(AT), we make good use of an algebraic property of the Kronecker product, that is, (B ⊗ C)vec(X) = vec(CXBT). After the conversion, the final prediction score matrix can be written as follows:
| Â = VdZTVTm | (8) |
KMDR-KS
In KMDR-KS, the Kronecker sum kernel is defined as K = Kd ⊕ Km. Similar to KMDR-KP, the final prediction score matrix of KMDR-KS is the same as eqn (8). However, for the Kronecker sum kernel, Λ = Λd ⊕ Λm. Therefore, the main difference between the two sub-algorithms is that they have different eigenvalue sets {λ1, λ2, …, λp}, that is, Λ* in KMDR-KS is different from Λ* in KMDR-KP.There is a parameter p in the construction of the link similarity matrix S. Here, we choose p = [n × q], where n is the size of kernel matrix K, and q ∈ [0, 1] is a proportion coefficient. The symbol [·] represents the Gauss rounding function. Notably, q was set as 0.25 in all experiments, and 0.25 was also chosen as the optimal parameter q in the method described by Kuang et al.31 This is equivalent to projecting the data onto the subspace spanned by the top 25% principal components.
Results
Performance evaluation
To evaluate the predictive capability of a method on a sparse set of known associations, we randomly divide all known associations of each disease into ten disjointed subsections, nine of which are used as testing samples and the remaining one is used as a training sample through multiple iterations. As diseases associated with only a few miRNAs may be insufficient to assess the capacity of the prediction method, we selected 22 human diseases, which are associated with at least 60 miRNAs, as test cases. Since the cosine similarities for diseases and miRNAs are constructed on the basis of known disease–miRNA associations, we need to recalculate the cosine value for each run when the known associations change. The area under the ROC curve (AUC) was computed to assess the quality of the predicted associations. AUC = 1 indicates perfect classification, whereas AUC = 0.5 reflects random classification. Additionally, considering that there are few known disease–miRNA associations, we also adopted a precision-recall (PR) curve, and the area under the PR curve (AUPR) served as a complementary quality measure.To demonstrate the effectiveness of the KMDR model, we compared its two sub-algorithms with six state-of-the-art models, namely, MIDP,18 MIDPE,18 RLSMDA,22 WBSMDA,19 KRLSM,23 and RKNNMDA.24 The parameters in MIDP, MIDPE, RLSMDA, KRLSM, and RKNNMDA are all chosen according to the author's recommendation.
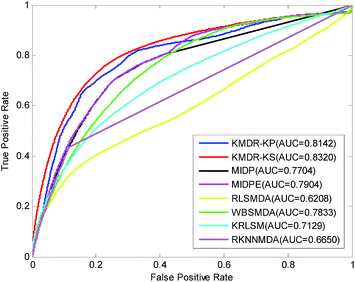
Table 1 lists in detail the AUC values of the 22 diseases for each method of comparison. As the table shows, KMDR-KP and KMDR-KS consistently outperform the other six computational approaches for the most selected diseases. In particular, the performance of KMDR built with the Kronecker sum kernel was consistently better than that of the Kronecker product kernel. KMDR-KS has the highest average AUC score, which is 0.8320, whereas the respective AUCs of KMDR-KP, MIDP, MIDPE, RLSMDA, WBSMDA, KRLSM, and RKNNMDA were 0.8142, 0.7704, 0.7904, 0.6208, 0.7833, 0.7129, and 0.6650. The average AUCs obtained by KMDR-KS were 1.78%, 6.16%, 4.16%, 21.12%, 4.87%, 11.91%, and 16.70% higher than those of the other six methods. Meanwhile, Fig. 2 shows the comparison of the ROC curves from each method.
| Disease name | #miRNAs | AUC | RKNNMDA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| KMDR-KP | KMDR-KS | MIDP | MIDPE | RLSMDA | WBSMDA | KRLSM | |||
| Breast neoplasms | 202 | 0.8168 | 0.8169 | 0.7250 | 0.7511 | 0.5418 | 0.7246 | 0.7541 | 0.7089 |
| Hepatocellular carcinoma | 214 | 0.7415 | 0.7571 | 0.6811 | 0.7188 | 0.5868 | 0.7184 | 0.6377 | 0.6635 |
| Non-small-cell lung carcinoma | 95 | 0.8454 | 0.8573 | 0.7380 | 0.7753 | 0.5742 | 0.8129 | 0.7279 | 0.7152 |
| Renal cell carcinoma | 107 | 0.7826 | 0.7991 | 0.6924 | 0.7331 | 0.5803 | 0.7553 | 0.6870 | 0.6579 |
| Squamous cell carcinoma | 80 | 0.8504 | 0.8726 | 0.7784 | 0.7911 | 0.6375 | 0.8230 | 0.6798 | 0.6750 |
| Colonic neoplasms | 78 | 0.8414 | 0.8585 | 0.8086 | 0.8289 | 0.6140 | 0.7750 | 0.6502 | 0.7036 |
| Colorectal neoplasms | 147 | 0.8082 | 0.8248 | 0.7191 | 0.7499 | 0.6395 | 0.6985 | 0.6558 | 0.6426 |
| Endometriosis | 62 | 0.7974 | 0.8130 | 0.7746 | 0.7840 | 0.5834 | 0.7739 | 0.6825 | 0.6063 |
| Esophageal neoplasms | 74 | 0.7665 | 0.7836 | 0.7298 | 0.7298 | 0.6898 | 0.7141 | 0.7001 | 0.6244 |
| Glioblastoma | 96 | 0.7777 | 0.8001 | 0.7178 | 0.7394 | 0.5604 | 0.7912 | 0.5966 | 0.6769 |
| Glioma | 71 | 0.8501 | 0.8665 | 0.7513 | 0.7798 | 0.5025 | 0.8265 | 0.7940 | 0.7573 |
| Head and neck neoplasms | 64 | 0.8317 | 0.8597 | 0.7994 | 0.8122 | 0.4387 | 0.8155 | 0.8269 | 0.6323 |
| Heart failure | 120 | 0.7690 | 0.7854 | 0.9116 | 0.9267 | 0.8493 | 0.7950 | 0.6574 | 0.6725 |
| Leukemia, myeloid, acute | 64 | 0.7983 | 0.8400 | 0.8430 | 0.8443 | 0.6798 | 0.8705 | 0.6568 | 0.6761 |
| Lung neoplasms | 132 | 0.8836 | 0.9027 | 0.8305 | 0.8595 | 0.7434 | 0.8509 | 0.7939 | 0.7460 |
| Medulloblastoma | 62 | 0.7875 | 0.7900 | 0.7704 | 0.7832 | 0.6367 | 0.7585 | 0.6443 | 0.6586 |
| Melanoma | 141 | 0.8199 | 0.8296 | 0.7764 | 0.7850 | 0.5479 | 0.7758 | 0.7364 | 0.6242 |
| Ovarian neoplasms | 114 | 0.8889 | 0.8949 | 0.8552 | 0.8793 | 0.5993 | 0.8503 | 0.8114 | 0.6362 |
| Pancreatic neoplasms | 99 | 0.8807 | 0.8961 | 0.8209 | 0.8406 | 0.7866 | 0.8436 | 0.7923 | 0.6617 |
| Prostatic neoplasms | 118 | 0.8093 | 0.8353 | 0.7576 | 0.7864 | 0.6535 | 0.7747 | 0.7423 | 0.5936 |
| Stomach neoplasms | 174 | 0.7608 | 0.7767 | 0.7425 | 0.7288 | 0.5318 | 0.6807 | 0.6763 | 0.6869 |
| Urinary bladder neoplasms | 92 | 0.8039 | 0.8440 | 0.7261 | 0.7606 | 0.6797 | 0.8028 | 0.7810 | 0.6104 |
| Average AUC | 0.8142 | 0.8320 | 0.7704 | 0.7904 | 0.6208 | 0.7833 | 0.7129 | 0.6650 | |
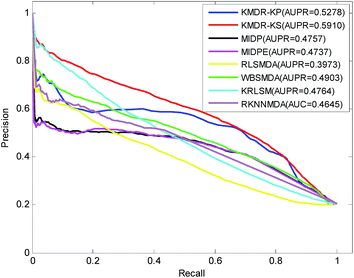
Fig. 3 displays the PR curves and the average AUPR scores of the above eight methods. It is obvious that the PR curves of KMDR-KP and KMDR-KS lie above those of MIDP, MIDPE, RLSMDA, WBSMDA, KRLSM, and RKNNMDA. The average AUPR values achieved by KMDR-KS were 6.32%, 11.53%, 11.73%, 19.37%, 10.07%, 11.46%, and 12.65% higher than those of the other seven methods. These prediction results suggest that the KMDR model performs well with diseases that are associated with only a few known miRNAs. This might be attributed to the fact that KMDR successfully combines the spaces of diseases and miRNAs into a single disease–miRNA space by using Kronecker sum. However, for two diseases, namely, “Heart Failure” and “Leukemia, Myeloid, Acute”, MIDPE and WBSMDA achieve higher AUCs than KMDR-KS; this could be because our method only adopts the topological structure of the disease–miRNA bipartite network.
Case studies
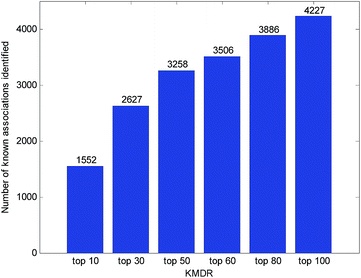
Usually, the top-ranked associations are more important for each disease. The number of correctly identified known disease–miRNA interactions under different top selections is shown in Fig. 4. For example, among the 5424 known disease–miRNA interactions, KMDR correctly detected 3258 (or 60.07%) known associations in the top 50 predictions. The result shows the effectiveness of KMDR in identifying confirmed disease–miRNA interactions.To further confirm the ability of KMDR to discover new miRNA–disease interactions, we present case studies of several important diseases (kidney neoplasms, breast neoplasms, and esophageal neoplasms). All known interactions included in the HMDD database are taken as the training set, and the non-interacting pairs of each disease are ranked according to the prediction scores. Predictive results were validated based on experimental literature and three recently updated disease–miRNA databases, namely, dbDEMC,26 miRCancer,27 and PhenomiR2.0.28
As a common urologic malignancy, the incidence and death rates of kidney cancer have been rising gradually. According to the report of the American Cancer Society in 2016, there would be approximately 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 new cases of kidney cancer, and 14
700 new cases of kidney cancer, and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 deaths, in America.33 Recent biological experiments have shown that many miRNAs are related to kidney cancer. Here, we implemented KMDR-KS to identify candidate kidney neoplasm-associated miRNAs. As a result, using the dbDEMC and miRCancer databases, all of the top 50 miRNA candidates were identified as being associated with kidney cancer (see Table 2). For the top 5 predicted candidates, hsa-mir-155 and hsa-mir-126 were found to be up-regulated in renal cell carcinoma,34,35 while hsa-mir-145, hsa-mir-200b, and hsa-mir-146a were identified as being down-regulated.36,37 Notably, only 7 known miRNAs were associated with kidney neoplasms in our gold standard dataset. Hence, this case study further demonstrates that the KMDR model is effective in predicting new associations for diseases that are associated with only a few known miRNAs.
240 deaths, in America.33 Recent biological experiments have shown that many miRNAs are related to kidney cancer. Here, we implemented KMDR-KS to identify candidate kidney neoplasm-associated miRNAs. As a result, using the dbDEMC and miRCancer databases, all of the top 50 miRNA candidates were identified as being associated with kidney cancer (see Table 2). For the top 5 predicted candidates, hsa-mir-155 and hsa-mir-126 were found to be up-regulated in renal cell carcinoma,34,35 while hsa-mir-145, hsa-mir-200b, and hsa-mir-146a were identified as being down-regulated.36,37 Notably, only 7 known miRNAs were associated with kidney neoplasms in our gold standard dataset. Hence, this case study further demonstrates that the KMDR model is effective in predicting new associations for diseases that are associated with only a few known miRNAs.
| Rank | miRNAs | Evidences | Rank | miRNAs | Evidences |
|---|---|---|---|---|---|
| 1 | hsa-mir-155 | dbDEMC | 26 | hsa-mir-1 | miRCancer |
| 2 | hsa-mir-145 | dbDEMC, miRCancer | 27 | hsa-mir-203 | dbDEMC, miRCancer |
| 3 | hsa-mir-200b | dbDEMC | 28 | hsa-mir-19b | dbDEMC |
| 4 | hsa-mir-146a | dbDEMC | 29 | hsa-mir-375 | dbDEMC |
| 5 | hsa-mir-126 | dbDEMC | 30 | hsa-mir-9 | dbDEMC |
| 6 | hsa-mir-200a | dbDEMC | 31 | hsa-mir-222 | dbDEMC |
| 7 | hsa-mir-16 | dbDEMC | 32 | hsa-let-7b | dbDEMC |
| 8 | hsa-mir-125b | dbDEMC | 33 | hsa-mir-210 | dbDEMC, miRCancer |
| 9 | hsa-mir-34a | dbDEMC | 34 | hsa-mir-10b | dbDEMC |
| 10 | hsa-mir-20a | dbDEMC | 35 | hsa-mir-214 | dbDEMC |
| 11 | hsa-let-7a | dbDEMC | 36 | hsa-let-7c | dbDEMC |
| 12 | hsa-mir-17 | dbDEMC | 37 | hsa-mir-195 | dbDEMC |
| 13 | hsa-mir-143 | dbDEMC | 38 | hsa-mir-29c | dbDEMC |
| 14 | hsa-mir-221 | dbDEMC | 39 | hsa-mir-218 | dbDEMC |
| 15 | hsa-mir-31 | dbDEMC | 40 | hsa-mir-182 | dbDEMC |
| 16 | hsa-mir-92a | dbDEMC | 41 | hsa-mir-486 | dbDEMC |
| 17 | hsa-mir-29b | dbDEMC | 42 | hsa-mir-150 | dbDEMC |
| 18 | hsa-mir-29a | dbDEMC | 43 | hsa-mir-27a | dbDEMC |
| 19 | hsa-mir-205 | miRCancer | 44 | hsa-mir-146b | dbDEMC |
| 20 | hsa-mir-223 | dbDEMC, miRCancer | 45 | hsa-mir-183 | dbDEMC, miRCancer |
| 21 | hsa-mir-18a | dbDEMC | 46 | hsa-mir-181b | dbDEMC |
| 22 | hsa-mir-19a | dbDEMC | 47 | hsa-mir-101 | dbDEMC |
| 23 | hsa-mir-199a | dbDEMC, miRCancer | 48 | hsa-mir-196a | dbDEMC |
| 24 | hsa-mir-181a | dbDEMC | 49 | hsa-mir-24 | dbDEMC |
| 25 | hsa-mir-429 | dbDEMC | 50 | hsa-mir-15b | dbDEMC |
Breast cancer is the most commonly diagnosed cancer in women, especially in developed countries. The American Cancer Society had estimated that during 2016, breast cancer would result in approximately 246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 new cases and 40
600 new cases and 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 female deaths in America.33 Previous studies have shown that multiple miRNAs have links with the progression of breast neoplasms. By implementing KMDR-KS to predict novel miRNA candidates associated with breast neoplasms, we confirmed that 45 out of the top 50 predicted miRNAs are present in dbDEMC, miRCancer, and PhenomiR2.0 (see Table 3). Furthermore, some potential candidates were validated by searching the literature on the PubMed website. Specifically, the expression of hsa-mir-378a (ranked 8th) increases during breast cancer formation.38 Hsa-mir-542 (ranked 13th) has been identified as being significantly down-regulated in breast cancer cells.39 In addition, hsa-mir-532 (ranked 26th) is markedly up-regulated in breast cancer tissues relative to normal tissues.40
450 female deaths in America.33 Previous studies have shown that multiple miRNAs have links with the progression of breast neoplasms. By implementing KMDR-KS to predict novel miRNA candidates associated with breast neoplasms, we confirmed that 45 out of the top 50 predicted miRNAs are present in dbDEMC, miRCancer, and PhenomiR2.0 (see Table 3). Furthermore, some potential candidates were validated by searching the literature on the PubMed website. Specifically, the expression of hsa-mir-378a (ranked 8th) increases during breast cancer formation.38 Hsa-mir-542 (ranked 13th) has been identified as being significantly down-regulated in breast cancer cells.39 In addition, hsa-mir-532 (ranked 26th) is markedly up-regulated in breast cancer tissues relative to normal tissues.40
| Rank | miRNAs | Evidences | Rank | miRNAs | Evidences |
|---|---|---|---|---|---|
| 1 | hsa-mir-106a | dbDEMC, PhenomiR2.0 | 26 | hsa-mir-532 | PMID: 24866763 |
| 2 | hsa-mir-142 | miRCancer, PhenomiR2.0 | 27 | hsa-mir-95 | dbDEMC, PhenomiR2.0 |
| 3 | hsa-mir-99a | dbDEMC, miRCancer, PhenomiR2.0 | 28 | hsa-mir-517a | dbDEMC, miRCancer, PhenomiR2.0 |
| 4 | hsa-mir-130a | dbDEMC, miRCancer, PhenomiR2.0 | 29 | hsa-mir-30e | miRCancer, PhenomiR2.0 |
| 5 | hsa-mir-138 | dbDEMC | 30 | hsa-mir-372 | dbDEMC, PhenomiR2.0 |
| 6 | hsa-mir-330 | dbDEMC, PhenomiR2.0 | 31 | hsa-mir-32 | dbDEMC, miRCancer, PhenomiR2.0 |
| 7 | hsa-mir-150 | dbDEMC, miRCancer, PhenomiR2.0 | 32 | hsa-mir-211 | dbDEMC, miRCancer, PhenomiR2.0 |
| 8 | hsa-mir-378a | PMID: 20889127 | 33 | hsa-mir-381 | dbDEMC, miRCancer, PhenomiR2.0 |
| 9 | hsa-mir-186 | dbDEMC, PhenomiR2.0 | 34 | hsa-mir-370 | dbDEMC, miRCancer, PhenomiR2.0 |
| 10 | hsa-mir-185 | dbDEMC, miRCancer, PhenomiR2.0 | 35 | hsa-mir-181c | dbDEMC, PhenomiR2.0 |
| 11 | hsa-mir-15b | dbDEMC, PhenomiR2.0 | 36 | hsa-mir-181d | dbDEMC, PhenomiR2.0 |
| 12 | hsa-mir-192 | dbDEMC, PhenomiR2.0 | 37 | hsa-mir-361 | PhenomiR2.0 |
| 13 | hsa-mir-542 | PMID: 22051041 | 38 | hsa-mir-2110 | dbDEMC |
| 14 | hsa-mir-650 | dbDEMC | 39 | hsa-mir-1303 | dbDEMC |
| 15 | hsa-mir-98 | dbDEMC, miRCancer, PhenomiR2.0 | 40 | hsa-mir-744 | dbDEMC |
| 16 | hsa-mir-130b | dbDEMC, PhenomiR2.0 | 41 | hsa-mir-1249 | Unconfirmed |
| 17 | hsa-mir-92b | dbDEMC | 42 | hsa-mir-376a | dbDEMC |
| 18 | hsa-mir-196b | dbDEMC, PhenomiR2.0 | 43 | hsa-mir-520e | dbDEMC, miRCancer, PhenomiR2.0 |
| 19 | hsa-mir-216a | dbDEMC, PhenomiR2.0 | 44 | hsa-mir-134 | dbDEMC, PhenomiR2.0 |
| 20 | hsa-mir-508 | Unconfirmed | 45 | hsa-mir-144 | dbDEMC, miRCancer |
| 21 | hsa-mir-574 | miRCancer | 46 | hsa-mir-190a | dbDEMC |
| 22 | hsa-mir-449b | dbDEMC | 47 | hsa-mir-421 | dbDEMC, miRCancer |
| 23 | hsa-mir-212 | dbDEMC, miRCancer, PhenomiR2.0 | 48 | hsa-mir-526b | dbDEMC, miRCancer, PhenomiR2.0 |
| 24 | hsa-mir-99b | dbDEMC, PhenomiR2.0 | 49 | hsa-mir-208a | dbDEMC, PhenomiR2.0 |
| 25 | hsa-mir-449a | dbDEMC, miRCancer, PhenomiR2.0 | 50 | hsa-mir-362 | miRCancer |
Esophageal cancer is the eighth most frequently diagnosed cancer worldwide, and it is considered the sixth leading cause of cancer-related death on account of its poor prognosis. Early detection and timely treatment of esophageal cancer is very helpful in improving the chance of a patient's survival. In our standard association dataset, 74 known miRNAs are related to esophageal cancer. Among the top 50 predicted candidates ranked by KMDR-KS, 47 miRNAs are corroborated by the three aforementioned databases (see Table 4). Additionally, hsa-mir-200b (ranked 4th) was supported by experimental literature as being correlated with esophageal neoplasms.41
| Rank | miRNAs | Evidences | Rank | miRNAs | Evidences |
|---|---|---|---|---|---|
| 1 | hsa-mir-17 | dbDEMC | 26 | hsa-mir-7 | dbDEMC |
| 2 | hsa-mir-125b | dbDEMC, PhenomiR2.0 | 27 | hsa-mir-124 | dbDEMC, miRCancer |
| 3 | hsa-mir-218 | dbDEMC, miRCancer | 28 | hsa-let-7g | dbDEMC |
| 4 | hsa-mir-200b | PMID: 24064224 | 29 | hsa-mir-224 | dbDEMC |
| 5 | hsa-mir-16 | dbDEMC | 30 | hsa-mir-195 | dbDEMC |
| 6 | hsa-mir-18a | dbDEMC | 31 | hsa-mir-127 | dbDEMC |
| 7 | hsa-mir-221 | dbDEMC, miRCancer | 32 | hsa-let-7f | dbDEMC |
| 8 | hsa-mir-10b | dbDEMC, miRCancer | 33 | hsa-mir-125a | dbDEMC |
| 9 | hsa-mir-182 | dbDEMC | 34 | hsa-let-7i | dbDEMC |
| 10 | hsa-mir-19b | dbDEMC | 35 | hsa-mir-93 | dbDEMC, PhenomiR2.0 |
| 11 | hsa-mir-1 | dbDEMC | 36 | hsa-mir-429 | dbDEMC |
| 12 | hsa-let-7d | dbDEMC | 37 | hsa-mir-151a | Unconfirmed |
| 13 | hsa-mir-146b | dbDEMC, miRCancer | 38 | hsa-mir-107 | dbDEMC |
| 14 | hsa-mir-222 | dbDEMC | 39 | hsa-mir-135a | dbDEMC |
| 15 | hsa-mir-133b | dbDEMC | 40 | hsa-mir-191 | dbDEMC |
| 16 | hsa-mir-181a | dbDEMC | 41 | hsa-mir-24 | dbDEMC |
| 17 | hsa-mir-181b | dbDEMC | 42 | hsa-mir-18b | dbDEMC |
| 18 | hsa-let-7e | dbDEMC | 43 | hsa-mir-106a | dbDEMC |
| 19 | hsa-mir-142 | dbDEMC | 44 | hsa-mir-103a | dbDEMC |
| 20 | hsa-mir-9 | dbDEMC | 45 | hsa-mir-302b | Unconfirmed |
| 21 | hsa-mir-30c | dbDEMC | 46 | hsa-mir-27b | dbDEMC, PhenomiR2.0 |
| 22 | hsa-mir-29b | dbDEMC | 47 | hsa-mir-96 | dbDEMC, miRCancer |
| 23 | hsa-mir-199b | dbDEMC | 48 | hsa-mir-30d | dbDEMC |
| 24 | hsa-mir-29a | dbDEMC | 49 | hsa-mir-106b | dbDEMC |
| 25 | hsa-mir-30a | dbDEMC | 50 | hsa-mir-138 | dbDEMC |
The results of the case studies fully illustrate that KMDR-KS performs well in predicting potential disease-associated miRNAs. Therefore, we further used KMDR-KS and KMDR-KP to rank potential candidates associated with each disease contained in HMDD (shown in ESI Tables S1 and S2†), in the hope that these prediction results will be validated by future biological experiments.
Discussion and conclusions
Identifying potential miRNA–disease associations could help discover novel biomarkers for clinical diagnosis, treatment, and prevention. Previous computational models remain difficult to use efficiently for diseases with a few known associated miRNAs. Therefore, a Kronecker kernel matrix dimension reduction model (KMDR) was implemented to identify hidden miRNA–disease associations. KMDR combined the spaces of miRNAs and diseases into a whole miRNA–disease space by using Kronecker product or Kronecker sum. Compared with six existing computational methods, KMDR achieved higher AUC values in most selected diseases. Moreover, case studies on kidney cancer, breast cancer, and esophageal cancer were done, and 100%, 96% and 96% of the top 50 miRNA candidates for each of these three important diseases were verified by the literature and by databases. These results have shown that KMDR can reliably identify disease–miRNA associations for clinical and experimental validation.The reliable performance of KMDR can be contributed to several factors. To begin with, our method combines the cosine similarity matrices of miRNAs and diseases into a larger miRNA–disease similarity matrix, which directly relates disease–miRNA pairs and could effectively improve the prediction performance. Second, negative miRNA–disease association samples are not needed in KMDR. Finally, KMDR is a global prediction model, which could be used to infer hidden miRNAs for all the diseases simultaneously.
Despite the efficiency and practicability of KMDR, there still exist some inevitable limitations that need further research. To begin with, like some other models,42–44 KMDR only depends on the topological structure of the miRNA–disease network, which means it cannot predict associations for a disease that does not exist within the network. To solve this problem, extensional biological information, like miRNA functional similarity data and disease semantic similarity data, can be integrated to expand the application range of KMDR. Second, our similarity matrices for KMDR might not be optimal in some scenarios. Finally, as the currently known miRNA–disease associations are insufficient, more information about diseases and miRNAs can be used for constructing more reliable disease-similarity and miRNA-similarity matrices, which may potentially improve prediction results. For example, we will integrate disease–gene interactions and miRNA-gene interactions in our future work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant 61572180 and Grant 61602283, Key Project of the Education Department of Hunan Province under Grant 17A037, and Hunan Provincial Innovation Foundation for Postgraduate under Grant CX2017B102.References
- D. P. Bartel, Cell, 2009, 136, 215–233 CrossRef CAS PubMed.
- X. Karp and V. Ambros, Science, 2005, 310, 1288–1289 CrossRef CAS PubMed.
- E. A. Miska, Curr. Opin. Genet. Dev., 2005, 15, 563–568 CrossRef CAS PubMed.
- P. Xu, M. Guo and B. A. Hay, Trends Genet., 2004, 20, 617–624 CrossRef CAS PubMed.
- I. Alvarez-Garcia and E. A. Miska, Development, 2005, 132, 4653–4662 CrossRef CAS PubMed.
- N. Lynam-Lennon, S. G. Maher and J. V. Reynolds, Biol. Rev., 2009, 84, 55–71 CrossRef PubMed.
- X. Chen, D. Xie, Q. Zhao and Z.-H. You, Briefings Bioinf., 2017 DOI:10.1093/bib/bbx130.
- Q. Xiao, J. Luo, C. Liang, J. Cai and P. Ding, Bioinformatics, 2018, 34, 239–248 CrossRef PubMed.
- Q. Zou, J. Li, L. Song, X. Zeng and G. Wang, Briefings Funct. Genomics, 2016, 15, 55–64 Search PubMed.
- W. Lan, J. Wang, M. Li, J. Liu, F. Wu and Y. Pan, IEEE/ACM Trans. Comput. Biol. Bioinf., 2016 DOI:10.1109/TCBB.2016.2586190.
- X. Chen, C. C. Yan, X. Zhang, Z.-H. You, Y.-A. Huang and G.-Y. Yan, Oncotarget, 2016, 7, 65257–65269 Search PubMed.
- J. Luo, P. Ding, C. Liang, B. Cao and X. Chen, IEEE/ACM Trans. Comput. Biol. Bioinf., 2017, 14, 1468–1475 CrossRef PubMed.
- X. Chen, Y.-W. Niu, G.-H. Wang and G.-Y. Yan, J. Biomed. Inf., 2017, 76, 50–58 CrossRef PubMed.
- Q. Jiang, Y. Hao, G. Wang, L. Juan, T. Zhang, M. Teng, Y. Liu and Y. Wang, BMC Syst. Biol., 2010, 4, S2 CrossRef PubMed.
- P. Xuan, K. Han, M. Guo, Y. Guo, J. Li, J. Ding, Y. Liu, Q. Dai, J. Li, Z. Teng and Y. Huang, PLoS One, 2013, 8, e70204 CAS.
- X. Chen, M.-X. Liu and G.-Y. Yan, Mol. BioSyst., 2012, 8, 2792–2798 RSC.
- H. Shi, J. Xu, G. Zhang, L. Xu, C. Li, L. Wang, Z. Zhao, W. Jiang, Z. Guo and X. Li, BMC Syst. Biol., 2013, 7, 101 CrossRef PubMed.
- P. Xuan, K. Han, Y. Guo, J. Li, X. Li, Y. Zhong, Z. Zhang and J. Ding, Bioinformatics, 2015, 31, 1805–1815 CrossRef CAS PubMed.
- X. Chen, C. C. Yan, X. Zhang, Z.-H. You, L. Deng, Y. Liu, Y. Zhang and Q. Dai, Sci. Rep., 2016, 6, 21106 CrossRef CAS PubMed.
- Z.-H. You, Z.-A. Huang, Z. Zhu, G.-Y. Yan, Z.-W. Li, Z. Wen and X. Chen, PLoS Comput. Biol., 2017, 13, e1005455 Search PubMed.
- J. Xu, C.-X. Li, J.-Y. Lv, Y.-S. Li, Y. Xiao, T.-T. Shao, X. Huo, X. Li, Y. Zou, Q.-L. Han, X. Li, L.-H. Wang and H. Ren, Mol. Cancer Ther., 2011, 10, 1857–1866 CrossRef CAS PubMed.
- X. Chen and G.-Y. Yan, Sci. Rep., 2014, 4, 5501 CrossRef CAS PubMed.
- J. Luo, Q. Xiao, C. Liang and P. Ding, IEEE Access, 2017, 2503–2513 CrossRef.
- X. Chen, Q.-F. Wu and G.-Y. Yan, RNA Biol., 2017, 14, 952–962 CrossRef PubMed.
- Y. Li, C. Qiu, J. Tu, B. Geng, J. Yang, T. Jiang and Q. Cui, Nucleic Acids Res., 2014, 42, D1070–D1074 CrossRef CAS PubMed.
- Z. Yang, L. Wu, A. Wang, W. Tang, Y. Zhao, H. Zhao and A. E. Teschendorff, Nucleic Acids Res., 2017, 45, D812–D818 CrossRef PubMed.
- B. Xie, Q. Ding, H. Han and D. Wu, Bioinformatics, 2013, 29, 638–644 CrossRef CAS PubMed.
- A. Ruepp, A. Kowarsch, D. Schmidl, F. Buggenthin, B. Brauner, I. Dunger, G. Fobo, G. Frishman, C. Montrone and F. J. Theis, Genome Biol., 2010, 11, R6 CrossRef PubMed.
- X. Chen, Y. Gong, D.-H. Zhang, Z.-H. You and Z.-W. Li, J. Cell. Mol. Med., 2018, 22, 472–485 CrossRef CAS PubMed.
- X. Chen, Z.-C. Jiang, D. Xie, D.-S. Huang, Q. Zhao, G.-Y. Yan and Z.-H. You, Mol. BioSyst., 2017, 13, 1202–1212 RSC.
- Q. Kuang, Y. Li, Y. Wu, R. Li, Y. Dong, Y. Li, Q. Xiong, Z. Huang and M. Li, Chemom. Intell. Lab. Syst., 2017, 162, 104–110 CrossRef CAS.
- R. Raymond and H. Kashima, in Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2010, Barcelona, Spain, September 20–24, 2010, Proceedings, Part III, ed. J. L. Balcázar, F. Bonchi, A. Gionis and M. Sebag, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 131–147, DOI:10.1007/978-3-642-15939-8_9.
- R. L. Siegel, K. D. Miller and A. Jemal, Ca-Cancer J. Clin., 2016, 66, 7–30 CrossRef PubMed.
- D. Juan, G. Alexe, T. Antes, H. Liu, A. Madabhushi, C. Delisi, S. Ganesan, G. Bhanot and L. S. Liou, Urology, 2010, 75, 835–841 CrossRef PubMed.
- T.-f. F. Chow, Y. M. Youssef, E. Lianidou, A. D. Romaschin, R. J. Honey, R. Stewart, K. T. Pace and G. M. Yousef, Clin. Biochem., 2010, 43, 150–158 CrossRef CAS PubMed.
- M. C. Lu, N. S. Lai, H. C. Chen, H. C. Yu, K. Y. Huang, C. H. Tung, H. B. Huang and C. L. Yu, Clin. Exp. Immunol., 2013, 171, 91–99 CrossRef CAS PubMed.
- M. Jung, H.-J. Mollenkopf, C. Grimm, I. Wagner, M. Albrecht, T. Waller, C. Pilarsky, M. Johannsen, C. Stephan, H. Lehrach, W. Nietfeld, T. Rudel, K. Jung and G. Kristiansen, J. Cell. Mol. Med., 2009, 13, 3918–3928 CrossRef PubMed.
- L. J. Eichner, M.-C. Perry, C. R. Dufour, N. Bertos, M. Park, J. St-Pierre and V. Giguère, Cell Metab., 2010, 12, 352–361 CrossRef CAS PubMed.
- Y. Yamamoto, Y. Yoshioka, K. Minoura, R.-u. Takahashi, F. Takeshita, T. Taya, R. Horii, Y. Fukuoka, T. Kato, N. Kosaka and T. Ochiya, Mol. Cancer, 2011, 10, 135 CrossRef CAS PubMed.
- C. Cava, G. Bertoli, M. Ripamonti, G. Mauri, I. Zoppis, P. A. D. Rosa, M. C. Gilardi and I. Castiglioni, PLoS One, 2014, 9, e97681 Search PubMed.
- H. Zhang, K. Zhang, L. Liao, L. Li, Z. Du, B. Wu, J. Wu, X. Xu, F. Zeng and B. Chen, Carcinogenesis, 2014, 35, 292–301 CrossRef CAS PubMed.
- J.-Q. Li, Z.-H. Rong, X. Chen, G.-Y. Yan and Z.-H. You, Oncotarget, 2017, 8, 21187–21199 Search PubMed.
- G. Li, J. Luo, Q. Xiao, C. Liang, P. Ding and B. Cao, IEEE Access, 2017, 5, 24032–24039 CrossRef.
- X. Chen, C. Clarence Yan, X. Zhang, Z. Li, L. Deng, Y. Zhang and Q. Dai, Sci. Rep., 2015, 5, 13877 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: One supplementary figure and two supplemental tables are available as excel files. See DOI: 10.1039/c7ra12491k |
| This journal is © The Royal Society of Chemistry 2018 |