Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cathodoluminescence of Y2O3:Ln3+ (Ln = Tb, Er and Tm) and Y2O3:Bi3+ nanocrystalline particles at 200 keV
Daniel den Engelsen*,
George R. Fern*,
Terry G. Ireland * and
Jack Silver*
* and
Jack Silver*
Centre for Phosphor and Display Materials, Wolfson Centre for Materials Processing, Brunel University London, Uxbridge, Middlesex UB8 3PH, UK. E-mail: jack.silver@brunel.ac.uk
First published on 2nd January 2018
Abstract
The cathodoluminescence (CL) spectra of nanocrystalline Y2O3:Tb3+ (0.3%), Y2O3:Er3+ (1%), Y2O3:Tm3+ (2%) and Y2O3:Bi3+ (1%) were recorded in a transmission electron microscope at 200 keV, low current density and various temperatures. The quenching energy of the intrinsic luminescence of the various Y2O3:Ln3+ (Ln = Tb, Er and Tm) phosphors was found to be 0.25 eV. The intrinsic luminescence and the strongest spectral transitions of Ln3+ in these three phosphors exhibit similar temperature behaviour at temperatures > −50 °C, viz. a small increase of the spectral radiance upon increasing the temperature. Increasing the temperature beyond −50 °C led to complete quenching of the intrinsic luminescence at room temperature, whereas the radiance of the Ln3+ spectral transitions only decreased slightly. An extended Jablonski diagram for the energy transfer from the self-trapped exciton states in Y2O3 to the Ln3+ and Bi3+ ions is proposed. This diagram also indicates why Tb3+ is a better quencher of the intrinsic luminescence in Y2O3 than Er3+ and Tm3+. The intrinsic luminescence of Y2O3:Bi3+ largely overlapped with the blue Bi3+ emission band, which made an accurate analysis of its temperature behaviour impossible. Nevertheless, we concluded that upon increasing the temperature energy from Bi3+ ions at the C3i sites is transferred to Bi3+ ions at C2 sites. From the temperature behaviour of the 539 nm transition of the 2H11/2 → 4I15/2 manifold of Y2O3:Er3+ the activation energy for this transition could be determined: viz. 0.078 eV (623 cm−1).
Introduction
Recently we have published a study on the intrinsic luminescence in cubic Y2O3 and Y2O3:Eu3+ generated in a transmission electron microscope (TEM).1 The intrinsic luminescence from Y2O3 consists of three broad emission bands: the strongest is in the near UV with a centre wavelength (λ0) at 353 nm (28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 cm−1) and two, much weaker, bands manifest at 675 nm (14
330 cm−1) and two, much weaker, bands manifest at 675 nm (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 cm−1) and 770 nm (12
810 cm−1) and 770 nm (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990 cm−1).1 This intrinsic luminescence from Y2O3 excited by high energy electrons is rather strong at temperatures < −50 °C and is quenched at room temperature.
990 cm−1).1 This intrinsic luminescence from Y2O3 excited by high energy electrons is rather strong at temperatures < −50 °C and is quenched at room temperature.
The intrinsic luminescence of Y2O3 in the near UV has been studied by scientists who hoped to enhance this luminescence for scintillator applications;2–9 the weak deep-red intrinsic luminescence bands at 675 nm and 770 nm have not been observed (or described) by other authors. In ref. 1 we also reported the quenching of the intrinsic luminescence by a mechanism other than temperature quenching, viz. doping of Y2O3 by rare earth ions, such as Nd3+, Eu3+, Tb3+ and Tm3+. This had already been observed by Wickersheim and Lefever10 in 1964 and later by Jacobsohn et al.3 and Tanner et al.11 Jacobson et al. observed a strong reduction of the intrinsic Y2O3 luminescence upon doping with Tb3+, while Hayes et al.7 mentioned weak intrinsic luminescence of Y2O3 upon doping with Eu3+. We explained this quenching mechanism in Y2O3:Eu3+ in terms of radiationless energy transfer from self-trapped excitons (STEs) in the Y2O3 lattice to the 5D4 level of the Eu3+ ion in the Y2O3 lattice.1 Radiationless energy transfer in phosphors may be considered as an example of resonance energy transfer described by Förster in 1948 (FRET).12 According to this theory the efficiency of radiationless energy transfer depends on the spectral overlap integral between a donor and acceptor state. Based on the theory of resonance energy transfer it is to be expected that there must be differences in the energy transfer from the excited intrinsic energy level of Y2O3 (donor state) to various rare earth dopants (acceptors). With this idea in mind we started an investigation of the intrinsic luminescence in Y2O3:Tb3+ (0.3%), Y2O3:Er3+ (1%), Y2O3:Tm3+ (2%) and Y2O3:Bi3+ (1%) by high energy cathodoluminescence (CL) in a TEM.
Experimental
Materials and synthesis
Yttrium oxide (99.99%, Ampere Industrie, France) and terbium(III) oxide (99.99%, Neo Performance Materials, UK), erbium oxide (99.99%, Neo Performance Materials, UK), thulium oxide (99.99%, Neo Performance Materials, UK) and bismuth(III) oxide (99.99%, Neo Performance Materials, UK) were used to prepare the lanthanide, bismuth and yttrium nitrate stock solutions. Urea, nitric acid, oxalic acid and isopropanol (Fisher Scientific, UK) were used for the syntheses. All chemicals were used as received. The general technique for controlled homogeneous precipitation of spherical monosized submicrometre rare earth oxide precursor particles, namely, the hydroxycarbonates, is by a single nucleation event, followed by uniform growth of nuclei. This is achieved using the slow aqueous thermal decomposition of urea where the reactants are added very slowly, deterring localised excess of reagent that would produce many nuclei and small particles that would form a floc. Thus, homogeneous precipitation is a technique that allows the slow addition of reactant, deterring localised excess of reagent, it is based on the slow hydrolysis of (or some other reaction) a solute, yielding a product that reacts to form a desired precipitate. When the above requirement is met hydrolysis will proceed uniformly throughout the solution, at a rate that is also, dependent on temperature. Precipitation will be slow, nucleation followed by particle growth will remove the reacting ions as they are produced inhibiting any further nucleation, formation of the particles being controlled by the concentration of reactants.The synthesis of spherical monosized submicrometre rare earth oxide precursor particles of Y2O3:Ln3+ and Y2O3:Bi3+ were prepared by the following method.
The oxides of the desired rare earth elements were digested in dilute nitric acid to form nitrate stock solutions (0.25 M) within a pH range of 1 to 3. To synthesise for example Y2O3:Bi3+ (Bi = 2.0 mol%) Y(NO3)3 (24.5 ml), Bi(NO3)3 (0.5 ml) and deionised water, (475 ml) were added to a one litre beaker and heated to boiling (this temperature was maintained throughout the reaction) at this point urea (15.01 g) was added. When turbidity was observed the solution was aged for one hour. The solution was then filtered whilst still hot (cooling could allow the uncontrolled nucleation of any residual reactants to form which would affect the monodispersity of the resulting hydroxycarbonate phosphor precursor particles). The precipitate was then washed three times with deionised water (100 ml), then dried in an oven at 80 °C for 8 hours. The precursor particles were then annealed in an alumina crucible in air at 980 °C 6 hours resulting in cubic spherical submicrometre Y2O3:Bi3+ phosphor particles.
The above method produces approximately 1.7 g of phosphor powder the precipitation method is scalable up to ten times of the example described above.
X-ray powder diffraction
The crystallinity of the prepared Y2O3:Tb3+ (0.3%), Y2O3:Er3+ (1%), Y2O3:Tm3+ (2%) and Y2O3:Bi3+ (1%) materials was checked by X-ray powder diffraction (XRPD) using a Bruker D8 Advance X-ray powder diffractometer fitted with a nickel-filtered copper source and a LynxEyet silicon strip detector. The analysis of the XRPD spectra has also been described in our previous work.1,13–16 These XRD analyses confirmed that our powder samples had the cubic bixbyite structure of Y2O3. The dopant concentration of the lanthanide ions or Bi3+ in Y2O3 was not separately checked.Transmission electron microscope
The submicron spherical Y2O3:Ln3+ and Y2O3:Bi3+ samples were investigated with a TEM (2100F, JEOL, Japan) equipped with a Schottky-type field emission gun. The TEM was equipped with a Vulcan CL detector, Gatan, USA, for imaging and spectroscopic purposes. This system used a Czerny–Turner spectrometer with back-illuminated CCD and gratings with 1200 or 2400 grooves per mm for collection of CL emission spectra. Light was collected from the sample using a mirror above and below the sample, which enabled a solid angle of about 5 sr, which is almost half of a sphere. This high solid angle made light collection highly efficient and enabled the collection of CL at low intensity. Unfortunately, the cooled detector of this spectrometer did not allow the recording of spectra at λ < 400 nm. A small cryostat connected to the sample holder enabled cooling of the samples in the TEM down to 102 K (171 °C); adjustment of the sample temperature anywhere between 102 K and 303 K was facile.CL-spectra were recorded with a focussed e-beam, spot size 1.5 nm, and defocussed e-beam, spot size ∼ 5 μm. The latter method was preferred, because the lower current density (about 7 orders of magnitude lower) had as consequence that specimen degradation due to the electron bombardment was avoided. Degradation due to the e-beam is easy to observe with phosphor specimens, because in that case the CL decreases as function of time due to lattice damage. This damage is due to the formation of defects or even recrystallization in the case of a focussed e-beam with a very small spot size. For Y2O3:Er3+ we have observed a CL decrease with a focussed e-beam of about 10% during 1 minute. In order to get sufficient luminescence with a defocussed e-beam, the specimens had to be thicker than 200 nm, preferably >1 μm, and the area from which the luminescence was collected must be larger than 1 μm as well. Thus, a rather large area of the sample was excited which impeded the collection of CL-spectra from individual nano-sized particles (using a focussed e-beam). For the CL-measurements in the TEM copper grids coated with thin carbon films having small holes (holey carbon films) were used as substrates.
Results
Microscope images
Fig. 1 and 2 present TEM images of the materials described in this report.Fig. 1 shows that the Y2O3:Tm3+ and Y2O3:Er3+ particles are spherical and have diameters of about 150 nm and 250 nm respectively. These spheres consist of crystallites, which are about 30 nm. The Y2O3:Tb3+ particles have more crystalline shapes and are smaller than 100 nm. Fig. 1c and d are scanning transmission electron microscope (STEM) images of Y2O3:1% Er3+: Fig. 1c is a high-angle annular dark-field (HAADF) image, while Fig. 1d is an image of the panchromatic luminescence. This luminescence originates mainly from the green Er3+ 4S3/2 → 4I15/2 multiplet. The scanning speed was adjusted to suppress smearing out of the image.
Fig. 2 shows STEM images of clusters of spherical Y2O3:Tm3+ and Y2O3:Bi3+ particles: Fig. 2a and c are HAADF images, while Fig. 2b and d are images of the panchromatic luminescence from the same cluster of particles shown in Fig. 2a and c respectively. For maximizing the CL of the samples, locations were selected on the holey-carbon-Cu-grids with some agglomeration of spheres to obtain sufficient thickness. Fig. 2 manifests typical examples of these locations. The CL-spectra recorded of Y2O3:Bi3+ refer to the cluster presented in Fig. 2c and d.
The luminescence that creates the panchromatic image of Fig. 2b is mainly from the blue emission from Tm3+ (the 1D2 → 3F4 multiplet), while that of Fig. 2d is from the blue and green emission bands of Bi3+, to be described hereafter.
The images of the panchromatic luminescence of the Y2O3:1% Er3+ and Y2O3:2% Tm3+ particles in Fig. 1d and 2b respectively are evidence for uniform Er3+ and Tm3+ doping in both one particle and all the particles: this is a vindication of the synthetic procedure. The non-uniformity seen in the particles in Fig. 1d refers to the boundaries of crystallites, which can also be observed in Fig. 1c. As mentioned in the previous section, thickness of the phosphor particles is an important parameter in homogeneous materials: the luminance increases as the thickness increases. This also refers to the present TEM study, in which the penetration depth of the impinging electrons is more than two orders of magnitude larger than the diameter of the particles. Particles on top of others yield more luminescence: this is clearly illustrated in Fig. 2. The luminance effect of thickness differences between the centre of a spherical particle and the edge can also be observed in Fig. 1d. However, the uniformity of the luminescence in Fig. 2d of Y2O3:1% Bi3+ is less convincing, because some particles show edges with slightly enhanced luminance. In a recent study on the panchromatic luminescence from phosphor particles in a scanning electron microscope (SEM) we have attributed the enhanced edge luminance to backscattered electrons from particles that are mainly situated below the actual particle.17 In a TEM the backscatter coefficient is much lower than in a SEM due to the high beam voltage; as a consequence, an enrichment of Bi3+ at the surface of the Y2O3:Bi3+ particles represented in Fig. 2d cannot be excluded.
Cathodoluminescence spectra
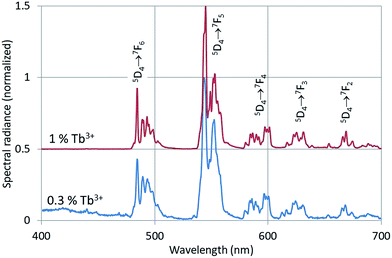
The CL-spectra of Y2O3:Tb3+ (0.3%), Y2O3:Er3+ (1%), Y2O3:Tm3+ (2%) and Y2O3:Bi3+ (1%) were recorded at 200 keV between −170 °C and +30 °C, usually in steps of 25 °C. In most cases a defocussed e-beam was used (TEM-mode) with a current density at the sample of ∼0.05 A cm−2. Fig. 3–5 present the CL spectra of Y2O3:Tb3+ (0.3% and 1%), Y2O3:Er3+ (1%) and Y2O3:Tm3+ (2%) respectively. In these figures only the spectra recorded at the minimum and/or minimum and maximum temperatures are shown for clarity reasons.The intrinsic luminescence of Y2O3:0.3% Tb3+ in Fig. 3 can be observed between 400 nm and 470 nm, whereas Y2O3:1% Tb3+ did not yield any intrinsic luminescence at this temperature. At room temperature the intrinsic luminescence in Y2O3:0.3% Tb3+ disappeared completely. As mentioned above, we could not detect the UV-part of the intrinsic luminescence of Y2O3. We measured λ0, the wavelength at the maximum, of the intrinsic luminescence of Y2O3 at 353 nm;1 however, this peak wavelength was also measured at other wavelengths by other scientists, see for instance Table 1 in ref. 1. By excitation of Y2O3 with X-rays Jacobsohn et al.3 measured 410 nm; by doping Y2O3 with 20 ppm Tb3+ they found that the peak wavelength moved to about 360 nm. The Tb3+ transitions in Fig. 3 have been assigned according to the published energy levels of Tb3+ in Y2O3.18 As we have indicated in our study on the intrinsic luminescence in undoped Y2O3 and Y2O3:Eu3+, the spectral radiance between 400 nm and 420 nm may be used to analyse the temperature behaviour of the intrinsic luminescence.
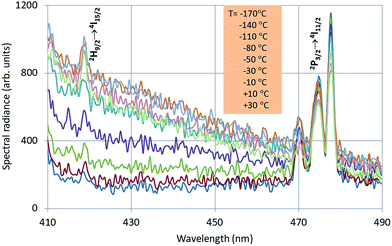
In Fig. 4 the intrinsic luminescence of Y2O3 can also be observed in the low temperature spectrum of Y2O3:Er3+ between 400 nm and 460 nm; this spectrum also shows intrinsic deep-red luminescence at about 675 nm. The peak wavelength of this deep-red luminescence cannot be determined exactly because of the 4F9/2 → 4I15/2 transition manifold. The reason that we can observe this deep-red intrinsic luminescence in Y2O3:Er3+ is probably the high current density of the focussed e-beam.
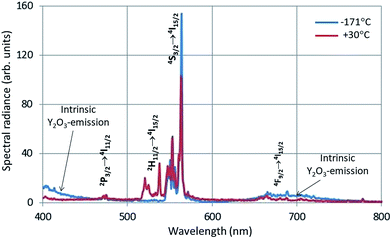 | ||
| Fig. 4 CL-spectra of Y2O3:1% Er3+ at −171 °C and 30 °C. Spectra recorded with a stationary focussed e-beam (STEM-mode). | ||
The Er3+ transitions in Fig. 4 have been assigned according to the published energy levels of Er3+ in Y2O3.19 As mentioned before, the stationary e-beam used to record the spectra presented in Fig. 4 caused some degradation of the sample. The analyses of the spectral data, to be presented hereafter, are based on data from a defocussed beam without e-beam degradation.
For Y2O3:Tb3+ and Y2O3:Er3+ CL spectra were recorded both with a focussed and with a defocussed e-beam. With a focussed, stationary e-beam the intrinsic luminescence became more intense compared to the Ln3+ luminescence, as presented in Table 1.
A very high current density of the e-beam is thus beneficial for the intrinsic luminescence; however, it is detrimental for the sample when long exposures are necessary. In ref. 1 we have shown that the radiance (integrated intensity) of the intrinsic luminescence is much larger than the radiance of the strongest Eu3+ peak: hence, from an energy point of view, Table 1 is misleading.
The CL-spectrum of Y2O3:2% Tm3+ at −165 °C also shows intrinsic luminescence between 400 nm and about 450 nm. The Tm3+ transitions in Fig. 5 have been assigned according to the published energy levels of Tm3+ in Y2O3.18 The deep-red intrinsic luminescence at about 675 nm cannot be clearly observed due to the 1G4 → 3F4 transition manifold of Tm3+. The radio-luminescence spectrum of Y2O3:0.15% Tm3+ was measured by Fujimoto et al.9 by excitation with 5.5 MeV-α-rays. They measured 360 nm for λ0 of the UV-intrinsic luminescence; they also reported another (smaller) emission band at about 460 nm, which must be attributed to the 1D2 → 3F4 Tm3+ multiplet.
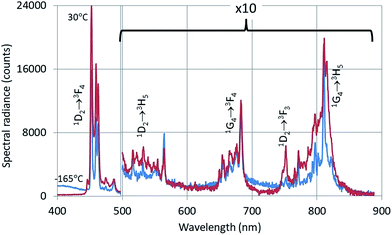 | ||
| Fig. 5 CL-spectra of Y2O3:2% Tm3+ at −165 °C and 30 °C. Spectra recorded with a defocussed e-beam (TEM-mode). Bandpass: 2 nm. | ||
Fig. 6 shows the CL-spectra of Y2O3:1% Bi3+ recorded at 200 kV and various temperatures.
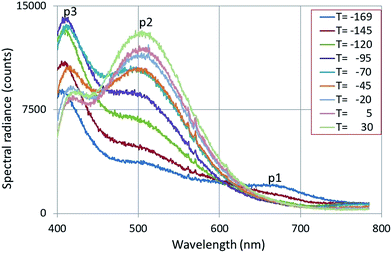 | ||
| Fig. 6 CL-spectra of Y2O3:1% Bi3+ recorded at 200 kV and various temperatures, indicated in degrees C. The emission bands p1, p2 and p3 are explained in the text. | ||
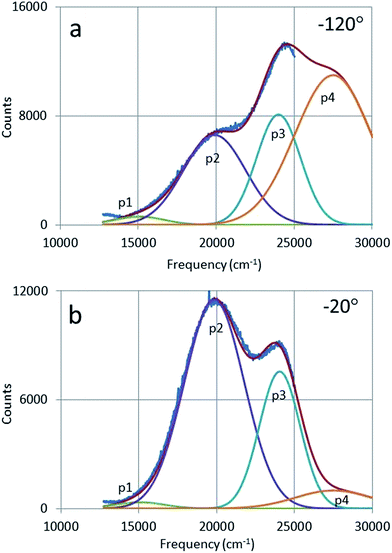
Fig. 6 shows three broad emission bands: p1 is the deep-red intrinsic emission of Y2O3, p2 and p3 are the green and blue emission bands of Y2O3:Bi3+ respectively.20,21 The spectra presented in Fig. 6 will be analysed by deconvolution hereafter. The λ0 of the green band p2 was found (after deconvolution) to be at 504 nm, which deviates considerably from 477 nm as reported by Jafer et al.21 by CL. Herein the λ0 of the blue band was found to be at 417 nm, which is close to 413 nm, reported by Jafer et al.21
Analysis of the spectra
In this section we shall describe the temperature behaviour of the intrinsic luminescence of Y2O3:Ln3+ and Y2O3:Bi3+ phosphors in terms of Arrhenius plots. Fig. 7 is a typical example of the intrinsic luminescence in Y2O3:Er3+.Since we could not measure the complete intrinsic luminescence band in the near UV with λ0 at 353 nm, the radiance (integrated intensity) of the intrinsic emission could not be evaluated. In analysing the intrinsic luminescence in Y2O3 and Y2O3:Eu3+,1 we found that identical results were obtained by using the spectral radiance at the top, SR353, and at some point at the flank of the intrinsic luminescence band, say SR412. This means that the full width at half maximum (FWHM) does not change upon varying the temperature. For the analyses we shall use the spectral radiance of the intrinsic luminescence at 412 nm, SR412, assuming that the intrinsic luminescence of Y2O3:Tb3+, Y2O3:Er3+ and Y2O3:Tm3+ all behaves identical to the luminescence in Y2O3:Eu3+. The selection of 412 nm is also based on the requirement to be sufficiently far from any interfering Ln3+ transition.
Fig. 8 is the Arrhenius plot of SR412 and SR551 of Y2O3:0.3% Tb3+.
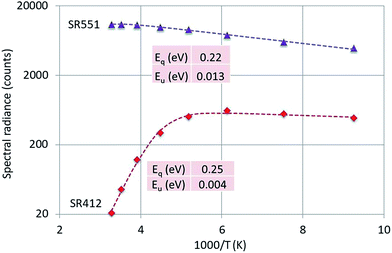 | ||
| Fig. 8 Arrhenius plot of SR412 and SR551 of Y2O3:0.3% Tb3+. Dashed curves are according to eqn (1), fitted to the experimental points. Only the calculated activation energies are indicated. | ||
The peak at 551 nm is not the strongest transition of the 5D4 → 7F5 multiplet as can be seen in Fig. 3. The 551 nm peak originates from cation sites with C2 symmetry, whereas the transition at 543 nm is a doublet consisting of peaks originating from cation sites with C2 and cation sites with C3i symmetry.22,23 Since the temperature behaviours of the C2 and C3i transitions are different due to energy transfer from the C3i states to the C2 states, SR551 is a better choice for the present analysis. As mentioned above, radiance (integrated intensity) is the preferred quantity to describe temperature behaviour. We have checked the temperature variation of the radiance of the 551 nm peak (by deconvolution using Lorentzian profiles) with the variation of SR551 (intensity at the maximum): these were identical. The reason is that the CL-spectra have been recorded with a rather large bandpass of 2 nm: the FWHM of the spectral transitions is then largely determined by the monochromator and thus (almost) equal for the various temperatures.
Fig. 8 presents that the temperature behaviour of the intrinsic luminescence represented by SR412 has a low temperature region, where the spectral radiance (SR) increases a little bit upon increasing the temperature, while in the high temperature region SR decreases strongly. This behaviour of SR can be represented by the following equation:
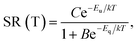 | (1) |
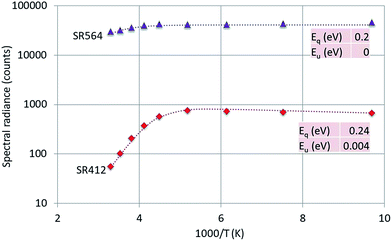 | ||
| Fig. 9 Arrhenius plot of SR412 and SR564 of Y2O3:1% Er3+. Dashed curves are according to eqn (1), fitted to the experimental points. Only the fitted activation energies are indicated. | ||
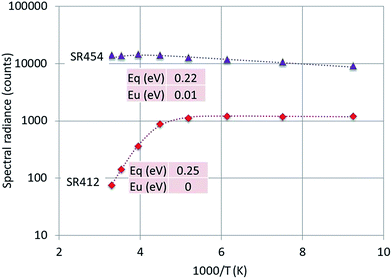 | ||
| Fig. 10 Arrhenius plot of SR412 and SR454 of Y2O3:2% Tm3+. Dashed curves are according to eqn (1), fitted to the experimental points. Only the fitted activation energies are indicated. | ||
The 564 nm peak is the strongest transition of the 4S3/2 → 4I15/2 manifold in Y2O3:Er3+ and the 564 nm peak itself is at least a doublet. If this peak has a contribution from a C3i transition, then this could explain the flat behaviour (Eu = 0) of SR564 at temperatures < −70 °C.
The luminescence peak at 454 nm is the strongest of the 1D2 → 3F4 manifold in the CL spectra of Y2O3:Tm3+ as depicted in Fig. 5. This peak consists of at least 4 transitions as indicated in the laser-activated high-resolution spectrum of Y2O3:Tm3+ described by Silver et al.:27 it is therefore obvious to assume that the C3i character of this CL-peak will be modest.
The graphs depicted in Fig. 8–10 show rather similar behaviour: slight increase of SR in the low temperature region upon increasing the temperature and quenching of the intrinsic luminescence at high temperatures. The quenching energy Eq for the intrinsic luminescence is about 0.25 eV for Y2O3:Tb3+, Y2O3:Er3+ and Y2O3:Tm3+, which is larger than Eq (0.14 eV) determined for Y2O3:Eu3+.1 We assume that Eq = 0.14 eV for Y2O3:Eu3+ is an underestimate, based on our new measuring technique with a defocussed e-beam in the TEM (which avoids beam degradation of the sample). The quenching energies Eq for the Ln3+ spectral peaks represented in Fig. 8–10 are also similar. It should be mentioned that the spread in Eq for these Ln3+ transitions is considerable, because the range of experimental values for these SRs is much smaller than one decade.
200 keV-cathodoluminescence in Y2O3:Bi3+
Fig. 11 shows the deconvolutions of the CL-spectra of Y2O3:Bi3+ at −120 °C and −20 °C. These spectra can be fitted well with 4 Gaussian profiles with a cm−1 base.The profiles p1, p2 and p3 were already defined in Fig. 6 and p4 is the UV-intrinsic luminescence, of which only the part in the visible (λ > 400 nm) could be measured. The FWHM and λ0 for p1 and p4 were taken from ref. 1 for these deconvolutions, while the amplitudes of p1 and p4 were fitted together with the in total 6 Gaussian parameters for p2 and p3. From the deconvoluted spectrum the radiances Ri of the profiles p2, p3 and p4 can be calculated by integration according to:
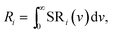 | (2) |
Fig. 12 is the Arrhenius plot of the radiances of p2, p3 and p4, which are the green band of Y2O3:Bi3+, the blue band and the intrinsic luminescence band respectively.
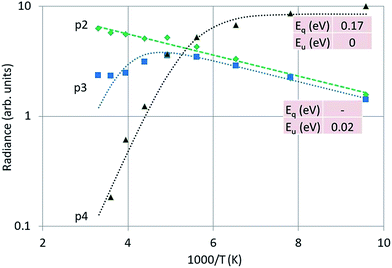 | ||
| Fig. 12 Arrhenius plot of the green emission band (p2), the blue emission band (p3) and the UV intrinsic luminescence (p4) of Y2O3:Bi3+. Dashed and dotted curves were fitted with eqn (1) to the experimental points, using radiance instead of spectral radiance. | ||
It should be stressed that the representation of the radiance of the intrinsic luminescence, p4, is not very accurate, because we could not measure at λ < 400 nm.
Significant in Fig. 12 is the deviation of parallelism of the p2 and p3 curves at temperatures > −70 °C. At higher temperatures the blue band decreases significantly, while the green band still grows. The blue emission band has been attributed to the 3Eu → 1Ag (C3i) transition by Jafer et al.,21 while these authors attributed the green band to the 3B → 1A (C2) transition. With this assignment in mind, it is tempting to assume that the kink in the curve for the blue band in Fig. 12 is due to energy transfer from Bi3+ at a C3i cation position to Bi3+ at a C2 position. This energy transfer is dependent on the distance between the two Bi3+ ions and should be much less at low Bi3+ concentrations. This was not tested in the present study.
Energy transfer in Y2O3:Ln3+ and Y2O3:Bi3+
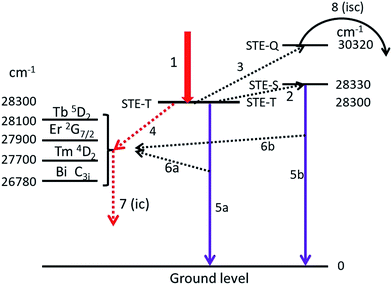
In this section we shall discuss the results that are presented in the preceding sections. In doing so we shall make use of an extended Jablonski diagram that visualizes the energy flows in the phosphors. Hayes et al.7 concluded from the optical detection of magnetic resonance that the intrinsic luminescence in Y2O3 originates from a triplet state. This conclusion poses a difficulty in constructing a Jablonski-type diagram of the energy flows, because radiation from a triplet state is usually slow (phosphorescence), whereas the decay time of the intrinsic luminescence in Y2O3 is rather short, between 15 and 200 ns.28,29 It should be mentioned that these decay times were determined at room temperature: at low temperature decay times are usually substantially longer.Fig. 13 is the extended Jablonski diagram of the energy flows in Y2O3:Ln3+ and Y2O3:Bi3+ upon bombardment with high energy electron. This diagram is speculative: it needs further confirmation by future work.
The construction of the energy diagram in Fig. 13 is based on the assumption that Y2O3 has three levels for the self-trapped exciton (STE), indicated by STE-T, STE-S and STE-Q. STE-T refers to a triplet state, STE-S refers to a singlet state and STE-Q indicates the level of the quenching state, where the intersystem crossing starts. In fact we need four STE-levels; however, to keep the diagram as simple as possible, we ignore here the deep-red intrinsic luminescence. When after being hit by high energy electrons, the almost thermalized electron–hole pairs in the lattice are trapped at STE-T, which is indicated by arrow 1. By phonon interactions the excitons can be promoted to STE-S (arrow 2) and at higher temperature to STE-Q (arrow 3). The location of the energy levels is indicated in cm−1, the levels for STE-T and STE-Q are derived from the Arrhenius plots in Fig. 8–10 and from ref. 1 for positioning STE-S (λ0 is 353 nm). The separation between STE-T and STE-S is only 0.004 eV (30 cm−1): at −170 °C the population density of STE-S is already over 50% of the population density of STE-T. We assume that energy can be transferred from the STE states of Y2O3 to excited states in Ln3+ and Bi3+ via three different mechanisms:
(1) From STE-T by radiationless transfer according to Förster's resonance energy transfer (FRET), indicated by arrow 4, to Ln3+ and to Bi3+;
(2) Via absorption of intrinsic luminescence, indicated by arrows 6a and 6b to Ln3+ and to Bi3+;
(3) From STE-Q by intersystem crossing, indicated by arrow 8.
The first two energy transfer mechanisms are dominant at low temperatures; the third is leading at high temperatures. When excitons arrive at STE-Q due to phonon interaction at high temperature, they can radiationless transfer energy to the dopants via intersystem crossing. This process will eventually empty the STE-T and STE-S states and at sufficiently high temperature, the intrinsic luminescence will be quenched completely. In the following we shall focus on the first two energy transfer mechanisms.
Arrows 5a and 5b represent the UV intrinsic luminescence. These two arrows indicate the complicated nature of the intrinsic luminescence, which shows fast and slow contributions to the decay.28,29 The slow decay component (>100 ns) is represented by arrow 5a (from STE-T), while the fast component from STE-S is represented by arrow 5b. Arrow 5b explains why the intrinsic luminescence increases slightly upon increasing the temperature from −170 °C to about −70 °C, while arrow 5a explains why there is still intrinsic luminescence in Y2O3 at about 1 K. The intrinsic luminescence at this very low temperature is supposed to be slow (triplet state). Unfortunately, we could not find literature data to verify this idea.
In order to understand why the Ln3+ and Bi3+ transitions also increase slightly in the low temperature region, it is assumed that Ln3+ and Bi3+ ions can also directly absorb intrinsic luminescence, as indicated by arrows 6a and 6b. The energy flow of the UV intrinsic luminescence (arrows 5a and 5b) is very large in Y2O3:Eu3+ at low temperatures;1 we assume that this is also the case in Y2O3:Tb3+, Y2O3:Er3+ and Y2O3:Tm3+.
The efficiency of the FRET-mechanism, represented by arrow 4 depends, among other parameters, strongly on the overlap between the spectra of the donor and acceptor states. A simple approximation of this overlap can be obtained by determining the energy difference between the donor and acceptor states: the smaller the energy difference, the larger the overlap and consequently, the larger the energy transfer. In the diagram of Fig. 13 we have indicated the energy levels of the relevant states of Ln3+ and Bi3+ that will be in resonance with STE-T (and STE-S). These energy levels were taken from Dieke's diagram,30 Table 1 in the publication of Gruber et al. for Y2O3:Er3+ (ref. 19) and from Boulon's data on Y2O3:Bi3+.20 It can be concluded from Fig. 13 that the spectral overlap between the intrinsic luminescence state (STE-T) with an energy of 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 and the 5D2 state of Tb3+ with an energy of about 28
300 cm−1 and the 5D2 state of Tb3+ with an energy of about 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 must be substantial: larger than the interactions with the nearby states of Er3+, Tm3+ and Bi3+. This qualitative consideration agrees favourably with our experimental evidence. The intrinsic luminescence of Y2O3 in Y2O3:0.3% Tb3+ is modest in the 0.3% material and completely absent in the 1% material, whereas it is still substantial in Y2O3:1% Er3+, Y2O3:2% Tm3+, Y2O3:1% Bi3+ and Y2O3:0.5% Eu3+,1 which have higher concentrations of dopants. The above consideration also agrees with the results of Jacobsohn et al.,3 who reported complete quenching of the intrinsic luminescence in Y2O3:Tb3+ at a doping level of 0.08% (at room temperature and X-ray excitation). In the case of Bi3+ the energy difference between the STE-T and the C3i levels, which is 28
100 cm−1 must be substantial: larger than the interactions with the nearby states of Er3+, Tm3+ and Bi3+. This qualitative consideration agrees favourably with our experimental evidence. The intrinsic luminescence of Y2O3 in Y2O3:0.3% Tb3+ is modest in the 0.3% material and completely absent in the 1% material, whereas it is still substantial in Y2O3:1% Er3+, Y2O3:2% Tm3+, Y2O3:1% Bi3+ and Y2O3:0.5% Eu3+,1 which have higher concentrations of dopants. The above consideration also agrees with the results of Jacobsohn et al.,3 who reported complete quenching of the intrinsic luminescence in Y2O3:Tb3+ at a doping level of 0.08% (at room temperature and X-ray excitation). In the case of Bi3+ the energy difference between the STE-T and the C3i levels, which is 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 − 26
300 − 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 = 1520 cm−1,20 is substantial. This is not favourable for effective FRET and it explains why the intrinsic luminescence in Y2O3:1% Bi3+ is rather strong. The FRET mechanism (arrow 4) is very fast and the subsequent radiationless conversion to lower energy levels in Ln3+ (not represented in Fig. 13), indicated by arrow 7, is fast as well. The decay from the Bi3+ C3i state to the ground state is 0.6 μs at room temperature and increases to about 2 μs at −170 °C.20 This is still fast enough to maintain the energy transfer via the arrows 4 and 7.
780 = 1520 cm−1,20 is substantial. This is not favourable for effective FRET and it explains why the intrinsic luminescence in Y2O3:1% Bi3+ is rather strong. The FRET mechanism (arrow 4) is very fast and the subsequent radiationless conversion to lower energy levels in Ln3+ (not represented in Fig. 13), indicated by arrow 7, is fast as well. The decay from the Bi3+ C3i state to the ground state is 0.6 μs at room temperature and increases to about 2 μs at −170 °C.20 This is still fast enough to maintain the energy transfer via the arrows 4 and 7.
4f–4f energy transfer in Y2O3:Er3+
The 4f–4f energy transfer in Y2O3:Er3+ has been studied extensively in our laboratories by laser-activated spectroscopy.26,31 The most obvious transfer is from the 4S3/2 state of Er3+ to the 2H11/2 state, which causes the spectral radiance of the 2H11/2 → 4I15/2 transition manifold to be substantially temperature-dependent: this can clearly be observed in Fig. 4. Because of this temperature dependency, this manifold is called hot band.31 For an accurate analysis of the temperature behaviour of this hot band of Y2O3:Er3+, the radiance of a transition is a better criterion than SR, because of the variation of the FWHM as a function of temperature.26 Via deconvolution the radiance of transitions can be determined.Fig. 14 presents the deconvolution of the 539 nm doublet, which is the transition with the largest wavelength of the 2H11/2 → 4I15/2 multiplet.
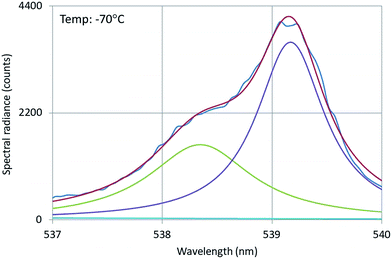 | ||
| Fig. 14 Deconvolution of the 539 nm doublet of Y2O3:Er3+. Recorded with a defocussed e-beam at 200 kV. Deconvolution with two Lorentzian profiles and least squares fitting to the experimental SR. | ||
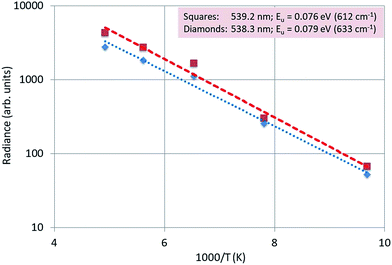
Fig. 15 is an Arrhenius plot of the radiances of the 539.2 nm and 538.3 nm peaks. The dotted and dashed lines were fitted to the experimental points with eqn (1): in this case there was no quenching, because the temperatures were not high enough to observe any quenching of the luminescence.
We found that the average activation energy for this doublet is 0.078 eV (623 cm−1), which is in good agreement with the value (0.08 eV (650 cm−1)) determined from the laser-activated spectra.26
Conclusion
CL-spectroscopy at 200 kV in a TEM has been combined in this study with scintillation research, which usually applies to other types of high-energy excitation sources such as X-rays, γ-rays and α-rays. In the present study we have applied a non-focussed e-beam (TEM-mode) at the sample to avoid e-beam degradation. In this case a rather large area of the sample is excited which impedes the collection of CL-spectra from individual nano-sized particles (using a focussed e-beam). With the defocussed e-beam it is possible to study temperature effects with CL-spectroscopy.The panchromatic images of the Y2O3:Ln3+ (Ln = Tb, Er and Tm) particles are evidence for uniform doping both in the single particles and also in all particles; this is again a vindication of the synthetic procedure, and ensures that we may trust that all the particles in each sample have the same luminous properties. This is important to allow trust in the Cl-data, which lead to the main conclusions of this work. The uniformity of the CL from Y2O3:Bi3+ particles is less convincing and may indicate that there is some enrichment of Bi3+ at the surface of the particles; however, if this is the case, it does not affect the conclusions that can be drawn from this work. More measurements will be necessary to investigate this possible non-uniformity of Bi3+ in Y2O3 in detail.
In this study we have shown that Y2O3:Ln3+ (Ln = Tb, Er and Tm) and Y2O3:Bi3+ show intrinsic luminescence at low temperature and excitation with 200 keV electrons. From Arrhenius-type analyses of the spectral transitions we have constructed an energy model that describes in detail the energy transfer from the self-trapped excitons to the Ln3+ levels. This model also shows why the quenching of the intrinsic luminescence in Y2O3 is more effective upon doping with Tb than doping with the other Ln3+ ions, due to Förster's resonance energy transfer mechanism.
From the temperature analyses of the CL-spectra of Y2O3:Bi3+ we could conclude that energy is transferred from Bi3+ ions at C3i sites to Bi3+ ions at C2 sites upon increasing the temperature. Until now, this type of energy transfer has been observed only in Y2O3 and Lu2O3 doped with the lanthanide ions such as Eu3+ and Tb3+.13,22,23,32 In 2006 Kravchenko et al.33 measured the magnetic properties of bismuth(III) oxy compounds and concluded that Bi2O3 is paramagnetic, which indicates that Bi3+ must have an unpaired electron in oxy compounds. This brings Bi3+ closer to the lanthanide family and makes its energy transfer from the centrosymmetric site to the non-symmetric site more obvious, but still far from clear. Analysis of the CL-spectra of the 2H11/2 → 4I15/2 transition manifold of Y2O3:Er3+ provided an accurate value of the activation energy that describes its temperature behaviour.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are grateful to the EPSRC and Technology Strategy Board (TSB) for funding the PURPOSE (TP11/MFE/6/1/AA129F; EP-SRC TS/G000271/1) and CONVERTED (JeS no. TS/1003053/1), PRISM (EP/N508974/1) and FAB3D programs. We are finally grateful to the TSB for funding the CONVERT program.References
- D. den Engelsen, G. R. Fern, T. G. Ireland, P. G. Harris, P. R. Hobson, A. Lipman, R. Dhillon, P. J. Marsh and J. Silver, J. Mater. Chem. C, 2016, 4, 7026–7034 RSC.
- A. Fukabori, L. An, A. Ito, V. Chani, K. Kamada, A. Yoshikawa, T. Ikegami and T. Goto, Ceram. Int., 2012, 38, 2119–2123 CrossRef CAS.
- L. G. Jacobsohn, B. L. Bennett, R. E. Muenchausen, J. F. Smith and D. W. Cooke, Proc. SPIE, 2006, 6321, 63210J CrossRef.
- R. L. Wood and W. Hayes, J. Phys. C: Solid State Phys., 1982, 15, 7209–7214 CrossRef CAS.
- T. C. de Oliveira, M. Souza da Silva, L. Menezes de Jesus, D. Vieira Sampaio, J. C. Alves dos Santos, N. R. da Silva Souza and R. Santos da Silva, Ceram. Int., 2014, 40, 16209–16212 CrossRef.
- G. Blasse and L. H. Brixner, Eur. J. Solid State Inorg. Chem., 1991, 28, 767–771 CAS.
- W. Hayes, M. J. Kane, O. Salminen and A. I. Kuznetsov, J. Phys. C: Solid State Phys., 1984, 17, L383–L387 CrossRef CAS.
- A. Fukabori, V. Chani, J. Pejchal, K. Kamada, A. Yoshikawa and T. Ikega, Opt. Mater., 2011, 34, 452–456 CrossRef CAS.
- Y. Fujimoto, T. Yanagida, Y. Yokota, A. Ikesue and A. Yoshikawa, Opt. Mater., 2011, 34, 448–451 CrossRef CAS.
- K. A. Wickersheim and R. A. Lefever, J. Electrochem. Soc., 1964, 111, 47–51 CrossRef CAS.
- P. A. Tanner, L. Fu and B. M. Cheng, J. Phys. Chem. C, 2009, 113, 10773–10779 CAS.
- T. Förster, Ann. Phys., 1948, 2, 55–75 CrossRef.
- D. den Engelsen, P. G. Harris, T. G. Ireland and J. Silver, ECS J. Solid State Sci. Technol., 2015, 4, R1–R9 CAS.
- D. den Engelsen, P. G. Harris, T. G. Ireland, R. Withnall and J. Silver, ECS J. Solid State Sci. Technol., 2013, 2, R201–R207 CrossRef CAS.
- X. Jing, T. Ireland, C. Gibbons, D. J. Barber, J. Silver, A. Vecht, G. Fern, P. Trogwa and D. C. Morton, J. Electrochem. Soc., 1999, 146, 4654–4658 CrossRef CAS.
- J. Silver, T. G. Ireland and R. Withnall, J. Electrochem. Soc., 2004, 151, H66–H68 CrossRef CAS.
- D. den Engelsen, P. G. Harris, T. G. Ireland, G. R. Fern and J. Silver, Ultramicroscopy, 2015, 157, 27–34 CrossRef PubMed.
- R. P. Leavitt, J. B. Gruber, N. C. Chang and C. A. Morrison, J. Chem. Phys., 1982, 76, 4775–4788 CrossRef CAS.
- J. B. Gruber, G. W. Burdick, S. Chandra and D. K. Sardar, J. Appl. Phys., 2010, 108, 023109 CrossRef.
- G. Boulon, J. Phys., 1971, 32, 333–347 CAS.
- R. M. Jafer, E. Coetsee, A. Yousif, R. E. Kroon, O. M. Ntwaeaborwa and H. C. Swart, Appl. Surf. Sci., 2015, 332, 198–204 CrossRef CAS.
- D. den Engelsen, P. G. Harris, T. G. Ireland, G. Fern and J. Silver, ECS J. Solid State Sci. Technol., 2015, 4, R145–R152 CrossRef CAS.
- D. den Engelsen, P. G. Harris, T. G. Ireland, G. Fern and J. Silver, ECS J. Solid State Sci. Technol., 2015, 4, R105–R113 CrossRef CAS.
- F. Baur, F. Glocker and T. Jüstel, J. Mater. Chem. C, 2015, 3, 2054–2064 RSC.
- J. Ueda, P. Dorenbos, A. J. J. Bos, A. Meijerink and S. Tanabe, J. Phys. Chem. C, 2015, 119, 25003–25008 CAS.
- D. den Engelsen, G. R. Fern, T. Ireland and J. Silver, J. Lumin. Search PubMed , submitted.
- J. Silver, M. I. Martinez-Rubio, T. G. Ireland, G. R. Fern and R. Withnall, J. Phys. Chem., 2003, 107, 1548–1553 CrossRef CAS.
- A. Fukabori, T. Yanagida, J. Pejchal, S. Maeo, Y. Yokota, A. Yoshikawa, T. Ikegami, F. Moretti and K. Kamada, J. Appl. Phys., 2010, 107, 073501 CrossRef.
- A. Fukabori, V. Chani, K. Kamada, T. Yanagida, Y. Yokota, F. Moretti, N. Kawaguchi and A. Yoshikawa, J. Cryst. Growth, 2011, 318, 823–827 CrossRef CAS.
- G. H. Dieke, Spectra and Energy Levels of rare Earth Ions in Crystals, Interscience, 1968 Search PubMed.
- J. Silver, M. I. Martinez-Rubio, T. G. Ireland, G. R. Fern and R. Withnall, J. Phys. Chem. B, 2001, 105, 948–953 CrossRef CAS.
- E. Zych, J. Phys.: Condens. Matter, 2002, 14, 5637–5650 CrossRef CAS.
- E. A. Kravchenko, V. G. Orlov and M. P. Shlykov, Russ. Chem. Rev., 2006, 75, 77–93 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |