Open Access Article
Open Access ArticleCan water continuously oxidize the PuO molecule? Mechanisms, topological analysis and rate constant calculations†
Wenxia Niua,
Feng Xie b,
Peng Li
b,
Peng Li *c,
Jie Mac,
Tao Gaod and
Huaqiang Yinb
*c,
Jie Mac,
Tao Gaod and
Huaqiang Yinb
aDepartment of Physics, Taiyuan Normal University, Taiyuan, 030031, China
bInstitute of Nuclear and New Energy Technology, Collaborative Innovation Center of Advanced Nuclear Energy Technology, Key Laboratory of Advanced Reactor Engineering and Safety of Ministry of Education, Tsinghua University, Beijing 100084, China
cSchool of Physics and Electronic Engineering, Shanxi University, Taiyuan, 030006, China. E-mail: lip@sxu.edu.cn
dInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, 610065, China
First published on 23rd January 2018
Abstract
A detailed description of the reaction mechanisms provides insights into the PuO continuously oxidized by water in the gas-phase. Two reaction pathways were located, isomerization and dehydrogenation, and the corresponding different products are closely examined. Our results indicated that it is difficult to oxidize PuO with a water molecule at room temperature. In the early stages of reaction, the reaction rate constants of the first O–H bond dissociation are very small. Once the dissociations of the O–H bonds were complete, the remaining process will be exothermic, and the best thermochemical conditions observed at dehydrogenation around 42.3 kcal mol−1. Minimum energy crossing points between the septuplet–quintet and septuplet–triplet PESs were searched. Electron localization function and atoms in molecules were performed to analyze the topological property of bonding evolution along the reactions. Rate constants were calculated between 298 and 1000 K by using variational transition-state theory including one-dimensional tunneling effects.
Introduction
Plutonium, which in some forms is used in most of the nuclear industry, has unique chemical and physical properties as well as strong chemical reactivity. When exposed to moisture and atmospheric components, the metal surface readily corrodes.1 An in-depth understanding of the corrosion mechanism is an important basis for seeking effective plutonium surface corrosion resistance methods. Besides, exploring the most stable plutonium oxide and whether plutonium oxide further oxidizes are also important issues in plutonium science.2,3 Therefore, over the last few decades, the reaction of plutonium with small molecules in the gas phase has attracted significant attention both in experimental1–12 and theoretical studies.13–21 In addition, the reaction of plutonium with water which can provide some insight into the corrosive mechanism of steam on nuclear fuel is a more imperative and challenging research field.In terms of experimental study, PuO2 solid reacts with water vapor to form PuO2+x, which was detected and characterized by mass spectrometric (MS) analysis.2,8 These studies yielded an extremely important insight, that PuO2+x is the stable oxides of plutonium, and H2 formed during the Pu + H2O reaction will continue to participate in the reaction and produce plutonium hydroxide PuOH. In a recent experimental study, the gas phase monopositive plutonyl ion PuO2+ reaction with water was investigated by employing electrospray ionization (ESI) mass spectrometry.10 The spectra of products PuO2(OH)+, PuO2+(H2O)4 and PuO2+(O2)(H2O)3 were detected. Because of the experimental specificity of PuO, there is no report of PuO being continuously oxidized by H2O in the experiment.
Undoubtedly, experimental investigations provide precious original information of the gas phase plutonium reacted with water. However, limitations still exist, and no direct structural and detailed mechanism information was obtained. On one hand, the potentially dangerous of plutonium brings difficulties and risks to the experimental study. On the other hand, the development and application of surface anti-corrosion experimental techniques require basic research provide detailed and in-depth understanding of the microscopic mechanism. As a crucial complement of experimental researches, these detailed information can reliably computed by density functional theory (DFT), and these theory methods have been successful used in the study of actinide corrosive reaction.22–27 In 2015 and 2017, Ao28,29 reported the existence of PuO and the formation of hyperstoichiometric PuO2 from first principle calculation. There results indicated that PuO is thermodynamically unstable at ambient pressure.
In our recent theoretical study,21 the mechanisms and molecular dynamics of the reaction of gas phase Pu atom with H2O were investigated by DFT computation. The reaction pathways shown in the following equations were determined.
| Pu + H2O → HPuOH → PuO + H2 | (1) |
| Pu + H2O → HPuOH → OPuH2 | (2) |
The PuO + H2 process was found as the minimum energy reaction channel of Pu + H2O reaction, with heat liberation around 36.7 kcal mol−1. Our previous theoretical studies have demonstrated that such reactions are usually as two-state reactivity, which means there are intersystem crossing between the potential surfaces of different spin multiplicity.26,27
In the work, we perform the DFT calculations combined with variational transition state theory, focusing on the investigation of detailed mechanism, topological properties and rate constants of gas phase PuO react with H2O molecules. From the electronic structure level, the microscopic mechanism of plutonium corrosion can be reasonably evaluated, and a reliable theoretical basis for the interpretation of the practical corrosions of plutonium will be provided.
Computational details
Different levels of methods were employed to optimize the geometries and locate transition states on the potential energy surface of the possible spin states. The B3LYP,30,31 B3PW91,32 PBE0 (ref. 33) and PW91PW91 (ref. 34) functions were used together with the Stuttgart–Dresden–Bonn relativistic effective core potential (SDD-RECP)35 for the Pu atom. The Pople type basis set 6-311++G(d,p) was adopted for O and H atoms.36 These calculations were implemented in the Gaussian 03 package.37 The located transition states on each potential energy surface have examined by intrinsic reaction coordinate (IRC) calculation, and the corresponding imaginary frequency connect the reactants and products correctly. The reported relative energies include the vibrational zero point energy (VZPE) corrections. This set of research methods has been successfully implemented in previous study on corrosion reaction of actinide systems. The minimum energy crossing point (MECP) between different spin potential surfaces of was identified using the program of sobMECP program38,39 and Gaussian 03.In order to get more in-depth bonding characteristic information along the pathway, the topological analysis including electron localization function (ELF)40,41 and atoms-in-molecules (AIM)42 as well as Mayer bond order43 were performed. The topological properties of the (3, −1) bond critical points (BCP) in the gradient field of the electron density were obtained. These analysis were performed with the Multiwfn package.44
Rate constants are calculated between 298 and 1000 K by using variational transition state (VTST) theory45 including one-dimensional tunneling effects (Wigner46 and Eckart47). All rate constant computations were carried out by using the KiSThelP program.48
Results and discussion
Although current computational methods have been successfully performed in the previous studies, we still verify the correctness of these methods in the plutonium oxide system. We calculated the vibrational frequencies of the PuO and PuO2 complexes and compared with the available experimental data, of which the results are collated in Table 1. As can be seen, the results from method schemes we adopted are in most cases closer to the available experimentally detected data.Structures and energetics
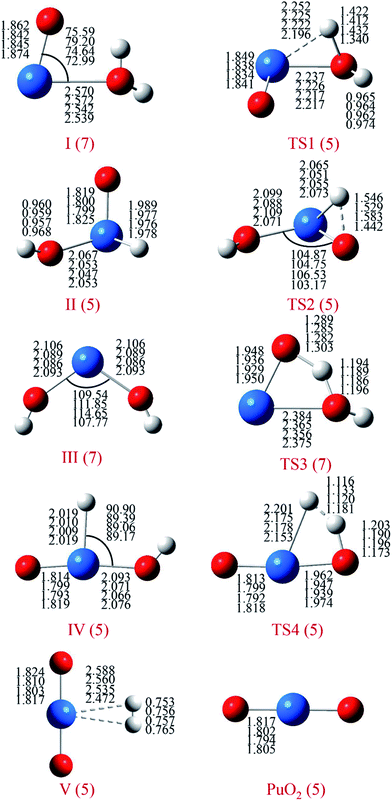
For each species on the different spin potential surfaces, several initial geometries were constructed, and optimized by full geometry without symmetry constrain at different levels of theory. Triplet, quintet, and septuplet spin states were taken into account. Geometric parameters of the lowest energy spin states for stationary species are presented in Fig. 1. It can be seen that the geometric parameters are relatively less dependence on the method, most bond lengths are within 0.05 Å of the difference. These angles agree to ±5°, except for the O–Pu–O bond of complex III.The potential energy profiles of PuO + H2O reactions are reported in Fig. 2 and 3, the corresponding relative energies are regarding the reactants' ground state asymptotes.
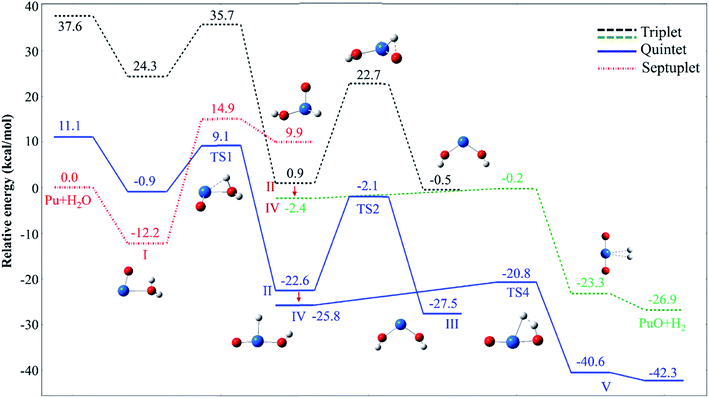 | ||
| Fig. 2 Potential energy profiles for the reaction of PuO + H2O (path A) at the PW91/SDD levels of theory. | ||
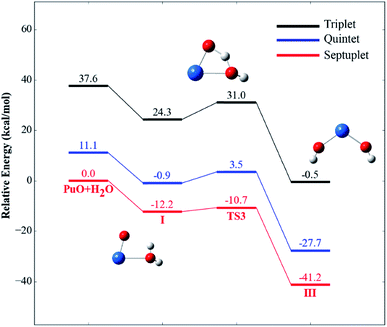 | ||
| Fig. 3 Potential energy profiles for the reaction of PuO + H2O (path B) at the PW91/SDD levels of theory. | ||
We have found that the PuO + H2O has similar mechanisms with the insertion reaction for actinide atoms in our previous studies from an overall perspective.17,21,26 Two reaction channels were found, isomerization and hydrogen elimination, and the formation of PuO2 + H2 is more thermodynamically favorable.
The reaction of PuO + H2O starts with the formation of the initial complex, OPu–OH2 (I), exothermic by as much as −12.2 kcal mol−1 at ground state septuplet spin state. Hereafter, the first O–H bond of water was activated, and the corresponding H atom will shift from O atom of water to PuO section. Our results show that there are two possible directions for this shift, one is perpendicular to the molecular plane and the H atom trapped by Pu atom; the other is in the molecular plane and the H atom trapped by O atom of PuO. Therefore, the reaction system overcomes two different transition states (TS1 and TS3) after complex I. For the sake of discussion, the TS1 path is named path A, and TS3 path is named path B, the corresponding potential energy profiles are plotted in Fig. 2 and 3, respectively.
As can be seen in Fig. 2, the path A, the system proceeds to form the first insertion intermediate (II) H–OPuOH through the TS1 in which the PuO is inserted into one of the O–H. The first transition state TS1 with an activation barrier of 9.1 kcal mol−1 at the PW91/SDD level, and the imaginary frequency of −1219.12 cm−1 correspond primarily to the migration of the H atom from the O atom to the Pu atom. In this process, the system involves crossings between surfaces of quintet and septuplet spin states, and the minimum energy path changes from septuplet to quintet state.
After the OHPuOH intermediate, the reaction will proceed along two channels. The first one is the isomerization of OHPuOH to form HO–Pu–OH (III). Alone the quintet state surface this intermediate carried on to isomerization via TS2 transition state, which lay 2.1 kcal mol−1 below the asymptotes, with an activation barrier of 20.5 kcal mol−1 at the PW91/SDD levels of theory. The imaginary frequency of TS2 was −1143.37 cm−1, corresponding to the movement of the second H atom from the O atom to the Pu atom. Our results on HO–Pu–OH predicted that this isomeric product have a septuplet (7A) ground state.
Another channel is dehydrogenation process. As can be seen, in this process, the intermediate II product first passes through a no-threshold isomerization process to form intermediate IV, and the corresponding molecular structure changes from triangular pyramid (II) to plane (IV). The change in energy during this process is relatively small, 3.2 kcal mol−1 with the PW91/SDD method. From IV, the second H atom migrating from oxygen to plutonium evolved into a hydrogen complex (H2) PuO, complex V in Fig. 2. This process needs to overcome a four-center transition state TS4, which lay 20.8 kcal mol−1 below the asymptotes, with an imaginary frequency of −1133.11 cm−1 and described a motion in which the two hydrogen atoms moving together. This dehydrogenation of PuO + H2O was calculated to be exothermic at −42.3 kcal mol−1 at PW91/SDD level of theory.
For path B, as shown in Fig. 3, the path B is also an isomerization process, and the isomeric product is HO–Pu–OH (III). Comparison of path A and path B reveals that these two channels have the same isomeric product but undergo two different transition states. Compared to the path A, the path B can be directly isomerism from the initial complex I, only need the system overcomes a transition state TS3. The TS3 lies at −10.7 kcal mol−1 below the reactant asymptote, and with an imaginary frequency of −1121.40 cm−1 and corresponds mainly to the movement of H atom from Oyl atom (the O atom of H2O molecule) to the O atom of PuO molecule.
The relative energies of selected stationary species for the PuO + H2O reaction at all the studied methods are collected in Table 2. We can see that energies were consistent in most case except for B3LYP/SDD which overestimated the relative energy of TS3 and TS4. In addition, we checked the 〈S2〉 values to ensure the spin contamination was minimal.
| I (7) | TS1 (5) | II (5) | TS2 (5) | TS3 (7) | III (7) | IV (5) | TS4 (5) | V (5) | PuO2 + H2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| a SDD for Pu and 6-311++G(d,p) for O and H atoms.b Expected value of S2 at the B3LYP/SDD level of theory.c Expected value of S2 at the B3PW91/SDD level of theory.d Expected value of S2 at the PW91/SDD level of theory.e Expected value of S2 at the PW91/SDD level of theory. | ||||||||||
| B3LYPa | 6.768 | 33.382 | 0.000 | 22.044 | 11.217 | −22.239 | −0.493 | 13.045 | −7.917 | −11.782 |
| B3PW91a | 6.817 | 32.309 | 0.000 | 18.603 | 8.921 | −26.223 | −0.948 | 8.646 | −9.354 | −16.192 |
| PBE0a | 3.508 | 31.321 | 0.000 | 24.927 | 7.171 | −27.324 | −0.296 | 9.859 | −9.764 | −12.983 |
| PW91a | 10.308 | 37.490 | 0.000 | 20.496 | 11.865 | −18.660 | −3.253 | 1.798 | −18.015 | −19.781 |
| 〈S2〉b | 12.026 | 6.862 | 6.068 | 6.703 | 12.020 | 12.009 | 6.083 | 6.072 | 6.064 | |
| 〈S2〉c | 12.032 | 6.893 | 6.075 | 6.732 | 12.026 | 12.015 | 6.083 | 6.077 | 6.064 | |
| 〈S2〉d | 12.032 | 6.915 | 6.076 | 6.788 | 12.025 | 12.013 | 6.087 | 6.079 | 6.067 | |
| 〈S2〉e | 12.030 | 6.643 | 6.089 | 6.503 | 12.025 | 12.015 | 6.071 | 6.066 | 6.054 | |
As discussed above, this reaction involves crossing between surfaces of quintet and septuplet spin states. It is worth mentioning that these intersystem crossings play an important role in the progress of the reaction, since it characterizes where the transition is most likely to take places. The MECPs between states of different spin have been located by the sobMECP method. We first determine the MECP between the septuplet and quintet surfaces in the region from complex I to TS1, marked as MECP(7–5), and the MECP between the septuplet and triplet surfaces in the region from TS1 to complex II, marked as MECP(7–3). The molecular structures of MECPs at the PW91/SDD level of theory are shown in Fig. 4. The MECP(7–5) has a nonplanar geometry in which the Pu–Oyl, Pu–H and O–H bond lengths are 2.218, 2.189 and 1.368 Å, respectively. This geometry is very similar to TS1, means that it is a late crossing point, leading to the barrier height from 14.9 to 9.1 kcal mol−1 at the PW91/SDD level. For the MECP(7–3), the Pu–Oyl and Pu–H bond lengths are 2.133 and 2.136 Å, and the H–Pu–Oyl angle is 57.86°.
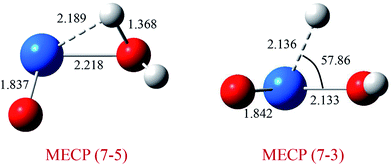 | ||
| Fig. 4 Structures and selected geometric parameters of MECP on the PuO + H2O potential energy surface optimized at the PW91/SDD levels of theory. Bond distances are in Å, and angles are in degrees. | ||
Analysis of the whole reaction of PuO + H2O, we found that the reaction mechanism is similar with the activation of H2O by actinide atoms and ions.21–24,50–52 The reaction mechanisms according to the universal channel proposed, the first step is the formation of a actinide –OH2 complex followed with an O–H bond broke by the insertion of the actinide molecule. After that the first insertion intermediate will be generated, and this process is usually the key step of the whole reaction, with the largest reaction coefficients. In addition, this process always involves a crossings between surfaces of different spin states, with the exception of Pu + H2O,21 which takes place alone the minimum energy path septuplet state surface. The following step is migration of second H atom of H2O molecule to the actinide, and the isomerization or hydrogen elimination are take places. Our previous studies show that this insertion intermediates have relatively long lifetimes to restructuring. Take Pu + H2O as an example,21 the lifetime of HPuOH intermediate was found to be almost 137 fs. From the perspective of energy barriers, it is difficult to oxidize PuO by water molecules than Pu atoms at room temperature. The activation energy barrier of the first O–H bond for PuO + H2O is 21.3 kcal mol−1 at PW91/SDD levels of theory, while this barrier for Pu + H2O is 15.8 kcal mol−1. This view is also confirmed in later reaction rate analysis.
Bonding characteristics
In this section, we conducted the ELF, AIM and Mayer bond orders analysis to get a deeper understanding of the bond characteristics evolution. It is worth emphasizing that ELF + AIM analysis are powerful tools to analyzing the nature of the interaction between atoms, and have been successfully used in the actinide system.47–53The ELF shaded surfaces with projection maps of stationary points on the PuO + H2O potential energy surface optimized at the PW91/SDD levels of theory are displayed in Fig. 5. The AIM parameters of the main BCPs of each species are listed in Table 3. These topological parameters include electron density ρ(r) and its Laplacian ∇2ρ(r), the kinetic G(r) and potential energy density V(r), H(r) is the total energy density. H(r) was used as a criterion,54 negative H(r) corresponds to covalent interactions and positive H(r) correspond to closed-shell interactions. λ1 and λ2 are the eigenvalues of the Hessian of the energy density, and ε = λ1/λ2 − 1 denotes the ellipticity of the BCP. The ε was used as a measure of asphericity of the curvature of the ρ(r) in BCP, and served as a criterion to indicate the π nature of bonds.55,56
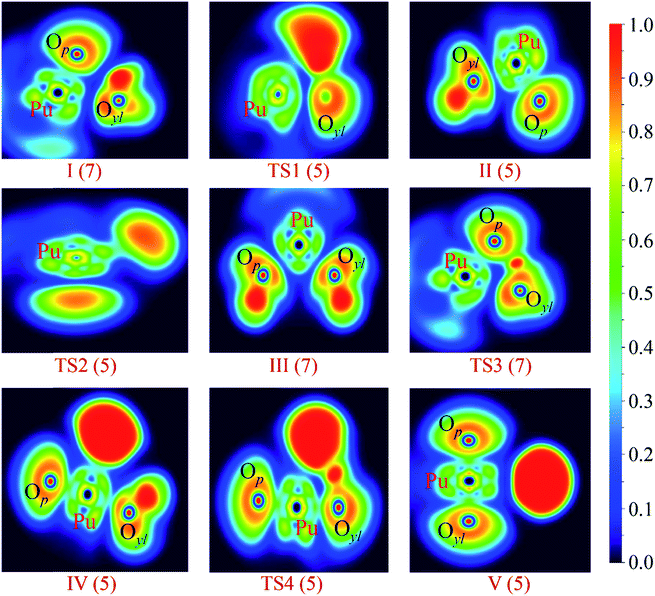 | ||
| Fig. 5 ELF shaded surfaces with projection maps of stationary points on the PuO + H2O potential energy surface optimized at the PW91/SDD levels of theory. | ||
| Species | ρ(r) | ∇2ρ(r) | G(r) | V(r) | H(r) | λ1 | λ2 | ε | |
|---|---|---|---|---|---|---|---|---|---|
| a Op is the O atom of PuO, and Oyl is the O atom of H2O. | |||||||||
| I (7) | Pu–Op | 0.222 | 0.476 | 0.268 | −0.416 | −0.148 | −0.353 | −0.329 | 0.073 |
| Pu–Oyl | 0.040 | 0.173 | 0.042 | −0.041 | 0.001 | −0.037 | −0.035 | 0.057 | |
| Op–H1 | 0.027 | 0.089 | 0.021 | −0.020 | 0.001 | −0.029 | −0.013 | 1.231 | |
| TS1 (5) | Pu–Op | 0.243 | 0.527 | 0.307 | −0.483 | −0.176 | −0.417 | −0.407 | 0.025 |
| Pu–Oyl | 0.091 | 0.348 | 0.104 | −0.121 | −0.017 | −0.125 | −0.116 | 0.078 | |
| O–H1 | 0.135 | −0.026 | 0.068 | −0.142 | −0.074 | −0.327 | −0.312 | 0.048 | |
| O–H2 | 0.348 | −2.326 | 0.071 | −0.724 | −0.653 | −0.017 | −0.016 | 0.063 | |
| II (5) | Pu–Op | 0.253 | 0.487 | 0.310 | −0.499 | −0.189 | −0.431 | −0.409 | 0.054 |
| Pu–Oyl | 0.131 | 0.513 | 0.172 | −0.217 | −0.045 | −0.192 | −0.180 | 0.067 | |
| Pu–H1 | 0.093 | 0.028 | 0.043 | −0.080 | −0.037 | −0.135 | −0.124 | 0.089 | |
| TS2 (5) | Pu–Op | 0.202 | 0.500 | 0.246 | −0.366 | −0.120 | −0.346 | −0.334 | 0.036 |
| Pu–Oyl | 0.126 | 0.482 | 0.161 | −0.203 | −0.042 | −0.182 | −0.174 | 0.046 | |
| Op–H1 | 0.111 | 0.058 | 0.061 | −0.107 | −0.046 | −0.221 | −0.198 | 0.116 | |
| TS3 (7) | Pu–Op | 0.185 | 0.437 | 0.212 | −0.316 | −0.104 | −0.285 | −0.257 | 0.109 |
| Pu–Oyl | 0.061 | 0.248 | 0.065 | −0.068 | −0.003 | −0.064 | −0.058 | 0.103 | |
| Op–H1 | 0.137 | −0.015 | 0.082 | −0.168 | −0.086 | −0.360 | −0.344 | 0.047 | |
| O–H1 | 0.181 | −0.342 | 0.088 | −0.262 | −0.174 | −0.593 | −0.572 | 0.037 | |
| III (7) | Pu–Op | 0.116 | 0.454 | 0.147 | −0.181 | −0.034 | −0.147 | −0.137 | 0.073 |
| Pu–Oyl | 0.116 | 0.454 | 0.147 | −0.181 | −0.034 | −0.147 | −0.137 | 0.073 | |
| Op–H1 | 0.353 | 2.309 | 0.077 | −0.732 | −0.655 | −1.651 | −1.650 | 0.001 | |
| O–H2 | 0.353 | 2.309 | 0.077 | −0.732 | −0.655 | −1.651 | −1.650 | 0.001 | |
| IV (5) | Pu–Op | 0.132 | 0.365 | 0.137 | −0.184 | −0.047 | −0.435 | −0.461 | 0.060 |
| Pu–Oyl | 0.258 | 0.371 | 0.289 | −0.486 | −0.197 | −0.185 | −0.187 | 0.011 | |
| Pu–H1 | 0.083 | 0.050 | 0.041 | −0.070 | −0.029 | −0.108 | −0.106 | 0.019 | |
| TS4 (5) | Pu–Op | 0.259 | 0.358 | 0.288 | −0.487 | −0.199 | −0.465 | −0.454 | 0.024 |
| Pu–Oyl | 0.178 | 0.354 | 0.181 | −0.275 | −0.094 | −0.297 | −0.282 | 0.053 | |
| Pu–H1 | 0.062 | 0.108 | 0.041 | −0.055 | −0.014 | −0.075 | −0.053 | 0.415 | |
| O–H2 | 0.199 | −0.404 | 0.087 | −0.277 | −0.190 | −0.635 | −0.621 | 0.023 | |
| H1–H2 | 0.095 | −0.085 | 0.028 | −0.077 | −0.049 | −0.187 | −0.171 | 0.094 | |
| V (5) | Pu–Op | 0.260 | 0.338 | 0.284 | −0.485 | −0.201 | −0.473 | −0.472 | 0.002 |
| Pu–Oyl | 0.260 | 0.338 | 0.284 | −0.485 | −0.201 | −0.473 | −0.472 | 0.002 | |
| H1–H2 | 0.249 | −0.966 | 0.002 | −0.245 | −0.243 | −0.832 | −0.824 | 0.010 | |
| Pu–H1H2 | 0.027 | 0.100 | 0.024 | −0.023 | 0.001 | −0.028 | −0.015 | 0.867 | |
As shown in Fig. 5, for first complex OPu–OH2, there is no disynaptic valence basin between Pu and Oyl atom, which means that there is no electron concentration between these two atoms. The AIM analysis results show that these is a (3, −1) BCP between Pu and Oyl atom, and the corresponding electron density ρ(r) is 0.04 and the H(r) is 0.001. Positive H(r) value means that Pu–Oyl interaction is a closed-shell interaction in complex I. In the case of TS1, the ELF and AIM results indicate that the Pu–Oyl bond is gradually formed in this process. Although the corresponding H(r) is small (−0.017), it is still an indicator of the increase in the electronic density of the Pu–Oyl BCP. Besides, the H(r) of the O–H1 bond is drops strongly compared to the O–H2 bond, which means that the O–H1 bond has a tendency to break.
In regard to the complex II, H–OPuOH, the ELF and AIM analysis shows that in this process the system involves a significantly change. The ELF result indicates that the disynaptic V(O–H1) basin has been replaced by the V(Pu–H1) basin, which means that the Pu–H1 bond was formed. The topological analysis shows there is a (3, −1) BCP between Pu and H1 atoms, and the H(r) is −0.080 reveals that this Pu–H1 bond belongs to covalent interactions. Besides, ELF and AIM analysis reveals the interaction of Pu–Oyl was strengthened, which was reflected by the increased H(r) of Pu–Oyl.
In terms of TS2, the ELF and AIM analysis indicates that there is no disynaptic V(Pu–H1) basin and (3, −1) BCP between Pu and H1 atoms, which means that this Pu–H1 bond has been broken in this process. Besides, the ρ(r) of Pu–Op and Pu–Oyl are decreasing, due to the sustained isomerization of molecular structure. In the case of the isomeric product HO–Pu–OH (III), the corresponding ELF projection map like a beautiful butterfly. From the ELF analysis, we can see that the Op–H2 bond has been formed as evidenced by the disynaptic V(Op–H2) basin. The AIM results reveal that these topological parameters have mirror symmetry, and all of these chemical bonds belong to covalent interactions.
The ELF and AIM analysis of the IV show that there are V(Pu–H1) and V(Pu–Oyl) disynaptic valence basins, and an increase in the ρ(r) of Pu–Oyl. In the case of TS4, these two H atoms are attracted to each other and gradually form bond, which proved by the V(H1–H2) disynaptic valence basin and the negative value of H(r) −0.049. This trend is more pronounced in the complex V. As can be seen in the Table 3, the H(r) of H1–H2 in V is −0.243, and there is a BCP between Pu atom and H1–H2 group with H(r) is 0.001, these values reveal that the Pu–(H1H2) interaction with the closed-shell characteristic.
In the case of the critical transition state TS3 in path B, the H1 atom has been bonded to the Op atom of PuO, as evidenced by the V(Op–H1) disynaptic valence basin and the corresponding H(r) is −0.086. Meanwhile, the interaction of Pu–Oyl was enhanced compared to the initial complex I. A higher ρ(r) (0.061) and more negative H(r) (−0.003) were found for Pu–Oyl in TS3 than in complex I.
As mentioned above, the ellipticity ε is the index of the π nature of the bonds. From Table 3, we can see that in complex I, the ε of Pu–Op and Pu–Oyl are 0.073 and 0.057 respectively. In comparison, both the ε of Pu–Op and Pu–Oyl in product V are 0.002. This trend reveals that the π nature of Pu–Op and Pu–Oyl was reduced as the reaction progresses.
Mayer bond orders analysis for all of the lowest-energy spin state species are listed in Table 4. As can be seen, the conclusions of Mayer bond order analysis are agree with the ELF and AIM analysis. In complex I, the Pu–Oyl bond order is 0.15 indicating there is no covalent interaction between these two atoms. As the PuO + H2O reaction proceeds, the interaction between Pu atom and ligands is strengthening, as evidenced by the increasing of the Pu–Oyl bond order.
| Species | I | TS1 | II | TS2 | TS3 | III | IV | TS4 | V |
|---|---|---|---|---|---|---|---|---|---|
| Pu–Op | 1.64 | 1.81 | 1.82 | 1.39 | 1.29 | 0.73 | 1.75 | 1.75 | 1.72 |
| Pu–Oyl | 0.15 | 0.39 | 0.80 | 0.79 | 0.37 | 0.73 | 0.90 | 1.18 | 1.72 |
| Pu–H1 | 0.66 | 0.93 | 0.72 | 0.89 | 0.67 | 0.11 | |||
| Pu–H2 | 0.23 | 0.11 | |||||||
| Op–H1 | 0.19 | 0.48 | 0.88 | ||||||
| O–H1 | 0.87 | 0.16 | 0.50 | 0.43 | |||||
| O–H2 | 0.91 | 0.88 | 0.87 | 0.87 | 0.90 | 0.88 | 0.87 | 0.49 | |
| H1–H2 | 0.89 |
Reaction rate constants
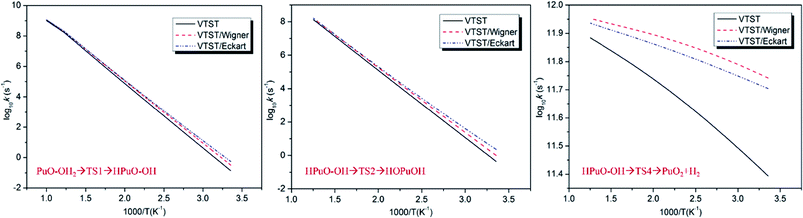
Rate coefficients (k) were calculated using the VTST method, and the energies and frequencies data used in this section were obtained by PW91/SDD in the reaction mechanism. In addition, the one-dimensional tunneling effects Wigner and Eckart were taken into account.Firstly, we calculated the variational effect of the titled reaction, the results indicate that both the barriers of classical potential energy (VMEP) and the ground state adiabatic potential energy (VGa) were located at the original transition state, which means that there is no variational effect, and kVTST is equal to the kTST. The concrete calculation of the rate constants is carried out according to the following expression45
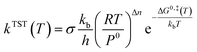 | (3) |
The predicted rate constants log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k with 1000/T graphics of PuO + H2O are presented in Fig. 6, and rate constants k at 298 and 600 K are collected in Table 5. By analyzing these data, we can see that the HPuO–OH → PuO2 + H2 is the fastest part of the whole reaction. The process of dissociating the O–H bond of H2O at room temperature is very slow, but as the temperature rises, this progress getting more faster. In contrast, the elevated temperature did not significantly increase the rate of dehydrogenation. By comparison, we found that the tunneling effects in the dehydrogenation process were more obvious than in the dissociating O–H bond one.
k with 1000/T graphics of PuO + H2O are presented in Fig. 6, and rate constants k at 298 and 600 K are collected in Table 5. By analyzing these data, we can see that the HPuO–OH → PuO2 + H2 is the fastest part of the whole reaction. The process of dissociating the O–H bond of H2O at room temperature is very slow, but as the temperature rises, this progress getting more faster. In contrast, the elevated temperature did not significantly increase the rate of dehydrogenation. By comparison, we found that the tunneling effects in the dehydrogenation process were more obvious than in the dissociating O–H bond one.
| T (K) | PuO–OH2 → HPuO–OH | HPuO–OH → HOPuOH | HPuO–OH → PuO2 + H2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| kVTST | kVTST/W | kVTST/Eck | kVTST | kVTST/W | kVTST/Eck | kVTST | kVTST/W | kVTST/Eck | |
| 298 | 0.135 | 0.317 | 0.548 | 0.434 | 0.987 | 2.271 | 2.47 × 1011 | 5.51 × 1011 | 5.06 × 1011 |
| 300 | 0.168 | 0.391 | 0.668 | 0.533 | 1.204 | 2.712 | 2.51 × 1011 | 5.55 × 1011 | 5.09 × 1011 |
| 350 | 1.70 × 10 | 3.36 × 10 | 4.64 × 10 | 4.37 × 10 | 8.40 × 10 | 1.31 × 102 | 3.39 × 1011 | 6.42 × 1011 | 5.83 × 1011 |
| 400 | 5.52 × 102 | 9.63 × 102 | 1.18 × 103 | 1.19 × 103 | 2.04 × 103 | 2.69 × 103 | 4.19 × 1011 | 7.04 × 1011 | 6.43 × 1011 |
| 450 | 8.37 × 103 | 1.32 × 104 | 1.53 × 104 | 1.58 × 104 | 2.46 × 104 | 2.95 × 104 | 4.88 × 1011 | 7.51 × 1011 | 6.69 × 1011 |
| 500 | 7.44 × 104 | 1.09 × 105 | 1.21 × 105 | 1.24 × 105 | 1.81 × 105 | 2.05 × 105 | 5.47 × 1011 | 7.85 × 1011 | 7.29 × 1011 |
| 550 | 4.49 × 105 | 6.25 × 105 | 6.75 × 105 | 6.78 × 105 | 9.31 × 105 | 1.02 × 106 | 5.97 × 1011 | 8.12 × 1011 | 7.60 × 1011 |
| 600 | 2.02 × 106 | 2.69 × 106 | 2.85 × 106 | 2.78 × 106 | 3.66 × 106 | 3.92 × 106 | 6.40 × 1011 | 8.34 × 1011 | 7.86 × 1011 |
Conclusions
The present work describes a systematic investigation of the gas phase PuO react with H2O molecule. The detailed mechanism, topological properties and rate constants were obtained. The main conclusions are summarized as follows,(1) Two reaction channels were found, there are isomerization and dehydrogenation. The later one was the minimum energy reaction pathway. Our results reveal that this process involve crossing between surfaces of quintet and septuplet spin states, and the corresponding MECPs were located.
(2) Topological property analysis can make us understand the nature of the bonding behavior along the reaction. Our ELF and AIM results show that at the beginning of the reaction, the PuO and H2O molecule are getting close to each other by electrostatic interaction and form an initial complex I, and Pu–Oyl interaction is a closed-shell interaction in this complex. As the reaction progresses, the covalent properties are gradually reflected between the Pu–Oyl atoms.
(3) The reaction rate constant results show that it is not easy to dissociate the first O–H bond by PuO at room temperature. Once the O–H bonds were dissociated, the remaining process will be exothermic.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (NSFC) (Grant No. 11604187, No. 11647040 and No. 11575099), and Open Fund of Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education (Tsinghua University, China).We are very grateful to Dr Sobereva for many helpful discussions and providing us with the Multiwfn package. We would like to thank the reviewers for the valuable suggestions on improving our paper.Notes and references
- J. M. Haschke, T. H. Allen and L. A. Morales, Los Alamos Sci., 2000, 26, 252–273 CAS.
- J. M. Haschke, T. H. Allen and L. A. Morales, Science, 2000, 287, 285–287 CrossRef CAS PubMed.
- P. A. Korzhavyi, L. Vitos, D. A. Andersson and B. Johansson, Nat. Mater., 2004, 4, 225–228 CrossRef PubMed.
- J. K. Gibson, Int. J. Mass Spectrom., 2000, 202, 19–29 CrossRef CAS.
- J. K. Gibson, J. Mass Spectrom., 2001, 36, 284–293 CrossRef CAS PubMed.
- M. Santos, J. Marçalo, A. Pires de Matos, J. K. Gibson and R. G. Haire, J. Phys. Chem. A, 2002, 106, 7190–7194 CrossRef CAS.
- J. K. Gibson, Int. J. Mass Spectrom., 2002, 216, 185–202 CrossRef CAS.
- J. M. Haschke, T. H. Allen and L. A. Morales, J. Alloys Compd., 2001, 314, 78–91 CrossRef CAS.
- J. K. Gibson, R. G. Haire, M. Santos, J. Marçalo and A. Pires de Matos, J. Phys. Chem. A, 2005, 109, 2768–2781 CrossRef CAS PubMed.
- D. Rios, M. C. Michelini, A. F. Lucena, J. Marçalo, T. H. Bray and J. K. Gibson, Inorg. Chem., 2012, 51, 6603–6614 CrossRef CAS PubMed.
- J. K. Gibson, R. G. Haire, J. Marçalo, M. Santos, A. Pires de Matos, M. K. Mrozik, R. M. Pitzer and B. E. Bursten, Organometallics, 2007, 26, 3947–3956 CrossRef CAS.
- J. K. Gibson, R. G. Haire, J. Marçalo, M. Santos, J. P. Leal, A. Pires de Matos, R. Tyagi, M. K. Mrozik, R. M. Pitzer and B. E. Bursten, Eur. Phys. J. D, 2007, 45, 133–138 CrossRef CAS.
- J. P. Blaudeau, S. A. Zygmunt, L. A. Curtiss, D. T. Reed and B. E. Bursten, Chem. Phys. Lett., 1999, 310, 347–354 CrossRef CAS.
- X. Wu and A. K. Ray, Phys. B, 2001, 293, 362–375 CrossRef CAS.
- Z. Cao and K. Balasubramanian, J. Chem. Phys., 2005, 123, 114309 CrossRef PubMed.
- L. V. Moskaleva, A. V. Matveev, J. Dengler and N. Rosch, Phys. Chem. Chem. Phys., 2006, 8, 3767–3773 RSC.
- B. Schimmelpfennig, T. Privalov, U. Wahlgren and I. Grenthe, J. Phys. Chem. A, 2003, 107, 9705–9711 CrossRef CAS.
- K. Balasubramanian, T. E. Felter, T. Anklam, T. W. Trelenberg and W. McLean II, J. Alloys Compd., 2007, 444–445, 447–452 CrossRef CAS.
- K. J. de Almeida and H. A. Duarte, Organometallics, 2009, 28, 3203–3211 CrossRef CAS.
- H. M. Steele, D. Guillaumont and P. Moisy, J. Phys. Chem. A, 2013, 117, 4500–4505 CrossRef CAS PubMed.
- P. Li, W. X. Niu, T. Gao and H. Y. Wang, ChemPhysChem, 2014, 15, 3078–3088 CrossRef CAS PubMed.
- M. d. C. Michelini, N. Russo and E. Sicilia, Angew. Chem., Int. Ed., 2006, 45, 1095–1099 CrossRef CAS PubMed.
- M. d. C. Michelini, N. Russo and E. Sicilia, J. Am. Chem. Soc., 2007, 129, 4229–4239 CrossRef CAS PubMed.
- B. Y. Liang, R. D. Hunt, G. P. Kushto, L. Andrews, J. Li and B. E. Bursten, Inorg. Chem., 2005, 44, 2159–2168 CrossRef CAS PubMed.
- E. Di Santo, M. C. Michelini and N. Russo, J. Phys. Chem. A, 2009, 113, 14699–14705 CrossRef CAS PubMed.
- P. Li, W. Niu, X. F. Tian, T. Gao and H. Y. Wang, J. Phys. Chem. A, 2013, 117, 3761–3770 CrossRef CAS PubMed.
- P. Li, W. Niu and T. Gao, RSC Adv., 2014, 4, 29806–29817 RSC.
- B. Ao, R. Qiu, H. Lu, X. Ye, P. Shi, P. Chen and X. Wang, J. Phys. Chem. C, 2015, 119, 101–108 CAS.
- R. Qiu, Y. Zhang and B. Ao, Sci. Rep., 2017, 7, 12167 CrossRef PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1998, 38, 3098–3100 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03 (Revision E.01), Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- T. Lu, sobMECP program, http://sobereva.com/286, accessed, 31 March 2017.
- J. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. R. Fassler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A quantum theory, Clarendon, Oxford, 1990 Search PubMed.
- I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Rev. Comput. Chem., 2007, 23, 125–232 CAS.
- E. Wigner, Z. J. Phys. Chem. B, 1932, 19, 203–216 Search PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303–1309 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- D. W. Green and G. T. Reedy, J. Chem. Phys., 1978, 69, 544–551 CrossRef CAS.
- P. Li, W. Niu, T. Gao and H. Y. Wang, Int. J. Quantum Chem., 2014, 114, 760–768 CrossRef CAS.
- P. Li, W. Niu, T. Gao and H. Y. Wang, J. Mol. Model., 2014, 20, 2466 CrossRef PubMed.
- P. Li, W. Niu and T. Gao, J. Radioanal. Nucl. Chem., 2015, 304, 489–499 CrossRef CAS.
- P. Li, W. Niu and T. Gao, RSC Adv., 2017, 7, 4291–4296 RSC.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627–628 (Angew. Chem., 1984, 96, 612–614) CrossRef.
- R. F. W. Bader, T. S. See, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068 CrossRef CAS.
- C. S. López, O. N. Faza, F. P. Cossío, D. M. York and A. R. de Lera, Chem.–Eur. J., 2005, 11, 1734–1738 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra12812f |
| This journal is © The Royal Society of Chemistry 2018 |