Open Access Article
Open Access ArticleElectrically tunable terahertz dual-band metamaterial absorber based on a liquid crystal
Zhiping Yin,
Yujiao Lu,
Tianyu Xia,
Weien Lai,
Jun Yang,
Hongbo Lu and
Guangsheng Deng
and
Guangsheng Deng *
*
Academy of Photoelectric Technology, Hefei University of Technology, Hefei, 230009, China. E-mail: dgsh@hfut.edu.cn
First published on 24th January 2018
Abstract
In this paper, a liquid crystal (LC) based tunable metamaterial absorber with dual-band absorption is presented. The proposed absorber is analysed both numerically and experimentally. The analysis shows that the two absorption peaks, originating from the new resonant structure, are experimentally detected at 269.8 GHz and 301.4 GHz when no bias voltage is applied to the LC layer. In order to understand the absorption mechanisms, simulation results for the surface current and power loss distributions are presented. Since liquid crystals are used as the dielectric layer to realize the electrically tunable absorber, a frequency tunability of 2.45% and 3.65% for the two absorption peaks is experimentally demonstrated by changing the bias voltage of the LC layer from 0 V to 12 V. Furthermore, the absorber is polarization independent and a high absorption for a wide range of oblique incidence is achieved. The designed absorber provides a way forward for the realization of tunable metamaterial devices that can be applied in multi-band detection and imaging.
1. Introduction
The terahertz (THz) waves ranging from 0.1 to 10 THz have attracted considerable attention from various researchers due to their emerging potential applications in imaging, sensing and spectroscopy.1–3 Several efforts have been made for advancing the THz devices,4–6 among which the THz absorber is believed to be a crucial component in developing THz detectors and sensors.The concept of a metamaterial absorber (MA) was promoted by Landy et al.7 The MAs have been widely investigated due to their low cost, small size and ultrathin thickness. Various structures, such as closed rings,8 split rings9 and cut-wire pairs,10 have been proposed for MAs. Currently, the research is focused on absorbers intended for detecting and spectroscopic imaging applications. Therefore, tunable and multiband MAs are of great importance. One possible way to achieve frequency tunability of MA is to reconstruct the geometries, but it cannot be applied in the case of dynamic tuning. A tunable MA based on electrostatically actuated MEMS cantilever11 or varactor loaded resonator12 has been proposed. However, the fabrication of such structures is complicated. Recently, a progress toward the improvement of tune method has been made by changing the material properties. Graphene13–17 and strontium titanate18,19 have been proposed for tunable metamaterials. Nevertheless, the fabrication of these kinds of devices is still a big challenge at current state-of-the-art. Semiconductor20,21 and superconductor22,23 were also adopted in tunable metamaterials, but the modulation of these devices requires harsh environment, which restricted their practical applications.
Liquid crystal (LC) is a promising candidate for tunable and dynamic metamaterials due to its voltage dependent birefringence. It has been widely employed to realize tunable metamaterials in recent years.24–26 Compared to other active mediums, the LC has several advantages. Firstly, the LC based metamaterial is cost-effectiveness and easy-to-manufacture. Secondly, it can be operated at room temperature with low bias voltages. Shrekenhamer et al.27 reported an electronically controlled MA based on the birefringence of LC cell at THz frequencies. Isić et al.28 and Wang et al.29 presented LC tunable THz absorbers with periodically arranged patch resonators. However, only one absorption peak frequency can be dynamically tuned for these works. To the best of authors' knowledge, LC based MA with multiple absorption peaks has been rarely reported. One of the main reasons is that the resonant structure of LC based MA is usually connected as a whole electrode. Hence, the existing multi-band absorber technologies by packing multiple discrete resonators within a unit cell are not suitable for LC based MAs.
In this paper, a polarization independent and tunable LC-based MA with two absorption peaks at THz frequencies is presented. Based on a new metamaterial unit cell structure, a LC and a dipole resonant mode are excited that are responsible for these two absorption peaks, respectively. The characteristics and the absorption mechanisms of the proposed MA are comprehensively investigated. Both the simulation and the measurement results have demonstrated that the two resonant frequencies can be dynamically tuned by adjusting the bias voltage of the LC layer.
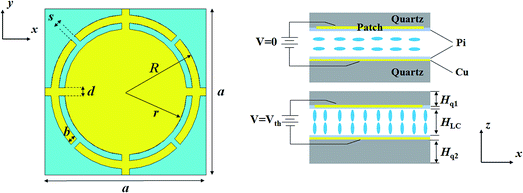
2. Design of the structure
The schematic view of the proposed tunable absorber unit cell is shown in Fig. 1. The unit cell is formed by using two parallel quartz plates that are separated by a cavity filled with the liquid crystal. Meanwhile, a patterned copper layer and a copper ground plane are printed on the inner surface of each quartz plate. In summary, the quartz plates serve not only to support the metal layers, but also to encapsulate the LC layer.The liquid crystal materials are composed of anisotropic molecules whose direction may change by an external electrical field. The orientation of the liquid crystal molecules and the permittivity of the LC layer along the electric field vector of the incident wave can be dynamically controlled by adjusting the bias voltage between the copper pattern layer and the metal ground. In order to control the orientation of the LC molecules in the absence of bias voltage, the inner surfaces of both copper layers are covered with polyimide (Pi) alignment layers. In the unbiased state (ε⊥), the long axis of the molecules is aligned parallel to the surface of the quartz due to the static action of the polymer alignment layer. The bias voltage, applied across the biasing layers, rotates the LC molecules. This provides maximum permittivity (ε∥), at the saturation state, while the direction is perpendicular to the cell walls. Therefore, the permittivity of the LC maybe electronically varied between these two states, i.e. Δεeff = ε∥ − ε⊥, where the absorption frequency of the absorber may also be shifted.
Table 1 lists the dimensions of the unit cell structure. Besides, the pattern layer and the ground plate were made of 500 nm thick copper, while the quartz plates were considered as a dielectric material with relative permittivity of 3.78 and dielectric loss tangent of 0.02. In the simulation, the copper was treated as a Drude model with plasma frequency of 1.12 × 1016 rad s−1 and collision frequency of 8.67 × 1013 rad s−1, respectively.30 Moreover, the LC material was assumed to be S200, and its permittivity in the unbiased state (ε⊥) and fully biased state (ε∥) were set to be 2.47 and 3.06, respectively.31
| Parameters | a | R | r | b | d | s | Hq1 | Hq2 | HLC |
| Values (μm) | 410 | 190 | 155 | 20 | 20 | 12 | 500 | 1000 | 45 |
The numerical time domain FDTD method is used to perform simulations, where the unit cell boundary conditions are applied in x and y directions. Since the proposed absorber has similar absorption characteristics for TE- or TM-polarized normal incident wave, the electromagnetic responses for the TE-polarized incident wave with electric field parallel to the x-axis are firstly investigated under the normal incidence.
The absorptivity of an absorber can be calculated by
| A = 1 − |S11|2 − |S21|2 | (1) |
The simulated absorption spectrum of the proposed MA in the unbiased state (εLC = 2.47) is shown in Fig. 2. In the simulation, the loss tangent of LC layer is set to be 0.02. The figure shows that two distinct absorption peaks, named mode f1 and f2, are located at 271 and 304.8 GHz with absorptivity of 97.1% and 95.3%, respectively. The simulation result provides a foundation for tuning of dual band absorption peaks with high absorptivity.
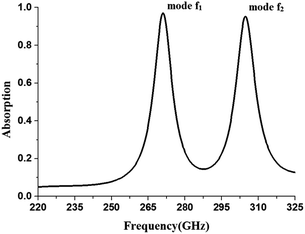 | ||
| Fig. 2 Absorption spectrum of the proposed metamaterial absorber with permittivity of LC εLC = 2.47 under the normal incidence of TE-polarized wave. | ||
3. Simulated results and discussions
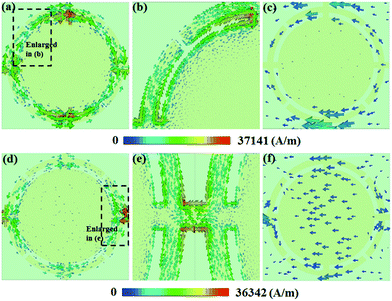
In order to demonstrate the intrinsic mechanism of the absorber, the surface current distributions on the copper pattern and the copper ground plane under TE-polarization are calculated corresponding to the two absorption peaks shown in Fig. 2. The simulated results are illustrated in Fig. 3.For mode f1, the surface current on the copper pattern mainly concentrates in the outer ring area as shown in Fig. 3(a). Moreover, the enlarged view shown in Fig. 3(b) indicates that an LC resonance mode is excited in each split-ring resonant area. Meanwhile, the surface current on the metal ground plane shown in Fig. 3(c) is reversed to that in Fig. 3(a), as the magnetic resonance is excited by the circulating currents between the two metallic layers. For mode f2, the surface current on the patterned layer is concentrated in the connecting bars between the two adjacent units, which excites the dipole resonances as shown in Fig. 3(d) and (e). Similarly, the magnetic response for the second resonance mode is also excited by the reversed surface current between the patterned and the ground layers.
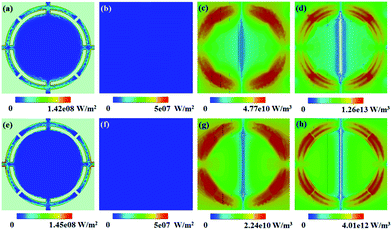
In order to further explore the absorption mechanism, the ohmic losses at the copper pattern layer and copper background, and the dielectric power loss densities in the quartz plate and the LC layer for the two peak absorption frequencies are calculated and the obtained results are shown in Fig. 4. It can be seen from the figure that the strength of the electric field determines the dielectric losses of the absorber in each dielectric layer, while the ohmic losses at the patterned copper layer are depended on the surface currents. Furthermore, it is observed that the most of the power losses is concentrated in the LC layer, where it contributes 67.2% and 69.9% of total losses for the two absorption peaks, respectively.
It is well known that the reflection depends on impedance, and is defined by:
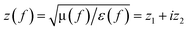 | (2) |
The retrieved impedance can be calculated by:32
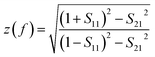 | (3) |
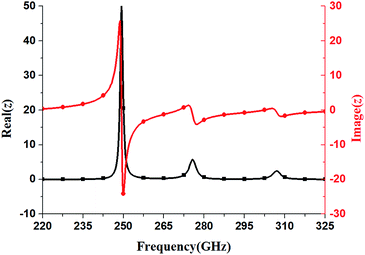
The normalized input impedance is illustrated in Fig. 5. It can be seen that the normalized input impedances at the peak absorption frequencies of 271 and 304.8 GHz are 0.881 + 0.177i and 0.946 + 0.383i, respectively. Furthermore, the normalized input impedance is approximately equal to the free-space impedance at each peak absorption frequency, wherein a little reflection from the structure is introduced. Additionally, the transmission from the structure is also zero due to the existence of the metal ground plane. Consequently, the incident wave is trapped in the structure and the energy is dissipated through dielectric and ohmic losses.
Now let's focus on the frequency tunability of the proposed dual band metamaterial absorber. As mentioned above, the measured permittivity of LC material S200 in the unbiased state (ε⊥) and the fully biased state (ε∥) were 2.47 and 3.06, respectively. In this paper, the LC is treated as a homogenous isotropic material and the effective index of the aligned nematic LC is given by33
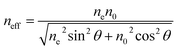 | (4) |
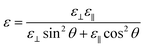 | (5) |
It can be concluded from eqn (5) that the LC permittivity is equal to ε⊥ for the initial case (θ = 0°), where the direction of the electric field vector in the LC layer is perpendicular to the LC molecular direction. With the increase of the bias voltage applied on the LC layer, the reorientation angle of the LC molecule gradually shifts towards the z axis and finally becomes parallel to the z axis (θ = 90°), as the LC permittivity increases to ε∥ at the fully-biased state.
The absorption spectra under the TE-polarized normal incidence excitation for the LC director angle values of θ = 0°, 30°, 45°, 60°, and 90° (corresponding to the dielectric constants of liquid crystal of εLC = 2.47, 2.595, 2.734, 2.888 and 3.06) are calculated and shown in Fig. 6. The spectra demonstrate the tunable performance of the proposed LC-based dual band absorber.
Fig. 6 shows two absorption peaks located at 271 and 304.8 GHz, for the initial alignment with LC molecular director parallel to the surface of the quartz. As the LC molecule is re-orientated from 0° to 90°, the two absorption peaks shift downwards to 261.5 and 290.8 GHz, accounting for 9.5 and 14 GHz frequency variation, respectively. From Fig. 6, the frequency tunability (fmod = Δf/fmax) for the two resonant modes is 3.51% and 4.59%, respectively. Moreover, the frequency tunability of mode f2 is relatively higher than mode f1, which can be attributed to the higher sensitivity to substrate material of dipole resonant mode.
In order to validate the performance of the proposed absorber under different polarization angles, the responses for the polarization angle variation, φ, under normal incidences are calculated and shown in Fig. 7. The figure shows that the proposed absorber is independent of wave polarization under normal incidence due to the structure symmetry.
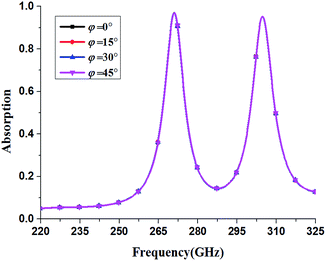 | ||
| Fig. 7 Absorption spectra for different polarization angles under the normal incident wave. The electric field is changed by an angle φ with respect to x-direction. | ||
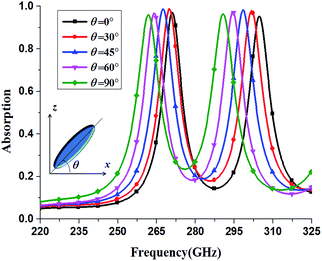
The proposed structure is further studied theoretically under oblique incidence. For TM-polarized incident wave, the proposed structure maintains absorption above 0.75 up to 60° incident angle for both absorption peaks as shown in Fig. 8(a). With the increase of incident angle, the resonance frequency nearly remains the same for mode f1. However, for mode f2, the resonance frequency shows a blue shift. For TE-polarized incident wave, the proposed structure maintains absorption above 0.8 up to 30° of oblique incidence for both f1 and f2 modes. Moreover, from Fig. 8(b), it is interesting that with the increase of incident angle, more resonance modes with high resonant intensity are excited, providing a characteristic of multi-band absorption with high absorptivity over wide incident angles.
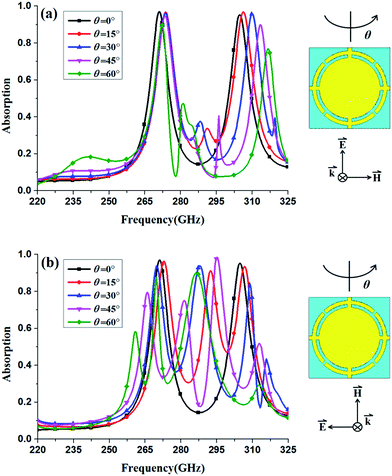 | ||
| Fig. 8 Absorption spectra of the proposed metamaterial absorber for different incident angles: (a) for TM-polarized incident wave and (b) for TE-polarized incident wave. | ||
4. Experimental verification
In order to experimentally verify the proposed absorber, an array of overall size of 2 cm × 2 cm, with 40 × 40 unit cells, was fabricated. The fabricated sample and the measurement setup are shown in Fig. 9. The setup contained an antenna connected to the Agilent N5224A vector network analyser via VNA extender VDI VNAX592, which was used for frequency range of 220–325 GHz. Moreover, a pair of THz lens were utilized to focus the THz beam, and an Agilent 33220A function signal generator was employed to produce the bias electronic field.Fig. 10 illustrates the measured absorptions of the fabricated sample at unbiased and biased states under TM-polarization. The differences between the measured and the simulated results for the resonant frequencies and the absorptions are mainly attributed to the inaccurate size of the sample due to the fabrication precision and the inaccuracy of the measurement.
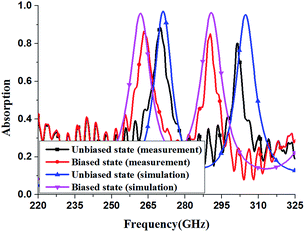 | ||
| Fig. 10 Simulated and measured absorption spectra at unbiased and biased states under the normal incidence of TE-polarized wave. | ||
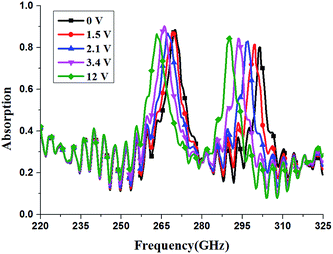
The frequency tunability of the absorber was obtained by measuring the absorption at different bias voltages as shown in Fig. 11. For mode f1, as the bias voltage increases from 0 to 12 V, the resonance frequency shifts downwards from 269.8 to 263.2 GHz, with a frequency tunability of 2.45%. For mode f2, a frequency tunability of 3.65% is achieved with the absorption frequency redshifts from 301.4 to 290.4 GHz. The measured frequency tunability of mode f2 is stronger than that of mode f1, which is in agreement with the simulated results. However, it should be noticed that the measured frequency tunability is much lower compared to the simulated results with a frequency tunability of 3.51% and 4.59% for mode f1 and f2, respectively. This is due to the fact that in experiment the liquid crystal molecules lying beyond the patterned electrode cannot be efficiently re-orientated. Moreover, the liquid crystal cells lying under the patterned electrode cannot be fully re-orientated.34 As a result, the measured performance of the absorber is worse than simulated results.
5. Conclusions
A THz tunable dual-band metamaterial absorber based on the liquid crystal is proposed in this paper. Based on a new metamaterial unit cell, the proposed structure experimentally provides two distinct absorption peaks at 269.8 and 301.4 GHz with absorptivity of 88.4% and 80.1%, respectively, when no bias voltage is applied. The absorption mechanism of the proposed structure is comprehensively investigated by the surface current distributions and the power loss distributions. The simulated results have demonstrated that the proposed absorber is polarization independent and is capable of providing high dual-band absorption for a wide range of incident angles under oblique incidence. The most important feature of the proposed absorber is that the dual-band absorption can be electrically tuned by simply adjusting the bias voltage of liquid crystal cavity from 0 to 12 V. Furthermore, the frequency tunability of 2.45% and 3.65% for the first and the second absorption peak, respectively, is experimentally demonstrated. The features of dual-band absorption and electric tunability validates that the proposed metamaterial absorber has significant potential applications in THz regime.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (grant no. 51607050) and Fundamental Research Funds for the Central Universities of China (grant no. JD2017JGPY0006).References
- M. Tonouchi, Cutting-edge terahertz technology, Nat. Photonics, 2007, 1, 97–105 CrossRef CAS.
- J. F. O'Hara, W. Withayachumnankul and I. Al-Naib, A review on thin-film sensing with terahertz waves, J. Infrared Millim. Terahertz Waves, 2012, 33, 245–291 CrossRef.
- M. Hangyo, Development and future prospects of terahertz technology, Jpn. J. Appl. Phys., 2015, 54, 120101 CrossRef.
- R. Filter, M. Farhat, M. Steglich, R. Alaee, C. Rockstuhl and F. Lederer, Tunable graphene antennas for selective enhancement of THz-emission, Opt. Express, 2013, 21, 3737–3745 CrossRef CAS PubMed.
- V. A. Trofimov and S. A. Varentsova, An effective method for substance detection using the broad spectrum THz signal: a ' terahertz nose', Sensors, 2015, 15, 12103–12132 CrossRef CAS PubMed.
- P. U. Jepsen, D. G. Cooke and M. Koch, Terahertz spectroscopy and imaging - Modern techniques and applications, Laser Photonics Rev., 2011, 5, 124–166 CrossRef CAS.
- N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith and W. J. Padilla, Perfect metamaterial absorber, Phys. Rev. Lett., 2008, 100, 207402 CrossRef CAS PubMed.
- D. Hu, H. Y. Wang and Q. F. Zhu, Design of six-band terahertz perfect absorber using a simple U-shaped closed-ring resonator, IEEE Photonics J., 2016, 8, 5500608 Search PubMed.
- B. X. Wang, G. Z. Wang, L. L. Wang and X. Zhai, Design of a five-band terahertz absorber based on three nested split-ring resonators, IEEE Photonics Technol. Lett., 2016, 28, 307–310 CrossRef.
- Y. J. Yoo, Y. J. Kim, J. S. Hwang, J. Y. Rhee, K. W. Kim, Y. H. Kim, H. Cheong, L. Y. Chen and Y. P. Lee, Triple-band perfect metamaterial absorption, based on single cut-wire bar, Appl. Phys. Lett., 2015, 106, 071105 CrossRef.
- F. R. Hu, Y. X. Qian, Z. Li, J. H. Niu, K. Nie, X. M. Xiong, W. T. Zhang and Z. Y. Peng, Design of a tunable terahertz narrow band metamaterial absorber based on an electrostatically actuated MEMS cantilever and split ring resonator array, J. Opt., 2013, 15, 055101 CrossRef.
- H. Yuan, B. O. Zhu and Y. Feng, A frequency and bandwidth tunable metamaterial absorber in x-band, J. Appl. Phys., 2015, 117, 173103 CrossRef.
- G. Yao, F. R. Ling, J. Yue, C. Y. Luo, J. Ji and J. Q. Yao, Dual-band tunable perfect metamaterial absorber in the THz range, Opt. Express, 2016, 24, 1518–1527 CrossRef CAS PubMed.
- G. S. Deng, P. Chen, J. Yang, Z. P. Yin and L. Z. Qiu, Graphene-based tunable polarization sensitive terahertz metamaterial absorber, Opt. Commun., 2016, 380, 101–107 CrossRef CAS.
- X. Y. He, P. Q. Gao and W. Z. Shi, A further comparison of graphene and thin metal layers for plasmonics, Nanoscale, 2016, 8, 10388–10397 RSC.
- X. Y. He, F. T. Lin, F. Liu and W. Z. Shi, Terahertz tunable graphene Fano resonance, Nanotechnology, 2016, 27, 485202 CrossRef PubMed.
- X. Y. He, Tunable terahertz graphene metamaterials, Carbon, 2015, 82, 229–237 CrossRef CAS.
- C. Y. Luo, D. Li, Q. Luo, J. Yue, P. Gao, J. Q. Yao and F. R. Ling, Design of a tunable multiband terahertz waves absorber, J. Alloys Compd., 2015, 652, 18–24 CrossRef CAS.
- B. X. Wang, X. Zhai, G. Z. Wang, W. Q. Huang and L. L. Wang, Frequency tunable metamaterial absorber at deep-subwavelength scale, Opt. Mater. Express, 2015, 5, 227–235 CrossRef.
- M. Desouky, A. M. Mahmoud and M. A. Swillam, Tunable mid IR focusing in InAs based semiconductor hyperbolic metamaterial, Sci. Rep., 2017, 7, 15312 CrossRef PubMed.
- Y. K. Bai, R. X. Wei, X. R. Ma and Y. Ma, Tunable metamaterial terahertz band-stop filter based on InSb, J. Infrared, Millimeter, Terahertz Waves, 2017, 36, 261–265 Search PubMed.
- S. Kalhor, M. Ghanaatshoar, T. Kashiwagi, K. Kadowaki, M. J. Kelly and K. Delfanazari, Thermal tuning of high-Tc superconducting Bi2Sr2CaCu2O8+δ terahertz metamaterial, IEEE Photonics J., 2017, 9, 1400308 Search PubMed.
- R. Singh, J. Xiong, A. K. Azad, H. Yang, S. A. Trugman, Q. X. Jia, A. J. Taylor and H. T. Chen, Optical tuning and ultrafast dynamics of high-temperature superconducting terahertz metamaterials, Nanophotonics, 2012, 1, 117–123 CrossRef CAS.
- Q. Zhao, L. Kang, B. Du, B. Li, J. Zhou, H. Tang, X. Liang and B. Z. Zhang, Electrically tunable negative permeability metamaterials based on nematic liquid crystals, Appl. Phys. Lett., 2007, 90, 011112 CrossRef.
- Q. K. Liu, Y. X. Cui, D. Gardner, X. Li, S. L. He and I. I. Smalyukh, Self-alignment of plasmonic gold nanorods in reconfigurable anisotropic fluids for tunable bulk metamaterial Applications, Nano Lett., 2010, 10, 1347–1353 CrossRef CAS PubMed.
- Z. X. Su, J. B. Yin and X. P. Zhao, Soft and broadband infrared metamaterial absorber based on gold nanorod/liquid crystal hybrid with tunable total absorption, Sci. Rep., 2015, 5, 16698 CrossRef CAS PubMed.
- D. Shrekenhamer, W. C. Chen and W. J. Padilla, liquid crystal tunable metamaterial perfect absorber, Phys. Rev. Lett., 2013, 110, 177403 CrossRef PubMed.
- G. Isić, B. Vasić, D. C. Zografopoulos, R. Beccherelli and R. Gajić, Electrically tunablecritically coupled terahertz metamaterial absorber based on nematic liquid crystals, Phys. Rev. Appl., 2015, 3, 064007 CrossRef.
- L. Wang, S. J. Ge, Z. X. Chen, W. Hu and Y. Q. Lu, Bridging the terahertz near-field and far-field observations of liquid crystal based metamaterial absorbers, Chin. Phys. B, 2016, 25, 094222 CrossRef.
- M. A. Ordal, R. J. Bell, R. W. Alexander, L. L. Long and M. R. Querry, Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W, Appl. Opt., 1985, 24, 4493–4499 CrossRef CAS PubMed.
- H. B. Lu, S. C. Jing, T. Y. Xia, J. Yang, Z. P. Yin and G. S. Deng, Measurement of LC dielectric constant at lower terahertz region based on metamaterial absorber, IEICE Electronics Express, 2017, 14, 20170469 CrossRef.
- D. Smith, D. Vier, Th. Koschny, G. Matmon and C. Soukoulis, Electromagnetic parameter retrieval from inhomogeneous metamaterials, Phys. Rev. E, 2005, 71, 036617 CrossRef CAS PubMed.
- I. C. Khoo, Liquid Crystal: Physical Properties and Nonlinear Optical Phenomena, Wiley, USA, 1995 Search PubMed.
- S. Bildik, S. Dieter, C. Fritzsch, W. Menzel and R. Jakoby, Reconfigurable folded reflectarray antenna based upon liquid crystal technology, IEEE Trans. Antennas Propag., 2015, 63, 122–132 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |