Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structure, polaron formation, and functional properties in transition-metal tungstates
Khang Hoang a,
Myungkeun Ohb and
Yongki Choi
a,
Myungkeun Ohb and
Yongki Choi *ab
*ab
aDepartment of Physics, North Dakota State University, Fargo, North Dakota 58108, USA. E-mail: yongki.choi@ndsu.edu
bMaterials and Nanotechnology Program, North Dakota State University, Fargo, North Dakota 58105, USA
First published on 23rd January 2018
Abstract
Transition-metal tungstates MWO4 (M = Co, Ni, Cu, Zn) have applications in many areas, including supercapacitors. A good understanding of the electronic structure is essential to understanding their functional properties. Here, we report a first-principles study of the materials using hybrid density-functional calculations. The electronic structure is analyzed with a focus on the nature of the electronic states near the band edges. We find that hole polarons can form at the Co lattice site in CoWO4 and the O site in NiWO4, CuWO4, and ZnWO4, resulting in the formation of Co3+ in the former and O− in the latter. The electrochemical activity observed in certain tungstate compounds, but not in others, appears to be related to the ability to form hole polarons on the transition-metal ions. The formation energy and migration barrier of the hole polaron in CoWO4 are also calculated and the results are employed to understand the reported p-type conductivity.
1 Introduction
Transition-metal tungstates MWO4 (M = Co, Ni, Cu, Zn) have been of interest for a wide range of applications, including supercapacitors,1,2 photocatalysts,3–5 scintillators,6 and sensors.7 The compounds possess the monoclinic (P2/c) wolframite-type structure,8–10 see Fig. 1, except CuWO4 whose symmetry is triclinically distorted with the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) due to the Jahn–Teller effect associated with the Cu2+ ion.10 CoWO4, for example, were shown to be a promising supercapacitor electrode material,1 suggesting that the Co3+/2+ redox couple may be active. Bharati et al.11 also reported that CoWO4 is a “p-type semiconductor” and its electronic conduction is likely to occur through hopping of small polarons. ZnWO4, on the other hand, was found not to show any electroactivity when used as a pseudocapacitive electrode material.12 As shown in previous studies, electronic structure and polaron formation can provide crucial information on the electrochemical properties of complex transition-metal oxides.13–15
due to the Jahn–Teller effect associated with the Cu2+ ion.10 CoWO4, for example, were shown to be a promising supercapacitor electrode material,1 suggesting that the Co3+/2+ redox couple may be active. Bharati et al.11 also reported that CoWO4 is a “p-type semiconductor” and its electronic conduction is likely to occur through hopping of small polarons. ZnWO4, on the other hand, was found not to show any electroactivity when used as a pseudocapacitive electrode material.12 As shown in previous studies, electronic structure and polaron formation can provide crucial information on the electrochemical properties of complex transition-metal oxides.13–15
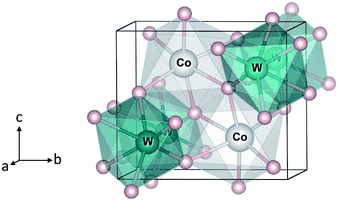 | ||
| Fig. 1 Crystal structure of monoclinic CoWO4. Large (gray) spheres are Co, medium (blue) spheres are W, and small (red) spheres are O. | ||
The electronic structure of the tungstates mentioned above has been investigated by several research groups using first-principles calculations based on density-functional theory (DFT) within the standard local-density or generalized gradient approximation and/or its extension DFT+U where U is the on-site Hubbard correction.16–19 The methods used in these previous studies are, however, often have limited predictive power because the electronic states in the materials (e.g., the transition-metal d and oxygen p states) are not treated on equal footing. Besides, to our knowledge, polaron formation in the compounds has not been studied. Recently, two transition-metal tungstates, FeWO4 and MnWO4, have been studied in detail and the results show that both hole and electron polarons can occur and participate in charge transport and electrochemical processes.15 It thus remains to be explored if polarons also form in the other tungstates.
We herein report a first-principles study of MWO4 (M = Co, Ni, Cu, Zn) using a hybrid DFT/Hartree–Fock method in which all electronic states in the materials are treated on equal footing. The focus of this work is on the electronic structure, particularly the nature of the electronic states near the band edges, in the different tungstate compounds, and the ability to stabilize an electron and/or hole polaron. We also explicitly investigate the formation of selected intrinsic point defects in CoWO4 as well as the migration of hole polarons and discuss its relevance to the observed p-type electronic conduction. The electronic structure of FeWO4 and MnWO4 is also reproduced and included for comparison.
2 Methods
The total-energy calculations are based on DFT, using the Heyd–Scuseria–Ernzerhof (HSE06) screened hybrid functional,20 the projector augmented wave (PAW) method,21 and a plane-wave basis set, as implemented in the Vienna Ab Initio Simulation Package (VASP).22 The Hartree–Fock mixing parameter and the screening length are set to their standard values of 0.25 and 10 Å, respectively. We use the standard PAW potentials in the VASP database which treat Mn 3d6 4s1, Fe 3d7 4s1, Co 3d8 4s1, Ni 3d9 4s1, Cu 3d10 4p1, Zn 3d10 4p2, W 6s2 5d4, and O 2s2 2p4 explicitly as valence electrons and the rest as core electrons. The plane-wave basis-set cutoff is set to 500 eV and spin polarization is included. The calculations of bulk properties in MWO4 (two formula units per unit cell) are carried out using a 5 × 4 × 5 k-point mesh. Point defects in CoWO4 are modelled using 2 × 2 × 2 (96-atom) monoclinic supercells. Integrations over the supercell Brillouin zone is carried out using the Γ point. In all calculations, structural relaxations are performed with the HSE06 functional and the force threshold is chosen to be 0.01 eV Å−1.The formation energy of a cobalt vacancy (VCo) with charge state q in CoWO4 is defined as
| Ef(VCoq) = Etot(VCoq) − Etot(bulk) + μCo + q(Ev + μe) + Δq, | (1) |
3 Results and discussion
3.1 Atomic and electronic structure
We start with the bulk properties of the tungstates. Fig. 1 shows the relaxed structure of monoclinic CoWO4; the structure of NiWO4 and ZnWO4 is similar. The lattice parameters of MWO4 are listed in Table 1. We find that the calculated values are in excellent agreement with the reported experimental ones.8–10| Experimental | Calculated | ||
|---|---|---|---|
| CoWO4 | a = 4.659 Å | Ref. 8 | a = 4.659 Å |
| b = 5.667 Å | b = 5.716 Å | ||
| c = 4.940 Å | c = 4.936 Å | ||
| β = 89.94° | β = 89.95° | ||
| NiWO4 | a = 4.599 Å | Ref. 9 | a = 4.612 Å |
| b = 5.660 Å | b = 5.675 Å | ||
| c = 4.906 Å | c = 4.906 Å | ||
| β = 90.03° | β = 89.92° | ||
| CuWO4 | a = 4.7095 Å | Ref. 10 | a = 4.772 Å |
| b = 5.8452 Å | b = 5.935 Å | ||
| c = 4.8885 Å | c = 4.871 Å | ||
| α = 88.353° | α = 87.70° | ||
| β = 92.508° | β = 93.27° | ||
| γ = 97.205° | γ = 98.89° | ||
| ZnWO4 | a = 4.6926 Å | Ref. 10 | a = 4.702 Å |
| b = 5.7213 Å | b = 5.755 Å | ||
| c = 4.9281 Å | c = 4.917 Å | ||
| β = 90.632° | β = 90.70° |
In CoWO4, Co is found to be stable as high-spin Co2+ with a magnetic moment of 2.73 μB; W is stable as W6+. Our calculations using 2 × 1 × 1 supercells of the unit cell shown in Fig. 1, similar to the 2 × 1 × 1 models for FeWO4 and MnWO4 described in ref. 15, indicate that the ferromagnetic (FM) and antiferromagnetic (AF) spin configurations are degenerate in energy.
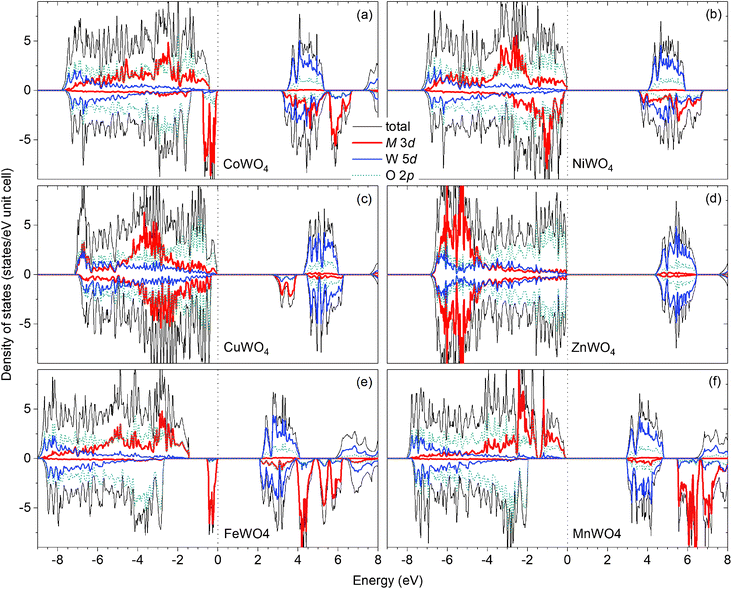
Fig. 2(a) shows the total and projected electronic density of states of CoWO4. Focusing on the electronic structure near the band edges, we find that the VBM is predominantly composed of the Co 3d states, whereas the conduction-band minimum (CBM) is predominantly the W 5d and Co 3d states. A detailed analysis of the electronic structure shows that each of the two Co atoms in the unit cell accounts for 39% of the electronic states at the VBM; at the CBM, each W accounts for 32% and each Co contributes 15%. The calculated band gap is 3.10 eV, a direct gap at the Γ point. This value is very close to the experimental value 2.80 eV estimated by Bharati et al.,11 obtained by assuming that the electronic conduction above 750 K is through band-like carriers.
As for NiWO4, Ni is stable as Ni2+ with a calculated magnetic moment of 1.74 μB. The FM and AF spin configurations NiWO4 are almost degenerate in energy; the FM configuration is higher in energy than the AF configuration with parallel spins within the Ni zigzag chains along the c axis but with adjacent chains coupled antiferromagnetically by only 8 meV per formula unit. Fig. 2(b) shows the electronic structure of NiWO4. The VBM of the compound is predominantly composed of the Ni 3d states and the O 2p states; each Ni atom in the unit cell accounts for 16% of the electronic states at the VBM and some O atoms contribute up to 10% each. The CBM, on the other hand, is predominantly composed of the W 5d states and the Ni 3d states; each W atom accounts for 28% and each Ni atom contributes 20%. NiWO4 has an indirect band gap of 3.41 eV. Experimentally, the compound was reported to have an optical band gap of 3.2 ± 0.2 eV.9
In CuWO4, Cu is found to be stable as Cu2+ with a magnetic moment of 0.76 μB. The electronic structure of the compound is shown in Fig. 2(c). We find that the VBM is predominantly composed of the O 2p states and some contribution from the Cu 3d states; specifically, the electronic states at the VBM have 12% from each Cu atom and some O atoms contributes up to 13% each. The CBM is, on the other hand, predominantly the Cu 3d states (29% from each Cu atom) and the W 5d states (17% from each W atom). CuWO4 is found to have an indirect band gap of 2.71 eV, comparable to the reported experimental value 2.3 eV.4
Finally, Zn in ZnWO4 is found to be stable as Zn2+ with a zero magnetic moment. Fig. 2(d) shows the electronic structure of ZnWO4. We find that the VBM is predominantly composed of the O 2ps states; some O atoms contribute up to 20% to the electronic states at the VBM. The CBM is, on the other hand, predominantly the W 5d states (each W atom contributes 40%) and there is a small contribution from the Zn 3d states (5% is from each Zn atom). ZnWO4 has a calculated (direct) band gap of 4.30 eV, comparable to the reported experimental value 3.98 eV.16
For comparison, the results for FeWO4 and MnWO4 are also included; see Fig. 2(e and f). As also reported ref. 15, the VBM of FeWO4 is predominantly composed of the Fe 3d states with each Fe atom accounts for 46% of the electronic states at the VBM; the CBM is predominantly the W 5d states with each W atom contributes 40%. The VBM of MnWO4 is, on the other hand, predominantly the Mn 3d states with each Mn atom accounts for 27%; the CBM is predominantly composed of the W 5d states with each W atom accounts for 39% of the states at the CBM.
The nature of the electronic structure near the band edges is thus different for different tungstates in the series, as expected. More importantly, our analysis provides a quantitative understanding of electronic structure formation. In the next section, we will examine the implications on defect formation in the materials, particularly on possible formation of polarons.
3.2 Hole polaron formation
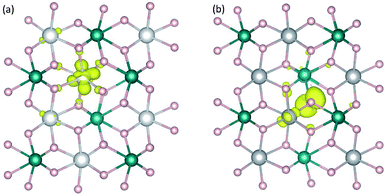
Calculations for polarons are carried out using the supercell models described in Section 2. For each compound, the creation of a free hole polaron involves removing one electron from the supercell, specifically from the highest occupied state; the creation of a free electron polaron, on the other hand, involves adding one electron to the supercell, i.e., to the lowest unoccupied state. The procedures are performed via controlling the total number of valence electrons in the system. The actual occupation of the removed or added electron is checked by examining changes in the charge density, local lattice environment, and magnetic moment. The removal and addition of electrons can be employed to represent oxidation and reduction processes, respectively.13–15We find that the removal of an electron from the CoWO4 supercell results in a high-spin Co3+ with a calculated magnetic moment of 3.16 μB, which can be regarded as a highly localized electron hole at one of the Co lattice sites. The local lattice environment is slightly distorted in the presence of the hole; the average Co3+–O bond length is 2.02 Å, compared to 2.10 Å of the Co–O bonds in the bulk. Since the lattice distortion is mainly within the first nearest neighbors of the hole, the localized hole can be regarded as a small hole polaron, hereafter denoted as ηCo+; see Fig. 3(a). The self-trapping energy (EST), defined as the formation-energy difference between the free hole and the hole polaron, is calculated to be 0.32 eV for ηCo+. We note that the low-spin Co3+ (0 μB) solution is higher in energy than the high-spin configuration by 0.50 eV. The formation of the hole polaron ηCo+ in CoWO4 can be understood in terms of the electronic structure discussed earlier according to which the electron has to be removed from the Co 3d states; see also Fig. 2(a).
The removal of an electron from the NiWO4, CuWO4, or ZnWO4 supercell, on the other hand, results in a highly localized electron hole at one of the O sites; i.e., one O2− is oxidized to O− with a magnetic moment of ∼0.7 μB. The local lattice environment is also distorted in the presence of this hole. O− can thus also be regarded as a small hole polaron, hereafter denoted as ηO+. Fig. 3(b) shows the charge density associated with ηO+ in NiWO4. The self-trapping energy is EST = 0.22 eV (in NiWO4), 0.05 eV (CuWO4), or 0.38 eV (ZnWO4). The very small EST value in the case of triclinic CuWO4 could be due to the Jahn–Teller distortion in the material's lattice environment. The main difference between these three tungstates and CoWO4 (as well as FeWO4 and MnWO4)15 is thus that the oxidation occurs on the transition metal in the latter whereas it can occur on the oxygen in the former. The results are therefore consistent with the electronic structure presented earlier in which the VBM of NiWO4, CuWO4, and ZnWO4 is composed mainly of the O 2p states. We note that, though a free hole polaron associated with Ni3+ cannot be stabilized in bulk NiWO4, it remains to be explored if it can occur in the presence of other defects or at/near the surface or interface where the lattice environment is different from that in the bulk.
Regarding electron polarons, we find that the addition of an electron to MWO4 (M = Co, Ni, Cu, Zn) results in an electron that is delocalized all over the supercell. The electron polaron associated with the reduction of W6+ to W5+ is thus not stable in these compounds, unlike in FeWO4 and MnWO4.15 The difference can be traced back to the electronic structure discussed earlier: there is a strong mixing between the M 3d and W 5d states at the CBM of MWO4 (M = Co, Ni, Cu, Zn). As a result, an electron when added to the materials (e.g., during a reduction process) cannot be localized on any particular W ion. In the case of MWO4 (M = Fe, Mn), the CBM is predominantly composed of the W 5d states, making it possible for the added electron to be localized.15
Finally, as mentioned earlier, some transition-metal tungstates such as CoWO4 (as well as FeWO4 and MnWO4) are electroactive,1,12,25 whereas other tungstates such as ZnWO4 are not active,12 when used as pseudocapacitive electrode materials. This can be ascribed to the fact that hole polarons associated with the transition metal can form in the former but not in the latter; i.e., the transition-metal (M) redox couple is active in MWO4 (M = Co, Fe, Mn). Given the interplay between the electronic structure and polaron formation, our work thus illustrates how a material's functional properties can be related to its electronic structure.
3.3 Electronic conduction in CoWO4
Let us now discuss in more detail the case of CoWO4 where the hole polaron ηCo+ is found to be stable. This defect can occur in the material in combination with other intrinsic point defects. Based on the results previously reported for FeWO4 and MnWO4,15 we consider only cobalt vacancies (VCo) since VCo2− (i.e., the removal of an Co2+ ion) is likely the lowest-energy negatively charged intrinsic point defect. Fig. 4 shows the calculated formation energies of ηCo+ and VCo (in charge states 2−, −, and 0). The slope in the energy plots indicates the charge state: positively (negatively) charged defects have positive (negative) slopes. The formation energies are obtained by assuming that CoWO4 is in equilibrium with WO3 (often used as one of the reactants in the synthesis of CoWO4) and air at 900 °C (the conditions under which the material is prepared).17 We note that the q = −1 and 0 charge states of VCo, nominally denoted as VCo− and VCo0, are not really stable; VCo− (V0Co) is, in fact, a defect complex of VCo2− and one (two) ηCo+.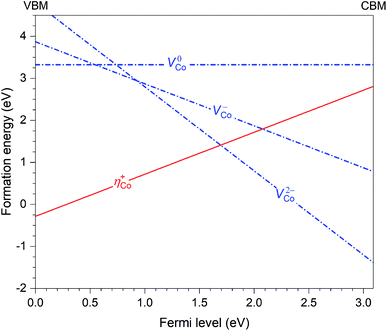 | ||
| Fig. 4 Formation energies of the hole polaron (ηCo+) and Co vacancies (VCo) in CoWO4, plotted as a function of Fermi level from the valence-band maximum (VBM) to the conduction-band minimum (CBM). | ||
Since ηCo+ and VCo2− are the dominant intrinsic point defects in the material, assuming the absence of any lower-energy negatively charged intrinsic defects or impurities, they determine the position of the Fermi level, which is at μinte = 1.67 eV, where charge neutrality is maintained; see Fig. 4. At this Fermi-level position, the formation energy of the two defects is 1.41 eV. We also estimate the migration barrier (Em) of the hole polaron, using the method as described in ref. 15 and references therein, and find that Em = 0.29 eV along the zigzag metal chain (i.e., c axis). For comparison, the migration barrier was reported to be 0.14 eV for ηFe+ in FeWO4 or 0.28 eV for ηMn+ in MnWO4.15
Given the low migration barrier, ηCo+ can participate in electronic transport that results in the p-type conductivity as observed in experiments.11 Bharati et al. reported that the activation energy in the extrinsic region (<750 K) is Ea = 0.64 eV, whereas Ea = 1.40 eV in the intrinsic region (>750 K). As discussed in detail in ref. 15 and 26, the lower limit of the activation energy is Em and the upper limit is Ef + Em. The calculated Em is thus lower than the experimental Ea in the extrinsic region, as expected. In the intrinsic region, our calculations give Ea = 1.70 eV. Experimentally, Bharati et al. argued that the conduction is band-type with an activation energy of 1.40 eV;11 however, given that our estimated activation energy is comparable, the conduction may actually still involve hopping of the small hole polarons ηCo+.
4 Summary
A hybrid density-functional study of the electronic structure and polaron formation has been carried out for transition-metal tungstates. The calculated lattice parameters and band gaps are in good agreement with experiments. The nature of the electronic structure at the valence-band top in CoWO4 allows for the formation of hole polarons (Co3+) at the transition metal site and hence active (Co3+/2+) redox couples, similar to what was reported for FeWO4 and MnWO4, whereas in NiWO4, CuWO4, and ZnWO4 hole polarons (O−) can be stabilized at the oxygen site. Electron polarons at the W site cannot be stabilized in MWO4 (M = Co, Ni, Cu, Zn), unlike in FeWO4 and MnWO4 where the electron polarons were reported to be stable. The difference between the tungstate compounds can be understood in terms of the calculated electronic structure. Finally, we find that hole polarons are responsible for the observed p-type conductivity in CoWO4.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported financially by the National Institute of General Medical Sciences of the National Institute of Health under Award No. R15GM122063. The calculations were carried out using computing resources at the Center for Computationally Assisted Science and Technology at North Dakota State University.References
- X. Xing, Y. Gui, G. Zhang and C. Song, Electrochim. Acta, 2015, 157, 15–22 CrossRef CAS.
- X. Xu, L. Pei, Y. Yang, J. Shen and M. Ye, J. Alloys Compd., 2016, 654, 23–31 CrossRef CAS.
- H. Jia, J. Stark, L. Q. Zhou, C. Ling, T. Sekito and Z. Markin, RSC Adv., 2012, 2, 10874–10881 RSC.
- C. R. Lhermitte and B. M. Bartlett, Acc. Chem. Res., 2016, 49, 1121–1129 CrossRef CAS PubMed.
- C. Zhang, H. Zhang, K. Zhang, X. Li, Q. Leng and C. Hu, ACS Appl. Mater. Interfaces, 2014, 6, 14423–14432 CAS.
- V. B. Mikhailik, H. Kraus, G. Miller, M. S. Mykhaylyk and D. Wahl, J. Appl. Phys., 2005, 97, 083523 CrossRef.
- C. M. Gonzalez, X. Du, J. L. Dunford and M. L. Post, Sens. Actuators, B, 2012, 173, 169–176 CrossRef CAS.
- J. B. Forsyth and C. Wilkinson, J. Phys.: Condens. Matter, 1994, 6, 3073 CrossRef CAS.
- P. Parhi, T. N. Karthik and V. Manivannan, J. Alloys Compd., 2008, 465, 380–386 CrossRef CAS.
- P. F. Schofield, K. S. Knight, S. A. T. Redfern and G. Cressey, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 102–112 CrossRef.
- R. Bharati, R. A. Singh and B. M. Wanklyn, J. Mater. Sci., 1981, 16, 775–779 CrossRef CAS.
- N. Goubard-Bretesché, O. Crosnier, C. Payen, F. Favier and T. Brousse, Electrochem. Commun., 2015, 57, 61–64 CrossRef.
- K. Hoang and M. Johannes, Chem. Mater., 2011, 23, 3003–3013 CrossRef CAS.
- M. D. Johannes, K. Hoang, J. L. Allen and K. Gaskell, Phys. Rev. B, 2012, 85, 115106 CrossRef.
- K. Hoang, Phys. Rev. Materials, 2017, 1, 024603 CrossRef.
- J. Ruiz-Fuertes, S. López-Moreno, J. López-Solano, D. Errandonea, A. Segura, R. Lacomba-Perales, A. Muñoz, S. Radescu, P. Rodríguez-Hernández, M. Gospodinov, L. L. Nagornaya and C. Y. Tu, Phys. Rev. B, 2012, 86, 125202 CrossRef.
- S. Dey, R. A. Ricciardo, H. L. Cuthbert and P. M. Woodward, Inorg. Chem., 2014, 53, 4394–4399 CrossRef CAS PubMed.
- S. Rajagopal, V. L. Bekenev, D. Nataraj, D. Mangalaraj and O. Y. Khyzhun, J. Alloys Compd., 2010, 496, 61–68 CrossRef CAS.
- C. Ling, L. Q. Zhou and H. Jia, RSC Adv., 2014, 4, 24692–24697 RSC.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- F. Li, X. Xu, J. Huo and W. Wang, Mater. Chem. Phys., 2015, 167, 22–27 CrossRef CAS.
- K. Hoang and M. D. Johannes, J. Mater. Chem. A, 2014, 2, 5224–5235 CAS.
| This journal is © The Royal Society of Chemistry 2018 |