Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Performance enhancement by vertical morphology alteration of the active layer in organic solar cells
Sheng Bi ab,
Zhongliang Ouyangc,
Qinglei Guod and
Chengming Jiang*ab
ab,
Zhongliang Ouyangc,
Qinglei Guod and
Chengming Jiang*ab
aKey Laboratory for Precision and Non-traditional Machining Technology of the Ministry of Education, Dalian University of Technology, Dalian 116024, P. R. China. E-mail: jiangcm@dlut.edu.cn
bInstitute of Photoelectric Nanoscience and Nanotechnology, Dalian University of Technology, Dalian 116024, P. R. China
cDepartment of Electrical and Computer Engineering, Center for Materials for Information Technology, The University of Alabama, Box# 870209, Tuscaloosa, AL 35487, USA
dDepartment of Material Science and Engineering, Frederick Seitz Material Research Laboratory, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
First published on 9th February 2018
Abstract
Bulk heterojunction organic solar cells (OSCs) have attracted worldwide attention due to their great potential as a green, flexible and low-cost renewable energy source. A vertical configuration in the active layer due to the aggregation of donor and acceptor molecules and the influence on the performance of OSCs deserve an in-depth study. In this study, five different vertical configurations of the active layer in OSCs were built up. The absorbance and indexes of the devices were theoretically analyzed. It was found that the configuration with the donor and acceptor molecules distributed equally exhibits the highest power conversion efficiency, followed by the configuration with the donor closer to the anode and the acceptor closer to the cathode, which matches experimental results well. Further analyses present the recombination, resistance, quantum efficiency and current leakage of all the configurations. It is anticipated that our results will promote the better understanding and development of the OSC field.
Organic solar cells (OSCs) have attracted worldwide attention due to advantages such as their low cost, flexibility, solution processability and energy saving abilities.1–6 The blend of polymer and fullerene morphology as produced via solution processing is complicated with impure phases, broad distribution of domain sizes and a vertical composition gradient.7–11,48 Vertical phase separation has been found to be one of the most common phenomena that exists in all OSCs.12–16 The distribution of donor and acceptor molecules is one of the key factors that has a great effect on charge separation and transportation. It is well known that nanoscale interpenetrating donor–acceptor network increases interfacial area, thereby enhancing exciton dissociation at the polymer–fullerene interface.
Therefore, several studies have been conducted to investigate the parameters influencing the formation of vertical phase separation, such as blend composition, post annealing, solvent evaporation rate and substrate surface energy.17–23 There have been substantial efforts to understand the morphology evolution in polymer:fullerene molecules out of the polymer phase, diffusion of fullerene molecules and aggregation of fullerene molecules into cluster domains. There are only three chief vertical configurations that exist in OSCs from experiment based on the way donor and acceptor molecules aggregate. Different formation of the active layers results in distinct OSC performance. Nonetheless, the mechanism of vertical aggregation of donor and acceptor molecules and the function of vertical configurations are still under debate.
In this work, the P3HT/PCBM system is used as a benchmark to simulate five different vertical configurations, which cover all the possibilities of donor and acceptor aggregation in the OSC active layer. Calculation models were established to simulate Gradient I, Gradient II, Top-down, Bottom-up and Homogeneous structures which represent different polymer:fullerene aggregations in the active layer of a regular structure organic solar cells. In these models, we perform thorough, systematic research on the optical properties of active layers and indexes of the device in the structure. The performance of these five configurations is exhibited by analysis of the open circuit voltage (Voc), short circuit current (Isc), fill factor (FF) and power conversion efficiency (PCE). The five vertical configurations achieved in the manuscript cannot be easily fabricated experimentally. Our work gives a clear and in-depth view of devices with almost all possibilities of donor and acceptor aggregation. The experimental results act as proof of the calculations. This gives an easy and accurate reference for deciding the vertical formation in organic solar cells. We anticipate that our findings will catalyze the development of these devices and push efficiency improvements.
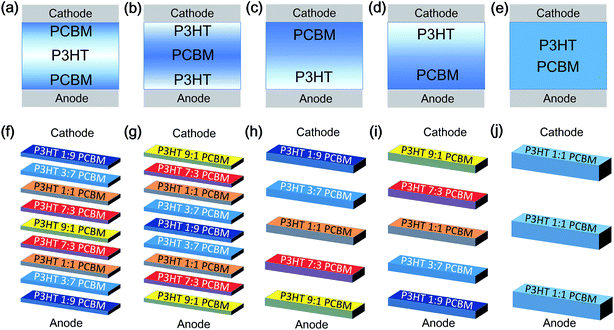
Semiconducting emissive thin film optical simulators (SETFOSs),5,24,25 developed by Fluxim AG, are employed to concretely reveal charge distribution inside PSCs. As schematically described in Fig. 1(a)–(e), it was found from experiment that the vertical configuration of the P3HT and PCBM blend layer can be separated into five different cases: P3HT or PCBM aggregates in the middle sandwiched by PCBM or P3HT aggregation, P3HT or PCBM configurations with Top-down aggregation, and P3HT/PCBM mixed uniformly. In order to simulate this experiment, models were built up to fit these five situations in Fig. 1(f)–(j), assuming that the top electrode is the cathode while the bottom electrode is the anode. The simulation was composed of five different concentration ratios of P3HT and PCBM layers: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9, 3
9, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7, 1
7, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 7
1, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 9
3 and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the sandwich structure, a P3HT 1
1. In the sandwich structure, a P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM layer was simulated at the top to represent dramatic PCBM aggregation. As the concentration of PCBM decreases and that of P3HT increases in the middle, P3HT 3
9 PCBM layer was simulated at the top to represent dramatic PCBM aggregation. As the concentration of PCBM decreases and that of P3HT increases in the middle, P3HT 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PCBM, P3HT 1
7 PCBM, P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM and P3HT 7
1 PCBM and P3HT 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 PCBM were used in series to serve as the gradient concentration of PCBM. P3HT 9
3 PCBM were used in series to serve as the gradient concentration of PCBM. P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM was introduced at the middle to represent a P3HT-rich layer, according to experiment. An increased concentration of PCBM, P3HT 7
1 PCBM was introduced at the middle to represent a P3HT-rich layer, according to experiment. An increased concentration of PCBM, P3HT 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 PCBM, P3HT 1
3 PCBM, P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM and P3HT 3
1 PCBM and P3HT 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PCBM was created subsequently, again with the concentration of P3HT decreased. Finally, P3HT 1
7 PCBM was created subsequently, again with the concentration of P3HT decreased. Finally, P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM was used as the PCBM-rich layer at the bottom. In the Gradient II configuration, the distribution of P3HT-rich and PCBM-rich is the opposite. P3HT 1
9 PCBM was used as the PCBM-rich layer at the bottom. In the Gradient II configuration, the distribution of P3HT-rich and PCBM-rich is the opposite. P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM is set up in the middle while P3HT 9
9 PCBM is set up in the middle while P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM is on both the top and bottom. The vertical configuration is dramatically changed in the Top-down configuration. At the very top, the P3HT 1
1 PCBM is on both the top and bottom. The vertical configuration is dramatically changed in the Top-down configuration. At the very top, the P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM layer is the PCBM-rich layer. The gradient concentration of P3HT 3
9 PCBM layer is the PCBM-rich layer. The gradient concentration of P3HT 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PCBM, P3HT 1
7 PCBM, P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM and P3HT 7
1 PCBM and P3HT 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 PCBM was subsequently created from top to bottom. P3HT 9
3 PCBM was subsequently created from top to bottom. P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM at the bottom demonstrated severe P3HT aggregation, and the distribution was the opposite in the Bottom-up profile, where the concentration of PCBM gradually increases from top to bottom while that of P3HT went in the other direction. A ratio of 1
1 PCBM at the bottom demonstrated severe P3HT aggregation, and the distribution was the opposite in the Bottom-up profile, where the concentration of PCBM gradually increases from top to bottom while that of P3HT went in the other direction. A ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 between P3HT and PCBM was used as the Homogeneous structure. It is worth noting that the total thicknesses of the active layer for all the structures is the same.
1 between P3HT and PCBM was used as the Homogeneous structure. It is worth noting that the total thicknesses of the active layer for all the structures is the same.
The simulation parameters used to reproduce the measurements are summarized in Table 1. The work function of the anode and cathode is 5.0 eV and 4.3 eV, respectively. The dielectric constant varies with the ratio between P3HT and PCBM. The dielectric constant for pure P3HT is 3 while that for pure PCBM is 3.9, and the dielectric constant changes linearly with the content.26–31 The parameters of mobility and Langevin recombination efficiency and optical charge generation efficiency for each P3HT/PCBM ratio are reasonably set. Since the acceptor (PCBM) carries holes, an increasing amount of acceptor leads to easier electron transportation, which results in the electron mobility improvement from P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM to P3HT 1
1 PCBM to P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM. The same goes for holes. The decreasing amount of donor (P3HT) produces the reduction in hole mobility, which matches the conclusions from experiment well.32,33 Also, according to previous experiments,34–37 the proper amount of P3HT and PCBM molecules (a fair amount of P3HT and PCBM) in the blend enormously stimulates charge separation and transportation and thus leads to a high optical charge generation efficiency and low Langevin recombination efficiency. In P3HT 9
9 PCBM. The same goes for holes. The decreasing amount of donor (P3HT) produces the reduction in hole mobility, which matches the conclusions from experiment well.32,33 Also, according to previous experiments,34–37 the proper amount of P3HT and PCBM molecules (a fair amount of P3HT and PCBM) in the blend enormously stimulates charge separation and transportation and thus leads to a high optical charge generation efficiency and low Langevin recombination efficiency. In P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM and P3HT 1
1 PCBM and P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM, high Langevin recombination efficiency originates from a smaller interface, where electron and hole pairs separate.34–37 And P3HT 9
9 PCBM, high Langevin recombination efficiency originates from a smaller interface, where electron and hole pairs separate.34–37 And P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM generates charge better than P3HT 1
1 PCBM generates charge better than P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM because of having more P3HT molecules helps with generation. The values for electron/hole mobility, Langevin recombination efficiency and optical charge generation efficiency were obtained from individual P3HT 9
9 PCBM because of having more P3HT molecules helps with generation. The values for electron/hole mobility, Langevin recombination efficiency and optical charge generation efficiency were obtained from individual P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM, P3HT 7
1 PCBM, P3HT 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 PCBM, P3HT 1
3 PCBM, P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM, P3HT 3
1 PCBM, P3HT 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PCBM and P3HT 1
7 PCBM and P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM OSC devices and match those from experimental results in the literature well.38–42 In the simulation of the multi-layer structure, these parameters were no longer changed.
9 PCBM OSC devices and match those from experimental results in the literature well.38–42 In the simulation of the multi-layer structure, these parameters were no longer changed.
| Parameter | P3HT 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM 1 PCBM |
P3HT 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 PCBM 3 PCBM |
P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM 1 PCBM |
P3HT 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 PCBM 7 PCBM |
P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 PCBM 9 PCBM |
|---|---|---|---|---|---|
| Electron mobility (m2 V−1 s−1) | 2 × 10−5 | 2 × 10−4 | 1 × 10−3 | 1.5 × 10−2 | 4 × 10−2 |
| Hole mobility (m2 V−1 s−1) | 7 × 10−3 | 2 × 10−3 | 7 × 10−4 | 2.5 × 10−4 | 5 × 10−5 |
| Langevin recombination efficiency | 0.05 | 0.15 | 0.2 | 0.12 | 0.05 |
| Optical charge generation efficiency | 0.2 | 0.6 | 0.8 | 0.52 | 0.1 |
| Dielectric constant | 3.09 | 3.27 | 3.45 | 3.63 | 3.81 |
For the experiment, P3HT (50 kDa) was commercially available from Rieke Metal Inc., and PCBM was purchased from NanoC and used as received. A 30 nm-thick poly(3,4-ethylenedioxy thiophene):poly(styrene sulfonate) (PEDOT:PSS) anode buffer layer, purchased from HC Stark, was spin-coated on top of the precleaned ITO substrate, which was treated with soap, acetone and isopropyl alcohol for 15 min and UV ozone for 20 min, then dried at 140 °C for 10 min in air. The P3HT–PCBM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.7 wt) was dissolved in 1,2-dichlorobenzene (DCB) and the resulting solution (concentration, 20 mg ml−1) was deposited at a speed of 900 rpm for 40 s on top of the PEDOT:PSS layer. Then the entire device was put in a vacuum oven and annealed at 140 °C for 20 min. An 80 nm Al layer was subsequently thermally evaporated at a pressure of 3 × 10−6 Torr. Current–voltage (I–V) characterization of the polymer photovoltaic cells was conducted using a computer-controlled measurement unit from Newport under AM1.5G illumination, 100 mW cm−2.
0.7 wt) was dissolved in 1,2-dichlorobenzene (DCB) and the resulting solution (concentration, 20 mg ml−1) was deposited at a speed of 900 rpm for 40 s on top of the PEDOT:PSS layer. Then the entire device was put in a vacuum oven and annealed at 140 °C for 20 min. An 80 nm Al layer was subsequently thermally evaporated at a pressure of 3 × 10−6 Torr. Current–voltage (I–V) characterization of the polymer photovoltaic cells was conducted using a computer-controlled measurement unit from Newport under AM1.5G illumination, 100 mW cm−2.
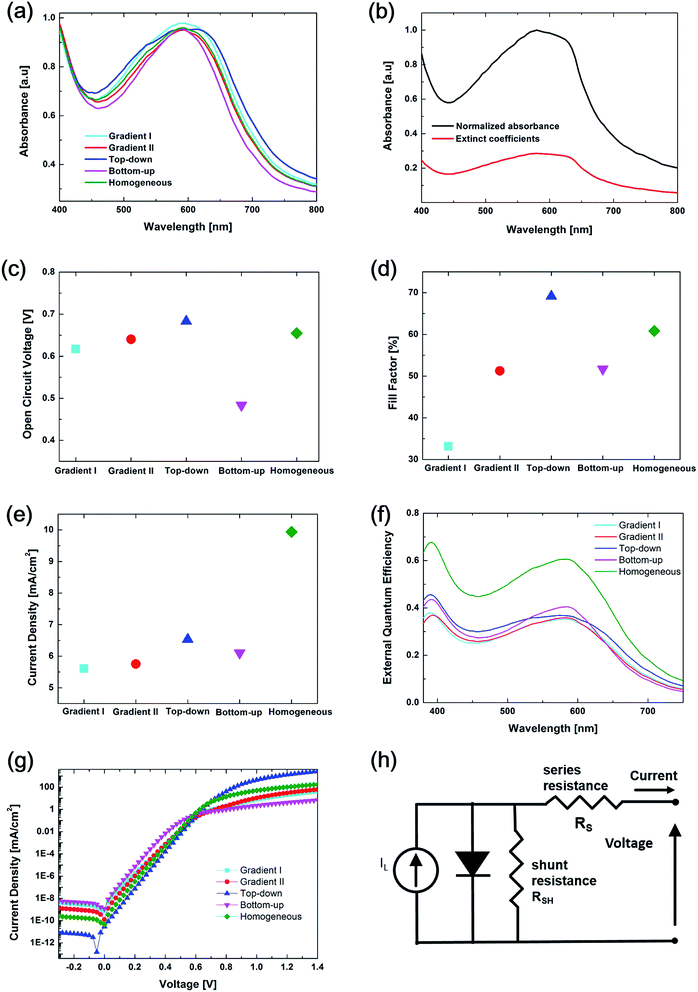
Fig. 2(a) shows the current density versus voltage (J–V) characteristics from a simulation of the regular OSC structure with different vertical configurations. The power-conversion efficiencies (PCEs) extracted from these J–V curves are summarized in Fig. 2(b). From the J–V curve, both Top-down and Homogeneous structures tend to have comparably square-shaped curves because of the easy charge carrier transportation, which leads to a relatively high fill factor. The shape of the curves in the Gradient I and Gradient II configurations tends to be S-shaped, which leads to a low fill factor. The open circuit voltage in the Bottom-up configuration is obviously much smaller than those in all the other configurations. The Homogeneous configuration tends to have the highest current density. The PCEs are 1.15%, 1.89%, 3.08%, 1.53% and 3.96% for the Gradient I, Gradient II, Top-down, Bottom-up and Homogeneous configurations, respectively.
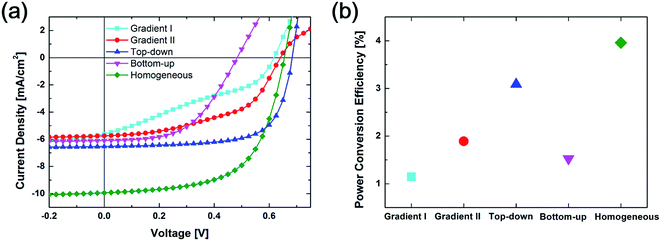 | ||
| Fig. 2 (a) J–V curve and (b) power conversion efficiency from Gradient I, Gradient II, Top-down, Bottom-up and Homogeneous configurations in simulation. | ||
The absorbance of a solar cell with different vertical compositions has been studied. As illustrated in Fig. 3(a), the absorbance of the different structures exhibits a similar trend, first dropping to 450 nm and then rising to 600 nm. Beyond 600 nm, the absorption decreases drastically with increasing wavelength. The Bottom-up configuration has the lowest overall absorbance, and there is no significant difference in absorption for the other four structures. This behavior can be explained using the complex refractive index ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = n + iκ. The imaginary part, κ, which is also called the extinction coefficient, plays a key role in the light absorbing process. The intensity of the electromagnetic wave that propagates through a material is proportional to exp(−4πκd/λ), where d and λ are the depth into the material and wavelength in the vacuum, respectively. Thus, light passing through a material with larger κ attenuates faster. In other words, light experiences stronger absorption across materials with higher κ values. Fig. 3(b) shows the wavelength dependence of extinction coefficients and the normalized absorbance for the P3HT 1
= n + iκ. The imaginary part, κ, which is also called the extinction coefficient, plays a key role in the light absorbing process. The intensity of the electromagnetic wave that propagates through a material is proportional to exp(−4πκd/λ), where d and λ are the depth into the material and wavelength in the vacuum, respectively. Thus, light passing through a material with larger κ attenuates faster. In other words, light experiences stronger absorption across materials with higher κ values. Fig. 3(b) shows the wavelength dependence of extinction coefficients and the normalized absorbance for the P3HT 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PCBM layer. It can be seen that the trend of extinction coefficients has been mimicked by the spectral absorbance. The slight difference between the absorbance for different configurations is probably a result of the reflection occurring at the interfaces between layers.
1 PCBM layer. It can be seen that the trend of extinction coefficients has been mimicked by the spectral absorbance. The slight difference between the absorbance for different configurations is probably a result of the reflection occurring at the interfaces between layers.
Open circuit voltage (Voc) variations based on different vertical configurations are shown in Fig. 3(c). The Top-down configuration has the highest value compared to the lowest value from the Bottom-up configuration. The values from Gradient I, Gradient II and Homogeneous configurations also vary greatly. The general expression is shown in eqn (1),43
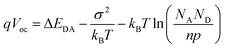 | (1) |
Fill factor variation, as shown in Fig. 3(d), can be expressed by eqn (2) and (3),44,45
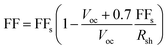 | (2) |
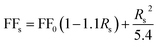 | (3) |
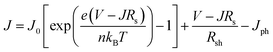 | (4) |
Current density variation is shown in Fig. 3(e). It depends on the amount of charge carrier generation and the resistance in the device. The External Quantum Efficiency (EQE), shown in Fig. 3(f), reflects the ratio between the number of generated electron–holes by excitons in the device and the number of incident photons. The Homogeneous configuration possesses the highest EQE value, which means a lot more electrons and holes in the device are generated by incident photons. As a result, a noticeably high current density occurs in the Homogeneous configuration. The EQE values of the Top-down and Bottom-up configurations are relatively similar and those of Gradient I and Gradient II are the lowest. The current densities of Gradient I, Gradient II and Bottom-up configurations have minor differences under the function of EQE, resistance and current leakage.
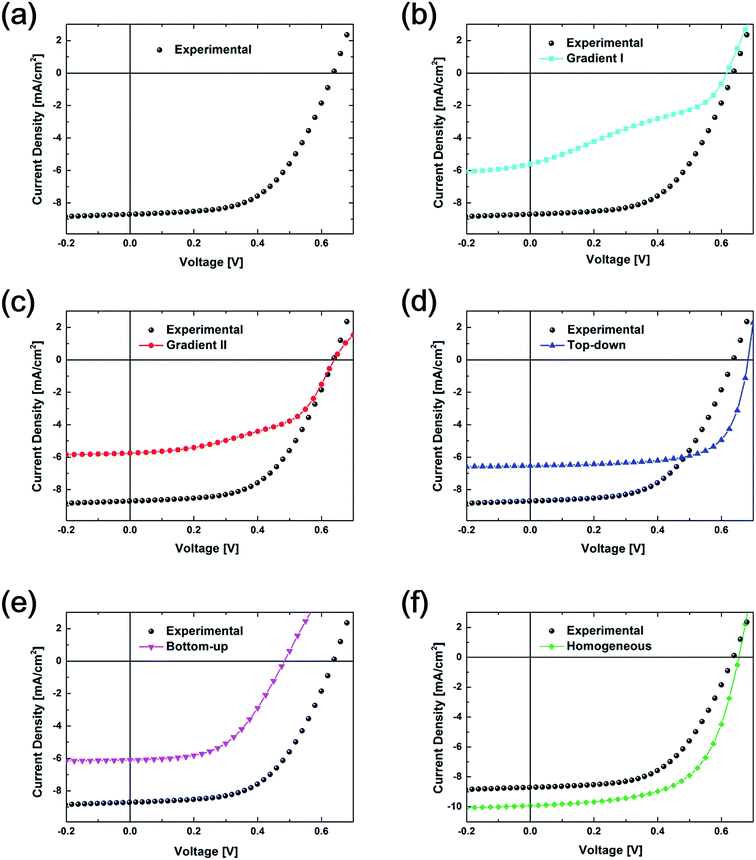
In order to calculate the goodness of fit between the experimental and computational results, a J–V curve comparison is carried out, as shown in Fig. 4. In Fig. 4(a), the J–V curve from the experiment with 3.1% PCE is presented. J–V curves from various vertical configurations are compared with those from experiment. Variance between each two curves was calculated as 13.9, 8.1, 3.8, 15.2, and 2.4 for the curves between the Gradient I, Gradient II, Top-down, Bottom-up, and Homogeneous configurations and experimental values, respectively. As a result, the data for the Homogeneous configuration is the closest to experimental data followed by the Top-down vertical configuration data.
To conclude, five vertical configurations have been successfully simulated. The vertical configuration has a dramatic effect on the performance of OSCs. It was found that the variation of PCE in different configurations comes from the quantum efficiency, resistance in the device and the current leakage under various circumstances. Uniform blending of the donor and acceptor results in the highest PCE. The acceptor being closer to the cathode and the donor being closer to the anode also gives a relatively high PCE. By comparing the variance between simulation and experimental data, the Homogeneous configuration has the most similar data to that from experiment. This finding emphasizes that a difference in vertical configuration can lead to a superior overall device performance and provides guidance for vertical configuration design in experiments. This gives an easy and accurate reference for deciding the vertical formation in organic solar cells. We anticipate that our findings will catalyze the development of OSCs and promote a better understanding in the field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was financially supported by the National Natural Science Foundation of China (NSFC, 51702035 and 51602056) and Dalian University of Technology, China, DUT16RC(3)051.Notes and references
- T. R. Andersen, H. F. Dam, M. Hosel, M. Helgesen, J. E. Carle, T. T. Larsen-Olsen, S. A. Gevorgyan, J. W. Andreasen, J. Adams, N. Li, F. Machui, G. D. Spyropoulos, T. Ameri, N. Lemaitre, M. Legros, A. Scheel, D. Gaiser, K. Kreul, S. Berny, O. R. Lozman, S. Nordman, M. Valimaki, M. Vilkman, R. R. Sondergaard, M. Jorgensen, C. J. Brabec and F. C. Krebs, Scalable, ambient atmosphere roll-to-roll manufacture of encapsulated large area, flexible organic tandem solar cell modules, Energy Environ. Sci., 2014, 7(9), 2925–2933 CAS.
- Y. Zhang, T. P. Basel, B. R. Gautam, X. M. Yang, D. J. Mascaro, F. Liu and Z. V. Vardeny, Spin-enhanced organic bulk heterojunction photovoltaic solar cells, Nat. Commun., 2012, 3, 1043 CrossRef PubMed.
- L. M. Kozycz, D. Gao, J. Hollinger and D. S. Seferos, Donor–Donor Block Copolymers for Ternary Organic Solar Cells, Macromolecules, 2012, 45(14), 5823–5832 CrossRef CAS.
- A. K. K. Kyaw, X. W. Sun, C. Y. Jiang, G. Q. Lo, D. W. Zhao and D. L. Kwong, An inverted organic solar cell employing a sol–gel derived ZnO electron selective layer and thermal evaporated MoO3 hole selective layer, Appl. Phys. Lett., 2008, 93(22), 221107 CrossRef.
- M. T. Neukom, S. Zuefle and B. Ruhstaller, Reliable extraction of organic solar cell parameters by combining steady-state and transient techniques, Org. Electron., 2012, 13(12), 2910–2916 CrossRef CAS.
- G. Li, R. Zhu and Y. Yang, Polymer solar cells, Nat. Photonics, 2012, 6(3), 153–161 CrossRef CAS.
- G. Li, V. Shrotriya, J. S. Huang, Y. Yao, T. Moriarty, K. Emery and Y. Yang, High-efficiency solution processable polymer photovoltaic cells by self-organization of polymer blends, Nat. Mater., 2005, 4(11), 864–868 CrossRef CAS.
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganas and J. V. Manca, On the origin of the open-circuit voltage of polymer-fullerene solar cells, Nat. Mater., 2009, 8(11), 904–909 CrossRef CAS PubMed.
- S. Alem, J. Lu, R. Movileanu, T. Kololuoma, A. Dadvand and Y. Tao, Solution-processed annealing-free ZnO nanoparticles for stable inverted organic solar cells, Org. Electron., 2014, 15(5), 1035–1042 CrossRef CAS.
- S.-S. Li, K.-H. Tu, C.-C. Lin, C.-W. Chen and M. Chhowalla, Solution-Processable Graphene Oxide as an Efficient Hole Transport Layer in Polymer Solar Cells, ACS Nano, 2010, 4(6), 3169–3174 CrossRef CAS PubMed.
- I. Jeon, S. Zeijkovic, K. Kondo, M. Yoshizawa and Y. Matsuo, Interface Engineering of Metal Oxides using Ammonium Anthracene in Inverted Organic Solar Cells, ACS Appl. Mater. Interfaces, 2016, 8(44), 29866–29871 CAS.
- Z. Z. Sun, K. Xiao, J. K. Keum, X. Yu, K. L. Hong, J. Browning, I. N. Ivanov, J. H. Chen, J. Alonzo, D. W. Li, B. G. Sumpter, E. A. Payzant, C. M. Rouleau and D. B. Geohegan, PS-b-P3HT Copolymers as P3HT/PCBM Interfacial Compatibilizers for High Efficiency Photovoltaics, Adv. Mater., 2011, 23(46), 5529–5535 CrossRef CAS PubMed.
- J. Y. Oh, W. S. Jang, T. I. Lee, J.-M. Myoung and H. K. Baik, Driving vertical phase separation in a bulk-heterojunction by inserting a poly(3-hexylthiophene) layer for highly efficient organic solar cells, Appl. Phys. Lett., 2011, 98(2), 023303 CrossRef.
- Y.-C. Huang, G. C. Welch, G. C. Bazan, M. L. Chabinyc and W.-F. Su, Self-vertical phase separation study of nanoparticle/polymer solar cells by introducing fluorinated small molecules, Chem. Commun., 2012, 48(58), 7250–7252 RSC.
- Y. Yan, X. Liu and T. Wang, Conjugated-Polymer Blends for Organic Photovoltaics: Rational Control of Vertical Stratification for High Performance, Adv. Mater., 2017, 29(20), 1601674 CrossRef PubMed.
- I. Jeon and Y. Matsuo, Vertical phase separation and light-soaking effect improvements by photoactive layer spin coating initiation time control in air-processed inverted organic solar cells, Sol. Energy Mater. Sol. Cells, 2015, 140, 335–343 CrossRef CAS.
- L. Zhang, X. Xing, L. Zheng, Z. Chen, L. Xiao, B. Qu and Q. Gong, Vertical phase separation in bulk heterojunction solar cells formed by in situ polymerization of fulleride, Sci. Rep., 2014, 4, 5071 CrossRef CAS PubMed.
- B. Xue, B. Vaughan, C.-H. Poh, K. B. Burke, L. Thomsen, A. Stapleton, X. Zhou, G. W. Bryant, W. Belcher and P. C. Dastoor, Vertical Stratification and Interfacial Structure in P3HT:PCBM Organic Solar Cells, J. Phys. Chem. C, 2010, 114(37), 15797–15805 CAS.
- Z. Xu, L.-M. Chen, G. Yang, C.-H. Huang, J. Hou, Y. Wu, G. Li, C.-S. Hsu and Y. Yang, Vertical Phase Separation in Poly(3-hexylthiophene): Fullerene Derivative Blends and its Advantage for Inverted Structure Solar Cells, Adv. Funct. Mater., 2009, 19(8), 1227–1234 CrossRef CAS.
- T. Song, Z. Wu, Y. Tu, Y. Jin and B. Sun, Vertical phase segregation of hybrid poly(3-hexylthiophene) and fullerene derivative composites controlled via velocity of solvent drying, Semicond. Sci. Technol., 2011, 26(3), 034009 CrossRef.
- M. Kim, J. Lee, S. B. Jo, D. H. Sin, H. Ko, H. Lee, S. G. Lee and K. Cho, Critical factors governing vertical phase separation in polymer-PCBM blend films for organic solar cells, J. Mater. Chem. A, 2016, 4(40), 15522–15535 CAS.
- M. Kim, J.-H. Kim, H. H. Choi, J. H. Park, S. B. Jo, M. Sim, J. S. Kim, H. Jinnai, Y. D. Park and K. Cho, Electrical Performance of Organic Solar Cells with Additive-Assisted Vertical Phase Separation in the Photoactive Layer, Adv. Energy Mater., 2014, 4(2), 1300612 CrossRef.
- Z. R. He, D. W. Li, D. K. Hensley, A. J. Rondinone and J. H. Chen, Switching phase separation mode by varying the hydrophobicity of polymer additives in solution-processed semiconducting small-molecule/polymer blends, Appl. Phys. Lett., 2013, 103(11), 113301 CrossRef.
- M. T. Neukom, N. A. Reinke and B. Ruhstaller, Charge extraction with linearly increasing voltage: A numerical model for parameter extraction, Sol. Energy, 2011, 85(6), 1250–1256 CrossRef CAS.
- S. Wenger, S. Seyrling, A. N. Tiwari and M. Graetzel, Fabrication and performance of a monolithic dye-sensitized TiO2/Cu(In,Ga)Se-2 thin film tandem solar cell, Appl. Phys. Lett., 2009, 94(17), 173508 CrossRef.
- J. Szmytkowski, Modeling the electrical characteristics of P3HT: PCBM bulk heterojunction solar cells: Implementing the interface recombination, Semicond. Sci. Technol., 2010, 25(1), 015009 CrossRef.
- P. W. M. Blom, V. D. Mihailetchi, L. J. A. Koster and D. E. Markov, Device physics of polymer : fullerene bulk heterojunction solar cells, Adv. Mater., 2007, 19(12), 1551–1566 CrossRef CAS.
- G. Juska, K. Genevicius, R. Osterbacka, K. Arlauskas, T. Kreouzis, D. D. C. Bradley and H. Stubb, Initial transport of photogenerated charge carriers in pi-conjugated polymers, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(8), 081201 CrossRef.
- J. Schafferhans, A. Baumann, A. Wagenpfahl, C. Deibel and V. Dyakonov, Oxygen doping of P3HT:PCBM blends: Influence on trap states, charge carrier mobility and solar cell performance, Org. Electron., 2010, 11(10), 1693–1700 CrossRef CAS.
- A. M. C. Ng, K. Y. Cheung, M. K. Fung, A. B. Djurisic and W. K. Chan, Spectroscopic ellipsometry characterization of polymer-fullerene blend films, Thin Solid Films, 2008, 517(3), 1047–1052 CrossRef CAS.
- H. Hoppe, N. Arnold, N. S. Sariciftci and D. Meissner, Modeling the optical absorption within conjugated polymer/fullerene-based bulk-heterojunction organic solar cells, Sol. Energy Mater. Sol. Cells, 2003, 80(1), 105–113 CrossRef CAS.
- M. Shibao, T. Morita, W. Takashima and K. Kaneto, Ambipolar transport in field-effect transistors based on composite films of poly(3-hexylthiophene) and fullerene derivative, Jpn. J. Appl. Phys., 2007, 46(4–7), L123–L125 CrossRef CAS.
- J. Nakamura, K. Murata and K. Takahashi, Relation between carrier mobility and cell performance in bulk heterojunction solar cells consisting of soluble polythiophene and fullerene derivatives, Appl. Phys. Lett., 2005, 87(13), 132105 CrossRef.
- E. von Hauff, V. Dyakonov and R. Parisi, Study of field effect mobility in PCBM films and P3HT : PCBM blends, Sol. Energy Mater. Sol. Cells, 2005, 87(1–4), 149–156 CrossRef CAS.
- C. Tanase, E. J. Meijer, P. W. M. Blom and D. M. de Leeuw, Unification of the hole transport in polymeric field-effect transistors and light-emitting diodes, Phys. Rev. Lett., 2003, 91(21), 216601 CrossRef CAS PubMed.
- A. Pivrikas, N. S. Sariciftci, G. Juska and R. Osterbacka, A review of charge transport and recombination in polymer/fullerene organic solar cells, Prog. Photovoltaics, 2007, 15(8), 677–696 CAS.
- A. Pivrikas, H. Neugebauer and N. S. Sariciftci, Charge Carrier Lifetime and Recombination in Bulk Heterojunction Solar Cells, IEEE J. Sel. Top. Quantum Electron., 2010, 16(6), 1746–1758 CrossRef CAS.
- Y. Yang, W. Chen, L. Dou, W.-H. Chang, H.-S. Duan, B. Bob and G. Li, High-performance multiple-donor bulk heterojunction solar cells, Nat. Photonics, 2015, 9(3), 190–198 CrossRef CAS.
- G. Li, V. Shrotriya, Y. Yao, J. Huang and Y. Yang, Manipulating regioregular poly(3-hexylthiophene): 6,6-phenyl-C-61-butyric acid methyl ester blends – route towards high efficiency polymer solar cells, J. Mater. Chem., 2007, 17(30), 3126–3140 RSC.
- W. Ma, J. Y. Kim, K. Lee and A. J. Heeger, Effect of the molecular weight of poly(3-hexylthiophene) on the morphology and performance of polymer bulk heterojunction solar cells, Macromol. Rapid Commun., 2007, 28(17), 1776–1780 CrossRef CAS.
- I.-W. Hwang, D. Moses and A. J. Heeger, Photoinduced carrier generation in P3HT/PCBM bulk heterojunction materials, J. Phys. Chem. C, 2008, 112(11), 4350–4354 CAS.
- Y.-T. Tsai, K. Goto, O. Yoshikawa, S. Mori, T. Sagawa and S. Yoshikawa, Charge Transporting Properties and Output Characteristics in Polythiophene: Fullerene Derivative Solar Cells, Jpn. J. Appl. Phys., 2011, 50(1), 01BC13 CrossRef.
- B. Qi and J. Wang, Open-circuit voltage in organic solar cells, J. Mater. Chem., 2012, 22(46), 24315–24325 RSC.
- B. Qi and J. Wang, Fill factor in organic solar cells, Phys. Chem. Chem. Phys., 2013, 15(23), 8972–8982 RSC.
- M. A. Green, Accuracy of Analytical Expressions For Solar-Cell Fill Factors, Sol. Cells, 1982, 7(3), 337–340 CrossRef CAS.
- J. D. Servaites, M. A. Ratner and T. J. Marks, Organic solar cells: A new look at traditional models, Energy Environ. Sci., 2011, 4(11), 4410–4422 CAS.
- C. Waldauf, M. C. Scharber, P. Schilinsky, J. A. Hauch and C. J. Brabec, Physics of organic bulk heterojunction devices for photovoltaic applications, J. Appl. Phys., 2006, 99(10), 104503 CrossRef.
- I. Jeon and Y. Matsuo, Polymer–Fullerene Solar Cells, Encyclopedia of Polymer Science and Technology, 2017, pp. 1–21 Search PubMed.
| This journal is © The Royal Society of Chemistry 2018 |