Open Access Article
Open Access ArticleJSFit: a method for the fitting and prediction of J- and S-shaped concentration–response curves†
Ze-Jun Wanga,
Shu-Shen Liu *ab and
Rui Qua
*ab and
Rui Qua
aKey Laboratory of Yangtze River Water Environment, Ministry of Education, College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China. E-mail: ssliuhl@263.net; Tel: +86-21-65982767
bState Key Laboratory of Pollution Control and Resource Reuse, College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China
First published on 9th February 2018
Abstract
Most monotonic S-shaped concentration–response curves (CRCs) can be satisfactorily described by a classical Hill equation. However, the Hill equation cannot effectively describe the non-monotonic J-shaped CRCs that display stimulation at low concentrations and inhibition at high concentrations. On the other hand, the physical meaning of the model parameters in current models describing the J-shaped CRCs is not very clear. It is well known that both toxicity experiments and the fitting process inevitably produce uncertainty. To effectively deal with the J-shaped concentration–response data with uncertainty and make the model parameters meaningful, we developed a method for the fitting of the J-shaped and/or S-shaped concentration–response data (simply called JSFit). The JSFit first uses one Hill equation (S-shaped) or combines with two Hill equations (J-shaped) for fitting, then nonlinear least squares fitting is performed by means of the Levenberg–Marquardt algorithm, and finally the observation-based confidence intervals of the fitting curve are constructed by the delta procedure. For the convenience of application, we wrote a computational program (JSFit) using the MATAB programming language and introduced automation of the initial parameters into the program. The JSFit was then successfully used in the fitting and prediction of the toxic data of pesticides, ionic liquids, antibiotics, and personal skin-care products on Vibrio Qinghaiensis sp.-Q67.
Introduction
Hormesis is a biphasic concentration–response relationship exhibiting low-concentration stimulation and high-concentration inhibition.1 Since the discovery of hormesis in the nineteenth century, many studies have described qualitatively the phenomena such as homeostasis, equilibrium, stability, and optimization throughout the scientific fields as diverse as physiology (e.g. temperature affecting the growth rate2), ecology (e.g. disturbances affecting species diversity3), and psychology (e.g. intensity of punishment affecting the rate of training4) and economics (e.g. tax rate affecting tax revenue4). In recent years, significant research has shown that hormesis can be induced by many chemicals, especially some poisonous and harmful substances such as persistent organic pollutants,5 pesticides,6 metal ions,7 antibiotic8 and ionic liquids.9,10 The quantitative description of the hormetic concentration–response relationship has become an important step for gaining a better understanding of hormesis and the influence and meaning of hormesis in environmental risk assessment.11Fortunately, a few models4,12–16 can be used to quantitatively describe the hormetic concentration–response relationship. The most widely used is the model with five parameters (simply M5) cited by Ge et al. in 2011.9 In 2013, several biphasic models were compared in terms of the goodness-of-fit (GoF) statistics of the adjusted coefficient of determination (Radj2), the root mean square error (RMSE), and the Akaike information criterion (AIC), where M5 gave the best description of hermetic data sets.11 Although the GoFs of these models were satisfactory, the model coefficients were far away from the values represented by their physical meaning.
Some scholars have directly fitted hormetic data using the sigmoidal equation, but this would miss some important information at low concentration. In 2016, de Garcia et al. used three logistic models, from a family of sigmoidal equations, to fit hormetic data of the bacterium Vibrio fischeri exposed to pharmaceuticals and personal care products for description of the concentration–response behaviour.17 Since most of the stimulative effects take place at low concentration levels, such as EC0 and EC5, some conclusions obtained from the sigmoid equation at these levels would not be correct.
In 2015, Di Veroli et al. developed an automated fitting procedure and software, named as Dr-Fit, to fit the concentration–response curves (CRCs) with multiple inflection points by a many Hill model.18 Without doubt the Dr-Fit software was a powerful tool for fitting CRC. However, because the number of data points was relatively few in the paper and as the experimental errors were not considered, the CRC model from the Dr-Fit can only be used to fit but not to predict.
In fact, there are some more or less errors with the experimental data points and fitting process, which are often ignored by scholars. So, it is necessary to examine the effects of experimental errors and fitting deviation on the CRC fitting in the construction of a CRC prediction model. Zhu et al.19 introduced confidence intervals (CIs): FCIs based on the function fitting and OCIs based on observation, into the CRC fitting. The CIs can be used to test the data points in turn and to judge whether there is a large deviation from the experimental data points, which could further improve the experimental method to a certain extent.
Because hormesis describes a biphasic concentration–response relationship, which is stimulation at low concentration and inhibition at high concentration, it is usually expressed as a J-shaped concentration–response relationship or CRC.20 In 2008, Beckon et al. constructed a new model based on the theory that the stimulation and inhibition effects in the two phases could be separated into two different and independent sensitivity threshold probability distributions.4 Trogl et al. used two sigmoid equations to model the hormetic curves.21 However, the regression coefficients in the models did not have any significant physical meaning. Therefore, it is necessary to enrich the physical meaning of the model coefficients in the development of a quantitative model.
The main purpose of this paper is to develop a model for the fitting and prediction of the monotonic S-shaped and/or non-monotonic J-shaped concentration–response data. In the model development, the observed concentration–response data are fitted to a Hill function (S-shaped) or an integration function from the product of two Hill functions, and then automatic initialization of the model coefficients is performed, and the CIs of the fitted CRCs are finally constructed. On the basis of the developed model, some characteristic parameters of J-shaped CRC are given. Furthermore, the outlier and reliability of the observational data are also analyzed.
Data and methods
Concentration–effect data set
The concentration–response/effect data set (C–E) used in this paper comes from the literature.22 The data set consists of toxic effects and luminescence inhibition ratios (each three replications) of 1-ethylpyridinium chloride ([epy]Cl) at 12 concentration levels in seven exposure times (0.25, 2, 4, 6, 8, 10 and 12 h) on Vibrio Qinghaiensis sp.-Q67 (Q67) (Table S1 in the ESI†). In the set, the CRCs of [epy]Cl in the first 0.25 h and 2 h are S-shaped, while those in the latter five times (4, 6, 8, 10 and 12 h) are J-shaped (Fig. S1†).General procedure of modelling
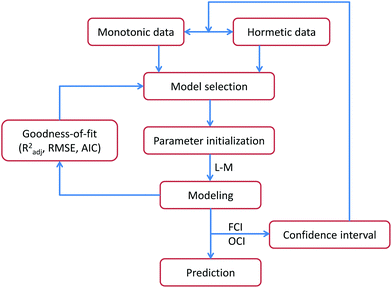
The modelling flow chart is shown in Fig. 1, and involves the steps: (1) for the monotonic and hormetic data, a suitable mathematical model is selected, such as a single Hill model or a product of two Hill models. (2) Calculus is used to analyze the specific meaning of each model coefficient, where its initial values are estimated by combining the information in the original experimental data (initialization). (3) On the basis of the Levenberg–Marquardt algorithm23 in MATLAB, experimental data are fitted by the selected model to obtain the model coefficients. (4) The GoFs, such as Radj2, RMSE and AIC, of the model are calculated to evaluate the fitting quality. (5) On the basis of the fitted CRC and experimental data, the FCIs and OCIs are constructed. The reliability of the experimental data is analyzed and outliers in the original experimental data are picked out. (6) Using the hold-out method,24 the predictive potential of the model is evaluated.Model coefficient estimation
For a monotonic concentration–response relationship, the CRC may be described quantitatively by the classical Hill equation.25,26 For a given concentration, C, the response/effect, E, can be calculated by the Hill equation with four parameters:
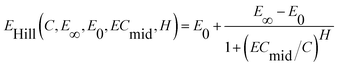 | (1) |
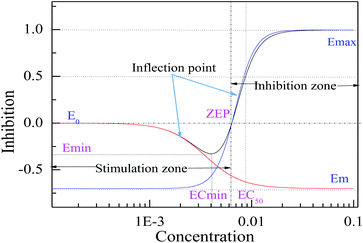
For a non-monotonic concentration–response relationship, the CRC can be described by an integration model combined with two Hill equations. The hormetic concentration (C)–effect (E) relationship has two inflection points,18 which determine the number of equations to be integrated, and one minimum, which is break point of the integration model (Fig. 2).
Therefore, by means of the break point, a hormetic concentration–response curve (HRC) could be split into two independent and separate Hill equations, named as two phases: one descendant phase (first phase) and one ascendant phase (second phase) (Fig. 2).
The monotonic CRC of each phase can be modelled by a Hill equation. For the first phase (the descendant phase), the Hill equation (eqn (1)) can be rewritten as follows:
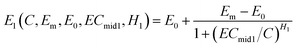 | (2) |
For the second phase (the ascendant phase), the Hill equation (eqn (1)) can be rewritten as follows:
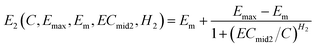 | (3) |
Combining eqn (2) with eqn (3), an integration model with seven parameters (called HM7-1 in this paper) can be obtained to describe the HRC. Since the minimum effect value of eqn (2) and (3) is Em (Fig. 2), the integration model needs to be divided by Em.
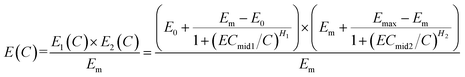 | (4) |
In many cases, E0 is often approximately zero and Emax approximately equals to 1. In this case, eqn (4) can be reduced to eqn (5) (called HM5).
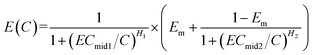 | (5) |
However, due to some reasons, like solubility, Emax is often less than 1, and eqn (5) is transformed into eqn (6) (called HM6).
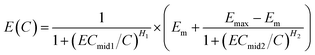 | (6) |
If E0 is not zero, the HRC is upward translated E0 units. Thus, eqn (6) is transformed into eqn (7) with seven parameters (called HM7-2):4
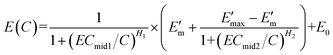 | (7) |
Model coefficient initialization
In the integration model, HM7-1 (eqn (4)), there are seven parameters: E0, Em, Emax, ECmid1, ECmid2, H1 and H2, to be estimated. In this paper, these parameters were called the model coefficients (MCj, j = 1, 2, …, 7). Currently, the estimation of the coefficients in the existing literature often requires the user to provide appropriate initial values to perform the iteration operations, which is very difficult to do for users who are not familiar with the algorithm and HRC. In this paper, an automatic initialization method was thus given on the basis of the specific meaning of the model coefficients.At first, coefficient estimation expressions were built by calculus and then the model parameters were estimated with discrete observation data points. The concentration–effect data set (Ci, Ei; i = 1, 2, …, n) was sorted by concentration from small to large, and then the initial values (MCj,0) of the seven model coefficients (MCj) were automatically assigned as follows:
| E0,0 = 0 or E0,0 = E1 | (8a) |
| Emax,0 = 1 or Emax,0 = En | (8b) |
| Em,0 = min(Ei) | (8c) |
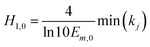 | (8d) |
| ECmid1,0 = Cj(min(kj)) | (8e) |
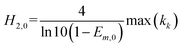 | (8f) |
| ECmid2,0 = Ck(max(kk)) | (8g) |
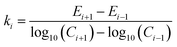 | (9) |
Model prediction evaluation
The hold-out method24 is used to evaluate the prediction ability of a model. The experimental C–E data were divided into two sets: a training set of no. 1, 3, 4, 6, 7, 9, 10 and 12 and a test set of no. 2, 5, 8 and 10. The training set was used to develop a model and the test set was used to validate the model's predictive power, which is expressed by the predictive determination coefficient, qext2, defined as follows:
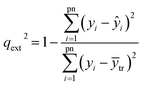 | (10) |
Goodness-of-fit
The goodness-of-fit (GoF) of a model is often expressed by the coefficient of determination (R2), Radj2, RMSE or AIC.28 The GoFs are defined as follows:
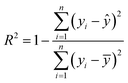 | (11) |
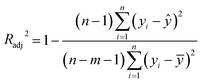 | (12) |
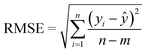 | (13) |
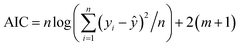 | (14) |
At present, there are five models: M1,12 M2,13 M3,15 M4 (ref. 4) and M5 (ref. 9) that can describe the J-shaped CRC (Table S2†). It has been proved that the M5 model is the best model among the five modes.11 The M5 model with five model coefficients can be written as follows:
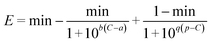 | (15) |
Confidence intervals
There are two kinds of CIs: the FCI based on function and the OCI based on observation. The FCI describes the uncertainty of the function fitting,29 and the OCI describes the uncertainty of both the experimental observation and the function fitting. The FCIs and OCIs can be calculated by the delta procedure as follows:19,30
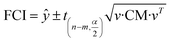 | (16) |
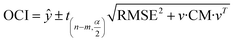 | (17) |
All the computations were implemented on the JSFit program developed in our laboratory and written using the MATLAB language.
Results
The fitting model of J- and S-shaped CRCs
Using the JSFit program, the CRC models of [epy]Cl at seven exposure time-points to Q67 were developed. The models included 20 J-shaped CRC models at the times of 4, 6, 8, 10 and 12 h and two S-shaped CRC models at the times of 0.25 h and 2 h (Table 1).| Time | Model | Em/E′m | ECmid1 (E-3)a | H1 | Emax/E′max | ECmid2 (E-3)a | H2 | E0 | Radj2 | RMSE | AIC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a E-3 represents the unit of data as 10−3 mol L−1. | |||||||||||
| 12 h | HM6 | −1.901 | 10.79 | 1.402 | 1.189 | 7.354 | 2.677 | 0.9955 | 0.03584 | −23.26 | |
| HM7-1 | −0.481 | 2.987 | 4.223 | 1.085 | 12.33 | 2.328 | −0.066 | 0.9972 | 0.02832 | −25.71 | |
| HM7-2 | −0.409 | 2.999 | 4.298 | 1.151 | 12.36 | 2.334 | −0.066 | 0.9972 | 0.02826 | −25.73 | |
| HM5 | −0.526 | 3.095 | 1.815 | 11.25 | 2.759 | 0.9931 | 0.04449 | −21.00 | |||
| 10 h | HM6 | −1.450 | 8.095 | 1.544 | 1.094 | 6.908 | 2.809 | 0.9944 | 0.04082 | −21.90 | |
| HM7-1 | −0.394 | 2.752 | 6.731 | 1.027 | 10.87 | 2.629 | −0.068 | 0.9985 | 0.02135 | −28.66 | |
| HM7-2 | −0.322 | 2.763 | 6.904 | 1.094 | 10.89 | 2.636 | −0.068 | 0.9985 | 0.02132 | −28.67 | |
| HM5 | −0.602 | 3.612 | 1.872 | 9.291 | 2.709 | 0.9934 | 0.04439 | −21.03 | |||
| 8 h | HM6 | −4.333 | 9.165 | 2.374 | 1.006 | 4.159 | 3.069 | 0.9963 | 0.03309 | −24.09 | |
| HM7-1 | −0.354 | 2.774 | 6.368 | 0.987 | 9.562 | 2.840 | −0.046 | 0.9989 | 0.01761 | −30.66 | |
| HM7-2 | −0.305 | 2.783 | 6.451 | 1.033 | 9.574 | 2.846 | −0.046 | 0.9989 | 0.01764 | −30.65 | |
| HM5 | −0.913 | 4.776 | 2.202 | 7.006 | 2.488 | 0.9962 | 0.03353 | −23.95 | |||
| 6 h | HM6 | −0.432 | 3.525 | 2.431 | 0.939 | 8.009 | 3.141 | 0.9987 | 0.01920 | −29.76 | |
| HM7-1 | −0.263 | 2.671 | 5.591 | 0.931 | 8.979 | 3.407 | −0.028 | 0.9995 | 0.01199 | −34.67 | |
| HM7-2 | −0.234 | 2.676 | 5.613 | 0.959 | 8.983 | 3.409 | −0.028 | 0.9995 | 0.01198 | −34.68 | |
| HM5 | −0.688 | 6.369 | 1.645 | 6.942 | 3.882 | 0.9979 | 0.02427 | −27.32 | |||
| 4 h | HM6 | −0.622 | 6.174 | 1.873 | 0.923 | 5.957 | 4.793 | 0.9987 | 0.01846 | −30.17 | |
| HM7-1 | −111.662 | 5.517 | 4.384 | 0.919 | 0.3921 | 1.822 | −0.095 | 0.9994 | 0.01209 | −34.58 | |
| HM7-2 | −6.706 | 5.413 | 4.388 | 0.940 | 1.894 | 1.907 | −0.024 | 0.9993 | 0.01348 | −33.45 | |
| HM5 | −153.843 | 4.900 | 4.367 | 0.1314 | 1.359 | 0.9960 | 0.03220 | −24.38 | |||
| 2 h | Hill | −0.038 | 0.753 | 8.006 | 2.869 | 0.9917 | 0.03686 | −22.96 | |||
| 0.25 h | Hill | −0.056 | 0.884 | 5.456 | 1.555 | 0.9967 | 0.02342 | −27.69 | |||
From Table 1, all the fitted Radj2s are larger than 0.99, while the RMSEs are less than 0.045 and AICs less than −21, which shows that all the CRC models had a good fitting ability to the observed data. In particular, the seven-parameter models, HM7-1 and HM7-2, were better than HM6 and HM5, with the Radj2s of HM7-1 and HM7-2 being larger than 0.998, RMSEs less than 0.022 and AICs less than −28.66, except for the models at 12 h. As shown above, the integrated HM7-1 or HM7-2 model could describe the J-shaped CRCs well, while the single Hill model could describe the S-shaped CRCs well.
The characteristic parameters of J-shaped CRCs
For the monotonic S-shaped CRC that can be described by one Hill equation with four model coefficients (Em, Emax, ECmid2 and H2), the four coefficients can fully characterize the shape and location of the S-shaped CRC, and the coefficients are the characteristic parameters. However, seven model coefficients in the integration model come from the two Hill equations and cannot really depict the specific shape and location of a J-shaped CRC. We think that at least five parameters, such as the median stimulative effect concentration in the descendant phase (left) (ECmsL), the minimum effect concentration (ECmin), the minimum effect or maximum stimulative effect (Emin), the median effect concentration (EC50) and the zero effect concentration point (ZEP), are needed to characterize the specific shape and location of a J-shaped CRC or hormetic CRC (HRC). Here, ECmin can be solved by letting the derivative of the J-shaped CRC to the concentration variable be zero: ∂E(C)/∂C = 0. Then, Emin can be solved by substituting the ECmin into eqn (4) or (7). The values of ECmsL, EC50 and ZEP can be solved by dichotomy, where we let the effect be Emin/2, 50% and 0, respectively. We called the four concentrations and one effect the characteristic parameters of a J-shaped CRC, and the characteristic parameters of [epy]Cl obtained from the HM7-1 or HM7-2 are shown in Table 2. The characteristic parameters are some important points on a J-shaped CRC and show the change regulation of the effect with the concentration, where each characteristic parameter is part of the J-shaped CRCs. However, the model coefficients were only used to construct the model, and they only indirectly reflect the change regulation of the effect with the concentration, but generally speaking, the model coefficients can't reflect the substantive characteristics of a J-shaped CRC.| Time | Model | ECmsL (E-3)a | ZEP (E-3)a | EC50 (E-3)a | ECmin (E-3)a | Emin |
|---|---|---|---|---|---|---|
| a E-3 represents the unit of data as 10−3 mol L−1. | ||||||
| 12 h | HM6 | 1.843 | 8.765 | 15.29 | 4.467 | −0.283 |
| HM7-1 | 2.241 | 8.696 | 15.40 | 4.169 | −0.303 | |
| HM7-2 | 2.249 | 8.693 | 15.40 | 4.169 | −0.304 | |
| HM5 | 1.767 | 8.909 | 15.05 | 4.365 | −0.274 | |
| 10 h | HM6 | 1.817 | 7.635 | 13.16 | 4.121 | −0.252 |
| HM7-1 | 2.241 | 7.542 | 13.29 | 3.715 | −0.283 | |
| HM7-2 | 2.351 | 7.542 | 13.29 | 3.715 | −0.283 | |
| HM5 | 1.796 | 7.702 | 13.07 | 4.074 | −0.248 | |
| 8 h | HM6 | 2.119 | 6.694 | 11.60 | 3.890 | −0.224 |
| HM7-1 | 2.361 | 6.663 | 11.65 | 3.631 | −0.237 | |
| HM7-2 | 2.363 | 6.661 | 11.65 | 3.631 | −0.237 | |
| HM5 | 2.011 | 6.754 | 11.55 | 3.936 | −0.215 | |
| 6 h | HM6 | 2.020 | 6.255 | 10.57 | 3.802 | −0.170 |
| HM7-1 | 2.261 | 6.195 | 10.62 | 3.589 | −0.182 | |
| HM7-2 | 2.267 | 6.193 | 10.62 | 3.589 | −0.182 | |
| HM5 | 1.893 | 6.305 | 10.52 | 3.936 | −0.162 | |
| 4 h | HM6 | 2.001 | 5.485 | 9.087 | 3.715 | −0.133 |
| HM7-1 | 2.225 | 5.468 | 9.120 | 3.758 | −0.139 | |
| HM7-2 | 2.227 | 5.470 | 9.124 | 3.802 | −0.140 | |
| HM5 | 2.273 | 5.348 | 9.342 | 5.470 | −0.146 | |
In JSFit program, at least five model coefficients, one effect (Em), two concentrations (ECmid1 and ECmid2) and two slopes (H1 and H2) are needed to construct a model, which implies that at least five characteristic parameters can fully characterize the J-shaped CRC, and the combination of four concentrations and one effect proposed in this paper is an optimal selection. When the characteristic parameter Emin is determined, the shape and location of the descendant phase can be characterized by two concentrations (ECmin and ECmsL), while the shape and location of the ascendant phase can be characterized by two concentrations (ZEP and EC50).
Whether a single model coefficient can reflect the change of the data depends on the model coefficient Em. Em is a virtual parameter that can reflect the size of Emin on a J-shaped CRC to a certain extent, but it is always less than the real Emin. When Em is closer to Emin, the model coefficient will be closer to the value (including characteristic parameters) on the J-shaped CRC. For example, at 12 h, when the model coefficient Em (from −190.1% to −48.1%) is close to Emin (about −30%), the model coefficient ECmid1, from 10.79 × 10−3 mol L−1 to 2.987 × 10−3 mol L−1, is close to the characteristic parameters of ECmsL (about 2.0 × 10−3 mol L−1), and the other model coefficients are close to the corresponding value for the J-shaped CRC.
Model coefficient initialization
On the one hand, because solution of the model coefficients is an iterative process, each coefficient to be solved requires an initial value. On the other hand, it is more difficult for people who are not familiar with programming to set the initial values. In this study, according to the physical meaning of the model coefficient, several reliable initial value equations were provided by combining discrete data with calculus (eqn (8(a–g))). According to the equations, the corresponding initial coefficients could be calculated. For a certain time, selecting the average value of observed effects (three replications), the slope vectors, ki (i = 2, 3, …, n−1) were calculated using eqn (9), and the initial values (MCj,0) could be obtained by eqn (8(a–g)). The initial values of the model coefficients are listed in Table 3.| Time | Em,0/E′m | ECmid1,0 (E-3) | H1,0 | Emax,0/E′max | ECmid2,0 (E-3) | H2,0 | E0,0 |
|---|---|---|---|---|---|---|---|
| 12 | −0.314 | 2.637 | 3.4036 | 0.979 | 12.41 | 2.671 | 0 |
| 10 | −0.286 | 2.637 | 3.5626 | 0.979 | 12.41 | 2.698 | 0 |
| 8 | −0.234 | 2.637 | 3.7687 | 0.963 | 8.531 | 2.843 | 0 |
| 6 | −0.179 | 2.637 | 3.8234 | 0.933 | 8.531 | 3.233 | 0 |
| 4 | −0.137 | 2.637 | 3.8365 | 0.904 | 8.531 | 3.285 | 0 |
| 2 | −0.048 | 0.793 | 8.531 | 2.410 | 0 | ||
| 0.25 | −0.038 | 0.841 | 8.531 | 1.730 | 0 |
From Table 3, the initial values (MCj,0) of HM7-1 and HM7-2 calculated by eqn (8(a–g)) have a strong regularity. For the J-shaped data set, E0,0 is 0 all the time, and Emax,0 is the twelfth effect (average value), which corresponds to the maximum concentration. Because the sixth concentration point of the 12 concentration levels has the minimum inhibitory effect, so Em,0 is the sixth effect of the data set. ECmid1,0 is the fifth concentration, and the corresponding slope is H1,0, because the slope of the fifth concentration point is the minimum in the descendant phase. At 4, 6 and 8 h, the ECmid2,0 is the eighth concentration, and the corresponding slope is H2,0, while for 10 and 12 h, ECmid2,0 is the ninth concentration and the corresponding slope is H2,0 based on the maximum slope of the ascendant phase. For S-shaped CRC, Em,0 and Emax,0 are the first and twelfth effects, which correspond to the minimum and maximum concentrations, respectively. Because the slope of the eighth concentration point is the maximum, ECmid2,0 is the eighth concentration, its corresponding slope is H2,0. For the HM6 and HM5 models, the corresponding values are chosen as the initial values of the model coefficients.
Model selecting
For the monotonic S-shaped concentration–effect data, there are two manifestations: the effect increasing with concentration (monotonic increasing S-shaped) and the effect decreasing with concentration (monotonic decreasing S-shaped). For the non-monotonic J-shaped/hormetic concentration–effect data, there are three categories:Hdata 1: the effect tends to 0 at low concentration and to 1 at high concentration.
Hdata 2: the effect tends to 0 at low concentration and is less than 1 at high concentration.
Hdata 3: the effect is larger than 0 at low concentration and less than 1 at high concentration.
According to the characteristics of the concentration–effect data, the appropriate model should be selected in the JSFit program. For monotonic increasing S-shaped data, the ascending Hill is chosen, while for monotonic descending S-shaped data, the descending Hill is selected. The ascending Hill and the descending Hill have different initial values for the model coefficients. For non-monotonic hormetic data, the model with fewer parameters should be chosen as much as possible to avoid overfitting. Therefore, the HM5 model is selected for Hdata 1, the HM6 model for Hdata 2, and the HM7-1 or HM7-2 model for Hdata 3.
Application of JSFit
JSFit can be used to fit the concentration–effect data with S-shaped and/or J-shaped CRC profiles, whether the data are from a single pollutant or mixture. Fig. S3† provides the experimental concentration–effect scatters and the fitting CRCs for some chemical and mixture examples, including pesticide metalaxyl (Met) using the ascending Hill model, ionic liquid [epy]Br using the HM5 model (belonging to Hdata 1), antibiotic polymyxin B sulfate (POL) using the HM7-1 model (Hdata 3), and a complex personal care product mixture using the HM6 model (Hdata 2). From Fig. S3,† various CRCs could be well fitted to the experimental data.Discussion
Model prediction evaluation
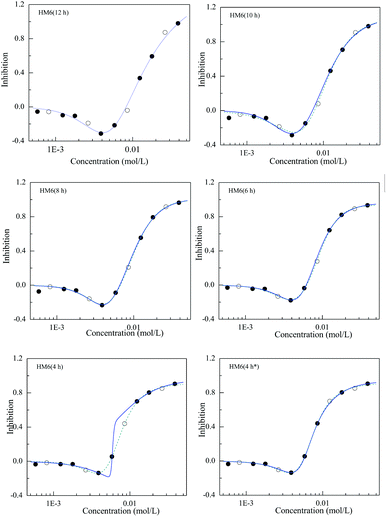
Due to the limited number of observation data, 1/3 of the J-shaped data was equidistantly selected as a test set, and the remaining 2/3 concentration–effect data were used as training sets. Because the effect at low concentration was near to 0, the model coefficient E0 could be ignored. Furthermore, it was found that HM6 was better than HM5. Therefore, HM6 was chosen to analyze the model prediction ability. The training set was used to model the J-shape data, and the effects of various concentrations in the test set were predicted by the training set model. The obtained qext2 values are listed in Table S3.† Fig. 3 depicts the relationships between the experimental points and the fitting curves of [epy]Cl at 12, 10, 8, 6 and 4 h. As can be clearly seen, apart from 4 h, all the experimental points at the other times almost fall on the fitting curves. The predictive qext2 values at 12, 10, 8 and 6 h were 0.9884, 0.9940, 0.9989 and 0.9954, respectively, which were the same as the estimated R2 (0.9978, 0.9954, 0.9966 and 0.9992), showing a good prediction ability of HM6.It is noted that the fitting curve (solid blue) of the lower left panel in Fig. 3 partly deviates from the dashed line based on all experimental data. However, if one data point (○) in the test set is adjusted, the fitting curve based on the training set overlaps with the curve based on all the experimental data (see the lower right panel in Fig. 3), which explains that the selection of the training set affects the predictive potential of HM6. So, the training set to be used to develop a predicable model has to contain enough data points and cannot lack some important information of CRC, such as the minimum effect or the up and down slope. In particular, the number of model coefficients selected should be as little as possible, i.e. using a simple model rather than a complex model18 and enough concentration–effect data to develop the CRC model.
Model comparison analysis
Currently, compared with other models (M1, M2, M3 and M4), the M5 model, which has been widely used to describe hormetically the concentration–response relationship, has a better fitting quality.9,11,22 However, the model coefficients obtained by the M5 model fitting the concentration–effect of [epy]Cl on Vibrio Qinghaiensis Q67 distort the physical meaning. For example, for the model coefficient min, the description of the minimum inhibitory ratio of hormetic CRCs is more than 0 sometimes.22 Although, the M5 model has such shortcomings, the fitting quality of M5 to the hormetic concentration–effect data is acceptable, which is the reason why it is so widely used.Five characteristic parameters (ECmsL, ECmin, Emin, EC50 and ZEP) propounded in this paper can characterize the specific shape and location of a J-shaped CRC or hormetic CRC (HRC). The model coefficient Em in HM5 is similar to min in M5, but the characteristic parameter Emin truly reflects the minimum effect of the J-shaped CRC. On the other hand, the fitting quality of HM5 is more optimal than M5, as seen from the results of three GoFs, Radj2, RMSE and AIC in Table 4 (also see Fig. S4†).
| GoFs | 4 h | 6 h | 8 h | 10 h | 12 h | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| HM5 | M5 | HM5 | M5 | HM5 | M5 | HM5 | M5 | HM5 | M5 | |
| Radj2 | 0.9960 | 0.9607 | 0.9979 | 0.9842 | 0.9962 | 0.9879 | 0.9934 | 0.9892 | 0.9931 | 0.9922 |
| RMSE | 0.03220 | 0.08343 | 0.02427 | 0.05475 | 0.03353 | 0.04939 | 0.04439 | 0.0469 | 0.04449 | 0.03906 |
| AIC | −24.38 | −14.46 | −27.32 | −18.85 | −23.95 | −19.92 | −21.03 | −20.46 | −21.00 | −22.37 |
Analysis of the confidence intervals
The confident intervals (CIs), FCIs or OCIs, can describe the uncertainty in toxicity experiments and the function fit. The confident interval width (CIW), defined as (CI+ − CI−)/2, can quantitatively reflect the fitting quality. The CIWs from some models, such as HM6, HM7-1, HM7-2 and HM5, change with the concentration, as shown in Fig. 4.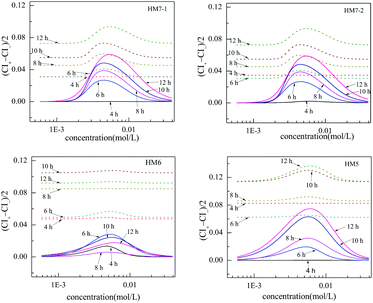 | ||
| Fig. 4 Plot of the width of confident intervals, (CI+ − CI−)/2, versus the concentration, where “—” and “⋯” are based on FCIs and OCIs of the fitted CRCs of [epy]Cl, respectively. | ||
It can clearly be seen that the variation regularity of CIW of HM7-1 is similar to that of HM7-2, whether the CIW is based on FCI or OCI. The CIW from HM6 was the minimum among the four models, while the CIW from HM5 was the maximum. For example, the CIW based on FCIs from HM6 at 12 h was 0.017, while that from HM5 was 0.075, and the CIW from HM5 is 4.4 times that from HM5. On the other hand, the changes of CIWs with concentration from the four models had a similar variation regularity, that is, the CIW based on FCIs increased from 0 to the maximum and then decreased from the maximum to 0, while the CIW based on OCIs increased from a small value to a maximum and then decreased from the maximum to another small value. On the whole, the CIW based FCIs values are less than those based on OCIs.
Although the variation regularity of the CIW based on OCIs from different models with concentration was similar to that on FCI, the steepness of change was smoother and the CIW value was larger. Since OCI is more dependent on RMSE, the difference in the CIW based on OCIs from different models can be estimated simply according to RMSE, thus the choice of model based on RMSE is equivalent to the choice of model based on OCIs.
Of course, we can also test the reliability and identify outliers in the original observation data. There is a way to judge outliers by utilizing an expanded uncertainty;31 however, this method is only used with repeat measurements made at the same concentration, and the more data are measured, the more accurate the test will be. For the CRCs data, the number of measurement effects at the same concentration was limited, and the variation regularity of the CRCs data with the change of concentration is known, so we cannot test the reliability and identify outliers by this method. Therefore, a method based on OCIs to identify outliers was developed. A confidence intervals relative error (REOCI) was used to quantitatively describe the relative deviation of the predictive value from the experimental value. The REOCI is defined as follows.
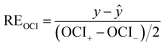 | (18) |
Substituting eqn (17) into eqn (18) gives:
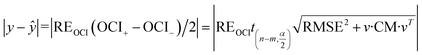 | (19) |
Referring to the expanded uncertainty31 and introducing an adjusting factor (λ) gives:
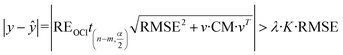 | (20) |
Therefore, when the following inequality is true, the corresponding data point can be considered as an outlier:
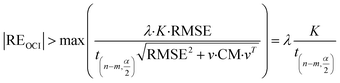 | (21) |
The ratio of the number of outliers in a CRC to all the data, Pout, and the ratio of the number of non-outliers to all the data, Prel, are respectively used to describe the proportion of outliers and the reliability of the CRC data.
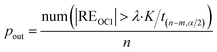 | (22) |
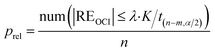 | (23) |
The above method based on OCIs was used to analyze the experimental concentration–effect data of [epy]Cl at four exposure times, and the results are listed in Table S4.† Although some Pout values were slightly larger than 0.05, the theoretical outliers were at most 1.8 of 36 experimental data points, while the number of outliers calculated by all the models was not more than 2, which still shows that the experimental data were reliable and this set of data was believable. The way to deal with these outliers is to use the average of other data instead of the outliers when computing.
Conclusions
To process the J-shaped concentration–response data with uncertainty, the JSFit method or program was developed to quantitatively and rationally fit the J-shaped (and the S-shaped) CRC. JSFit could automatically initialize the model coefficients on the basis of the specific meaning of each model coefficient and then constructs the observation-based confident intervals (OCIs) of the CRC. Also, it was used to analyze the reliability and outliers of the experimental CRC data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to the National Natural Science Foundation of China (21677113 and 21377097) for their financial support.References
- E. J. Calabrese and L. A. Baldwin, Hum. Exp. Toxicol., 2002, 21, 91–97 CAS.
- B. Bjornsson, A. Steinarsson and M. Oddgeirsson, ICES J. Mar. Sci., 2001, 58, 29–38 CrossRef.
- J. H. Connell, Science, 1978, 199, 1302–1310 CAS.
- W. Beckon, C. Parkins, A. Maximovich and A. V. Beckon, Environ. Sci. Technol., 2008, 42, 1308–1314 CrossRef CAS PubMed.
- Y. X. Chen, K. L. Shen, C. F. Shen, L. Chen and X. C. Chen, J. Hazard. Mater., 2010, 180, 773–776 CrossRef CAS PubMed.
- H. M. Qiu, J. J. Geng, H. Q. Ren, X. M. Xia, X. R. Wang and Y. Yu, J. Hazard. Mater., 2013, 248, 172–176 CrossRef PubMed.
- X. M. Zou, X. Y. Xiao, Y. He, L. J. Hu, C. Hu and X. F. Huang, J. Hazard. Mater., 2017, 322, 454–460 CrossRef CAS PubMed.
- Y. Liu, S. Chen, X. Chen, J. Zhang and B. Y. Gao, J. Hazard. Mater., 2015, 297, 83–91 CrossRef CAS PubMed.
- H. L. Ge, S. S. Liu, X. W. Zhu, H. L. Liu and L. J. Wang, Environ. Sci. Technol., 2011, 45, 1623–1629 CrossRef CAS PubMed.
- Z. Y. Yu and J. Zhang, J. Hazard. Mater., 2016, 312, 114–122 CrossRef CAS PubMed.
- X. W. Zhu, S. S. Liu, L. T. Qin, F. Chen and H. L. Liu, Ecotoxicol. Environ. Saf., 2013, 89, 130–136 CrossRef CAS PubMed.
- P. Brain and R. Cousens, Weed Res., 1989, 29, 93–96 CrossRef.
- P. H. Vanewijk and J. A. Hoekstra, Ecotoxicol. Environ. Saf., 1993, 25, 25–32 CrossRef CAS.
- O. Schabenberger, B. E. Tharp, J. J. Kells and D. Penner, Agron. J., 1999, 91, 713–721 CrossRef CAS.
- N. Cedergreen, C. Ritz and J. C. Streibig, Environ. Toxicol. Chem., 2005, 24, 3166–3172 CrossRef CAS PubMed.
- L. T. Qin, S. S. Liu, H. L. Liu and Y. H. Zhang, Chemosphere, 2010, 78, 327–334 CrossRef CAS PubMed.
- S. O. de Garcia, P. A. Garcia-Encina and R. Irusta-Mata, Ecotoxicology, 2016, 25, 141–162 CrossRef PubMed.
- G. Y. Di Veroli, C. Fornari, I. Goldlust, G. Mills, S. B. Koh, J. L. Bramhall, F. M. Richards and D. I. Jodrell, Sci. Rep., 2015, 5, 14701 CrossRef CAS PubMed.
- X. W. Zhu, S. S. Liu, H. L. Ge and Y. Liu, China Environ. Sci., 2009, 29, 113–117 CAS.
- E. J. Calabrese, Homeopathy, 2015, 104, 69–82 CrossRef PubMed.
- J. Trogl, G. Kuncova, L. Kubicova, P. Parik, J. Halova, K. Demnerova, S. Ripp and G. S. Sayler, Folia Microbiol., 2007, 52, 3–14 CrossRef CAS.
- R. Qu, S. S. Liu, Q. F. Zheng and T. Li, Sci. Rep., 2017, 7, 43473 CrossRef PubMed.
- M. Cui, Y. Zhao, B. B. Xu and X. W. Gao, Int. J. Heat Mass Transfer, 2017, 107, 747–754 CrossRef.
- Nurhayati, I. K. Hadihardaja, I. Soekarno and M. Cahyono, Informatics, Management, Engineering, and Environment (Time-E 2014), Ieee, 2014 2nd International Conference on Technology, 2014, pp. 228–233 Search PubMed.
- H. Prinz, J. Chem. Biol., 2010, 3, 37–44 CrossRef PubMed.
- J. Trogl and K. Benediktova, Int. J. Environ. Res., 2011, 5, 989–998 CAS.
- X. Y. Huang, D. H. Yang, P. Tong and Y. J. Zhou, Bull. Seismol. Soc. Am., 2016, 106, 2877–2899 CrossRef.
- K. Yamaoka, T. Nakagawa and T. Uno, J. Pharmacokinet. Biopharm., 1978, 6, 165–175 CrossRef CAS PubMed.
- J. Tarasinska, Stat. Probabil. Lett., 2005, 73, 125–130 CrossRef.
- J. R. Donaldson and R. B. Schnabel, Technometrics, 1987, 29, 67–82 CrossRef.
- Y. C. Kuang, M. P. L. Ooi, A. Rajan and S. Demidenko, Ieee, 2015 Ieee International Instrumentation and Measurement Technology Conference (I2mtc), 2015, pp. 1729–1734 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra13220d |
| This journal is © The Royal Society of Chemistry 2018 |