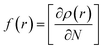Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of rotameric conformations of substituted imidazo-[1,2-a]pyrazine: experimental and theoretical approaches†
Gulshan Kumar ,
Richa Goel,
Kamaldeep Paul and
Vijay Luxami
,
Richa Goel,
Kamaldeep Paul and
Vijay Luxami *
*
School of Chemistry and Biochemistry, Thapar University, Patiala-147004, India. E-mail: vluxami@thapar.edu
First published on 7th March 2018
Abstract
The different rotameric conformations of imidazo-[1,2-a]pyrazine have been synthesized and characterized by means of different experimental techniques, such as NMR, FTIR, and absorption spectroscopy and quantum chemical calculations. The different conformations were stabilized by hydrogen bonds, such as OH⋯N, ArH⋯N and ArH⋯ArH. The ground state optimizations and potential energy surface (PES) scanning profiles produced using density functional theory (DFT) show two stable rotameric forms for each molecule. The relative population of the conformations is affected by the strength of the hydrogen bonds. The calculated absorption spectra and isotopic shielding constants were acquired by time-dependent density functional theory (TD-DFT) and gauge invariant atomic orbitals (GIAO)-DFT, respectively. The strength of the hydrogen bonding interactions that resulted in the different conformations was studied by quantum theory of atoms in molecules (QTAIM).
1. Introduction
The heterocyclic compounds are essential candidates in the chemical, biological, agricultural, and veterinary fields.1,2 Among the various heterocycles, imidazo[1,2-a]pyrazine is an aza-heterocyclic compound that has applications as an anticancer agent,3 cardiac stimulating agent and uterine relaxant,4 antihyperglycemic agent,5 antihypertensive agent,6 antiulcer agent,7 antibronchospastic agent8 etc.,9–11 The properties of compounds as an application candidate depend upon the molecular structure of the compound and can be tuned by altering the molecular modification, and orientation of the compound.12The spatial and chemical constraints in molecular systems give rise to different spatial arrangements or conformations. These conformations can be governed by non-covalent interactions, such as van der Waals interactions, hydrogen bonding, and steric hindrance significantly.12–15 These non-covalent interactions are the deciding forces in building supramolecular assemblies, and thus, this is a fascinating area in structural chemistry. These interactions connect together the synthons and building blocks of supramolecular structures.12,15 Among the noncovalent interactions, hydrogen bonds, such as C–H⋯O, N–H⋯O, O–H⋯N, C–H⋯π, O–H⋯π, and π–π interactions, have a conclusive role in controlling molecular conformations. Thus, the implication of such interactions in conformational analysis would result in new conformations of compounds in the solid, solution and gas phase. These interactions lock the molecular configurations through hydrogen bonding, and thus, permit the formation of different conformations.16–24 Thus, the exact structure determination of a molecule is important and a big subject of research itself in science. Structural determination requires tough conformational analysis by means of experimental and theoretical calculations.
For decades, correct structural information has been very helpful in describing many chemical, physical and biological processes, such as reaction mechanisms and photophysical processes, and in designing molecular machines and understanding their functioning, etc.25,26 The problem of exact structure determination is solved by experimental (e.g. spectroscopic techniques), single crystal X-ray diffraction (SCXRD) and theoretical (quantum chemical calculations) tools. Spectroscopic techniques, such as FTIR, NMR, absorption spectroscopy etc., provide very specific information about functional groups and their orientation, and thus, they are promising tools in solving molecular structures. Also, SCXRD provides the exact molecular configuration following good structural refinement, but it requires high-quality crystals and growing good quality crystals is not always an easy task. Therefore, conformer assignment requires experimental data from different techniques, and data analysis exercises, and thus is always a challenging task through experimental techniques. Therefore, the use of computational tools is the best alternative to predict an accurate structure via different quantum chemical methods. Quantum chemical calculations can be used to predict the spectroscopic values for different possible structures. The correlation of experimental and theoretical results is also a good parameter to confirm the exact molecular structure. During a literature survey, we found some reports on the conformational examination of organic compounds by mean of experimental and theoretical techniques, but the conformation of imidazo-[1,2-a]pyrazine has not been determined.27–32 In this work, we have synthesized a series of imidazo-[1,2-a]pyrazine derivatives that exhibit different rotameric conformations. These rotameric conformations were further purified by column chromatography. Moreover, the rotamers were characterized through NMR, UV and quantum chemical calculations. Furthermore, the experimental data have been correlated with the calculated values to gain insight into the rotameric structures.
2. Experimental section
2.1. Material and methods
All the chemicals used for synthesis were purchased from Sigma-Aldrich Chemical Ltd., Loba Chemie etc. depending upon their availability. All the solvents used were of spectroscopic grade and purchased from Spectrochem and Rankem Ltd. All chemicals and solvents were used without further purification. The progress of the chemical reaction was monitored by thin-layer chromatography (TLC). Melting points were recorded using the open capillary tube method and were uncorrected. 1H NMR and 13C NMR spectra were recorded on a JEOL ECS-400 MHz spectrometer at ambient temperature in CDCl3 with TMS as an internal reference. All chemical shifts were reported in ppm relative to the reference. Mass spectra of the synthesised compounds were recorded using a Waters Micromass Q-Tof micro mass spectrometer. The absorption spectra were recorded on a SHIMADZU-2600 spectrophotometer using quartz cuvettes of 1 cm path length.2.2. Synthesis
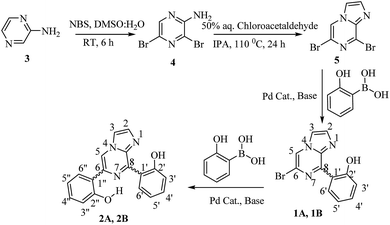
2-Aminopyrazine was used as the starting material, which was brominated with N-bromosuccinimide (NBS) in DMSO and H2O at room temperature for 6 hours. The resultant 2-amino-3,5-dibromopyrazine (4)33 was cyclized with chloroacetaldehyde in iso-propyl alcohol to obtain 6,8-dibromo-imidazo[1,2-a]pyrazine (5). Subsequently, a Suzuki–Miyaura cross-coupling reaction was performed with 6,8-dibromo-imidazo[1,2-a]pyrazine and 2-hydroxyphenyl boronic acid in the presence of a palladium catalyst and afforded the substituted mono- and di-arylated products (1 and 2, Scheme 1).342.3. Computational details
All theoretical calculations were performed using the GAUSSIAN-03W program.35 The geometry optimizations for all molecules were carried out at the DFT/B3LYP level of theory using the 6-31++G(d,p) basis set.36–38 Frequency calculations were performed on the obtained optimized structures at the same level of theory. The potential energy surfaces for the dihedral angles were acquired using DFT at the B3LYP/6-31+g* level of theory to identify the local minima. The theoretical absorption spectra were calculated from the vertical excitation energies using the time-dependent density functional theory (TD-DFT) method. The NMR shielding tensors were calculated using the GAIO method.39 The conformational optimization was performed in different solvents (CH3CN and CHCl3) for the optimized structures using a self-consistent reaction field (SCRF) approach coupled with the integral equation formation of polarizable continuum model (IEFPCM) solvation method. Topological analysis of the electron distribution was conducted on selected conformations according to Bader's “Quantum Theory of Atoms in Molecule (QTAIM)”.40 QTAIM calculations were carried out using the Multiwfn program41 to evaluate the nature and strength of the hydrogen bonds present in the different conformations.3. Results and discussion
3.1. Synthesis of 2-amino-3,5-dibromopyrazine (4)33
N-Bromosuccinamide (14.95 g, 83.99 mmol) was added over 50 min to a mixture of 2-aminopyrazine (3.80 g, 40 mmol) in 80 ml of DMSO and 2 ml of H2O below 15 °C. The mixture was then stirred for 6 h at room temperature. After completion of the reaction, the mixture was extracted with water and ethyl acetate. The ethyl acetate layer was dried over Na2SO4 and concentrated under vacuum. The crude product was purified by column chromatography using hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate (9
ethyl acetate (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as an eluent. White solid; yield: 90%; mp 115–116 °C; 1H NMR (CDCl3, 400 MHz): δ 5.12 (bs, 1H, NH2), 8.04 (s, 1H, C6H); 13C NMR (CDCl3, 100 MHz): δ 123.5, 123.9, 143.1, 151.8; MS (EI): m/z 254 (M+ + 1).
1) as an eluent. White solid; yield: 90%; mp 115–116 °C; 1H NMR (CDCl3, 400 MHz): δ 5.12 (bs, 1H, NH2), 8.04 (s, 1H, C6H); 13C NMR (CDCl3, 100 MHz): δ 123.5, 123.9, 143.1, 151.8; MS (EI): m/z 254 (M+ + 1).
3.2. Synthesis of 6,8-dibromo-imidazo[1,2-a]pyrazine (5)34
To 2-amino-3,5-dibromopyrazine (5.0 g, 19.8 mmol) in 100 ml of isopropyl alcohol (IPA), a 50% aqueous solution of chloroacetaldehyde (99 mmol) was added dropwise. The reaction mixture was refluxed at 110 °C for 24 h. After the completion of the reaction, the reaction mixture was cooled to room temperature and then extracted with water and chloroform. The chloroform layer was dried over sodium sulphate and concentrated under vacuum to get the crude product. The product was purified by column chromatography using hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate (6
ethyl acetate (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) as an eluent to obtain a pure compound as a white solid. Yield: 80%; mp: 163–165 °C; 1H NMR (CDCl3, 400 MHz): δ 7.80 (d, J = 0.92 Hz, 1H, C2H), 7.86 (d, J = 1.36 Hz, 1H, C3H), 8.29 (s, 1H, C5H); 13C NMR (CDCl3, 100 MHz): δ 115.9, 119.3, 119.9, 137.0, 137.4, 142.5; MS (EI): m/z 278 (M+ + 1).
4) as an eluent to obtain a pure compound as a white solid. Yield: 80%; mp: 163–165 °C; 1H NMR (CDCl3, 400 MHz): δ 7.80 (d, J = 0.92 Hz, 1H, C2H), 7.86 (d, J = 1.36 Hz, 1H, C3H), 8.29 (s, 1H, C5H); 13C NMR (CDCl3, 100 MHz): δ 115.9, 119.3, 119.9, 137.0, 137.4, 142.5; MS (EI): m/z 278 (M+ + 1).
3.3. Synthesis of compound 1
A vial equipped with a stirring bar was charged with 6,8-dibromo-imidazo[1,2-a]pyrazine (5) (0.5 g, 1.8 mmol), Cs2CO3 (0.6 g, 1.8 mmol) and boronic acid (1.8 mmol), dissolved in CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (9
H2O (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 100 °C under an inert atmosphere. Then, 5 mol% of Pd(PPh3)4 was added and the vial was capped. The reaction mixture was refluxed for 7–12 h. After the completion of the reaction (monitored by TLC), the reaction mixture was cooled, and then extracted with water and chloroform. The organic layer was dried over Na2SO4, filtered and concentrated under vacuum to obtain the crude product. The residue was purified by silica gel (60–120 mesh) column chromatography using hexane
1) at 100 °C under an inert atmosphere. Then, 5 mol% of Pd(PPh3)4 was added and the vial was capped. The reaction mixture was refluxed for 7–12 h. After the completion of the reaction (monitored by TLC), the reaction mixture was cooled, and then extracted with water and chloroform. The organic layer was dried over Na2SO4, filtered and concentrated under vacuum to obtain the crude product. The residue was purified by silica gel (60–120 mesh) column chromatography using hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate as an eluent. Two different coloured solid products, 1A and 1B, were obtained.
ethyl acetate as an eluent. Two different coloured solid products, 1A and 1B, were obtained.
3.4. Synthesis of compound 2
A vial equipped with a stirring bar was charged with 6-bromo-8-substituted-imidazo[1,2-a]pyrazine (1A or 1B) (0.1 g, 0.323 mmol), Cs2CO3 (0.105 g, 0.323 mmol) and 2-hydroxyphenylboronic acid (0.323 mmol), dissolved in CH3CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (9
H2O (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 100 °C under an inert atmosphere. Then, 5 mol% of Pd(PPh3)4 was added, the vial was capped and the mixture was refluxed for 6–12 h. After the completion of the reaction (monitored by TLC), the reaction mixture was cooled, and then extracted with water and chloroform. The organic layer was dried over Na2SO4, filtered and concentrated under vacuum to obtain the crude product. The residue was purified by silica gel (100–200 mesh) column chromatography using hexane
1) at 100 °C under an inert atmosphere. Then, 5 mol% of Pd(PPh3)4 was added, the vial was capped and the mixture was refluxed for 6–12 h. After the completion of the reaction (monitored by TLC), the reaction mixture was cooled, and then extracted with water and chloroform. The organic layer was dried over Na2SO4, filtered and concentrated under vacuum to obtain the crude product. The residue was purified by silica gel (100–200 mesh) column chromatography using hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate as an eluent. Two new different compounds, namely 2A and 2B, were obtained with respect to their starting reactants 1A and 1B.
ethyl acetate as an eluent. Two new different compounds, namely 2A and 2B, were obtained with respect to their starting reactants 1A and 1B.
Interestingly, the molecular mass from ESI-MS was found to be the same for compounds 1A and 1B (Fig. S3, and S7†), and likewise for 2A and 2B (Fig. S14, and S19†), but with different NMR signals (Fig. S1, S8, S5, S6, S12, S13, S17 and S18†). Furthermore, all the synthesized compounds have different absorption maxima (Fig. S10 and S21†), and characteristic FTIR signals (Fig. S4, S8, S15 and S20†), which clearly indicates that the obtained compounds 1A and 1B are isomeric forms of each other, as are 2A and 2B. The obtained compounds have a rigid architecture, except for rotation around the single bond connecting the phenyl ring to the imidazo-[1,2-a]pyrazine moiety. Therefore, the only possibility is for the isomeric forms to be different rotameric conformations. Thus, in order to determine the accurate structures of the possible conformers of compounds 1 and 2, theoretical calculations were performed.
3.5. Geometry optimization and reactivity of compound 1
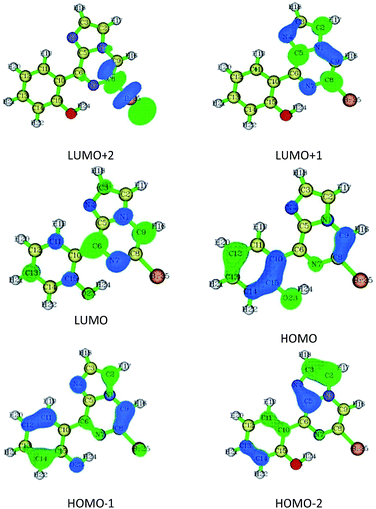
Compound 1 was optimized, and was further subjected to Fukui indices analysis, which is widely used to predict the reactivity indices in order to observe the reactive sites (electrophilic and nucleophilic sites) present on a molecule.42 Fukui functions are the partial derivatives of electron density with respect to the number of electrons present.where ρ(r) denotes the electron density, and N is the number of electrons present in the molecular system. Generally, the indices are calculated for the HOMO and LUMO, and represent the nucleophilicity and electrophilicity index, respectively. Reactive sites in the molecular system have larger Fukui index values (Fig. 1).
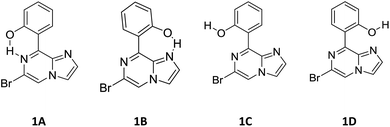
1. Compound 1 has rotational flexibility with respect to the single bond joining the hydroxy phenyl ring and the rigid imidazo-[1,2-a]pyrazine ring. Therefore, a conformational search was carried out using the rotational potential energy surface (PES) produced by DFT at the B3LYP/6-31+G* level. All possible conformations of compound 1 at local minima are shown in Scheme 2.
2. The obtained structures at local minima were analyzed to determine their relative Boltzmann contributions. From the Boltzmann distribution principle, any conformers with a free energy in the region of 5 kcal mol−1 can make some contribution to the Boltzmann population at room temperature (RT). Thus, the contributing conformers have been further optimized using DFT at the B3LYP/6-31++G(d,p) level and confirmed as having no imaginary frequencies.
3. The absorption spectra and NMR chemical shifts were computed for each of the optimized conformers using the TD-DFT and GIAO methods.
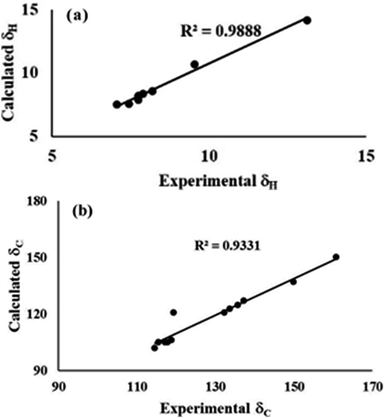
4. The experimental and calculated data for the absorption spectra, FTIR signals, and NMR shielding tensors were compared and evaluated to determine the structure of the compounds.
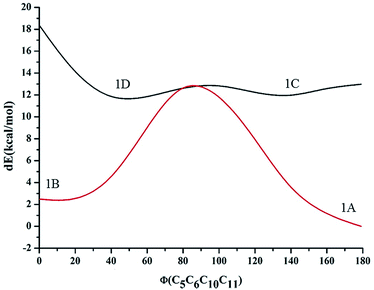 | ||
| Fig. 2 Energy variation (in kcal mol−1) of the different conformations for compound 1 along with the dihedral angle between the imidazole moiety and the phenolic moiety in the ground state. | ||
| Conformer | ΔE (kcal mol−1) | Boltzmann distribution (%) |
|---|---|---|
| 1A | 0.000 | 92.5 |
| 1B | 1.488 | 7.5 |
| 1C | 9.948 | 0 |
| 1D | 23.845 | 0 |
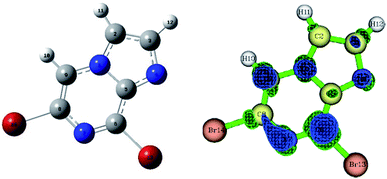
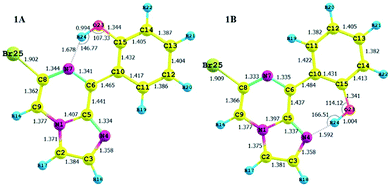
The calculated charges on the H24 [0.505 (NBO)], N7 [−0.571 (NBO)] and O23 [−0.677 (NBO)] atoms establish an intramolecular dipolar interaction between a phenolic hydrogen (O23–H24) and the pyrazine nitrogen (N7) of the imidazole moiety.
The calculated non-bonded distance between N7 and H24 bonded to O23 [d (N7⋯H24) = 1.678 Å] is less than the sum of the van der Waals radii of hydrogen and nitrogen. The smaller distance and columbic interaction with opposite charges on H24 and N7 support six-membered intramolecular hydrogen bonding.
The calculated charges on the H24 [+0.520 (NBO)], N4 [−0.539 (NBO)] and O23 [−0.560 (−0.712 (NBO))] atoms establish an intramolecular dipolar interaction between a phenolic hydrogen (O23–H24) and the pyrrole nitrogen (N4).
The non-bonded distance between the phenolic hydrogen and pyrrole nitrogen [d (H24⋯N4) = 1.592 Å], which is less than the sum of the van der Waals radii of hydrogen and nitrogen, supports hydrogen bonding. The smaller distance and columbic interaction with opposite charges on H24 and N4 confirmed the seven-membered intramolecular hydrogen bonding.
In addition to the N⋯H–O hydrogen bonding interactions in conformers 1A and 1B, there are ArH⋯N interactions, where the aromatic hydrogen of the phenolic moiety interacts with the pyrrole nitrogen for conformer 1A and the imidazole nitrogen for conformer 1B. These interactions are weak in nature, as confirmed by the interaction distances and topological parameters. Thus, conformer 1B exhibits seven-membered intramolecular hydrogen bonding, which is less stable than the six-membered hydrogen bonding exhibited by conformer 1A, and this could be the reason for the low Boltzmann contribution for conformer 1B.
Additionally, both conformers 1A and 1B were free from interelectronic repulsion, which is present in conformers 1C and 1D. Furthermore, the hydrogen bonding interaction was also estimated by QTAIM calculations using the Multiwfn program (Table 2).
| Compound | Interactions | BCP | d (Å) | ∠D⋯HA | ∇2ρ | V(r) | G(r) | H(r) | EHB |
|---|---|---|---|---|---|---|---|---|---|
| 1A | |||||||||
| N⋯HO | (3, −1) | 1.68 | 146.77 | 0.1303 | −0.0452 | 0.0419 | −0.0063 | −14.18 | |
| ArH⋯N | (3, −1) | 2.19 | 129.10 | 0.0637 | −0.0131 | 0.0145 | −0.0014 | −4.11 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| 1B | |||||||||
| N⋯HO | (3, −1) | 1.59 | 166.51 | 0.1295 | −0.0581 | 0.0453 | −0.0129 | −18.22 | |
| ArH⋯N | (3, −1) | 2.25 | 102.36 | 0.0812 | −0.0137 | 0.0170 | −0.0033 | −4.39 | |
| Bond | MBO at 6-31G** | LBO at 6-31++G** | ||
|---|---|---|---|---|
| 1A | 1B | 1A | 1B | |
| N4–H24 | — | 0.1867 | — | 0.0011 |
| N7–H24 | 0.1497 | — | 0.0006 | — |
| C15–O23 | 1.0574 | 1.0746 | 0.5981 | 0.5917 |
| O23–H24 | 0.7432 | 0.7011 | 0.5103 | 0.4638 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C etc. were observed for both conformers 1A and 1B. All computed band positions are in good agreement with the experimental values for both conformers. However, the OH stretching vibrations, which are usually environmentally dependent, suggestively distinguish both conformations. The free O–H stretching vibration occurs in the range of 3500–3700 cm−1, and the hydrogen bonded O–H stretching vibration is usually observed in the range of 3200–3600 cm−1.45,46 The computed frequency results showed the O–H stretching band at 3230.25 cm−1 in FTIR for conformer 1A. Experimentally a broad O–H stretching band is observed at 3158 cm−1 for conformer 1A (Fig. S4†). The computed and experimental FTIR values for conformer 1B were at 2999.47 cm−1 and 3069 cm−1, respectively (Fig. S8†). The broadness in the band also confirmed the presence of intramolecular hydrogen bonding. The difference in the FTIR values of the O–H bands for 1A and 1B revealed that the OH bond was slightly weak in conformer 1A relative to 1B. As discussed earlier, the more polarized nature of the O–H bond as indicated by LBO bond order analysis and the strong hydrogen bonding indicated by QTAIM analysis for conformer 1B further weaken the O–H bond strength for 1B. Therefore, the FTIR values were in good agreement with the observations from topology analysis, hydrogen bond strength, and LBOs.
C etc. were observed for both conformers 1A and 1B. All computed band positions are in good agreement with the experimental values for both conformers. However, the OH stretching vibrations, which are usually environmentally dependent, suggestively distinguish both conformations. The free O–H stretching vibration occurs in the range of 3500–3700 cm−1, and the hydrogen bonded O–H stretching vibration is usually observed in the range of 3200–3600 cm−1.45,46 The computed frequency results showed the O–H stretching band at 3230.25 cm−1 in FTIR for conformer 1A. Experimentally a broad O–H stretching band is observed at 3158 cm−1 for conformer 1A (Fig. S4†). The computed and experimental FTIR values for conformer 1B were at 2999.47 cm−1 and 3069 cm−1, respectively (Fig. S8†). The broadness in the band also confirmed the presence of intramolecular hydrogen bonding. The difference in the FTIR values of the O–H bands for 1A and 1B revealed that the OH bond was slightly weak in conformer 1A relative to 1B. As discussed earlier, the more polarized nature of the O–H bond as indicated by LBO bond order analysis and the strong hydrogen bonding indicated by QTAIM analysis for conformer 1B further weaken the O–H bond strength for 1B. Therefore, the FTIR values were in good agreement with the observations from topology analysis, hydrogen bond strength, and LBOs.Thus, the synthesized conformers have been optimized in the form of 1A and 1B. Both conformers 1A and 1B have a planar geometry and were found to be stabilised by six- and seven-membered hydrogen bonding, respectively. The stability and strength of the hydrogen bonds were established by QTAIM. The observed and calculated spectral data for NMR and FTIR were found to be in good correlation for each conformer.
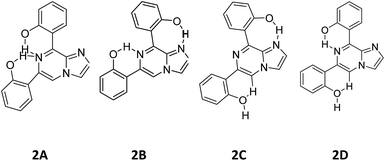
3.6. Structural analysis of compound 2
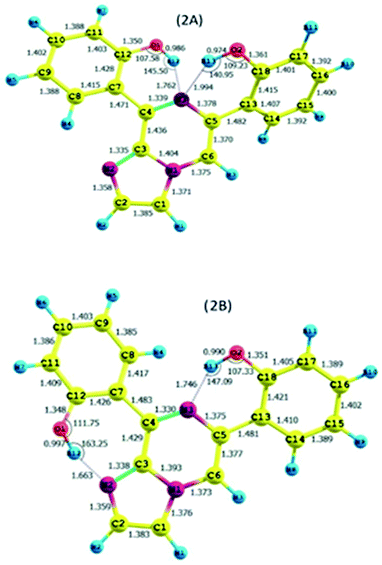
As discussed above, the isomeric forms of compound 1 were found to have 1A and 1B geometry. Subsequently, the separated isomers were reacted with another boronic acid and this resulted in two new compounds. Therefore, the conformers that resulted from the second substitution could have the possible structures shown in Scheme 3. Conformer 1A, stabilized by six-membered hydrogen bonding, could further result in either form 2A or 2B. Therefore, compound 2 was first optimized based on conformer 2A using the same protocol as for compound 1. The optimized geometry was confirmed by it having no imaginary frequencies. Furthermore, the optimized structure of conformer 2A was analysed through potential energy surface analysis for a dual dihedral scan of two phenolic moieties with the imidazo-[1,2-a]pyrazine moiety with variation from 0° to 180° at a step size of 20 degrees. The Boltzmann contributions of significant structures with a relative energy of 5 kcal mol−1 on the potential energy surface were considered for further analysis. Four conformers represented by 2A, 2B, 2C and 2D were found to be within the Boltzmann energy limit for a significant contribution (Fig. 7). The relative energy and Boltzmann distributions for all conformers at the minima have been calculated in Table 4. All the conformers were found to be stabilized by hydrogen bonding, established by the interaction distance primarily. Conformer 2B was found to be the most stable with the highest contribution of 91.9%, followed by conformer 2A with an ∼6.7% contribution. On the other hand, 2C and 2D have negligible Boltzmann distributions. The molecular structures with adequate Boltzmann distributions have been optimized and analyzed by frequency calculations. The optimized structures for the conformers are shown in Fig. 8 along with their characteristic structural parameters, such as bond lengths and bond angles. The stabilization of the conformers has been discussed on the basis of hydrogen bonding.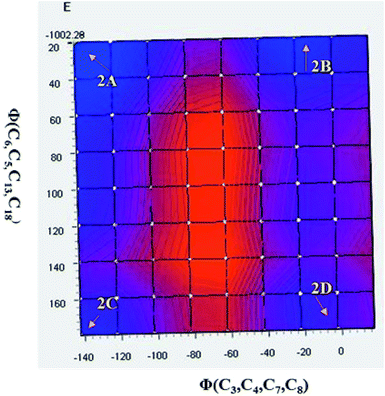 | ||
| Fig. 7 Potential energy surface for the dual dihedral angle between the imidazole moiety and a phenolic moiety in the ground state for compound 2, with four conformers at local minima. | ||
| Conformer | ΔE (kcal mol−1) | Boltzmann distribution (%) |
|---|---|---|
| 2A | 1.530 | 6.96 |
| 2B | 0 | 91.91 |
| 2C | 18.508 | 0 |
| 2D | 2.627 | 1.09 |
The calculated charges on the H12 [0.522 (NBO)], O1 [−0.699 (NBO)], H13 [0.519 (NBO)], O2 [−0.677 (NBO)] and N3 [−0.567 (NBO)] atoms establish N⋯H–O intramolecular dipolar interactions between a phenolic hydrogen and the pyrazine nitrogen of the imidazole moiety. The calculated non-bonded distance between the phenolic hydrogen (H12, H13) and pyrazine nitrogen (N3) [d (N3⋯H12) = 1.762 Å, and d (N3⋯H13) = 1.994 Å] has been found to be less than the sum of the van der Waals radii of hydrogen and nitrogen. The smaller distance and columbic interaction with opposite charges on H12, H13 and N3 support six-membered intramolecular hydrogen bonding.
The calculated charges on the H12 [0.525 (NBO)], O1 [−0.710 (NBO)], N2 [−0.512 (NBO)], H13 [0.523 (NBO)], O2 [−0.722 (NBO)] and N1 [−0.540 (NBO)] atoms establish N⋯H–O intramolecular dipolar interactions between a phenolic hydrogen and the pyrazine/pyrrole nitrogen of the imidazole moiety.
The calculated non-bonded distances between the phenolic hydrogen (H12, H13) and pyrazine/pyrrole nitrogen (N3/N2) [d (N2⋯H12) = 1.663 Å, and d (N3⋯H13) = 1.764 Å] were found to be less than the sum of the van der Waals radii of hydrogen and nitrogen. The smaller distance and columbic interaction with opposite charges on H12, H13 and N3 support six-membered intramolecular hydrogen bonding.
Additionally, both conformers 2A and 2B were free from interelectronic repulsion. Furthermore, the nature of the hydrogen bonding interaction was estimated by QTAIM calculations using the Multiwfn program.
| Compound | Interaction | BCP | d (Å) | ∠D⋯HA | ∇2ρ | V(r) | G(r) | H(r) | EHB |
|---|---|---|---|---|---|---|---|---|---|
| 2A | |||||||||
| N⋯HO | (3, −1) | 1.994 | 140.95 | 0.0742 | −0.0197 | 0.0191 | −0.0006 | −06.18 | |
| N⋯HO | (3, −1) | 1.762 | 145.50 | 0.1151 | −0.0354 | 0.0321 | −0.0033 | −11.10 | |
| ArH⋯N | (3, −1) | 2.265 | 123.12 | 0.0577 | −0.0110 | 0.0127 | 0.0017 | −3.45 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| 2B | |||||||||
| N⋯HO (7HB) | (3,−1) | 1.663 | 163.25 | 0.1240 | −0.0437 | 0.0374 | −0.0064 | −13.71 | |
| N⋯HO (6HB) | (3, −1) | 1.746 | 147.09 | 0.1165 | −0.0364 | 0.0327 | −0.0036 | −11.42 | |
| ArH⋯HAr | (3, −1) | 2.144 | 0.0471 | −0.0056 | 0.0087 | 0.0030 | −1.76 | ||
| Bond | MBO at 6-31G** | LBO at 6-31++G** | ||
|---|---|---|---|---|
| 2A | 2B | 2A | 2B | |
| N2–H12 | — | 0.1702 | — | — |
| N3–H12 | 0.1268 | — | — | — |
| N3–H13 | 0.0764 | 0.1317 | — | — |
| C12–O1 | 1.0336 | 1.0451 | 0.5755 | 0.5775 |
| C18–O2 | 0.9226 | 1.0342 | 0.5455 | 0.5775 |
| O1–H12 | 0.7663 | 0.7261 | 0.5433 | 0.4993 |
| O2–H13 | 0.8114 | 0.7565 | 0.6042 | 0.5364 |
Thus, the differences in the signals for the NMR, FTIR, and absorption peaks for the two compounds and their correlation with theoretical calculations clearly predict the specific orientation of the rotamers.
4. Conclusions
In summary, we have successfully synthesized a series of imidazo-[1,2-a]pyrazines, possessing different rotameric conformations, which were further purified by column chromatography. Theoretical investigation of the accurate structure of the different rotameric forms was done through PES and hydrogen bond strength analysis. The obtained rotameric forms were found to be stabilized by intramolecular hydrogen bond locking, which was further established by QTAIM analysis. The Laplacian and Mayer bond order (LBO/MBO) revealed that differences in bond strength for the different conformations, and thus distinctions in the vibrational frequency and NMR signals, assisted in the recognition of the accurate structure for the different conformations.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
VL thanks DST-INSPIRE (IFA12-CH-59), New Delhi for the fellowship and financial assistance. We also thank SAI Labs, Thapar University, Patiala for NMR and SAIF, Panjab University, Chandigarh for mass analysis.Notes and references
- A. Padwa and S. K. Bur, Tetrahedron, 2007, 63, 5341–5378 CrossRef CAS PubMed.
- T. Eicher, S. Hauptmann and A. Speicher, The Chemistry of Heterocycles: Structures, Reactions, Synthesis, and Applications, John Wiley & Sons, 2013 Search PubMed.
- N. Sanghai, V. Jain, R. Preet, S. Kandekar, S. Das, N. Trivedi, P. Mohapatra, G. Priyadarshani, M. Kashyap and D. Das, Med. Chem. Commun., 2014, 5, 766–782 RSC.
- C. Sablayrolles, J. C. Milhavet, E. Rechenq, J. P. Chapat, G. H. Cros, M. Boucard, J. J. Serrano and J. H. McNeill, J. Med. Chem., 1984, 27, 206–212 CrossRef CAS PubMed.
- L. C. Meurer, R. L. Tolman, E. W. Chapin, R. Saperstein, P. P. Vicario, M. M. Zrada and M. MacCoss, J. Med. Chem., 1992, 35, 3845–3857 CrossRef CAS PubMed.
- W. C. Lumma Jr, W. C. Randall, E. Cresson, J. R. Huff, R. D. Hartman and T. Lyon, J. Med. Chem., 1983, 26, 357–363 CrossRef CAS.
- J. J. Kaminski, D. Perkins, J. Frantz, D. M. Solomon, A. J. Elliott, P. Chiu and J. F. Long, J. Med. Chem., 1987, 30, 2047–2051 CrossRef CAS PubMed.
- P. A. Bonnet, A. Michel, F. Laurent, C. Sablayrolles, E. Rechencq, J. C. Mani, M. Boucard and J. P. Chapat, J. Med. Chem., 1992, 35, 3353–3358 CrossRef CAS PubMed.
- R. Goel, V. Luxami and K. Paul, Org. Biomol. Chem., 2015, 13, 3525–3555 CAS.
- J. Liu, D. Guiadeen, A. Krikorian, X. Gao, J. Wang, S. B. Boga, A.-B. Alhassan, Y. Yu, H. Vaccaro and S. Liu, ACS Med. Chem. Lett., 2015, 7, 198–203 CrossRef PubMed.
- S. M. González, S. Rodríguez-Arístegui, A. I. Hernández, C. Varela, E. G. Cantalapiedra, R. M. Álvarez, A. R. Hergueta, J. R. Bischoff, M. I. Albarrán and A. Cebriá, Bioorg. Med. Chem. Lett., 2017, 27, 2536–2543 CrossRef PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- S. A. Sharber, R. N. Baral, F. Frausto, T. E. Haas, P. Müller and S. W. Thomas III, J. Am. Chem. Soc., 2017, 139, 5164–5174 CrossRef CAS PubMed.
- E. L. Eliel and S. H. Wilen, Stereochemistry of Organic Compounds, John Wiley & Sons, 2008 Search PubMed.
- E. Peresypkina, A. Virovets and M. Scheer, Cryst. Growth Des., 2016, 16, 2335–2341 CAS.
- V. S. Kumar, F. C. Pigge and N. P. Rath, Cryst. Growth Des., 2004, 4, 651–653 CAS.
- S. P. Thomas, M. S. Pavan and T. N. Guru Row, Cryst. Growth Des., 2012, 12, 6083–6091 CAS.
- C. R. Jones, P. K. Baruah, A. L. Thompson, S. Scheiner and M. D. Smith, J. Am. Chem. Soc., 2012, 134, 12064–12071 CrossRef CAS PubMed.
- M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873–13900 RSC.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- C. B. Aakeröy, J. Desper, B. Leonard and J. F. Urbina, Cryst. Growth Des., 2005, 5, 865–873 Search PubMed.
- Y. Umezawa, S. Tsuboyama, K. Honda, J. Uzawa and M. Nishio, Bull. Chem. Soc. Jpn., 1998, 71, 1207–1213 CrossRef CAS.
- W. Saenger and G. Jeffrey, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin, 1991 Search PubMed.
- H. Huang, L. Yang, A. Facchetti and T. J. Marks, Chem. Rev., 2017, 117, 10291–10318 CrossRef CAS PubMed.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- E. A. Neal and S. M. Goldup, Chem. Commun., 2014, 50, 5128–5142 RSC.
- T. Lei, X. Xia, J.-Y. Wang, C.-J. Liu and J. Pei, J. Am. Chem. Soc., 2014, 136, 2135–2141 CrossRef CAS PubMed.
- S. P. Thomas, K. Shashiprabha, K. Vinutha, S. P. Nayak, K. Nagarajan and T. G. Row, Cryst. Growth Des., 2014, 14, 3758–3766 CAS.
- C. Zhu, A. U. Mu, Y.-H. Lin, Z.-H. Guo, T. Yuan, S. E. Wheeler and L. Fang, Org. Lett., 2016, 18, 6332–6335 CrossRef CAS PubMed.
- X. Chen, M. Addicoat, E. Jin, L. Zhai, H. Xu, N. Huang, Z. Guo, L. Liu, S. Irle and D. Jiang, J. Am. Chem. Soc., 2015, 137, 3241–3247 CrossRef PubMed.
- A. G. Gerbst, A. V. Nikolaev, D. V. Yashunsky, A. S. Shashkov, A. S. Dmitrenok and N. E. Nifantiev, Sci. Rep., 2017, 7, 8934 CrossRef PubMed.
- L. Čechová, E. Procházková, I. Císařová, M. Dračínský and Z. Janeba, Chem. Commun., 2014, 50, 14892–14895 RSC.
- B. Jiang, C.-G. Yang, W.-N. Xiong and J. Wang, Bioorg. Med. Chem., 2001, 9, 1149–1154 CrossRef CAS PubMed.
- R. Goel, V. Luxami and K. Paul, RSC Adv., 2014, 4, 9885–9892 RSC.
- M. J. Frisch and A. B. Nielsen, Gaussian 03 Programmer's Reference, Gaussian, 2003 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- U. Koch and P. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- H. H. Freedman, J. Am. Chem. Soc., 1961, 83, 2900–2905 CrossRef CAS.
- R. Silverstein, G. Bassler and T. Morrill, Spectroscopic Determination of Organic Compounds, Wiley, New York, 1981 Search PubMed.
- C. F. Matta, J. Hernández-Trujillo, T. H. Tang and R. F. Bader, Eur. J. Chem., 2003, 9, 1940–1951 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 1H NMR, 13C NMR, MS, FTIR, predicted absorption spectra and their correlation, and molecular orbitals. See DOI: 10.1039/c7ra13617j |
| This journal is © The Royal Society of Chemistry 2018 |