Soft magnetic nanocomposites based on adaptive matrix of wormlike surfactant micelles

Abstract

The paper describes a new type of soft magnetic nanocomposite (SMN) based on a transient network of wormlike surfactant micelles with embedded oppositely charged submicron particles of magnetite acting as cross-linking agents. We study the change of the rheological properties of the SMNs with different contents of particles in response to magnetic field. We show that even at low field strengths the system acquires solid-like behavior, which can be attributed to the aggregation of particles into chain-like/column structures. A solid-like behavior appears at a rather small volume fraction of particles (0.002–0.04) indicating weak restrictions imposed by the matrix to the reorganization of particles under magnetic field, which can be due to the self-assembled structure of the micellar network. In the oscillatory rheological measurements, SMNs show a linear viscoelastic response in an unusually wide region of values of strain, magnetic field strength and content of particles, which is caused by the viscoelastic contribution of the micellar network. Upon gradual increase of magnetic field strength H, the dynamic moduli G′ and G′′ demonstrate slow growth followed by a sharp rise with a scaling law H^3.0 and reach a plateau at 0.15 T. The highest values of the storage modulus G′ in SMNs are close to those in magnetorheological fluids with liquid Newtonian carrier, where particles move freely and the G′ value is defined by the interactions of magnetized particles and chain-like/columns structures. SMNs have a yield stress, which grows with the increase of magnetic field strength and finally levels off just at the same magnetic field strength at which the G′ and G′′ values reach a plateau indicating the saturation of the particles magnetization. The concentration dependencies of the elastic modulus and yield stress suggest the transition from chain-like to columnar structures of the particles. The new SMNs possessing the features of both magnetic fluids and magnetic gels have promising potential in a wide range of applications requiring responsiveness to magnetic field.

---

1. Introduction

Smart or adaptive materials attract considerable interest because of their ability to drastically change their properties under the action of external stimuli. One of the most attractive and easily implemented types of smart materials represent systems responsive to magnetic field that include magnetorheological fluids, ferrofluids, magnetoactive elastomers, magnetic gels etc.^1–9 These materials change the mechanical properties by several orders of magnitude in magnetic fields up to 1 T. This outstanding feature makes these materials very promising for applications in mechanical systems that require the active control of vibrations including shock absorbers, seismic vibration dampers, control valves, artificial joints and so on.^3–5,10,11

Magnetorheological fluids (MRFs) are usually composed of micron- or submicron-sized magnetic particles dispersed in a non-magnetisable carrier liquid.^4,5 They demonstrate very fast transition from a liquid to a nearly solid state, when magnetic field is applied. This behaviour is attributed to magnetization of the particles resulting in their aggregation due to dipole–dipole attraction,^5,8 which can lead to the formation of a network of chain-like particles aggregates spreading throughout the volume of the fluid. As the interparticle attraction decreases rather sharply with increasing distance between the particles, the formation of chain-like structures depends on the concentration of particles (that is on the average distance between them) and on the value of magnetic field strength determining the degree of magnetization of the particle (that is its magnetic dipole moment). During the aggregation, initially the single-width chain-like structures form and grow in length. Then, these structures can aggregate laterally building up wider columns.¹² The proposed mechanism of lateral aggregation involves the coalescence through torque-driven zippering motion.¹ It was suggested that the coarsening is driven by a local variation of the magnetic field around the initial chain-like structures caused by some topological defects.

Usually, in MRFs, the aggregation of magnetized particles is observed already at rather small concentrations of particles: 0.1–5 vol%.^5,13–15 However, these fluids suffer from some drawbacks. One of them is the nonlinear rheological response, which comes out with increasing strain amplitude.¹⁶ Another important drawback is an insufficient sedimentation stability. Indeed, usually the magnetic particles of rather large size are used to provide strong sensitivity to magnetic field. Also, the particles have much higher density than the carrier fluid. Such big and heavy particles have tendency to settle. Exacerbating the problem is that the particles strive to aggregate with each other in order to reduce the surface energy and sometimes because of the remnant magnetization. To overcome this problem different approaches have been proposed including the use of thixotropic agents,¹⁶ viscous¹⁷ or viscoplastic¹⁸ media. These approaches change the initial rheological properties and restrict the mobility of the particles required for structure formation under the action of magnetic field.

A wide range of linear rheological response and a strongly improved sedimentation stability can be obtained by using magnetic elastomers/gels.^3,19–22 But in these materials, chemical network limits considerably the mobility of particles and as a consequence the magnetic response. To get a significant magnetic response in this case it is necessary to use a high amount of particles (above 10 vol%) and fields above 0.1 T.

Recently, a new carrier for magnetic particles based on solutions of entangled wormlike micelles (WLMs) of surfactant was proposed.⁹ This carrier provides a high sedimentation stability because the particles incorporate into the transient micellar network by linking to the energetically unfavourable end-caps of micellar chains through fusion with the surfactant layer on their surface. The obtained SMNs do not phase separate during several months.⁹ In addition to improved sedimentation stability, WLM solutions can provide some other advantages as a carrier for magnetic particles. First, being formed by weak non-covalent interactions the WLMs can be easily reorganized^23–29 and one can expect that they will not restrict the mobility of particles under the action of magnetic field. Second, in oscillatory measurements, the neat WLM solutions demonstrate a linear viscoelastic region^30–32 in a wide range of strain and one can anticipate that it will remain in the presence of particles. Thus, the WLM network seems to be promising for the application as a matrix for magnetic fluid. However, the behaviour of these systems under magnetic field is almost unstudied.

Thus, the present paper is aimed at the investigation of the effect of magnetic field on the rheological properties of new SMNs composed of the solutions of entangled WLMs of surfactant and submicron-sized magnetite particles. The WLMs were formed from cationic surfactant erucyl bis-(hydroxyethyl) methylammonium chloride (EHAC) in the presence of low molecular weight salt potassium chloride (which is necessary to obtain long WLMs) and negatively charged 250 nm magnetite particles. As a result of these studies we demonstrate that in magnetic field, in addition to their high sedimentation stability the SMNs possess a broad region of linear viscoelastic response and high values of elastic moduli even at rather small volume fraction of particles (0.002–0.04). The obtained data contribute to the general understanding of the behaviour of the MRFs and can have important practical applications taking into account the valuable properties of the elaborated SMNs.

2. Experimental section

2.1 Materials

The WLMs were prepared from a cationic surfactant EHAC with a long mono-unsaturated C22 tail C₈H₁₇CH=CHC₁₂H₂₄N(CH₂CH₂OH)₂CH₃Cl. The surfactant solution containing 25 wt% 2-propanol was provided by Akzo Nobel. For purification from 2-propanol the crude EHAC solution was diluted 10 times with deionized water and then freeze-dried. The absence of 2-propanol in the obtained EHAC powder was proved by ¹H NMR spectroscopy. Potassium chloride (purity > 99%) from Acros Organics was used as received. Distilled water was purified by a Milli-Q system (Millipore).

Submicron particles of magnetite Fe₃O₄ were supplied by Aldrich. These particles have the average diameter of ca. 250 nm and the following magnetic characteristics: saturation magnetization 100 emu g⁻¹, residual magnetization 19 emu g⁻¹, coercive force 95 Oe.⁹ They demonstrate a ferrimagnetic behaviour.¹⁶ The sign of the surface charge of magnetite particles depends on pH: in acidic medium it is positive, in basic medium it becomes negative as a result of deprotonation of OH groups.³⁴ In the present study, the pH was kept at 11 to provide strong negative charge of the surface of particles.

SMNs were prepared following the procedure developed by us previously.⁹ Magnetite powder was added to surfactant solution and vortexed. Then some quantity of 15 wt% stock solution of salt was added and the resulting system was stirred with IKA Ultra-Turrax T25 homogenizer during at least 25 min at a rate of 5200 rpm. Then the SMNs thus prepared were left undisturbed for seven days to allow them to release air bubbles. The volume fraction of magnetite particles was varied from 0.002 to 0.04. The phase separation in the SMNs was examined by visual observation during 2 months storage at 25 °C.

2.2 Rheological measurements

The rheological properties of the SMNs in magnetic field were investigated with a commercial rheometer Physica MCR 301 (Anton Paar, Austria). All experiments were run at 20 °C set to ±0.1 °C accuracy by a Peltier temperature control device. The measuring system geometry was a special nonmagnetic 20 mm diameter parallel-plate set. The gap thickness between the plates was 300 μm in all measurements. Since we have chosen the most used gap thickness for such kind of experiments, it allowed us to compare quantitatively our results with the references avoiding the possible influence of the gap thickness on the viscoelasticity of the samples.^35,36 The magnetic field from 0.001 T to 1 T was generated in the direction perpendicular to shear with the magnetic cell of the rheometer. At each magnetic field strength, the samples were kept in the measurement cell at least 15 minutes before testing, since relaxation and reorganization processes in this system require rather long time because of high viscosity²¹ and long relaxation time³⁷ of EHAC solutions. The results were repeatable when the magnetic field strength was elevated either gradually or by high step changing. The magnetic field produced by the cell has a weak radial gradient with a pseudo-plateau at medium radial distance.³⁸ Such weak inhomogeneity of the field has to be taken into account only in highly concentrated magnetic systems.³⁸ In the present work, dilute suspensions of particles were used, and therefore, the field is assumed to be homogeneous. For strain sweep measurements, the frequency was kept at 1 rad s⁻¹. For frequency sweep measurements, the strain amplitude was picked from linear viscoelastic range. Yield stress was measured from stress–strain curves obtained in steady-state regime of applied shear stress.

3. Results and discussion

3.1 Viscoelastic carrier fluid

Viscoelastic transient network of entangled WLMs of EHAC surfactant was used as effective carrier for submicron magnetite particles.⁹ The micellar network provides strong viscoelasticity to the solution: highly viscous response at long-time shear stress action and gel-like response at the short-time action.^{30–32,39,40} Such solutions are promising candidates for SMN preparation because they have an extremely wide region of linear viscoelasticity.^32,39 For the present study, we used 0.6 wt% solution of EHAC in the presence of 1.5 wt% potassium chloride. This solution shows simple Maxwellian viscoelastic behaviour with a single relaxation time both with and without magnetite particles as was demonstrated earlier.^9,37 The relaxation time τ_R determined from the frequency ω_c at the intersection of G′(ω) and G′′(ω) dependences equals to 90 s for EHAC solution and 165 s for EHAC solution with 0.3 vol% of particles.

3.2 Linear viscoelastic response

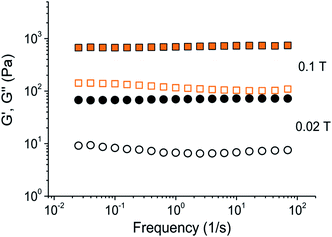
On Fig. 1 storage G′ and loss G′′ moduli are presented as a function of frequency of the applied stress at a fixed amplitude (shear strain) 1% under different magnetic field strengths. It is seen that in magnetic field, the SMN demonstrates a linear solid-like behaviour: both moduli are almost independent of frequency and the storage modulus G′ significantly exceeds the loss modulus G′′ within the studied range of frequencies. Note that in the absence of magnetic field the same sample exhibits viscoelastic liquid behaviour expressed in viscous liquid response with G′′ > G′ at low frequencies and elastic gel-like response with G′ > G′′ and a plateau modulus G₀ at middle and high frequencies.⁹ Therefore, the application of magnetic field induces the transition from liquid-like to solid-like behaviour. Solid-like rheological response is commonly attributed to the field-induced magnetization of the suspended particles^4,5,41,42 leading to their attraction to each other that results in the formation of anisometric chain-like aggregates aligned along the magnetic field lines (Fig. 2), which are perpendicular to the direction of flow. The longest chain-like structures spreading from one plate of the measurement cell to another induce the increase of the storage modulus G′, whereas shorter structures (so-called “free” strings) contribute to the loss modulus G′′.¹⁷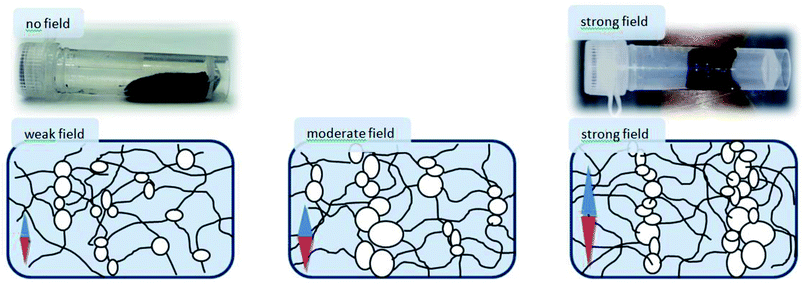

Fig. 1 Frequency dependence of storage G′ (filled symbols) and loss G′′ (open symbols) moduli at a constant strain of 1% and different magnetic field strengths of 0.02 T (black circles) and of 0.1 T (orange squares) for the SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

Fig. 2 (Top) Photo on the left represents SMN in liquid-like state (without magnetic field) and photo on the right demonstrates SMN in solid-like state (under the action of a strong magnetic field). (Bottom) Schematic representation of the variation of particles/WLM network structure with increasing magnetic field strength corresponding to regions I, II and III depicted on Fig. 4. Arrows indicate the direction of the magnetic field lines.

The SMNs in liquid-like state (without field) and in solid-like state (at quite strong magnetic field) are shown on photos in Fig. 2. In the absence of the field the SMN flows (left photo), whereas SMN exposed to the field does not flow, keeps its shape and stays near the magnet poles (right photo) due to magnetic forces that induce the formation of chain-like structures of particles and compel them to locate in higher field area.

From Fig. 1 it is seen that in the present system, the storage modulus G′ is higher than the loss modulus G′′ by an order of magnitude. The observed rheological behaviour of SMNs (Fig. 1) is quite different from that of classical MRFs based on Newtonian liquids, where the storage G′ and the loss G′′ moduli are usually close to each other in medium fields.^17,36,44 The high G′/G′′ ratio can be related to viscoelastic impact of the matrix – entangled network of WLMs^25,37,43 that will be discussed further.

A linear solid-like behaviour rather similar to that in SMNs (Fig. 1) was observed for micron-size carbonyl iron particles dispersed in highly viscous silicon oil¹⁷ but only at extremely low strain amplitude 0.01% (100 times lower than in the present system). Basically, the behaviour of SMNs is more reminiscent to that often observed in magnetic elastomers/gels demonstrating a high ratio of storage and loss moduli G′/G′′^19,20,45,46 attributed to viscoelasticity of the network matrix. However, in elastomers, a pronounced increase of the moduli in magnetic field can be achieved only at high volume fraction of magnetic particles,^19,47,48 which is required to form percolated chain-like structures inside a polymer network despite the restrictions imposed by the matrix to the mobility and the rearrangements of embedded particles. By contrast, the SMN under study provides high moduli G′ and G′′ at rather small volume fraction of particles (0.002–0.04), because it is based on “living” self-assembled matrix, which can be easily reorganized to follow the displacement of particles induced by the field. Thus, under magnetic field the SMNs even with rather small content of particles demonstrate a solid-like behaviour attributed to chain-like structures of the magnetized particles and a high G′/G′′ ratio related to viscoelastic properties of WLM network.

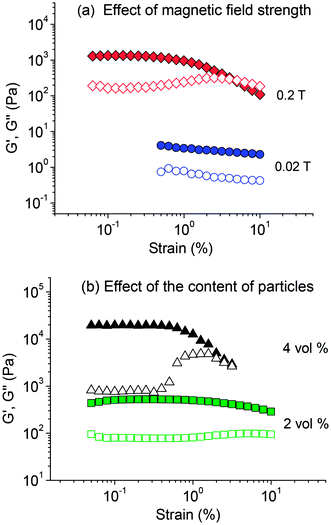
Fig. 3 shows the evolution of storage G′ and loss G′′ moduli with the amplitude of the applied strain. It is seen that at low strain the both moduli are almost unchanged, which corresponds to linear viscoelasticity regime. At higher strain, the system deviates from the linear viscoelasticity: the storage modulus decreases, whereas simultaneously the loss modulus increases and then passes through maximum. This behaviour is usually associated with the breakage of chain-like structures of particles:^5,34,45 it reduces the fraction of aggregates attached to both plates of the measuring cell thus decreasing G′, at the same time it augments the fraction of “free” strings thereby enhancing the loss modulus G′′. The deviations from linear viscoelasticity are more pronounced at higher strength of magnetic field (Fig. 3a) and at higher content of magnetic particles (Fig. 3b) that is in the cases, when stronger chain-like/column structures are formed. Thick and rigid columns break even at moderate strain amplitude deformation, thus giving input to nonlinear viscoelasticity. At the same time, thin and flexible columns that are formed at lower particles volume fraction and lower magnetic strength can contribute to linear viscoelasticity. It should be noted that in the systems under study the region of linear viscoelasticity is enormously wide (Fig. 3). For instance, for the sample containing 2 vol% of magnetite particles (Fig. 3b) the linear viscoelastic response is observed until a strain of at least 5% at magnetic field as high as 1 T. This property is quite important taking into account that many magnetorheological devices are exploited under dynamic conditions in linear viscoelasticity region.⁴⁴ In classic MRFs representing submicron magnetic particles suspended in Newtonian non-magnetisable liquid, the viscoelastic response to oscillating applied stress is mainly nonlinear, whereas the linear viscoelasticity region is very short being limited to extra low strain amplitudes (less than 0.01–0.5%) at moderate field (0.1 T).^{16,17,21,36,49,50} For instance, dilute suspension of submicron magnetite particles in viscous oil shows a linear viscoelasticity range until as low strain as 0.003%.³⁶ Micron iron particles suspended in silicon oil of very high viscosity (0.34 Pa s) also have rather short linear viscoelasticity region (up to 0.1%).⁴⁴ This drawback restricts considerably the possibility of utilization of such MRFs in the area, where oscillatory shear stress is periodically applied, for instance, in damper applications for vibration control. On the other hand, much longer linear viscoelasticity region was observed in magnetic polymer gels,^19,45,51 which was attributed to linear response of the polymer network itself.

Fig. 3 Variation of storage G′ (filled symbols) and loss G′′ (open symbols) moduli as a function of strain at constant frequency of 1 rad s⁻¹ (a) for SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC at different magnetic field strengths of 0.2 T (red diamonds) and 0.02 T (blue circles) and (b) for SMNs containing 2 vol% (green squares) or 4 vol% (black triangles) magnetite particles and 0.6 wt% EHAC at magnetic field strength of 1 T. Solvent: 1.5 wt% aqueous solution of KCl.

A broad range of linear viscoelasticity in SMNs under study can be provided in a similar way by WLM network. However, one can expect an additional stabilization effect of WLMs on chain-like structures of particles. Note that magnetite particles under study are negatively charged. Therefore, when such similarly charged particles start to aggregate under the action of magnetic field, they should overcome the electrostatic repulsion between them. Oppositely charged surfactant molecules intercalating between the particles will eliminate the repulsion⁵² thus favouring the growth and stabilization of chain-like aggregates. Therefore, the SMNs under study possess a wide region of linear viscoelastic properties, where the storage modulus is higher than the loss modulus and both of them are independent of time and amplitude of the harmonic stress. The observed properties suggest that SMNs are very promising for numerous magnetorheological applications under dynamic conditions.

3.3 Dynamic elastic moduli

The evolution of the dynamic moduli G′ and G′′ with gradual increase of magnetic field from 0.001 T to 1 T is illustrated on Fig. 4. It is seen that the graphs for both G′ and G′′ show quite similar S-shaped growth curves. On each curve, three different regions can be distinguished: initial slow growth (region I) followed by a sharp rise (region II) and a plateau (region III).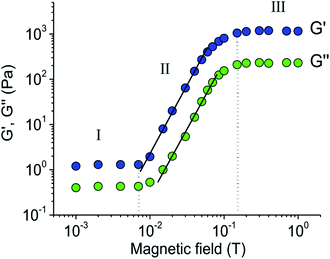

Fig. 4 Effect of magnetic field strength on storage G′ and loss G′′ moduli of SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

In region I, the moduli only slightly increase with magnetic field. In this region, the magnetic field is so weak that the particles are only scarcely magnetized³⁶ and therefore cannot form elongated aggregates, which could affect the dynamic moduli. At these conditions, the values of the moduli are determined by the contribution of viscoelastic WLM network, and their slight enhancement can be assigned to the restricted reptation of WLMs arising as a result of the displacement of particles guided by magnetic field.

When the field strength reaches 0.007 T, the both moduli start to rise dramatically indicating the transition to region II (Fig. 4). Such pronounced enhancement of the rheological properties is due to the formation of chain-like structures, which becomes possible, when the magnetic forces start to overcome the network–particles interactions. Note that the particles embedded into WLM network begin to form the chain-like structures at quite low field conditions. Comparison with the literature data³⁶ shows that inside the network the motion of the particles induced by magnetic forces starts at the same strength of magnetic field as it would be in low viscous Newtonian liquid carrier indicating that the WLMs do not restrict the displacement of the particles. Most probably, this is related to the ability of WLMs to continuously break and reform at relatively short timescales⁴³ thus making easy the rearrangement of micellar network in response to the relocation of the particles.

In region II, the increase of G′ and G′′ with the strength of magnetic field H proceeds according to the same scaling law: G′ ∼ H^3.0±0.2 and G′′ ∼ H^3.0±0.2 (Fig. 4). This law is even much stronger than that predicted theoretically^41,42,53 for MRFs: G′ ∼ H². As the theoretical estimates were obtained for single-width chains, this may indicate the formation of column structures in our system. An increase of G′ stronger than H² in MRFs with submicron magnetite was previously observed by de Vicente.⁵⁴ It was attributed to the addition of side chains to the single-width chains of particles. One can suggest that in the present system the surfactant favours the aggregation of particles into columns. As discussed above, it may proceed via intercalation of cationic surfactant molecules between negatively charged magnetite particles. Also, strong increase of G′ can be provided by viscoelastic WLM bridges formed between the aggregates of particles (Fig. 2).

At magnetic field of 0.15 T the moduli G′ and G′′ level off (regime III). This indicates the saturation of the particles magnetization so that further increase of the field strength does not affect the chain-like/column structures in the system.^36,42 Note that the saturation field strength observed here (0.15 T) is the same as for submicron magnetite particles in liquid carrier.^33,36,45 The highest values of the storage modulus G′ are also comparable to those observed in MRFs with submicron magnetite particles of the same concentration,³⁶ but the loss modulus G′′ in the present system is much lower than in MRFs. This indicates to lower dissipation part in the viscoelastic response of the SMNs in comparison with MRFs, which may be due to the linking of the particles and their aggregates to viscoelastic WLM network. Overall, in the present system the total increase of the moduli G′ and G′′ induced by the field exceeds 3 orders of magnitude (Fig. 4). It indicates that at high field, the viscoelasticity of the SMNs is dominated by the impact of chain-like/columnar structures formed by the particles, and the contribution of WLM network is negligible.

The evolution of the viscoelastic properties of the SMNs at increasing magnetic field was further examined by analysing the variation of the loss factor G′′/G′ data. On the dependence of the loss factor G′′/G′ on the magnetic field strength H (Fig. 5) one can see two plateaus (at low and at high field strengths, respectively) with a minimum between them. As was discussed above, the plateau at low magnetic field (H < 0.007 T) is determined by the viscoelasticity of WLM network, whereas the second plateau observed at H > 0.15 T is due to the saturation of particles magnetization. The minimum between the two plateaus corresponds to the structural transition induced by magnetic field.

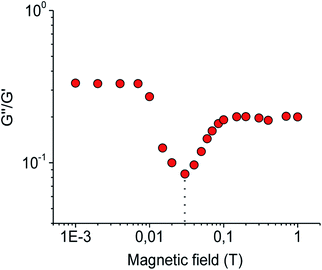Fig. 5 Effect of magnetic field strength on the loss factor G′′/G′ of SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

Note that in many magnetorheological soft materials increasing magnetic field strength leads to the increase of the loss factor followed by its saturation^46,55,56 indicating that the behaviour of the curve (Fig. 5) at higher magnetic field strength (H > 0.03 T) is governed by magnetic particles. This allows us to suggest that the part of the curve at lower magnetic field strength (H < 0.03 T) corresponds to the dominant impact of viscoelastic matrix. From Fig. 5 it is seen that in this part, the enhancement of H from 0.007 to 0.03 T leads to a decrease of the loss factor G′′/G′. Here the both moduli G′ and G′′ begin to grow (Fig. 4) due to the formation of chain-like structures of particles, and the elastic impact prevails over viscous one: G' > G′′. As the aggregates of particles that are formed at this rather low magnetic field strength H are suggested to be small, one can suppose that the predominantly elastic response is provided by WLM chains connected to these aggregates of particles.

At higher magnetic field strength (H > 0.03 T) the magnetic interactions between the particles become stronger and their effect on the both moduli G′ and G′′ start to dominate over the impact of WLM network. The increase of the loss factor G′′/G′ at H > 0.03 T suggests that more energy is dissipated as a function of the applied field. This can be attributed to the strengthening of the aggregates of particles with increasing magnetic field, which hampers them to follow the oscillating strain.

As to viscoelastic WLM matrix, at strong magnetic field (H > 0.03 T) it is suggested to easily reorganize to accommodate itself to the restructuration of the particles. The accommodation proceeds via breaking and reformation of particles/WLM junctions.⁹ In this reorganized system, the WLMs connect just formed chain-like structures of particles and built a common network with them as illustrated in Fig. 2. This peculiarity distinguishes WLM network from a polymeric one, in which under the action of magnetic field the polymer chains stretch in order to permit the displacement of particles linked to them.¹⁹ This restricts the movement of particles in the polymeric matrix. By contrast, self-assembled WLMs give free rein to particles and form a new network accommodating the new aggregates of particles.

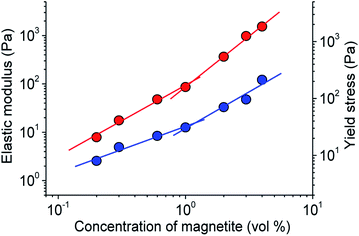
Fig. 6 shows the variation of storage modulus G′ with the concentration of magnetite particles φ under magnetic field of 1 T corresponding to saturation region. On this plot, one can distinguish two power-law dependences: G′ ∼ φ^1.5±0.1 (at φ < 1 vol%) and G′ ∼ φ^2.1±0.1 (at φ > 1 vol%). According to literature data,^16,57,58 the change of the power law can be attributed to the transition from chain-like structures of the magnetic particles to column structures, when the concentration of particles increases. Close value of the exponent (2.2 ± 0.4) in a similar range of concentrations of particles (0.5–5 vol%) was observed for submicron magnetite particles suspended in silicon oil containing polyethylene.³⁶ From Fig. 6 it is seen that at high content of particles, the elastic modulus gets the value of 1.5 kPa, which exceeds the plateau modulus of the parent WLM network by 3 orders of magnitude.

Fig. 6 Elastic storage modulus G′ at magnetic field strength of 0.2 T (red circles) and static yield stress at magnetic field strength of 1 T (blue circles) as a function of the concentration of magnetite particles in SMN containing 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

Thus, the SMNs composed of WLM network with embedded submicron magnetite particles demonstrate linear viscoelastic response in unusually wide region of values of strain, magnetic field strength and content of particles. The highest values of G′ are mostly consistent with theoretical predictions for MRF with liquid Newtonian carrier, where particles move freely and the value of storage modulus G′ is defined by magnetized particles interactions and chain like/columns structures thus indicating to weak restrictions imposed by the WLM matrix, which can be attributed to “living” nature of micellar network.^28–30

3.4 Yield stress

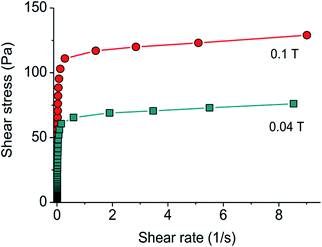
The above-described measurements were carried out at low stress in the pre-yield regime thus providing insight into initial undisturbed structure of the system. Higher stress can disrupt the structure. The minimum stress required to move the chain-like structures is called static (or frictional) yield stress. This yield stress is often associated with the slip of the aggregates along the measuring plates rather than the breaking of their chain-like structure under the shear.^5,17,59 Dependencies of the shear stress on the shear rate at different magnetic field strengths are shown on Fig. 7. It is seen that the shear rate starts to accelerate above a certain stress value, which represents a static yield stress of the sample τ_y. Further, we will call it just yield stress. From Fig. 7 it is evident that the yield stress τ_y increases with magnetic field strength, which can be due to stronger chain-like skeleton of the particles.

Fig. 7 Shear stress as a function of shear rate at different magnetic field strengths: 0.04 T (olive squares) and 0.1 T (red circles) for SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

The dependence of the yield stress τ_y on magnetic field strength is shown in Fig. 8. It is seen that at low magnetic field (H < 0.01 T) no yield stress is observed indicating that the interactions between the particles are too weak to construct percolated aggregates. The yield stress appears at H ≈ 0.01 T and grows with further increase of magnetic field strength according to power law of τ_y ∼ H^0.8±0.1 (Fig. 8), which can be attributed to the reinforcement of chain-like structures formed by the particles. Finally, the yield stress levels off just at the same magnetic field strength at which the G′ and G′′ values reach a plateau (cf. Fig. 3 and 8) indicating the saturation of the particles magnetization. The maximum value of the yield stress observed here (100 Pa) is comparable to that of MRF with submicron magnetite particles.¹³

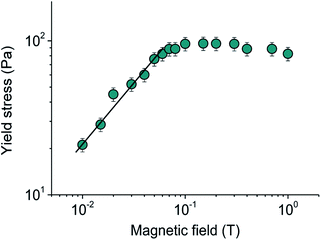Fig. 8 Effect of magnetic field strength on the static yield stress τ_y of SMN containing 3 vol% magnetite particles and 0.6 wt% EHAC. Solvent: 1.5 wt% aqueous solution of KCl.

Fig. 6 presents the dependence of the yield stress τ_y on the concentration of magnetite particles at constant value of magnetic field H = 1 T corresponding to saturation region. The dependence consists of two power-laws: τ_y ∼ φ^0.8±0.1 and τ_y ∼ φ^1.3±0.2 changing at φ ≈ 1 vol%. The first exponent 0.8 is in good agreement with the linear dependence of the yield stress on the particles content predicted by Ginder⁴² and confirmed by several experimental results for dilute dispersions.^13,16 At larger content of particles, the exponent becomes higher – (1.3 ± 0.2). Similar behaviour was observed previously for micron carbonyl iron^16,58 and micron magnetite¹⁶ in silicone oil. The change of the concentration dependence of the yield stress at larger content of particles was explained by the transition from chain-like to column structures of the magnetic particles with increasing their concentration. Highly compact column structures restrict the deformation, which results in larger yield stress values.^16,57 Note that similar two power-law dependence on the concentration of magnetic particles was also observed for the elastic modulus (Fig. 6), and the transition between the two power law dependences proceeded at the same concentration of magnetite (1 vol%). Thus, the changeover from chain-like aggregates to columnar structures at increasing concentration of aggregating magnetite particles is reflected both on the evolution of elasticity modulus (measured at pre-yield low strains) and yield stress (determined at higher strains).

4. Conclusions

In this paper, the viscoelastic properties of SMNs composed of submicron magnetite particles dispersed in WLM network were studied under the action of magnetic field at different volume fraction of particles. It was observed that the SMNs combine features typical for MRFs based on Newtonian liquid with some features of magnetorheological elastomers/gels. Similar to magnetic elastomers/gels SMNs demonstrate a broad range of linear viscoelasticity and a high ratio of storage and loss moduli G′/G′′ attributed to viscoelastic contribution of the network matrix. At the same time, in contrast to elastomers, the SMNs provide high moduli G′ and G′′ at rather small volume fraction of particles (0.002–0.04), because WLMs do not hinder the field-induced rearrangement of particles, as it occurs in polymeric networks. Simultaneously, the elastic modulus G′ and the yield stress of the SMN gain high values comparable to MRFs, where particles are located in Newtonian liquid carrier and a network does not restrict their motion driven by field. This feature is explained by “living” character of bonds between WLMs and magnetic particles, which does not hinder the aggregation of the particles.

A broad region of linear viscoelasticity demonstrated by SMNs allows one to measure mechanical properties of the SMNs under oscillating stress thus modelling conditions of the practical applications of magnetoresponsive smart materials as damping and amortization material. Thus, transient network of entangled WLM is a promising matrix for preparation of SMNs with prospective mechanical properties suitable for various implications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Russian Foundation for Basic Research and Moscow City Government (project No. 15-33-70046 “mol_a_mos”).

References

1. G. Bossis, O. Volkova, S. Lacis and A. Meunier, Magnetorheology: Fluids, Structures and Rheology, Ferrofluids, Lecture Notes in Physics, ed S. Odenbach, Springer, Berlin, 2002, vol. 594, pp. 202–230.
2. S. Odenbach, J. Phys.: Condens. Matter, 2004, 16, R1135–R1150.
3. G. Filipcsei, I. Csetneki, A. Szilgyi and M. Zrinyi, Magnetic Field-Responsive Smart Polymer Composites, Advances in Polymer Science, Oligomers, Polymer Composites, Molecular Imprinting, Springer, Berlin, 2007, vol. 206, pp. 137–189.
4. B. J. Park, F. F. Fang and H. J. Choi, Soft Matter, 2010, 6, 5246–5253.
5. J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710.
6. C. Echeverria and C. Mijangos, Langmuir, 2011, 27, 8027–8035.
7. Y. Zhou, N. Sharma, P. Deshmukh, R. K. Lakhman, M. Jain and R. M. Kasi, J. Am. Chem. Soc., 2012, 134, 1630–1641.
8. J. Faraudo, J. S. Andreu and J. Camacho, Soft Matter, 2013, 9, 6654–6664.
9. V. A. Pletneva, V. S. Molchanov and O. E. Philippova, Langmuir, 2015, 31, 110–119.
10. S. S. Abramchuk, E. Y. Kramarenko, G. V. Stepanov, L. V. Nikitin, G. Filipcsei, A. R. Khokhlov and M. Zrinyi, Polym. Adv. Technol., 2007, 18, 883–890.
11. O. V. Stolbov, Y. L. Raikher and M. Balasoiu, Soft Matter, 2011, 7, 8484–8487.
12. J. M. Martin and J. Odinek, Phys. Rev. Lett., 1992, 69, 1524–1528.
13. F. Vereda, J. De Vicente, J. P. Segovia-Gutiérrez and R. Hidalgo-Alvarez, J. Phys. D: Appl. Phys., 2011, 44, 425002.
14. D. I. Santiago-Quiñonez and C. Rinaldi, Soft Matter, 2012, 8, 5327–5333.
15. A. Barabanova, V. Molchanov, O. Philippova and A. Khokhlov, Macromol. Symp., 2014, 337, 80–86.
16. B. D. Chin, J. H. Park, M. H. Kwon and O. O. Park, Rheol. Acta, 2001, 40, 211–219.
17. J. Claracq, J. Sarrazin and J.-P. Montfort, Rheol. Acta, 2004, 43, 38–49.
18. P. J. Rankin, A. T. Horvath and D. J. Klingenberg, Rheol. Acta, 1999, 38, 471–477.
19. T. Mitsumata, A. Honda, H. Kanazawa and M. Kawai, J. Phys. Chem. B, 2012, 116, 12341–12348.
20. V. V. Sorokin, E. Ecker, G. V. Stepanov, M. Shamonin, G. J. Monkman, E. Y. Kramarenko and A. R. Khokhlov, Soft Matter, 2014, 10, 8765–8776.
21. H.-N. An, B. Sun, S. J. Picken and E. Mendes, J. Phys. Chem. B, 2012, 116, 4702–4711.
22. A. V. Ryzhkov, P. V. Melenev, M. Balasoiu and Y. L. Raikher, J. Chem. Phys., 2016, 145, 074905.
23. D. A. Kuryashov, O. E. Philippova, V. S. Molchanov, N. Y. Bashkirtseva and I. N. Diyarov, Colloid J., 2010, 72, 230–235.
24. E. Oikonomou, G. Bokias, J. K. Kallitsis and I. Iliopoulos, Langmuir, 2011, 27, 5054–5061.
25. V. S. Molchanov and O. E. Philippova, J. Colloid Interface Sci., 2013, 394, 353–359.
26. A. V. Shibaev, M. V. Tamm, V. S. Molchanov, A. V. Rogachev, A. I. Kuklin, E. E. Dormidontova and O. E. Philippova, Langmuir, 2014, 30, 3705–3714.
27. A. V. Shibaev, V. S. Molchanov and O. E. Philippova, J. Phys. Chem. B, 2015, 119, 15938–15946.
28. Y. Feng, Z. Chu and C. A. Dreiss, Smart Wormlike Micelles: Design, Characteristics and Applications, Springer-Verlag, Berlin, Heidelberg, 2015.
29. A. L. Kwiatkowski, H. Sharma, V. S. Molchanov, A. S. Orekhov, A. L. Vasiliev, E. E. Dormidontova and O. E. Philippova, Macromolecules, 2017, 50, 7299–7308.
30. L. J. Magid, J. Phys. Chem. B, 1998, 102, 4064–4074.
31. R. Oda, J. Narayanan, P. A. Hassan, C. Manohar, R. A. Salkar, F. Kern and S. J. Candau, Langmuir, 1998, 14, 4364–4572.
32. Giant Micelles: Properties and Applications, ed. R. Zana and E. W. Kaler, CRC Press, Boca Raton, 2007.
33. J. Wu, L. Pei, S. Xuan, G. Yan and X. Gong, J. Magn. Magn. Mater., 2016, 408, 18–25.
34. C. Galindo-Gonzalez, S. Gantz, L. Ourry, F. Mammeri, S. Ammar-Merah and A. Ponton, Macromolecules, 2014, 47, 3136–3144.
35. M. T. López-López, L. Rodriguez-Arco, A. Zubarev, L. Iskakova and D. G. Durán, J. Appl. Phys., 2010, 108, 083503.
36. J. de Vicente, J. P. Segovia-Gutiérrez, E. Andablo-Reyes, F. Vereda and R. Hidalgo-Alvarez, J. Chem. Phys., 2009, 131, 194902.
37. A. L. Kwiatkowski, V. S. Molchanov, A. S. Orekhov, A. L. Vasiliev and O. E. Philippova, J. Phys. Chem. B, 2016, 120, 12547–12556.
38. M. T. López-López, A. Gómez-Ramirez, L. Rodriguez-Arco, D. G. Durán, L. Iskakova and A. Zubarev, Langmuir, 2012, 28, 6232–6245.
39. C. A. Dreiss, Soft Matter, 2007, 3, 956–970.
40. K. Trickett and J. Eastoe, Adv. Colloid Interface Sci., 2008, 144, 66–74.
41. T. C. B. McLeish, T. Jordan and M. T. Shaw, J. Rheol., 1991, 35, 427–448.
42. J. M. Ginder, L. C. Davis and L. D. Elie, Int. J. Mod. Phys. B, 1996, 10, 3293–3303.
43. V. S. Molchanov and O. E. Philippova, Colloid J., 2009, 71, 249–255.
44. W. H. Li, G. Chen and S. H. Yao, Smart Mater. Struct., 1999, 8, 460–468.
45. T. Mitsumata, T. Wakabayashi and T. Okazaki, J. Phys. Chem. B, 2008, 112, 14132–14139.
46. V. S. Molchanov, G. V. Stepanov, V. G. Vasiliev, E. Y. Kramarenko, A. R. Khokhlov, Z.-D. Xu and Y.-Q. Guo, Macromol. Mater. Eng., 2014, 299, 1116–1125.
47. G. V. Stepanov, S. S. Abramchuk, D. A. Grishin, L. V. Nikitin, E. Y. Kramarenko and A. R. Khokhlov, Polymer, 2007, 48, 488–495.
48. Q. Chen, S. Gong, J. Moll, D. Zhao, S. K. Kumar and R. H. Colby, ACS Macro Lett., 2015, 4, 398–402.
49. Y. Otsubo, Colloids Surf., 1991, 58, 73–86.
50. M. Parthasarathy, K. H. Ahn, B. Belongia and D. J. Klingenberg, Int. J. Mod. Phys. B, 1994, 8, 2789–2809.
51. H. An, S. J. Picken and E. Mendes, Polymer, 2012, 53, 4164–4170.
52. O. E. Philippova, L. A. Chtcheglova, N. S. Karybiants and A. R. Khokhlov, Polym. Gels Networks, 1998, 6, 409–421.
53. J. E. Martin and R. A. Anderson, J. Chem. Phys., 1996, 104, 4814–4827.
54. J. de Vicente and J. Ramirez, J. Colloid Interface Sci., 2007, 316, 867–876.
55. M. R. Jolly, J. D. Carlson, B. C. Munoz and T. A. Bullions, J. Intell. Mater. Syst. Struct., 1996, 7, 613–622.
56. H. An, S. J. Picken and E. Mendes, Soft Matter, 2010, 6, 4497–4503.
57. X. Tang, Y. Chen and H. Conrad, Structure and interaction force in a model magnetorheological model, in Electro-Rheological Fluids, Magneto-Rheological Suspensions and Associated Technology, ed. W. A. Bullough, World Scientific, Singapore, 1996, pp. 603–612.
58. O. Volkova, G. Bossis, M. Guyot, V. Bashtovoi and A. Reks, J. Rheol., 2000, 44, 91–104.
59. J. L. Viota, A. V. Delgado, J. L. Arias and J. D. G. Durán, J. Colloid Interface Sci., 2008, 324, 199–204.

---