Open Access Article
Open Access ArticleTheoretical study on the reaction mechanism of the thermal cis–trans isomerization of fluorine-substituted azobenzene derivatives†
Xiao-Mei Liua,
Xing-Yi Jinb,
Zhi-Xiang Zhanga,
Jian Wang *a and
Fu-Quan Bai
*a and
Fu-Quan Bai *a
*a
aInstitute of Theoretical Chemistry, Laboratory of Theoretical and Computational Chemistry, International Joint Research Laboratory of Nano-Micro Architecture Chemistry, Jilin University, Changchun 130023, People's Republic of China. E-mail: abbott@jlu.edu.cn; baifq@jlu.edu.cn
b1st Department of Neurosurgery, China–Japan Union Hospital, Jilin University, Xiantai Street No. 126, Changchun 130033, People's Republic of China
First published on 23rd March 2018
Abstract
This research was based on the quantum chemical calculations of a set of valid photoswitches of azobenzene compounds, with the aim of describing their thermal isomerization. The influences of familiar fluorine substitution and additional electron-donating groups (EDGs) and electron-withdrawing groups (EWGs) on the para-position were also systematically studied. The results show that the presence of fluorine in different ortho-positions has a distinct effect on the molecular orbital distribution of the E isomer, which realizes the purpose of splitting the n → π* transition between the E and Z isomers. On this basis, further para-substitution can allow tunability on the order of the energy level to the molecular orbitals through their influence on the conjugation pattern of the compound. It is the modification of the substituent on these positions that allows the photoisomerization to proceed under visible wavelength light surroundings. The thermal Z → E isomerization mechanism has also been analyzed, and a detailed comparison of these compounds has been made with respect to the thermal half-life τ1/2, and the rate constants kZ–E. The results reveal that isomerization is thought to be a process of globally structural change, during which the effect of the substituents is determined by the extent of their influence on the conjugated system.
Introduction
Molecular photoswitches have aroused widespread interest in recent years.1–5 Because of their unique photochromic characteristics,6 they have been widely used in molecular data storage,7–9 photopharmacology,10 optochemical genetics,11 materials science,12 and biomolecules13,14 among other areas. Over the past few decades, most research has been focused on azobenzenes,15 spiropyrans,16 diarylethenes,17 and stilbenes18 which are all characterized by photoisomerization. Among these molecules, azobenzene, which is based on the diatomic structure N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, has unique structural characteristics and can be used for optical control under different conditions.19–21 Therefore, it is treated as a classical photochromic compound.
N, has unique structural characteristics and can be used for optical control under different conditions.19–21 Therefore, it is treated as a classical photochromic compound.
The azobenzene molecule exists in trans- (E) and cis- (Z) configurations, where the approximately planar structure of the former makes it more stable than the latter. Knie and colleagues measured the absorption spectra of both isomers in acetonitrile (ACN) solution using an ultra-performance liquid chromatograph (UPLC).22 The characteristic absorption spectra present in the trans-isomer of azobenzene are the π → π* absorption (λmax = 317 nm; ε = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1) in the ultraviolet region and the n → π* absorption (λmax = 444 nm; ε = 400 M−1 cm−1) in the visible region.23 The π-electron system of the azobenzene compound is easily modified by altering the substituent, which can change its absorption peaks. More importantly, its isomerization process is reversible. In many cases, the ease of the isomerization reaction of azobenzene is related to its cis- and trans-conformations. It is significant to regulate the cis → trans isomerization process under certain conditions. In general, azobenzene-based photoswitches refer to isomerization under ultraviolet (UV) light irradiation. However, as UV light can cause damage to organisms, its application in biological systems is restricted. To break this restriction, a common strategy is to make the absorption spectra of isomers shift using the substituent effect on benzene. Siewertsen et al. reported a bridged azobenzene derivative with a large separation of the n → π* band in the cis- and trans-isomers, which exhibits improved performance in terms of photoisomerization compared with azobenzene.24 Yang et al. reported the synthesis of a BF2–azo complex and the separation of the n → π* transition in cis- and trans-isomers, herewith achieving efficient conversion of the two isomers in the visible region.25 Subsequently, the trans–cis isomerization of the BF2–azo compound in the near-infrared region (NIR) is achieved by introducing electron-donating groups into the para-position.26 From the perspective of theoretical calculations, our group studied the thermal cis-to-trans isomerization of BF2–azo compounds with respect to para-substitution with electron-donating groups.27 Both theoretical and experimental results demonstrated that the larger the separation of the n → π* absorption bands between the cis- and trans-isomers, the better the conversion rate of both isomerizations. However, this conclusion only relates to para-substitution, leaving the question of the effect of other substitutions unanswered.
000 M−1 cm−1) in the ultraviolet region and the n → π* absorption (λmax = 444 nm; ε = 400 M−1 cm−1) in the visible region.23 The π-electron system of the azobenzene compound is easily modified by altering the substituent, which can change its absorption peaks. More importantly, its isomerization process is reversible. In many cases, the ease of the isomerization reaction of azobenzene is related to its cis- and trans-conformations. It is significant to regulate the cis → trans isomerization process under certain conditions. In general, azobenzene-based photoswitches refer to isomerization under ultraviolet (UV) light irradiation. However, as UV light can cause damage to organisms, its application in biological systems is restricted. To break this restriction, a common strategy is to make the absorption spectra of isomers shift using the substituent effect on benzene. Siewertsen et al. reported a bridged azobenzene derivative with a large separation of the n → π* band in the cis- and trans-isomers, which exhibits improved performance in terms of photoisomerization compared with azobenzene.24 Yang et al. reported the synthesis of a BF2–azo complex and the separation of the n → π* transition in cis- and trans-isomers, herewith achieving efficient conversion of the two isomers in the visible region.25 Subsequently, the trans–cis isomerization of the BF2–azo compound in the near-infrared region (NIR) is achieved by introducing electron-donating groups into the para-position.26 From the perspective of theoretical calculations, our group studied the thermal cis-to-trans isomerization of BF2–azo compounds with respect to para-substitution with electron-donating groups.27 Both theoretical and experimental results demonstrated that the larger the separation of the n → π* absorption bands between the cis- and trans-isomers, the better the conversion rate of both isomerizations. However, this conclusion only relates to para-substitution, leaving the question of the effect of other substitutions unanswered.
Recently, Bleger synthesized a series of ortho-fluoroazobenzenes and published a systematical analysis of their photophysical and photochemical performance.28 According to the results, substitution on the ortho-position by fluorine can also shift the absorption of azobenzene bathochromic, an effect which is more obvious with the increase of fluorine. Moreover, because there is a distinct spectroscopic shift, photoisomerizations become possible under visible irradiation. Although similar to the BF2–azo compound mentioned above, the effect of ortho-fluoro substitution is still unknown and worth in-depth study. Furthermore, it is intriguing to explore the effect of combining both ortho- and para-substitution in one azobenzene. According to this strategy, a series of ortho-fluoroazobenzenes 1–4 as shown in Fig. 1 were selected systematically in this work. Additionally, the effects of electron-donating groups (EDGs) and electron-withdrawing groups (EWGs) on para-positions are also considered, such as compounds 5, 6, 7, 8 and 9. We give an in-depth examination of the substituent effect on the isomerization of azobenzene in terms of geometry of the structures, molecular orbital information, absorption spectra, energy barrier for the isomerization pathway and thermal half-lives of these compounds. Ultimately, this research is intended to promote the rational design of molecular photoswitches.
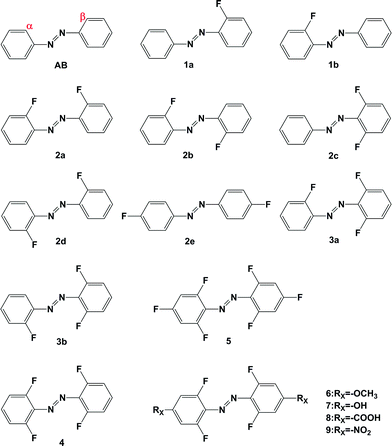 | ||
| Fig. 1 Molecular structure of azobenzene compounds (α and β represent fluorine atom substitution at different ortho-positions, respectively). | ||
Computational details
In this paper, all quantum chemical calculations were carried out using the Gaussian 09 suite of programs (D.01).29 The density-functional theory (DFT)30,31 method was used to calculate the ground state, and the time-dependent density-functional theory (TD-DFT)32–34 method was utilized to investigate properties under the excited state. With respect to timeliness and accuracy, various functions including M06, M06L, M06-2X, PBE0 and B3LYP were evaluated.35 After comparison, B3LYP was selected in geometry optimization of cis- and trans-configurations. It was found that geometry optimization of the absorption spectra of the cis- and trans-configurations calculated using B3LYP functional were in good agreement with the experimental data (see Table S1†). In addition, we tested the different basis sets, among which the most suitable for our system was 6-311G* (see Table S2†). On this basis, vibration frequency analysis was performed in order to ascertain the stability of the molecular structure. Taking into account solvent effects, this was performed using the self-consistent reaction field theory with the polarizable continuum model (PCM) for the ACN solvent.36Based on the conventional transition state theory (TST),37,38 flexible scanning of the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C for the molecule was implemented in an attempt to obtain the transition state. Intrinsic reaction coordinates (IRCs) were operated to identify the accuracy of the transition state. The thermal reaction rates constants kZ–E at a temperature of 298.15 K and a pressure of 1 atm were calculated using KiSThelp program software.39 The effect of one-dimensional (1D) Wigner tunneling (WT) on the reaction rate was also taken into consideration.40 In order to gain more reliable results, we needed to consider the WT coefficient of the 1D Wigner tunneling to correct the reaction rate:
N–C for the molecule was implemented in an attempt to obtain the transition state. Intrinsic reaction coordinates (IRCs) were operated to identify the accuracy of the transition state. The thermal reaction rates constants kZ–E at a temperature of 298.15 K and a pressure of 1 atm were calculated using KiSThelp program software.39 The effect of one-dimensional (1D) Wigner tunneling (WT) on the reaction rate was also taken into consideration.40 In order to gain more reliable results, we needed to consider the WT coefficient of the 1D Wigner tunneling to correct the reaction rate:
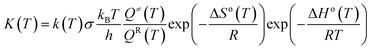 | (2.1) |
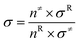 | (2.2) |
The thermal transition rate constants k are calculated using the standard Eyring's transition state theory model with the WT coefficient correct:
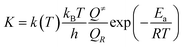 | (2.3) |
Here, Ea represents the reaction energy barrier, which is equal to the energy difference between the transition state and the reactant, k(T) is given by ref. 39 and 41:
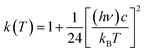 | (2.4) |
Results and discussion
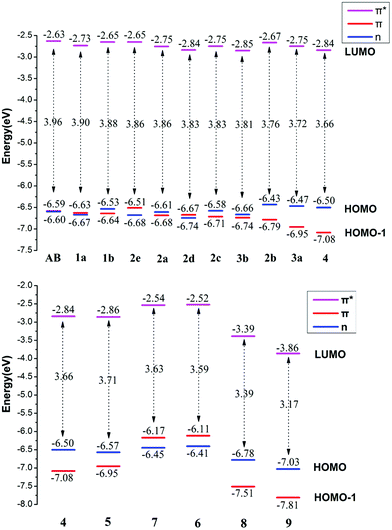
According to molecular orbital theory, the transition involved in the excitation of the S1 state and S2 state can be assigned to n → π* and π → π* for azobenzene, respectively. By applying different substituents, corresponding transition bands may also shift, which can be treated as an approach for regularity. In this study, the vertical absorption spectra of molecules were calculated. Detailed analysis of the nature of their Frontier molecular orbital and energy levels were also proposed. In addition, we explored the thermal cis–trans isomerization rate and the thermal stability of the Z isomers to give guidance on a new azobenzene molecular photoswitch design.Absorption properties
The absorption spectrum properties are shown in Fig. 2, Tables 1 and S3.† The spatial distribution and energy levels of relevant molecular orbitals in the E isomers are shown in Fig. 3 and 4 and Table S4.† The results are consistent with the experimental data.22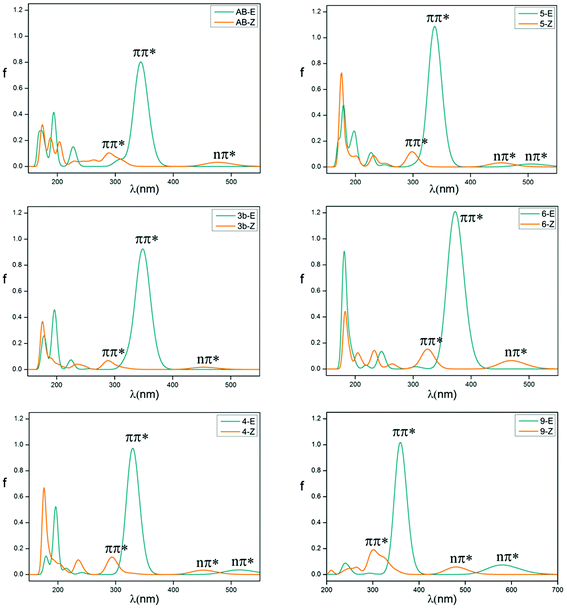 | ||
| Fig. 2 Vertical electronic absorption spectra of azobenzene compounds of E (blue line) and Z (yellow) isomers. | ||
| π–π* | n–π* | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λE (nm) | f | λZ (nm) | f | λE (nm) | f | λZ (nm) | f | ΔλE–Z (nm) | Deg (°) | |
| Azobenzene | 344 | 0.893 | 310 | 0.071 | 482 | 0.000 | 477 | 0.050 | 5 | 0 |
| 2e | 350 | 0.912 | 300 | 0.027 | 470 | 0.000 | 478 | 0.058 | 8 | 0 |
| 1a | 350 | 0.885 | 317 | 0.027 | 486 | 0.000 | 470 | 0.047 | 16 | 0 |
| 1b | 341 | 0.871 | 312 | 0.012 | 495 | 0.000 | 471 | 0.054 | 24 | 3.85 |
| 2a | 346 | 0.848 | 322 | 0.017 | 500 | 0.000 | 466 | 0.052 | 34 | 3.00 |
| 2d | 355 | 0.883 | 319 | 0.026 | 491 | 0.000 | 457 | 0.045 | 34 | 0.02 |
| 2c | 343 | 0.931 | 315 | 0.013 | 502 | 0.002 | 463 | 0.050 | 39 | 8.07 |
| 3b | 349 | 0.915 | 323 | 0.014 | 508 | 0.000 | 454 | 0.048 | 54 | 0 |
| 2b | 336 | 0.751 | 319 | 0.005 | 506 | 0.012 | 466 | 0.058 | 40 | 23.10 |
| 3a | 333 | 0.693 | 323 | 0.021 | 507 | 0.027 | 460 | 0.056 | 47 | 35.24 |
| 4 | 330 | 0.936 | 327 | 0.015 | 514 | 0.036 | 452 | 0.053 | 62 | 40.10 |
| 5 | 338 | 1.008 | 310 | 0.010 | 505 | 0.021 | 453 | 0.062 | 52 | 2.94 |
| 6 | 373 | 1.346 | 331 | 0.052 | 490 | 0.001 | 469 | 0.129 | 21 | 9.38 |
| 7 | 364 | 1.188 | 325 | 0.048 | 490 | 0.005 | 465 | 0.105 | 25 | 26.77 |
| 8 | 344 | 1.126 | 340 | 0.023 | 549 | 0.078 | 468 | 0.083 | 81 | 50.46 |
| 9 | 359 | 1.090 | 350 | 0.026 | 580 | 0.082 | 480 | 0.097 | 100 | 50.86 |
 | ||
| Fig. 3 Molecular orbital profiles of the E isomers of azobenzene compounds. Notes: L, H and H-1 represent LUMO, HOMO and HOMO-1 respectively. | ||
For azobenzene, the contribution to the lowest unoccupied molecular orbital (LUMO) and highest occupied molecular orbital (HOMO) is derived from the π* orbital and the π orbital, while the energy level of the n orbital is lower than that of the π orbital and becomes HOMO-1. The absorption spectra results show that the n → π* transition absorption band of the E isomer is dipole-forbidden. However, this is permitted in the Z isomer and the oscillation strength is relatively larger. This phenomenon is similar to 2e. For 1–4 with ortho-fluorines, their absorption spectra and the order of n and π orbital are regularly changed, which is relevant to the position of fluorine (α and β positions are indicated in Fig. 1). The results of the absorption spectra show that the π → π* transition bands in both isomers are mainly localized in the ultraviolet region and the intensity of each E isomer is much greater than that of the Z isomer. Compared with azobenzene, for all ortho-fluoroazobenzenes, the n → π* absorption wavelengths of Z isomers show a hypochromatic shift, compared with a bathochromic shift in E isomers. Moreover, the difference value ΔλE–Z increases along with the amount of fluorine, resulting in the n → π* splitting between the E and Z isomers. According to the comparison among 2a, 2c, and 3a, it seems that the substitution on the α-position will lead to an n orbital rise and π orbital decrease, while the π* orbital remains almost unaffected. This means that the energy gap between n and π* decreases and the absorption bathocromic shifted. A similar phenomenon can also be found between 1b and 2b, or 3b and 4. On the other hand, compared 1b with 2a (2c with 3b), one may infer that substitution on the β-position will decrease all three orbitals, especially the π* orbital. Therefore, the energy gap between n and π* decreases correspondingly. One more noteworthy feature is that the n → π* transition becomes permitted in the E isomer and the oscillation strength increases from 1 to 4. This is attributed to the change of distribution to HOMO. Despite 2d, the HOMOs in the other compounds are all assigned as n orbitals which exhibit a heterogeneous phase distribution on the N and adjacent α-F atoms. This heterogeneity induces the intermolecular steric effect and increases the dihedral angle between the two benzenes. With the increase of fluorine, the structural distortion becomes more evident and a direct change in HOMO can be detected, which is that the distribution on benzene increases and could be assigned as n orbital mixed with π orbital. It is this mixture that allows the n → π* transition. The results above demonstrate that the position and amount of fluorine substitution can bring an obvious influence on not only the arrangement of orbital energy levels, which may even involve a change in order, but also the distribution of the n orbital. It is this influence that makes the absorption band of the n → π* transition bathochromic-shifted to ensure the photochromic isomerization occurs under visible wavelengths. However, there are different results when two fluorine atoms are added to the benzene para-position. In 2e, the π and π* orbitals rise and the n orbital decreases, and the energy gap between n and π* increases. Therefore, this will lead to n–π* transition bands of the trans-isomer hypochromatic. Nevertheless, the n–π* transitions have almost no shift in the cis-isomer.
On the basis of 4, the effect of para-substitution has been also tested. When fluorine is connected to the para-position of benzene in 5, the level of the n orbital reduces while that of the π orbital rises and the π* orbital still remains invariant. In addition, both EDGs (–OH, –OCH3) and EWGs (–COOH, –NO2) are also considered. In 6 and 7, three orbitals n, π, π* all rise to some extent. HOMO switches to the π orbital, which leads to a decrease in the dihedral angle between the two benzenes. However, the band for the n → π* transition shows a hypochromatic shift. In 8 and 9, a contrary phenomenon in that the three orbitals are decreased is detected, together with further bathochromic shift on the n → π* transition band and structural distortion, which is similar to the β-F substitution. As a whole, the amplitude of fluctuation in the n orbital is relatively small, whereas it is much more obvious in the π and π* orbitals whose distributions are related to the conjugation pattern of the compounds. In other word, regardless of the difference in electron-donating or -withdrawing ability, the substituents mentioned above mainly affect the conjugated system of the E isomer. Accordingly, one may infer that this can be applied to give tunability to the fluctuation of molecular orbitals to achieve the goal of shifting bands.
Thermal stability of the Z isomers
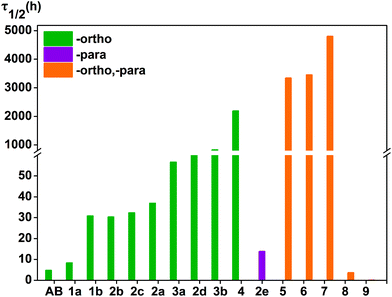
In order to better understand the influence of substituents on the thermal stability of the Z isomers, we calculated the half-live of cis-azobenzene derivatives at room temperature in ACN (see Table 2 and Fig. 5). It has previously been experimentally demonstrated that the polarity of the solvent promotes the stability of the cis-isomers of the azobenzene molecules,22 and there are similarities with our work. In order to maintain consistency with the experiments, we have chosen ACN with good polarity as the solvent in this work.| ΔG≠ [kJ mol−1] | ΔH≠ [kJ mol−1] | ΔS≠ [J mol−1 k−1] | kZ–E [S−1] | τ1/2 [h] | |
|---|---|---|---|---|---|
| Azobenzene | 98.39 | 99.60 | 4.06 | 4.10 × 10−5 | 4.7 |
| 1a | 99.83 | 103.08 | 10.90 | 2.33 × 10−5 | 8.3 |
| 1b | 103.06 | 104.51 | 4.88 | 6.26 × 10−6 | 30.8 |
| 2a | 103.54 | 107.48 | 13.21 | 5.21 × 10−6 | 36.9 |
| 2b | 103.05 | 105.41 | 7.92 | 6.36 × 10−6 | 30.3 |
| 2c | 103.22 | 105.20 | 6.65 | 5.96 × 10−6 | 32.3 |
| 2d | 105.95 | 109.68 | 12.49 | 1.95 × 10−6 | 98.8 |
| 2e | 101.08 | 104.00 | 9.78 | 1.40 × 10−5 | 13.7 |
| 3a | 104.62 | 108.71 | 13.74 | 3.40 × 10−6 | 56.6 |
| 3b | 111.23 | 114.90 | 12.30 | 2.32 × 10−7 | 829.3 |
| 4 | 113.66 | 115.60 | 6.51 | 8.80 × 10−8 | 2187.6 |
| 5 | 114.73 | 115.17 | 1.45 | 5.77 × 10−8 | 3336.2 |
| 6 | 114.84 | 114.78 | −0.21 | 5.58 × 10−8 | 3448.2 |
| 7 | 115.66 | 115.13 | −1.76 | 4.02 × 10−8 | 4794.9 |
| 8 | 97.68 | 101.83 | 13.92 | 5.35 × 10−5 | 3.6 |
| 9 | 87.54 | 92.56 | 16.85 | 3.14 × 10−3 | 0.1 |
At this temperature, the thermal half-life of Z-azobenzene is 4.7 h, and the thermal stability of the Z isomer of 1a is slightly better than that of Z-azobenzene, with a thermal half-life of τ1/2 = 8.3 h. 1b is more stable, and the half-life is 30.8 h at room temperature. Thermal stability is similar in the 2a, 2b and 2c of the Z isomer compounds, for which the half-lives are 36.9, 30.3 and 32.3 h, respectively. The thermal half-life of 2d is 98.8 h and thermal stability was better than 3a. The thermal half-life of 2e is τ1/2 = 13.7 h, which is less than the thermal stability of compound 1b. Three fluorine atoms are added to the azobenzene ortho-position, and their Z isomers have excellent thermal stability. The thermal half-life of 3a is τ1/2 = 56.6 h and 3b is τ1/2 = 829.3 h. Among the Z isomers of a number of ortho-fluoroazobenzene derivatives, 4 exhibits a high thermal stability with a half-life of τ1/2 = 2187.6 h. It is obvious that the σ-electron-withdrawing group fluorine is attached to the ortho-position to heighten the thermal stability of the Z isomer.
The effect described above is attributed to the change in the dipole moment of the Z isomer (μ(Z)) and the transition state (μ≠) (see Table 3). In the polar solvent ACN solution, the thermal stability of the Z isomer increases when the dipole moment value of the Z isomer (μ(Z)) is greater than that of the transition state (μ≠). This applies not only to ortho-substituted azobenzene derivatives, but also to para-substituted azobenzene compounds.
| E(Z) [kJ mol−1] | μ(Z) [D] | E(≠) [kJ mol−1] | μ(≠) [D] | μ(E) [D] | μ(Z) − μ(≠) [D] | μ(Z) − μ(E) [D] | ΔE = E(≠) − E(Z) [kJ mol−1] | |
|---|---|---|---|---|---|---|---|---|
| Azobenzene | 59.24 | 4.29 | 164.16 | 4.37 | 0.00 | −0.08 | 4.29 | 104.92 |
| 1a | 55.96 | 4.71 | 164.15 | 3.58 | 1.64 | 1.12 | 3.07 | 108.19 |
| 1b | 48.84 | 5.61 | 158.87 | 5.04 | 1.73 | 0.57 | 3.88 | 110.03 |
| 2a | 45.36 | 6.33 | 158.13 | 4.23 | 3.12 | 2.10 | 3.21 | 112.77 |
| 2b | 38.99 | 6.55 | 149.82 | 4.23 | 0.53 | 2.32 | 6.03 | 110.83 |
| 2c | 44.66 | 5.57 | 154.76 | 3.12 | 1.42 | 2.45 | 4.15 | 110.10 |
| 2d | 54.52 | 4.62 | 169.35 | 4.58 | 0.00 | 0.04 | 4.62 | 114.84 |
| 2e | 62.77 | 1.56 | 172.08 | 4.26 | 0.00 | −2.70 | 1.56 | 109.31 |
| 3b | 42.83 | 5.92 | 163.14 | 4.78 | 1.89 | 1.14 | 4.03 | 120.31 |
| 3a | 34.79 | 6.91 | 148.76 | 4.61 | 1.61 | 2.30 | 5.30 | 113.98 |
| 4 | 31.79 | 6.90 | 152.73 | 4.23 | 0.21 | 2.68 | 6.69 | 120.94 |
| 5 | 35.52 | 4.19 | 155.87 | 2.44 | 0.11 | 1.75 | 4.08 | 120.35 |
| 6 | 38.90 | 7.54 | 158.75 | 2.78 | 0.09 | 4.77 | 7.45 | 119.85 |
| 7 | 38.65 | 6.45 | 158.60 | 2.12 | 0.31 | 4.33 | 6.14 | 119.95 |
| 8 | 30.32 | 3.70 | 136.94 | 7.62 | 3.29 | −3.92 | 0.41 | 106.62 |
| 9 | 30.87 | 1.46 | 127.97 | 8.39 | 0.02 | −6.93 | 1.44 | 97.10 |
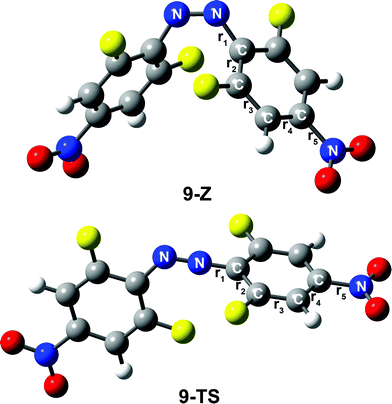
In addition, different substituents are added to the para-position of compound 4, and the thermal stability of the cis-isomer also changes. In fact, when the para-substituents of 4 are –OCH3 and –OH, the thermal stability of the Z isomer of the compound increased significantly. For instance, the half-lives of the Z isomers of 6 and 7 are 3348.2, 4794.9 h, respectively. Conversely, linking –COOH or –NO2 to the para-position of compound 4 can greatly reduce the thermal stability of the cis-isomer. Obviously, the half-lives of the Z isomers of compounds 8 and 9 are shortened significantly. The half-lives of compounds 8 and 9 are 3.6 h and 0.1 h, respectively, and their thermal stability is less than that of azobenzene. It is noteworthy that the thermal stability of compound 5 is higher than that of 4. To explain this phenomenon, we list the bond lengths of the cis and transition states of compounds 5–9. The chemical bond label is shown in Fig. 6. During the transition from the cis configuration to the transition state, the bond lengths of compounds 5–9 varied regularly (see Table 4). Compounds 5, 6 and 7 undergo minor changes in each of the corresponding chemical bonds during the transition of the cis-to-transition-state. However, the corresponding bond lengths of compounds 8 and 9 vary greatly. In other words, compared with 5, 6 and 7, compounds 8 and 9 have a greater influence on the conjugation system.
| r1 [Å] | r2 [Å] | r3 [Å] | r4 [Å] | r5 [Å] | |
|---|---|---|---|---|---|
| 5-Z | 1.428 | 1.399 | 1.384 | 1.386 | 1.344 |
| 5-TS | 1.318 | 1.423 | 1.379 | 1.390 | 1.347 |
| 6-Z | 1.423 | 1.404 | 1.377 | 1.403 | 1.349 |
| 6-TS | 1.317 | 1.429 | 1.372 | 1.407 | 1.347 |
| 7-Z | 1.423 | 1.402 | 1.380 | 1.398 | 1.353 |
| 7-TS | 1.317 | 1.428 | 1.374 | 1.402 | 1.351 |
| 8-Z | 1.426 | 1.400 | 1.380 | 1.396 | 1.491 |
| 8-TS | 1.313 | 1.420 | 1.369 | 1.405 | 1.468 |
| 9-Z | 1.426 | 1.400 | 1.382 | 1.389 | 1.477 |
| 9-TS | 1.309 | 1.423 | 1.367 | 1.401 | 1.437 |
Therefore, the transition from the cis-to-transition-state becomes significantly easier. As a result, the thermal stability of the cis-isomer decreases and the rate of reaction increases.
In addition, the influence of the substituent on the dipole moment of the compound cannot be ignored. For compounds 1–4, the number of ortho-fluorine atoms increases, resulting in an increase in the dipole moment of the cis-isomer and a small change in the dipole moment in the transition state.
Therefore, the transition of the cis-isomer to the transition state becomes difficult, the energy barrier of the reaction increases, and the thermal stability of the cis-isomer increases. During the transition of the cis-isomer to the transition state, although the dipole moment direction has also changed within 45°, the general values are almost the same (see Fig. S1 and Table S5†). Peculiarly, in compounds 2e, 8 and 9, the value of the dipole moment of the cis-isomer to the transition state was significantly increased from 1–3 to 6–8 Debye, and the dipole moment direction was obviously changed. The polar solvent is propitious to promote the stability of the transition state more than for the cis-isomers in this time; consequently, the cis-isomers have relatively low thermal stability when the para-position is substituted to reduce the whole dipole moment of the azobenzene molecules. Compared with 4, the dipole moment of the cis-isomer and transition state of compound 5 decreases. The energy barrier of the reaction is also high, resulting in an increase in the stability of the cis-isomer. For compounds 6 and 7, the transition state dipole moment decreases with increase of the cis-isomer dipole moment. The energy barrier of the cis-to-transition-state transition increases, and the cis-isomer stability increases. In contrast to 6 and 7, the dipole moment of the cis-isomers of compounds 8 and 9 decreases and the dipole moment of the transition states increases. The reduction of the energy barrier leads to an increase in the reaction rate, which leads to a lower thermal stability of the cis-isomer. Among the cis-isomers of these molecules, compounds 7 and 9 have the highest and the lowest thermal stability, respectively.
In short, the thermal stability of the Z isomer of ortho-fluoroazobenzenes increases as the number of fluorine atoms increases. In the para-substituted azobenzene compounds, the thermal stability of the Z isomers varies with different substituents. We can verify this finding by measuring the rate kZ–E of the Z → E isomerization. The thermal transition rate is given as eqn (3.1) in the Eyring theory, and the thermal half-life from Eyring is given by eqn (3.2).
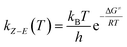 | (3.1) |
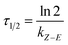 | (3.2) |
In the ortho-substituted azobenzene compounds, the energy of the transition state decreases, and the energy of the cis-isomer of the molecule is also reduced. Further, the latter decreases more significantly, resulting in an increase in the reaction energy barrier and a decrease in the reaction rate. For the para-substituted azobenzene derivatives, the para-substituted substituent of 6/7 is –OCH3/–OH, the thermal stability of the cis-isomer increases, and the rate of the reaction slows down. In 2e, the thermal stability of the cis-isomers is poor. Moreover, the energy barrier for its transition from the cis-isomer to the transition state is small. Its cis–trans isomerization rate is accordingly very fast. However, when para-substituents are –COOH and –NO2, the thermal stability of the cis-isomer of compounds 8 and 9 decreases and the rate of the reaction increases (see Fig. 7). The reaction rate is not related to whether the para-substituent is EDG or EWG. Overall, it can be seen that the stronger the bonding ability between the para-substituent and the conjugated system, the faster the isomerization reaction.
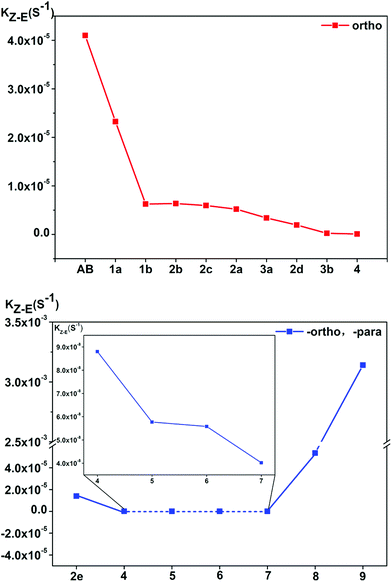 | ||
| Fig. 7 The thermal cis → trans isomerization reaction rates kZ–E of the azobenzene derivative compounds, the inset is a plot of the reaction rate for compounds 4–7 at more precise coordinate. | ||
In this work, we mainly studied the properties of ortho-fluoroazobenzene compounds, including the photochemical properties of the E isomer and the thermal stability of the Z isomer. In fact, the thermal stability of the Z isomer is a precondition for the photochemistry reaction. It is easy to conclude that the longer the half-life of the Z isomer, the better the thermal stability. Therefore, the trans–cis light conversion rate is advanced, and improvements in photoswitch performance are observed.
Concluding remarks
The introduction of fluoro substituents at the ortho-position of azobenzene provides a simple approach to optimize the properties of photoswitches. Due to the effective segregation of the n → π* bands of the E and Z isomers and extended half-life of the Z isomer at room temperature, it is possible to avoid the use of ultraviolet light to achieve high light conversion. The thermal stability of the cis-isomer depends on the influence of the substituent on the conjugated system. With increases in the bonding degree between the substituent and the conjugated system, the impact of the substituent increases, the thermal stability of the cis-isomer is reduced, and the rate of cis-to-trans isomerization accelerates. In addition, the substituents also affect the conjugate system of the E isomer. Substituents affect the resonance conjugation mode by affecting the π and π* orbitals of the compounds. Thus, molecular orbital fluctuations can be adjusted so that the n → π* band of the compound can be shifted to separate n → π* transition bands of the cis–trans isomers. This allows cis–trans isomerization of azobenzene compounds in the visible region, which has a very important significance in terms of practical applications.Compared with azobenzene, compound 9 has the largest n–π* band separation in the cis and trans isomers and also shows the faster cis–trans isomerization rate at room temperature. The cis-isomer of compound 7 shows the best thermal stability, with a half-life of up to 4795 h at room temperature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the State Key Development Program for Basic Research of China (Grant No. 2013CB834801) and the Natural Science Foundation of China (Grant No. 21573088) and Young Scholar Training Program of Jilin University and Open Project Funding of Beijing National Laboratory for Molecular Sciences (BNLMS).Notes and references
- J. Moreno, F. Schweighoefer, J. Wachtveitl and S. Hecht, Chem.–Eur. J., 2016, 22, 1070–1075 CrossRef CAS PubMed.
- B. E. Tebikachew, H. B. Li, A. Pirrotta, K. Börjesson, G. C. Solomon, J. Hihath and K. Moth-Poulsen, J. Phys. Chem. C, 2017, 121, 7094–7100 CAS.
- H. Tian and S. J. Yang, Chem. Soc. Rev., 2004, 33, 85–97 RSC.
- A. C. Whalley, M. L. Steigerwald, X. Guo and C. Nuckolls, J. Am. Chem. Soc., 2007, 129, 12590–12591 CrossRef CAS PubMed.
- T.-T. Yin, Z.-X. Zhao, L.-Y. Yu and H.-X. Zhang, Org. Electron., 2017, 48, 154–164 CrossRef CAS.
- H. K. Cammenga, V. N. Emel'yanenko and S. P. Verevkin, Ind. Eng. Chem. Res., 2009, 48, 10120–10128 CrossRef CAS.
- G. Berkovic, V. Krongauz and V. Weiss, Chem. Rev., 2000, 100, 1741–1753 CrossRef CAS PubMed.
- M. Irie, Chem. Rev., 2000, 100, 1685–1716 CrossRef CAS PubMed.
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277 CrossRef CAS PubMed.
- W. A. Velema, W. Szymanski and B. L. Feringa, J. Am. Chem. Soc., 2014, 136, 2178–2191 CrossRef CAS PubMed.
- L. Sjulson and G. Miesenboeck, Chem. Rev., 2008, 108, 1588–1602 CrossRef CAS PubMed.
- M.-M. Russew and S. Hecht, Adv. Mater., 2010, 22, 3348–3360 CrossRef CAS PubMed.
- M. Andresen, M. C. Wahl, A. C. Stiel, F. Grater, L. V. Schafer, S. Trowitzsch, G. Weber, C. Eggeling, H. Grubmuller, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13070–13074 CrossRef CAS PubMed.
- S. Samanta, A. A. Beharry, O. Sadovski, T. M. McCormick, A. Babalhavaeji, V. Tropepe and G. A. Woolley, J. Am. Chem. Soc., 2013, 135, 9777–9784 CrossRef CAS PubMed.
- D. Bleger, Z. Yu and S. Hecht, Chem. Commun., 2011, 47, 12260–12266 RSC.
- C. Kaiser, T. Halbritter, A. Heckel and J. Wachtveitl, ChemistrySelect, 2017, 2, 4111–4123 CrossRef CAS.
- Z.-X. Zhang, F.-Q. Bai, L. Li and H.-X. Zhang, New J. Chem., 2015, 39, 1634–1642 RSC.
- H.-H. Yao, H.-H. Cheng, C.-H. Cheng, C.-K. Lin, J.-S. Yang and I. C. Chen, Phys. Chem. Chem. Phys., 2016, 18, 28164–28174 RSC.
- H. M. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825 RSC.
- A. A. Beharry and G. A. Woolley, Chem. Soc. Rev., 2011, 40, 4422–4437 RSC.
- J. Dokić, M. Gothe, J. Wirth, M. V. Peters, J. Schwarz, S. Hecht and P. Saalfrank, J. Phys. Chem. A, 2009, 113, 6763–6773 CrossRef PubMed.
- C. Knie, M. Utecht, F. Zhao, H. Kulla, S. Kovalenko, A. M. Brouwer, P. Saalfrank, S. Hecht and D. Bleger, Chem.–Eur. J., 2014, 20, 16492–16501 CrossRef CAS PubMed.
- T.-T. Yin, Z.-X. Zhao and H.-X. Zhang, Org. Electron., 2018, 52, 61–70 CrossRef CAS.
- R. Siewertsen, H. Neumann, B. Buchheim-Stehn, R. Herges, C. Naether, F. Renth and F. Temps, J. Am. Chem. Soc., 2009, 131, 15594–15595 CrossRef CAS PubMed.
- Y. Yang, R. P. Hughes and I. Aprahamian, J. Am. Chem. Soc., 2012, 134, 15221–15224 CrossRef CAS PubMed.
- Y. Yang, R. P. Hughes and I. Aprahamian, J. Am. Chem. Soc., 2014, 136, 13190–13193 CrossRef CAS PubMed.
- Y.-P. Wang, Z.-X. Zhang, M. Xie, F.-Q. Bai, P.-X. Wang and H.-X. Zhang, Dyes Pigm., 2016, 129, 100–108 CrossRef CAS.
- D. Bleger, J. Schwarz, A. M. Brouwer and S. Hecht, J. Am. Chem. Soc., 2012, 134, 20597–20600 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kita, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramill, R. E. Gomperts, O. Stratmann, A. J. Yazyev, R. Austin, C. Cammi, J. W. Pomelli, R. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. Frenette, M. Hatamimoslehabadi, S. Bellinger-Buckley, S. Laoui, J. La, S. Bag, S. Mallidi, T. Hasan, B. Bouma, C. Yeleswarapu and J. Rochford, J. Am. Chem. Soc., 2014, 136, 15853–15856 CrossRef CAS PubMed.
- S. Knippenberg, M. V. Bohnwagner, P. H. P. Harbach and A. Dreuw, J. Phys. Chem. A, 2015, 119, 1323–1331 CrossRef CAS PubMed.
- N. Boens, V. Leen, W. Dehaen, L. Wang, K. Robeyns, W. Qin, X. Tang, D. Beljonne, C. Tonnele, J. M. Paredes, M. J. Ruedas-Rama, A. Orte, L. Crovetto, E. M. Talavera and J. M. Alvarez-Pez, J. Phys. Chem. A, 2012, 116, 9621–9631 CrossRef CAS PubMed.
- Y. Kubota, Y. Ozaki, K. Funabiki and M. Matsui, J. Org. Chem., 2013, 78, 7058–7067 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- K. Raghavachari, Theor. Chem. Acc., 2000, 103, 361–363 CrossRef CAS.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef PubMed.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 200–203 CrossRef CAS.
- N. B. Jaufeerally, H. H. Abdallah, P. Ramasami and H. F. Schaefer, J. Phys. Chem. A, 2013, 117, 5567–5577 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Absorption properties, molecular orbitals and computational methods for azobenzene compounds. See DOI: 10.1039/c8ra01132j |
| This journal is © The Royal Society of Chemistry 2018 |