Open Access Article
Open Access ArticleDFT prediction of a novel molybdenum tetraboride superhard material
Yong Pan *a,
Xiaohong Wanga,
Songxia Lia,
Yanqiong Lib and
Ming Wenb
*a,
Xiaohong Wanga,
Songxia Lia,
Yanqiong Lib and
Ming Wenb
aSchool of Material Science and Engineering, Southwest Petroleum University, Chengdu 610500, China. E-mail: panyong10@mails.jlu.edu.cn; Fax: +86-028-83037406; Tel: +86-028-83037401
bState Key Laboratory of Advanced Technologies for Comprehensive Utilization of Platinum Metals, Kunming, 650106, China
First published on 16th May 2018
Abstract
Although transition metal borides (TMBs) are promising superhard materials, the research and development of new TMB superhard materials is still a great challenge. Naturally, the Vickers hardness of TMBs is related to the 3D-network chemical bonding, in addition to the valence electron density and covalent bonds. In this paper, we apply ab initio calculations to explore the structural stability, Vickers hardness and hardening mechanism of MoB4 tetraboride. Four possible tetraborides are predicted based on the phonon dispersion model. We find that MoB4 with monoclinic structure (C2/m) and orthorhombic structure (Immm) are dynamically stable at the ground state. The calculated Vickers hardness of MoB4 with monoclinic and orthorhombic structures is 41.3 GPa and 40.0 GPa, respectively. We suggest that the high hardness is derived from the 3D-network B–B covalent bond owing to bond synergistic effects. On the other hand, the Vickers hardness of MoB4 decreases gradually with increasing pressure. The calculated results show that the hardness of MoB4 is attributed to the B/G ratio and c/a ratio. Finally, we predict that MoB4 is a new superhard material.
1. Introduction
The research and development of new superhard materials is still a growing interest owing to the increasing demand for their industrial applications. Among all the superhard materials, transition metal borides (TMBs) are attractive and promising candidates because of their high Vickers hardness, high elastic modulus, excellent thermal stability and electronic properties etc.1–9 Over the last few years, a large number of TMBs have been widely investigated.10–15 Despite some TMBs being potential superhard materials,16,17 controversy remains about the intrinsic hardness of TMBs. One is that the measured Vickers hardness of TMBs fails to agree with the theoretical results.18 The other important reason is that numerous TMBs are not superhard materials because of theirs structural features and bonding characteristics.19–22To explore new superhard materials, recent works have proposed that alloying is a good path to improve the hardness of TMBs.23,24 The Vickers hardness of WB4 with alloying elements of 6 at% Hf, 8 at% Zr and 8 at% Ti increases from 43.3 GPa to 51.6 GPa, 55.9 GPa and 50.9 GPa, respectively.17 The measured Vickers hardness of Y0.5Sc0.5B12, Zr0.5Sc0.5B12 and Zr0.5Y0.5B12 is 45.2 GPa, 48.0 GPa and 45.8 GPa, respectively.25 Low concentration of Mo can effectively improve the Vickers hardness of WB4.26 However, the Vickers hardness of ternary borides is sensitive to the concentration of the alloying element. Kaner et al. have found that high concentration of Re weakens the Vickers hardness of WB4.26 In particular, the hardening mechanism of ternary boride becomes very complex due to the charge interaction between elements. The development of ternary TMBs superhard material is faced with the great challenge. Thus, the search for binary TMBs superhard material is still of great significant.
According to the equation of Vickers hardness: HV = 1854.4P/d2, it is clear that the hardness of a solid is determined by the applied load and indent mark in micrometer. Thus, we suggest that the Vickers hardness of TMBs depends on the chemical bonding of the direction of applied load, in addition to the valence electron density and covalent bond. There is no doubt that 3D-network chemical bonding can effectively improve the incompressibility and hardness. For example, although the valence electron density of 3d-Cr and 4d-Zr is smaller than that of 5d-W and 5d-Re, CrB4 and ZrB4 can be regarded as potential superhard materials due to the 3D-network B–B covalent bond.27,28 As mentioned above, tetraboride with 3D boron network is expected to show superhardness. Unfortunately, the structural stability of tetraborides is still a great dilemma for the development of TMBs superhard materials.
We report on a new MoB4 tetraboride and those structural features influence the intrinsic hardness of MoB4. The likely hardening mechanism behind the hardness vs. pressure is provided in these cases. We predict that MoB4 with monoclinic C2/m structure and orthorhombic Immm structure are new superhard material. Importantly, we propose that the intrinsic hardness of TMBs is attributed to arrangement of chemical bonding along the applied load, which is related to the c/a ratio and B/G ratio.
2. Models and theoretical methods
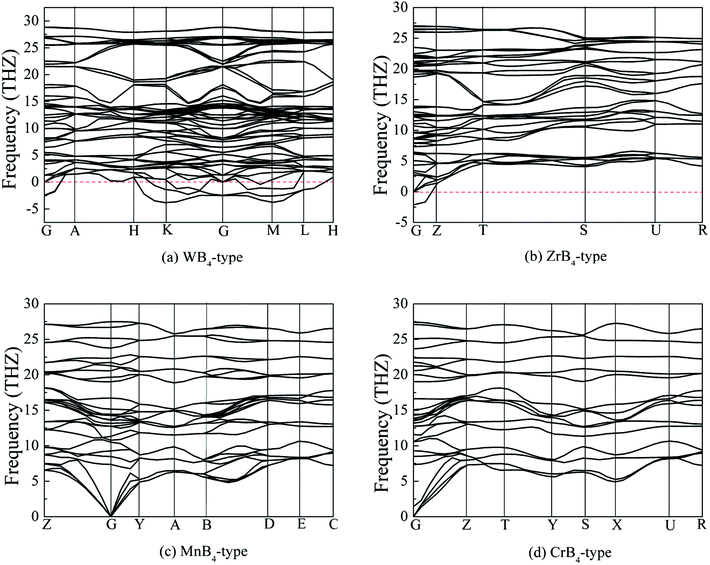
To guarantee the 3D boron network, tetraboride is a very attractive structure. As we know, WB4 with hexagonal structure (space group: P63/mmc) is a tetraboride.29 In this structure, W atoms occupy the Wyckoff 2b(0, 0, 0.2500) and 2c(0.6667, 0.3333, 0.7500) sites, and B atoms locate at the 12i(0, 0.3347, 0) and 4f(0.6653, 0.6653, 0.500) sites, respectively. It is observed that hexagonal prism is composed of 12 B atoms, which can improve the deformation resistance and intrinsic hardness. Although the calculated Vickers hardness of WB4 is about 46.2 GPa, this structure is unstable at the ground state.30–32 On the other hand, other TMB4 (TM = Re, Mo and Os) with WB4-type structures are not superhard materials.According to the above design principles, we find that the existences of CrB4 with orthorhombic structure (Immm),33 ZrB4 with orthorhombic structure (Cmcm)28,34 and MnB4 with monoclinic structure (C2/m)35 have the 3D boron network, which may improve the deformation resistance and enhance the intrinsic hardness. Therefore, in this paper, we consider and design these tetraborides. The structural models of MoB4 with four possible structures are shown in Fig. 1.
According to the Inorganic Crystal Structure Database (ISCD), we apply this idea to investigate potential structure of MoB4. Four structures were considered: WB4-type structure (P63/mmc), ZrB4-type structure (Cmcm), MnB4-type structure (C2/m) and CrB4-type structure (Immm), respectively. All calculations in this paper were performed by using the DFT within generalized-gradient-approximation (GGA) with PBE functional,36 as implemented in CASTEP code.37 The interactions between the electrons and ions were adopted by using the ultrasoft pseudopotential.38 In addition, the electronic configurations of Mo atom and B atom were 4p64d55s1 and 2s22p,1 respectively. After the converged test, the cutoff energy of plane wave was 400 eV. The k-point grids of 11 × 11 × 8, 17 × 17 × 5, 13 × 13 × 19 and 18 × 18 × 13 for WB4-type structure, ZrB4-type structure, MnB4-type structure, and CrB4-type structure were treated, respectively. During the structural optimization, the periodic boundary condition (PBC) of a system was adopted and all atoms in a system were fully relaxed. In this paper, the elastic properties of MoB4 were calculated by the stress tensor vs. strain method.39,40 The dynamically stable of MoB4 is estimated by the PHONON code. Importantly, the Vickers hardness (HV) of MoB4 is given by:41
| HV = 2(k2G)0.585 − 3 | (1) |
3. Results and discussion
The structural stability of a boride is determined not only by the thermodynamically stable but also by the dynamically stable.42,43 Although the structural information and mechanical properties of MoB4 with WB4-type hexagonal structure have been studied over the last years,44–46 the dynamically stable of MoB4 is unknown. Therefore, we are not sure that MoB4 is stable at the ground state. To investigate the stable structure, following, we consider the formation enthalpy and phonon dispersion of MoB4 with four structures based on ab initio calculations.Table 1 lists the calculated lattice parameters, c/a ratio, density, formation enthalpy and bond length of MoB4. We can see that the calculated formation enthalpy of these structures is smaller than zero, indicating that these structures are thermodynamically stable at the ground state. Importantly, the calculated formation enthalpy of MoB4 with WB4-type hexagonal structure is about −7.3598 eV per atom, which is bigger than that of ZrB4-type, MnB4-type and CrB4-type structures. Therefore, we can conclude that our predicted MoB4 structure is more thermodynamically stable than that of WB4-type structure.
| Phase | Method | a | b | c | c/a | ρ | Ef | B–B | Mo–B |
|---|---|---|---|---|---|---|---|---|---|
| WB4-type | Cal | 5.279 | 6.591 | 1.249 | 5.81 | −7.3598 | 1.691 | 2.405 | |
| Exp47 | 5.214 | 6.358 | |||||||
| ZrB4-type | Cal | 5.225 | 3.059 | 9.954 | 1.906 | 5.81 | −7.7562 | 1.743 | 2.371 |
| MnB4-type | Cal | 5.785 | 5.767 | 2.959 | 0.511 | 5.45 | −7.7949 | 1.775 | 2.206 |
| CrB4-type | Cal | 4.973 | 5.767 | 2.959 | 0.595 | 5.45 | −7.7947 | 1.776 | 2.206 |
In addition to thermodynamically stable, dynamically stable also plays a key role in structural stability. To examine the dynamically stable, Fig. 2 shows the calculated phonon dispersion curves of MoB4 with four structures. It is found that the experimental MoB4 with hexagonal structure is a dynamically unstable because there are some imaginary phonon frequencies in this structure. This result is consistent with the previous viewpoint.46 In addition, ZrB4-type structure is also a dynamically unstable at the ground state. Importantly, we find that MoB4 with MnB4-type and CrB4-type structures are dynamically stable because no imaginary phonon frequencies are observed in the two structures. As mentioned above, we can conclude that MoB4 with MnB4-type and CrB4-type structures are stable.
Obviously, we suggest that the structural stability of MoB4 is related to the structural feature and chemical bonding. As listed in Table 1, the calculated lattice parameters of WB4-type structure are a = 5.279 Å and c = 6.591 Å, respectively, which are in good agreement with experimental data.47 This structural feature is similar to the WB4.48 The calculated bond length of B–B covalent bond and Mo–B bond is about 1.691 Å and 2.405 Å, which are in excellent agreement with the other theoretical result.44
For MnB4-type structure, the calculated lattice parameters are a = 5.785 Å, b = 5.767 Å and c = 2.959 Å, respectively. In this structure, Mo atom occupies the Wyckoff 2a(0, 0, 0) site, and B atom locates at the 8j(0.1889, 0.3461, 0.1889) site, respectively. For CrB4-type structure, the calculated lattice parameters are a = 5.785 Å, b = 5.767 Å and c = 2.959 Å, respectively. In this structure, Mo atom occupies the Wyckoff 2a(0, 0, 0) site, and B atom locates at the 8n(0.1889, 0.6540, 0) site, respectively. Obviously, the B atom positions in CrB4-type structure are shifted in comparison to MnB4-type structure. The structural discrepancy is shown in Fig. 1.
Although the structural feature of MnB4-type and CrB4-type structures is similar, the structural feature of MnB4-type and CrB4-type structures is different from the WB4-type structure. From Fig. 1, we can see that the bond cage of CrB4-type structure is composed of 12 B atoms. Note that Mo atom locates at the center of the B bond cage. This structural feature is very similar to the CrB4.49 Therefore, the 3D-network B–B covalent bond can improve the structural stability and mechanical properties. However, the structural feature of MnB4-type structure is slightly different from CrB4-type structures. The B atom migration adjusts the B bond cage, which is composed of 10 B atoms. As a result, the atomic configuration changes the charge interaction between B atoms, and alters the properties.
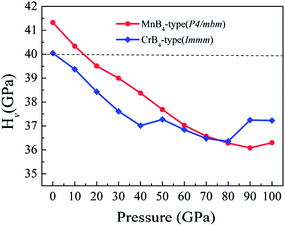
To explore the Vickers hardness of MoB4, Fig. 3 shows the calculated Vickers hardness of MoB4 as a function of pressure (0–100 GPa). Based on the structural stability, we consider two stable MoB4 structures: MnB4-type and CrB4-type structures, respectively. Surprisingly, the calculated Vickers hardness of MnB4-type structure and CrB4-type structure is about 41.3 GPa and 40.0 GPa, respectively, which are much bigger than that of WB4-type structure (24.8 GPa).44 This result is demonstrated by the elastic modulus and B/G ratio.50 The calculated bulk modulus of MnB4-type structure and CrB4-type structure is 279.1 GPa and 279.5 GPa, respectively, which is slightly smaller than that of WB4.51 However, the calculated shear modulus of MnB4-type structure and CrB4-type structure is 249.6 GPa and 245.7 GPa, respectively. The calculated Young's modulus of MnB4-type structure and CrB4-type structure is 576.8 GPa and 570.1 GPa, respectively. Obviously, the calculated shear modulus and Young's modulus of MoB4 are larger than that of WB4, implying that MoB4 has a strong shear deformation resistance and high elastic stiffness in comparison to WB4.
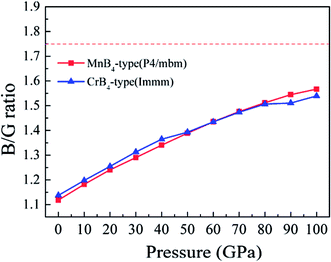
In addition, the Vickers hardness of TMBs is indirectly measured by the B/G ratio. The general trend is, the smaller the B/G ratio, the higher the hardness for a solid. According to the ab initio calculations, the calculated B/G ratio of MnB4-type structure and CrB4-type structure is 1.12 and 1.14, respectively, which is smaller than that of WB4 hexagonal structure (1.22).52 This result also affirms that the Vickers hardness of our predicted MoB4 structure is higher than that of WB4.
According to the structural feature (see Fig. 1), we suggest that the high hardness of MoB4 with these structures is mainly determined by the 3D-network B–B covalent bond. For CrB4-type structures, B12 bond cage (12 B atoms) is composed of three different B–B covalent bonds, which can effectively improve the deformation resistance under applied load. Although the structural feature of MnB4-type structure is slightly different from CrB4-type structure, B8 bond cage (8 B atoms) is composed of two different B–B covalent bonds (1.775 Å and 1.946 Å) and one type of Mo–B bond (2.206 Å). As a result, this structural feature can improve the Vickers hardness of MoB4. As mentioned above, it is concluded that our predicted MoB4 tetraboride is a promising superhard material.
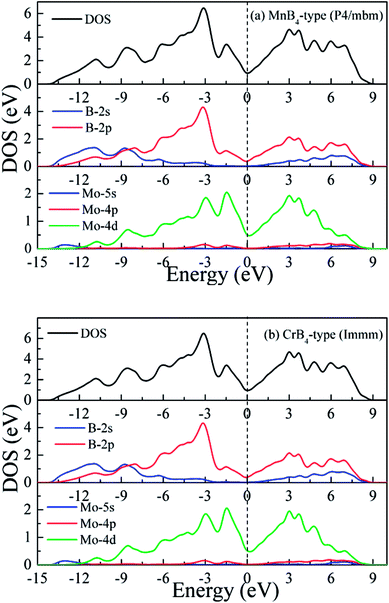
To gain further insight into chemical bonding, Fig. 4 shows the calculated total and partial density of states (DOS) of MoB4 with two structures. The black vertical dashed of DOS indicates the Fermi level (EF). The calculated DOS profiles show that the some bands across the EF, meaning that MoB4 exhibits the degree of metallic behavior. This result is demonstrated by the band structure. Importantly, we can see that the DOS profile of MoB4 is contributed by Mo-4d state, B-2s state and B-2p state. The localized hybridization between Mo atom and the B atom forms the Mo–B bond (see Table 1). It is worth noticing that B-2s state embeds into B-2p state. As a result, the localized hybridization between B atoms can form the B–B covalent bond. In particular, the 3D-network B–B covalent bonds improve the intrinsic hardness of MoB4.
On the other hand, we further find that the calculated Vickers hardness of MoB4 decreases gradually with increasing pressure. In particular, the calculated Vickers hardness of MoB4 is smaller than 40 GPa when pressure is bigger than 10 GPa. This result indicates that pressure can weaken the Vickers hardness of MoB4, which is consistent with the previous experimentally.13,17 However, the trend of Vickers hardness of MoB4 is different from the variation of elastic modulus. To examine the correlation between elastic modulus and the pressure, Fig. 5 displays the calculated bulk modulus, shear modulus and Young's modulus of MoB4 as a function of pressure. It is obvious that the calculated elastic modulus of MoB4 increases with increasing pressure. We suggest that this trend is attributed to the chemical bonding.
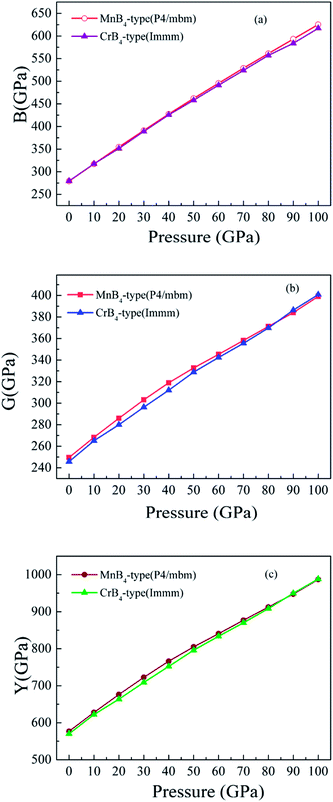 | ||
| Fig. 5 Calculated elastic modulus of MoB4 as a function of pressure. (a) Bulk modulus vs. pressure, (b) shear modulus vs. pressure, and (c) Young's modulus vs. pressure, respectively. | ||
Fig. 6 shows the calculated bond length of B–B covalent bond and Mo–B bond as a function of pressure. With increasing pressure, the calculated bond length of B–B covalent bond and Mo–B bond decrease. That is to say, high pressure obviously improves the coulomb repulsion and shorter core electron overlap, which leads to lattice shrinkage. This is why pressure enhances the elastic modulus of MoB4. However, the variation of elastic modulus does not demonstrates the trend of Vickers hardness. Therefore, we suggest that the variation of Vickers hardness of TMBs is related to other factors.
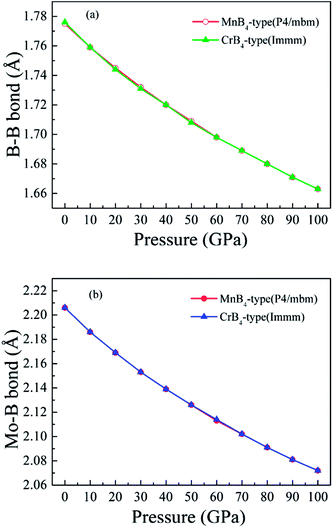 | ||
| Fig. 6 Calculated bond length of chemical bonding as a function of pressure. (a) B–B covalent bond, and (b) Mo–B bond, respectively. | ||
It is worth noting that the Vickers hardness of MoB4 is indirectly reflected by the B/G ratio (brittle or ductile behavior). To reveal the Vickers hardness, Fig. 7 shows the calculated B/G ratio of MoB4 as a function of pressure. It is obvious that the calculated B/G ratio of MoB4 increases with increasing pressure. The trend is similar to the Vickers hardness. Although MoB4 shows the brittle behavior with increasing pressure, pressure weakens the brittle behavior. It indirectly affirms that high pressure reduces the Vickers hardness of MoB4.
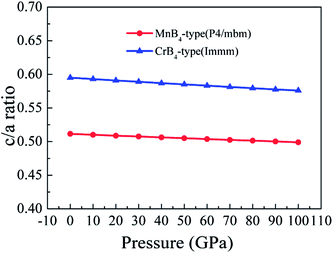
Importantly, the Vickers hardness of a material is determined by the indent mark in micrometer based on the equation of Vickers hardness. For a solid, the volume deformation resistance and shear deformation resistance are related to the a-axis and c-axis, respectively. This is why the bulk modulus and shear modulus does not reflect the Vickers hardness of a solid. Therefore, we assume that the trend of Vickers hardness is related to the c/a ratio because the c/a ratio reflects the degree of deformation resistance. To demonstrate the idea, Fig. 8 shows the calculated c/a ratio of MoB4 as a function of pressure. It is found that the calculated c/a ratio of MoB4 decreases with increasing pressure. Therefore, high pressure aggravates the coulomb repulsion between Mo atom and the B atom along the c-axis. According to the Vickers principles, c-axis is just the direction of applied load. That is to say, the Vickers hardness of a solid mainly depends on the bond strength of chemical bonding along the c-axis. Owing to bond synergistic effects, the 3D-network B–B covalent bond can improve the deformation resistance. From Fig. 8, we can see that the calculated c/a ratio of MnB4-type structure is smaller than that of CrB4-type structures. The result is related to the bonding state along the c-axis (see Fig. 1). Therefore, we suggest that the hardness of transition metal borides is also determined by the variation of c/a ratio.
On the other hand, transition metal borides exhibit a degree of metallic behavior in comparison to other superhard materials. To examine their electronic properties, Fig. 9 shows the calculated band structure of MoB4 with MnB4-type and CrB4-type structures. The horizontal dotted line indicates the Fermi level (EF). It is observed that there is the electronic overlap between the top of the valence band and the conduction band, implying that MoB4 also shows the electronic properties. This result is similar to other TMBs.
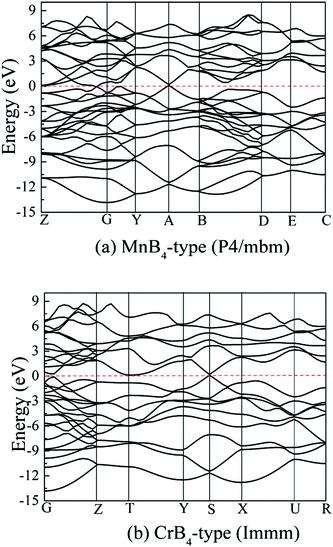 | ||
| Fig. 9 Calculated band structure of MoB4, (a) MnB4-type structure and (b) CrB4-type structure, respectively. | ||
4. Conclusion
In summary, our ab initio calculations have revealed that 3D-network B–B covalent bond can effectively enhance the Vickers hardness of TMBs. The hardening mechanism of TMBs is related to the c/a ratio and B/G ratio. To demonstrate the idea, we use the ab initio calculations to systematically investigate the structural stability, structural information, elastic modulus, Vickers hardness, electronic properties and electronic structure of MoB4. Four possible MoB4 tetraborides are predicted. According to the formation enthalpy and phonon dispersion, we deny MoB4 with WB4-type hexagonal structure and predict new MoB4 structures (C2/m and Immm). The calculated lattice parameters of MnB4-type structure are a = 5.785 Å, b = 5.767 Å and c = 2.959 Å, respectively. The lattice parameters of CrB4-type structure are a = 5.785 Å, b = 5.767 Å and c = 2.959 Å, respectively. In particular, we find that the calculated Vickers hardness of MnB4-type structure and CrB4-type structure is 41.3 GPa and 40.0 GPa, respectively. The calculated chemical bonding shows that the high hardness of MoB4 is attributed to the 3D-network B–B covalent bonds. With increasing pressure, the Vickers hardness of MoB4 decreases, in contrary to the elastic modulus of MoB4 increases. This result is similar to the other TMBs. We suggest that the trend of hardness derives from the B/G ratio and c/a ratio. Therefore, we predict that MoB4 is a new superhard material.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by National Natural Science Foundation of China (Grant No. 51564025), State Key Laboratory of Advanced Technology for Comprehensive Utilization of Platinum Metals (Grant No. SKL-SPM-201816) and the important Project of Nature Science Foundation of Yunnan (No. 2017FA029). We also thank Lady Yun Zheng for discussion.References
- G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506 CrossRef PubMed.
- S. Carenco, D. Portehault, C. Boissiere, N. Mezailles and C. Sanchez, Chem. Rev., 2013, 113, 7981–8065 CrossRef PubMed.
- J. P. Scheifers, Y. Zhang and B. P. T. Fokwa, Acc. Chem. Res., 2017, 50, 2317–2325 CrossRef PubMed.
- Y. Pan and B. Zhou, Ceram. Int., 2017, 43, 8763–8768 CrossRef.
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef PubMed.
- L. P. Ding, P. Shao, F. H. Zhang, C. Lu, L. Ding, S. Y. Ning and X. F. Huang, Inorg. Chem., 2016, 55, 7033–7040 CrossRef PubMed.
- S. Wei, D. Li, Y. Lv, Z. Liu, F. Tian, D. Duan, B. Liu and T. Cui, J. Alloys Compd., 2016, 688, 1101–1107 CrossRef.
- B. Chu, D. Li, K. Bao, F. Tian, D. Duan, X. Sha, B. Liu and T. Cui, J. Alloys Compd., 2014, 617, 660–664 CrossRef.
- Y. Pan, H. Huang, X. Wang and Y. Lin, Comput. Mater. Sci., 2015, 109, 1–6 CrossRef.
- D. Koumoulis, C. L. Turner, R. E. Taylor and R. B. Kaner, J. Phys. Chem. C, 2016, 120, 2901–2907 Search PubMed.
- Y. Zhang, L. Wu, B. Wan, Y. Zhao, R. Gao, Z. Li, J. Zhang, H. Gou and H. K. Mao, Phys. Chem. Chem. Phys., 2016, 18, 2361–2368 RSC.
- B. J. Suh, X. Zong, Y. Singh, A. Niazi and D. C. Johnston, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144511 CrossRef.
- A. Latini, J. V. Rau, R. Teghil, A. Generosi and V. R. Alberini, ACS Appl. Mater. Interfaces, 2010, 2, 581–587 Search PubMed.
- Z. Li, D. Zheng, Z. Ding, Y. Li, B. Yao, Y. Li, X. Zhao, G. Yu, Y. Tang, W. Zheng and X. Liu, Mater. Res. Bull., 2016, 74, 188–191 CrossRef.
- Y. Pan and Y. Lin, JOM, 2017, 69, 2009–2013 CrossRef.
- H. Y. Niu, J. Q. Wang, X. Q. Chen, D. Z. Li, Y. Y. Li and P. Lazar, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144116 CrossRef.
- G. Akopov, M. T. Yeung, C. L. Turner, R. Mohammadi and R. B. Kaner, J. Am. Chem. Soc., 2016, 138, 5714–5721 CrossRef PubMed.
- J. B. Levine, J. B. Betts, J. D. Garrett, S. Q. Guo, J. T. Eng, A. Migliori and R. B. Kaner, Acta Mater., 2010, 58, 1530–1535 CrossRef.
- A. G. V. D. Geest and A. N. Kolmogorov, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2014, 46, 184–204 CrossRef.
- X. Zhang, E. Zhao, Z. Wu, K. Li and Q. Hou, Comput. Mater. Sci., 2014, 95, 377–383 CrossRef.
- L. P. Ding, X. Y. Kuang, P. Shao and X. F. Huang, Inorg. Chem., 2014, 53, 3471–3479 CrossRef PubMed.
- A. L. Ivanovskii, Prog. Mater. Sci., 2012, 57, 184–228 CrossRef.
- Q. F. Gu, G. Krauss and W. Steurer, Adv. Mater., 2008, 20, 3620–3626 CrossRef.
- M. T. Yeung, J. Lei, R. Mohammadi, C. L. Turner, Y. Wang, S. H. Tolbert and R. B. Kaner, Adv. Mater., 2016, 28, 6993–6998 CrossRef PubMed.
- G. Akopov, M. T. Yeung, Z. C. Sobell, C. L. Turner, C. W. Lin and R. B. Kaner, Chem. Mater., 2016, 28, 6605–6612 CrossRef.
- R. Mohammadi, C. L. Turner, M. Xie, M. T. Yeung, A. T. Lech, S. H. Tolbert and R. B. Kaner, Chem. Mater., 2016, 28, 632–637 CrossRef.
- A. Knappschneider, C. Litterscheid, D. Dzivenko, J. A. Kurzman and R. Sechadri, Inorg. Chem., 2013, 52, 540–542 CrossRef PubMed.
- X. Zhang, J. Qin, X. Sun, Y. Xue, M. Ma and R. Liu, Phys. Chem. Chem. Phys., 2013, 15, 20894–20899 RSC.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2015, 115, 185502 CrossRef PubMed.
- Q. Tao, D. Zheng, X. Zhao, Y. Chen, Q. Li, Q. Li, C. Wang, T. Cui, Y. Ma, X. Wang and P. Zhu, Chem. Mater., 2014, 26, 5297–5302 CrossRef.
- Y. Liang, Z. Fu, X. Yuan, S. Wang, Z. Zhong and W. Zhang, Europhys. Lett., 2012, 98, 66004 CrossRef.
- C. Zang, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 180101 CrossRef.
- S. Wang, X. Yu, J. Zhang, Y. Zhang, L. Wang, D. He and Y. Zhao, Journal of Superhard Materials, 2014, 36, 279–287 CrossRef.
- K. I. Portnoi, V. M. Romashov and L. N. Burobina, Powder Metall. Met. Ceram., 1970, 9, 577–580 CrossRef.
- S. Andersson and J. O. Carlsson, Acta Chem. Scand., 1970, 24, 1791–1799 CrossRef.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef.
- Y. Pan, Y. Lin, H. Wang and C. Zhang, Mater. Des., 2015, 86, 259–265 CrossRef.
- Y. Pan, J. Zhang, C. Jin and X. Chen, Mater. Des., 2016, 108, 13–18 CrossRef.
- X. Q. Chen, H. Y. Niu, D. Z. Li and Y. Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef.
- Y. Pan, P. Mao, H. Jiang, Y. Wan and W. Guan, Ceram. Int., 2017, 43, 5274–5282 CrossRef.
- Y. Pan and W. M. Guan, Phys. Chem. Chem. Phys., 2017, 19, 19427–19433 RSC.
- M. Zhang, H. Wang, H. Wang, T. Cui and Y. Ma, J. Phys. Chem. C, 2010, 114, 6722–6725 Search PubMed.
- M. Zhang, H. Yan, G. ZHang and H. Wang, J. Phys. Chem. C, 2012, 116, 4293–4297 Search PubMed.
- M. Zhang, H. Yan, Q. Wei and H. Wang, Comput. Mater. Sci., 2013, 68, 371–378 CrossRef.
- T. Lundstrom and I. Rosenberg, J. Solid State Chem., 1973, 6, 299–305 CrossRef.
- M. Wang, Y. W. Li, T. Cui, Y. M. Ma and G. T. Zou, Appl. Phys. Lett., 2008, 93, 101905 CrossRef.
- Y. Pan, Y. H. Lin, M. Wen and Q. N. Meng, RSC Adv., 2014, 4, 63891–63896 RSC.
- Y. Pan, Y. Lin, Q. Xue, C. Ren and H. Wang, Mater. Des., 2016, 89, 676–683 CrossRef.
- M. Mazdziarz and T. Moscicki, Mater. Chem. Phys., 2016, 179, 92–102 CrossRef.
- X. Li, Y. Tao and F. Peng, J. Alloys Compd., 2016, 687, 579–585 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |