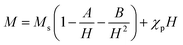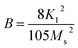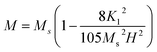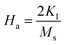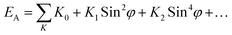DOI:
10.1039/C8RA02455C
(Paper)
RSC Adv., 2018,
8, 19600-19609
Investigation of crystal structure, microstructure and low temperature magnetic behavior of Ce4+ and Zn2+ co-doped barium hexaferrites (BaFe12O19)
Received
20th March 2018
, Accepted 21st May 2018
First published on 29th May 2018
Abstract
Ce4+ and Zn2+ co-doped barium hexaferrites (BFO) have been synthesized via a citrate-nitrate autocombustion route. Phase purity has been confirmed by high resolution (HR) powder X-ray diffraction analysis. Rietveld refinement on HR-XRD data has been carried out to reveal the crystal structure, bond angles and bond lengths. High-resolution scanning electron microscope (HR-SEM) has been used to study the effect of Ce4+ and Zn2+ on microstructure. Magnetic behavior of co-doped barium hexaferrites in the low temperature regime, 2–300 K has been studied. Further, it has been explained on the basis of superexchange interactions and formation of Bloch walls due to the presence of imperfections in the doped samples. It has been found that BFO changes hard to soft magnetic behavior when the temperature is decreased from 300 K to 2 K. Moreover, doping of Ce4+ and Zn2+ at Fe3+ site also brings similar effects which strengthens with decreasing temperature.
1. Introduction
Hexaferrites are widely used in electronic industries as microwave absorbers, permanent magnets, magnetic recording, data storage, etc. owing to their notable dielectric and magnetic properties.1–3 Due to low price, outstanding chemical stability and easy synthesis,4 M-type hexaferrites are the most extensively investigated among the common six types of hexaferrites.4 Recently, BaFe12O19 (BFO), an M-type hexaferrite, has attracted the attention of scientific community because of its tunable coercive field (Hc), reasonably high saturation magnetization (Ms), high Curie temperature (Tc), low eddy current losses and high electrical resistivity.5–7 By the means of suitable cationic substitutions at Ba2+ and/or Fe3+ site, saturation magnetization and coercivity of BFO can be tailor-made as per the requirements. However, while deciding outcomes of substitutions, the crystal structure of hexaferrites plays a vital role. The unit cell of BaFe12O19 is arranged by stacking R (BaFe6O11) and S (Fe6O8) blocks in RSR*S* sequence where ‘*’ denotes rotation of block along c-direction of the hexagonal unit cell by 180°.8 The R block is comprised of three hexagonal layers of oxygen with one oxygen ion in the middle layer substituted by Ba ion, while S block has two hexagonal layers with four oxygen ions in each. Five different interstitial sites are occupied by Fe3+ ions out of which octahedral 2a and tetrahedral 4f1 sites are in the S block, bipyramidal 2b and octahedral 4f2 are in R block, and octahedral 12k site resides at R–S interface. In these interstitial sites, metal ions residing in 2a, 2b and 12k sites have spin up while in 4f1 and 4f2 have spin down. Total 12 Fe3+ ions in the formula unit are distributed on various interstitial sites as 6 ions at 12k, 2 ions at 4f1 and 4f2 each and 1 ion at 2a and 2b each.9 Since, 8 of the Fe3+ ions are arranged such that their spins are in the upward direction while those of remaining 4 Fe3+ ions are in the downward direction. Therefore, the observed net magnetic moment per formula unit is due to 4 Fe3+ ions in upward direction. Considering the electronic configuration of Fe3+, it has 5 unpaired electrons in 3d orbitals. Thus, each Fe3+ ion has net magnetic moment of 5 μB. Hence, barium hexaferrite has net magnetic moment of 20 μB per formula unit.
During the recent past decades, few investigations were reported on the effect doping and co-doping of various metal ions at Ba2+ and Fe3+ sites. Single substitution of metal ions such as La,9 Al,10 Bi,11 Ti,12 Sc,13 Ce,14 etc. and different cationic combinations such as Co–Ti,15 Bi–Ti,15 Ru–Ti,16 Zn–Sn,17 Sc–Mg,18 Zn–Ti,19 Co–Sn,20 etc. as co-dopants at Fe3+ site in BaFe12O19 were investigated for their magnetic properties. It was observed that if Fe3+ ion is replaced by some non-magnetic ion, such as Zn2+, the saturation magnetization (MS) is increased due to the preferred filling of tetrahedral sites by Zn2+ ions. Since Zn2+ has no net magnetic moment, therefore, it reduces the net magnetic moment in the opposite direction, eventually rendering enhanced net magnetic moment or saturation magnetization per unit formula.3 On the other hand, if magnetic cation is substituted at Fe3+ site, the net magnetic moment will be affected by magnetic response of dopant cation. For example, the effect of doping of Co2+, a magnetic cation with 3 μB net magnetic moment on Fe3+ site was studied and observed that the net magnetization is decreased as well as the coercive field. Due to one less charge on Co2+ as compared to Fe3+, the strength of crystal field and magnetic interaction among magnetic ions decreases leading to low coercive field.21 A few researchers reported the effect of Ce3+ doping at both Ba2+ and Fe3+ sites in BaFe12O19.14,22 They observed that on doping Ce3+ ion at Ba2+ site, saturation magnetization increases first and then decreases after a certain concentration (10% Ce3+). However, no definite trend was observed for coercive field.14 In contrast, on doping of Ce3+ at Fe3+ site decreases the saturation magnetization because of less magnetic moment of Ce3+ ion as compared to Fe3+. The coercive field was found to increase slightly with increasing Ce3+ concentration.22 Albeit, there is an uncertainty of the oxidation state of cerium as +3 and site preference of Ce3+ ion between Ba2+ and Fe3+ sites based on the ionic radii of these ions. All the above-mentioned reports are mainly concerned with the high temperature magnetic behavior of these hexaferrites. Therefore, it is considered worthwhile to study the magnetic behavior in low temperature region since this will strengthen the understanding of the magnetic aspects of these hexaferrites.
In the present investigation, Zn–Ce co-doped barium hexaferrites, BaFe12−2xCexZnxO19 with x = 0, 0.1 and 0.3 have been synthesized via citrate-nitrate auto-combustion route. The magnetic behavior of synthesized hexaferrites has been investigated in low temperature regime (2–300 K). The magnetic properties are further explained by superexchange interactions and formation of Bloch walls due to imperfections.
2. Experimental work
2.1 Sample preparation
BaFe12−2xCexZnxO19 (x = 0.0, 0.1, 0.3) nano-crystalline powders were synthesized using citrate nitrate auto-combustion route. Synthesized compositions were designated as BFO (x = 0), BFCZO1 (x = 0.1) and BFCZO3 (x = 0.3). Barium carbonate (99% purity, Sigma Aldrich), ammonium ceric nitrate (99% purity, Qualikems, India), Fe(NO3)3·9H2O (98% purity, Fisher Scientific), Zn(NO3)2·9H2O (96% purity, Fisher Scientific) and citric acid (99.5% purity, Loba Chemie, India) were used as the starting materials. Stoichiometric amount of BaCO3 was weighed and dissolved in dilute nitric acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) to obtain Ba(NO3)2 followed by heating at 413 K till complete dryness. Ceric ammonium nitrate, barium nitrate, zinc nitrate, ferric nitrate and citric acid were then dissolved in double distilled water separately to make an aqueous transparent solution. All the prepared aqueous nitrate solutions were then added to the citric acid solution keeping the citrate to nitrate molar ratio (C/N) ∼0.3 for controlled and smooth combustion.23 The final mixed solution was then heated continuously at 473 K with continuous slow stirring. During heating, all the excess water evaporated, and the mass became viscous and turned into a gel. The gel slowly foamed followed by ignition and burnt into ash within a very short time-period. The ash was then collected and grounded using agate mortar-pestle. The ground powder was then calcined at 1373 K for 4 h in air. The calcined powders were then mixed with 2% PVA and pressed uniaxially under a load of 50 kN to form cylindrical pellets of diameter ∼12 mm and thickness ∼1.5 mm. The pellets were sintered in five steps using an electrical furnace (Lenton, made in UK). In the first step, the temperature was raised to 773 K with a heating rate of 2 K min−1 and held at this temperature for 1 h to remove the binder. The temperature was then raised to 1573 K (heating rate 5 K min−1) and held there for 6 h and finally cooled down to the room temperature.
4) to obtain Ba(NO3)2 followed by heating at 413 K till complete dryness. Ceric ammonium nitrate, barium nitrate, zinc nitrate, ferric nitrate and citric acid were then dissolved in double distilled water separately to make an aqueous transparent solution. All the prepared aqueous nitrate solutions were then added to the citric acid solution keeping the citrate to nitrate molar ratio (C/N) ∼0.3 for controlled and smooth combustion.23 The final mixed solution was then heated continuously at 473 K with continuous slow stirring. During heating, all the excess water evaporated, and the mass became viscous and turned into a gel. The gel slowly foamed followed by ignition and burnt into ash within a very short time-period. The ash was then collected and grounded using agate mortar-pestle. The ground powder was then calcined at 1373 K for 4 h in air. The calcined powders were then mixed with 2% PVA and pressed uniaxially under a load of 50 kN to form cylindrical pellets of diameter ∼12 mm and thickness ∼1.5 mm. The pellets were sintered in five steps using an electrical furnace (Lenton, made in UK). In the first step, the temperature was raised to 773 K with a heating rate of 2 K min−1 and held at this temperature for 1 h to remove the binder. The temperature was then raised to 1573 K (heating rate 5 K min−1) and held there for 6 h and finally cooled down to the room temperature.
2.2 Characterization
HR-Powder X-ray diffraction patterns of calcined and sintered samples were recorded using Rigaku High-Resolution X-ray Diffractometer to confirm the phase purity. Data were collected in the diffraction angle (2θ) range 20–90° with a very slow scan rate. Rietveld refinement was carried out on HR-XRD data to determine the lattice parameters and crystal structure. In order to study the microstructure, polishing of sintered pellets was done using emery papers of grade 1/0, 2/0, 3/0, and 4/0 (Sia, Switzerland) followed by polishing on a velvet cloth using diamond paste of grade 1/4-OS-475 (HIFIN). The pellets were then thermally etched at 1473 K for 15 min, and micrographs were recorded using FEI NOVA NANOSEM 450. To study the magnetic behavior of these hexaferrite samples, the pellets were cut into cuboidal pieces of dimension 4 mm × 2 mm × 2 mm. M–T plots were recorded in the temperature range 2–300 K under both ZFC (zero field cooled) and FC (field cooled) conditions. M–H loops for all the samples were recorded at 2 K and 300 K while varying external magnetic field from −2 to 2 Tesla. Magnetic studies were performed using VSM (Quantum design, Model-MPMS 3, EM-QM, USA).
3. Results and discussion
3.1 Structural analysis
To confirm the phase purity of synthesized hexaferrites, HR-XRD was carried out on sintered samples in 2θ range, 20–100°. Fig. 1 shows the high-resolution X-ray diffraction patterns for BFO, BFCZO1 and BFCZO3. Both BFO and BFCZO1 were found to be a single phase solid solution. In BFCZO3, there were some extra peaks identified due to ceria (CeO2). However, there were no peaks observed corresponding to ZnO or any other Zn based compounds in all the compositions. This implies that the solubility limit of cerium in hexaferrite was reached in the composition BFCZO3 while Zn was still soluble. HR-XRD data were analyzed by using X'Perthighscore to find out initial unit cell parameters and space group. All the peaks in BFO and BFCZO1 were indexed based on JCPDS card number 78-0132. The crystal structure of BFO was found to be hexagonal with P63/mmc space group.
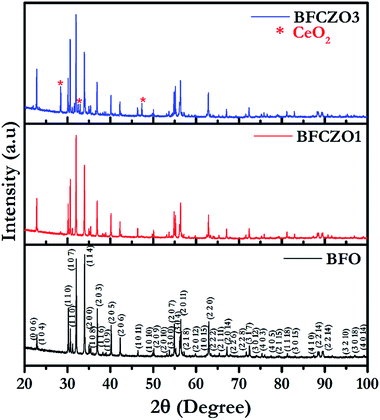 |
| | Fig. 1 High-resolution X-ray diffraction patterns for BFO, BFCZO1 and BFCZO3. | |
To further reveal the detailed structural parameters, Rietveld refinement was carried out on HR-XRD data of all the compositions using FullProf software.24 In the composition, BFCZO3 extra peaks corresponding to ceria (CeO2) were excluded during Rietveld refinement of its HR-XRD data. During the refinement, zero correction, scale factor, lattice parameters, line widths, asymmetry parameters, atomic positions and thermal parameters were refined simultaneously. The shape of peaks was described by pseudo-Voigt function and background was expressed by linear interpolation between a set of selected background points. The fitting was judged by the goodness of fit along with low values of reliable factors such as weighted profile factor (Rwp), expected weighted profile factor (Rexp), Bragg factor (RB) and χ2 as included in Table 1. All the refinements were found to be a good match with experimentally observed data. Fig. 2(a) and (b) shows the Rietveld refinement fitted patterns of BFO and BFCZO1 respectively. All the important refined parameters are given in Tables 1 and 2 and bond lengths and bond angles are reported in Tables 3 and 4 respectively. Bond lengths and bond angles for the composition, BFCZO3 are not included due to presence of ceria as an extra phase in this composition. Lattice parameters of BFO closely match with the previously reported data.25 With increasing doping concentration of Ce4+ and Zn2+ at the Fe3+ site, the lattice parameters were found to be increased. The lattice parameter ‘c’ was increased more as compared to ‘a or b’ which is due to presence of multiple Fe3+ sites along c-axis as compared to a and b-axis. It is interesting to note from Table 2 that Biso for Fe3+ at trigonal bipyramidal (TBP) is high as compared to that in octahedral and tetrahedral sites. In addition, the Fe–O average bond length in TBP site is significantly high as compared to average bond length in octahedral and tetrahedral sites. This indicates that Fe3+ at TBP site has high dynamics due to thermal energy. Furthermore, the bond angles (see Table 4) also deviates from standard bond angles in octahedra, tetrahedra and TBP sites. The existence of large bond lengths, high dynamics of Fe3+ at TBP site due to thermal energy coupled with significant deviation of bond angles from standard values would affect the magnetic exchange interaction in these ferrites which is discussed in detail in Section 3.3.
Table 1 Cell parameters and other reliable parameters of Rietveld analysis for BFO, BFCZO1 and BFCZO3
| Parameters |
BFO |
BFCZO1 |
BFCZO3 |
| a (Å) |
5.8908 |
5.8959 |
5.8993 |
| b (Å) |
5.8908 |
5.8959 |
5.8993 |
| c (Å) |
23.2075 |
23.2259 |
23.2422 |
| Rp |
30.7 |
38.4 |
49.4 |
| Rwp |
17.3 |
25.2 |
31.8 |
| Rexp |
15.4 |
14.6 |
16.3 |
| RB |
6.87 |
13.47 |
14.3 |
| χ2 |
1.26 |
2.98 |
3.78 |
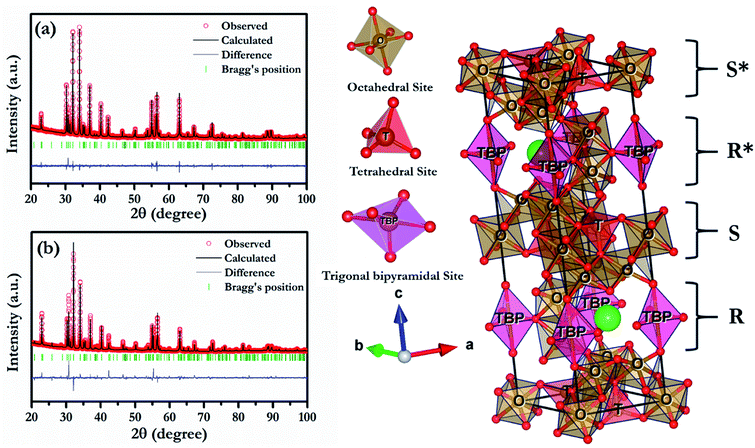 |
| | Fig. 2 Rietveld refinement patterns of (a) BFO, (b) BFCZO1 and schematic of BFO. | |
Table 2 Refined structural parameters of Rietveld analysis for BFO and BFCZO1
| Atoms |
BaFe12O19 (BFO) |
BaCe0·1Zn0·1Fe11·8O19 (BFCZO1) |
| X |
Y |
Z |
Biso |
X |
Y |
Z |
Biso |
| Ba |
0.6667 |
0.3333 |
0.2500 |
0.78 |
0.6667 |
0.3333 |
0.2500 |
0.31 |
| Fe1 |
0.0000 |
0.0000 |
0.0000 |
0.90 |
0.0000 |
0.0000 |
0.0000 |
0.56 |
| Fe2 |
0.0000 |
0.0000 |
0.2500 |
2.17 |
0.0000 |
0.0000 |
0.2500 |
3.68 |
| Fe3 |
0.3333 |
0.6667 |
0.0282 |
0.59 |
0.3333 |
0.6667 |
0.0281 |
0.24 |
| Zn |
— |
— |
— |
— |
0.3333 |
0.6667 |
0.0281 |
0.23 |
| Fe4 |
0.3333 |
0.6667 |
0.1908 |
0.69 |
0.3333 |
0.6667 |
0.1940 |
1.06 |
| Ce |
— |
— |
— |
— |
0.3333 |
0.6667 |
0.1940 |
1.06 |
| Fe5 |
0.1681 |
0.3374 |
−0.1086 |
0.59 |
0.1684 |
0.3369 |
−0.1098 |
0.22 |
| O1 |
0.0000 |
0.0000 |
0.1480 |
0.58 |
0.0000 |
0.0000 |
0.1253 |
2.28 |
| O2 |
0.3333 |
0.6667 |
−0.0565 |
0.89 |
0.3333 |
0.6667 |
−0.0868 |
1.18 |
| O3 |
0.1802 |
0.3605 |
0.2500 |
0.32 |
0.1970 |
0.3942 |
0.2500 |
1.67 |
| O4 |
0.1629 |
0.3257 |
0.0517 |
0.15 |
0.1777 |
0.3553 |
0.0469 |
0.34 |
| O5 |
0.5033 |
0.0068 |
0.1467 |
0.07 |
0.5083 |
0.0167 |
0.1249 |
1.14 |
Table 3 Different Fe–O (Me–O) and average bond lengths for BFO and BFCZO1; O-octahedral, TBP-trigonal bipyramidal, T-tetrahedral
| Site |
Bond type |
Bond length (Å) |
Average bond length (Å) |
| BFO |
BFCZO1 |
BFO |
BFCZO1 |
| Fe1 (2a, O) |
Fe1–O4 |
2.04994 |
2.11640 |
2.04994 |
2.11640 |
| Fe2 (2b, TBP) |
Fe2–O1 |
2.36694 |
2.89557 |
2.05031 |
2.37576 |
| Fe2–O3 |
1.83923 |
2.01255 |
| Fe3 (4f1, T) |
Fe3–O2 |
1.96591 |
2.66889 |
1.85881 |
1.90412 |
| Fe3–O4 |
1.82311 |
1.64920 |
| Fe4 (4f2, O) |
Fe4–O3 |
2.08050 |
1.90391 |
2.04747 |
2.15324 |
| Fe4–O5 |
2.01444 |
2.40258 |
| Fe5 (12k, O) |
Fe5–O1 |
1.94911 |
1.75753 |
2.01572 |
1.91466 |
| Fe5–O2 |
2.06924 |
1.76621 |
| Fe5–O4 |
2.14641 |
2.29335 |
| Fe5–O5 |
1.89156 |
1.68877 |
Table 4 Me1–O–Me2 (Me![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe) bond angles for BFO and BFCZO1
Fe) bond angles for BFO and BFCZO1
| Bond type |
BFO |
BFCZO1 |
| Fe1–O4–Fe3 |
126.7153 |
133.5897 |
| Fe1–O4–Fe5 |
93.3023; 93.3011 |
88.3533; 88.3464 |
| Fe2–O1–Fe5 |
117.9775 |
101.8584 |
| Fe2–O3–Fe4 |
138.6468 |
136.9580 |
| Fe3–O2–Fe5 |
125.7317 |
107.5496 |
| Fe4–O3–Fe4 |
82.7063 |
86.0841 |
| Fe4–O5–Fe5 |
127.8448; 127.8131 |
118.7285; 118.7063 |
| Fe5–O2–Fe5 |
89.3373 |
111.3225 |
| Fe5–O5–Fe5 |
100.5177 |
119.4773 |
3.2 Site preference of Ce4+ and Zn2+
It has been reported in previous studies that Zn2+ prefers 4f1 site among all the available Fe3+ sites.3 However, there is an uncertainty with site preference of Ce. A few studies suggested that the Ce preferably occupy Ba-site,14 meanwhile, other reports claimed that Ce prefers Fe-site.22 In the present study, we have assumed that Ce would occupy the Fe-site and hence synthesized compounds accordingly. Considering the ionic radius of Ce4+ (0.87 Å)26 and Ba2+(1.61 Å),26 it is clear that if Ce4+ replaces Ba2+, then final lattice parameters should decrease. But, in the current study, lattice parameters were found to increase with increasing Ce4+ concentration. Moreover, the ionic radius of Ce4+ (0.87 Å)26 is much closer to Fe3+(0.78 Å)26 as compared to Ba2+(1.61 Å).26 Thus Ce4+ would prefer Fe3+ site instead of Ba2+ site. For further investigations, HR-XRD of BFO and BFCZO1 was compared. Interestingly, the intensities of a few reflections such as (006), (008) and (107) were increased substantially as depicted in Fig. 3 while rest of the pattern remained unaltered. The schematic of BFO with (006), (008) and (107) planes is shown in Fig. 3. It is observed from the Fig. 3 that these planes contain only Fe sites. Therefore, the intensities of HR-XRD profiles will differ only in these directions. Hence, it can be concluded that Ce4+ ions occupy Fe3+ sites instead of Ba2+.
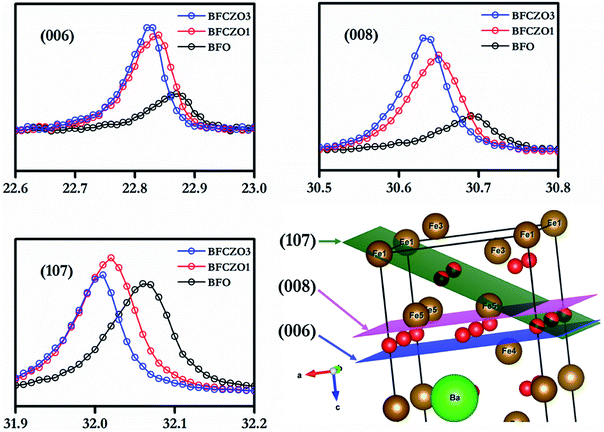 |
| | Fig. 3 Comparison of (006), (008) and (107) HR-XRD profiles and intersections of these planes in unit cell. | |
3.3 Microstructural analysis
Microstructure plays a key role in defining magnetic properties of hexaferrites.27–29 In hexaferrites c-axis is easy axis of magnetization.30 If the grain growth occurs favorably along c-direction, then it will affect the coercive field of the material.31 This eventually can change the behavior of the sample from hard magnetic to a typical soft magnetic. In addition, the grain size also can affect the magnetic behavior.27 For example, in case of smaller grains there would be high pinning of magnetic moments at the grain boundaries resulting into high coercive field.32 In contrast, a single crystal or a single grain would have almost negligible coercive field if studied while applying external field along c-axis (easy axis). This type of behavior was reported in previous studies.32
The microstructure of these hexaferrites was studied using HR-SEM. Images of fractured surface of BFO, BFCZO1 and BFCZO3 are depicted in Fig. 4a, c and d respectively. Grains with plate-like shape having high aspect ratio appears to grow along the c-axis. It is interesting to note that the aspect ratio of grains in BFO is very large which decreases substantially on substitution of Zn2+ and Ce4+. In the composition, BFCZO3, large hexagonal shaped grains were observed. However, the average grain size increases with increasing dopant concentrations. The average grain size was measured assuming grains of spherical shape. The average grain size of BFO, BFCZO1 and BFCZO3 was found to be 0.61 μm, 1.32 μm and 2.49 μm respectively. It can be inferred by comparing the grain size that doping of Ce4+ and Zn2+ suppresses grain growth specially along c-axis. It is noted that addition of Ce4+ and Zn2+ favors the formation of grains with high volume. These large hexagonal grains may be consisting of multi-domains.33 The effect of multi-domain grains on magnetization of these hexagonal ferrites is further discussed in Section 3.4. Fig. 4(b) shows the EDX elemental mapping of BFO sample. It was inferred from the compositional analysis that the stoichiometry of different atoms was well maintained as per requirement in M-type hexaferrites.
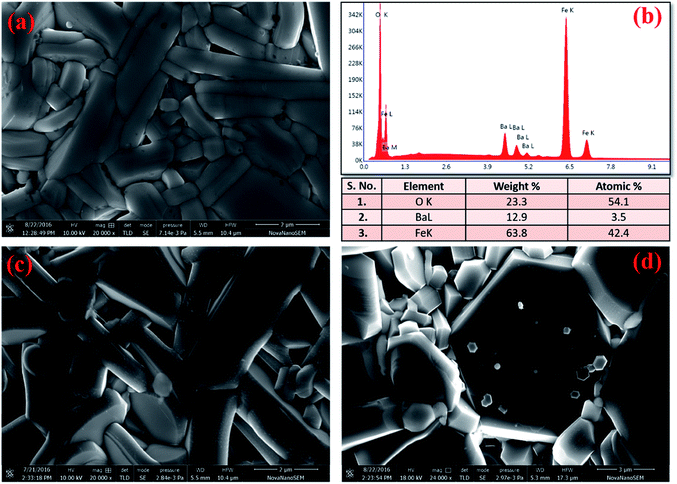 |
| | Fig. 4 HR-SEM images of (a) BFO, (c) BFCZO1, (d) BFCZO3 and (b) EDX elemental mapping results for BFO. | |
3.4 Magnetic properties
Variation of Magnetization with temperature, in the temperature range 2–300 K, for both FC (cooling and heating in the presence of 300 Oe external magnetic field) and ZFC (cooling in absence of magnetic field and heating in presence of 300 Oe external magnetic field) conditions is depicted in Fig. 5. All the synthesized compositions exhibited an increasing trend of magnetization in both ZFC and FC conditions. The net magnetization in FC condition was higher than that in ZFC because the sample was cooled in presence of 300 Oe external field during FC. The net magnetization increased with decreasing temperature. This increase in magnetization is due to the stability of magnetic moments and strong coupling between magnetic dipoles at low temperature.34 At 300 K, the net magnetization doesn't become zero which shows that the Curie temperature lies beyond this temperature range. The Curie temperature in these hexaferrites was reported to be around 500 K.35 Interestingly, the net magnetic moment increases with doping of Ce4+ and Zn2+. As stated earlier, Zn2+, a non-magnetic ion, prefers 4f1 site. Since, 4f1 site carries the magnetic moment in opposite direction to net magnetic moment of the unit cell, therefore replacing Fe3+ by a non-magnetic ion, Zn2+, on this particular site would eventually enhance the net magnetization.3 On the other hand, Ce4+ replaces one of the Fe3+ ions at three octahedra sites, 12k, 4f2 and 2a. Thus, the effect of Ce4+ on net magnetization is rather difficult to predict. However, to gain impetus into the effect of Ce4+ doping on net magnetization, it is important to compare the magnetic behavior of BFCZO1 and BFCZO3. From the Fig. 5, it is noticed that increase in net magnetization of BFCZO1 as compared to BFO is ∼3 emu/gm while in BFCZO3 its ∼1.6 emu gm−1 with respect to BFCZO1. Thus, in BFCZO1, the increase in net magnetization is due to combined effect of Ce4+ and Zn2+. Whereas, further increased magnetization in BFCZO3 seems to be due to the occupation of 4f1 site by Zn2+ and partial occupation of Ce4+ on 4f2 site, since in this composition Ce4+ is not fully blended in solid solution as observed in HR-XRD. Therefore, it can be expected that Ce4+ preferably favors 4f2 site. However, exact site occupation of Ce4+ is still uncertain.
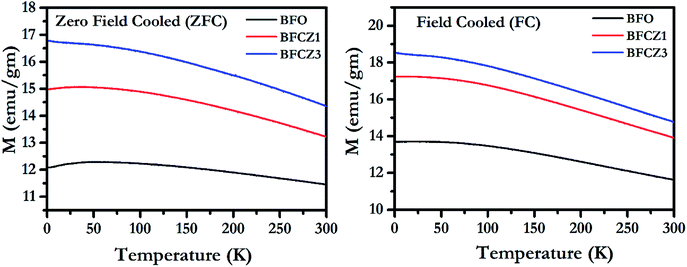 |
| | Fig. 5 Magnetization vs. temperature plot for BFO, BFCZO1 and BFCZO3 in both ZFC and FC conditions. | |
Fig. 6(a) and 7(a) show the M–H hysteresis loop of BFO, BFCZO1 and BFCZO3 at 300 K and 2 K respectively, in the range of −2 to +2 Tesla. All the compositions were saturated in this range of external magnetic field. The values of saturation magnetization (MS), remanent magnetization (MR) and coercive field (HC) are given in Table 5. The saturation magnetization (MS) was calculated using Law of approach to saturation (LAS)36 described by eqn (1).
| |
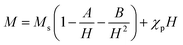 | (1) |
where,
Ms is saturation magnetization, ‘
A’ is inhomogeneity parameter,
χp is the high field susceptibility and ‘
B’ is anisotropy parameter. For hexagonal ferrites, ‘
B’ can be expressed by
eqn (2):
36| |
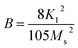 | (2) |
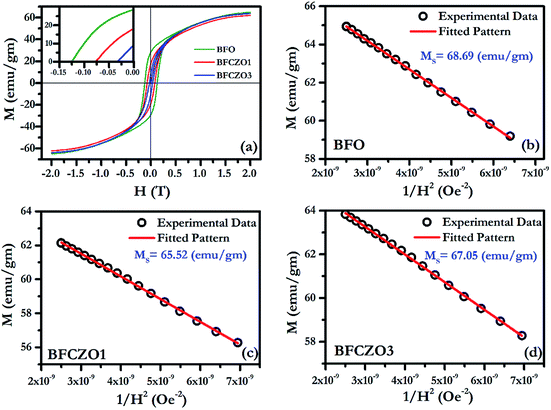 |
| | Fig. 6 (a) M–H hysteresis loop for BFO, BFCZO1 and BFCZO3 at 300 K, (b), (c) and (d) Fitting of M–H data in high field regime for BFO, BFCZO1 and BFCZO3 respectively. | |
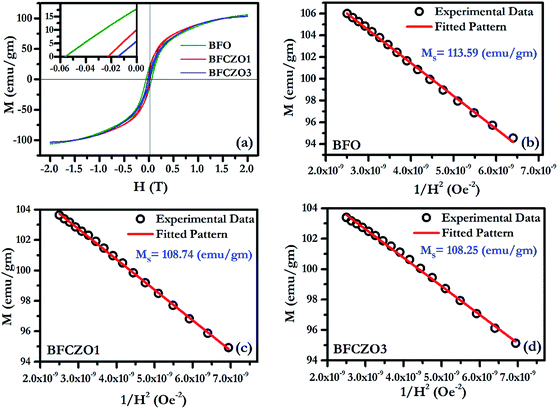 |
| | Fig. 7 (a) M–H hysteresis loop for BFO, BFCZO1 and BFCZO3 at 2 K, (b), (c) & (d) Fitting of M–H data in high field regime for BFO, BFCZO1 and BFCZO3 respectively. | |
Table 5 Saturation magnetization, coercive field, remanent magnetization, MR/MS ratio, anisotropy field (HA) and magnetocrystalline anisotropy constant (K1) for all the compositions at 300 K and 2 K
| Compositions/properties |
300 K |
2 K |
| BFO |
BFCZO1 |
BFCZO3 |
BFO |
BFCZO1 |
BFCZO3 |
| MS (emu gm−1) |
68.69 |
65.52 |
67.05 |
124.91 |
117.28 |
117.44 |
| HC (Oe) |
1238 |
752 |
306 |
558 |
227 |
146 |
| MR (emu gm−1) |
28 |
18 |
7 |
18 |
10 |
6 |
| MR/MS |
0.41 |
0.27 |
0.10 |
0.14 |
0.08 |
0.05 |
| HA (×104) |
7.24 |
7.02 |
6.81 |
8.01 |
6.68 |
6.52 |
| K1 (×106) |
2.49 |
2.30 |
2.28 |
4.55 |
3.63 |
3.53 |
Moreover, at the sufficiently high magnetic field the value of A/H and χP in eqn (1) are negligible in case of hexaferrites as explained by Neel37 and Brown.38 Thus, the eqn (1) can be written as follows:
| |
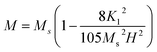 | (3) |
To calculate the saturation magnetization (MS) and K1, M–H curve data at high external field were fitted with the eqn (3). The fitted curves, according to the equation above, for all the compositions at 300 K and 2 K are depicted in Fig. 6(b–d) and 7(b–d) respectively. On the basis of MS and K1, the values of the anisotropy field (Ha) can be calculated by the eqn (4):33,39
| |
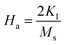 | (4) |
where,
HA is anisotropy field,
MS is saturation magnetization and
K1 is magneto-crystalline anisotropy (MCA) constant. The values of
K1 and
HA are listed in
Table 5. The degree of MCA is defined by
HA, in A m
−1, and anisotropy constant
K1 is a measure of the difficulty to move the magnetization out of preferred (easy) direction in the crystal lattice.
4,40 MCA is related to the energy needed to turn a magnetization vector from the preferred low energy, or easy direction, to a difficult, higher energy orientation, represented by the anisotropy constants
K1 and
K2. For single hexagonal crystals the total anisotropy energy (
EA) is given by the sum:
41| |
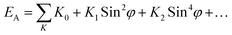 | (5) |
where
K0 = the energy to magnetize along the easy axis, and
φ = the angle between the direction of magnetization and the
c-axis. The higher order terms (
K2,
K3…) are negligible for uniaxial ferrites.
42 K0 has a low value as the easy axis is a low energy orientation.
4 Thus, for M-type hexaferrites the anisotropy constant becomes
K1.
At 300 K, maximum saturation magnetization, 68.69 emu gm−1 was found in BFO. Interestingly, doping of Ce4+ and Zn2+ in BFO reduces MR and HC substantially while MS remains almost invariant as shown in Table 5. The effect of Ce4+ and Zn2+ on magnetic behavior of these samples can be explained on the basis of the presence of large grains with low aspect ratio. These large grains can be considered as comprised of multiples crystallites. Kittel43 suggested that if the crystallite size surpasses a critical diameter, Bloch walls will be created spontaneously.32 Due to presence of these multiple crystallites, there will be randomly oriented multiple domains with a net magnetization in a single grain. Thus, at 300 K, after doping with Ce4+ and Zn2+, presence of excessive additional domains would help to decrease the remanent magnetization and coercive field. However, it was observed by Rathenau et al.32 that the formation of Bloch walls is not constrained to particle size; rather it depends upon the presence of imperfections. In the present case, due to introduction of Ce and Zn, presence of defects such as oxygen vacancies can be expected. Presence of these vacancies (imperfections) would enhance Bloch wall formation around the imperfections and hence result in the reduced remanent magnetization and coercive field. To further verify this, we have calculated MR/MS ratio, anisotropy constant K1 and highest coercive force (HA) (see Table 5). It has been observed that the MR/MS ratio is 0.40 for BFO which is closer to 0.50, values for well oriented samples.42 In case of BFCZO1 and BFCZO3, it reduced to 0.27 and 0.10 respectively. These low values of MR/MS imply the enhanced disorientated domains and hence low MR and HC. From the Table 5, it can be observed that MR reduced by ∼35% and ∼75% in BFCZO1 and BFCZO3 respectively as compared to BFO. HC decreased by ∼40% and ∼76% in BFCZO1 and BFCZO3 respectively.
The scenario at low temperature (2 K) is quite similar to 300 K. At 2 K, the saturation magnetization becomes almost double in all the compositions. The remanent magnetization and coercive field also follow similar trend with increasing Ce4+ and Zn2+ concentrations. But, the remanent magnetization and coercive field in BFO decrease manifold at low temperature. To understand this behavior, one has to consider exchange interactions in these hexaferrites.44 Generally, in metals, the magnetic spins are linked to each other via direct exchange which becomes negligible over longer distances. In these ferrimagnets, the distance between two magnetic ions is not adequate, due to presence of oxygen ions, for direct exchange. Thus, magnetic moments are linked by superexchange interactions. The interaction of opposing magnetic spins via an intermediate oxygen atom (Me1–O–Me2) (Me-magnetic ion and O-oxygen) is known as superexchange interaction.45 The magnitude of superexchange interaction can be estimated by Me1–O–Me2 bond angles and bond lengths. An angle of 180° (Me1–O–Me2) would cause strongest interaction effect and 90° weakest, and the effect becomes negligible over Me–O distance of 3 Å, as suggested by Anderson.46 In the present case, to evaluate the effect of superexchange interaction we have calculated all the possible Me–O bond lengths and Me–O–Me bond angles, as listed in Tables 3 and 4 All the bond lengths in BFO and BFCZO1 are less than 3 Å. Therefore, superexchange interactions are significant at all the Fe3+ sites. The average bond length follows TBP > O > T order at 300 K. Thus, tetrahedra Fe3+ sites have strongest interaction while TBP sites have the weakest interaction. Furthermore, as observed in HR-XRD, the thermal parameter is also high for Fe3+ ions at TBP site. This leads to weak exchange interaction and hence less contribution in net magnetization at 300 K. At 2 K, it is expected that all the sites are frozen and superexchange interactions are enhanced. However, as observed from Tables 3 and 4, the Me–O–Me bond angles around 4f1 and 4f2 site are rather closer to 180° thus the interaction would be strong in these sites as compared to the other sites. Hence, at low temperature, it can be hypothesized that when external magnetic field is applied, all the magnetic moments are being forced to align in the direction of external field. As the external field is reduced slowly, due to strong interactions of magnetic moments in opposite directions (4f1 and 4f2 sites), they tend to return to their original position. In this way, they also force to relax the magnetic moments which are in the direction of net magnetization resulting in low remanent magnetization and coercive force. To further verify the hypothesis, we have calculated the MR/MS ratio, anisotropy constant K1 and anisotropy field HA at 300 K and 2 K. Interestingly, MR/MS ratio decreases from 0.41 to 0.14 while the values of K1 and HA increased substantially as compared to the values obtained at 300 K in BFO. As a whole, all these values will decrease remanent magnetization and coercive force as discussed above. However, a decreasing trend of K1 and HA, an anomalous behavior, was observed with doping of Ce4+ and Zn2+ in BFO. In doped compositions, BFCZO1 and BFCZO3, due to presence of non-magnetic ions, the superexchange interaction would be weakened. Hence, the anisotropy constant K1 and highest coercive force HA would also decrease, as observed from Table 5. The effect doping Ce4+ and Zn2+ collectively, changes its behavior from hard to soft magnet.
4. Conclusions
In summary, BaFe12−2xCexZnxO19 (x = 0.0, 0.1, 0.3) samples were successfully synthesized via citrate-nitrate auto-combustion route and conventional sintering at 1573 K. High-resolution X-ray diffraction and scanning electron microscopy studies were carried out to reveal the phase purity and morphology. Rietveld refinement of HR-XRD data was done to divulge the structural parameters such as lattice parameters, bond angles, bond lengths, thermal parameters and atomic positions. Magnetic behavior all the samples were studied in low temperature regime, 2–300 K. With decreasing temperature, all the samples convert their behavior from hard to soft magnet. The doping of Ce4+ and Zn2+ in BFO suppresses the c-axis preferred grain growth and enhances the average grain size. The presence of these non-magnetic ions in BFO helped to decrease the remanent magnetization at 300 K and 2 K altering their behavior from hard to soft magnet. The magnetic behavior was explained on the Bloch wall formation and superexchange interactions.
Conflicts of interest
There are no conflicts of interest to declare.
References
- A. Ghasemi, S. E. Shirsath, X. Liu and A. Morisako, J. Appl. Phys., 2011, 109, 07A507 CrossRef.
- Ü. Özgür, Y. Alivov and H. Morkoç, J. Mater. Sci. Mater. Electron., 2009, 20, 789–834 CrossRef.
- Z. W. Li, C. K. Ong, Z. Yang, F. L. Wei, X. Z. Zhou, J. H. Zhao and A. H. Morrish, Phys. Rev. B, 2000, 62, 6530–6537 CrossRef.
- R. C. Pullar, Prog. Mater. Sci., 2012, 57, 1191–1334 CrossRef.
- W. Gong, G. C. Hadjipanayis and R. F. Krause, J. Appl. Phys., 1994, 75, 6649–6651 CrossRef.
- P. Campbell, Permanent Magnet Materials and their Application, Cambridge University Press, Cambridge, 1994 Search PubMed.
- S. Castro, M. Gayoso, J. Rivas, J. M. Greneche, J. Mira and C. Rodríguez, J. Magn. Magn. Mater., 1996, 152, 61–69 CrossRef.
- R. C. Pullar, Prog. Mater. Sci., 2012, 57, 1191–1334 CrossRef.
- C. Wu, Z. Yu, K. Sun, J. Nie, R. Guo, H. Liu, X. Jiang and Z. Lan, Sci. Rep., 2016, 6, 36200 CrossRef PubMed.
- V. N. Dhage, M. L. Mane, A. P. Keche, C. T. Birajdar and K. M. Jadhav, Phys. B, 2011, 406, 789–793 CrossRef.
- P. Winotai, S. Thongmee and I. M. Tangab, Mater. Res. Bull., 2000, 35, 1747–1753 CrossRef.
- P. A. Mariño-Castellanos, J. Anglada-Rivera, A. Cruz-Fuentes and R. Lora-Serrano, J. Magn. Magn. Mater., 2004, 280, 214–220 CrossRef.
- P. Borisov, J. Alaria, T. Yang, S. R. C. McMitchell and M. J. Rosseinsky, Appl. Phys. Lett., 2013, 102, 1–6 CrossRef.
- Z. Mosleh, P. Kameli, A. Poorbaferani, M. Ranjbar and H. Salamati, J. Magn. Magn. Mater., 2016, 397, 101–107 CrossRef.
- A. G. Belous, O. I. V’yunov, E. V. Pashkova, V. P. Ivanitskii and O. N. Gavrilenko, J. Phys. Chem. B, 2006, 110, 26477–26481 CrossRef PubMed.
- A. M. Alsmadi, I. Bsoul, S. H. Mahmood, G. Alnawashi, K. Prokeš, K. Siemensmeyer, B. Klemke and H. Nakotte, J. Appl. Phys., 2013, 114, 4–12 CrossRef.
- H. C. Fang, Z. Yang, C. K. Ong, Y. Li and C. S. Wang, J. Magn. Magn. Mater., 1998, 187, 129–135 CrossRef.
- Y. Tokunaga, Y. Kaneko, D. Okuyama, S. Ishiwata, T. Arima, S. Wakimoto, K. Kakurai, Y. Taguchi and Y. Tokura, Phys. Rev. Lett., 2010, 105, 17–20 CrossRef PubMed.
- P. Wartewig, M. K. Krause, P. Esquinazi, S. Rösler and R. Sonntag, J. Magn. Magn. Mater., 1999, 192, 83–99 CrossRef.
- F. Sandiumenge, B. Martínezxavier, X. Batlle, S. Gali and X. Obradors, J. Appl. Phys., 1992, 72, 4608 CrossRef.
- M. G. Shalini and S. C. Sahoo, AIP Conf. Proc., 2016, 1728, 020445 CrossRef.
- R. A. Pawar, S. S. Desai, Q. Y. Tamboli, S. E. Shirsath and S. M. Patange, J. Magn. Magn. Mater., 2015, 378, 59–63 CrossRef.
- K. Tanwar, N. Jaiswal, D. Kumar and O. Parkash, J. Alloys Compd., 2016, 684, 683–690 CrossRef.
- J. Rodrigues-Carvajal, Lab. Leon Brillouin, CEA-CNRS, Fr., 2000.
- P. B. Braun, The crystal structures of a new group of ferromagnetic compound, 1957 Search PubMed.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925–946 CrossRef.
- M. Hillert, Acta Metall., 1965, 13, 227–238 CrossRef.
- J. Dho, E. K. Lee, J. Y. Park and N. H. Hur, J. Magn. Magn. Mater., 2005, 285, 164–168 CrossRef.
- S. Ram, H. Krishnan, K. Rai and K. Narayan, Jpn. J. Appl. Phys., 1989, 28, 604–608 CrossRef.
- X. Zhang, Z. Yue, S. Meng and L. Yuan, J. Appl. Phys., 2015, 116, 243909 CrossRef.
- M. Sugimoto, J. Am. Ceram. Soc., 1999, 82, 269–280 CrossRef.
- G. W. Rathenau, Rev. Mod. Phys., 1953, 25, 297–301 CrossRef.
- C. Kittel, Rev. Mod. Phys., 1949, 21, 541–583 CrossRef.
- H. Kojima, Handb. Ferromagn. Mater., 1982, vol. 3, pp. 305–391 Search PubMed.
- L. Jahn and H. G. Muller, Phys. Status Solidi, 1963, 35, 723–730 CrossRef.
- T. Miyazaki and H. Jin, The Physics of Ferromagnetism, Oxford University Press, 2012, vol. 158 Search PubMed.
- L. Néel, J. Phys. Radium, 1948, 9, 184–192 CrossRef.
- W. F. Brown, Phys. Rev., 1941, 60, 139–147 CrossRef.
- A. Moitra, S. Kim, S. G. Kim, S. C. Erwin, Y. K. Hong and J. Park, Comput. Condens. Mat., 2014, 1, 45–50 CrossRef.
- B. T. Shirk, J. Appl. Phys., 1969, 40, 1294 CrossRef.
- C. Heck, Magnetic Materials and their Applications, London: Butterworth, 1974 Search PubMed.
- J. Smit and H. P. J. Wijn, Ferrites: physical properties of ferrimagnetic oxides in relation to their technical applications, Philips' Technical Library, Eindhoven, Netherlands, 1959, p. 369 Search PubMed.
- C. Kittel, Phys. Rev., 1948, 73, 810–811 CrossRef.
- L. Néel, Proc. Phys. Soc., Sect. A, 1952, 65, 869–885 CrossRef.
- H. Kramers, Physica, 1934, 1, 182–192 CrossRef.
- P. W. Anderson, Phys. Rev., 1950, 79, 705–710 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Deepankar Sri Gyan,
Prashant Gupta,
Shukdev Pandey,
OmParkash and
Devendra Kumar
*,
Deepankar Sri Gyan,
Prashant Gupta,
Shukdev Pandey,
OmParkash and
Devendra Kumar
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) to obtain Ba(NO3)2 followed by heating at 413 K till complete dryness. Ceric ammonium nitrate, barium nitrate, zinc nitrate, ferric nitrate and citric acid were then dissolved in double distilled water separately to make an aqueous transparent solution. All the prepared aqueous nitrate solutions were then added to the citric acid solution keeping the citrate to nitrate molar ratio (C/N) ∼0.3 for controlled and smooth combustion.23 The final mixed solution was then heated continuously at 473 K with continuous slow stirring. During heating, all the excess water evaporated, and the mass became viscous and turned into a gel. The gel slowly foamed followed by ignition and burnt into ash within a very short time-period. The ash was then collected and grounded using agate mortar-pestle. The ground powder was then calcined at 1373 K for 4 h in air. The calcined powders were then mixed with 2% PVA and pressed uniaxially under a load of 50 kN to form cylindrical pellets of diameter ∼12 mm and thickness ∼1.5 mm. The pellets were sintered in five steps using an electrical furnace (Lenton, made in UK). In the first step, the temperature was raised to 773 K with a heating rate of 2 K min−1 and held at this temperature for 1 h to remove the binder. The temperature was then raised to 1573 K (heating rate 5 K min−1) and held there for 6 h and finally cooled down to the room temperature.
4) to obtain Ba(NO3)2 followed by heating at 413 K till complete dryness. Ceric ammonium nitrate, barium nitrate, zinc nitrate, ferric nitrate and citric acid were then dissolved in double distilled water separately to make an aqueous transparent solution. All the prepared aqueous nitrate solutions were then added to the citric acid solution keeping the citrate to nitrate molar ratio (C/N) ∼0.3 for controlled and smooth combustion.23 The final mixed solution was then heated continuously at 473 K with continuous slow stirring. During heating, all the excess water evaporated, and the mass became viscous and turned into a gel. The gel slowly foamed followed by ignition and burnt into ash within a very short time-period. The ash was then collected and grounded using agate mortar-pestle. The ground powder was then calcined at 1373 K for 4 h in air. The calcined powders were then mixed with 2% PVA and pressed uniaxially under a load of 50 kN to form cylindrical pellets of diameter ∼12 mm and thickness ∼1.5 mm. The pellets were sintered in five steps using an electrical furnace (Lenton, made in UK). In the first step, the temperature was raised to 773 K with a heating rate of 2 K min−1 and held at this temperature for 1 h to remove the binder. The temperature was then raised to 1573 K (heating rate 5 K min−1) and held there for 6 h and finally cooled down to the room temperature.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe) bond angles for BFO and BFCZO1
Fe) bond angles for BFO and BFCZO1