Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enhancement of dissipated energy by large bending of an organic single crystal undergoing twinning deformation†
Sajjad Husain Mir a,
Yuichi Takasaki
a,
Yuichi Takasaki ab,
Emile R. Engela and
Satoshi Takamizawa
ab,
Emile R. Engela and
Satoshi Takamizawa *a
*a
aDepartment of Materials System Science, Graduate School of Nanobioscience, Yokohama City University, 22-2 Seto, Kanazawa-ku, Yokohama, Kanagawa 236-0027, Japan. E-mail: staka@yokohama-cu.ac.jp
bKanagawa Institute of Industrial Science and Technology, Shimoimaizumi, 705-1 Ebina, Kanagawa 243-0435, Japan
First published on 14th June 2018
Abstract
We demonstrate exceptional twinning deformation in a molecular crystal upon application of mechanical stress. Crystal integrity is preserved and the deformation is associated with a large bending angle (65.44°). This is a new strategy to increase the magnitude of the dissipated energy in an organic solid comparable to that seen in alloys. By X-ray crystallographic analysis it was determined that a large molecular rearrangement at the twinning interface preserves the crystal integrity. Drastic molecular rearrangement at the twinning interface helps to preserve hydrogen bonding in the molecular rotation, which facilitates the large bending angle. The maximum shear strain of 218.81% and dissipated energy density of 1 MJ m−3 can significantly enhance mechanical damping of vibrations.
Introduction
Twinning deformation is a type of plastic deformation that has been extensively investigated in metal alloys, mostly from the perspective of physics and materials science.1 There are only a few examples of twinning deformation reported for organic crystals. This could be due to the typical fragility and tiny size of organic crystals. The dissipated energy (Ed) derived from twinning deformation of alloys and organic single crystals depends on the following factors: (i) coercive stress (σc) and (ii) bending angle (θ), given as (Ed = σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). In alloys the required magnitude of σc is larger than in the case of molecular crystals, deriving a significant magnitude of Ed. However, the value of θ is usually smaller in alloys than in organic crystals. The Ed value in alloys (usually 103 to 104 kJ m−3) is much higher than in typical organic solids (approximately 102 kJ m−3). Application of a relatively smaller σc in the deformation of organic single crystals can produce a large θ without crystal cleavage. Achievement of a large θ paves the way for new design principles to increase the value of Ed in organic single crystals. Moreover, alloys have polycrystalline properties so on average θ is reduced due to their isotropic nature, whereas, in organic single crystals the composition is almost anisotropic and associated with comparatively higher values of θ which is advantageous for achieving enhancing Ed.
θ). In alloys the required magnitude of σc is larger than in the case of molecular crystals, deriving a significant magnitude of Ed. However, the value of θ is usually smaller in alloys than in organic crystals. The Ed value in alloys (usually 103 to 104 kJ m−3) is much higher than in typical organic solids (approximately 102 kJ m−3). Application of a relatively smaller σc in the deformation of organic single crystals can produce a large θ without crystal cleavage. Achievement of a large θ paves the way for new design principles to increase the value of Ed in organic single crystals. Moreover, alloys have polycrystalline properties so on average θ is reduced due to their isotropic nature, whereas, in organic single crystals the composition is almost anisotropic and associated with comparatively higher values of θ which is advantageous for achieving enhancing Ed.
Some of the reports of twinning deformation in single crystals relate to organometallic compounds such as ferrocene2 and tetramethyle-tetraselenafulvalene (TMTSF)2X3 (X = ClO4, PF6, AsF6, and NO3), while among organic solids the following examples have been reported: 1,3,5-tribromo-2,4,6-triiodobenzene,4 1,3,5-trichloro-2,4,6-triiodobenzene,4 L-lysine monohydrochloride dihydrate,5 and adipic acid doped with 3-methyl adipic acid.6 Studies of twinning deformation in such organic or organometallic solids are underdeveloped in contrast to the studies in metallic solids7 involving a control of their mechanical durability or deformability.
Recently, our research group has reported some stress-induced twinning deformation in organic single crystals,8–11 supported with experimental evidence by microscopic observations, X-ray crystal structure analysis, and force measurements. For example, the organosuperelastic crystals of the planar molecule 3,5-difluorobenzoic acid8 showed exceptional twinning. Crystal of 5-chloro-2-nitroaniline9 exhibited twinning ferroelasticity. The flexible rod shaped adipic acid molecule showed ferroelasticity driven by conformational change.10 Finally, a non-planar 4,4′-dicarboxydiphenyl ether11 exhibited ferroelasticity by partial ring flipping. However, the bending angles in these crystals were 27.8°, 49.21°, 44.65°, and 16.9°, respectively. Moreover, the Ed value of these crystals is not so high as compared to that of alloys. Herein, we investigated twinning deformation in a single crystal of 2-methyl-5-nitro-benzoic acid (C7H8NO4). Our results indicate exceptional mechanical twinning with an unprecedentedly large bending angle and large coercive stress, which requires drastic molecular rearrangement at the twinning interface to preserve the hydrogen bonding and avoid crystal cleavage. These factors contribute towards a large Ed, which is an important property for mechanical damping of vibrations.
Results and discussion
2-Methyl-5-nitrobenzoic acid (C7H8NO4) (1) (Scheme 1) is a beige colored aromatic compound with a high melting point of 184 °C. 1 is an important simple compound serving as a raw material for pharmaceuticals, agrochemicals, and dyes. Well-shaped, pale yellow colored rods with typical lengths of 0.2–1.0 mm and thicknesses of 0.1–0.3 mm were obtained by recrystallization of 1 from acetone at 298 K.Twinning deformation was induced in a single crystal by the application of compression stress perpendicular to (110)α0 and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
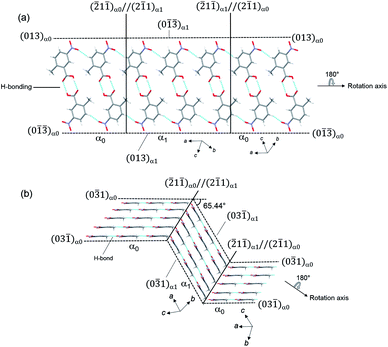
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)α0 (mother domain: α0) crystal faces at 298 K. The crystal deformed in a diffusionless manner (Fig. 1a). The bending angle is estimated to be 65.44° between α0 and α1 (α1: twinned domain), which corresponds to the angle between (0
0)α0 (mother domain: α0) crystal faces at 298 K. The crystal deformed in a diffusionless manner (Fig. 1a). The bending angle is estimated to be 65.44° between α0 and α1 (α1: twinned domain), which corresponds to the angle between (0![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1)α0 and (03
1)α0 and (03![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )α1, which agrees well with the value 64.28° obtained by measurement from the optical microscope (Fig. 1a). It is surprising that such a large bending can be achieved without considerably damaging the crystal.
)α1, which agrees well with the value 64.28° obtained by measurement from the optical microscope (Fig. 1a). It is surprising that such a large bending can be achieved without considerably damaging the crystal.
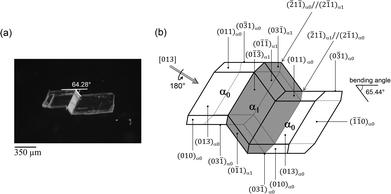 | ||
| Fig. 1 (a) Optical image of the twinned crystal, prepared by compression on crystal surface (110)α0, [013] and (b) crystal face indices of the mechanically twinned crystal. | ||
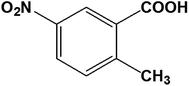
Single-crystal X-ray structure analysis confirmed the twinning deformation under shear force. Both the α0 and α1 crystal structures have an identical crystal structure with the same symmetry i.e. triclinic crystal system and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group12 (Table S1†). According to the indices of crystal faces in the bent shape as shown in Fig. 1b, the twinning interface is (
space group12 (Table S1†). According to the indices of crystal faces in the bent shape as shown in Fig. 1b, the twinning interface is (![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1
1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )α0//(2
)α0//(2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)α1. The α1 domain is related to α0 domain by a 180° rotation about the axis along [013]α0 (Fig. 1b). The deformation requires drastic molecular rearrangement when the interface passes through the molecule. Considering the lattice correspondence require to achieve the bent crystal shape, the continuity of hydrogen bonding across the interface connecting α0 and α1 domains should be ensured by adjustment of the molecular orientations facing at the interface and the strength of hydrogen bonding between molecules at the interface. Molecules at the twining interface are surrounded by four other neighboring molecules, that keeps hydrogen bonding stronger on passing of rotational plane. We presume this facilitates large bending without crystal cleavage. A similar speculation was indicated in the elastic curvature of an organic single crystal.13 Typical O–H⋯O hydrogen bonding between carboxylic acid groups occurs along [013] with the C–O distance of 2.639 Å (intermolecular dotted lines in Fig. 2b). In addition, there are C–H⋯O interactions along [0
1)α1. The α1 domain is related to α0 domain by a 180° rotation about the axis along [013]α0 (Fig. 1b). The deformation requires drastic molecular rearrangement when the interface passes through the molecule. Considering the lattice correspondence require to achieve the bent crystal shape, the continuity of hydrogen bonding across the interface connecting α0 and α1 domains should be ensured by adjustment of the molecular orientations facing at the interface and the strength of hydrogen bonding between molecules at the interface. Molecules at the twining interface are surrounded by four other neighboring molecules, that keeps hydrogen bonding stronger on passing of rotational plane. We presume this facilitates large bending without crystal cleavage. A similar speculation was indicated in the elastic curvature of an organic single crystal.13 Typical O–H⋯O hydrogen bonding between carboxylic acid groups occurs along [013] with the C–O distance of 2.639 Å (intermolecular dotted lines in Fig. 2b). In addition, there are C–H⋯O interactions along [0![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1] between the aromatic hydrogen H and O on the nitro group with C–O distance of 2.673 Å. The combination of O–H⋯O and C–H⋯O hydrogen bonds constitutes 2D arrangement in the plane of (013)α0. The hydrogen bonding between carboxylic acid groups is the dominant force over weak van der Waals interactions between nitro and aromatic hydrogen atoms.
1] between the aromatic hydrogen H and O on the nitro group with C–O distance of 2.673 Å. The combination of O–H⋯O and C–H⋯O hydrogen bonds constitutes 2D arrangement in the plane of (013)α0. The hydrogen bonding between carboxylic acid groups is the dominant force over weak van der Waals interactions between nitro and aromatic hydrogen atoms.
The maximum strain of 1 is expected to be 218.81% from tanθ, where θ is the bending angle. This calculated maximum strain is higher than for previous reports on organic crystals that have comparatively smaller bending angles than 1. For example, the strain values for (TMTSF)2ClO4,14a (TMTSF)2PF6,14c 3,5 difluorobenzoic acid,8 and 5-chloro-2-nitroaniline9 are 33.3%, 36%, 52.7% and 115.9%, respectively. Moreover, the strain value is higher than for certain twinned metals. For examples, the values for gold nanopillars15a and copper nanowires15b are 5% and 7.2%, respectively.
We also conducted compression measurements of a single-crystal specimen. Despite the large bending angle and the brittleness of the crystal we could successfully induce twinning by loading stress along the long axis of the crystal (Fig. 3a). We prevented crystal breakage by avoiding stress perpendicular to the crystal surface. Because we presume if stress is perpendicular to the surface, components of the stress are in opposite direction at the interface, thats causes seperation of the crystal at the twining interface. Whereas, compression causes effective stress components in the direction as shown in Fig. 3a that prevents crystal breakage at the interface on twinning deformation. Therefore, a stress–strain curve was obtained by compressing the crystal via the crystal surface (110)α0 (Fig. 3a), which derives the effective force along the angle 57.28° between twinning interface and effective shear. The effective stress that causes twining deformation was derived by applying the formula (Feff/cross-sectional area of the α0/α1 boundary), i.e. (13.40 × 10−15 m2) (Fig. 3a). One end of a single-crystal was fixed to a glass stage with a glue. A glass jig was then pushed against the (110)α0 crystal surface at a constant speed of 30 μm min−1 (ESI, Movie S1†). As shown in Fig. 3c, stress was detected after the glass jig reached the crystal surface and an increase in the loading force began (3c(i and ii)). The effective stress reached 6.891 MPa at which point the twinning interface was generated (3c(ii)). The coercive stress achieved is the largest amongst all reports.8–11 The α1 domain started to grow from both sides of the crystal. The growth of the α1 domain was not smooth, producing spikes (3c(ii and iii)) in the curve. This could be ascribed to the generation of the multiple domains. On holding the displacement of the jig, the α1 remained present and strain was recorded by removing the stress (iii and iv). The estimated dissipated strain energy was calculated as 1000 kJ m−3 (0.6796 kJ kg−1, and 123.109 J mol−1). Based on the equation (Ed = σc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), the Ed value of 1 is 65.24 times larger than the corresponding value for 3,5-difluorobenzoic acid i.e. 15.47 kJ m−3 (0.010 kJ kg−1, 1.642 J mol−1),8 and 4.67 times larger than in the case of 5-chloro-2-nitroaniline i e. 216 kJ m−3 (0.136 kJ kg−1, 23.46 J mol−1).9 This large value of Ed is comparable to that of alloys and much higher than typical for organic solids. Since Ed is a derivative of the applied shear stress (σ) and deformation angle (θ) of the crystal, such dissipated energy density is expected to be increased by enlarging the bending angle of the crystal, which in this case is 64.28° (Fig. 1a), and/or the required shear stress for the deformation. The high dissipated energy will be effective for the damping of mechanical vibrations.
θ), the Ed value of 1 is 65.24 times larger than the corresponding value for 3,5-difluorobenzoic acid i.e. 15.47 kJ m−3 (0.010 kJ kg−1, 1.642 J mol−1),8 and 4.67 times larger than in the case of 5-chloro-2-nitroaniline i e. 216 kJ m−3 (0.136 kJ kg−1, 23.46 J mol−1).9 This large value of Ed is comparable to that of alloys and much higher than typical for organic solids. Since Ed is a derivative of the applied shear stress (σ) and deformation angle (θ) of the crystal, such dissipated energy density is expected to be increased by enlarging the bending angle of the crystal, which in this case is 64.28° (Fig. 1a), and/or the required shear stress for the deformation. The high dissipated energy will be effective for the damping of mechanical vibrations.
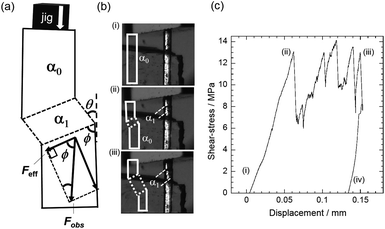 | ||
| Fig. 3 Measurement of stress–strain curve, (a) cartoon illustration of crystal deformation pattern and force components, (b) snapshots of the twinning deformation of shear-stress (i–iii) (Movie S1†) with inset sketches of the deformation pattern, and (c) stress–strain curve at 298 K. | ||
Conclusions
We confirmed a new strategy to increase Ed in organic single crystal, which typically bears smaller stress than those of metallic solids. Large bending angle in twinning ferroelastic deformation enables a wider crystal deformation range for the realization of large energy od dissipation. The relationship between effective bending angle and Ed can be clearly measured in single crystals without breakage by microscopic and macroscopic experiments. The maximum strain and the Ed value in 1 is, to the best of our knowledge, the largest reported molecular crystals, facilitated by large deformation but with a smaller shear force. Such controllability paves the way for new design principles to increase the value of Ed in organic single crystals. The combination of small σc and large Ed makes organic ferroelastic materials promising for applications in mechanical damping, with high susceptibility to absorb weak shocks effectively by their small volume.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by SUZUKI, KISTEC, 2016–2018 Strategic Research Promotion (SK2810) fund of Yokohama City University for S. T., and the JSPS KAKENHI grants 17H06368 (grant-in-aid for Scientific Research on Innovative Areas), 17K19143 (grant-in-aid for Challenging Research (Pioneering)) for S. T. and 16H0710 (grant-in-aid for Research Activity start-up) for Y. T.Notes and references
- D. Zhang, L. Jiang, B. Zheng, J. M. Schoenung, S. Mahajan, E. J. Lavernia and I. J. Beyerlein, Deformation Twinning (Update), Reference Module in Materials Science and Materials Engineering, 2016, DOI:10.1016/B978-0-12-803581-8.02878-2.
- Y. Miyamoto and S. Takamizawa, Dalton Trans., 2015, 44, 5688–5691 RSC.
- H. Schwenk, K. Neumair, K. Andres, F. Wudl and E. Aharon-Shalom, Mol. Cryst. Liq. Cryst., 1982, 79, 277 CrossRef.
- C. M. Reddy, M. T. Kirchner, R. C. Gundakaram, K. A. Padmanabhan and G. R. Desiraju, Chem.–Eur. J., 2006, 12, 2222 CrossRef PubMed.
- R. Bandyopadhyay and D. J. W. Grant, Pharm. Res., 2002, 19, 491 CrossRef.
- L. Williams-Seton, R. J. Davey, H. F. Lieberman and R. G. Pritchard, J. Pharm. Sci., 2000, 89, 346 CrossRef PubMed.
- I. Yoshida, D. Monma, K. Lino, K. Otsuka, M. Asai and H. Tsuzuki, J. Alloys Compd., 2003, 355, 79–84 CrossRef.
- S. Takamizawa and Y. Takasaki, Angew. Chem., Int. Ed., 2015, 54, 4815–4817 CrossRef PubMed.
- S. H. Mir, Y. Takasaki, E. R. Engel and S. Takamizawa, Angew. Chem., Int. Ed., 2017, 56, 15882–15885 CrossRef PubMed.
- S. H. Mir, Y. Takasaki and S. Takamizawa, Phys. Chem. Chem. Phys., 2018, 20, 4631 RSC.
- E. R. Engel, Y. Takasaki, S. H. Mir and S. Takamizawa, R. Soc. Open Sci., 2018, 5, 171146 CrossRef PubMed.
- Crystal data of 1 for the α0 phase (mother phase) at 298 K (CCDC-1831132): triclinic, P
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 7.611 (15) Å, b = 10.47 (2) Å, c = 10.55 (2) Å, α = 89.45 (3)°, β = 81.45 (3)°, γ = 76.75 (3)°, V = 810 (3) Å3, Z = 4, Dcalc. = 1.485 Mg m−3, R1 = 0.0601, wR2 = 0.1786 for 1243 reflections with I > 2σ(I) (for 1674 reflections (2759 total measured)), goodness-of-fit on F2 = 1.071, largest diff. peak (hole) = 0.233 (−0.243) e Å3. The α1 phase (twinned phase) at 298 K (CCDC-1831133): triclinic, P
, a = 7.611 (15) Å, b = 10.47 (2) Å, c = 10.55 (2) Å, α = 89.45 (3)°, β = 81.45 (3)°, γ = 76.75 (3)°, V = 810 (3) Å3, Z = 4, Dcalc. = 1.485 Mg m−3, R1 = 0.0601, wR2 = 0.1786 for 1243 reflections with I > 2σ(I) (for 1674 reflections (2759 total measured)), goodness-of-fit on F2 = 1.071, largest diff. peak (hole) = 0.233 (−0.243) e Å3. The α1 phase (twinned phase) at 298 K (CCDC-1831133): triclinic, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , a = 7.636 (13) Å, b = 10.426 (19) Å, c = 10.520 (18) Å, α = 89.28 (3)°, β = 81.80 (3)°, γ = 76.32 (3)°, V = 805 (2) Å3, Z = 4, Dcalc. = 1.494 Mg m−3, R1 = 0.1016, wR2 = 0.3546 for 1500 reflections with I > 2σ(I) (for 1554 reflections (2769 total measured)), goodness-of-fit on F2 = 1.161, largest diff. peak (hole) = 0.466 (−0.431) e Å−3. CCDC-1831132, 1831133 contain the supplementary crystallographic data for this paper.
, a = 7.636 (13) Å, b = 10.426 (19) Å, c = 10.520 (18) Å, α = 89.28 (3)°, β = 81.80 (3)°, γ = 76.32 (3)°, V = 805 (2) Å3, Z = 4, Dcalc. = 1.494 Mg m−3, R1 = 0.1016, wR2 = 0.3546 for 1500 reflections with I > 2σ(I) (for 1554 reflections (2769 total measured)), goodness-of-fit on F2 = 1.161, largest diff. peak (hole) = 0.466 (−0.431) e Å−3. CCDC-1831132, 1831133 contain the supplementary crystallographic data for this paper. - A. K. Saini, K. Natarajan and S. M. Mobin, Chem. Commun., 2017, 53, 9870 RSC.
- (a) H. Schwenk, K. Andres, F. Wudl and E. Aharon-Shalom, J. Phys., 1983, 44, 1041–1045 CrossRef; (b) K. Kawabata, Y. Hosokawa, T. Kawauchi and T. Sambongi, Ferroelectrics, 2001, 251, 199–205 CrossRef; (c) K. Kawabata, T. Saga, K. Matsuda, K. Nenoto and T. Sambongi, Europhys. Lett., 2003, 64, 118–123 CrossRef.
- (a) K. A. Afanasyev and F. Sansoz, Nano Lett., 2007, 7, 2056 CrossRef; (b) Y. Yue, P. Liu, Z. Zhang, X. Han and E. Ma, Nano Lett., 2011, 11, 3151 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1831132 and 1831133. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8ra02499e |
| This journal is © The Royal Society of Chemistry 2018 |