Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate potential energy surfaces for the first two lowest electronic states of the Li (2p) + H2 reaction†
Liwei Fu ,
Dequan Wang
,
Dequan Wang * and
Xuri Huang*
* and
Xuri Huang*
Laboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun, People’s Republic of China. E-mail: dequan_wang@jlu.edu.cn
First published on 25th April 2018
Abstract
The accuracy of three-dimensional adiabatic and diabatic potential energy surfaces is calculated using ab initio methods and is numerically fitted for the two lowest electronic states 1 and 22A′ of the LiH2 system, which are very important for the Li (2p) + H2 reaction. The finite difference method is performed to generate the mixing angles, which are used to educe the diabatic potential from the adiabatic potential. The accurate conical intersection (CI) is studied in this work with three different basis sets. The energy of the conical intersection is slightly lower (nearly 0.12 eV) than that of the perpendicular intermediate on the first excited state. By analyzing the potential energy surfaces in this work we can suggest that the most possible reaction pathway for the title reaction is Li (2p) + H2 → LiH2 (22A′) (C2v) → CI → LiH2 (12A′) (C2v) → LiH⋯H → LiH (X1∑g+) + H. The conical intersection and (22A′) intermediate may play a vital role in the title reaction.
1 Introduction
In recent years, lithium chemistry has been thought to play an important role in early cosmic evolution.1–10 In the standard Big Bang model, the first star object was formed by gas composed of H, He and Li and some of its isotopes, which means that the chemistry of the early universe is very simple.11,12 The formation and depletion of LiH molecules play an important role in stellar evolution and galactic lithium production.2,3 The Li + H2 reaction is considered as an important pathway of LiH formation.7,8A large number of theoretical studies were essential for identifying and understanding the LiH2 system. The investigation of the electronic potential energy surface (PES) was the first essential ingredient. Several 3D-PESs for the ground-state (12A′) of the LiH2 system have been well constructed in the past decade13–18 and been used for dynamics studies.19–33
The reaction, Li (2p) + H2 → H + LiH (X), is endoergic by 1624 cm−1.20 The reaction of Li (2s) + H2 → H + LiH (X) on the ground state requires an amount of energy for initiation. Many studies20,34–36 proved that Li + H2 reactions are considered to follow surface hopping mechanisms by Li insertion into the H–H bond to yield the LiH product. In these conditions the nonadiabatic couplings should be taken into account. The nonadiabatic potential energy surfaces are very interesting for dynamic studies. Up to now, there are two PESs available in the literature that can be used to study non-adiabatic processes for the Li (2p) + H2 → H + LiH reaction. The first is the Hsiao and co-workers surface17 obtained in 2011. The second one is the He and co-workers surface,37 which was investigated in 2016. Hsiao and his co-workers calculated the non-adiabatic PES for the LiH2 system at the HF/CAS/MRCI level. In Hsiao’s work, the ground state 12A′ and the lowest excited state 22A′ were calculated using 10a′ and 2a′′ active spaces with the multi-reference configuration interaction (MRCI) method. The potential energies for the excited and ground states have been fitted to the analytical expression in terms of the many-body expansion function. The LiH2 configurations were sampled in the ranges r = 0.5–7.0 Å, R = 0.8–7.0 Å, and θ = 1–89° with the Jacobi coordinates (R, r, θ). The work found that the crossing seam lies at the HLiH bending angle ϕ = 35–45° and the Li–H distance R3 = 2.0–2.3 Å while the other LiH distance is fixed at 1.6 Å. Quasi-classical trajectory calculations on the fitted energy function were performed and good results were obtained. He and co-workers37 performed a global diabatic PES, which was correlated with the ground state 12A′ and the first excited state 22A′ of the Li (2p) + H2 reaction. These potential energies were calculated with two regions, the Li–H2 reactant region and the H–LiH product region. The energies were scanned in the ranges RLi–HH = 0.0–30.0a0, rHH = 0.6–30.0a0, θ = 0.0–90.0°, and RH–LiH = 0.0–30.0a0, rLiH = 1.3–30.0a0, θ = 0.0–90.0° for the reactant region and the product region, respectively. Then the authors converted the adiabatic energies to diabatic potential energies and fitted the diabatic potential energies by the NN method. In this way, an accurate global diabatic PES was performed. In the present work, the authors calculate the LiH2 adiabatic potential energies in a larger range and with more data points than before and use a more accurate fitting method to improve the PES level. The conical intersection point is accurately studied too.
The main differences between the present work and former work are as follows: firstly, the atom distances of r(H–H) and R(Li–HH) are scanned to 32 Å, which is larger than those done before and ensures that all of the dynamic studies are in the accurate scan area; secondly, a more accurate fit method, the three dimensional B-spline method, is used to make sure that accurate PESs are obtained; thirdly, many more geometries (83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930) are generated for every adiabatic potential energy.
930) are generated for every adiabatic potential energy.
The outline of the present work is as follows. The second chapter introduces the calculation method for the adiabatic energies. The adiabatic and diabatic PESs of LiH2 are presented in the third chapter. The fourth chapter shows a simple summary for the present work.
2 Computational methods
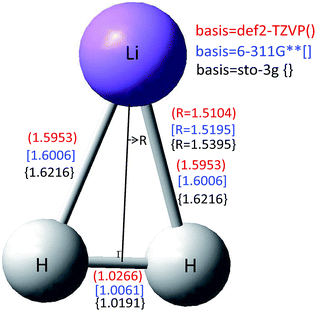
In this work, the ab initio calculations have been carried out at the HF/MSSCF/MRCI level with the MOLPRO 2012 package38 using the large basis sets (aug-cc-pV5Z) and a full-valence active space involving five valence electrons in ten orbitals was employed in the MSSCF procedure. Furthermore, one 1s orbital of the lithium atom was kept doubly occupied. In the subsequent MRCI calculations, one 1s orbital of the lithium atom was frozen. In this system, we use the Jacobi coordinates (r, R, θ) to characterize this three-body system, in which r indicates the bond length of the two hydrogen atoms, R shows the distance of the lithium atom from the center of mass of the two hydrogen atoms, and θ represents the angle between the r an R vectors. We sampled the LiH2 configurations in the ranges r = 0.4–32 Å, R = 0.0–32 Å, and θ = 0.0–90.0°. For θ = 0.0–30°, the angle grid is 5°. 164 r points and 55 R points were used with different step sizes and 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 geometries were chosen to generate the ab initio energy points in this region. For θ = 40.0–90.0°, the angle grid was enlarged to 10° and 63 r points and 55 R points were used, so 20
140 geometries were chosen to generate the ab initio energy points in this region. For θ = 40.0–90.0°, the angle grid was enlarged to 10° and 63 r points and 55 R points were used, so 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 geometries were achieved here. A total of 83
790 geometries were achieved here. A total of 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 geometries were generated for every adiabatic potential energy. These large number points warrant the quality of the following fitting PESs. Inside the whole scan field the procedure interpolates the surfaces using the three dimensional B-spline method.
930 geometries were generated for every adiabatic potential energy. These large number points warrant the quality of the following fitting PESs. Inside the whole scan field the procedure interpolates the surfaces using the three dimensional B-spline method.
Considering the two coupling states of LiH2, the diabatic energies Hdii can be obtained in terms of our fitted adiabatic energies Eai by
Hd11 = cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αEa1 + sin2 αEa1 + sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αEa2; αEa2;
| (1) |
Hd22 = sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αEa1 + cos2 αEa1 + cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αEa2; αEa2;
| (2) |
Hd12 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α(Ea2 − Ea1); α(Ea2 − Ea1);
| (3) |
| Hd12 = Hd21. | (4) |
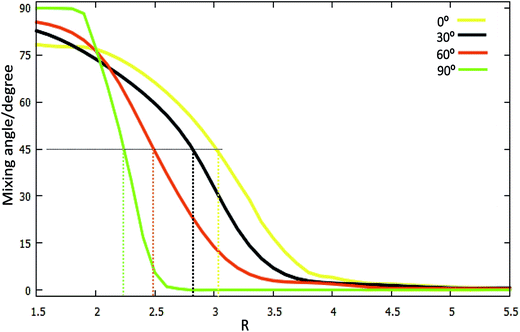
Hd11 and Hd22 are the corresponding diabatic energies for the diabatic PES; Hd12 and Hd21 are the coupling potential energies between the two diabatic states. The mixing angle α was obtained by the finite difference method39–43 using the Molpro program.
3 Results
In this work, we calculated the three dimensional adiabatic and diabatic PESs for the LiH2 system. For easy to understand and discuss these PESs, we regard the ground state energy of the Li (2s) atom to be 0 eV, far away from that of the equilibrium structure of H2.3.1 Diatomic atom potential energy
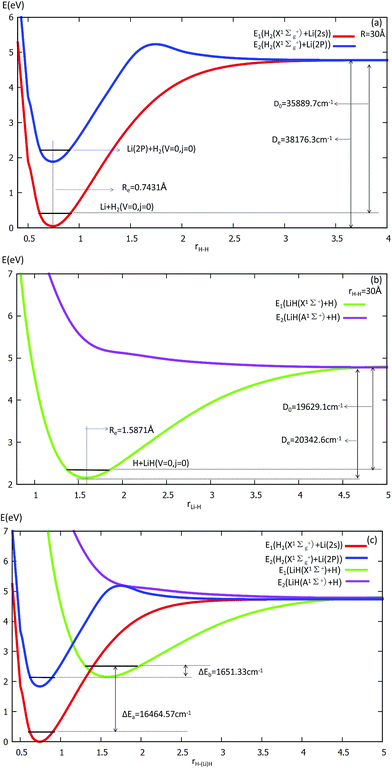
The equilibrium structures and electronic energies for the diatomic molecules (H2 and LiH) are derived from our fitting PES. To obtain the H2 PES, we fixed R = 30 Å and θ = 90.0°. For deriving the LiH PES, we fixed r = 30 Å and θ = 0.0°. The detailed results are shown in Fig. 1 and listed in Table 1. Our fitting PESs display that the difference of the Li (2s) and Li (2p) energies is 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803.2 cm−1. From panel (a) in Fig. 1, one can see that the equilibrium distance (Re) of H2 is 0.7431 Å and the dissociation energy (De) is 35
803.2 cm−1. From panel (a) in Fig. 1, one can see that the equilibrium distance (Re) of H2 is 0.7431 Å and the dissociation energy (De) is 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889.7 cm−1, which are in good agreement with the experimental results of 0.74144 Å (ref. 45) and 36
889.7 cm−1, which are in good agreement with the experimental results of 0.74144 Å (ref. 45) and 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118.06 cm−1,46 respectively.
118.06 cm−1,46 respectively.
 | ||
| Fig. 1 Potential energy surfaces (in eV) are plotted as a function of the distances r(H–H) and r(Li–H) (in Å) at the angle θ = 0° in Jacobi coordinates. | ||
| Species | Parameter | This work | Lee’s worka | Experimental |
|---|---|---|---|---|
| a Ref. 20.b Ref. 44.c Ref. 45.d Ref. 46.e Ref. 47. | ||||
| Li | ΔE (2p ← 2s) [cm−1] | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803.2 803.2 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 914 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904b 904b |
| H2 (X1Σg+) | Re [Å] | 0.7431 | 0.743 | 0.7414c |
| De [cm−1] | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 176.3 176.3 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868 868 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288c 288c |
|
| D0 [cm−1] | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889.7 889.7 |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 687 687 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 118.06d 118.06d |
|
| LiH (X1Σ+) | Re [Å] | 1.5871 | 1.60 | 1.5956e |
| De [cm−1] | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342.6 342.6 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287.7e 287.7e |
|
| D0 [cm−1] | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629.1 629.1 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 011 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.8e 589.8e |
|
Panel (b) in Fig. 1 exhibits that Re = 1.5871 Å and De = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629.1 cm−1 for LiH. These are in good accordance with Stwalley’s experimental results of 1.59558 Å and 19
629.1 cm−1 for LiH. These are in good accordance with Stwalley’s experimental results of 1.59558 Å and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.8 cm−1,47 respectively.
589.8 cm−1,47 respectively.
Energy curves for the two lowest states of the H2 and LiH are shown at panel (c) in Fig. 1.
From panel (a) one can see that the curve of the first excited state includes two parts of the PES, i.e. H2 (singlet) + Li (2p) and H2 (triplet) + Li (2s). When r(H–H) becomes larger, the energies of H2 (triplet) + Li (2s) and that of H2 (singlet) + Li (2s) are degenerate, so the two curves approach the same point. This characteristic is also suited to the LiH PES curve. As shown in panel (c), when the three atoms are far away from each other, the energies of every curve approach the same point.
3.2 Three-dimensional adiabatic potential energy surfaces
The three-dimensional adiabatic potential energy surfaces (3D-PESs) of LiH2 are plotted in Fig. 2, 3 and Fig. S1A–6A† for θ = 0.0°, 15.0°, 30.0°, 60.0°, and 90.0°, respectively.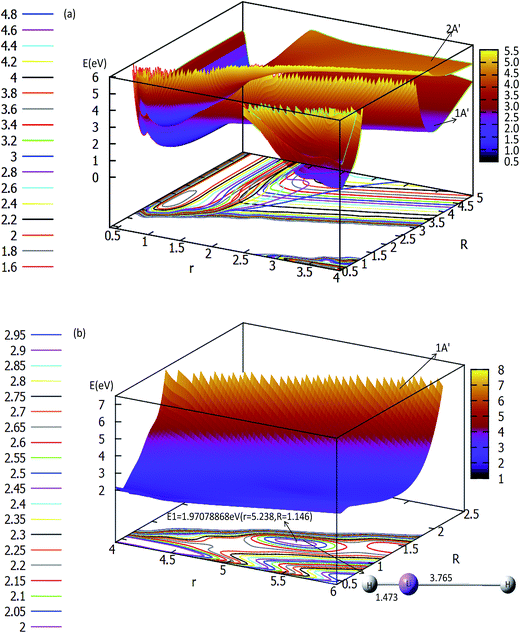 | ||
| Fig. 2 Two potential energy surfaces (in eV) and contour plots of the potential energy surface as a function of distances r and R (in Å) at the angle θ = 0° in Jacobi coordinates. | ||
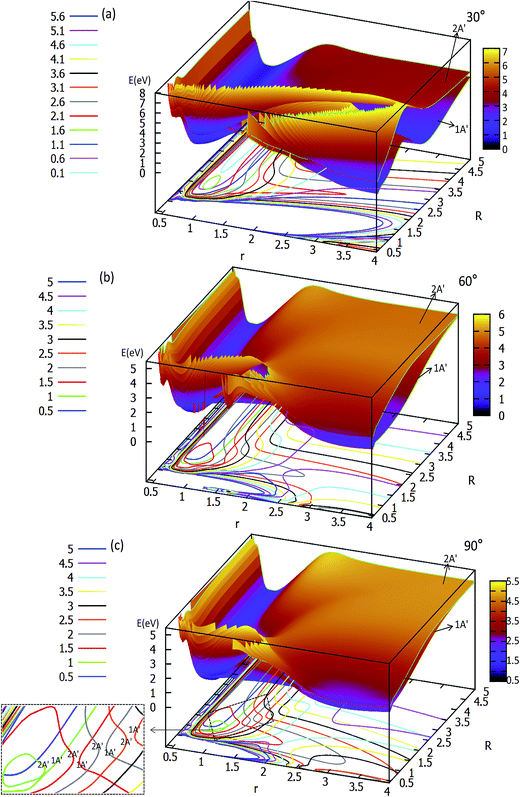 | ||
| Fig. 3 Two potential energy surfaces (in eV) and contour plots of the potential energy surface as a function of distances r and R (in Å) for the different angles θ = 30°, 60° and 90°. | ||
The panel (a) in Fig. 2 is a multi plot of the ground state LiH2 (12A′) and the first excited state LiH2 (22A′) PESs with θ = 0°. The separated figures are plotted in panels (a) and (b) in Fig. S1A.† From panel (a) in Fig. 2 and panel (a) in Fig. S1A†, one can find that for the ground state reaction, the entrance, which is the reaction starting from the reactants, of Li (2s) + H2 has no reaction barrier, and the PES has no minimum geometries. But for the lowest excited state of LiH2 (22A′) there is a minimum when θ = 0.0° (see panel (a) in Fig. 2 and panel (b) in Fig. S1A†). The corresponding geometry of this minimum is r(H–H) = 0.741 Å and r(LiH) = 1.838 Å, and the energy of this structure is 0.1686 eV lower than that of the entrance for this linear structure. Panel (b) in Fig. 2 is enlarged, plotting the product part (LiH (X1Σg+) + H). This panel reveals that first a Li–H⋯H complex is formed in the ground state reaction pathway, then after a reaction barrier the system reaches the LiH (X1Σg+) + H product. The geometry of this collinear complex is r(Li–H) = 1.473 Å and r(H–H) = 3.765 Å, and the corresponding energy is 1.9708 eV higher than that of the entrance.
The ground state and the first excited state of the LiH2 PESs for θ = 15° are plotted in Fig. S2A† and Fig. S3A.† The features of these PESs are similar to that of θ = 0°. Firstly, there is a minimum structure on the first excited PES (see panel (a) in Fig. S2A† and panel (d) in Fig. S3A†), and its energy is 1.618 eV higher than that of the ground state entrance, and it is 0.2191 eV lower than that of the entrance of the excited state. Secondly, there is a product complex in the ground state PES, and the energy of this complex is 2.0830 eV higher than that of ground state entrance. The product complex for this θ = 15° is 0.1122 eV higher than that of θ = 0°. This result indicates that the production is in the small θ range. For obtaining the accurate PESs of the product part, a small grid both for the angle and for the distance is used to scan the energies for this area.
The two lowest adiabatic PESs of LiH2 for θ = 30° and θ = 60° are plotted in panels (a) and (b) in Fig. 3, respectively. The characteristics of the PESs for these two angles are different from that of 0° and 15°, i.e. there is no product complex in these PESs. The consistent feature of these four angles PESs is that there is a minimum in the first excited state. The minimum energies are 0.311 eV and 0.747 eV lower than those of the entrance for 30° and 60°, respectively. The detailed minimum geometry is shown in panel (b) in Fig. S4A† and Fig. S5A.†
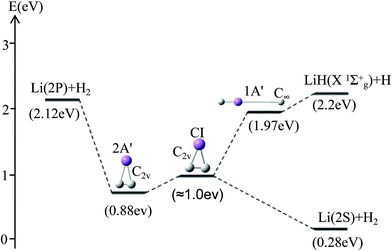
For θ = 90° the PESs of the lowest two states of LiH2 are multi plotted in panel (c) in Fig. 3 and the separated plot is shown in panels (a) and (b) in Fig. S6A.† As with the other angle PESs, there is no minimum on the ground state and there is one minimum on the first excited state. The energy of this minimum is 0.975 eV lower than that of the entrance energy. The energy of this minimum is the lowest in the excited state, so it is the global minimum for the first excited state. From the contour plot of the lowest two PESs of LiH2 (see panel (c) in the Fig. 3), the 1 eV energies are shown with the green ring and the adjacent green curve contour line for (22A′) and (12A′) LiH2, respectively. These two lines are nearly coinciding when the geometries are in the ranges r ≈ 1.0 Å and 1.5 < R < 2.0 Å. The 2 and 12A′ states lie very close to each other in these geometries. So the conical intersection for the title system is in this area. In other words, the surface transition from the 22A′ to 1A′ state frequently occurs in this area. According to the above discussions, we can come to the conclusion that the most possible reaction pathway (see Fig. 4) for Li (2p) + H2 → LiH (X) + H is as follows: firstly, the lithium atom attacks H2 to form the perpendicular (C2v) LiH2 (22A′) intermediate; secondly, the system passes the conical intersection and the electron transits from the 22A′ to 12A′ surface; and lastly, LiH2 (12A′) separates into two parts product LiH (X) + H. Comparing Fig. 1 and 3 one can see that the energy of the conical intersection (nearly 1 eV) is lower than that of Li (2P) + H2 (nearly 2 eV) (hence no reaction barrier), so the required kinetic energy for the Li (2p) + H2 → LiH (X) + H reaction is just the endothermic energy of the reaction. That means that the reaction starts from the reactants Li (2P) + H2 and proceeds through the most possible reaction pathway to reach the products LiH (X) + H. There is no higher energy transition state, the only collision energy needed is the difference in energy between the products and reactants, i.e. the endothermicity (1624 cm−1) of the reaction.
3.3 Three dimensional diabatic potential energy surfaces
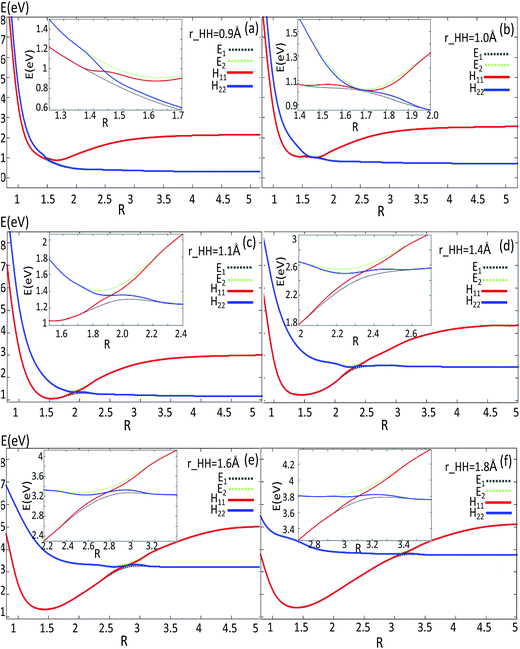 | ||
| Fig. 7 Adiabatic and diabatic potentials (in eV) as a function of distance R (in Å) for the fixed angles θ = 90° at r = 0.9 Å, r = 1.1 Å, r = 1.4 Å, r = 1.6 Å, r = 1.8 Å in Jacobi coordinates. | ||
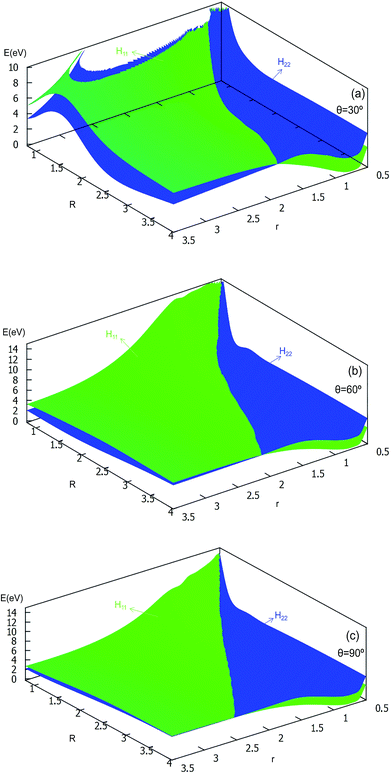 | ||
| Fig. 8 Diabatic potential energy surfaces (in eV) as a function of distances r and R (in Å) at the different angles θ = 30°, θ = 60°, θ = 90° in Jacobi coordinates. | ||
The 2D diabatic potentials for θ = 30°, 60°, and 90° are plotted in Fig. 8. In this figure, the green surfaces describe the H11 potential, and the blue surfaces show the H22 potential. According to these three panels one can conclude that when the two hydrogen atoms are at a short distance the ground state of the title system is H11 potential. If the distance of the two hydrogen atoms is increased (the title system after the cross point), the H22 potential energy are the ground state energy. Furthermore, these three panels exhibit that the cross points are nearly on the same line for each angle.
4 Conclusions
We present ab initio calculated adiabatic potential energy surfaces of the ground state (12A′) and the first excited state (22A′) for the LiH2 system by the MOLPRO quantum chemistry package in Jacobi coordinates. In total 83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 930 geometries were used to generate every state’s adiabatic potential, so an accurate and larger region of configuration space for the potential energy surfaces for the ground and the first excited states is produced. For obtaining the accurate diabatic potentials, mixing angles were derived with a finite difference method. The conical intersection geometries for the two lowest states were also studied in this work with three different basis sets.
930 geometries were used to generate every state’s adiabatic potential, so an accurate and larger region of configuration space for the potential energy surfaces for the ground and the first excited states is produced. For obtaining the accurate diabatic potentials, mixing angles were derived with a finite difference method. The conical intersection geometries for the two lowest states were also studied in this work with three different basis sets.
Our work has predicted some essential features of these two lowest states. There is a global minimum, i.e. a perpendicular (C2v) intermediate, on the first excited state LiH2 (22A′) potential. The conical intersection appeared near the intermediate, and the energy of this conical intersection is slightly higher (≈0.12 eV) than that of the intermediate. Comparing Fig. 1 and 3 one can see that the energy of the conical intersection (nearly 1 eV) is lower than that of Li (2P) + H2 (nearly 2 eV) (hence no reaction barrier), so the required kinetic energy for the Li (2p) + H2 → LiH (X) + H reaction is just the endothermic energy of the reaction. That means, the reaction starts from the reactants Li (2P) + H2, proceeds through the most possible reaction pathway to reach the products LiH (X) + H, and there is no higher energy transition state. The only collision energy needed is the difference in energy between the products and reactants, i.e. the endothermicity (1624 cm−1) of the reaction. There is a complex LiH⋯ H with angle θ = 0° on the 12A′ potential. So the most possible reaction pathway for Li (2P) + H2 → LiH + H is as follows: firstly, the Li (2P) atom attacks H2 and forms a perpendicular (C2v) LiH2 (22A′) intermediate; secondly, the intermediate passes the conical intersection reaching the LiH2 (12A′) potential; thirdly, a partial electron of the lithium atom transfers to one hydrogen atom, then the Li–H bond is formed and the H–H bond is broken to form a LiH⋯H complex; lastly, the complex separates into the LiH (X1Σg+) + H product.
It is worth performing the full dynamical study with these global diabatic potential energy surfaces. We will continue this work in the following study. We will make sure that in the following work we can obtain more interesting results.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21373099, 21573090, 21673092), the Jilin Province Science and Technology Development Plan (20150101005JC) and the Ministry of Education of China (20130061110020).References
- D. Galli and F. Palla, Astron. Astrophys., 1998, 335, 403–420 CAS.
- M. Signore, G. Vedrenne, P. D. Bernardis, V. Dubrovich, P. Encrenaz, R. Maoli, S. Masi, G. Mastrantonio, B. Melchiorri, F. Melchiorri and P. E. Tanzili, Astrophys. J., Suppl. Ser., 1994, 92, 535–537 CrossRef CAS.
- R. Maoli, F. Melchiorri and D. Tosti, Astrophys. J., 1994, 425, 372–381 CrossRef CAS.
- S. Lepp and J. M. Shull, Astrophys. J., 1984, 280, 465–469 CrossRef CAS.
- P. C. Stancil, A. Loeb, M. Zaldarriaga, A. Dalgarno and S. Lepp, Astrophys. J., 2002, 580, 29–35 CrossRef CAS.
- V. K. Dubrovich and A. A. Lipovka, Astron. Astrophys., 1995, 296, 301–306 CAS.
- P. C. Stancil and A. Dalgarno, Astrophys. J., 1997, 479, 543–546 CrossRef CAS.
- S. Bovino, M. Wernli and F. A. Gianturco, Astrophys. J., 2009, 699, 383–387 CrossRef CAS.
- E. Bodo, F. A. Gianturco and R. Martinazzo, Phys. Rep., 2003, 384, 85–119 CrossRef CAS.
- N. J. Clarke, M. Sironi, M. Raimondi, S. Kumar, F. A. Gianturco, E. Buonomo and D. L. Cooper, Chem. Phys., 1998, 233, 9–27 CrossRef CAS.
- S. Lepp, P. C. Stancil and A. Dalgarno, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, R57–R80 CrossRef CAS.
- F. A. Gianturco and P. G. Giorgi, Phys. Rev. A, 1996, 54, 4073–4077 CrossRef CAS.
- L. J. Dunne, J. N. Murrell and P. Jemmer, Chem. Phys. Lett., 2001, 336, 1–6 CrossRef CAS.
- K. H. Kim, Y. S. Lee, T. Ishida and G. H. Jeung, J. Chem. Phys., 2003, 119, 4689–4693 CrossRef CAS.
- M. Wernli, D. Caruso, E. Bodo and F. A. Gianturco, J. Phys. Chem. A, 2009, 113, 1121–1128 CrossRef CAS PubMed.
- F. V. Prudente, J. M. C. Marques and A. M. Maniero, Chem. Phys. Lett., 2009, 474, 18–22 CrossRef CAS.
- M. Hsiao, K. Lin and Y. Hung, J. Chem. Phys., 2011, 134, 034119 CrossRef PubMed.
- J. C. Yuan, D. He and M. D. Chen, Phys. Chem. Chem. Phys., 2015, 17, 11732–11739 RSC.
- N. J. Clarke, M. Sironi, M. Raimondi, S. Kumar, F. A. Gianturco, E. Buonomo and D. L. Cooper, Chem. Phys., 1998, 233, 9–27 CrossRef CAS.
- H. S. Lee, Y. S. Lee and G. H. Jeung, J. Phys. Chem. A, 1999, 103, 11080–11088 CrossRef CAS.
- H. Berriche, J. Mol. Struct.: THEOCHEM, 2004, 682, 89–96 CrossRef CAS.
- H. Berriche and C. Tlili, J. Mol. Struct.: THEOCHEM, 2004, 678, 11–16 CrossRef CAS.
- E. Bodo, F. A. Gianturco, R. Martinazzo and M. Raimondi, Eur. Phys. J. D, 2001, 15, 321–329 CrossRef CAS.
- R. Padmanaban and S. Mahapatra, J. Theor. Comput. Chem., 2006, 5, 871–885 CrossRef CAS.
- R. Padmanaban and S. Mahapatra, J. Phys. Chem. A, 2006, 110, 6039–6046 CrossRef CAS PubMed.
- R. Padmanaban and S. Mahapatra, J. Chem. Phys., 2002, 117, 6469–6477 CrossRef CAS.
- P. Defazio, C. Petrongolo, P. Gamallo and M. Gonzalez, J. Chem. Phys., 2005, 122, 214303 CrossRef PubMed.
- K. C. Lin and R. Vetter, Int. Rev. Phys. Chem., 2002, 21, 357–383 CrossRef CAS.
- T. Roy, T. R. Rao and S. Mahapatra, Chem. Phys. Lett., 2011, 501, 252–256 CrossRef CAS.
- S. Gomez-Carrasco, L. Gonzalez-Sanchez, N. Bulut, O. Roncero, L. Banares and J. F. Castillo, Astrophys. J., 2014, 784, 55 CrossRef.
- T. Roy and S. Mahapatra, J. Chem. Phys., 2012, 136, 174313 CrossRef PubMed.
- R. Padmanaban and S. Mahapatra, J. Chem. Phys., 2004, 121, 7681–7691 CrossRef CAS PubMed.
- G. Sha, J. Yuan, C. Meng and M. Chen, Chem. Res. Chin. Univ., 2013, 29, 956–961 CrossRef CAS.
- J. J. Chen, Y. M. Hung, D. K. Liu, H. S. Fung and K. C. Lin, J. Chem. Phys., 2001, 114, 9395–9401 CrossRef CAS.
- S. Bililign, B. C. Hattaway, T. L. Robinson and G. H. Jeung, J. Chem. Phys., 2001, 114, 7052–7058 CrossRef CAS.
- T. J. Martines, Chem. Phys. Lett., 1997, 272, 139–147 CrossRef.
- D. He, J. Yuan, H. Li and M. Chen, Sci. Rep., 2016, 6, 25083 CrossRef CAS PubMed.
- MOLPRO, http://www.molpro.net.
- M. Peric, R. J. Buenker and S. D. Peyerimho, Mol. Phys., 1990, 71, 673–691 CrossRef CAS.
- G. Hirsch, R. J. Buenker and C. Petrongolo, Mol. Phys., 1990, 70, 835–848 CrossRef CAS.
- M. H. Alexander, J. Chem. Phys., 1993, 99, 6014–6026 CrossRef CAS.
- H. J. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5802–5807 CrossRef.
- C. Petrongolo, G. Hirsch and R. J. Buenker, Mol. Phys., 1990, 70, 825–834 CrossRef CAS.
- C. E. Moore, Atomic Energy levels, National Bureau Standards (U.S.), Cir. No. 467; G. P. O: Washington DC, 1971, p. 4 Search PubMed.
- K. P. Huker and G. Herzberg, Molecular Spectra and Molecular Structure, Van Nostrand Reinhold, New York, 1979, p. 4 Search PubMed.
- E. E. Eyler and N. Melikechi, Phys. Rev. A: At., Mol., Opt. Phys., 1993, 48, R18 CrossRef CAS.
- W. C. Swalley and W. T. Zemke, J. Phys. Chem. Ref. Data, 1993, 22, 87–112 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02504e |
| This journal is © The Royal Society of Chemistry 2018 |