 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of H2 and N2 treatment for B2H6 dosing process on TiN surfaces during atomic layer deposition: an ab initio study†
Hwanyeol Parka,
Sungwoo Lee a,
Ho Jun Kimb,
Daekwang Wooc,
Se Jun Parkc,
Kangsoo Kimc,
Euijoon Yoon*ad and
Gun-Do Lee
a,
Ho Jun Kimb,
Daekwang Wooc,
Se Jun Parkc,
Kangsoo Kimc,
Euijoon Yoon*ad and
Gun-Do Lee *ad
*ad
aDepartment of Materials Science and Engineering, Seoul National University, Seoul 08826, Korea. E-mail: eyoon@snu.ac.kr; gdlee@snu.ac.kr
bDepartment of Mechanical Engineering, Dong-A University, Busan 49315, South Korea
cMemory Thin Film Technology Team, Giheung Hwaseong Complex, Samsung Electronics, 445-701, South Korea
dResearch Institute of Advanced Materials and Inter-University Semiconductor Research Center, Seoul National University, Seoul 08826, South Korea
First published on 8th June 2018
Abstract
For the development of the future ultrahigh-scale integrated memory devices, a uniform tungsten (W) gate deposition process with good conformal film is essential for improving the conductivity of the W gate, resulting in the enhancement of device performance. As the memory devices are further scaled down, uniform W deposition becomes more difficult because of the experimental limitations of the sub-nanometer scale deposition even with atomic layer deposition (ALD) W processes. Even though it is known that the B2H6 dosing process plays a key role in the deposition of the ALD W layer with low resistivity and in the removal of residual fluorine (F) atoms, the roles of H2 and N2 treatments used in the ALD W process have not yet been reported. To understand the detailed ALD W process, we have investigated the effects of H2 and N2 treatment on TiN surfaces for the B2H6 dosing process using first-principles density functional theory (DFT) calculations. In our DFT calculated results, H2 treatment on the TiN surfaces causes the surfaces to become H-covered TiN surfaces, which results in lowering the reactivity of the B2H6 precursor since the overall reactions of the B2H6 on the H-covered TiN surfaces are energetically less favorable than the TiN surfaces. As a result, an effect of the H2 treatment is to decrease the reactivity of the B2H6 molecule on the TiN surface. However, N2 treatment on the Ti-terminated TiN (111) surface is more likely to make the TiN surface become an N-terminated TiN (111) surface, which results in making a lot of N-terminated TiN (111) surfaces, having a very reactive nature for B2H6 bond dissociation. As a result, the effect of N2 treatment serves as a catalyst to decompose B2H6. From the deep understanding of the effect of H2 and N2 during the B2H6 dosing process, the use of proper gas treatment is required for the improvement of the W nucleation layers.
1. Introduction
As the demand for miniaturized and highly integrated devices in the electronics industry increases, conformal film deposition techniques that can precisely control thickness at the atomic scale are becoming very important.1,2 Nitride materials, such as titanium nitride, silicon nitride, have been deposited using conventional deposition systems such as low-pressure chemical vapor deposition (LPCVD)3,4 and plasma-enhanced chemical vapor deposition (PECVD).5,6 Another deposition technique, atomic layer deposition (ALD),7–9 is the most prevalent technique for the fabrication of new memory devices due to the excellent step coverage and high conformality on extremely high aspect ratio structures. The ALD processes utilize well-controlled sequential surface reactions to achieve uniform and conformal films.10,11As one of the indispensable materials in the fabrication of future memory devices, tungsten (W) has been used in the metal gate deposition process due to the capability of depositing lower resistive films than other candidate materials, which results in the enhancement of the device performance.12,13 In the fabrication of memory devices, tungsten films have most widely been deposited using the ALD process by alternatively exposing W precursors such as tungsten hexafluoride (WF6) and reducing agents such as diborane (B2H6) in an ABAB… sequence. In the ALD W processes, the B2H6 dosing process plays a critical role in the deposition of W films with low resistivity and in the removal of residual fluorine (F) atoms on the surface.14–16 However, since the aspect ratio increases as the size of the memory device becomes smaller, it becomes difficult to deposit a thin film having excellent step coverage and conformality due to the problem of a seam or void being formed in the process of filling the W metal gate. This problem is a major obstacle to the development of future memory devices.17,18 To tackle this problem, the theoretical comprehension of the ALD W process is required due to the experimentally limited observations on the sub-nanometer scale. During the ALD W process, H2 and N2 molecules are used as both a purging gas at the purge time and a dilute gas (5% B2H6 + 95% H2 or N2) at the B2H6 dosing time.15 Although a few experimental results on ALD W have been reported, there has been no theoretical report on the effect of H2 and N2 treatment used in the ALD W process.
In our previous study, we reported that the severe problems, such as seams or voids, in filling the W metal gate for memory devices could be attributed to the difference in the deposition rate of the W film depending on the orientations of the TiN surfaces by analyzing the dissociation reaction of B2H6 on three different TiN surfaces using the density functional theory (DFT)19 calculation method. Since this previous study does not give information on the H2 and N2 treatment for the B2H6 dosing process, we want to report how important the use of proper gas treatment could be for B2H6 bond dissociation.
Previous ab initio molecular dynamics (AIMD) simulation results have shown that the presence of N vacancies catalyzes N2 dissociative chemisorption on the TiN (001) surface. N2 dissociation is never observed at the defect-free TiN (001) surface.20 The phenomena were also observed for the vanadium nitride (001) surface.21 D. G. Sangiovanni et al. demonstrated that the Ti and N adatom diffusion mechanism on TiN (001) involves direct hopping onto a lower layer and push-out/exchange by classical molecular dynamics (CMD) and AIMD simulations at temperatures ranging from 1200 to 2400 K.22–25 They also carried out Ti and N adatom migration pathways on the TiN (111) surface and showed that Nad species are considerably more mobile than Tiad on TiN (111), contrary to their previous results on TiN (001) by CMD based on the modified embedded atom method (MEAM) at temperatures ranging from 600 to 1800 K.26 A similar study was also carried out by Yuan Ren et al., showing that the diffusion energy of the Ti adatom is greater than that of the N adatom, confirmed by first principles calculations.27 C. Tholander et al. reported that Ti, Al, and N adatom mobilities on TiN (001), (011) and (111) surfaces, in general, are fastest on TiN (001), slower on (111), slowest on (011).28
In this study, we present a first-principles study based on DFT calculations to investigate the effects of H2 and N2 treatment on TiN surfaces for the B2H6 dosing process. In the first step, the decomposition processes of H2 and N2 treatment on the TiN surface were carefully analyzed. Then, in the second step, the decomposition processes of B2H6 molecules on the H2- and N2-treated TiN surfaces were analyzed to determine H2 and N2 treatment effects, respectively. From our calculated results in this study, the structure of the TiN surfaces can be changed as the TiN surface is exposed to large amounts of H2 or N2 molecules during the B2H6 dosing process. As a result, the changed structure of the TiN surfaces can have a significant impact on the ALD W process because the underlying surfaces can have significant effects on the characteristics of the subsequent W nucleation layers.29,30 The TiN surfaces have been widely utilized as a glue/barrier layer for subsequent W nucleation.31 Three different planes of TiN surfaces, TiN (001), Ti-terminated TiN (111), and N-terminated TiN (111) were taken into account because poly-crystalline TiN layers with (001) and (111) preferred orientations were mainly observed in the deposition of TiN films.32,33 The dissociative reaction pathways and reaction energetics of both H2 and N2 on three different TiN surfaces were investigated to explore the effect of H2 and N2 treatment for the B2H6 dosing process. It is expected that the comparative analysis of both H2 and N2 would give us insight into how important the use of proper gas treatment could be for improving the quality of the subsequent W layer during the W ALD process. This study will help to understand how H2 and N2 treatment plays an important role in the B2H6 dissociation reaction and ultimately provide new important information for improving the W ALD process.
2. Computational methods
In our theoretical results, all DFT calculations were performed using the Vienna ab initio simulation package (VASP) program with the Perdew–Burke–Ernzerhof (PBE) functional in the generalized gradient approximation (GGA).34,35 We used the PBE-D2 functional with a correction to the conventional Kohn–Sham DFT energy to treat the vdW interactions for all TiN surface calculations.36 The projector augmented wave (PAW) method was used to describe the interaction between valence electrons and ion cores.37 TiN (001) and TiN (111) surfaces with the B1-NaCl structure were used as the reactive surfaces with the B2H6 precursor. The optimized lattice parameter of TiN was a0 = 4.259 Å, which overestimated, somewhat, the experimental value (a0 = 4.24 Å)38 since PBE functionals generally tend to overestimate the lattice parameters. Compared to our PBE based calculated lattice parameter, previous research papers for DFT calculations of TiN reported that an optimized lattice parameter of TiN using the PBE functional is close to 4.254 Å.25,39 Another related paper using the Armiento Mattsson (AM05) approximation reported yields of 4.220 Å.40 For the TiN (001) surface, a 4-layer slab of (2 × 2) supercell with 64 atoms was considered. For comparison, the TiN surfaces with Ti-terminated and N-terminated (111) orientations were considered with a 5-layer slab of (2 × 2) supercell with 45 atoms.For all TiN surfaces, such as TiN (001), Ti-terminated TiN (111), and N-terminated TiN (111), vacuum gaps with values of 23.7 Å, 25.4 Å, and 25.6 Å, respectively, in the z-direction were included to avoid interactions between adjacent slabs. Valence orbitals were described by a plane-wave basis set with the cutoff energy of 400 eV. Electronic energies were calculated with a self-consistent-field (SCF) tolerance of 10−4 eV on the total energy. Ultrasoft Vanderbilt-type pseudopotentials41 were used to describe the interactions between ions and electrons. A 3 × 3 × 3 Monkhorst k-point mesh for bulk TiN was chosen. The Brillouin zone for three different TiN surfaces was sampled with a 3 × 3 × 1 Monkhorst–Pack k-point mesh. Geometry optimization was performed by minimizing the forces of all atoms to less than 0.02 eV Å−1 with the total energy of the system converged to within 10−4 eV during self-consistent iterations. In addition, we calculated total energies for various configurations to determine the energy barrier for the dissociative adsorption of H2 and N2 on the TiN surfaces in the first step, and for one of B2H6 on H-covered TiN surfaces in the second step.
To optimize adsorption structures, we considered two orientations and three positions of H2 and N2 on the three different TiN surfaces. The details of all six cases are shown in the ESI (Fig. S1–S3†). The optimized adsorption structures with the lowest energies (ESI, Tables S1–S3†) were used in this paper. We also checked three orientations and three positions of B2H6 on both H-covered Ti-terminated TiN (111) and H-covered N-terminated TiN (111) surfaces. The details of all nine cases are shown in the ESI (Fig. S4 and S5†). The optimized adsorption structures with the lowest energies (ESI, Tables S4 and S5†) were used in this paper. To find the optimized reaction path for the B2H6 bond dissociation on the H-covered TiN (111) surface, we considered three reaction paths, namely, path a, path b, and path c in the ESI (Fig. S8 and S9†). The optimized reaction path (path a) with the lowest overall reaction energy (ESI, Tables S8 and S9†) was used in this paper. To check the differences between PBE-D2 based calculations for convergence criteria of forces, such as 20 meV Å−1, and 1 meV Å−1, we carried out DFT calculations of H2 and N2 dissociative reactions on three TiN surfaces in the ESI (Table S10†). In those calculations, energy profiles with very similar results were obtained for two cases, i.e., PBE-D2 (<20 meV Å−1), PBE-D2 (<1 meV Å−1). To be more specific, the difference in activation energies between the two cases is very small (maximum difference: 0.007 eV, minimum difference: 0). Moreover, the difference in reaction energies between the two cases was not found. We believe it is reasonable to use the criteria of forces less than 20 meV Å−1.
It is worth noting that PBE-D2 generally results in a well-known and physically understood estimation of the dissociative reactions of molecules on various surfaces. Various computational approaches can be utilized to correct the shortcomings of approximate DFT calculations, including GW corrections42 or some exact Hartree–Fock (HF) exchange in the modern hybrid density functional (B3LYP, PBE0, HSE, etc.),43–45 which can lead to substantially improved band gaps; however, they are significantly computationally demanding. Since all our DFT calculations are addressed to bond dissociative reactions of various molecules, we believe it is reasonable and quantitative to investigate the dissociative reactions of various molecules on TiN surfaces using the PBE-D2 theory. In addition, PBE-D2 predictions have proven useful for prediction of the dissociative reactions of various molecules on different surfaces as shown by the numerous studies on the dissociation of different large molecules on Au (gold),46 oxygen reduction reaction on Co(acetylaetonate)2,47 water dissociation on mackinawite (FeS),48,49 and the dissociative reaction of silicon precursor on Si.50
To calculate the transition state, the distance between the two dissociative atoms was slightly separated, and energy relaxation was performed with the constrained distance. The same procedures were carried out until the force between two dissociative atoms became almost zero at the saddle point energy. This procedure for the calculation of the transition state is required to find not only the accurate final state but also transition state, especially in complicated systems such as B2H6 dissociation. After this procedure, we used the nudged elastic band method51 using the calculated final state to check the accurate transition state. During surface relaxation in our DFT calculations, no obvious surface reconstruction was found in different surfaces, such as TiN (001), Ti-terminated TiN (111), N-terminated TiN (111), which has been confirmed in another report.52
3. Results and discussion
3.1. H2 and N2 dissociative chemisorption on TiN (001)
The optimized structures of the initial, transition and final states for the H2 and N2 dissociative chemisorption step on the TiN (001) surface are shown in Fig. 1(a) and (b). The calculated energy diagram of H2 and N2 decomposition on the three different TiN surfaces is shown in Fig. 4. The initial state (IS) in Fig. 1(a) presents the optimized structure with the lowest adsorption energy of H2 on the surface. The final state (FS) in Fig. 1(a) shows that dissociated H atoms from H2 molecule react with titanium atoms of the TiN (001) surface after H–H bond dissociation because the binding energy on titanium sites of the TiN (001) surface is 0.42 eV larger compared to the nitrogen sites in our calculated results.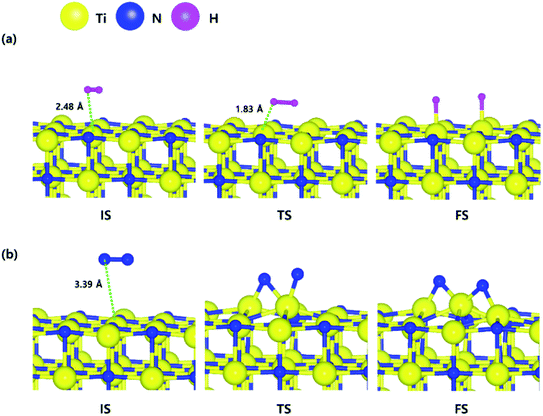 | ||
| Fig. 1 The optimized initial, transition, and final structures of the dissociative chemisorption step for (a) H2 and (b) N2 on the TiN (001) surface. | ||
The reaction energy can be calculated as the energy difference between the initial state and the final state. As shown in Fig. 4, the calculated reaction energy of H2 on the TiN (001) surface is 1.04 eV, which shows that the reaction is endothermic and energetically unfavorable. The activation energy from the initial state to the final state is 1.68 eV with the transition state as shown in Fig. 4. The N2 dissociative chemisorption step on the TiN (001) surface is shown in Fig. 1(b). It was found that the reaction energy is 3.25 eV (Fig. 4), which indicates that the reaction is thermodynamically endothermic and unfavorable. The activation energy from the initial state to the final state is 4.92 eV with the transition state as shown in Fig. 4.
3.2. H2 and N2 dissociative chemisorption on Ti-terminated TiN (111)
The decomposition mechanism of H2 and N2 was also studied on the Ti-terminated TiN (111) surface to estimate the difference between TiN (001) and TiN (111) surfaces. The optimized initial, transition, and final structures of H2 and N2 on the Ti-terminated TiN (111) surface are shown in Fig. 2. It was found that dissociated H atoms and N atoms in the final state were adsorbed on the hollow site made by three Ti atoms (Site number 3 in Fig. S2†). As shown in Fig. 2(a) and 4, it was found that the reaction energy of H2 is −2.10 eV, which indicates that the reaction is exothermic and energetically favorable. The activation energy from the initial state to the final state is 0.11 eV with the transition state as shown in Fig. 4, indicating that this reaction has a small energy barrier. As shown in Fig. 2(b) and 4, the adsorption energy of N2 is −3.44 eV, showing that the adsorption is energetically favorable. The reaction energy of N2 is −2.06 eV in Fig. 4, which indicates that the reaction is exothermic. The activation energy from the initial state to the final state is 0.92 eV with the transition state as shown in Fig. 4. The energy diagram for the H2 and N2 decomposition on Ti-terminated TiN (111) differs from the TiN (001) as illustrated in Fig. 4. It demonstrates that both H–H and N–N bond dissociation steps on the Ti-terminated TiN (111) surfaces are more facile than the TiN (001) surface due to the smaller activation energies of dissociation on the Ti-terminated TiN (111) surface. Moreover, the reactions of both H2 and N2 are energetically favorable, with their reaction energies of −2.10 eV, −2.06 eV, respectively. The high reactivity of both molecules on the Ti-terminated TiN (111) surface is most likely to be because the surface has triple dangling bonds per atom, which make the surface even more reactive than the TiN (001) surface. To be more specific, the number of dangling bonds on the Ti-terminated TiN (111) surface is more than that of the TiN (001), so that the bond dissociation of both H2 and N2 is more favorable on the former. This analysis was confirmed by the higher adsorption of both H and N atoms on the Ti- terminated (111) surface compared to the TiN (001) surface as shown in Table 1. Due to the aforementioned reasons, this surface can also reduce the energy barriers of the H2 and N2 decomposition as compared to the TiN (001) surface.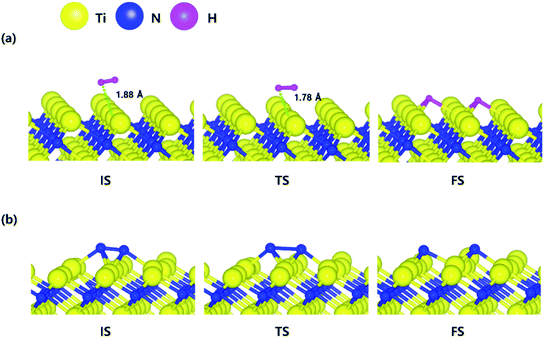 | ||
| Fig. 2 The optimized initial, transition, and final structures of the dissociative chemisorption step for (a) H2 and (b) N2 on the Ti-terminated TiN (111) surface. | ||
| Surface | H | N |
|---|---|---|
| TiN (001) | 2.93 | 5.79 |
| Ti-terminated TiN (111) | 4.61 | 11.0 |
| N-terminated TiN (111) | 5.73 | Not bound |
3.3. H2 and N2 dissociative chemisorption on N-terminated TiN (111)
The optimized initial, transition, and final structures of H2 and N2 on the N-terminated TiN (111) surface are displayed in Fig. 3. It was found that dissociated H atoms in the final state were adsorbed on the hollow site made by three N atoms (Site number 3 in Fig. S3†). As shown in Fig. 3(a) and 4, the reaction energy of H2 is −4.66 eV, which indicates that the reaction is exothermic. The activation energy from the initial state to the final state is 0.26 eV with the transition state, indicating that this reaction requires a low energy barrier. However, as for the N2 in Fig. 3(b) and 4, the reaction energy of N2 is 1.24 eV, which indicates that the reaction is endothermic. In this case, N2 molecules were not dissociated on the surface. The activation energy from the initial state to the final state is 1.45 eV with the transition state. We found that the H–H bond breaking on the N-terminated TiN (111) surfaces was much more facile compared to those of both TiN (001) and Ti-terminated TiN (111) surfaces, as shown in Fig. 4. This result is primarily because the binding energy (Eb = 5.73 eV) of H atoms on the N-terminated TiN (111) surface is the highest among the three different TiN surfaces, as shown in Table 1. Furthermore, the decomposition of H2 on the N-terminated TiN (111) surface is energetically favorable due to the downhill reaction and small energy barrier for H–H bond breaking. However, the N-terminated TiN (111) surface was not advantageous for breaking the N–N bond because N2 was not dissociated on the N-terminated TiN (111) surface. Although the N2 molecule has a larger bond dissociation energy (Edissosciation = 9.45 eV)53 than H2 (Edissosciation = 4.36 eV)53 due to the triple bonding nature of N2, this N2 molecule could be dissociated on the Ti-terminated TiN (111) surface. We suggest that this phenomenon is attributed to a large binding energy (Eb = 11.0 eV) of the N atom on the Ti-terminated TiN (111) surface, as depicted in Table 1.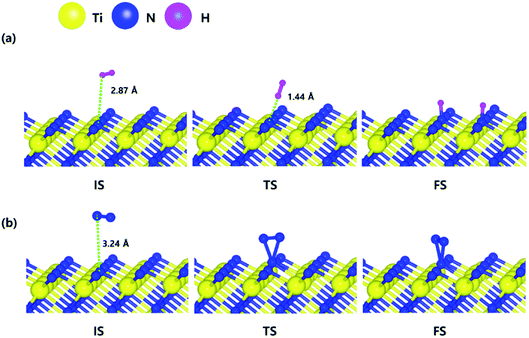 | ||
| Fig. 3 The optimized initial, transition, and final structures of the dissociative chemisorption step for (a) H2 and (b) N2 on the N-terminated TiN (111) surface. | ||
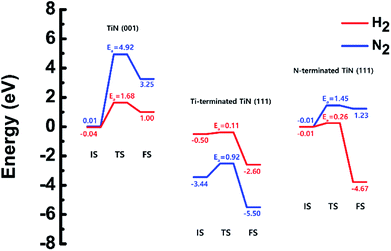 | ||
| Fig. 4 Calculated energy diagram of H2 and N2 decomposition on the TiN (001), the Ti-terminated TiN (111), and N-terminated TiN (111) surface. | ||
3.4. The effect of N2 treatment on TiN surfaces during the ALD process
As mentioned in Section 3.1, it is difficult to decompose both H2 and N2 on the TiN (001) surface because of the reactions in Fig. 4 are energetically unfavorable. However, since Ti-terminated TiN (111) can decompose H2 and N2 as shown Fig. 4, H-covered Ti-terminated TiN (111) and N-terminated TiN (111) surfaces can be made. In the case of N terminated TiN (111), the N–N bond dissociation is not possible, but H–H bond dissociation is possible, so the H-covered N-terminated TiN (111) surface can be made. Fig. 2(b) and 4 show that N2 treatment on the Ti-terminated TiN (111) surface is more likely to make the surface an N-terminated TiN (111) surface, which results in making a lot of N-terminated TiN (111) surfaces under the ALD process. Our previous study19 has shown that the N-terminated TiN (111) surface among the three TiN surfaces is the best surface for the B2H6 decomposition reaction. The combination of our previous study19 and this study provides new information on the effect of N2 treatment, which plays the role of a catalyst to decompose B2H6. Since both the results from our previous study and this study explain the effect of N2 treatment well enough, we have focused on the investigation of the H2 effect in this study. The decomposition processes of B2H6 on both the H covered Ti-terminated TiN (111) and the H-covered N-terminated TiN (111) surface were analyzed in detail to investigate the effect of H2 treatment. For the TiN (001) surface, the H-covered TiN (001) surface is excluded from the text because it is energetically unstable and H atoms on the surface are desorbed as H2.3.5. B2H6 dissociative chemisorption on H-covered Ti-terminated TiN (111)
Based on the results shown in Section 3.2, when the Ti-terminated TiN (111) surface is subjected to H2 treatment, the H2 molecule can be easily decomposed because of the low energy barrier for H2 bond dissociation on the surface, and thus the H-covered Ti-terminated TiN (111) surface can be made. Fig. 5 shows the decomposition reaction mechanism of B2H6 molecules when the H-covered Ti-terminated TiN (111) surface is formed after H2 treatment. Fig. 5(a) shows the first reaction step where the H atoms of the B2H6 molecules adsorbed on the TiN surface react with the H atoms on the TiN surface, desorbing H2, and the remaining B2H5 is bound to the surface. It was found that the dissociated B2H5 molecule is adsorbed on the hollow site made by three Ti atoms (Site number 4 in Fig. S4†). The reaction energy is 0.77 eV in Fig. 6, indicating that the reaction is endothermic. The activation energy is 1.24 eV with the transition state in Fig. 6. Fig. 5(b) shows the second reaction step where the H atoms of the B2H5 molecules adsorbed on the surface react with the H atom of the TiN surface then desorb into H2. As for the second reaction step, it shows that the reaction energy is −0.11 eV with an activation energy of 1.33 eV in Fig. 6.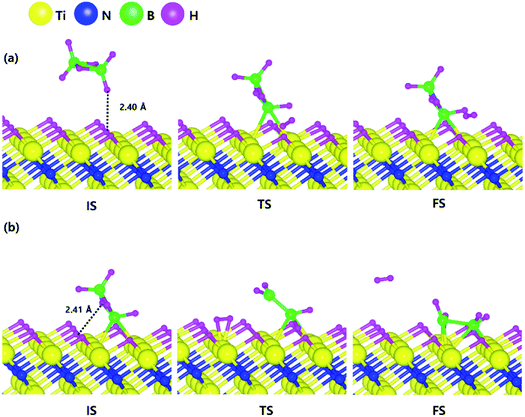 | ||
| Fig. 5 Dissociative chemisorption of B2H6 on the H-covered Ti-terminated TiN (111) surface: (a) the first reaction step (b) the second reaction step. | ||
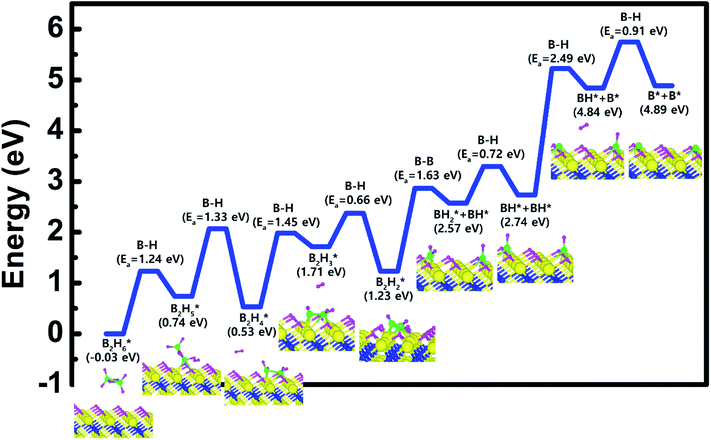 | ||
| Fig. 6 Calculated energy diagram of B2H6 decomposition on the H-covered Ti-terminated TiN (111) surface. | ||
To complete the overall reaction energetics of B2H6 for the optimized reaction path, the calculated energy diagram of B2H6 decomposition on the H-covered Ti-terminated TiN (111) surface is displayed in Fig. 6. The detailed structures of B2H6 during the overall reaction pathway on the surface for transition state calculations can be found in the ESI (Fig. S6†). During the reaction of the B2H6 precursor, this calculation shows that the overall reaction process is endothermic, with a calculated overall reaction energy of 4.92 eV in Table 2. This result indicates that the B2H6 dissociative chemisorption on H-covered Ti-terminated TiN (111) is energetically unfavorable due to the uphill reactions and high activation energies that range from a minimum of 0.66 eV to a maximum of 2.49 eV in Table 2. This implies that the low reactivity of B2H6 with the surface is due to the presence of the H-covered surface, compared to our previous results,19 as shown in Table 2, reporting that the dissociative reaction of B2H6 is energetically favorable on Ti-terminated TiN (111) surface. As a result, an effect of the H2 treatment on the surface is to passivate the TiN surface to prevent it from reacting with the B2H6 molecule.
| Surface | Bond dissociation | Ea,minimum (eV) | Ea,maximum (eV) | Erxn,overall (eV) | Note |
|---|---|---|---|---|---|
| H-covered Ti-terminated TiN (111) | B–B & B–H | 0.66 | 2.49 | 4.92 | This study |
| H-covered N-terminated TiN (111) | B–B & B–H | 0.40 | 1.65 | 1.26 | This study |
| Ti-terminated TiN (111) | B–B & B–H | 0.07 | 0.93 | −0.88 | Our previous study19 |
| N-terminated TiN (111) | B–B & B–H | Barrier-less | 0.39 | −19.0 | Our previous study19 |
3.6. B2H6 dissociative chemisorption on H-covered N-terminated TiN (111)
Based on the results shown in Section 3.3, when the N-terminated TiN (111) surface is subjected to H2 treatment, the H2 molecule can be easily dissociated because of the low barrier for the H2 bond dissociation on the surface, and thus the H-covered N-terminated TiN (111) surface can be made. Fig. 7 shows the decomposition reaction mechanism of B2H6 molecules when the H-covered N-terminated TiN (111) surface is formed after H2 treatment. Fig. 7(a) shows the first reaction step where the H atoms of the B2H6 molecule adsorbed on the TiN surface react with the H atoms on the TiN surface, desorbing H2, and the remaining B2H5 binds to the surface. The reaction energy is −0.38 eV in Fig. 8, indicating that the reaction is exothermic. The activation energy is 0.87 eV with the transition state in Fig. 8. Fig. 7(b) shows the second reaction step where the H atom of the B2H5 molecule adsorbed on the surface reacts with the H atom of the TiN surface to be desorbed into H2. As for the second reaction step, it shows that the reaction energy is 0.04 eV with an activation energy of 1.07 eV in Fig. 8.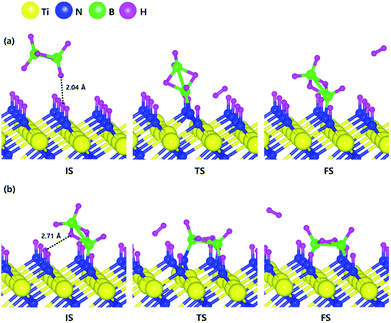 | ||
| Fig. 7 Dissociative chemisorption of B2H6 on the H-covered Ti-terminated TiN (111) surface: (a) the first reaction step (b) the second reaction step. | ||
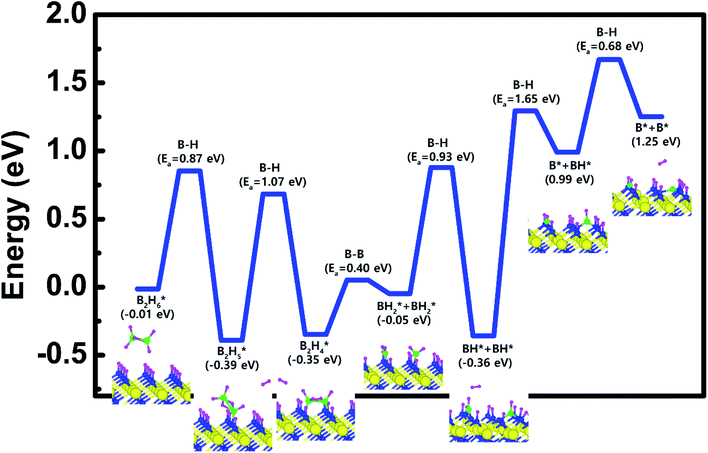 | ||
| Fig. 8 Calculated energy diagram of B2H6 decomposition on the H-covered N-terminated TiN (111) surface. | ||
The entire energy diagram for the B2H6 decomposition on the H-covered N-terminated TiN (111) is illustrated in Fig. 8. The detailed structures of B2H6 during the overall reaction pathway on the surface for transition state calculations can be found in the ESI (Fig. S7†). During the reaction of the B2H6 precursor, this calculation shows that the overall reaction process is endothermic with a calculated overall reaction energy of 1.26 eV in Table 2. Although the overall reaction from the 1st reaction step to the 7th reaction step (ESI, Fig. S7†) is energetically unfavorable, B2H6 dissociative reactions can occur from the 1st reaction step to the 5th reaction step because the overall reaction energy from the 1st to 5th step is −0.35 eV as shown in Fig. 8, meaning that the reaction is energetically favorable. From the 5th reaction step, two remaining BH species are difficult to dissociate due to the uphill reactions of B–H bond breaking with energy barriers of 1.65 eV, and 0.68 eV, respectively in Fig. 8.
Unlike the H-covered Ti-terminated TiN (111), the H-covered N-terminated TiN (111) surface can dissociate the B2H6 molecule into BH species up to 5th reaction step. We suggest that those remaining BH species and H atoms would be desorbed as BF3 and HF from WF6 in the next ALD cycle.
However, compared to the N-terminated TiN (111) in our previous results,19 the dissociative reaction of B2H6 is much more favorable on the N-terminated TiN (111) surface than the H-covered N-terminated TiN (111) surface as shown in Table 2. This implies that the low reactivity of B2H6 with the surface is attributed to the presence of an H-covered surface. As a result, an effect of the H2 treatment on the surface is to passivate the TiN surface to prevent it from reacting with the B2H6 molecules.
4. Discussion
Table 2 shows the minimum and maximum activation energies, and overall reaction energies required for B2H6 bond dissociation on the H-covered TiN and the TiN surfaces. The information on the TiN (001) surface is excluded because it is difficult to make an H-covered surface as mentioned above in Section 3.4. In addition, it was reported in our previous study that the B2H6 dissociative reaction on the TiN (001) surface is energetically unfavorable,19 meaning that the TiN (001) is not suitable for the B2H6 dosing process.As shown in Table 2, B2H6 dissociative reactions on both the H-covered Ti-terminated TiN (111) surface and the H-covered N-terminated TiN (111) surface require large overall reaction energies and activation energies, meaning that those reactions are energetically unfavorable. However, B2H6 dissociative reactions on both the Ti-terminated TiN (111) surface and the N-terminated TiN (111) surface are exothermic, meaning that those reactions are energetically favorable. In conclusion, H2 treatment on both Ti-terminated TiN (111) surface and N-terminated TiN (111) surface converts these surfaces into H-covered surfaces, leading to the degradation of the B2H6 dissociative reactions. As a result, H2 treatment has an effect of passivating the TiN surfaces. However, an effect of N2 treatment on the TiN surface is more likely to make the surface an N-terminated TiN (111) surface under the ALD process as mentioned above in Section 3.4, which leads to a lot of N-terminated TiN (111) surfaces. Table 2 shows that the B2H6 dissociative reaction on the N-terminated TiN (111) surface is much more energetically favorable than the Ti-terminated TiN (111) surface because it has a much lower reaction energy. As a result, N2 treatment has the effect of making the TiN surfaces more reactive for B2H6 bond dissociation. In the next ALD cycle after the B2H6 dosing process, the WF6 molecule is generally used for W deposition. Since boron (B) adatoms on the TiN surface would react with the F atoms of WF6, the BF3 desorption process would occur on the surface and therefore, a uniform W film could be deposited.
Our results imply that making a lot of N-terminated TiN (111) surfaces, by N2 treatment, plays an important role in improving the properties of the subsequent W nucleation layers during the W ALD process because easily dissociated B adatoms on the surface could dissociate the WF6 molecule and desorb into BF3. Since W nucleation layers are experimentally difficult to grow using only WF6 molecules without the B2H6 dosing process,54 B2H6 should be easily dissociated on the TiN surfaces for obtaining high-quality W nucleation layers during the W ALD process. Although H2 molecules play a role in lowering the reactivity of B2H6 on the TiN surfaces, this molecule can be useful to remove residual F atoms, which degrade the quality of the W layer. It has been reported that ALD W deposition under H2 exposure helps to remove residual F atoms by the desorption of HF.55 The previous experimental results and our theoretical results provide insight into how to design the ALD W deposition process to develop the W films for highly integrated devices.
5. Conclusions
In summary, we investigated the effects of H2 and N2 treatment on TiN surfaces for the B2H6 dosing process based on DFT calculation. Since the H2 molecule is easily dissociated on both Ti-terminated TiN (111) and N-terminated TiN (111) surfaces, H-covered Ti-terminated TiN (111) and H-covered N-terminated TiN (111) surfaces can be made. In our DFT calculated results, H2 treatment on the TiN surfaces convert the surfaces into H-covered TiN surfaces, which results in lowering the reactivity of the B2H6 precursor since the overall reactions of the B2H6 on the H-covered TiN surfaces are energetically less favorable than the TiN surfaces. As a result, an effect of the H2 treatment is to decrease the reactivity of the B2H6 molecule on the TiN surface. However, N2 treatment on the Ti-terminated TiN (111) surface is more likely to make the surface an N-terminated TiN (111) surface, which results in making a lot of N-terminated TiN (111) surfaces with very reactive nature for B2H6 bond dissociation. As a result, the effect of N2 treatment serves as a catalyst to decompose B2H6. Although the N2 molecule is more useful for B2H6 bond dissociation than H2 in regard to the reactivity, the H2 molecule has a greater advantage for the removal of residual F atoms than N2. From the understanding of the effect of H2 and N2 during the B2H6 dosing process, the use of proper gas treatment is required for the improvement of the W nucleation layers. These results imply that the deep understanding of the role of H2 and N2 treatment will provide insight for improving the W ALD process for future memory devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Euijoon Yoon and Gun-Do Lee acknowledge support from the Supercomputing Center/Korea Institute of Science and Technology Information with supercomputing resources (KSC-2017-C3-0013), from the Joint Program for Samsung Electronics Co., Ltd. (SEC), BK21PLUS SNU Materials Division for Educating Creative Global Leaders (21A20131912052), and from the National Research Foundation of Korea (NRF) grant funded by the Korea government (RIAM NRF-2016R1D1A1A02937045).References
- S. Bin Baek, D. H. Kim and Y. C. Kim, Appl. Surf. Sci., 2012, 258, 6341–6344 CrossRef.
- M. C. Schwille, T. Schossler and J. Barth, J. Vac. Sci. Technol., A, 2017, 35(1), 01B118 Search PubMed.
- W. Huang, X. Wang, M. Sheng, L. Xu, F. Stubhan, L. Luo, T. Feng, X. Wang, F. Zhang and S. Zou, Mater. Sci. Eng., B, 2003, 98, 248–254 CrossRef.
- A. El Amrani, A. Bekhtari, B. Mahmoudi, A. Lefgoum and H. Menari, Vacuum, 2011, 86, 386–390 CrossRef.
- N. Sharma, M. Hooda and S. K. Sharma, Journal of Materials, 2014, 2014, 1–8 CrossRef.
- B. C. Joshi, G. Eranna, D. P. Runthala, B. B. Dixit, O. P. Wadhawan and P. D. Yyas, Indian J. Eng. Mater. Sci., 2000, 7, 303–309 Search PubMed.
- W.-J. Lee, J.-H. Lee, C. O. Park, Y.-S. Lee, S.-J. Shin and S.-K. Rha, J. Korean Phys. Soc., 2004, 45, 1352–1355 Search PubMed.
- J. W. Klaus, A. W. Ott, A. C. Dillon and S. M. George, Surf. Sci., 1998, 418, L14–L19 CrossRef.
- C. A. Murray, S. D. Elliott, D. Hausmann, J. Henri and A. LaVoie, ACS Appl. Mater. Interfaces, 2014, 6(13), 10534–10541 Search PubMed.
- S. M. George, Chem. Rev., 2010, 110, 111–131 CrossRef PubMed.
- S. J. Won, J. R. Kim, S. Suh, N. I. Lee, C. S. Hwang and H. J. Kim, ACS Appl. Mater. Interfaces, 2011, 3, 1633–1639 Search PubMed.
- S.-H. Kim, N. Kwak, J. Kim and H. Sohn, J. Electrochem. Soc., 2006, 153(10), 887–893 CrossRef.
- S.-H. Kim and J.-K. Kim, et al., Electrochem. Solid-State Lett., 2006, 9(3), C54–C57 CrossRef.
- J. Klaus, S. Ferro and S. George, Thin Solid Films, 2000, 360, 145 CrossRef.
- C.-H. Kim, et al., J. Electrochem. Soc., 2009, 156(9), H685–H689 CrossRef.
- G. Wang, Q. Xu, T. Yang, J. Xiang, J. Xu, J. Gao, C. Li, J. Li, J. Yan, D. Chen, T. Ye, C. Zhao and J. Luoz, ECS J. Solid State Sci. Technol., 2014, 3(4), 82–85 CrossRef.
- T. Omstead, G. C. D'Couto, S.-H. Lee, P. Wongsenkaum, J. Collins and K. Levy, Solid State Technol., 2002, 51, 45 Search PubMed.
- S.-H. Kim, E.-S. Hwang, S.-H. Pyi, H.-J. Sun, J.-W. Lee, J.-K. Kim, N. Kawk, H. Sohn and J. Kim, J. Electrochem. Soc., 2005, 152, C408 CrossRef.
- H. Park, S. Lee, Ho J. Kim, E. Yoon and G.-D. Lee, RSC Adv., 2017, 7, 55750–55755 RSC.
- D. G. Sangiovanni, D. Edströma, L. Hultman, I. Petrov, J. E. Greene and V. Chirita, Surf. Sci., 2014, 624, 25–31 CrossRef.
- D. G. Sangiovanni, A. B. Mei, L. Hultman, V. Chirita, I. Petrov and J. E. Greene, J. Phys. Chem. C, 2016, 120, 12503–12516 Search PubMed.
- D. G. Sangiovanni, A. B. Mei, L. Hultman, V. Chirita, I. Petrov and J. E. Greene, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 035406 CrossRef.
- D. Edströma, D. G. Sangiovanni, L. Hultman, V. Chirita, I. Petrov and J. E. Greene, Thin Solid Films, 2014, 558, 37–46 CrossRef.
- D. G. Sangiovanni, D. Edströma, L. Hultman, I. Petrov, J. E. Greene and V. Chirita, Surf. Sci., 2014, 627, 34–41 CrossRef.
- D. G. Sangiovanni, D. Edströma, L. Hultman, V. Chirita, I. Petrov and J. E. Greene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155443 CrossRef.
- D. G. Sangiovanni, F. Tasnádi, L. Hultman, I. Petrov, J. E. Greene and V. Chirita, Surf. Sci., 2016, 649, 72–79 CrossRef.
- Y. Ren, X. Liu, X. Tan and E. Westkämper, Comput. Mater. Sci., 2013, 77, 102–107 CrossRef.
- C. Tholander, B. Alling, F. Tasnádi, J. E. Greene and L. Hultman, Surf. Sci., 2014, 630, 28–40 CrossRef.
- S.-H. Kim, S. Yeom, N. Kwak and H. Sohn, J. Electrochem. Soc., 2008, 155, D148 CrossRef.
- G. Ramanath, H. Kim, H. S. Goindi, M. J. Frederick, C.-S. Shin, R. Goswami, I. Petrov and J. E. Greene, AIP Conf. Proc., 2002, 612, 10 CrossRef.
- C.-H. Kim, I.-C. Rho, S.-H. Kim, Y.-S. Sohn, H.-S. Kang and H.-S. Kim, Electrochem. Solid-State Lett., 2009, 12(3), H80–H83 CrossRef.
- U. C. Oh and J. H. Je, J. Appl. Phys., 1993, 74, 1692 CrossRef.
- J. H. Je, D. Y. Noh, H. K. Kim and K. S. Liang, J. Appl. Phys., 1997, 81, 6126 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef PubMed.
- P. E. Blochl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- N. Schoenberg, Acta Chem. Scand., 1954, 8, 213 CrossRef.
- D. G. Sangiovanni, V. Chirita and L. Hultman, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 104107 CrossRef.
- D. G. Sangiovanni, B. Alling, P. Steneteg, L. Hultman and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054301 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- W. G. Aulbur, L. Jönsson and J. W. Wilkins, Solid State Phys., 1999, 54, 1–218 Search PubMed.
- J. K. Perry, J. Tahir-Kheli and W. A. Goddard III, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 144510 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- K. Lassoued, M. Seydou, F. Raouafi, F. Larbi, P. Lang and B. Diawara, Adsorption, 2018, 24, 191–201 CrossRef.
- N. Wang, Y. Liu, J. Zhao and Q. Cai, RSC Adv., 2016, 6, 79662 RSC.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Chem. Phys., 2016, 144, 174704 CrossRef PubMed.
- N. Y. Dzade, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2016, 120, 21441–21450 Search PubMed.
- J.-H. Yang, S.-B. Baek and Y.-C. Kim, J. Nanosci. Nanotechnol., 2014, 14, 7954–7960 CrossRef PubMed.
- G. Henkelman and H. Jónsson, J. Phys. Chem., 2000, 113, 9978–9985 CrossRef.
- D. Gall, S. Kodambaka, M. A. Wall, I. Petrov and J. E. Greene, J. Appl. Phys., 2003, 93, 9087 CrossRef.
- J. A. Dean, Lange's handbook of chemistry, McGraw-Hill, 15th edn, 1998, pp. 599–610 Search PubMed.
- J. W. Klaus, S. J. Ferro and S. M. George, Thin Solid Films, 2000, 360, 145–153 CrossRef.
- B. Kalanyan, P. C. Lemaire, S. E. Atanasov, M. J. Ritz and G. N. Parson, Chem. Mater., 2016, 28, 117–126 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02622j |
| This journal is © The Royal Society of Chemistry 2018 |
