Theoretical insights into the reaction mechanisms between 2,3,7,8-tetrachlorodibenzofuran and the methylidyne radical

Abstract

To explore the potential role of the methylidyne radical (CH) in the transformation of 2,3,7,8-tetrachlorodibenzofuran (TCDF), in this study, the detailed reaction mechanisms between TCDF and CH radical have been systematically investigated employing the B3LYP method of density functional theory (DFT) in combination with the atoms in molecules (AIM) theory and ab initio molecular dynamics. It was found that the title reaction is a multi-channel reaction, i.e., the CH radical can attack the C–X (X = C, Cl, H, O) bonds of TCDF via the insertion modes, resulting in the formation of 13 products. Thermodynamically, the whole reaction processes are exothermic and spontaneous since all the enthalpy and Gibbs free energy changes are negative values in the formation processes. Moreover, the thermodynamic stability of the products is controlled by the distribution of the single unpaired electron. Kinetically, the most favorable reaction channel is the insertion of the CH radical into the C–C bond except for the C atoms attached to the chlorine atom. Moreover, the dominant products have been further confirmed by the molecular dynamics. Meanwhile, the IR spectra and hyperfine coupling constants of the dominant products have been investigated to provide helpful information for their identification experimentally. In addition, the reactivity of the CH radical toward the F- and Br-substituted TCDFs has also been investigated. Expectedly, the present findings can enable us to better understand the reactivity of the CH radical toward organic pollutants analogous to TCDF in the atmosphere.

---

1. Introduction

Nowadays, the control, reduction, and conversion of persistent organic pollutants (POPs) have become important global environmental problems because POPs have posed a serious threat to human health and the ecological environment. As representative POPs, polychlorinated dibenzofurans (PCDFs) have been studied extensively due to their highly toxicological effects (e.g., dermal toxicity, immunotoxicity, and carcinogenicity, etc.) and widespread occurrence in the environment. It is well recognized that the major sources of PCDFs are incineration and thermal decomposition of waste materials involving chlorine as well as natural combustion processes (e.g., volcanic activity). Up to now, many studies have been carried out to gain a better understanding of the formation^1–8 and degradation^9–25 of PCDFs experimentally and theoretically. Especially, for the degradation of PCDFs, many methods have been proposed, such as microbial degradation, photocatalytic decomposition, and high temperature degradation, etc. Obviously, the unique stable structures of PCDFs limit their degradation in practice. Actually, only a few active free radicals, such as OH, NO₃, and H radicals, can react with PCDFs. Thus, it is necessary to seek new species which can react with PCDFs so as to provide useful clues to the transformation and degradation of PCDFs for experiments.

As one of the most reactive radical species, the methylidyne radical (CH) is well known to be of great importance in various fields, such as combustion chemistry, dense interstellar clouds, and planetary atmospheres. Its extreme reactivity arises from the presence of one singly occupied and one vacant non-bonding molecular orbital localized on the carbon atom.³⁷ Therefore, CH radical can react with most species ranging from small alkanes,^28–31 alkene,^28,32–38 alkyne,^{28,33,37–39} pyrrole,⁴¹ acrolein⁴² to large polycyclic aromatic hydrocarbons like anthracene (C₁₄H₁₀),⁴³ providing an alternative way to synthesize long-chain or ring-expanded hydrocarbons and complex organic molecules. For example, CH radical can react with pyrrole to produce the ring expansion product pyridine,⁴¹ where CH radical can be readily prepared experimentally via the photolysis of bromoform at room temperature. The cyclic versus linear isomers produced by the reaction of the CH radical with small unsaturated hydrocarbons involving ethylene, acetylene, allene, and methylacetylene have been investigated experimentally and theoretically.⁴⁵ Recently, the reactions of the CH radical with C₃H₈, CH₄, C₃H₆, and C₃H₄ have been systematically investigated theoretically by Ribeiro et al.^30–33 providing new insights into the detailed reaction mechanisms for the CH radical chemistry. As a general rule, more and more studies suggest that the reactions of the CH radical with other species can occur barrierlessly⁴⁴ and are high exothermicity.⁴⁰

Inspired by the highly reactive CH radical in the above studies^26–47 as well as the specific geometry of PCDFs containing the different types of C–X (X = C, Cl, H, O) bonds, we wonder if PCDFs can react with CH radical so as to change their geometries and even properties. If so, what are the detailed reaction mechanisms and the dominant reaction products? Moreover, how about the properties of the dominant products, such as IR and hyperfine coupling constants (hfcc's)? In addition, do the PCDFs derivatives, such as F- and Br- substituted species, also have similar reactivity with CH radical? Obviously, the clarification of the above questions will enable us to have a better understanding of the potential reactivity of CH radical in the atmosphere.

Unfortunately, the above questions remain unclear to the best of our knowledge. Therefore, in this study, taking the 2,3,7,8-tetrachlorodibenzofuran (TCDF) as model compound of PCDFs, its reaction with CH radical has been systematically investigated employing the density functional theory (DFT) method in combination with ab initio molecular dynamics. As a result, the detailed reaction mechanisms, thermodynamic information, and kinetic data for the title reaction have been clarified at the molecular level. Hopefully, the present results not only can clarify the potential reactivity of the highly reactive CH radical with TCDF and provide new insights into the transformation and degradation of TCDF in the atmosphere, but also can provide helpful information to promote the progress of the relevant experiments.

2. Computational methods

Nowadays, the density functional theory (DFT) method has been widely applied in computational chemistry since its reliability and efficiency in predicting the geometries and properties has been verified by a lot of studies including the CH radical.^{30–34,46–57} Therefore, all the species in the whole reactions have been fully optimized at the B3LYP/6-311++G** level of theory. Subsequently, vibrational frequency analysis has been performed at the same level of theory to identify the nature of the optimized structures. Moreover, intrinsic reaction coordinate (IRC) calculations were performed to further verify that the calculated transition states indeed connected the reactants and products.^58,59 In addition, single-point energy calculations have been performed at the B3LYP/AUG-cc-pVTZ level of theory to further refine the energy parameters for the formation of the initial intermediates and the main reaction pathways. As shown in Tables 1 and 2, both levels of theory can give consistent results with each other. For the sake of consistency, the results at the B3LYP/6-311++G** level of theory have been discussed below if not noted otherwise, where all the energy parameters are corrected by the zero-point vibrational energy (ZPVE). All the Cartesian coordinates of the optimized species and the IRC plots for all the pathways have been given in the ESI† for reference.

Table 1 The calculated relative energies (ΔE_rela) of initial intermediates and the enthalpy and Gibbs free energy changes (ΔH and ΔG) in the formation process of them^a

Intermediates	ΔErela	ΔH	ΔG
a All the energy parameters are relative to the initial reactants. All the units are in kcal mol^−1. The data before and after the slash refer to the results of the F- and Br-substituted cases, respectively. The data in bracket refer to the results at the B3LYP/AUG-cc-pVTZ level of theory including the ZPVE corrections at the B3LYP/6-311++G** level of theory.
IM1	−53.74[−52.88]	−54.98[−54.12]	−44.99[−44.14]
	(−53.33/−54.86)	(−54.59/−56.08)	(−44.55/−46.19)
IM2	−53.87[−52.95]	−55.12[−54.20]	−45.10[−44.18]
	(−53.31/−55.13)	(−54.59/−56.37)	(−44.50/−46.43)
IM3	−43.71[−43.36]	−44.89[−44.54]	−35.06[−34.71]
	(−41.33/−44.23)	(−42.47/−45.44)	(−32.75/−35.58)
IM4	−35.71[−34.95]	−36.98[−36.22]	−26.89[−26.13]
	(−36.83/−35.60)	(−38.12/−36.89)	(−27.94/−26.81)
IM5	−37.10[−36.37]	−38.32[−37.60]	−28.32[−27.59]
	(−38.20/−37.01)	(−39.42/−38.25)	(−29.39/−28.27)
IM6	−45.08[−44.69]	−46.26[−45.87]	−36.43[−36.04]
	(−43.10/−45.47)	(−44.24/−46.67)	(−34.48/−36.80)
IM7	−52.65[−51.75]	−53.89[−52.98]	−43.90[−43.00]
	(−52.07/−53.88)	(−53.32/−55.11)	(−43.31/−45.19)
IM8	−52.67[−51.71]	−53.91[−52.96]	−43.89[−42.94]
	(−51.89/−54.00)	(−53.16/−55.24)	(−43.11/−45.29)
IM9	−8.35[−10.64]	−8.88[−11.17]	−0.58[−2.87]
IM10	−8.78[−10.92]	−9.33[−11.47]	−0.98[−3.13]

---

Table 2 The relative energies (ΔE_rela) for the transition state relative to the initial reactants, the energy barriers, and the ΔH and ΔG during the interconversion processes^a

Reactions	TSs	ΔErela			ΔH	ΔG
a All the units are in kcal mol^−1. The direction from left to right is defined as the forward reaction. The data in parentheses refer to the results without considering the ZPVE corrections. The data before and after the slash refer to the results of the F- and Br-substituted cases, respectively. The data in bracket refer to the results using the AUG-cc-pVTZ basis set.
IM1 ⇌ IM2	TS1	−53.49	0.25	0.38	−0.14	−0.11
IM1 ⇌ P1	TS2	−52.22[−51.64]	1.52[1.25]	49.52[50.74]	−48.01[−49.51]	−48.18[−49.68]
		−52.12/−53.37	1.21/1.49	52.52/47.73	−51.26/−46.24	−51.50/−46.56
IM2 ⇌ P1	TS3	−51.10[−50.35]	2.77[2.60]	50.64[52.03]	−47.87[−49.44]	−48.07[−49.64]
		−49.49/−52.44	3.82/2.70	55.15/48.66	−51.26/−45.95	−51.55/−46.32
IM3 ⇌ P1	TS4	−43.96	−0.25(0.28)	57.77	−58.10	−58.11
		[−43.61]	[−0.25(0.28)]	[58.77]	[−59.09]	[−59.11]
		−41.66/−44.54	−0.33(0.06)	62.98/56.56	−63.38/−56.89	−63.30/−57.17
			/−0.31(0.19)
IM10 ⇌ IM2	TS5	−0.95	7.83	52.92	−45.79	−44.12
IM4 ⇌ IM5	TS6	−35.07	0.64	2.03	−1.34	−1.43
IM4 ⇌ P2	TS7	−34.53	1.18	2.41	−1.17	−1.14
		−35.45/−34.51	1.38/1.09	2.20/2.66	−0.73/−1.51	−0.80/−1.43
IM5 ⇌ P3	TS8	−37.24	−0.14(0.14)	3.47	−3.75	−3.33
		[−36.54]	[−0.17(0.11)]	[3.49]	[−3.80]	[−3.38]
		−38.37/−37.12	−0.17(0.09)	4.15/3.57	−4.51/−3.81	−4.01/−3.36
			/−0.12(0.17)
P2 ⇌ P3	TS9	−37.25	−0.30(0.32)	3.46	−3.92	−3.62
		−38.05/−37.45	−0.40(0.13)	4.47/3.24	−5.08/−3.66	−4.67/−3.38
			/−0.28(0.07)
IM4 ⇌ P4	TS10	−1.04[−1.00]	34.67[33.95]	99.89[100.46]	−65.22[−66.50]	−65.62[−66.91]
IM6 ⇌ P4	TS11	−45.05[−44.68]	0.03[0.01]	55.88[56.78]	−55.94[−56.85]	−56.08[−56.99]
		−43.44/−45.50	−0.35(0.21)	60.95/54.73	−61.39/−54.80	−61.33/−55.66
			/−0.03(0.87)
IM7 ⇌ IM8	TS12	−52.31	0.34	0.35	−0.03	0.01
IM7 ⇌ P4	TS13	−51.01[−50.37]	1.64[1.37]	49.93[51.09]	−48.32[−49.74]	−48.61[−50.04]
		−50.85/−52.23	1.22/1.65	53.54/48.00	−52.31/−46.36	−52.50/−47.27
IM8 ⇌ P4	TS14	−49.48[−48.75]	3.19[2.97]	51.46[52.71]	−48.29[−49.77]	−48.62[−50.09]
		−47.85/−50.97	4.04/3.03	56.54/49.26	−52.48/−46.23	−52.70/−47.17
IM9 ⇌ IM8	TS15	−0.61	7.73	52.06	−45.03	−43.32
IM7 ⇌ P5	TS16	−1.72	50.93	104.23	−53.31	−53.40
P1 ⇌ P6	TS17	27.74	129.47	147.52	−18.16	−17.74
IM9 ⇌ P7	TS18	4.02	12.37	112.07	−100.38	−99.10
IM9 ⇌ P8	TS19	4.16	12.51	118.10	−106.31	−104.75
P7 ⇌ P8	TS20	−101.54	6.51	12.40	−5.94	−5.64
P5 ⇌ P7	TS21	−22.06	83.89	85.99	−2.05	−2.38
P5 ⇌ P8	TS22	−22.14	83.82	91.80	−7.99	−8.02
IM8 ⇌ P8	TS23	−25.31	27.36	88.62	−61.28	−61.43
IM9 ⇌ IM10	TS24	−0.99	7.36	7.79	−0.45	−0.41
IM10 ⇌ P9	TS25	4.86	13.64	111.62	−98.62	−97.48
IM10 ⇌ P10	TS26	5.16	13.94	117.79	−104.54	−103.04
P9 ⇌ P10	TS27	−101.81	4.96	10.82	−5.93	−5.56
IM6 ⇌ P11	TS28	−0.81	44.27	108.67	−64.44	−64.15
P1 ⇌ P12	TS29	−14.23	87.51	94.71	−7.16	−6.92
P4 ⇌ P13	TS30	−5.48	95.46	107.73	−12.30	−11.96

---

To clarify the structural features and the nature of the interatomic interactions for the initial intermediates and products, atoms in molecules (AIM) theory was employed on the basis of the optimized structures. In the AIM analyses, the interatomic interaction is indicated by the presence of a bond critical point (BCP). The corresponding strength can be estimated from the magnitude of the electron density (ρ_bcp) at the BCP. Similarly, the ring structures can be confirmed by the existence of a ring critical point (RCP). Additionally, the nature of the interatomic interaction can be predicted from the topological parameters at the BCP, such as the Laplacian (∇²ρ_bcp) and energy density (H_bcp). For example, the interatomic interactions are characterized by the covalent bonds (shared interaction) and the H-bonds as well as van der Waals interactions (closed-shell interaction) if ∇²ρ_bcp < 0 and ∇²ρ_bcp > 0, respectively. In addition, it was also reported that the interatomic interactions should be partially covalent if ∇²ρ_bcp > 0 and H_bcp < 0.^60,61

To better confirm the presence of the non-covalent interactions in the selected products, the reduced density gradient (RDG) analysis was performed on the basis of the optimized structures. In this method, the different weak interactions can be intuitively illustrated using different colors in real space.⁶²

To further clarify the interconversion among the initial intermediates and the formation processes of the products, ab initio molecular dynamics has been carried out at the B3LYP/6-311G** level of theory using the Atom Centered Density Matrix Propagation (ADMP) approach based on the optimized initial intermediates.^63–65 Here, the dynamics calculations were performed with NVT ensemble at 298.15 K and the total simulation time is 1.0 ps with a time stepsize of 0.5 fs.

All the calculations have been performed using Gaussian 09 program.⁶⁶

3. Results and discussion

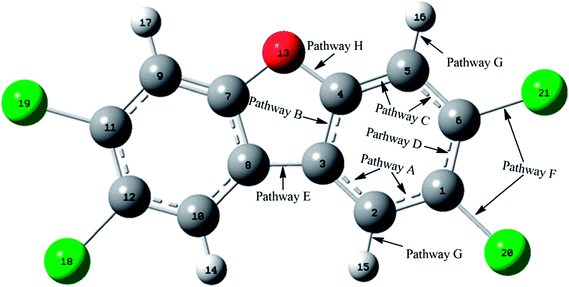
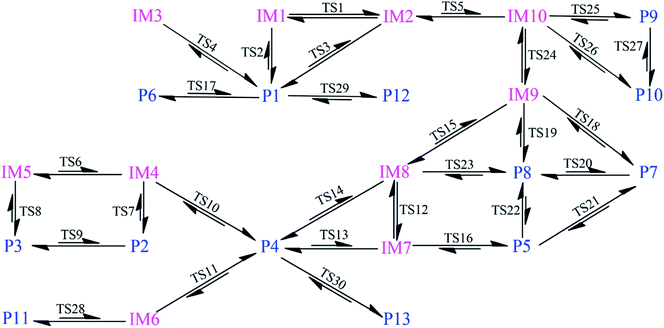
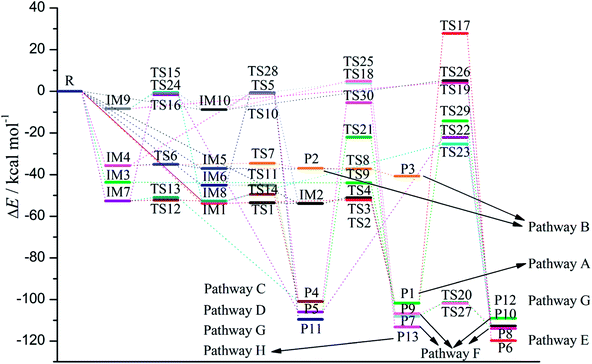
As shown in Fig. 1, the reaction of CH radical with TCDF is a multi-channel reaction via the insertion mode. In details, the whole reaction can be divided into four categories according to the type of the inserted bonds, i.e., the C–C (Pathways A–E), C–Cl (Pathway F), C–H (Pathway G), and C–O bond (Pathway H), respectively.

Fig. 1 The positions of the C–X (X = C, Cl, H, O) bonds of TCDF attacked by CH radical.

As shown in Fig. 2, as the first step of the whole reaction, ten initial intermediates named as IM1–IM10 have been located barrierlessly, where the corresponding thermodynamic data have been summarized in Table 1. Obviously, the formation processes of them are spontaneous and strongly exothermic reactions except for IM9 and IM10, which can be reflected from the negative values of the enthalpy and Gibbs free energy changes (ΔH and ΔG). As for the formation of IM9 and IM10, small values have been observed for the ΔH and ΔG, implying the unfavorable formation of them thermodynamically. Subsequently, thirteen products P1–P13 and thirty transition states TS1–TS30 have been located in the interconversion processes among intermediates and products, where the relevant thermodynamic parameters and the energy barriers for the interconversion processes have been summarized in Table 2. For the sake of simplicity, the interconversion relationship among the initial intermediates, transition states, and products have been illustrated in Fig. 3. Moreover, the whole reaction profiles for the title reaction have been shown in Fig. 4.

Fig. 2 The optimized initial intermediates (IM), transition states (TS), and products in the reaction of TCDF with CH radical.

Fig. 3 Schematic diagram for the interconversion among initial intermediates and products. The short arrow denotes the high energy barrier needed to overcome and the two-way arrow refers to the similar forward and reverse energy barriers.

Fig. 4 The reaction profiles for the reaction between TCDF and CH radical.

3.1 Reaction pathways and the interconversions among intermediates

As shown in Fig. 5, many ring critical points have been observed in the initial intermediates and products except for IM9 and IM10, suggesting that additional ring structures have been formed for TCDF when the CH radical is introduced. Moreover, as presented in Table 3, the negative values of ∇²ρ_bcp at the BCPs suggests that the formed bonds between the CH radical and TCDF should be covalent in nature. On the other hand, for the initial intermediates IM9 and IM10, the positive ∇²ρ_bcp and negative H_bcp at BCP between the C atom of the CH radical and Cl atom of TCDF have been observed, indicating that the corresponding interaction is partially covalent.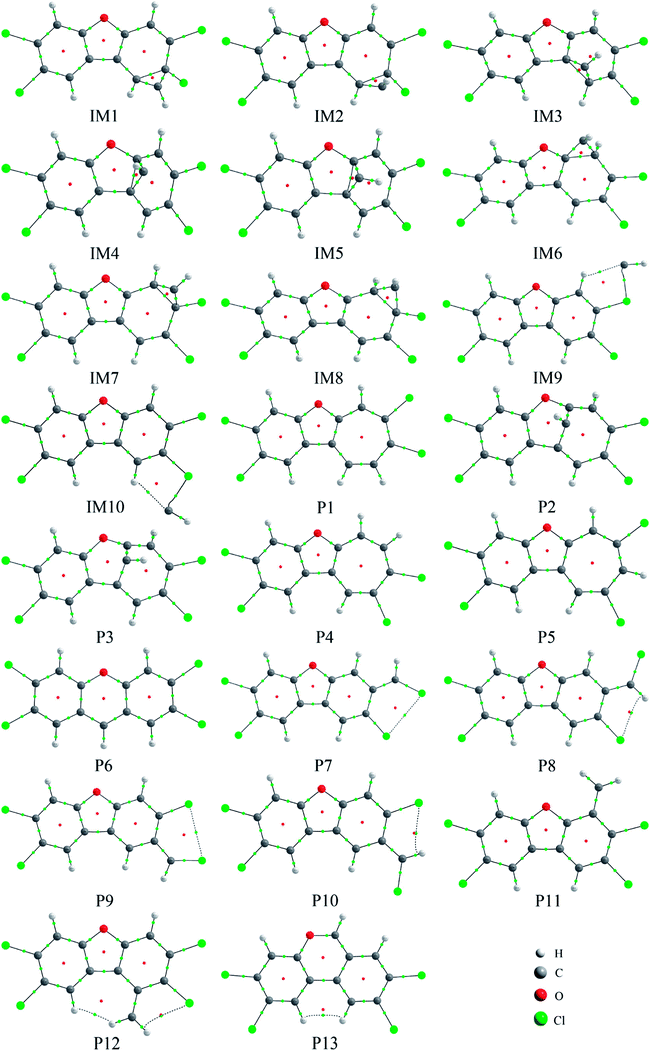

Fig. 5 The molecular graphs for the initial intermediates and products, where the BCP and RCP are denoted as small green and red dots, respectively.

Table 3 The topological parameters for the selected BCPs in the initial intermediates and products^a

Species	BCP	ρbcp	∇^2ρbcp	Vbcp	Gbcp	Hbcp
a Atomic numbering refers to Fig. 2. The ρbcp, ∇^2ρbcp, Vbcp, Gbcp, and Hbcp is electron density, the Laplacian of the electron density, potential energy density, kinetic energy density, and energy density at the BCP, respectively.
IM1	C1 – C22	0.2655	−0.5642	−0.3437	0.1013	−0.2423
	C2 – C22	0.2510	−0.4894	−0.3128	0.0952	−0.2176
IM2	C1 – C22	0.2640	−0.5524	−0.3400	0.1009	−0.2390
	C2 – C22	0.2541	−0.5054	−0.3187	0.0962	−0.2225
IM3	C2 – C22	0.2608	−0.5541	−0.3296	0.0955	−0.2341
	C3 – C22	0.2564	−0.5234	−0.3223	0.0957	−0.2266
IM4	C3 – C22	0.2430	−0.4407	−0.3003	0.0951	−0.2053
	C4 – C22	0.2671	−0.5773	−0.3443	0.1000	−0.2443
IM5	C3 – C22	0.2525	−0.4992	−0.3166	0.0959	−0.2207
	C4 – C22	0.2646	−0.5662	−0.3396	0.0990	−0.2406
IM6	C4 – C22	0.2691	−0.5909	−0.3462	0.0992	−0.2470
	C5 – C22	0.2543	−0.5095	−0.3185	0.0955	−0.2229
IM7	C5 – C22	0.2475	−0.4697	−0.3072	0.0949	−0.2123
	C6 – C22	0.2679	−0.5792	−0.3477	0.1014	−0.2462
IM8	C5 – C22	0.2508	−0.4852	−0.3130	0.0958	−0.2171
	C6 – C22	0.2661	−0.5649	−0.3434	0.1011	−0.2423
IM9	Cl21 – C22	0.0904	0.0614	−0.0820	0.0487	−0.0333
IM10	Cl20 – C22	0.0904	0.0607	−0.0819	0.0486	−0.0334
P1	C1 – C22	0.2792	−0.7172	−0.3365	0.0786	−0.2579
	C2 – C22	0.3259	−0.9353	−0.4733	0.1197	−0.3536
P2	C3 – C22	0.2697	−0.6614	−0.3211	0.0779	−0.2432
	C4 – C22	0.2824	−0.7287	−0.3489	0.0834	−0.2655
P3	C3 – C22	0.2763	−0.6890	−0.3400	0.0839	−0.2562
	C4 – C22	0.2862	−0.7418	−0.3669	0.0907	−0.2762
P4	C4 – C22	0.3017	−0.8479	−0.3969	0.0925	−0.3044
	C5 – C22	0.3071	−0.8482	−0.4162	0.1021	−0.3141
P5	C1 – C22	0.2868	−0.7536	−0.3582	0.0849	−0.2733
	C6 – C22	0.3087	−0.8511	−0.4263	0.1067	−0.3195
P6	C3 – C22	0.2953	−0.7939	−0.3783	0.0899	−0.2884
	C8 – C22	0.2953	−0.7938	−0.3783	0.0899	−0.2884
P7	C6 – C22	0.2970	−0.7854	−0.3867	0.0952	−0.2915
	Cl21 – C22	0.2051	−0.3055	−0.2234	0.0735	−0.1499
P8	C6 – C22	0.3022	−0.8157	−0.3985	0.0973	−0.3012
	Cl21 – C22	0.2024	−0.2997	−0.2199	0.0725	−0.1474
P9	C1 – C22	0.2927	−0.7643	−0.3749	0.0919	−0.2830
	Cl20 – C22	0.2043	−0.3021	−0.2223	0.0734	−0.1489
P10	C1 – C22	0.2979	−0.7948	−0.3869	0.0941	−0.2928
	Cl20 – C22	0.2015	−0.2962	−0.2188	0.0724	−0.1464
P11	C5 – C22	0.3045	−0.8350	−0.4102	0.1007	−0.3095
P12	C2 – C22	0.3078	−0.8515	−0.4166	0.1018	−0.3147
P13	C4 – C22	0.3110	−0.8653	−0.4227	0.1032	−0.3195
	O13 – C22	0.2735	−0.0999	−0.7395	0.3573	−0.3822

---

(1) Pathway A. As displayed in Fig. 1 and 2, in this pathway, CH radical attacks the C1–C2 and C2–C3 bonds of TCDF, leading to the formation of three intermediates IM1, IM2, and IM3 characterized by the three-membered ring structure. As shown in Fig. 3 and 4, IM1 and IM2 can interconvert into each other via the transition state TS1, i.e., IM1 ⇌ IM2, where the forward (reverse) energy barrier and the enthalpy changes (free energy changes) are 0.25(0.38) kcal mol⁻¹ and −0.14(−0.11) kcal mol⁻¹, respectively. Obviously, this interconversion process is a spontaneous and exothermic reaction and can occur easily due to the low energy barrier.

Subsequently, the initial intermediates IM1, IM2, and IM3 undergo the corresponding transition states TS2, TS3, and TS4 to form the product P1, i.e., IM1 → TS2 → P1, IM2 → TS3 → P1, and IM3 → TS4 → P1, where P1 is characterized by a planar seven-membered ring structure. The energy barriers of the three processes are 1.52, 2.77, and −0.25(0.28) kcal mol⁻¹ respectively, where the value in parentheses is the result without considering the ZPVE corrections. Moreover, the above processes are spontaneous and highly exothermic reactions, where the corresponding enthalpy (Gibbs free energy) changes are −48.01(−48.18), −47.87(−48.07), and −58.10(−58.11) kcal mol⁻¹, respectively. Therefore, P1 should be the dominant product and the pathway IM3 → TS4 → P1 is the optimal pathway to produce it.

(2) Pathway B. As displayed in Fig. 1 and 2, in this pathway, CH radical attacks the C3–C4 bond of TCDF. Similar to Pathway A, two three-membered ring intermediates IM4 and IM5 have been formed. As shown in Fig. 3 and 4, they can interconvert into each other through the transition state TS6, i.e., IM4 → TS6 → IM5, where the forward (reverse) energy barrier and the enthalpy (Gibbs free energy) changes are 0.64(2.03) and −1.34(−1.43) kcal mol⁻¹, respectively. Therefore, IM4 and IM5 are easy to interconvert into each other.

Subsequently, the initial intermediates IM4 and IM5 can undergo the corresponding transition states TS7 and TS8 to produce the ring-expanded products P2 and P3, i.e., IM4 → TS7 → P2 and IM5 → TS8 → P3. For the two processes, the energy barriers are 1.18 and −0.14(0.14) kcal mol⁻¹ respectively, where the value in parentheses is the result without considering ZPVE corrections. Moreover, the above processes are exothermic and spontaneous processes, where the corresponding enthalpy (Gibbs free energy) changes are −1.17(−1.14) and −3.75(−3.33) kcal mol⁻¹, respectively. Therefore, it is easy to convert into products P2 and P3 for IM4 and IM5.

(3) Pathway C. As displayed in Fig. 1 and 2, in this pathway, CH radical attacks the C4–C5 and C5–C6 bonds of TCDF, leading to the formation of three three-membered ring intermediates IM6, IM7, and IM8. Here, IM7 and IM8 can interconvert into each other through the transition state TS12, i.e., IM7 ⇌ IM8, where the forward (reverse) energy barrier and the enthalpy (Gibbs free energy) changes are 0.34(0.35) and −0.03(0.01) kcal mol⁻¹, respectively. Obviously, the above conversion process can proceed easily thermodynamically and kinetically.

After then, the above three intermediates can undergo the corresponding transition states to produce the ring-expanded product P4, i.e., IM6 → TS11 → P4, IM7 → TS13 → P4, and IM8 → TS14 → P4, where the energy barriers are 0.03, 1.64, and 3.19 kcal mol⁻¹, respectively. Moreover, the above processes are exothermic and spontaneous processes, where the corresponding enthalpy (Gibbs free energy) changes are −55.94(−56.08), −48.32(−48.61), and −48.29(−48.62) kcal mol⁻¹, respectively. Therefore, similar to products P1–P3, P4 should also be the dominant product. In addition, as presented in Table 2, IM4 can also convert into P4 thermodynamically, where the corresponding enthalpy and Gibbs free energy changes are −65.22 and −65.62 kcal mol⁻¹, respectively. However, the high energy barrier of 34.67 kcal mol⁻¹ suggests that it is difficult to occur for this process. Therefore, the IM6 → TS11 → P4 process should be the optimal pathway to produce product P4.

(4) Pathway D. As displayed in Fig. 1 and 2, in this pathway, CH radical can be inserted into the C1–C6 bond of TCDF, leading to the formation of the ring-expanded product P5. Further IRC analyses suggest that P5 is derived from the initial intermediate IM7, i.e., IM7 → TS16 → P5. However, the calculated energy barrier of 50.93 kcal mol⁻¹ for this process is too high to occur although it is an exothermic and spontaneous process thermodynamically. Here, the corresponding enthalpy and Gibbs free energy changes are −53.31 and −53.40 kcal mol⁻¹, respectively. Therefore, it is difficult to obtain P5 in practice.

(5) Pathway E. As displayed in Fig. 1 and 2, in this pathway, CH radical can be inserted into the C3–C8 bond of TCDF, leading to the formation of the ring-expanded product P6. Further IRC analyses suggest that P6 is derived from the conversion of P1 via TS17, i.e., P1 → TS17 → P6. However, the calculated energy barrier of 129.47 kcal mol⁻¹ suggests that it is infeasible to take place for this process although it is favorable thermodynamically as can be seen from the negative enthalpy and Gibbs free energy changes.

(6) Pathway F. As displayed in Fig. 1 and 2, in this pathway, CH radical attacks the two C–Cl bonds of TCDF, leading to the formation of two initial intermediates IM9 and IM10. As shown in Fig. 3 and 4, IM9 and IM10 can interconvert into each other via the transition state TS24, where the forward (reverse) energy barrier and the enthalpy (Gibbs free energy) changes are 7.36(7.79) and −0.45(−0.41) kcal mol⁻¹, respectively. In addition, it was found that IM10 can convert into IM2 via TS5 with an energy barrier of 7.83 kcal mol⁻¹. Meanwhile, it is also favorable for this conversion process thermodynamically, where the corresponding enthalpy and Gibbs free energy changes are −45.79 and −44.12 kcal mol⁻¹, respectively.

Subsequently, IM9 and IM10 can undergo corresponding transition states to produce products P7–P10, i.e., IM9 → TS18 → P7, IM9 → TS19 → P8, IM10 → TS25 → P9, and IM10 → TS26 → P10, where the energy barrier of each process is 12.37, 12.51, 13.64, and 13.94 kcal mol⁻¹, respectively. Moreover, all the above reaction processes are exothermic and spontaneous processes, where the corresponding enthalpy (Gibbs free energy) changes are −100.38(−99.10), −106.31(−104.75), −98.62(−97.48), and −104.54(−103.04) kcal mol⁻¹, respectively. Additionally, it was also found that IM8 can be converted into P8 via TS23 with an energy barrier of 27.36 kcal mol⁻¹, implying that it is difficult to proceed under normal conditions. Compared with the products P1–P4 mentioned above, the formation of the products P7–P10 requires higher energy barriers to overcome. Moreover, as the precursors to the products P7–P10, IM9 and IM10 are unfavorable to be formed thermodynamically relative to the other intermediates. Therefore, products P7–P10 should be the secondary products of the title reaction.

(7) Pathway G. As displayed in Fig. 1 and 2, in this pathway, CH radical can be inserted into C–H bond of TCDF, i.e., C5–H16 and C2–H15 bonds, leading to the formation of two products P11 and P12. Further IRC analyses suggest that P11 and P12 are derived from the conversion of IM6 and P1 via the transition states TS28 and TS29, respectively. The calculated enthalpy (Gibbs free energy) changes of −64.44(−64.15) and −7.16(−6.92) kcal mol⁻¹ suggest that the above two conversion processes are spontaneous and exothermic processes thermodynamically. On the other hand, the calculated high energy barriers (44.27 and 87.51 kcal mol⁻¹) suggest that those processes are difficult to proceed. Therefore, the possibility of obtaining the products P11 and P12 should be small.

(8) Pathway H. As displayed in Fig. 1 and 2, in this pathway, CH radical attacks the C4–O13 bond of TCDF, leading to the formation of the ring-expanded product P13. Further IRC analyses suggest that P13 is derived from the conversion of P1 via TS30 with an energy barrier of 95.46 kcal mol⁻¹. Obviously, it is difficult to obtain P13 due to the high energy barrier.

3.2 Analyses of stability and interconversion of products

3.2.1 Stability analysis. As shown in Fig. 6, we have calculated the relative energies among all the products relative to the isolated reactants. Obviously, the relative stability orders among the products should be as follows: P6 > P8 > P13 > P10 > P11 > P12 > P7 > P9 > P5 > P1 > P4 > P3 > P2. To further clarify the correlation between the stability of the products and the single electron distributions, we have investigated the spin density of the products.

Fig. 6 The relative energy of each product relative to the separated monomers.

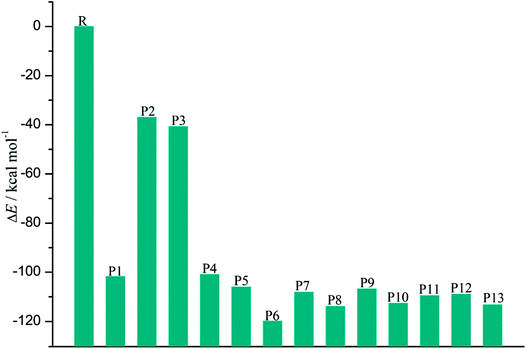
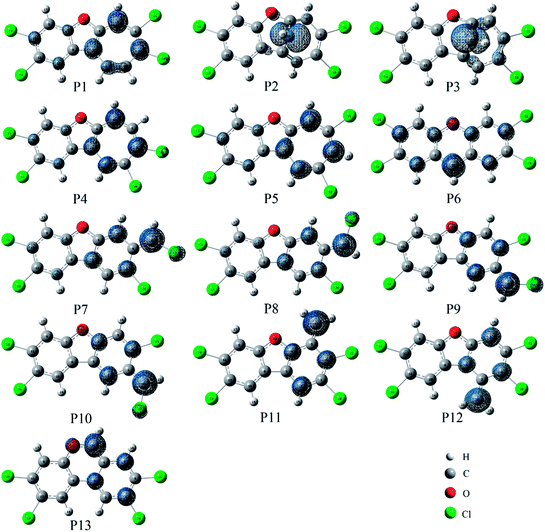
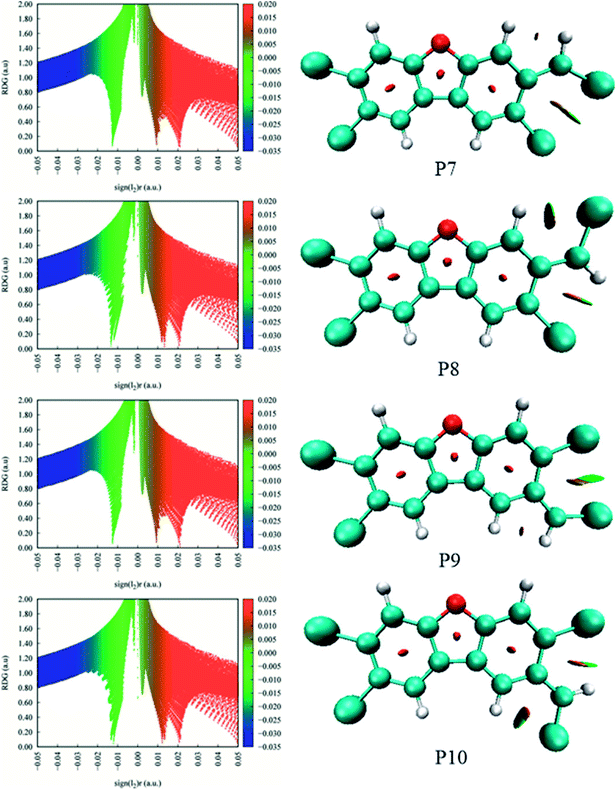
As shown in Fig. 7, the distributions of the unpaired electron in the products are different depending on the position of the inserted CH radical. According to the degree of the delocalization of the unpaired electron, the products can be divided into four groups, namely, (1) P6, (2) P7–P13, (3) P1, P4, and P5, (4) P2 and P3. In more details, for the most stable product P6, its single electron is distributed widely around the C atom of the inserted CH radical and its adjacent two rings. For the second group, the single electron is mainly distributed on the C atom of the inserted CH radical and its adjacent ring. As shown in Fig. 6, the stabilities of these products including P7–P13 are also similar to each other. Here, note that P8 is more stable than P7, which should be due to the favorable intramolecular H-bonds in P8. To further clarify this point, we have carried out the RDG analysis of P7 and P8. As displayed in Fig. 8, two intramolecular H-bonds H16⋯Cl21 and H23⋯Cl20 in P8 can be confirmed by the appearance of the corresponding spikes between H and Cl atoms. However, two repulsion interactions including the H16⋯H23 and Cl20⋯Cl21 atoms can be observed in P7. Similarly, the same phenomena can also be observed in P9 and P10. As for the third group including the products P1, P4, and P5, their single electrons are mainly distributed on the selected ring associated with the inserted CH radical. As for the forth group including the least stable products P2 and P3, the single electron is only localized on the C atom of the inserted CH radical. Obviously, the above analyses suggest that the stability of the products is mainly controlled by the distribution of the single electron overall, i.e., the wider the single electron distribution is, the more stable the product is.

Fig. 7 Spin density maps of the products. The isodensity contours are 0.005 electron per bohr³.

Fig. 8 RDG analyses for the products P7–P10.

3.2.2 The interconversion among products. Besides the interconversion among the initial intermediates mentioned above, as shown in Fig. 3, the different products can also be interconverted into each other. For example, for the following processes, i.e., (1) P1 → TS17 → P6, (2) P1 → TS29 → P12, (3) P2 → TS9 → P3, (4) P4 → TS30 → P13, (5) P5 → TS21 → P7, (6) P5 → TS22 → P8, (7) P7 → TS20 → P8, and (8) P9 → TS27 → P10, the enthalpy (Gibbs free energy) changes are −18.16(−17.74), −7.16(−6.92), −3.92(−3.62), −12.30(−11.96), −2.05(−2.38), −7.99(−8.02), −5.94(−5.64), and −5.93(−5.56) kcal mol⁻¹, respectively. So, all the above processes are exothermic and spontaneous reactions thermodynamically as can be seen from the negative values of the enthalpy and Gibbs free energy changes. At the same time, the energy barriers of the above interconversion processes are 129.47, 87.51, −0.30(0.32), 95.46, 83.89, 83.82, 6.51, and 4.96 kcal mol⁻¹, respectively, where the data in parentheses refer to the results without considering ZPVE corrections. Obviously, only the processes (3), (7), and (8) are feasible due to their low energy barriers kinetically. Particularly, the energy barrier of process (3) disappears after considering the ZPVE corrections, further suggesting the easy conversion from P2 to P3.

As presented in Table 2, for the formation processes of the products P1–P4, the corresponding energy barriers are no more than 4 kcal mol⁻¹, indicating that these reactions can occur easily. On the contrary, as for the products P5 and P6, they are difficult to be formed as can be seen from the high energy barriers, where the corresponding energy barriers are 50.93 and 129.47 kcal mol⁻¹, respectively. Similarly, the same is also true for the products P11–P13. As for the products P7–P10, the corresponding energy barriers ranging from 12.37 to 13.94 kcal mol⁻¹ are higher than those of the products P1–P4. Moreover, the initial intermediates IM9 and IM10 associated with the formation of P7–P10 are unfavorable thermodynamically. As a result, the formation of the products P7–P10 has no competitive with the P1–P4. In addition, given the fact that the product P2 is very easy to convert to P3 as mentioned above, we can say that P1, P3, and P4 should be the most favorable products of the title reaction.

3.3 Molecular dynamics analysis

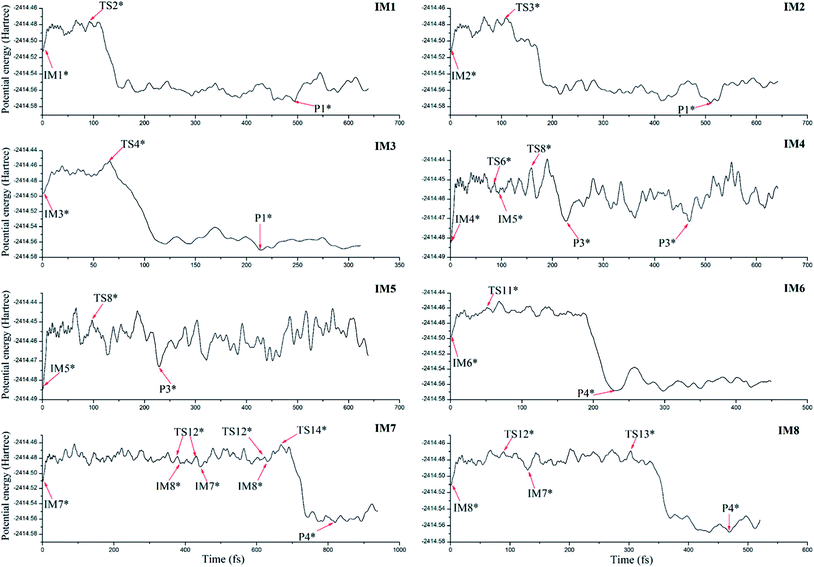
To further confirm the possibility of the formation of the dominant products and their dynamic stability, ab initio molecular dynamics has been performed on the basis of the optimized initial intermediates. Here, only the initial intermediates IM1-IM8 have been considered due to the low thermodynamic stability of the initial intermediates IM9 and IM10 as mentioned above.

As shown in Fig. 9, for the initial intermediates IM1, IM2, and IM3, they have been finally converted to product P1 at different time scales, where the corresponding transition states TS2, TS3, and TS4 can be observed during the dynamic processes. Similarly, for IM4 and IM5, they have been finally converted to product P3. Here, the conversion from IM4 to IM5 via TS6 has also been observed. As for IM6, IM7, and IM8, the product P4 has been obtained after the corresponding conversion. Therefore, the formed initial intermediates can be easily converted to the products P1, P3, and P4, which is also consistent with the above analyses.

Fig. 9 The changes of potential energy of the initial intermediates along with the simulation time, where asterisk denotes the geometry similar to the optimized intermediate, transition state, and product.

3.4 IR spectra and hyperfine coupling constants of the dominant products

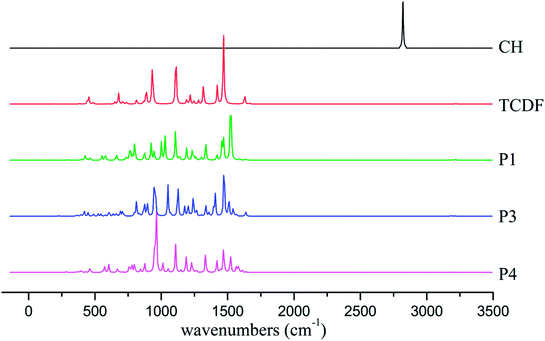
To provide useful information for the detection and identification of the products using IR and electron spin resonance (ESR) techniques, the IR spectra and the hyperfine coupling constants (hfcc's) of the dominant products including P1, P3, and P4 have been analyzed.

As shown in Fig. 10, the characteristic absorption peaks of the CH radical and TCDF appear at about 2821 and 1469 cm⁻¹, corresponding to the stretching vibration of the C–H bond and the rocking vibration of the C–H bond in the ring, respectively. However, the former C–H vibration disappears in the products. As for the latter, they can still be observed at about 1522 cm⁻¹ (P1), 1472 cm⁻¹ (P3), and 1470 cm⁻¹ (P4), respectively. Moreover, the IR absorption peaks of each product have their own characteristics. For example, for the product P1, a strong absorption peak could be observed at about 1107 cm⁻¹, corresponding to the rocking vibration of the C–H bond in the non-reactive ring. For the product P3, a strong absorption peak occurs at about 947 cm⁻¹, which mainly corresponds to the distortion vibration of the two rings. As for the product P4, its characteristic absorption peak appears at about 962 cm⁻¹, which mainly corresponds to the stretching vibration of the C–C bond in the reactive ring. Obviously, these different features of the IR spectra of the products can provide some help in the identification of them using the gas-phase vibrational spectrum experimentally.

Fig. 10 IR spectra of monomers and the dominant products.

In view of the fact that the products have short lifespan and high reactivity due to the existence of the single unpaired electron, so it is difficult to detect and characterize them experimentally. At present, the electron spin resonance (ESR) technique is one of the effective spectroscopic methods to detect free radicals via providing the hfcc's. In the case of lacking relevant experimental information, theoretical predictions are highly desirable. As shown in Table 4, depending on the specific products, all the results of the hfcc's are different in signs and values except for four chlorine atoms. For example, the hfcc's of ¹³C1 are 9.9 (P1), 1.2 (P3), and −8.1 G (P4), respectively. Especially, as for the C22 atom of the introduced CH radical, the hfcc is −3.0, 73.5, and 9.4 G in P1, P3, and P4, respectively. Obviously, the different hfcc results can be used to identify the different products experimentally.

Table 4 The calculated hyperfine coupling constants of the atoms in P1, P3, and P4^a

Atom numberings	Atom	P1	P3	P4
a All the units are in Gauss.
1	^13C	9.9	1.2	−8.1
2	^13C	−1.0	8.8	2.9
3	^13C	5.7	−1.1	2.6
4	^13C	−9.4	−9.7	−7.3
5	^13C	10.6	7.7	−10.7
6	^13C	−11.5	0.1	13.8
7	^13C	2.2	−0.4	1.8
8	^13C	−5.5	6.8	−4.3
9	^13C	−2.6	0.5	−2.2
10	^13C	2.8	0.6	2.2
11	^13C	3.8	−0.2	3.2
12	^13C	−3.5	1.0	−2.9
13	^17O	0.1	−0.5	0.1
14	^1H	−2.4	0.2	−2.0
15	^1H	−2.7	−0.4	−5.3
16	^1H	−9.9	0.3	3.1
17	^1H	0.8	−0.1	0.7
18	^35Cl	0.0	0.0	0.0
19	^35Cl	0.1	0.0	0.1
20	^35Cl	0.2	0.2	−0.1
21	^35Cl	−0.1	0.1	0.3
22	^13C	−3.0	73.5	9.4
23	^1H	−1.6	−8.8	−8.9

---

3.5 Substitution effects

To further validate the feasibility of the reactions between CH radical and other TCDF derivatives, the reactions of F- and Br-substituted TCDFs with CH radical have been investigated on the basis of the above reactions, where only the selected pathways associated with the dominant products P1, P3, and P4 have been considered. As displayed in Fig. 11, similar to the above reactions without substitution, the initial intermediates, transition states, and products involved in the reactions have also been located, where the relevant geometries before and after substitution were similar to each other. Moreover, as shown in Tables 1 and 2, the calculated thermodynamic and kinetic data, such as enthalpy changes, Gibbs free energy changes, and energy barriers are also similar to those before substitution. For example, the whole reaction processes are exothermic and spontaneous thermodynamically as can be seen from the negative enthalpy and Gibbs free energy changes. Meanwhile, each pathway has low energy barrier, which is no more than 5 kcal mol⁻¹. Therefore, similar to TCDF, its derivatives can also react with CH radical in the gas phase, resulting in the transformation of them in geometry and property. Certainly, relevant experiments are required to further confirm this point in the future.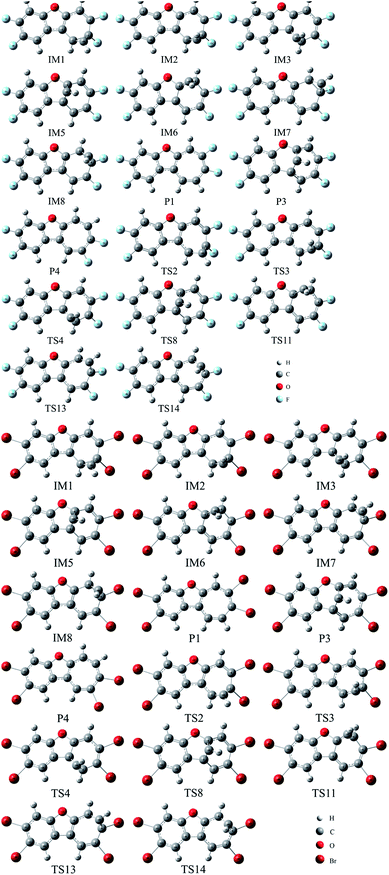

Fig. 11 The optimized initial intermediates (IM), transition states (TS), and the products in the reactions of F- and Br-substituted TCDFs with CH radical.

4. Conclusions

In this study, all of the possible reaction modes for the insertion of the CH radical into the C–X(X = C, Cl, H, O) bonds of TCDF have been systematically investigated employing B3LYP method in combination with the ab initio molecular dynamics. As a result, it was found that CH radical can react with TCDF via the insertion modes, i.e., an initial intermediate is formed firstly followed by the formation of a more stable product characterized by an expanded six- or seven-membered ring structure. Thermodynamically, the whole reaction processes are spontaneous and exothermic reactions and the thermodynamic stability of the products is controlled by the distribution of the single unpaired electron. Kinetically, the most favorable reaction channel is the insertion of the CH radical into the C–C bond except for the C atoms attached to the chlorine atom, producing the seven-membered ring compound. The dominant products have been further confirmed by the molecular dynamics. Moreover, the different distinct characteristics of IR and hyperfine coupling constants can provide some help in the detection and identification of the dominant products experimentally. In addition, similar to TCDF, the F- and Br-substituted TCDFs can also react with CH radical thermodynamically and kinetically. Expectedly, the present results can provide new insights into the transformation of TCDF and the potential role of CH radical in the atmosphere. Certainly, more extensive experiments are highly required to further confirm these computational results in the future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by National Natural Science Foundation of China (21577076, 21303093), Natural Science Foundation of Shandong Province (ZR2018MB020), and the Doctoral Foundation of Shandong Province (ZR2016BB20, ZR2017BB055).

References

1. L. L. Zou, Y. W. Ni, Y. Gao, F. M. Tang, J. Jin and J. P. Chen, Chemosphere, 2018, 195, 491–497.
2. E. N. Sappington, A. Balasubramani and H. S. Rifai, Chemosphere, 2015, 133, 82–89.
3. X. L. Wang, Y. W. Ni, H. J. Zhang, X. P. Zhang and J. P. Chen, Environ. Sci. Technol., 2012, 46, 12234–12240.
4. X. Wang, H. Zhang, Y. Ni, Q. Du, X. Zhang and J. Chen, Environ. Sci. Technol., 2014, 48, 4361–4367.
5. M. Salamanca, C. Chandia and A. Hernandez, Sci. Total Environ., 2016, 573, 1397–1405.
6. H. Dwyer and N. J. Themelis, Waste Manag., 2015, 46, 242–246.
7. N. V. Heeb, M. D. Rey, M. Zennegg, R. Haag, A. Wichser, P. Schmid, C. Seiler, P. Honegger, K. Zeyer, J. Mohn, S. Burki, Y. Zimmerli, J. Czerwinski and A. Mayer, Environ. Sci. Technol., 2015, 49, 9273–9279.
8. N. V. Heeb, M. Zennegg, R. Haag, A. Wichser, P. Schmid, C. Seiler, A. Ulrich, P. Honegger, K. Zeyer, L. Emmenegger, P. Bonsack, Y. Zimmerli, J. Czerwinski, M. Kasper and A. Mayer, Environ. Sci. Technol., 2013, 47, 6510–6517.
9. A. C. Hieke, R. Brinkmeyer, K. M. Yeager, K. Schindler, S. Zhang, C. Xu, P. Louchouarn and P. H. Santschi, Mar. Biotechnol., 2016, 18, 630–644.
10. A. Hidayat and S. Tachibana, Int. Biodeterior. Biodegrad., 2013, 77, 51–55.
11. M. Govindan and I. S. Moon, Chem. Eng. J., 2015, 272, 145–150.
12. N. Palanisami, S. J. Chung and I. S. Moon, J. Ind. Eng. Chem., 2015, 28, 28–31.
13. P. Liljelind, J. Unsworth, O. Maaskant and S. Marklund, Chemosphere, 2001, 42, 615–623.
14. E. Finocchio, G. Busca and M. Notaro, Appl. Catal., B, 2006, 62, 12–20.
15. T. Daikoku, M. Takemoto, Y. Yoshida, T. Okuda, Y. Takahashi, K. Ota, F. Tokuoka, A. T. Kawaguchi and K. Shiraki, Aerosol Air Qual. Res., 2015, 15, 1469–1484.
16. L. Y. Huang, G. J. Su, Y. X. Liu, L. W. Li, S. Liu, H. J. Lu and M. H. Zheng, RSC Adv., 2014, 4, 25453–25460.
17. M. F. Yu, X. Q. Lin, X. D. Li, T. Chen and J. H. Yan, Aerosol Air Qual. Res., 2016, 16, 2011–2022.
18. P. C. Hung, S. H. Chang, C. C. Ou-Yang and M. B. Chang, Chemosphere, 2016, 144, 50–58.
19. Y. Hajizadeh, J. A. Onwudili and P. T. Williams, Waste Manag., 2011, 31, 1194–1201.
20. A. Kawashima, M. Katayama, N. Matsumoto and K. Honda, Chemosphere, 2011, 83, 823–830.
21. K. Zhang, S. M. Sun and H. Zhang, RSC Adv., 2015, 5, 81153–81161.
22. X. M. Sun, C. X. Zhang, Y. Y. Zhao, J. Bai, Q. Z. Zhang and W. X. Wang, Environ. Sci. Technol., 2012, 46, 8148–8155.
23. C. X. Zhang, X. M. Sun, Y. S. Xu, C. S. Qi and J. H. Zhang, J. Environ. Chem. Eng., 2014, 2, 1098–1103.
24. W. X. Pan, Y. Y. Qi, R. X. Wang, Z. Han, D. J. Zhang and J. H. Zhan, Chemosphere, 2013, 91, 157–164.
25. Q. X. Zhou, Y. L. Yong, W. W. Ju, X. Y. Su, X. H. Li, C. Y. Wang and Z. B. Fu, Curr. Appl. Phys., 2018, 18, 61–67.
26. N. Love, R. N. Parthasarathy and S. R. Gollahalli, Int. J. Green Energy, 2011, 8, 113–120.
27. F. V. Tinaut, M. Reyes, B. Gimenez and J. V. Pastor, Energy Fuels, 2011, 25, 119–129.
28. K. McKee, M. A. Blitz, K. J. Hughes, M. J. Pilling, H. B. Qian, A. Taylor and P. W. Seakins, J. Phys. Chem. A, 2003, 107, 5710–5716.
29. P. Fleurat-Lessard, J. C. Rayez, A. Bergeat and J. C. Loison, Chem. Phys., 2002, 279, 87–99.
30. J. M. Ribeiro and A. M. Mebel, J. Phys. Chem. A, 2014, 118, 9080–9086.
31. J. M. Ribeiro and A. M. Mebel, Mol. Phys., 2015, 113, 1865–1872.
32. J. M. Ribeiro and A. M. Mebel, J. Phys. Chem. A, 2016, 120, 1800–1812.
33. J. M. Ribeiro and A. M. Mebel, Phys. Chem. Chem. Phys., 2017, 19, 14543–14554.
34. Y. Li, H. L. Liu, Z. J. Zhou, X. R. Huang and C. C. Sun, J. Phys. Chem. A, 2010, 114, 9496–9506.
35. A. J. Trevitt, M. B. Prendergast, F. Goulay, J. D. Savee, D. L Osborn, C. A. Taatjes and S. R. Leone, J. Phys. Chem. A, 2013, 117, 6450–6457.
36. F. Zhang, P. Maksyutenko and R. I. Kaiser, Phys. Chem. Chem. Phys., 2012, 14, 529–537.
37. F. Goulay, A. J. Trevitt, G. Meloni, T. M. Selby, D. L. Osborn, C. A. Taatjes, L. Vereecken and S. R. Leone, J. Am. Chem. Soc., 2009, 131, 993–1005.
38. J. C. Loison and A. Bergeat, Phys. Chem. Chem. Phys., 2009, 11, 655–664.
39. L. R. McCunn, B. L. FitzPatrick, M. J. Krisch, L. J. Butler, C. W. Liang and J. J. Lin, J. Chem. Phys., 2006, 125, 133306.
40. H. Thiesemann, J. MacNamara and C. A. Taatjes, J. Phys. Chem. A, 1997, 101, 1881–1886.
41. S. Soorkia, C. A. Taatjes, D. L. Osborn, T. M. Selby, A. J. Trevitt, K. R. Wilson and S. R. Leone, Phys. Chem. Chem. Phys., 2010, 12, 8750–8758.
42. J. F. Lockyear, O. Welz, J. D. Savee, F. Goulay, A. J. Trevitt, C. A. Taatjes, D. L. Osborn and S. R. Leone, J. Phys. Chem. A, 2013, 117, 11013–11026.
43. F. Goulay, C. Rebrion-Rowe, L. Biennier, S. D. Le Picard, A. Canosa and B. R. Rowe, J. Phys. Chem. A, 2006, 110, 3132–3137.
44. D. G. Johnson, M. A. Blitz and P. W. Seakins, Phys. Chem. Chem. Phys., 2000, 2, 2549–2553.
45. A. J. Trevitt and F. Goulay, Phys. Chem. Chem. Phys., 2016, 18, 5867–5882.
46. E. Mazarei and S. H. Mousavipour, J. Phys. Chem. A, 2017, 121, 8033–8047.
47. F. Goulay, A. J. Trevitt, J. D. Savee, J. Bouwman, D. L. Osborn, C. A. Taatjes, K. R. Wilson and S. R. Leone, J. Phys. Chem. A, 2012, 116, 6091–6106.
48. K. Xu, W. Wang, W. Wei, W. Feng, Q. Sun and P. Li, J. Phys. Chem. A, 2017, 121, 7236–7245.
49. C. Guo, W. Wang, W. Feng and P. Li, RSC Adv., 2017, 7, 12775–12782.
50. W. Wang, C. Guo, W. Feng, Q. Sun and P. Li, RSC Adv., 2017, 7, 32419–32426.
51. P. Li, W. Wang, Q. Sun, Z. Li, A. Du, S. Bi and Y. Zhao, ChemPhysChem, 2013, 14, 2737–2743.
52. P. Li, Z. Shen, W. Wang, Z. Ma, S. Bi, H. Sun and Y. Bu, Phys. Chem. Chem. Phys., 2010, 12, 5256–5267.
53. W. Feng, C. Ren, W. Wang, C. Guo, Q. Sun and P. Li, Theor. Chem. Acc., 2016, 135, 190.
54. W. Feng, C. Ren, W. Wang, C. Guo, Q. Sun and P. Li, RSC Adv., 2016, 6, 48099–48108.
55. W. Wang, X. Zhang, P. Li, Q. Sun, Z. Li, C. Ren and C. Guo, J. Phys. Chem. A, 2015, 119, 796–805.
56. P. Li, Z. Ma, W. Wang, Y. Zhai, H. Sun, S. Bi and Y. Bu, Phys. Chem. Chem. Phys., 2011, 13, 941–953.
57. P. Li, Z. Ma, W. Wang, R. Song, Y. Zhai, S. Bi, H. Sun and Y. Bu, Phys. Chem. Chem. Phys., 2011, 13, 5931–5939.
58. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
59. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
60. L. F. Pacios, J. Phys. Chem. A, 2004, 108, 1177–1188.
61. W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841.
62. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
63. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
64. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
65. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
66. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian, Inc., Wallingford CT, 2013.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra03046d

---