Space-filling open microfluidic channels designed to collect water droplets

Abstract

A flexible polymer film was coated with titanium oxide and a fluoroacrylate polymer to make the surface superhydrophobic and then patterned with superhydrophilic open microfluidic channels consisting of fractal branching structures. The lateral transport of liquid driven by the imbalance of the Laplace pressure in the flow channels with a width gradient allowed the collection of tiny aqueous droplets from the entire surface of the film at the converging point at the center within a second. The proposed fractal patterns were well-defined (i.e., mathematically determined in a unique manner) space-filling trees with only a few geometrical parameters. With the optimized geometrical parameters, the fluid volume collected to the film center (2.0 mm radius, 7.3% of total pattern area) reached 74% ± 9%, where the areal density of liquid was 12 times higher than that of an unpatterned surface.

---

Introduction

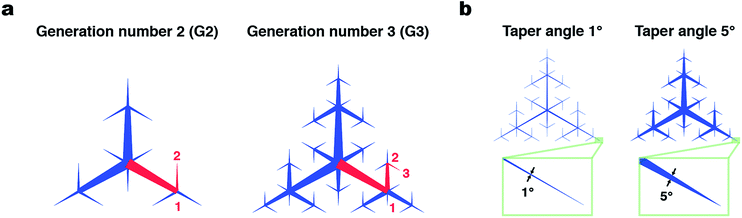
Techniques to harvest water from vapor and tiny droplets have been developed for use in dry areas such as deserts. In these techniques, vapor is condensed to form droplets on a substrate surface through elaborate microscopic wettability patterning,^1,2 the structure of which is often inspired by living organisms.^3–6 Another important element in water harvesting following vapor condensation is the collection of condensed droplets from a large area of substrate surface. Generally, gravity has been used to drive transfer of condensed droplets into a collection reservoir;^5–7 little attention has been paid to active long-range transport of water droplets.⁸ Recently, there has been progress in open microfluidics designed to directionally transport liquid on a surface by means of wettability and topography patterning.^9–12 Collection of tiny water droplets from a large surface area in a controlled manner can be a useful methodology for efficient collection and accumulation of aqueous analyte solutions. For example, perspiration is secreted from sweat glands on the skin surface, where it forms tiny droplets. Perspiration is useful for non-invasive sensing because it contains biomarkers such as lactate, potassium, and cortisol.¹³ A few pioneering studies on the efficient capture of perspiration have recently been published.^14–16 Mechanisms to efficiently collect droplets from a large surface area may allow more reliable sensing using perspiration, which is inherently present in small volumes.

Here, we develop a flexible plastic film with patterned surface wettability designed to collect tiny droplets from the entire film surface and accumulate them at a single point at the film center (Fig. 1). We use tapered superhydrophilic open microfluidic channels developed by the Megaridis group^5,6,17 to laterally transport droplets on the film surface driven by Laplace pressure imbalance. The channels on the film surface form branching patterns called space-filling trees that cover the entire surface area. The hyperbranched superhydrophilic channels have fractal (i.e., self-similar) triangular branching patterns with gradually narrowing width. The patterns are uniquely determined by two geometrical parameters: branching generation number G and taper angle α (Fig. 2); the side length of the outer triangle was fixed in this work. With this design, superhydrophilic channels cover the entire surface, which means that any droplet that makes contact with the surface has a high chance of being driven into the superhydrophilic channels and then the film center.

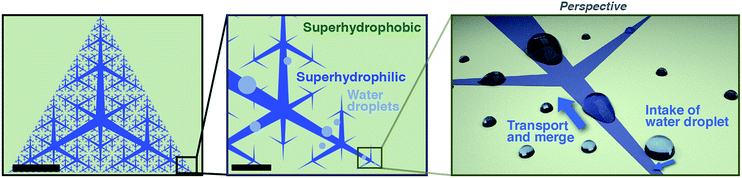Fig. 1 Design of space-filling open microfluidic channels (left and middle) and a schematic of droplet collection (right). Scale bars: 5 mm (left), 500 μm (middle).

Fig. 2 Geometrical parameters of the patterns. (a) Generation number G and (b) taper angle α.

Open tree-like hydrophilic microfluidic channels to collect droplets have recently been reported,⁸ but the present work differs from this previous study from a few aspects. First, the present study uses fractal space-filling patterns that cover the entire surface by nature and allow efficient water collection. Second, the pattern is automatically generated by recursive drawing, which enables extensive exploration of various patterns obtained by changing a few parameters; in comparison, the previous study used arbitrary handwriting of tree-shaped patterns and considerable effort was required to modify the pattern. Furthermore, our patterning method uses photolithography through a photomask, which has high throughput regardless of how complex the pattern is, unlike the direct laser writing used in the previous study.

Experimental

Materials

Anatase TiO₂ nanoparticles (<25 nm diameter) were purchased from Sigma-Aldrich Japan (Tokyo, Japan). Capstone® ST-100 was kindly gifted by DuPont (Tokyo, Japan). Polyethylene terephthalate (PET) films were kindly gifted by Teijin Limited (Tokyo, Japan). All other reagents and materials were purchased from Sigma-Aldrich Japan and Wako Chemicals (Osaka, Japan) and used as received.

Superhydrophobic coating

TiO₂ nanoparticles (1.5 g) and Capstone ST-100 (2.5 g) were added to ethanol (17.7 mL) and then sonicated by a tip sonicator (Branson, Sonifier 250) for 2 min at room temperature to form a suspension. The suspension was used for spraying within one day to avoid precipitate formation. The suspension was sprayed onto the surface of a PET film with a thickness of 75 μm by manually moving a spray nozzle (Anest Iwata, LPH-50-102G) above the film. The coated film was then dried in an oven at 60 °C overnight to obtain superhydrophobic coating with a thickness of 16.7 ± 2.8 (standard deviation) μm.

Superhydrophilic patterning of the coated PET film

Various space-filling and other patterns were generated by a custom script (https://github.com/hirokai/SpaceFilling) and drawn onto a 2 inch emulsion mask (Konica Minolta, HV1-18). Following standard development procedures, desired photomasks were produced. The photomask was placed on top of the coated PET film prepared above, and UV light with a wavelength of 365 nm was irradiated onto the film through the photomask for 30 min using a UV lamp (Hamamatsu, model L9588-01A) located 21.4 cm from the film surface, in which the UV intensity was 74 mW cm⁻².

Droplet collection experiment

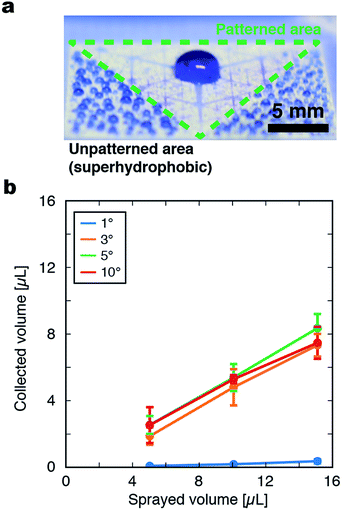
To measure the collection efficiency of the film surfaces by optical microscopy, colorless or blue water droplets were sprayed on the surface of each film through a spray nozzle (Everoy Spray Nozzles, MMA50) from above with a distance of 4 cm for 5 s with an air pressure of 0.02 MPa. The arithmetic and Sauter mean diameters of droplets sprayed from the nozzle were estimated to be 8 μm and 17 μm. The collected mass of liquid was imaged by an optical microscope (Keyence, VW-6000) with 30× magnification. The outline of the liquid was manually fitted with a Bezier curve and the internal volume was calculated by approximation to radially symmetric shapes using the equation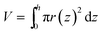 , where z is the distance from the film surface, h is the height of the droplet, and r(z) is the radius of the droplet at a distance of z (Fig. S1†). The collected volume was defined as the volume within a 2 mm radius from the center, and the collection efficiency was defined as the ratio of the collected volume and the total volume sprayed on the patterned area. Three samples were measured for every set of conditions. Observation of the dynamics of the droplet transport with high time resolution was conducted by a high-speed microscope (Keyence, VW-9000) with 1000 frames per s during spraying blue water droplets from a spray.

To image the surface morphology of the collected liquid, aqueous droplets containing opaque red paint (to increase reflection to that needed for the imaging) were sprayed on the film surface through a spray nozzle (Everoy Spray Nozzles, MMA50) for 5 s with an air pressure of 0.02 MPa. The height map of the liquid was obtained by a laser scanner (Keyence, VR-3000) with 12× magnification. The baseline of the height map was subtracted, and the radial density profile was defined as the relative areal density with respect to the radius of a triangular strip (Fig. S10†), which was calculated by a custom Python script with NumPy, SciPy, and scikit-image packages. One or two samples were measured for every set of conditions.

Results and discussion

Effects of superhydrophobic coating and UV irradiation on the wettability of the PET film surface

As a material for wettability patterning, we chose a mixture of titanium(IV) oxide (TiO₂) anatase nanoparticles and fluoroacrylate polymer (DuPont Capstone® ST-100) according to a previous report.¹⁷ The mixture of TiO₂ nanoparticles and Capstone ST-100 was intrinsically superhydrophobic, and spray coating of the mixture on a film surface made the film superhydrophobic. When the coated film was irradiated with ultraviolet (UV) light, the surface dramatically changed to become superhydrophilic. This switching of wettability enabled fine spatial patterning of surface wettability with high contrast by simply irradiating UV light through a photomask.

We first examined the effects of coating with TiO₂ and Capstone ST-100 and subsequent UV irradiation on the surface wettability of a PET film. The contact angle of a water droplet on the initial PET film surface was 74°. After the mixture of TiO₂ and Capstone ST-100 suspended in ethanol was sprayed on the PET film, the contact angle of a water droplet on the surface increased to 156°, which indicated that the PET film surface became superhydrophobic. After irradiation with UV light for 10 min, the contact angle dramatically decreased to 7°, which indicated the surface became superhydrophilic. These changes were consistent with those in a previous report.¹⁷ When UV light was irradiated on the superhydrophobic coating, the TiO₂ nanoparticles facilitated photocatalytic cleavage of the superhydrophobic fluoroalkyl chain of Capstone ST-100 (ref. 18). In addition, the surface of the TiO₂ nanoparticles became superhydrophilic. These made the irradiated surface of the mixture superhydrophilic.

Collection of droplets by space-filling superhydrophilic channels on the superhydrophobic surface

Hyperbranching superhydrophilic channels were patterned on the superhydrophobic film by irradiation of the film with UV light through a photomask. To investigate the behavior of water droplets on the film, microdroplets were sprayed on the film by a spray gun at a rate of 0.60 μL cm⁻² s⁻¹ (Fig. S2†). When droplets were sprayed on an unpatterned superhydrophobic surface, droplets on the film surface remained separated as spheres with a diameter of a few hundred micrometers. When sprayed on a coated film uniformly irradiated with UV light, the sprayed droplets spread all over the surface and formed a flat water film. In contrast, when droplets were sprayed on a film patterned with space-filling superhydrophilic channels, they immediately merged into a large coalesced droplet at the center of the pattern (Fig. 3a). A possible mechanism for such droplet collection by the pattern is as follows. Droplets sprayed on the superhydrophilic regions immediately spread on the surface and merge with each other, forming a large, flat, and continuous liquid phase that fills the width of the superhydrophilic channels. In addition, droplets sprayed outside the superhydrophilic regions may also become trapped in a superhydrophilic channel once they become large enough. The merged mass of liquid is then laterally transported toward the film center driven by the Laplace pressure imbalance inside the tapered superhydrophilic channels. During lateral transport, the liquid masses repeatedly merge with each other at the branch nodes.

Fig. 3 (a) Image of a water droplet accumulated at the center of the pattern after spraying with tiny droplets. (b) Dependence of the collected volume of a droplet at the film center (within a 2 mm radius) on the total volume of sprayed liquid. Patterns with G = 6 with α = 1°, 3°, 5°, and 10° were used. Three samples were measured for every set of conditions.

The relationship between the volume of collected liquid at the film center and total volume of sprayed droplets that was experimentally measured was consistent with the above mechanism; when the total volume of droplets sprayed on the surface was increased, the collected amount at the film center increased monotonically (Fig. 3b). The droplet transport process by the pattern with G = 6 and α = 5° was observed by a high-speed microscope (Fig. S3, ESI Movies 1 and 2†). The transient pinning of liquid masses at the nodes of branching paths was observed, followed by their disappearance when they merged into the larger liquid mass at another node closer to the film center. This transient accumulation at the node may suggest that sufficient wetting of the connecting superhydrophilic path or the accumulation of the droplet at the node to a certain extent is necessary for the droplet transport toward the center of the pattern.

The effects of geometric parameters of the pattern on water collection behaviors

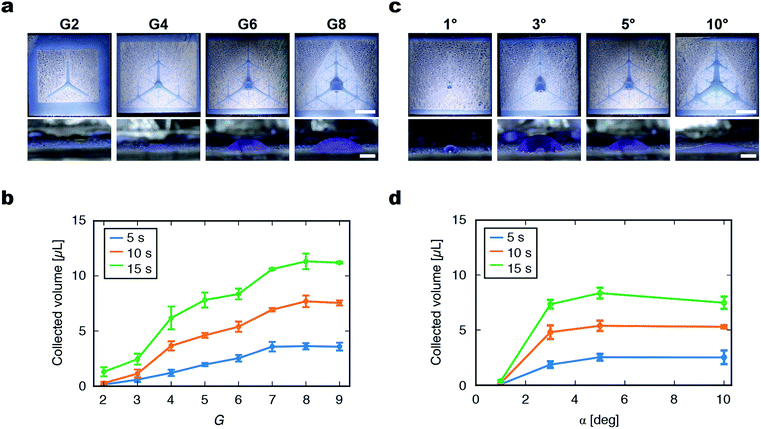
The fractal superhydrophilic patterns used in this study can be dramatically varied by modulating their G and α, which may lead to substantial changes of the water collection properties of the patterned films. From purely geometrical considerations, when G is increased by one, the maximum lateral distance between a point on the film and superhydrophilic channels (d_x,y in Fig. S4†) halves (Fig. S5 and S6†). Therefore, the chance of a droplet being trapped in a superhydrophilic channel increases with G. The path length, which is the distance that the droplet travels to reach the film center, increases with G, but the maximum path length converges to the distance between the center and vertex of a triangle. The area fraction of the superhydrophilic area increases linearly with G. Interestingly, the characteristics of fractal patterns make it possible to efficiently place superhydrophilic channels all over the film surface (i.e., max (d_x,y) decreases exponentially with G) while maintaining sufficiently low area fraction and path length.

To experimentally investigate the effects of geometrical parameters on droplet collection performance, the degree of accumulation of the liquid at the film center was measured for patterned films with various G and α. As G of the pattern was raised from 2 to 8, all of the patterns displayed the lateral transport and accumulation of droplets at the center of the pattern (Fig. 4a). As G increased, the collected droplet at the film center became larger, although the collected droplet was flatter with a larger radius. To quantitatively evaluate the behavior of droplet collection by the patterned film, the volume ratio of the collected liquid at the film center (within a 2 mm radius) to the total sprayed droplets was calculated. The collected liquid volume increased with the increase of G and plateaued at G = 7, 8, and 9. The plateauing for G > 7 could be attributed to the fine superhydrophilic patterns around the film center causing the lateral spreading of the droplet that spans overlapping closed paths (Fig. S7†). The advantage of the fractal space-filling patterning was demonstrated by comparing with the pattern with tree-like hierarchical structures with arbitrary branching⁶ (Fig. S8†). Although these two kinds of patterns appear similar, the collection efficiency of non-fractal tree-like structures was 25% ± 7% and significantly lower than the best collection efficiency obtained with the fractal space-filling patterns (74% ± 9% for G = 8 and α = 5°). This indicates that the automatically generated fractal patterns can cover the surface effectively thus collect droplets efficiently, which is difficult to achieve by manual design of tree-like patterns with low degree of branching (Table S1†).

Fig. 4 Collection of water droplets by various patterns. (a) Photographs of the top (top row) and side (bottom row) of collected droplets after spraying for 10 s on patterned films with various G and α = 5°. (b) The collected volume of liquid by patterns with various G and α = 5°. (c) Photographs of the top (top row) and side (bottom row) of collected droplets after spraying for 10 s on patterns with G = 6 and various α. (d) The collected volume of liquid by patterns with G = 6 and various α. Collected volume was defined as the volume of liquid within a 2 mm radius from the center of the pattern. The spray rate was 0.60 μL cm⁻² s⁻¹ for all measurements, and three samples were measured for every set of conditions. Spraying times in (b) and (d) were 5 s (blue), 10 s (orange), and 15 s (green). Scale bars in (a) and (c) are 5 mm (top) and 1 mm (bottom). The color balance of side view photographs was adjusted to clearly visualize the droplets.

Surface wetting of the superhydrophilic channel is necessary for lateral transport to occur. From this viewpoint, we hypothesized that a smaller superhydrophilic area with smaller α would be more desirable to maximize the collected volume. When α was varied, the maximum collected volume was obtained at α = 3° (Fig. 4d). When α was too small (1°), lateral transport of the solution was poor. This is probably because the Laplace pressure was not sufficient to drive droplet movement. When α = 10°, the lateral transport of droplets was observed, but the liquid mass was flat and some liquid was trapped at the film periphery, which resulted in the plateauing or slight decrease of collection efficiency.

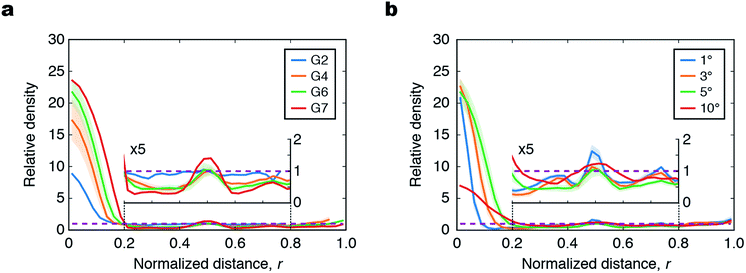
In addition to the collection efficiencies evaluated above, we also measured 2D height maps of the liquid at the film center by a 3D surface profiler (Fig. S9†), and calculated the radial density profile to quantify the distribution of liquid with respect to the normalized distance from the center (r) (Fig. 5 and S10†). If the liquid was spread uniformly over the entire surface, the density profile would be a horizontal line with a relative density of unity (purple dashed lines in Fig. 5); the deviation from this horizontal line indicates how the liquid is accumulated around the center and branching nodes of the film. As G increased from 2 to 7, the density increased at the center (r < 0.2) and first branching node (r = 0.5), whereas that at the other parts decreased (Fig. 5a). This indicates that the patterns with higher G collect more liquid from a larger area than that of patterns with lower G because of their more widespread superhydrophilic channels. The more pronounced accumulation at the center for the patterns with higher G is consistent with the results of microscopy observation in Fig. 4b.

Fig. 5 Radial density profiles of the surface of various patterns with collected liquid. (a) Patterns with various generation numbers G and a taper angle α of 5°. (b) Patterns with G = 6 with various α. The sample number N was 1 or 2, and the shaded regions indicate the standard error of the mean (for the conditions with N = 2). Purple dashed lines represent uniform distribution.

When different α were compared, the pattern with α = 5° showed the maximum accumulation of liquid at the film center (Fig. 5b). For the pattern with α = 1°, the volume of liquid trapped at the branching nodes (at r = 0.5, 0.75, and 0.375) was larger than those of the patterns with α = 3° and 5°. This is because the Laplace pressure imbalance induced by the pattern with α = 1° was insufficient to transport droplets from the branching nodes toward the film center. When α was increased to 10°, the peaks at the film center and branching nodes became broader and the accumulation at the film center was markedly attenuated. This is because the liquid spread over the wide area of the superhydrophilic channels. For the laser scanning measurements, commercial aqueous red paint was diluted in water to form droplets that reflected laser light. The surface tension of this liquid was lower (37.0 ± 2.0 mN m⁻¹; the average and standard deviation of five samples measured by the pendant drop method) than that of the water with aqueous blue ink used in Fig. 4 (75.2 ± 5.8 mN m⁻¹), which led to reduced spreading of the liquid to the superhydrophilic channel and the slightly inferior droplet transport compared to that of water for the patterns with a small value of α.

Although the present work focused on the collection of sprayed droplets, comparison of liquid volume and droplet size between the conducted experiment and actual human perspiration may give an insight into potential applicability of the present work to perspiration collection on skin. Perspiration is secreted from sweat pores typically with a density of 200 pores per cm², and the rate of perspiration is 1.3 μL min⁻¹ cm⁻² at a high perspiration state.¹⁹ In terms of volume, spraying for 5 s in our experiment corresponds to the perspiration on skin for 2 min. In terms of the droplet size, the average diameter of sprayed droplets in our experiment was in the order of 10 μm, and the diameter of a perspiration droplet grows to more than 10 μm at the sweat pore after 0.01 s of perspiration. The experimental conditions in which the developed wettability-patterned films were tested are relevant to perspiration on skin, which suggests that the developed film may be potentially useful for perspiration collection on the skin within a few minutes.

Conclusions

In the present study, we demonstrated the ability of fractal branching of hierarchical wettability patterns to collect droplets in a directional manner. The volume of liquid collected at the film center (2.0 mm radius, 7.3% of the total pattern area) reached 74% ± 9% of the total volume of sprayed droplets for the pattern with G = 8 and α = 5°, which corresponds to an areal density of liquid that is 12 times higher than that of an unpatterned surface. The water-collecting films developed in the present work represent an important step forward to collecting small volumes of aqueous solution from skin using 2D open microfluidics. The developed films are potentially useful for the collection and sensing of perspiration, although there are several challenges that remain to be addressed, such as placing the film on skin with an appropriate gap and draining the collected perspiration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partly supported by the Center of Innovation Program (COI-Stream) and Creation of Innovation Centers for Advanced Interdisciplinary Research Area Program from the Japan Science and Technology Agency (JST), Regional Innovation Strategy Support Program “Knowledge-based Medical Device Cluster/Miyagi Area”, and Grant-in-Aid for Scientific Research A (25246016), Challenging Exploratory Research (15K13315), and Grant-in-Aid for Young Scientists (B) (17K14096) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. We thank Natasha Lundin, PhD, from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.

Notes and references

1. R. P. Garrod, L. G. Harris, W. C. E. Schofield, J. McGettrick, L. J. Ward, D. O. H. Teare and J. P. S. Badyal, Langmuir, 2007, 23, 689.
2. Y. Hou, M. Yu, X. Chen, Z. Wang and S. Yao, ACS Nano, 2015, 9, 71.
3. L. Zhai, M. C. Berg, F. Ç. Cebeci, Y. Kim, J. M. Milwid, M. F. Rubner and R. E. Cohen, Nano Lett., 2006, 6, 1213.
4. H. Zhu, Z. Guo and W. Liu, Chem. Commun., 2016, 52, 3863.
5. A. Ghosh, S. Beaini, B. J. Zhang, R. Ganguly and C. M. Megaridis, Langmuir, 2014, 30, 13103.
6. P. S. Mahapatra, A. Ghosh, R. Ganguly and C. M. Megaridis, Int. J. Heat Mass Transfer, 2016, 92, 877.
7. H. Bai, L. Wang, J. Ju, R. Sun, Y. Zheng and L. Jiang, Adv. Mater., 2014, 26, 5025.
8. M. Wang, Q. Liu, H. Zhang, C. Wang, L. Wang, B. Xiang, Y. Fan, C. F. Guo and S. Ruan, ACS Appl. Mater. Interfaces, 2017, 9, 29248.
9. N. M. Oliveira, A. I. Neto, W. Song and J. F. Mano, Appl. Phys. Express, 2010, 3, 085205.
10. H. Gau, S. Herminghaus, P. Lenz and R. Lipowsky, Science, 1999, 283, 46.
11. C.-H. Hsu, C. Chen and A. Folch, Lab Chip, 2004, 4, 420.
12. R. Seemann, M. Brinkmann, E. J. Kramer, F. F. Lange and R. Lipowsky, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 1848.
13. Z. Sonner, E. Wilder, J. Heikenfeld, G. Kasting, F. Beyette, D. Swaile, F. Sherman, J. Joyce, J. Hagen, N. Kelley-Loughnane and R. Naik, Biomicrofluidics, 2015, 9, 031301.
14. R. Peng, Z. Sonner, A. Hauke, E. Wilder, J. Kasting, T. Gaillard, D. Swaille, F. Sherman, X. Mao, J. Hagen, R. Murdock and J. Heikenfeld, Lab Chip, 2016, 16, 4415.
15. A. Koh, D. Kang, Y. Xue, S. Lee, R. M. Pielak, J. Kim, T. Hwang, S. Min, A. Banks, P. Bastien, M. C. Manco, L. Wang, K. R. Ammann, K.-I. Jang, P. Won, S. Han, R. Ghaffari, U. Paik, M. J. Slepian, G. Balooch, Y. Huang and J. A. Rogers, Sci. Transl. Med., 2016, 8, 366ra165.
16. J. Choi, D. Kang, S. Han, S. B. Kim and J. A. Rogers, Adv. Healthcare Mater., 2017, 6, 1601355.
17. A. Ghosh, R. Ganguly, T. M. Schutzius and C. M. Megaridis, Lab Chip, 2014, 14, 1538.
18. K. Tadanaga, J. Morinaga, A. Matsuda and T. Minami, Chem. Mater., 2000, 12, 590.
19. S. D. Henkin, P. L. Sehl and F. Meyer, Int. J. Sports Physiol. Perform., 2010, 5, 359–366.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra02655f

---