Open Access Article
Open Access ArticleElectrical and thermal properties of silver nanowire fabricated on a flexible substrate by two-beam laser direct writing for designing a thermometer†
Gui-Cang He *a,
Heng Lub,
Xian-Zi Dongb,
Yong-Liang Zhangc,
Jie Liub,
Chang-Qing Xie*a and
Zhen-Sheng Zhao*b
*a,
Heng Lub,
Xian-Zi Dongb,
Yong-Liang Zhangc,
Jie Liub,
Chang-Qing Xie*a and
Zhen-Sheng Zhao*b
aKey Laboratory of Microelectronic Devices & Integrated Technology, Institute of Microelectronics, Chinese Academy of Sciences, Beijing 100029, P. R. China. E-mail: heguicang@ime.ac.cn; xiechangqing@ime.ac.cn
bLaboratory of Organic NanoPhotonics, CAS Key Laboratory of Bio-Inspired Materials and Interfacial Science, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, No. 29, Zhongguancun East Road, Beijing, 100190, P. R. China. E-mail: zhaozhsh@mail.ipc.ac.cn
cDepartment of Applied Physics, The Hong Kong Polytechnic University, Hong Kong, P. R. China
First published on 11th July 2018
Abstract
Accurate knowledge of electrical conductivity and thermal conductivity temperature dependence plays a crucial role in the design of a thermometer. Here, by using a two-beam laser direct writing system, an individual silver nanowire (AgNW) with well-defined dimensions is fabricated on a polyethylene terephthalate (PET) substrate. The temperature dependence of the resistivity of the fabricated AgNW is measured ranging from 10 to 300 K, and fitted with the Bloch–Grüneisen formula. The residual resistivity ((1.62 ± 0.20) × 10−7 Ω m) of the AgNW is larger than that of the bulk material (1 × 10−11 Ω m). The electron–phonon coupling constant of the AgNW is (1.08 ± 0.13) × 10−7 Ω m, which is larger than that of the bulk silver (5.24 × 10−8 Ω m). Moreover, the Debye temperature of the AgNW is 199.30 K and is lower than that of the bulk silver (235 K). The Lorenz number of the fabricated AgNW is found to decrease as the temperature increases. Besides, the Lorenz number (2.66 × 10−7 W Ω K−2) is larger than the Sommerfeld value (2.44 × 10−8 W Ω K−2) at room temperature. The measurement results allow one to design a thermometer in the temperature range 40–300 K. The flexibility of the AgNW is also excellent, and the resistance increase of the AgNW is only 2.58% when the AgNW bending about 1000 times with a bending radius of 1 mm.
1 Introduction
It is well known that the electrical conductivity and thermal conductivity of metallic nanomaterials is much better compared to non-metallic nanomaterials. The applications of metallic nanomaterial under different temperature conditions rely on an accurate knowledge of the electrical conductivity and thermal conductivity temperature dependence. According to Wiedemann–Franz law, the ratio of the conductivities for heat and electricity of pure bulk metals is proportional to the absolute temperature; the proportionality coefficient of the ratio is called Lorenz number. The Lorenz number is equal to the Sommerfeld value (2.44 × 10−8 W Ω K−2) if the electron gas is highly degenerate, and if the electron mean free path is the same for electrical and thermal conductivities.1 To investigate the Lorenz number of the metal nanowire could verify validity of the Wiedemann–Franz law in metallic nanomaterials. Recently, the temperature dependence of resistance of the metallic nanowires has attracted considerable interest.2–4 The metallic nanowire plays an important role in applications as metallic interconnects in electronic devices. In fact, a systematical investigation on the temperature dependence of the metallic nanowire’s resistance can not only facilitate a comprehensive understanding of the fundamental physics, such as electron–phonon interaction and structural scattering process inside the nanowire, but also provide both quantitative and qualitative characterization of future electronic and thermal devices based on metallic nanowires. Besides, designing nanoscale devices with special performance based on the property of the metallic nanowire could open a new way for metallic nanowire application.Much effort has been devoted to research of thermoelectric properties of metallic nanowires. For example, Cheng et al.5 characterized the thermal and electrical transport of silver nanowire (AgNW) at temperatures down to 35 K. They found that the Lorenz number of the AgNW (5.2 × 10−8 Ω W K−2 at 292 K) is much larger than that of bulk one (2.44 × 10−8 Ω W K−2 at 292 K), and decreases with temperature decreasing due to phonon-assisted electron energy transfer across grain boundaries.6 Ou et al. investigated the thermal conductivity and electrical resistivity of nickel nanowire in the temperature range from 15 K to 300 K.7 It was found that the temperature dependence of the thermal conductivity and the Lorenz number differs from the bulk case. Kojda et al. studied the temperature dependent thermoelectric and structural properties of AgNW in the temperature range of 1.4 K to room temperature, and observed the transition from diffusive transport to quasi ballistic one dimensional transport in a single metallic nanowire.8 The thermoelectric properties of metallic nanowire have been studied extensively. However, evidence for the validity of the Wiedemann–Franz law in metallic nanowires or thin films remains inconclusive.9 Metallic nanowire fabricated by different methods may have different inner structures, and electrical and thermal properties of metallic nanowires determined by not only the material alone, but also its size.10,11 It is very important to investigate the electrical and thermal properties of metallic nanowires for future applications.
In this work, AgNWs were fabricated by a two-beam laser direct writing system on a polyethylene terephthalate (PET) substrate under optimized experimental conditions. Then the temperature dependence of resistance of the AgNW was measured in the temperature range of 10 K to 300 K, and fitted with the Bloch–Grüneisen formula. The residue resistance, electron–phonon coupling constant and Debye temperature of the AgNW have been obtained from the fitting data, respectively. The temperature dependence of the Lorenz number of the AgNW was investigated in the temperature range of 40 K to 300 K. It was found that the Lorenz number decreased with increasing temperature, and it is larger than the Sommerfeld value at room temperature due to the high resistivity and the high defect concentration of the AgNW. Based on the linear trend of changes in AgNW resistance in the range of 40 K to 300 K, a thermometer has been designed. We also discuss the temperature error of the thermometer due to the measured resistance error of the AgNW. Besides, the AgNW on the PET substrate exhibits excellent flexibility.
2 Experimental section
Preparation of materials
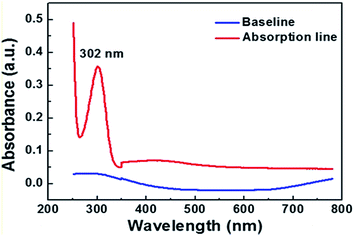
Materials for photoreduction consisted of diamine silver ions (DSI) as the silver source and a nitrogen-atom containing alkyl carboxylate (n-decanoylsarcosine sodium, NDSS) as the surfactant.12 Typically, 0.0340 g of AgNO3 was dissolved in 1.8 mL of water, and 0.2 mL of ammonia (25 wt%) water was added to it, so a solution of DSI was formed. Then, 0.0525 g of nitrogen-atom containing alkyl carboxylate (n-decanoylsarcosine sodium, NDSS) was dissolved in 1 mL water and mixed with 1 mL diammine silver ions solution. The silver ion aqua consists of 1 mL of DSI solution (0.05 M) and 1 mL of NDSS solution (0.099 M). We also have fabricated AgNW with different concentration of AgNO3 solution, but it did not generate a AgNW with compact and smooth morphology under other concentrations of AgNO3 solution (the detailed information is illustrated in the ESI 1†).Fig. 1 shows the optical absorption spectra of a mixture of DSI and NDSS solutions, a peak at 302 nm appears on the absorption band. This absorption band with a peak at 302 nm originates from the AgNO3, as an absorption band with a peak at 302 nm is found in the spectra of the DSI and pure AgNO3 solution (Fig. S2a and b†). But the absorption band does not appear in the corresponding wavelength range of a pure ammonia solution and a pure NDSS solution (Fig. S2c and d†). Besides, the remarkable absorption band is not observed at the laser wavelength of 780 nm and 442 nm in all spectra of solution. This implies that the photo-induced reduction reaction was associated with exciting the chemicals by a multiphoton absorption process.13,14
The two-beam laser direct writing system
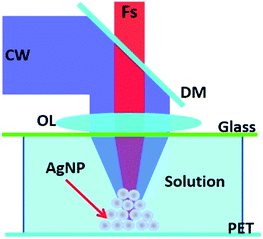
A two-beam laser direct writing system was used to fabricate the AgNWs on a PET substrate.14 As shown in Fig. 2, a femtosecond (fs) laser (Tsunami, Spectra-Physics) and a continuous wave (CW) laser (He-Cd laser, IK5751I-G) are overlapped together by a dichroic mirror (DM) and focused by an oil objective lens (OL) (Olympus, N.A. = 1.42, × 60) into the sample. The silver ion aqua is sandwiched between a glass and a PET substrate. The fs laser with a centre wavelength of 780 nm, a pulse width of 120 fs, and a repetition rate of 80 MHz is used as the excitation source to induce Ag nanoparticles from the sample. The CW laser with a wavelength of 442 nm (He-Cd laser, IK5751I-G) works as optical tweezers15,16 to make the Ag nanoparticles gather together by an optical trapping force.17,18 The beam radius of pulse laser and CW laser is 3 mm and 5 mm, respectively. For the Gaussian beams of pulse laser and CW laser, the distances where the light intensity falls to 1/e of the value in the center point are about 1.5 mm and 2.5 mm, respectively (the calculation method is illustrated in the ESI 3†).The AgNWs were generated at the focuses of the two lasers. The AgNWs could be fabricated on a PET substrate by a two-beam laser with the movement of a piezo stage.
A AgNW with compact and smooth surface can be fabricated on a PET substrate by a two-beam laser direct writing system under certain experimental conditions. The power density at the focus point of the pulse laser and CW laser are 6.45 × 1011 mW m−2 and 8.41 × 1012 mW m−2, respectively. The scanning speed (v) of the laser focus is 0.003 mm s−1. The scanning electron microscope (SEM, QUANTA FEG 250 USA) image and atomic force microscope (AFM, Bruker Multimode 8) image of the AgNWs that fabricated using this method are shown in Fig. S3.† The actual cross section of the AgNW is a triangle. The average width of the AgNW is 210 nm with the height of 92 nm. It must be mentioned that a single pulse laser can hardly fabricate a continuous AgNW on a PET substrate. If all the other process parameters are fixed, the single pulse laser can induce only some discrete Ag nanoparticles, and the two-beam laser can fabricate the compact and smooth AgNWs (detailed information is illustrated in the ESI 5†).
The resistance of AgNW measurement
The electrical measurement were performed in a vacuum environment, using a Keilthley 4200-SCS semiconductor system and the CRX-4K cryogenic probe station in a clean and shielded box in dark conditions. Two silver electrodes were deposited on the both ends of the AgNW by radio frequency magnetron sputtering (QPrep 400-BASE). Two golden conical probes were placed in contact with two deposited electrodes, then applying impressed voltage to detect the corresponding current.As shown in Fig. 3, the AgNW was fabricated on a PET substrate under certain experimental conditions (Pf = 6.45 × 1011 mW m−2, Pc = 8.41 × 1012 mW m−2, v = 0.003 mm s−1). The two silver electrodes were deposited on both ends of the AgNW by radio frequency magnetron sputtering. The distance (l) between two electrodes is 80 μm. The AFM image of the AgNW is shown in Fig. 3(b). The cross-section area (S) of the AgNW can be obtained from it. The measured I–V curve of the AgNW is shown in Fig. 3(c). The resistance (R) of the AgNW is obtained by the fitting line of the experimental values. The resistivity of the AgNW is calculated from the equation ρ = RS/L. In order to accurately calculate the resistivity of the AgNW, we chose three positions on the AgNW to obtain the cross section. The cross section of the AgNW is shaped like a triangle, the cross-sectional area can be approximated as a triangular area (Fig. S5†). We calculated resistivity of the AgNW using average area of the three triangulars at the different positions on the AgNW. The resistivity ((2.01 ± 0.25) × 10−7 Ω m) of AgNW fabricated by our method is lower than that of AgNW fabricated by femtosecond laser direct writing (2.31 × 10−7 Ω m),19 solution-based controlled ink jetting (2.61 × 10−6–5.76 × 10−7 Ω m)20 and ice-templating assembly method (∼4.65 × 10−4 Ω m).21 This indicates that the electric conductivity of the AgNW has been enhanced under the present experimental conditions. The CW beam of our method is acting as tweezers, which could strongly focuses the Ag nanoparticles to form the compact nanowires with a smooth surface. The nanowire with compact and smooth morphology would greatly reduce the effect of the surfaces and grain scattering on the resistivity of the nanowire. Thus, the resistivity of the AgNW fabricated by the two-beam laser direct writing system is lower than others. Materials with nanometric dimensions exhibit higher electrical resistivity due to additional scattering centers for the conduction electrons, mainly from surfaces and grain boundaries.22,23 Therefore, the resistivity of the AgNW fabricated by a two-beam laser direct writing system is still larger than that of the bulk silver (1.59 × 10−7 Ω m) at room temperature.
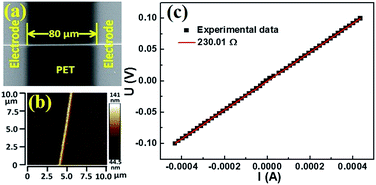 | ||
| Fig. 3 Measured resistance of the AgNW. (a) SEM image of the AgNW. (b) AFM image of the AgNW. (c) The AgNW I–V curve. | ||
3 Results and discussion
Electrical property
In order to investigate the variation on changes of the AgNW resistance with temperature, the resistance of the AgNW was measured in the temperature range from 10 K to 300 K. Here, we discuss the properties of the AgNW when its temperature was below 300 K. The AgNW was fabricated on a PET flexible substrate. If the temperature is very high, the substrate will melt and the AgNW may be destroyed. As shown in Fig. 4, the resistance of the AgNW hardly changes with the decreasing temperature when its temperature was below 20 K. Thus, we investigated the properties of the AgNW in the temperature range from 300 K to 10 K. In a nonmagnetic metallic crystalline solid, the temperature dependence of the resistance arises mainly from the electron–phonon interaction and can be explained in the framework of the Boltzmann transport theory using the Bloch–Grüneisen formula:24
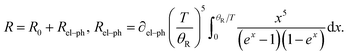 | (1) |
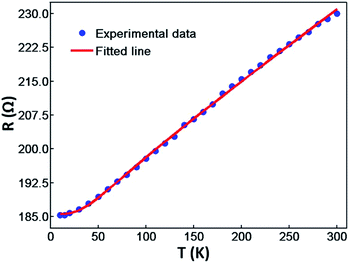 | ||
| Fig. 4 The temperature dependent electrical resistance of the AgNW and the fitted curve with the Bloch–Grüneisen formula. | ||
The measured resistances of the AgNW are fitted with respect to eqn (1), as shown in Fig. 4. The resistance fitting data are in good agreement with the measured data of the AgNW resistance. This indicates the AgNW fabricated by a two-beam laser direct writing system is a typical good metal. The residue resistance, Debye temperature and electron–phonon coupling constant of the AgNW can be obtained from the fitting data. The residue resistance results from impurities, grain boundary scatterings, surface scatterings of the electrons. Structural morphology of a composite always has direct influence on the charge transport mechanism.25 The residual resistivity ((1.62 ± 0.20) × 10−7 Ω m) of the AgNW is larger than that of the bulk material (1 × 10−11 Ω m).5 This is due to the AgNW being made up by Ag nanoparticles with a size of 20 nm.12 Moreover, NDSS molecules used as the surfactant in the silver ion aqua still remain in the AgNW.26 Consequently, the impurity, grain boundary and surface scattering of the electrons in the AgNW would be enhanced.
The electron–phonon coupling constant of the AgNW is (1.08 ± 0.13) × 10−7 Ω m, and it is greater than the electron–phonon coupling constant of the bulk silver (5.24 × 10−8 Ω m).2 This indicates the phonon electron collision frequency is higher and the energy exchange between the phonon and electron is much more frequent.27 The Debye temperature of the AgNW is 199.30 K and it is lower than the Debye temperature of the bulk silver (235 K). The reduced Debye temperature results from phonon softening due to grain boundary and surface scattering of the electrons in the AgNW. The atoms at the surface of the AgNW missing bonds result in the change of the vibration amplitude and the vibration frequency, and subsequently decrease the Debye temperature. Moreover, grain boundary and point defects, also can soften phonons and contribute to the decrease of the Debye temperature. Similar phenomenon is also observed in gold, platinum, copper, silver nanowires or nanofilms.28,29
Thermal property
Metallic nanowires are widely used in large-scale integrated circuits as interconnecting wires. A deep understanding of the mechanism of heat transport in AgNW is of great importance to the development of microelectronic industry. The relationship between the electrical resistance and the electrical current’s square is linear (Fig. 5(a)). Thus, the effect of thermal convection and radiation can be neglected, the transfer model has been built. The thermal conductivity of the AgNW can be expressed as:5
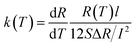 | (2) |
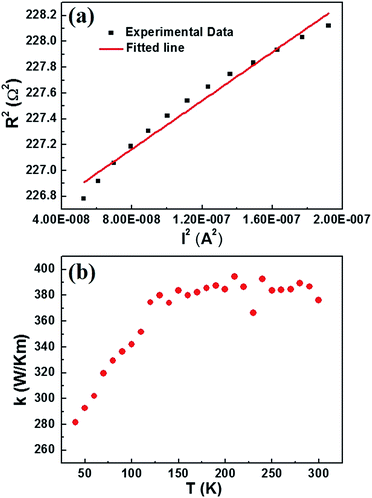 | ||
| Fig. 5 (a) The linear relationship between the electrical resistance and the electrical current’s square at a temperature of 290 K. (b) The temperature dependent thermal conductivity of the AgNW. | ||
In Fig. 5(b), the thermal conductivity of the AgNW is plotted as a function of temperature. The thermal conductivity of the AgNW increases with increasing temperature in the range of 30 K to 130 K, and the conductivity is relatively stable in the temperature range from 130 K to 300 K. This phenomenon has also been observed in nickel nanowires.6
According to the Wiedemann–Franz law, the Lorenz number of the metal is equal to Sommerfeld value (2.44 × 10−8 W Ω K−2). If the temperature is not very low (about more than 200 K), Lorenz number is a constant and has nothing to do with the kinds of the metal. But some research found that the Lorenz number of the metallic nanowire is changed with temperature.3,7 Here, the Lorenz number of the AgNW fabricated by a two-beam laser direct writing system is investigated. The Lorenz number is given by8
| L(T) = ρ(T)k(T)/T. | (3) |
The Lorenz number of the AgNW as a function of temperature is plotted in Fig. 6. The Lorenz number depends on the defect concentration, which can be expressed by the fraction R0/Rel–ph.8,9 Because the defect concentration is very high (R0/Rel–ph ≈ 4), the Lorenz number of the AgNW decreases with increasing temperature. This phenomenon has been observed in platinum and gold nanowires,30 and gold nanofilm.31 indicating that the Lorenz number is not a constant and the Wiedemann–Franz law is no longer valid in nanomaterial.32,33
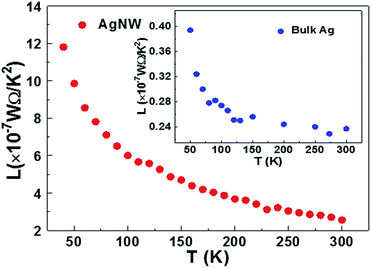 | ||
| Fig. 6 The temperature dependence of the Lorenz number of the AgNW (inset is the temperature dependence of the Lorenz number of the bulk silver). | ||
In order to compare the Lorenz number of AgNW and bulk Ag with the changing temperature, the Lorenz number of the bulk Ag was calculated according to eqn (3) (detailed information is illustrated in the ESI 7†). As shown in Fig. 4, at temperatures lower than 200 K, the Lorenz numbers of AgNW and bulk silver have the same trends, and the Lorenz number decreased sharply with increasing temperature. At temperatures higher than 200 K, the Lorenz number of AgNW decreased slowly with increasing temperatures. The Lorenz number of the bulk silver slightly varies with temperature, and it’s very close to the Sommerfeld value (2.44 × 10−8 W Ω K−2). The Lorenz number of AgNW at 290 K (2.66 × 10−7 W Ω K−2) is larger than the Sommerfeld value (2.44 × 10−8 W Ω K−2). The much larger Lorenz numbers are also observed in gold and platinum nanofilms of other work.30 This indicates that the thermal electron mean free path is larger than the electrical mean free path. That is because this value includes the contribution of the phonon-assisted electron energy transfer through the grain boundaries.5 In fact, the electron scattering at the boundaries has different effects on the energy transport for thermal conductivity and momentum transport for electrical conductivity.9
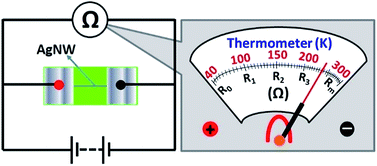
Thermometer designing
Similar to other nanowires,2,26 the resistance of the AgNW fabricated by the two-beam laser direct writing system linearly varied with the temperature in range of 40 K to 300 K. Therefore, a thermometer was designed based on this property. The environmental temperature can be determined through measuring the resistance of the AgNW at different temperatures, if the relationship between the AgNW resistance and the temperature is obtained. A schematic diagram of the thermometer is shown in Fig. 7. The temperature scale on the thermometer is determined by the change of resistance to temperature.To investigate the temperature error of the designed thermometer and the AgNW resistance accuracy with the temperature, the resistance of the AgNW was measured with decreasing and increasing temperatures in the temperature range between 40 K and 300 K, respectively. As shown in Fig. 8, the resistance changes linearly with the temperature variation. The temperature of the thermometer is determined by 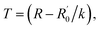 here, R is the measured resistance of the AgNW,
here, R is the measured resistance of the AgNW, 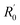 and k are the intercept and the slope of the fitted line. The slopes of the fitted lines of the AgNW resistance dependence, on decrease and increase in temperature, are 0.1294 ± 0.0010 and 0.1231 ± 0.0009, respectively. As shown in Fig. 8, the AgNW resistance error of the two fitted lines increased with increasing temperature. Correspondingly, the maximum error of the thermometer temperature is about 15 K at 300 K, the minimum error is about 7 K at 40 K. The resistance of the AgNW was measured using a Keilthley 4200-SCS semiconductor system and the CRX-4K cryogenic probe station in a clean and shielded box in the dark condition. Due to the thermal expansion and contraction of the golden probes of CRX-4K cryogenic probe station, the probes positions had to be changed while measuring the AgNW resistances at different temperature. Under certain temperature, the measured resistances are different if the probes were moved to different positions on the electrodes. The main source of error comes from the change in position of the probes contacting the two electrodes on both ends of the AgNW. AgNWs are usually not stable in air due to its oxidation. In order to prolong its shelf life and the repeatability of this thermometer, the AgNW should be covered by polydimethylsiloxane (PDMS). The PDMS can protect the AgNW and avoid its oxidation. Besides, the flexibility of the AgNW will be kept, because the flexibility of PDMS is superior to the PET substrate of AgNW.
and k are the intercept and the slope of the fitted line. The slopes of the fitted lines of the AgNW resistance dependence, on decrease and increase in temperature, are 0.1294 ± 0.0010 and 0.1231 ± 0.0009, respectively. As shown in Fig. 8, the AgNW resistance error of the two fitted lines increased with increasing temperature. Correspondingly, the maximum error of the thermometer temperature is about 15 K at 300 K, the minimum error is about 7 K at 40 K. The resistance of the AgNW was measured using a Keilthley 4200-SCS semiconductor system and the CRX-4K cryogenic probe station in a clean and shielded box in the dark condition. Due to the thermal expansion and contraction of the golden probes of CRX-4K cryogenic probe station, the probes positions had to be changed while measuring the AgNW resistances at different temperature. Under certain temperature, the measured resistances are different if the probes were moved to different positions on the electrodes. The main source of error comes from the change in position of the probes contacting the two electrodes on both ends of the AgNW. AgNWs are usually not stable in air due to its oxidation. In order to prolong its shelf life and the repeatability of this thermometer, the AgNW should be covered by polydimethylsiloxane (PDMS). The PDMS can protect the AgNW and avoid its oxidation. Besides, the flexibility of the AgNW will be kept, because the flexibility of PDMS is superior to the PET substrate of AgNW.
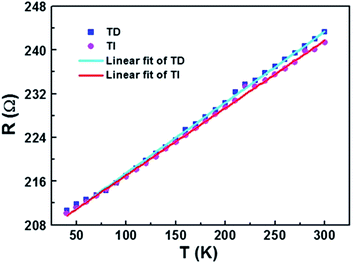 | ||
| Fig. 8 The measured resistances and the fitted lines of the AgNW changed with decreasing (TD, ■ —) and increasing (TI, ● —) temperature. | ||
Conventionally, a thermistor is used to fabricate a traditional resistance thermometer. An indicating instrument connects the thermistor by a metal wire, which is encapsulated in glass. But the core component of our designed thermometer is a AgNW, which is on a flexible PET substrate. Thus, our designed thermometer can be exploited and used to monitor the temperature variation on a micro/nano scale. It is also robust due to the flexibility of the PET substrate.
Flexibility of AgNW
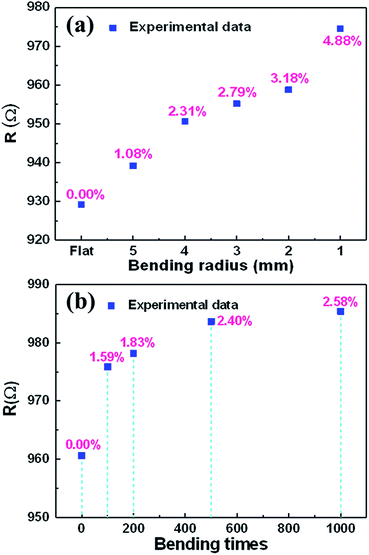
AgNWs are common conducting materials for fabrication of flexible electronics.34 The resistance stability of the AgNW with different mechanical bending radius and bending times is very important for application in flexible electronics. The resistance of the AgNW under different bending radii was measured, shown in Fig. 9(a). Under different bending statuses, the AgNW on the PET substrate exhibited a slight increase in resistance. The resistance increased only 4.88%, when the bending radii decreased down to 1 mm. Fig. 9(b) shows the changes in relative resistances of the AgNW with the bending times, revealing a negligible increasing (2.58%) during 1000 bending cycles with the bending radius of 1 mm. Besides, the I–V behavior of the AgNW under all different bending statuses exhibited a similar linear increase of the current when the sweeping voltage increased, indicating good ohm contact among AgNPs in the AgNW (Fig. S6†). Thus, the flexibility of the AgNW fabricated on a PET substrate by a two-beam laser direct writing system is excellent.4 Conclusions
In conclusion, an individual AgNW has been fabricated by the two-beam laser direct writing system on the PET substrate, and further the electrical conductivity and thermal conductivity were comprehensively investigated. The temperature dependence on resistance of the AgNW was measured in the temperature range of 10–300 K and fitted with the Bloch–Grüneisen formula. It is found that the residual resistivity ((1.62 ± 0.20) × 10−7 Ω m) and electron–phonon coupling constant ((1.08 ± 0.13) × 10−7 Ω m) of the AgNW are much larger than those of the bulk material. The Debye temperature of the AgNW is 199.30 K, which is lower than that of the bulk silver (235 K). This indicates that the size and the structure of the AgNW affect the transport of the electrons and phonons in the AgNW. The Lorenz number of the AgNW decreases with increasing temperature. At room temperature, it (2.66 × 10−7 W Ω K−2) is larger than Sommerfeld value (2.44 × 10−8 W Ω K−2). This may be due to the fact that electron scattering at the boundaries has different effects on the energy transport for thermal conductivity and momentum transport for electrical conductivity. Based on the linear trend of changes in resistance of the AgNW in temperature range from 40 to 300 K, a thermometer was designed. The maximum and minimum temperature error of the thermometer are about 15 K at 300 K and 7 K at 40 K, respectively. The flexibility of the AgNW fabricated on a PET substrate by a two-beam laser direct writing system is excellent. The resistance increased by only 2.58% when the AgNW was bent about 1000 times with a bending radius of 1 mm.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the financial support of the National Key research and Development Program of China (Grant No. 2016YFA0200501).Notes and references
- G. S. Kumar and G. Prasad, J. Mater. Sci., 1993, 28, 4261–4272 CrossRef.
- A. Bid, A. Bora and A. K. Raychaudhuri, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035426 CrossRef.
- F. Völklein, H. Reith, T. W. Cornelius, M. Rauber and R. Neumann, Nanotechnology, 2009, 20, 325706 CrossRef PubMed.
- S. Pud, A. Kisner, M. Heggen, D. Belaineh, R. Temirov, U. Simon, A. Offenhäusse, Y. Mourzina and S. Vitusevich, Small, 2013, 9, 846–852 CrossRef PubMed.
- Z. Cheng, L. Liu, S. Xu, M. Lu and X. Wang, Sci. Rep., 2015, 5, 10718 CrossRef PubMed.
- A. D. Wang, L. Jiang, X. W. Li, Y. Liu, X. Z. Dong, L. T. Qu, X. M. Duan and Y. F. Lu, Adv. Mater., 2015, 27, 6238–6243 CrossRef PubMed.
- M. N. Ou, T. J. Yang, S. R. Harutyunyan, Y. Y. Chen, C. D. Chen and S. J. Lai, Appl. Phys. Lett., 2008, 92, 063101 CrossRef.
- D. Kojda, R. Mitdank, M. Handwerg, A. Mogilatenko, M. Albrecht, Z. Wang, J. Ruhhammer, M. Kroener, P. Woias and S. F. Fischer, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024302 CrossRef.
- T. M. Tritt, Thermal Conductivity: Theory, Properties, and Applications, Springer, New York, 2004, p. 170 Search PubMed.
- W. Wu, S. H. Brongersma, M. V. Hove and K. Maex, Appl. Phys. Lett., 2004, 84, 2838–2840 CrossRef.
- W. Steinhögl, G. Schindler, G. Steinlesberger and M. Engelhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 075414 CrossRef.
- Y. Y. Cao, N. Takeyasu, T. Tanaka, X. M. Duan and S. Kawata, Small, 2009, 5, 1144–1148 Search PubMed.
- G. C. He, M. L. Zheng, X. Z. Dong, F. Jin, J. Liu, X. M. Duan and Z. S. Zhao, Sci. Rep., 2017, 7, 41757 CrossRef PubMed.
- G. C. He, M. L. Zheng, X. Z. Dong, J. Liu, F. Jin and Z. S. Zhao, Appl. Phys. Lett., 2017, 110, 263113 CrossRef.
- L. Novotny, R. X. Bian and X. S. Xie, Phys. Rev. Lett., 1997, 29, 645–648 CrossRef.
- G. C. He, M. L. Zheng, X. Z. Dong, J. Liu, X. M. Duan and Z. S. Zhao, AIP Adv., 2017, 7, 035203 CrossRef.
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156–159 CrossRef.
- K. Svoboda and S. M. Block, Opt. Lett., 1994, 19, 930–932 CrossRef PubMed.
- B. B. Xu, D. D. Zhang, X. Q. Liu, L. Wang, W. W. Xu, M. Haraguchi and A. W. Li, Opt. Lett., 2014, 39, 434–437 CrossRef PubMed.
- Z. Zhang, X. Zhang, Z. Xin, M. Deng, Y. Wen and Y. Song, Adv. Mater., 2013, 25, 6714–6718 CrossRef PubMed.
- H. L. Gao, L. Xu, F. Long, Z. Pan, Y. X. Du, Y. Lu, J. Ge and S. H. Yu, Angew. Chem., Int. Ed., 2014, 53, 4561–4566 CrossRef PubMed.
- H. Marom, J. Mullin and M. Eizenberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 045411 CrossRef.
- T. Zhou and D. Gall, Phys. Rev. B, 2018, 97, 165406 CrossRef.
- P. James and B. Bailey, in Solid-State Physics Introduction to the Theory, Springer-Verlag Berlin Heidelberg, Heidelberg, Germany, 2007, Ch. 4, pp. 214–265 Search PubMed.
- A. Ghosh, M. Miaha, C. Majumdera, S. Baga, D. Chakravortyb and S. K. Saha, Nanoscale, 2018, 10, 5539–5549 RSC.
- B. B. Xu, H. Xia, L. G. Niu, Y. L. Zhang, K. Sun, Q. D. Chen, Y. Xu, Z. Q. Lv, Z. H. Li, H. Misawa and H. B. Sun, Small, 2010, 6, 1762–1766 CrossRef PubMed.
- M. I. Kaganov, I. M. Lifshitz and L. V. Tanatarov, J. Exp. Theor. Phys, 1957, 4, 173–178 Search PubMed.
- W. Zhang, S. H. Brongersma and Z. Li, J. Appl. Phys., 2007, 101, 06703 Search PubMed.
- S. Kim, H. Suhl and I. K. Schuller, Phys. Rev. Lett., 1997, 78, 322–325 CrossRef.
- H. D. Wang, J. H. Liu, X. Zhang and K. Takahashi, Int. J. Heat Mass Transfer, 2013, 66, 585–591 CrossRef.
- H. Lin, S. Xu, X. Wang and N. Mei, Small, 2013, 9, 2585–2594 CrossRef PubMed.
- I. S. Beloborodov, A. V. Lopatin, F. W. J. Hekking, R. Fazio and V. M. Vinokur, Europhys. Lett., 2005, 69, 435–441 CrossRef.
- H. D. Wang, J. H. Liu, X. Zhang, Z. Y. Guo and K. Takahashi, Heat Mass Transfer, 2011, 47, 893–898 CrossRef.
- S. Chen, M. Su, C. Zhang, M. Gao, B. Bao, Q. Yang, B. Su and Y. Song, Adv. Mater., 2015, 27, 3928–3933 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra03280g |
| This journal is © The Royal Society of Chemistry 2018 |