DOI:
10.1039/C8RA03900C
(Paper)
RSC Adv., 2018,
8, 27900-27918
Theoretical-computational modeling of charge transfer and intersystem crossing reactions in complex chemical systems†
Received
7th May 2018
, Accepted 23rd July 2018
First published on 6th August 2018
Abstract
In this paper we present a theoretical-computational methodology specifically aimed at describing processes involving internal conversion or intersystem crossing, from atomistic (semiclassical) simulations and, hence, very suitable for treating complex atomic-molecular systems. The core of the presented approach is the evaluation of the diabatic perturbed energy surfaces of a portion of the whole system, treated at the quantum level and therefore preventively selected, in semi-classical interaction with the atomic-molecular environment. Subsequently, the estimation of the coupling between the diabatic surfaces and the inclusion of the obtained observables within a properly designed kinetic model allows the reconstruction of the whole phenomenology directly comparable to the experimental (typically kinetic) data. Application to two systems has demonstrated that the proposed approach can represent a valuable tool, somewhat complementary to other methods based on explicit quantum-dynamical approaches, for the theoretical-computational investigations of large and complex atomic-molecular systems.
1 Introduction
The Born–Oppenheimer (BO) approximation, i.e. the separation of electronic and nuclear degrees of freedom and the consequent possible use of classical physics to model the nuclear motion, has always dominated our mental representation of the chemical processes. However it is well known that the success of BO approximation for the quantitative resolution of whatever problem concerning electronic structure or chemical dynamics is limited to such phenomena in which the coupling between nuclear and electronic subsystems, i.e. non-adiabatic coupling, can be considered as negligible. These phenomena are usually termed as adiabatic because they can be considered as determined by the motion of nuclei on a single (electronic) potential energy surface (PES) with no crossing with any other PES. The deviation from adiabaticity is anything but uncommon in chemistry and the introduction of corrections beyond the BO approximation become in these cases essential.1–3 As a matter of fact typical possibly non-BO phenomena such as Charge-Transfer (CT), energy transfer or spin transitions (Intersystem Crossing, ISC) play a key role in many of the processes occurring, for example, in biological systems or material science4–11 and hence their modeling is of great intellectual and practical relevance. Nowadays a number of elegant theories and efficient algorithms are available for studying in great detail such effects in the dynamics of small to medium-sized molecular systems12–27 both in the gas-phase and even taking into account coupling with external baths (see for example28 and references therein cited). However the modeling of non-BO effects in complex molecular systems at atomistic level, e.g. reactions in solution, are still very challenging even though, because of their appeal, several procedures have been proposed in the last years either based on the Marcus theory or Fermi golden rule29–31 or involving more advanced procedures32–47 In this context, particularly inspired by approaches taking into account the dynamical effects of the perturbing environment,48 including mixed quantum-classical (QM/MM) methods based on the surface-hopping procedure,49–52 we have recently proposed a theoretical-computational methodology which makes use of Molecular Dynamics (MD) simulations and the Perturbed Matrix Method (PMM),54,55 for evaluating the possible crossing between different perturbed diabatic energy surfaces in large-sized atomic-molecular systems.53 Such a methodology, hereafter termed as MD-PMM, is based on the evaluation, at each step of a MD simulation, of the perturbed eigenstates (e.g. electronic) of a pre-selected species (hereafter termed as Quantum Center, QC) in semi-classical interaction with the atomistic environment (e.g. the solvent). In this respect MD-PMM, should be perceived as somewhat complementary to the already cited procedures designed for non-BO processes as relies in the extended phase-space sampling of the whole system, allowing the modeling of atomic-molecular systems whose complexity, far beyond the limitations of explicit quantum-dynamical approaches, is an essential and indispensable ingredient for the reliability of the final result. All the applications carried out so far56–58 have been characterized by two common features. Firstly, all the investigated processes have been limited to Electron Transfer (ET) reactions, i.e. CT reactions formally involving a complete donor to acceptor electron transfer, characterized by donor and acceptor species which can be treated as electronically independent (i.e. independent QCs), at least as far as the evaluation of their energy is concerned. In all these cases we have factorized the donor–acceptor couple states, hence termed as diabatic, as the product of the donor and acceptor perturbed eigenstates obtained by MD-PMM either fixing the exchanging charge in the donor or in the acceptor moiety.53 Secondly, in all the above applications we have systematically assumed purely adiabatic behaviours, i.e. processes characterized by an instantaneous quantum relaxation on the adiabatic state (the BO Hamiltonian eigenstate), without addressing the possible dynamical effects leading to diabatic transitions. In this study we extend our approach to explicitly estimate the possible diabatic behaviour by means of the method proposed in the 30's of the last century by Landau, Zener and Stueckelberg59–61 which represents an efficient approximation to model the quantum dynamics of chemical systems possibly undergoing non-BO behaviour, i.e. when the BO Hamiltonian eigenstates are very close in energy, avoiding the use of non-adiabatic coupling. Moreover, in the present paper we no longer assume CT reactions with electronic independent donor and acceptor,53 extending the kinetic model to be used and addressing more thoroughly the issues of the definition and role of the diabatic states and the productive intermediate (i.e. the transition region, vide infra). Compared to other QM/MM similar methodologies based on the Landau–Zener or related approaches,62,63 our method is based on three peculiar aspects: (i) a diabatic rather than an adiabatic representation of the relevant electronic states is involved; (ii) an extended, in principle exhaustive, QC-environment phase-space sampling for the reactive events can be achieved with virtually no limitations in the definition of the perturbation environment; (iii) the reactive events statistics obtained is used to construct a complete master equation for the reaction kinetics allowing to fully reproduce the experimentally observed process. Two case studies are presented in this paper. In the first application we have studied the photoinduced CT reaction of the DMN(4)DCNE in tetrahydrofurane (THF), where DMN stands for 1,4-dimethoxynaphthalene and DCNE stands for 1,2-dicyanoethylene We will hereafter refer to this species as simply DMN. (see Fig. 1). In the experiment of transient absorption spectroscopy,64–66 DMN is irradiated at 308 nm and prepared into a localized excited state which then undergoes a unimolecular charge transfer process with a time-constant of 360 fs in THF as schematically reported in Fig. 2. In the second application we have tested the reliability of our approach for a photoinduced ISC reaction, namely the singlet-triplet transition in fluorenilydene (FL, see Fig. 3) in solution.67,68 In the related experiment the singlet FL is generated by the photodetachment of N2 moiety from 9-diazofluorene (FL-N2) and shows a solvent dependent ISC rate characterized by a time-constant of 440 ps in acetonitrile (ACN) and 88 ps in apolar medium (cyclohexane). In both the investigated cases, despite the utilized approximations required for a numerical implementation of the theoretical method, our approach reveals rather accurate in reproducing the observed kinetics.
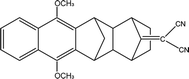 |
| | Fig. 1 Chemical Structure of DMN. | |
 |
| | Fig. 2 Schematic view of the photo-induced charge transfer reaction in DMN. | |
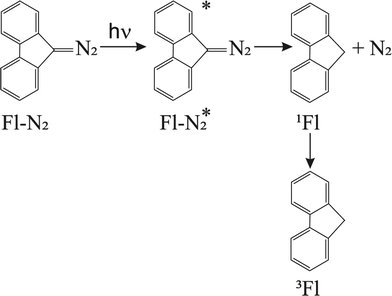 |
| | Fig. 3 Reaction scheme for the photogeneration of singlet FL and subsequent unimolecular decay into triplet FL. | |
2 Theory
2.1 General considerations
Non covalent CT or ISC reactions (i.e. CT or ISC reactions not involving any covalent bond disruption/formation) comprise a large variety of processes which, although all characterized by a large variation of a quantum property/observable ideally corresponding to a complete electron-transfer from a donor (D) to an acceptor (A) group for the former or to the complete spin transition for the latter, can involve rather different mechanisms thus possibly requiring different modeling approaches. In fact, such reactions must be considered as a sudden and dramatic change of such a property/observable of the reactive system, as provided by any kind of time-dependent perturbation inducing the exchange of the electronic distribution/spin state in two (first neighbour in energy) Hamiltonian eigenstates, typically occurring within tiny perturbation regions (the transition regions) where such eigenstates are close in energy. However, according to the type of time-dependent perturbation (i.e. the semiclassical perturbation) and vibronic states involved, the reaction inherent mechanism is different.
It is now necessary to introduce a set of definitions/assumptions to be used:
• As usual we assume that we can properly divide the simulated system into the QC, where the reaction occurs and that needs to be treated at quantum mechanical level and its environment, perturbing the QC quantum states, which we treat at semiclassical atomistic level.
• With QC adiabatic states we define the true Hamiltonian eigenstates of the perturbed QC: either the electronic eigenstates (adiabatic electronic states) or the vibronic eigenstates (adiabatic vibronic states) possibly including the effects of the nuclei-electron coupling (non-adiabatic coupling) which become non-negligible when the adiabatic electronic states are degenerate or quasi-degenerate.
• With QC diabatic states we define the Hamiltonian eigenstates (either the electronic eigenstates or the vibronic BO eigenstates) of the perturbed QC as obtained constraining the electron distribution or the spin state to be fixed in either the reactant (R) or the product (P) chemical condition, according to the choice of the R and P chemical species made to describe properly the reaction. Moreover, we always assume for the diabatic states the corresponding non-adiabatic coupling being (approximately) negligible.
• We assume that each possible reactive event can be properly described by two QC adiabatic states which are virtually indistinguishable from the corresponding diabatic states except within tiny perturbation regions, i.e. the transition regions (TR's) including the crossing of the diabatic energy surfaces (conical intersection), where each adiabatic state is a mixture of the diabatic ones and the reaction event occurs (i.e. the adiabatic states can be expressed as linear combinations of the two diabatic states, thus allowing to treat each reactive event within the reduced two-dimensional subspace defined by the diabatic states, see Fig. 4). We always consider that outside the transition regions the statistical ensemble for the reaction (the reactive ensemble) can be thought as constructed by reactive trajectories with the QC dynamical quantum state coinciding with a given adiabatic state and hence virtually identical to either the R or P QC diabatic state. Therefore, for each trajectory of the reactive ensemble representative of e.g. the R → P reaction, the QC is always in the R state when entering the TR (i.e. at the beginning of the transition process) and in either the R or P state when exiting the TR (i.e. when the transition process is completed) and thus the dynamics of the reactive ensemble can be properly described by usual chemical kinetics equations for the diabatic states interconversion (i.e. we consider the QC-environment system as a quantum dissipative system within the Markoff approximation69–71). Only within the TR's we need to consider the explicit quantum dynamics of each reactive trajectory as within such limited perturbation regions the Markoff approximation is typically inapplicable and the QC quantum state dynamics possibly involves significant mixing of the diabatic/adiabatic states.
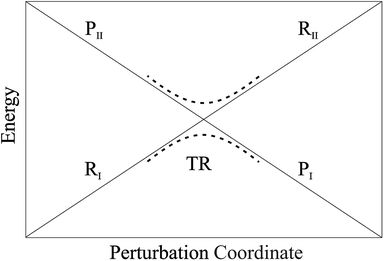 |
| | Fig. 4 Schematic picture of the diabatic (solid lines) and adiabatic (dashed lines) energy surfaces as a function of the perturbation coordinate, the latter representing the environment perturbing field (i.e. providing the QC-environment interaction) as well as the QC semi-classical internal motions, if present. | |
• We assume that, due to its tiny dimension, each TR crossing be fast enough to avoid any relevant change of the QC diabatic states involved, which can be considered as time-independent during the whole event with a virtually constant coupling term and linear time-dependent energies. Therefore, by also assuming that such a limited crossing time for the diabatic state definition may correspond to a virtually infinite relaxation time for the QC dynamical quantum state, we can use the Landau–Zener approach59 to obtain the diabatic/adiabatic behaviour of the transition, i.e. the probability for the R and P state as obtained by the QC dynamical quantum state emerging from the TR (note that the presence of the diabatic states coupling in the Hamiltonian matrix expressed in the diabatic basis set, makes the typically much smaller non-adiabatic coupling negligible). For each possible reactive event the QC transition, occurring within the TR, may involve a perturbation interval varying from the whole TR providing the complete CT or ISC process (i.e. for fully adiabatic transitions corresponding to a complete hop from one diabatic state to the other) to virtually no perturbation interval around the diabatic states energy crossing providing the reactive flux over either the R or P diabatic state energy surface and hence not involving any CT or ISC process (i.e. for fully diabatic transitions corresponding to a complete hop from one adiabatic state to the other).
In the following theory subsections we describe in details first (The TR based reaction scheme) how to model the kinetics for each CT or ISC reaction step, i.e. involving only diabatic energy crossings due to a single P diabatic state, on the basis of the TR properties. Subsequently (the diabatic states) we specifically address the issue of the definition of proper diabatic states and related energies to be used, employing the PMM framework (within the dipolar approximation) for both CT and ISC reactions. Finally, (the general model for the reaction kinetics) we derive a general and efficient model for the reaction kinetics considering CT and ISC processes possibly involving several reaction steps due to the presence of productive diabatic energy crossings involving several P diabatic states.
2.2 The TR based reaction scheme
In general, whenever the system crosses a TR, during the reactive dynamics, a possible reaction event can occurs according to the usual scheme shown in Fig. 4 where we describe the process in terms of the energy surfaces of the adiabatic and diabatic states involved in the reaction. From the figure, beyond the TR itself, we can identify four different chemical states (RI, RII and PI, PII) corresponding to perturbation regions where the adiabatic states I and II are virtually identical either to the R or the P diabatic state. According to Fig. 4, within the definitions and assumptions described above, for a TR crossing process characterized by a given adiabatic fraction χ as provided by the Landau–Zener approximation (i.e. 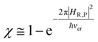 with HR,P the reactant–product coupling and vcr the absolute value of the diabatic energy difference time derivative at the crossing) we can schematize the R → P reaction occurring through the TR crossing as shown in Fig. 5 where A and B stand for either the I or II adiabatic surface index and the TRRA represents the TR chemical state as obtained by the reactive trajectories entering the transition region from RA (i.e. the reactive trajectories moving over an energy surface comprised within the A adiabatic and R diabatic surfaces).
with HR,P the reactant–product coupling and vcr the absolute value of the diabatic energy difference time derivative at the crossing) we can schematize the R → P reaction occurring through the TR crossing as shown in Fig. 5 where A and B stand for either the I or II adiabatic surface index and the TRRA represents the TR chemical state as obtained by the reactive trajectories entering the transition region from RA (i.e. the reactive trajectories moving over an energy surface comprised within the A adiabatic and R diabatic surfaces).
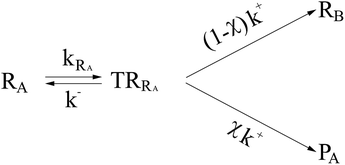 |
| | Fig. 5 Reaction scheme for the R → P reaction as occurring through the TR crossing. | |
Given its tiny dimension and the typically high vcr values, we have kRA ≪ k+ + k− implying the stationary condition for TRRA
| | |
[TṘRA] = [kRA[RA] − (k+ + k−)][TRRA] ≅ 0
| (1) |
hence providing
| |
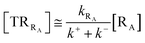 | (2) |
From eqn (2) we then obtain
| |
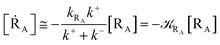 | (3) |
| |
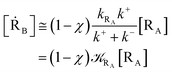 | (4) |
| |
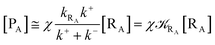 | (5) |
Note that in the present extended treatment we no longer assume any equilibrium53 within TR (implying k+ ≅ k−) as in typical ET and ISC reactions the transition region mean residence time is shorter than the autocorrelation mean time of the crossing velocity, thus implying k− ≅ 0. It is also worth to note that within the condition kRA ≪ k+ + k− motivating the stationary approximation we have [TṘRA]/[ṘA] ≅ [TRRA]/[RA] ≅ 0 and so the kinetics of [RA] is virtually indistinguishable from that of [RA] + [TRRA] or any combination of [RA] with a TRRA subpopulation (in particular the fraction time decay of the reactive trajectories not yet passed through the diabatic surfaces crossing, although possibly within the transition region).
The previous equations refer to the reaction as occurring via a single crossing process characterized by a given value of χ. In general, for the same R and P diabatic states, many possible crossing events characterized by different χ values can occur and, therefore, eqn (3)–(5), must be generalized considering different reactant subpopulations in fast interconversion, each reacting via given χl,![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l values, providing
RA,l values, providing
| |
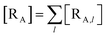 | (6) |
| |
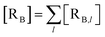 | (7) |
| |
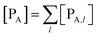 | (8) |
| |
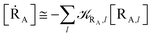 | (9) |
| |
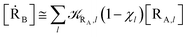 | (10) |
| |
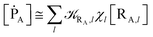 | (11) |
Eqn (9)–(11) can be simplified by considering that each [RA,l]/[RA] be stationary (i.e. [RA,l]/[RA] ≅ ρl with ρ˙l ≅ 0) within the reasonable assumption of statistical independent ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l and χl (i.e. 〈
RA,l and χl (i.e. 〈![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,lχl〉 ≅ 〈
RA,lχl〉 ≅ 〈![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l〉 〈χl〉), thus allowing to write
RA,l〉 〈χl〉), thus allowing to write
| |
[ṘA] ≅ −![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA[RA] RA[RA]
| (12) |
| |
[ṘB] ≅ ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA(1 − α)[RA] RA(1 − α)[RA]
| (13) |
| |
[ṖA] ≅ ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RAα[RA] RAα[RA]
| (14) |
with
| |
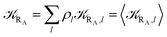 | (15) |
| |
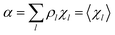 | (16) |
Eqn (12)–(17) provide the link between the kinetic model and the computational data as obtained by our MD-PMM method. In fact, by means of proper MD simulations it is rather straightforward to evaluate for a given R and P diabatic states couple the distribution of the time-lengths needed to reach the diabatic energy surfaces crossings in the reactant ensemble of trajectories and thus to reconstruct the [RA] kinetic trace with the corresponding rate constant (![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA), as we obtained in previous papers.53,56–58 Moreover, from the ensemble of the diabatic surfaces crossings as provided by the reactive trajectories it is also possible to obtain α = 〈χl〉 by simply evaluating by means of the Landau–Zener approach the adiabatic fraction at each crossing and then averaging over the crossings.
RA), as we obtained in previous papers.53,56–58 Moreover, from the ensemble of the diabatic surfaces crossings as provided by the reactive trajectories it is also possible to obtain α = 〈χl〉 by simply evaluating by means of the Landau–Zener approach the adiabatic fraction at each crossing and then averaging over the crossings.
2.3 The diabatic states
In order to obtain the information necessary to model the reaction kinetics, each CT or ISC reaction event needs to be modeled by proper R and P diabatic states. Unfortunately, such diabatic states depend on the specific choice of the QC observables/properties selected to define the corresponding reactants and products chemical conditions and thus, in principle, different diabatic states for the same reaction could be used. In line with our previous paper,53 when considering adiabatic ET reactions with electronically independent D and A species we can use the (constrained) D or A location of the exchanging electron to define via PMM the proper diabatic states to be used. However, in the present extended treatment we neither assume full adiabatic behavior nor the D and A electronic independence, thus requiring for CT reactions a different, more general, definition of the diabatic states (note that in order to estimate the diabatic effects we need to evaluate the D–A coupling). The treatment of the possible diabatic behavior implies that we cannot rely anymore on the electronic states only but inclusion of the vibrational effects is mandatory, thus requiring the explicit use of diabatic vibronic states.
2.3.1 CT reactions. In typical CT reactions, for each reactive event, the two relevant QC adiabatic states can be well approximated by linear combinations of only two unperturbed Hamiltonian eigenstates, i.e. the electronic or BO vibronic eigenstates of the isolated QC we always consider with well separated electronic Hamiltonian eigenvalues, thus ensuring a negligible non-adiabatic coupling. Therefore, a simple well suited choice for the diabatic states in CT reactions is to use the two QC unperturbed BO vibronic eigenstates best corresponding to the R and P electronic condition, respectively (the treatment of more complex cases involving adiabatic states defined by higher dimensional linear combinations of the unperturbed eigenstates and/or quasi-degenerate unperturbed electronic eigenstates is beyond the scope of the present paper). Note that for CT reactions we disregard any magnetic interaction (i.e. the QC Hamiltonian eigenstates are also spin eigenstates), assuming that only CT reactions involving diabatic states corresponding to the same spin eigenstate can occur (i.e. CT processes involving also a spin transition are assumed to be fully diabatic and hence irrelevant for the reaction).53 We always consider the R population semiclassical vibrational coordinates (i.e. the QC nuclear semiclassical internal coordinates providing only small harmonic-like fluctuations with little or no effect on the QC quantum properties except, of course, the electronic energy) as fully relaxed for each position of the QC conformational coordinates ξc (i.e. the QC nuclear internal semiclassical coordinates providing relevant structural changes), with hence the relevant R diabatic vibronic state involving a ξc-dependent quantum vibrational state and semiclassical vibrational coordinates, if present, relaxed to the ξc-dependent minimum energy position over the (electronic) R-energy surface (i.e. we disregard the small local fluctuations in modeling the reaction kinetics). However, for a given R diabatic vibronic state several P diabatic vibronic states (with semiclassical coordinates at the same position of the R state) are to be considered for the reaction, as different quantum vibrational states of the P electronic diabatic state could be involved in productive reaction events (i.e. the corresponding diabatic energy crossings do not provide fully diabatic transitions). It is worth to note that within the approximation we use of R-energy minimized semiclassical vibrational coordinates, the diabatic R and P electronic states involved in the reaction (i.e. the unperturbed electronic states Φ0e,R, Φ0e,P functions of the electronic coordinates as expressed within the internal QC reference of frame which is fully defined by the QC nuclear positions) can be considered as parametrical functions of only the conformational coordinates ξc and internal coordinates β corresponding to the QC nuclear quantum vibrational degrees of freedom, as it follows from the roto-translational invariance of the unperturbed electronic states (we clearly adopt the usual approximation of roto-translational invariance of the unperturbed vibrational states, i.e. fully uncoupled vibrational and roto-translational motions, and thus each ξc position fully determines also the local unperturbed vibrational modes). Within the PMM approach, using ξc-dependent energy minimized semiclassical vibrational coordinates, for each QC ξc, β configuration the corresponding orthonormal unperturbed electronic eigenstates Φ0e,j, eigenfunctions of the unperturbed (gas-phase) QC for a given spin eigenstate, provide the basis set for constructing the perturbed electronic Hamiltonian matrix (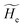 ) within the dipolar approximation
) within the dipolar approximation| |
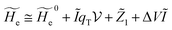 | (18) |
| |
[![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) 1]j,j′ = −E⋅〈Φ0e,j| 1]j,j′ = −E⋅〈Φ0e,j|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |Φ0e,j′〉 |Φ0e,j′〉
| (19) |
where 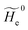 is the unperturbed electronic Hamiltonian matrix (diagonal within the chosen basis set), qT and
is the unperturbed electronic Hamiltonian matrix (diagonal within the chosen basis set), qT and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) are the QC total charge and dipole operator,
are the QC total charge and dipole operator, ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) and E are the electric potential and field as exerted by the environment on the QC centre of mass and Φ0e,j(ξc, β) becoming parametrically functions of only the QC conformational ξc coordinates when considering also the β coordinates as relaxed to their ξc-dependent energy minimized position as obtained in a reference eigenstate (e.g. the ground state), thus disregarding any explicit quantum vibrational effect73 (note that the use of electronic coordinates within the internal QC reference of frame requires that both
and E are the electric potential and field as exerted by the environment on the QC centre of mass and Φ0e,j(ξc, β) becoming parametrically functions of only the QC conformational ξc coordinates when considering also the β coordinates as relaxed to their ξc-dependent energy minimized position as obtained in a reference eigenstate (e.g. the ground state), thus disregarding any explicit quantum vibrational effect73 (note that the use of electronic coordinates within the internal QC reference of frame requires that both ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) and E must be also expressed within the internal QC reference of frame or, equivalently, that 〈Φ0e,j|
and E must be also expressed within the internal QC reference of frame or, equivalently, that 〈Φ0e,j|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |Φ0e,j′〉 be expressed in the reference of frame providing E). Finally, ΔV includes all the other terms treated as a simple short range potential and Ĩ is the identity matrix. Note that we assume, as usual, the R and P quantum vibrational modes as fully defined within the same QC internal coordinates subspace (i.e. the diabatic states share the same QC semiclassical configurational subspace) and thus in both diabatic states the same ξc, β coordinates can be used. The eigenvalues and eigenvectors of
|Φ0e,j′〉 be expressed in the reference of frame providing E). Finally, ΔV includes all the other terms treated as a simple short range potential and Ĩ is the identity matrix. Note that we assume, as usual, the R and P quantum vibrational modes as fully defined within the same QC internal coordinates subspace (i.e. the diabatic states share the same QC semiclassical configurational subspace) and thus in both diabatic states the same ξc, β coordinates can be used. The eigenvalues and eigenvectors of 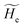 provide the actual perturbed electronic energies and eigenstates (adiabatic electronic states) while its elements corresponding to the diabatic electronic states of the CT reaction of interest (i.e. Φ0e,R, Φ0e,P) can be used to obtain the diabatic electronic energy change (electronic transition energy) Δ
provide the actual perturbed electronic energies and eigenstates (adiabatic electronic states) while its elements corresponding to the diabatic electronic states of the CT reaction of interest (i.e. Φ0e,R, Φ0e,P) can be used to obtain the diabatic electronic energy change (electronic transition energy) Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e
e| |
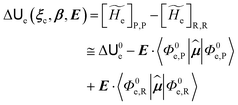 | (20) |
| |
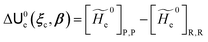 | (21) |
and the R, P electronic coupling term 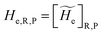
| |
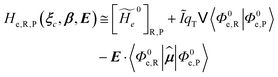 | (22) |
with clearly 〈Φ0e,R|Φ0e,P〉 and 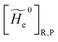 always zero except for the special case Φ0e,R = Φ0e,P (i.e. the diabatic vibronic states involve the same diabatic electronic state and hence 〈Φ0e,R|Φ0e,P〉 = 1 and Δ
always zero except for the special case Φ0e,R = Φ0e,P (i.e. the diabatic vibronic states involve the same diabatic electronic state and hence 〈Φ0e,R|Φ0e,P〉 = 1 and Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e = 0). Such a peculiar condition which is uncommon and requires a specific treatment will not be further discussed and in the following of this paper we will consider only the typical case of diabatic vibronic states involving different (non-degenerate in the unperturbed condition) diabatic electronic states.
e = 0). Such a peculiar condition which is uncommon and requires a specific treatment will not be further discussed and in the following of this paper we will consider only the typical case of diabatic vibronic states involving different (non-degenerate in the unperturbed condition) diabatic electronic states.Eqn (20)–(22) can be used for evaluating the complete transition energy (i.e. the diabatic vibronic energy change) Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) and, within the Landau–Zener approach, the fraction of adiabatic transitions (χ) in a R → P event involving a given ϕ0v,R,l(ξc, β) → ϕ0v,P,l′(ξc, β) vibrational state transition where ϕ0v,R,l, ϕ0v,P,l′ are, respectively, harmonic-like vibrational states of the diabatic electronic states Φ0e,R and Φ0e,P as obtained within the R and P electronic energy minima relevant for the R → P process (note that the vibrational states are functions of the internal coordinates β and only parametrically functions of the conformational coordinates ξc). Therefore, for a given possible reaction event (i.e. diabatic energy surfaces crossing) the corresponding complete transition energy and diabatic fraction 1 − χ are
and, within the Landau–Zener approach, the fraction of adiabatic transitions (χ) in a R → P event involving a given ϕ0v,R,l(ξc, β) → ϕ0v,P,l′(ξc, β) vibrational state transition where ϕ0v,R,l, ϕ0v,P,l′ are, respectively, harmonic-like vibrational states of the diabatic electronic states Φ0e,R and Φ0e,P as obtained within the R and P electronic energy minima relevant for the R → P process (note that the vibrational states are functions of the internal coordinates β and only parametrically functions of the conformational coordinates ξc). Therefore, for a given possible reaction event (i.e. diabatic energy surfaces crossing) the corresponding complete transition energy and diabatic fraction 1 − χ are
| |
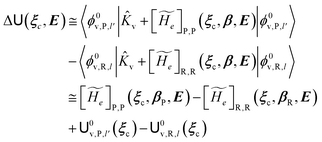 | (23) |
and
| |
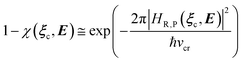 | (24) |
| |
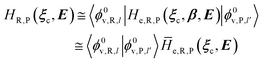 | (25) |
| |
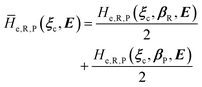 | (26) |
with
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) v
v the kinetic energy operator for the nuclear quantum vibrational coordinates,
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) 0v,R,l
0v,R,l,
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) 0v,P,l′
0v,P,l′ the unperturbed quantum vibrational energies corresponding to
ϕ0v,R,l and
ϕ0v,P,l′, respectively (
i.e. we disregard the perturbing electric field effects on the vibrational energy difference),
βR(
ξc) and
βP(
ξc) the
ξc-dependent minimum energy positions of the quantum vibrational coordinates
β for the R and P diabatic states and in
eqn (24) the crossing velocity
vcr (
i.e. the absolute value of the transition energy time derivative) as well as the conformational coordinates and the perturbing field are all to be evaluated at the crossing (
i.e. when Δ
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
= 0) thus providing the constant coupling term for the Landau–Zener formula. Note that typically |〈
ϕ0v,R,l|
ϕ0v,P,l′〉〈
Φ0e,R|
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif)
|
Φ0e,P〉|≪|〈
Φ0e,P|
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif)
|
Φ0e,P〉 − 〈
Φ0e,R|
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif)
|
Φ0e,R〉| thus allowing, within the whole TR, to consider the variation of
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) R,P
R,P as approximately negligible compared to the nearly linear variation of Δ
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif)
. Finally,
eqn (25) can be really accurate when the
βR and
βP minima are close enough to allow considering
He,R,P virtually constant within the relevant
β range, with
He,R,P(
ξc,
βR,
E) ≅
He,R,P(
ξc,
βP,
E) significantly different from zero (
i.e. really negligible non-adiabatic coupling).
2.3.2 ISC reactions. In ISC reactions the R → P transition virtually coincides with a QC spin eigenstate transition and hence, introducing the (electrons) spin eigenstates σRσP (with σR ≠ σP), the perturbed electronic-spin eigenstates Φe,RσR and Φe,PσP as obtained neglecting any magnetic interaction and provided within PMM by diagonalizing the perturbed electronic Hamiltonian matrix given by eqn (18) and (19) for the R and P spin eigenstate respectively, can be used as proper diabatic electronic-spin states. Therefore, the electronic transition energy can be simply obtained by Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e =
e = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,P −
e,P − ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,R where
e,R where ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,R,
e,R, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,P are eigenvalues of the electronic Hamiltonian matrix corresponding to the R and P magnetic state, respectively, and the electronic coupling term corresponding to the R, P element of the perturbed electronic Hamiltonian matrix (including the magnetic interactions) expressed within the diabatic electronic-spin basis set, is given by
e,P are eigenvalues of the electronic Hamiltonian matrix corresponding to the R and P magnetic state, respectively, and the electronic coupling term corresponding to the R, P element of the perturbed electronic Hamiltonian matrix (including the magnetic interactions) expressed within the diabatic electronic-spin basis set, is given by| |
He,R,P ≅ 〈Φe,RσR|Ĥso|Φe,PσP〉 = η†R![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) soηP soηP
| (27) |
where Ĥso is the spin–orbit Hamiltonian operator, ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) so is the corresponding matrix and ηRηP the unit vectors representing Φe,RσR and Φe,PσP within the same basis set used to express the spin–orbit matrix (i.e. the unperturbed basis set). Note that typically 〈Φe,RσR|Ĥso|Φe,PσP〉 is only slightly dependent on the perturbation and hence virtually constant within the TR.
so is the corresponding matrix and ηRηP the unit vectors representing Φe,RσR and Φe,PσP within the same basis set used to express the spin–orbit matrix (i.e. the unperturbed basis set). Note that typically 〈Φe,RσR|Ĥso|Φe,PσP〉 is only slightly dependent on the perturbation and hence virtually constant within the TR.Therefore, using as diabatic vibronic-spin states the R and P perturbed vibronic-spin BO eigenstates (each, typically, almost identical to a specific unperturbed eigenstate), in ISC reaction events the complete transition energy and the diabatic fraction are
| |
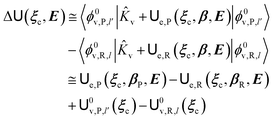 | (28) |
and
| |
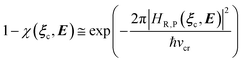 | (29) |
| |
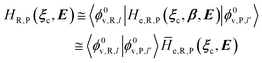 | (30) |
| |
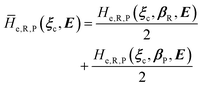 | (31) |
where we used the same notation employed for CT reactions and disregarded the typically small effects of perturbation on quantum vibrational modes, thus utilizing the unperturbed vibrational states of the unperturbed electronic states best corresponding to the pertubed electronic-spin R and P eigenstates.
2.4 The general model for the reaction kinetics
From the previous considerations and approximations we can outline the general reaction scheme by considering a single R diabatic vibronic state (typically the vibronic state involving the vibrational ground state) possibly crossing with several P diabatic vibronic states involving the vibrational states providing a non-negligible chemical flux for the R → P reaction (typically vibrational states within the energy range defined by the vibrational ground state as lower bound and the vibrational state corresponding to the R → P vertical transition as upper bound). In Fig. 6 and 7 we show a schematic picture of such diabatic state energy surfaces and the corresponding reaction scheme with rate constants for each reaction step obtained according to eqn (12)–(14). Note that we disregard in the reaction scheme any P → R back reaction as we assume a basically irreversible R → P process, possibly involving a fast products quantum and/or semiclassical vibrational relaxation. Moreover, we can safely consider in the reaction scheme that for each ith reaction step the corresponding αi (the mean adiabatic fraction as obtained averaging over all the crossings involved in the ith reaction step, see eqn (16)) is invariant for Ri → Ri+1 and Ri+1 → Ri as it only depends on the properties at the diabatic surfaces crossings of the ith reaction step, being necessarily unrelevant for the 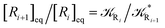 equilibrium constant (i.e. the equilibrium constant must be independent of the diabatic-adiabatic TR traversing behavior).
equilibrium constant (i.e. the equilibrium constant must be independent of the diabatic-adiabatic TR traversing behavior).
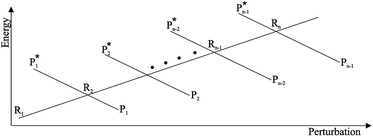 |
| | Fig. 6 Schematic picture of the diabatic state energy surfaces involved in the reaction. | |
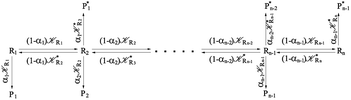 |
| | Fig. 7 Reaction scheme according to Fig. 6. | |
In order to obtain general, simple analytic expressions for the kinetics defined by Fig. 6 and 7, we need to introduce approximations suited to accurately describe typical CT and ISC reactions. A simplified condition can be obtained by using the irreversible reaction step approximation described below.
2.4.1 The irreversible reaction step approximation. The irreversible reaction step approximation is based on assuming that for each reactive trajectory involved in the R1 → Rn or equivalently in the Rn → R1 transition, no inversion of the chemical flux is possible for all the relevant reaction steps (i.e. we assume completely irreversible reaction steps from R1 to Rn or equivalently from Rn to R1, for the R1 → Rn or the Rn → R1 process respectively, see Fig. 5 and 6). Such an ideal condition, implying that the intermediates R2, R3,…, Rn−1 are characterized by different ensembles in the R1 → Rn and Rn → R1 transitions, is a proper approximation of the actual reaction only when the mean residence time of the intermediates region is not larger than the R1 → P1 (or Rn → Pn−1) transition energy time derivative (i.e. the intermediates traversing velocity) autocorrelation mean time, as typically occurring in many CT and ISC reactions (note that R1 and Rn differently from the intermediates are assumed to have inner equilibrium during the reaction). Therefore, within the irreversible reaction step approximation the rate equations for the R1 → Rn process can be obtained considering in Fig. 6 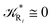 , providing
, providing| |
[Ṙ1] ≅ −![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (32) |
| |
[Ṙ2] ≅ (1 − α1)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] − R1[R1] − ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R2[R2] R2[R2]
| (33) |
| |
[Ṙi] ≅ (1 − αi−1)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri−1[Ri−1] − Ri−1[Ri−1] − ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri[Ri] Ri[Ri]
| (35) |
| |
[Ṙn] ≅ (1 − αn−1)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Rn−1[Rn−1] Rn−1[Rn−1]
| (37) |
while for the Rn → R1 process the rate equations are obtained considering ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri ≅ 0 and hence
Ri ≅ 0 and hence| |
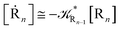 | (38) |
| |
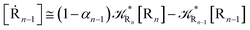 | (39) |
| |
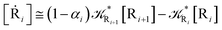 | (41) |
| |
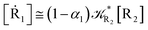 | (43) |
We can proceed further by considering that the irreversible reaction step approximation necessarily implies much faster transitions between neighboring intermediates than the R1 → R2 and Rn → Rn−1 rates, thus allowing to assume the stationary condition for all the intermediates (i.e. [Ṙ2] ≅ [Ṙ3] ≅ ⋯ ≅ [Ṙn−1] ≅ 0). Therefore, the rate equations for the R1 → Rn process provide
| |
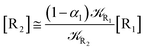 | (44) |
| |
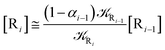 | (46) |
| |
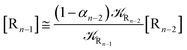 | (48) |
and hence using
eqn (44)–(48) into
eqn (37), we can write
| |
[Ṙ1] ≅ −![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (49) |
| |
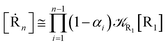 | (50) |
| |
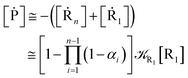 | (51) |
where
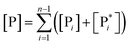
. Similarly, for the R
n → R
1 process we have
| |
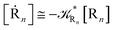 | (52) |
| |
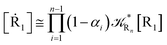 | (53) |
| |
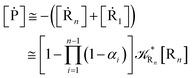 | (54) |
clearly showing that we can obtain the kinetics of the R
n → R
1 transition from that of the R
1 → R
n transition simply exchanging R
1 with R
n and
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1
R1 with
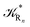
. These last equations can be further simplified considering that from
eqn (24),
(25),
(29) and
(30) for each
ith reaction step, assuming the R diabatic vibronic state involving the
l vibrational state, we have
| |
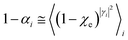 | (55) |
| |
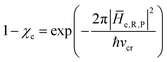 | (56) |
| | |
γi = 〈ϕ0v,R,l|ϕ0v,P,i〉
| (57) |
with
γi depending only on the conformational coordinates
ξc, 1 −
χe a function of the conformational coordinates and the perturbing field, independent of the reaction step, and the angle brackets with the
i subscript in
eqn (55) indicating averaging over the
ith reaction step ensemble (
i.e. the average is obtained over all the crossings of the
ith reaction step). Realizing that for each reaction step
γi is close to zero and can be considered as virtually constant and 0 ≤ 1 −
χe ≤ 1, we can write
| |
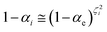 | (58) |
| | |
1 − αe ≅ 〈(1 − χe)〉i
| (59) |
where
αe is invariant for all the reaction steps and
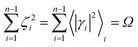
with 0 ≤
Ω ≤ 1. The use of
eqn (58) into
eqn (49)–(54) then provides for the R
1 → R
n kinetics
| |
[Ṙ1] ≅ −![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (61) |
| |
[Ṙn] ≅ (1 − αG)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (62) |
| |
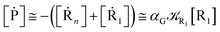 | (63) |
and for the R
n → R
1 kinetics
| |
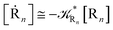 | (64) |
| |
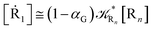 | (65) |
| |
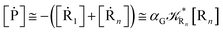 | (66) |
where 1 −
αG = (1 −
αe)
Ω and so the global adiabatic fraction is
αG = 1 − (1 −
αe)
Ω.
From eqn (61)–(66) it follows that within the irreversible reaction step approximation the complete reaction kinetics (involving the R1, Rn interconversion) can be obtained by using the scheme shown in Fig. 8, providing
| |
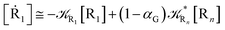 | (67) |
| |
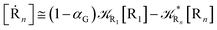 | (68) |
| |
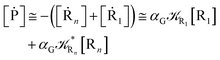 | (69) |
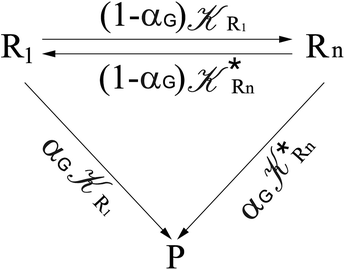 |
| | Fig. 8 Simplified reaction scheme according to the irreversible reaction step approximation (see text) when assuming stationary state conditions for all the intermediates. | |
Eqn (67) and (68) can be easily solved by diagonalizing the kinetic matrix of the rate constants, furnishing a biexponential time behavior as general solution for both R1 and Rn. However, it is of particular interest to consider the two typical approximate solutions as obtained assuming the stationary condition either for Rn or for R1. In the former case (i.e. [Ṙn] ≅ 0 and hence 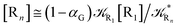 ) we have
) we have
| |
[Ṙ1] ≅ −αG(2 − αG)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (70) |
| |
[Ṗ] ≅ −[Ṙ1] ≅ αG(2 − αG)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] R1[R1]
| (71) |
providing, with [R
1]
0 the initial R
1 species concentration (
i.e. at the beginning of the R
n stationary state condition) and neglecting the R
n concentration (
i.e. [P] ≅ [R
1]
0 − [R
1]),
| |
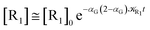 | (72) |
| |
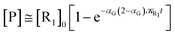 | (73) |
For the latter case (i.e. [Ṙ1] ≅ 0 and hence 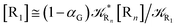 ) we can write
) we can write
| |
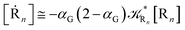 | (74) |
| |
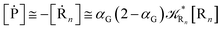 | (75) |
providing, with [R
n]
0 the initial R
n species concentration (
i.e. at the beginning of the R
1 stationary state condition) and neglecting the R
1 concentration (
i.e. [P] ≅ [R
n]
0 − [R
n]),
| |
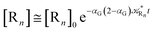 | (76) |
| |
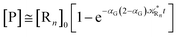 | (77) |
These last approximations furnish a very simple model of the reaction kinetics with a trivial exponential decay for R1 and Rn, respectively, as typically observed experimentally (note that eqn (70)–(73) implies 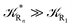 and eqn (74)–(77) implies
and eqn (74)–(77) implies 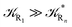 ). Remarkably, eqn (70)–(77) clearly show that within the irreversible reaction step approximation when Ω ≅ 1 and thus 1 − αG ≅ 1 − αe and αG ≅ αe, no explicit vibrational effect is present in the complete reaction kinetics and hence for such a condition in the limit αe → 1 eqn (70)–(77) reduce essentially to the expressions we derived and used in previous papers (ref), based on assuming fully adiabatic ET reactions when neglecting any explicit vibrational effect. Such a result well explains the accuracy of the simpler purely electronic approach utilized previously, indicating that in most typical ET reactions Ω ≈ 1 and αe ≈ 1 thus providing a kinetic behavior equivalent to adiabatic reactions involving purely electronic diabatic states.
). Remarkably, eqn (70)–(77) clearly show that within the irreversible reaction step approximation when Ω ≅ 1 and thus 1 − αG ≅ 1 − αe and αG ≅ αe, no explicit vibrational effect is present in the complete reaction kinetics and hence for such a condition in the limit αe → 1 eqn (70)–(77) reduce essentially to the expressions we derived and used in previous papers (ref), based on assuming fully adiabatic ET reactions when neglecting any explicit vibrational effect. Such a result well explains the accuracy of the simpler purely electronic approach utilized previously, indicating that in most typical ET reactions Ω ≈ 1 and αe ≈ 1 thus providing a kinetic behavior equivalent to adiabatic reactions involving purely electronic diabatic states.
Interestingly, eqn (70)–(77) can be also combined to treat the special case where an intermediate Rr plays at the same time the role of R1 in eqn (70)–(73) and of Rn in eqn (74)–(77), being hence involved in two reactive paths resulting in two products chemical states (P+ and P−), as described by the reaction scheme of Fig. 9. In fact, for such a condition, involving the stationary state for both R1 and Rn, we clearly have (defining now [P] = [P+] + [P−])
| |
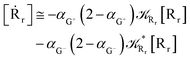 | (78) |
| |
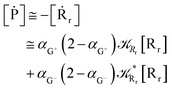 | (79) |
providing, with [R
r]
0 the initial R
r species concentration (
i.e. at the beginning of the R
1, R
n stationary state condition) and neglecting the R
1 and R
n concentrations (
i.e. [P] ≅ [R
r]
0 − [R
r]),
| |
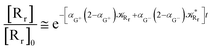 | (80) |
| |
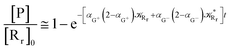 | (81) |
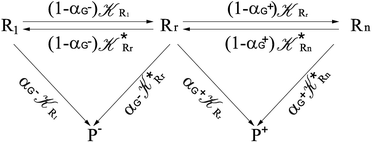 |
| | Fig. 9 Simplified reaction scheme according to the irreversible reaction step approximation (see text) when considering the Rr intermediate as a non-stationary reactants state. | |
Finally, in case the accessible conformational space is too extended for accurately using eqn (58) and neglecting the effects of conformational transitions (e.g. the relevant change of the unperturbed eigenstate electronic distribution, possibly requiring the change of the MD force field and/or the diabatic states to be used), the presented model should be employed to describe the reaction kinetics within different conformational states, each defined by a proper ξc subspace, thus allowing to reconstruct the whole reaction kinetics in terms of single subspace kinetics and conformational interconversions. Moreover, when more than a single R diabatic vibronic state is significantly present in the reactive ensemble (i.e. not only the vibrational ground state of the R diabatic electronic state involved in the reaction is thermally accessible or we deal with a vibrationally non-equilibrium R ensemble), the general model described applies in principle to the kinetics due to each R diabatic vibronic state with the whole kinetics given by their combination. However, when realizing that usually for the reactions of interest the R ensemble can be considered at thermal equilibrium with most of the accessible excited vibrational states (i.e. vibrational states with energies relatively close to the ground state energy) providing a kinetics similar to the vibrational ground state one, we can typically assume that the whole kinetics can be approximately given by the kinetics due only to the R vibronic state corresponding to the vibrational ground state, thus allowing to neglect the explicit evaluation of the kinetics due to the excited vibrational states. In order to significantly simplify the application of the model we will make use in general of such an approximation and in the present work we always consider only the R vibrational ground state to model the reaction kinetics.
3 Computational details
3.1 Computational strategy
Before entering into the details of the computational procedures utilized in this study, we provide a brief outline of the underlying strategy. First of all it is important to further remark that the whole study, based on the MD-PMM procedure, requires the production of MD simulations and quantum-chemical calculations (QCC) carried out on the pre-selected isolated (gas-phase) QC which can be treated either as a rigid54,55 or flexible moiety.72 In both the investigated cases the experimental measurements, we are referring to, were carried out starting from photo-generated species, i.e. the electronically excited DMN for the CT reaction and singlet FL for the ISC reaction, at a well-defined wavelength. For this reason the first step of the work is the theoretical-computational modeling of the equilibrium spectra in solution of the solvated precursors, namely: DMN in THF for the CT reaction and FL-N2 in ACN for ISC reaction. At this purpose we utilized the widely documented MD-PMM procedure for modeling the equilibrium absorption spectra in solution73,74 where the chromophore represents the QC perturbed by the electric field produced by the solvent molecules along an equilibrium MD simulation, hereafter termed as EqMD. From the obtained spectra we then extracted a number of MD configurations, falling in the experimental excitation range with an accuracy of ±0.5 nm, providing the whole set of initial conditions (position and associated momentum of all the atoms) to be used for studying the relaxation processes by means of relatively short non-equilibrium MD simulations, hereafter termed as NonEqMD (see for example ref. 72). Specifically, in each trajectory we have evaluated the time requested for entering the TR (see Theory section) and, finally, such a swarm of time-values has been utilized in conjunction with the specific model (see Theory section) for reconstructing the whole kinetics. Note that the NonEqMD simulations, again propagated in the NVT ensemble, were initiated using the coordinates and associated momenta of the perturbing environment as obtained by the extracted configurations while changing the QC force-field, i.e. atomic charges and bond lengths and angles. This last procedure reflects the basic approximation of the model, i.e. we have disregarded the ultrafast radiationless events (e.g. internal vibrational redistribution), known to take place essentially within the chromophore, upon the vertical excitation. For a general discussion on these last approximations we invite the reader to refer to the cited literature.72
3.2 Molecular Dynamics simulations
All the simulations were carried out using the Gromacs package,75 version 5.0.2 For the QCs we adopted the Lennard-Jones terms from the Gromos force-field76 while the atomic point charges,77 bond lengths, bond angles and torsion angles were obtained by standard QM calculations in vacuum (see the next subsection) both for the ground (in the EqMD simulations) and for the involved excited states (in the NonEqMD). The parameters for the solvents, i.e. acetonitrile78 and tetrahydrofurane83 were taken from the literature. For the EqMD simulations, after an initial energy minimization, the whole system was gradually heated from 50 K to the desired temperature using short (20 ps) MD simulations. The temperature was kept constant using the velocity rescaling algorithm.79 The LINCS algorithm80 was employed to constrain all bond lengths. Long range electrostatic interactions were computed by the particle mesh Ewald method81 with 34 wave vectors in each dimension and a 4th order cubic interpolation and a cut-off of 1.1 nm was used. For the NonEqMD simulations we adopted the same protocol previously described for EqMD but, obviously, not including the equilibration procedure. All the simulations were carried out in the NVT ensemble with the box adjusted to reproduce the correct solvent bulk density at the experimental temperature and pressure. This latter condition has been achieved by adjusting the solute–solvent box in order to reach the same calculated pressure of a box of pure solvent, simulated at the same temperature and at the corresponding experimental density.82 For the CT reaction we utilized a cubic box of 4.6 nm length filled with THF83 and one molecule of DMN. For the ISC reaction we utilized a cubic box of 3.5 nm length filled with ACN and one molecule of FL (or FL-N2 for the initial evaluation of the spectrum for preparing the initial conditions). Essential dynamics analysis84 was used for characterizing the QC conformational fluctuations of the FL-N2 and FL moieties only as DMN can be considered a rigid or semirigid molecule with hence either no structural fluctuations or only local semi-classical vibrations neglected within our QCC calculations.
Additional details of the utilized force-field (i.e. Gromos-format topologies) are reported in the ESI.†
3.3 Unperturbed quantum states and properties
All the gas-phase QCC necessary for evaluating both the force-field of the systems and the unperturbed basis set and properties for constructing the quantum Hamiltonian to be used, were carried out in the framework of the Density Functional Theory (DFT)85 using the hybrid B3LYP functional86,87 in conjunction with 6-311G** basis set. Time-Dependent Density Functional Theory (TD-DFT)88 was used with the same functional and basis set for evaluating the optimized geometries and the related properties of the involved excited states. We wish to remark that, in spite of the well known limitations of this level of theory, our choice was driven by the documented good performances of these calculations at a limited computational cost. Any attempt of studying the sensitivity of our results on the level of theory of the gas-phase QCC was out of the scope of the present study. The energy minimizations, vibrational frequency calculations and atomic-charge evaluations were carried out with the Gaussian09 package.89 The calculations of the unperturbed eigenstates and corresponding operator matrix elements were carried out in the framework of the linear90 and quadratic91 response theory using the Dalton package.92 The same package and the same level of theory was also utilized for the calculation of the spin–orbit coupling matrix element. Note that for this latter calculation the restricted-open formalism was adopted for the description of the triplet state. The use of different packages was due to practical reasons, i.e. efficiency of Gaussian09 package in the optimization of geometries in electronically excited states, and to the peculiar features of the packages themselves, e.g. complete evaluation of transition dipole matrix only possible in the Dalton package. Note that in order to avoid inconsistency of our unperturbed data, we used the B3LYPGauss version implemented in the Dalton suite. Additional details on QCC (i.e. optimized geometries) are reported in the ESI.†
4 Applications
4.1 Photoinduced CT reaction
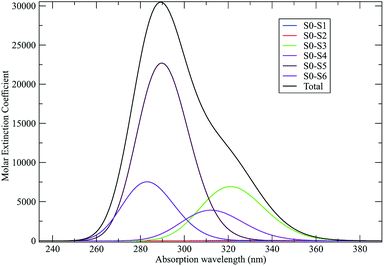
As discussed in the Theory section the perturbed electronic eigenstates outside the transition regions are usually almost identical to the unperturbed ones, allowing the use of the proper unperturbed eigenstate properties to construct the MD force field to be used (in particular for the ground state which is virtually unaffected by the perturbation). In Fig. 10 we show the DMN absorption spectrum as obtained via the PMM/MD approach (within the vertical transition approximation73) using the EqMD simulation performed in the ground state ensemble (i.e. the MD force field was constructed utilizing the DMN unperturbed ground state properties). From the figure it is evident that in correspondence of the excitation wavelength (308 nm) experimentally used to start the reaction process,64–66 most of the electronic transitions involves the third excited state which was then used to define the reactive ensemble (i.e. the excited-DMN simulation was propagated using the geometry and the atomic charges as obtained in the unperturbed third excited state, see below).
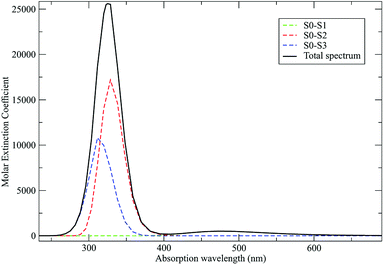 |
| | Fig. 10 Calculated absorption spectrum for DMN in THF. Molar extinction coefficient is reported in M−1 cm−1. | |
As a preliminary step, necessary for the construction of the force field for the NonEqMD simulations involving the perturbed S3 state, we need to check if, and how much, the third perturbed electronic excited state resembles the unperturbed S3 electronic state. At this purpose we have collected from the EqMD trajectory a number of 40 configurations found to absorb between 307.5 and 308.5 nm. In correspondence of each of them we have projected the perturbed (instantaneous at time zero of the reaction) S3 electronic state onto the unperturbed S3 one. The results, shown in Fig. 11, clearly confirm that in the initial reactive ensemble the perturbed S3 electronic state is almost identical, as expected, to the unperturbed S3 electronic state, allowing the use of the latter for constructing the MD force field generating the NonEqMD trajectories (the same analysis confirms also a similar correspondence for the other perturbed electronic eigenstates). On the basis of such a resemblance between perturbed and unperturbed electronic states, it is interesting to focus our attention on the QCC providing the DMN minimum energy structures and the related properties in the ground (S0) and first three excited (S1, S2 and S3) unperturbed electronic (singlet) eigenstates.
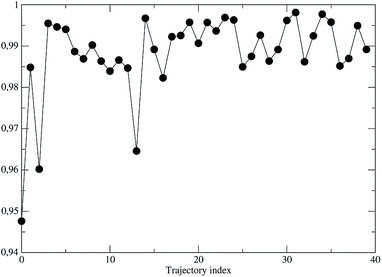 |
| | Fig. 11 Projections of the perturbed S3 electronic eigenstate onto the unperturbed S3 electronic eigenstate for the 40 initial configurations of the NonEqMD trajectories. | |
The results schematically reported in Fig. 12 indicate that the S0 → S1 excitation should be followed by the variation of the angle between the C(CN)2 plane and the aliphatic bicyclo moiety. On the other hand the S2 and S3 equilibrium geometries should be rather similar to the S0 geometry. Moreover, from the analysis of the dipole moments, reported in the Fig. 13, we can also observe that while the unperturbed S3 state has an electronic distribution similar to the ground state, both the unperturbed S1 and S2 states show a drastic modification of the electronic density, i.e. a sharp CT-state. It follows that the experimentally observed photoinduced CT events presumably involves the unperturbed S3 and S2 excited states as the R and P diabatic electronic states of the reaction.
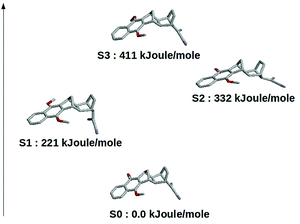 |
| | Fig. 12 Schematic view of the optimized (in vacuo) DMN in the ground and first three (singlet) excited states. | |
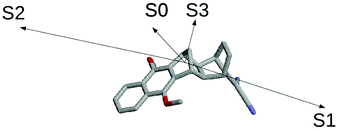 |
| | Fig. 13 Schematic view of the S0, S1, S2 and S3 dipole moments. | |
In order to verify that the unperturbed S2 and S3 electronic eigenstates are fully consistent with the proper diabatic electronic states to be used, we analyzed the 40 NonEqMD trajectories monitoring, for each of them, the energies corresponding to the unperturbed S3 and S2 eigenstates (i.e. the diabatic electronic energies corresponding to diagonal elements of the perturbed electronic Hamiltonian matrix) and the perturbed S3 and S2 eigenstates (i.e. the adiabatic electronic states) squared projections along the S3 and S2 unperturbed eigenstates providing the fractional amount of these unperturbed eigenstates in the definition of each adiabatic state (i.e. the diabatic state probabilities). In Fig. 14 we show, for one trajectory, such properties close to the energy crossing. From the figure it is evident that the perturbed electronic S3 eigenstate, virtually identical to the unperturbed S3 eigenstate just before the crossing, sharply becomes almost identical to the unperturbed S2 eigenstate while an almost specular behavior is occurring for the perturbed S2 eigenstate (the slight deviations from the ideal behaviour are due to the weak coupling of the other unperturbed eigenstates, disregarded in the model). Such results demonstrate that the S3 → S2 unperturbed eigenstate transition is an accurate approximation of the CT reaction, confirming that these unperturbed electronic eigenstates furnish the proper R and P diabatic electronic state, respectively, thus allowing the use of the corresponding reduced two-dimensional subspace to model the reactive events. Note that in the analysis of the NonEqMD trajectories the electronic energies and eigenstates (i.e. the electronic Hamiltonian matrix) are obtained at the R chemical state structure and hence the diabatic electronic energy crossings are approximately equivalent to the diabatic vibronic energy crossings involving the P diabatic vibronic state corresponding to the vertical transition. Therefore, the negative electronic transition energy always found before the first crossing, implies that the Rn → R1 reaction scheme is to be used.
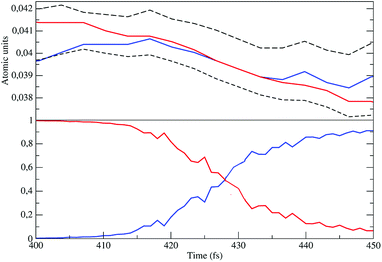 |
| | Fig. 14 Diabatic perturbed electronic energies (upper panel), including the S3 and S2 electronic Hamiltonian eigenvalues (dashed lines), and the perturbed S3 diabatic state probabilities (lower panel) close to the crossing. | |
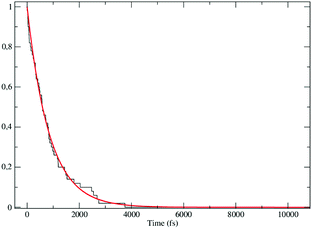
The distribution of the time lengths to reach the first diabatic energy crossing (the first S3 → S2 unperturbed eigenstate energy crossing) provides the rate constant 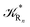 to be used in eqn (74)–(77), corresponding to the purely adiabatic kinetics53 (see Fig. 15) and hence for the complete reaction kinetics model we also need to evaluate the diabatic fraction 1 − αG = (1 − αe)Ω. For the present CT reaction, similarly to most of the typical CT reactions, the initial relevant vibronic crossing involves the P vibronic diabatic state corresponding to the vertical transition, with hence the largest vibrational state overlap, associated to a highly excited and strongly anharmonic P vibrational state. Such a condition avoids the use of any computationally explicit evaluation of the vibrational effects, necessarily based on the assumption of either the harmonic or slightly anharmonic behaviour of the P vibrational states of interest (note that for the R chemical state we consider only the diabatic vibronic state corresponding to the ground vibrational state). Therefore, for the present CT reaction in order to obtain an achievable efficient computational model and on the basis of the high density in energy of the relevant P vibronic states involved in the first reaction steps and corresponding large vibrational state overlaps, we assume Ω ≈ 1 and hence αG ≈ αe thus reducing the evaluation of the diabatic fraction to the purely electronic Landau–Zener factor, see eqn (55)–(60). As discussed in the Theory section such an assumption can be considered a reasonable approximation in typical CT reactions, at least when the initial reaction step involves the P vibronic state corresponding to the R → P vertical transition. From Fig. 15 we obtained
to be used in eqn (74)–(77), corresponding to the purely adiabatic kinetics53 (see Fig. 15) and hence for the complete reaction kinetics model we also need to evaluate the diabatic fraction 1 − αG = (1 − αe)Ω. For the present CT reaction, similarly to most of the typical CT reactions, the initial relevant vibronic crossing involves the P vibronic diabatic state corresponding to the vertical transition, with hence the largest vibrational state overlap, associated to a highly excited and strongly anharmonic P vibrational state. Such a condition avoids the use of any computationally explicit evaluation of the vibrational effects, necessarily based on the assumption of either the harmonic or slightly anharmonic behaviour of the P vibrational states of interest (note that for the R chemical state we consider only the diabatic vibronic state corresponding to the ground vibrational state). Therefore, for the present CT reaction in order to obtain an achievable efficient computational model and on the basis of the high density in energy of the relevant P vibronic states involved in the first reaction steps and corresponding large vibrational state overlaps, we assume Ω ≈ 1 and hence αG ≈ αe thus reducing the evaluation of the diabatic fraction to the purely electronic Landau–Zener factor, see eqn (55)–(60). As discussed in the Theory section such an assumption can be considered a reasonable approximation in typical CT reactions, at least when the initial reaction step involves the P vibronic state corresponding to the R → P vertical transition. From Fig. 15 we obtained 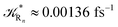 (corresponding to the purely adiabatic mean lifetime of ≈735 fs) and from the first diabatic energy crossing ensemble αG ≈ αe = 0.675 ± 0.035 providing, within our model, the complete rate constant for the reaction
(corresponding to the purely adiabatic mean lifetime of ≈735 fs) and from the first diabatic energy crossing ensemble αG ≈ αe = 0.675 ± 0.035 providing, within our model, the complete rate constant for the reaction 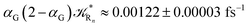 corresponding to a mean lifetime of ≈822 ± 20 fs (the noise indicated is always the estimated standard error). The reported theoretical-computational results reasonably well reproduce the experimental mean lifetime64–66 (≈360 fs), indicating that the employed theoretical-computational model captures the essential physics of the CT reaction.
corresponding to a mean lifetime of ≈822 ± 20 fs (the noise indicated is always the estimated standard error). The reported theoretical-computational results reasonably well reproduce the experimental mean lifetime64–66 (≈360 fs), indicating that the employed theoretical-computational model captures the essential physics of the CT reaction.
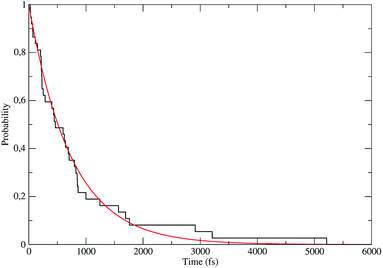 |
| | Fig. 15 Kinetic trace for the fully adiabatic CT reaction. | |
For the sake of clarity we have schematized the whole procedure, employed to obtain the results described in this subsection, in the flow-chart reported in Fig. 16.
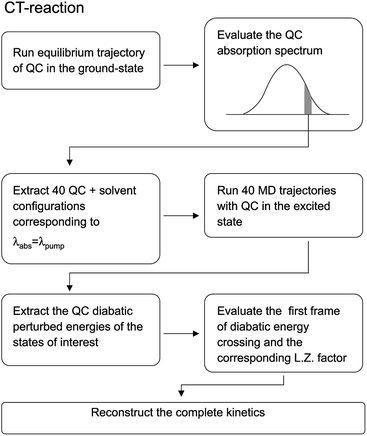 |
| | Fig. 16 Schematic representation of the relevant steps involved in the computational procedure described in the text. | |
4.2 ISC reaction
The singlet-triplet reaction of carbene-like systems has represented a long-time benchmark for QM calculations.93 The main problem is related to the correct evaluation of the singlet–triplet (S–T) energy gap which is very difficult to accurately obtain with low-cost calculations such as Hartree–Fock or DFT, even when using a relatively large atomic basis set. For this reason we decided to use the unperturbed QC calculations for both the singlet and triplet magnetic states, scaling the obtained energies in order to reproduce the experimentally estimated gas-phase S–T ground state energy gap (i.e. we scaled the T electronic ground state energy, keeping fixed the calculated T excitation energies).67,68 Differently from DMN, treated as a rigid or semirigid QC, FL needs to be considered a flexible QC. Specifically, we have included in the MD-PMM calculations, beyond the usual local semiclassical vibrations, the effects of the FL conformational fluctuations basically corresponding to fluctuations within the subspace defined by the low-frequency out-of-plane vibrational modes. At this purpose we have evaluated the geometry-dependent S and T unperturbed electronic eigenstates and properties, as described in detail in our previous publication,72 using the essential dynamics analysis.84 For the sake of brevity this part of the study has been reported in the ESI.† Similarly to the CT reaction, also in this case we have extracted 40 initial FL configurations from the FL-N2 spectrum (reported in Fig. 17) within the wavelength range 307.5–308.5 nm (i.e. the excitation range experimentally used).
 |
| | Fig. 17 Calculated absorption spectrum (molar extinction coefficient in M−1 cm−1) for FL-N2 in ACN. | |
The obtained MD trajectories of the singlet ground state FL, providing the NonEqMD ensemble for the S → T reaction (i.e. the R → P transition), clearly indicate that the S diabatic vibronic ground state energy is always initially lower than the T diabatic vibronic ground state energy, thus implying that the initial relevant vibronic crossing involves the T vibronic diabatic ground state, with hence in general a limited vibrational state overlap, and the relevant intermediates are associated to only the first excited and virtually harmonic T vibrational states (for the definition of the diabatic states and energies for ISC reactions see the Theory section). Such a condition requires/allows the explicit evaluation of the vibrational effects considering all the T vibrational states involved in the relevant stationary intermediates (note that for the S chemical state we consider only the diabatic vibronic ground state). For the present ISC reaction only the T vibrational ground and first three excited states (i.e. the first two excitations of the ≈214 cm−1 mode and the first excitation of the ≈428 cm−1 mode) are significant as no trajectory can reach diabatic vibronic energy crossings involving other T vibrational states. The distribution of the time lengths to reach the first diabatic energy crossing (the vibronic ground to ground S → T diabatic energy crossing) provides the rate constant ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 to be used in eqn (70)–(73), corresponding to the purely adiabatic kinetics53 (see Fig. 18). The complete reaction kinetics model can then be obtained evaluating the diabatic fraction 1 − αG = (1 − αe)Ω where αe is provided by the electronic Landau–Zener factor, see eqn (55)–(60), and Ω includes only the vibrational state overlaps of the S ground state with the T ground and first three excited vibrational states. In order to evaluate the relevant vibrational state overlaps for estimating Ω, we made use of the Duschinsky transformation94 providing the T normal mode coordinates in terms of the S ones. Such a procedure applied to a flexible QC consists, in principle for each fixed QC conformational coordinates configuration and environment perturbation, of the following steps:
R1 to be used in eqn (70)–(73), corresponding to the purely adiabatic kinetics53 (see Fig. 18). The complete reaction kinetics model can then be obtained evaluating the diabatic fraction 1 − αG = (1 − αe)Ω where αe is provided by the electronic Landau–Zener factor, see eqn (55)–(60), and Ω includes only the vibrational state overlaps of the S ground state with the T ground and first three excited vibrational states. In order to evaluate the relevant vibrational state overlaps for estimating Ω, we made use of the Duschinsky transformation94 providing the T normal mode coordinates in terms of the S ones. Such a procedure applied to a flexible QC consists, in principle for each fixed QC conformational coordinates configuration and environment perturbation, of the following steps:
 |
| | Fig. 18 Kinetic trace for the fully adiabatic ISC reaction. | |
• The evaluation of the S and T energy minimized structures and, after mass-weighted least square fitting of the T structure onto the corresponding S one (i.e. after removal of the relative roto-translation), of the corresponding normal mode coordinates and frequencies given by the eigenvectors and eigenvalues of the (mass-weighted) Hessian matrices.
• Projection of the T energy minimized structure and Hessian eigenvectors onto the S Hessian eigenvectors taken as axis of the reference frame in the mass-weighted space with origin in the S energy minimized structure, thus providing the T energy minimized structure and normal mode coordinates in terms of the S ones.
• Such a transformation allows to evaluate the vibrational state overlaps by integration of the S and T vibrational wavefunction product over the S normal mode coordinates.
It is worth to note that quantum normal modes typically correspond to only a subset of the Hessian eigenvectors, as most of the QC configurations do not correspond to a full space energy minimum and only the high frequency modes can be truly considered harmonic-like quantum vibrational modes. For sake of simplicity and considering the limited FL conformational freedom and the weak perturbation effects on the quantum vibrational modes and frequencies,95 we only considered such a transformation as obtained in the full space energy minimized S and T structures neglecting the perturbation effects (i.e. we disregard the effects due to both the conformational fluctuations and environment perturbation). Moreover by inspecting the squares of the elements of the Duschinsky matrix, i.e. the matrix given by the squared inner products of the S and T Hessian eigenvectors (see Fig. 19), we can safely conclude that within a good approximation no relevant mixing of the quantum modes is provided by the R → P transition, allowing to consider each T quantum vibrational mode as essentially coinciding with the S one of equal frequency with only a significant shift of the minimum energy position. Such evidence results in a considerable reduction of complexity for the calculation of the vibrational state overlaps, allowing to approximate the required multi-coordinates integral into the simple product of single-coordinate integrals with each integral corresponding to a single-mode vibrational state overlap.
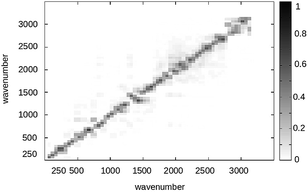 |
| | Fig. 19 Squares of the elements of the Duschinsky matrix for the FL S and T vibrational states. | |
By using the approximations described we obtained the estimate of αG (resulting rather close to zero), then providing the complete rate constant for the reaction αG(2 − αG)![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 ≈ 2αG
R1 ≈ 2αG![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 ≈ 0.0032 ± 0.0004 ps−1 corresponding to a mean lifetime of ≈312 ± 40 ps (the noise indicated is always the estimated standard error). The reported theoretical-computational results well reproduce the experimental mean lifetime67,68 (≈440 ps), indicating that the employed theoretical-computational model captures the essential physics of the ISC reaction. Interestingly, experimental evidences67,68 showed that in cyclohexane (a virtually apolar and very weakly interacting solvent) the FL S → T reaction is strongly accelerated with a reaction mean lifetime of ≈88 ps, indicating the relevant effects of the polar environment perturbation. In order to test the accuracy of our theoretical-computational methodology we performed, similarly to the previous case, MD simulations of the FL QC in vacuo, providing the NonEqMD ensemble for the gas-phase reaction. In this latter case the S diabatic vibronic ground state energy is always initially in between the energies of two T diabatic vibronic states (involving the first excited vibrational states of the T electronic ground state) as a consequence of the relevant increase of the S electronic ground state energy, thus requiring the use of eqn (78)–(81). For the gas-phase condition our results provide for the complete rate constant a corresponding mean lifetime of 16 ± 4 ps, clearly showing the dramatic acceleration of the kinetics due to the missing QC-solvent interaction and therefore possibly well explaining the experimentally observed rate constant increase in cyclohexane.
R1 ≈ 0.0032 ± 0.0004 ps−1 corresponding to a mean lifetime of ≈312 ± 40 ps (the noise indicated is always the estimated standard error). The reported theoretical-computational results well reproduce the experimental mean lifetime67,68 (≈440 ps), indicating that the employed theoretical-computational model captures the essential physics of the ISC reaction. Interestingly, experimental evidences67,68 showed that in cyclohexane (a virtually apolar and very weakly interacting solvent) the FL S → T reaction is strongly accelerated with a reaction mean lifetime of ≈88 ps, indicating the relevant effects of the polar environment perturbation. In order to test the accuracy of our theoretical-computational methodology we performed, similarly to the previous case, MD simulations of the FL QC in vacuo, providing the NonEqMD ensemble for the gas-phase reaction. In this latter case the S diabatic vibronic ground state energy is always initially in between the energies of two T diabatic vibronic states (involving the first excited vibrational states of the T electronic ground state) as a consequence of the relevant increase of the S electronic ground state energy, thus requiring the use of eqn (78)–(81). For the gas-phase condition our results provide for the complete rate constant a corresponding mean lifetime of 16 ± 4 ps, clearly showing the dramatic acceleration of the kinetics due to the missing QC-solvent interaction and therefore possibly well explaining the experimentally observed rate constant increase in cyclohexane.
For the sake of clarity we have schematized the whole procedure, employed to obtain the results described in this subsection, in the flow-chart reported in Fig. 20.
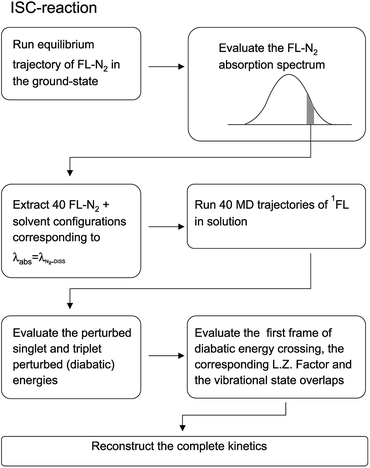 |
| | Fig. 20 Schematic representation of the relevant steps involved in the computational procedure described in the text. | |
5 Conclusions
The simulation of non-adiabatic phenomena is an extremely important issue for fundamental and practical reasons but, at the same time, is an extremely challenging task. Nowadays a large number of elegant and efficient theoretical-computational approaches, based on explicit Quantum-Dynamical (QD) or QM/MM simulations at different levels of approximation, are available for describing in great detail the energetics and the dynamics of such events for moderately sized molecular systems for a limited time-range. Much more problematic is the description of such processes for complex molecular systems spanning phase-space regions and relaxation time-ranges prohibitively large for explicit QD simulations. In this context we have presented, in this paper, a theoretical-computational methodology specifically designed at this purpose. The core of our approach is the evaluation of the diabatic perturbed energy surfaces of a preventively selected Quantum system in semi-classical interaction with its atomic-molecular environment, directly from the atomistic simulations of the whole molecular system. Subsequently, the estimation of the coupling between the diabatic surfaces and the inclusion of the obtained observables within a properly designed kinetic model allows the reconstruction of the whole phenomenology directly comparable to the experimental (typically kinetic) data. This last point together with the specific use of a diabatic representation and of the PMM framework allowing to sample large phase-space regions and relaxation lifetimes, characterize our method compared to similar QM/MM approaches. Application to two systems has demonstrated the accuracy and efficiency of the proposed method for the theoretical-computational investigations of reactive events within large and complex atomic-molecular systems, hence showing that it is a valuable tool complementary to the QD-based approaches.
Supplementary material
See supplementary material for: (i) molecular dynamics files (Gromacs-format); (ii) optimized structures utilized for MD-PMM calculations; (iii) essential dynamics analysis.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors thank CINECA (Italy) for the Iscra-C grant code IscrC-CCAE. Mr Renato Di Bartolomeo (University of l'Aquila) is acknowledged for his help in the preparation of the manuscript.
References
- S. Mahapatra, Excited Electronic States and Nonadiabatic Effects in Contemporary Chemical Dynamics, Acc. Chem. Res., 2009, 42, 1004–1015 CrossRef PubMed.
- D. Yarkony, Nonadiabatic Quantum Chemistry-Past, Present, and Future, Chem. Rev., 2012, 112, 481–498 CrossRef PubMed.
- B. F. E. Curchod and T. J. Martinez, Ab Initio Nonadiabatic Quantum Molecular Dynamics, Chem. Rev., 2018, 118, 3305–3336 CrossRef PubMed.
- G. J. Kavarnos, Fundamentals of photoinduced electron transfer, VCH, New York, 1993 Search PubMed.
- Photoinduced Electron Transfer Parts A–D, ed. M. A. Fox and M. Chanon, Elsevier, Amsterdam, 1988 Search PubMed.
- Photoinduced Electron Transfer. Parts I–IV, ed. J. Mattay, Elsevier, Amsterdam, 1988 Search PubMed.
- Heterogenoeus Photoinduced Electron Transfer, ed. M. Gratzel, CRC Publishers, Boca Raton, 1988 Search PubMed.
- J. R. Norris Jr and D. Meisel, Photochemical Energy Conversion, Elsevier, New York, 1989 Search PubMed.
- Organic Light Emitting Devices: Synthesis, Properties and Applications, ed. K. Mullen and U. Scherf, Wiley-VCH, Weinheim, 2006 Search PubMed.
- Highly Efficient OLEDs with Phosphorescent Materials, ed. H. Yersin, Wiley-VCH, Weinheim, 2008 Search PubMed.
- G. Scholes and G. R. Fleming, Energy transfer in photosynthesis, Adv. Chem. Phys., 2005, 132, 57–129 CrossRef.
- J. C. Tully, in Modern Methods for Multidimensional Dynamics Computations in Chemistry, ed. D. L. Thompson, World Scientific, Singapore, 1998 Search PubMed.
- X. Sun and W. H. Miller, Semiclassical initial value representation for electronically nonadiabatic molecular dynamics, J. Chem. Phys., 1997, 106, 6346–6353 CrossRef.
- M. Ben-Nun and T. J. Martinez, Nonadiabatic molecular dynamics: validation of the multiple spawning method for a multidimensional problem, J. Chem. Phys., 1998, 108, 7244–7257 CrossRef.
- I. Horenko, C. Salzmann, B. Schmidt and C. Schutte, Quantum-classical Liouville approach to molecular dynamics: surface hopping Gaussian phase-space packets, J. Chem. Phys., 2002, 117, 11075–11088 CrossRef.
- M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, NEWTON-X: a surface-hopping program for nonadiabatic molecular dynamics., Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33 Search PubMed.
- C. A. Schwerdtfeger, A. V. Soudackov and S. Hammes-Schiffer, Nonadiabatic dynamics of electron transfer in solution: explicit and implicit solvent treatments that include multiple relaxation time scales, J. Chem. Phys., 2014, 140, 034113 CrossRef PubMed.
- W. C. Pfalzgraff, A. Kelly and T. E. Markland, Nonadiabatic Dynamics in Atomistic Environments: Harnessing Quantum-Classical Theory with Generalized Quantum Master Equations, J. Phys. Chem. Lett., 2015, 6, 4743–4748 CrossRef PubMed.
- P. Huo and D. F. Coker, Partial linearized density matrix dynamics for dissipative, non-adiabatic quantum evolution, J. Chem. Phys., 2011, 135, 201101 CrossRef PubMed.
- R. Kapral and G. Ciccotti, Mixed quantum-classical dynamics, J. Chem. Phys., 1999, 110, 8919–8929 CrossRef.
- F. F. de Carvalho, M. E. F. Bouduban, B. F. E. Curchod and I. Tavernelli, Nonadiabatic Molecular Dynamics Based on Trajectories, Entropy, 2014, 16, 62–85 CrossRef.
- A. Jain and J. E. Subotnik Surface Hopping, Transition State Theory, and Decoherence II. Thermal Rate Constants and Detailed Balance, J. Chem. Phys., 2015, 143, 134107 CrossRef PubMed.
- I. Burghardt, M. Nest and G. A. Worth, Multiconfigurational system-bath dynamics using Gaussian wave packets: energy relaxation and decoherence induced by a finite-dimensional bath, Chem. Phys., 2003, 119, 5364–5378 Search PubMed.
- B. Lasorne, M. A. Robb and G. A. Worth, Direct quantum dynamics using variational multi-configuration Gaussian wavepackets. Implementation details and test case, Phys. Chem. Chem. Phys., 2007, 9, 3210–3227 RSC.
- H. Wang, Multilayer Multiconfigurational Time-Dependent Hartree Theory, J. Phys. Chem. A, 2015, 119, 7951–7956 CrossRef PubMed.
- F. Agostini, A. Abedi, Y. Suzuki and E. K. U. Gross, Mixed Quantum-Classical Dynamics on the Exact Time-Dependent Potential Energy Surface: A Fresh Look at Non-Adiabatic Processes, Mol. Phys., 2013, 111, 3625–3640 CrossRef.
- F. Di Maiolo, M. Masino and A. Painelli, Terahertz-pulse driven modulation of electronic spectra: modeling electron-phonon coupling in charge-transfer crystals, Phys. Rev. B, 2017, 96, 075106 CrossRef.
- W. Xie, M. Xu, S. Bai and Q. Shi, Mixed Quantum-Classical Study of Nonadiabatic Curve Crossing in Condensed Phases, J. Phys. Chem. A, 2016, 120, 3225–3232 CrossRef PubMed.
- R. A. Marcus, Electron Transfer Past and Future, Adv. Chem. Phys., 1999, 106, 1–6 Search PubMed.
- A. K. Manna and B. D. Dunietz, Charge-transfer rate constants in zinc-porphyrin-porphyrin-derived dyads: a Fermi golden rule first-principles-based study, J. Chem. Phys., 2014, 141, 121102 CrossRef PubMed.
- Y. Zhao and W. Z. Liang, Charge transfer in organic molecules for solar cells: theoretical perspective, Chem. Soc. Rev., 2012, 41, 1075 RSC.
- A. Soudackov and S. Hammes-Schiffer, Derivation of rate expressions for nonadiabatic proton-coupled electron transfer reactions in solution, J. Chem. Phys., 2000, 113, 2385–2396 CrossRef.
- A. Hazra, A. V. Soudackov and S. Hammes-Schiffer, Role of solvent dynamics in ultrafast photoinduced proton-coupled electron transfer reactions in solution, J. Phys. Chem. B, 2010, 114, 12319–12332 CrossRef PubMed.
- Comparisons of Classical and Quantum Dynamics, in Volume III of Advances in Classical Trajectory Methods, ed. W. L. Hase, JAI Press, Inc., Greenwich 1998 Search PubMed.
- A. Warshel, Dynamics of reactions in polar solvents. semiclassical trajectory studies of electron-transfer and proton-transfer reactions, J. Phys. Chem., 1982, 86, 2218–2224 CrossRef.
- X. Chen and R. J. Silbey, Excitation Energy Transfer in a Non-Markovian Dynamical Disordered Environment: Localization, Narrowing, and Transfer Efficiency, J. Phys. Chem. B, 2011, 115, 5499–5509 CrossRef PubMed.
- F. Sterpone, M. Ceccarelli and M. Marchi, Linear Response and electron transfer in complex biomolecular systems and a reaction center protein, J. Phys. Chem. B, 2003, 107, 11208 CrossRef.
- J. Blumberger and M. L. Klein, Reorganization free energies for long-range electron transfer in a porphyrin-binding four-helix bundle protein, J. Am. Chem. Soc., 2006, 128, 13854–13867 CrossRef PubMed.
- K. Ando, Solvent nuclear quantum effects in electron transfer reactions II. Molecular dynamics study on methanol solution, J. Chem. Phys., 2001, 114, 9040 CrossRef.
- L.-W. Ungar, M. D. Newton and G. A. Voth, Classical and Quantum Simulation of Electron Transfer Through a Polypeptide, J. Phys. Chem. B, 1999, 103, 7367–7382 CrossRef.
- M. Cascella, A. Magistrato, I. Tavernelli, P. Carloni and U. Rothlisberger, Role of protein frame and solvent for the redox properties of azurin from Pseudomonas aeruginosa, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19641–19646 CrossRef PubMed.
- W. R. Duncan and O. V. Prezhdo, Theoretical studies of photoinduced electron transfer in dye-sensitized TiO2, Annu. Rev. Phys. Chem., 2007, 58, 143–184 CrossRef PubMed.
- T. Kowalczyk, L.-P. Wang and T. Van Voorhis, Simulation of Solution Phase Electron Transfer in a Compact Donor–Acceptor Dyad, J. Phys. Chem. B, 2011, 115, 12135–12144 CrossRef PubMed.
- V. Cantatore, G. Granucci and M. Persico, Simulation of the pi-pi* photodynamics of azobenzene: decoherence and solvent effects, Comput. Theor. Chem., 2014, 1040, 126–135 CrossRef.
- J. Cerezo, Y. Liu, N. Lin, X. Zhao, R. Improta and F. Santoro, Mixed Quantum/Classical Method for Nonadiabatic Quantum Dynamics in Explicit Solvent Models: The ÏĂÏĂ*/nÏĂ* Decay of Thymine in Water as a Test Case, J. Chem. Theory Comput., 2018, 14, 820–832 CrossRef PubMed.
- S. Thallmair, J. P. P. Zauleck and R. de Vivie-Riedle, Quantum Dynamics in an Explicit Solvent Environment: A Photochemical Bond Cleavage Treated with a Combined QD/MD Approach, J. Chem. Theory Comput., 2015, 11, 1987–1995 CrossRef PubMed.
- P. Huo, S. Bonella, L. Chen and D. Coker, Linearized approximations for condensed phase non-adiabatic dynamics: multi-layered baths and Brownian dynamics implementation, Chem. Phys., 2010, 370, 87–97 CrossRef.
- M. Tachiya, Generalization of the Marcus equation for the electron-transfer rate, J. Phys. Chem., 1993, 97, 5911 CrossRef.
- W. Credo Chung, S. Nanbu and T. Ishida, QM/MM Trajectory Surface Hopping Approach to Photoisomerization of Rhodopsin and Isorhodopsin: The Origin of Faster and More Efficient Isomerization for Rhodopsin, J. Phys. Chem. B, 2012, 116, 8009–8023 CrossRef PubMed.
- L. M. Frutos, T. Andruniow, F. Santoro, N. Ferré and M. Olivucci, Tracking the excited-state time evolution of the visual pigment with multiconfigurational quantum chemistry, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 7764–7769 CrossRef PubMed.
- O. Weingart, P. Altoe', M. Stenta, A. Bottoni, G. Orlandi and M. Garavelli, Product formation in rhodopsin by fast hydrogen motions, Phys. Chem. Chem. Phys., 2011, 13, 3645–3648 RSC.
- N. O. Carstensen, QM/MM surface-hopping dynamics of a bridged azobenzene derivative, Phys. Chem. Chem. Phys., 2013, 15, 15017–15026 RSC.
- A. Amadei, I. Daidone and M. Aschi, A general theoretical model for electron transfer reactions in complex systems, Phys. Chem. Chem. Phys., 2012, 14, 1360 RSC.
- M. Aschi, R. Spezia, A. Di Nola, A. Amadei and X. Chem, Phys. Lett., 2001, 344, 374 Search PubMed.
- A. Amadei, M. D'Alessandro, M. D'Abramo and M. Aschi, Theoretical characterization of electronic states in interacting chemical systems, J. Chem. Phys., 2009, 130, 08410 CrossRef PubMed.
- M. Aschi, M. D'Abramo and A. Amadei, Photoinduced electron transfer in a dichromophoric peptide: a numerical experiment, Theor. Chem. Acc., 2016, 135, 132 Search PubMed.
- G. Piacente, A. Amadei, M. D'Abramo, I. Daidone and M. Aschi, Theoretical-computational modeling of photo-induced charge separation spectra and charge recombination kinetics in solution, Phys. Chem. Chem. Phys., 2014, 16(38), 20624–20638 RSC.
- L. Zanetti-Polzi, M. Aschi, A. Amadei and I. Daidone, Alternative Electron-Transfer Channels Ensure Ultrafast Deactivation of Light-Induced Excited States in Riboflavin Binding Protein, J. Phys. Chem. Lett., 2017, 8(14), 3321–3327 CrossRef PubMed.
- L. Landau, Zur Theorie der Energieubertragung II. Phys. Zeit, der Sowjetunion, 1932, vol. 2, pp. 46–51 Search PubMed.
- C. Zener, Non-Adiabatic Crossing of Energy Levels, Proc. R. Soc. London, 1932, 137, 696–702 CrossRef.
- C. G. Stueckelberg, Theorie der unelastischen Stosse zwischen Atomen, Helv. Phys. Acta, 1932, 5, 369 Search PubMed.
- C. Zhu and H. Nakamura, Theory of non adiabatic transitions for general two-state curve crossing problems I. Nonadiabatic tunneling case, J. Chem. Phys., 1994, 101, 10630 CrossRef.
- C. Zhu and H. Nakamura, Theory of non adiabatic transitions for general two-state curve crossing problems II. Landau–Zener case, J. Chem. Phys., 1995, 102, 7448 CrossRef.
- J. M. Warman, K. J. Smit, M. P. de Haas, S. A. Jonker, M. N. Paddon-Row, A. M. Oliver, J. Kroon, H. Oevering and J. W. Verhoeven, Long-distance Charge Recombination within Rigid Molecular Assemblies in Nondipolar Solvent, J. Phys. Chem., 1991, 95, 1979–1987 CrossRef.
- M. Seischab, T. Lodenkemper, A. Stockmann, S. Schneider, M. Koeberg, M. R. Roest, J. W. Verhoeven, J. M. Lawson and M. N. Paddon-Row, Phys. Chem. Chem. Phys., 2000, 2, 1889–1897 RSC.
- J. W. Verhoeven, On the role of spin correlation in the formation, decay and detection of long-lived, intramolecular charge transfer states, J. Photochem. Photobiol., C, 2006, 7, 40–60 CrossRef.
- J. Wang, J. Kubicki, H. Peng and M. S. Platz, Influence of Solvent on Carbene Intersystem Crossing Rates, J. Am. Chem. Soc., 2007, 130, 6604–6609 CrossRef PubMed.
- J. Wang, J. Kubicki, E. F. Hilinski, S. L. Mecklenburg, T. L. Gustafson and M. S. Platz, Ultrafast Study of 9-Diazofluorene: Direct Observation of the First Two Singlet States of Fluorenylidene, J. Am. Chem. Soc., 2007, 129, 13689–13690 Search PubMed.
- U. Fano, Description of States in Quantum Mechanics by Density Matrix and Operator Techniques, Rev. Mod. Phys., 1957, 29, 74 CrossRef.
- W. H. Loisell, Quantum Statistical Properties of Radiations, Wiley, New York, 1973 Search PubMed.
- K. Blum, Density Matrix Theory and Applications, Plenum Press, New York, 1996 Search PubMed.
- M. Aschi, V. Barone, B. Carlotti, I. Daidone, F. Elisei and A. Amadei, Photoexcitation and relaxation kinetics of molecular systems in solution: towards a complete in silico model, Phys. Chem. Chem. Phys., 2016, 18(41), 28919–28931 RSC.
- M. D'Alessandro, M. Aschi, C. Mazzuca, A. Palleschi and A. Amadei, Theoretical modeling of UV-Vis absorption and emission spectra in liquid state systems including vibrational and conformational effects: the vertical transition approximation (Erratum), J. Chem. Phys., 2013, 139, 139902 CrossRef.
- M. D'Abramo, M. Aschi and A. Amadei, Theoretical modeling of UV-Vis absorption and emission spectra in liquid state systems including vibrational and conformational effects: explicit treatment of the vibronic transitions, J. Chem. Phys., 2013, 140(16), 164104 CrossRef PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: a message-passing parallel molecular dynamics implementation., Comput. Phys. Commun., 1995, 91, 43–56 CrossRef.
- W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular Simulation: The GROMOS96 Manual and User Guide, Hochschulverlag AG an der ETH Zürich, Zürich, 1996 Search PubMed.
- B. H. Besler, K. M. Merz Jr and P. A. Kollman, Atomic charges derived from semiempirical methods, J. Comput. Chem., 1990, 21, 431–439 CrossRef.
- X. Grabuleda, C. Jaime and P. A. Kollman, Molecular dynamics simulation studies of liquid acetonitrile: new six-site model, J. Comput. Chem., 2000, 21, 901–908 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2017, 126, 014101 CrossRef PubMed.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. C. E. M. Frajie, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 81, 1463 CrossRef.
- T. A. Darden, D. M. York and L. G. Pedersen, Particle mesh Ewald: an Nlog(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089 CrossRef.
- S. Del Galdo and A. Amadei, The unfolding effects on the protein hydration shell and partial molar volume: a computational study, Phys. Chem. Chem. Phys., 2016, 18, 28175–28182 RSC.
- J. M. Briggs, T. Matsui and W. L. Jorgensen, Monte Carlo simulations of liquid alkyl ethers with the OPLS potential functions, J. Comput. Chem., 1990, 11, 958–971 CrossRef.
- A. Amadei, A. B. Linssen and H. J. Berendsen, Essential dynamics of proteins, Proteins, 1993, 17(4), 412–425 CrossRef PubMed.
- R. G. Parr and W. Yang, Density functional theory of atoms and molecules, Oxford University Press, New York, 1999 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 32(2), 785–789 CrossRef.
- A. D. Becke, Density-functional thermochemistry III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648 CrossRef.
- M. A. L. Marques and E. K. U. Gross, Time-dependent density functional theory, Annu. Rev. Phys. Chem., 2004, 55, 427–455 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- P. Jorgensen, H. J. A. Jensen and J. Olsen, Linear response calculations for large scale multiconfiguration self-consistent field wave functions, J. Chem. Phys., 1988, 89, 3654 CrossRef.
- T. D. Poulsen, P. R. Ogilby and K. V. Mikkelsen, Quadratic response of molecules in a nonequilibrium and equilibrium solvation model: Generalizations to include both singlet and triplet perturbations, J. Chem. Phys., 1999, 111, 2678 CrossRef.
- C. Angeli, K. L. Bak, V. Bakken, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, T. Enevoldsen and B. Fernandez, et al., Release Dalton, 2011 Search PubMed.
- H. Lee Woodcock, D. Moran, B. R. Brooks, P. v. R. Schleyer and H. F. Schaefer III, Carbene Stabilization by Aryl Substituents. Is Bigger Better?, J. Am. Chem. Soc., 2007, 129, 3763–3770 CrossRef PubMed.
- F. Duschinsky, Acta Physicochim URSS, 1937, 7, 551 Search PubMed.
- L. Zanetti-Polzi, M. Aschi, A. Amadei and I. Daidone, Simulation of the Amide I Infrared Spectrum in Photoinduced Peptide Folding/Unfolding Transitions, J. Phys. Chem. B, 2013, 117, 12383–12390 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the force fields; optimized geometries. See DOI: 10.1039/c8ra03900c |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b
*b

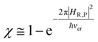 with HR,P the reactant–product coupling and vcr the absolute value of the diabatic energy difference time derivative at the crossing) we can schematize the R → P reaction occurring through the TR crossing as shown in Fig. 5 where A and B stand for either the I or II adiabatic surface index and the TRRA represents the TR chemical state as obtained by the reactive trajectories entering the transition region from RA (i.e. the reactive trajectories moving over an energy surface comprised within the A adiabatic and R diabatic surfaces).
with HR,P the reactant–product coupling and vcr the absolute value of the diabatic energy difference time derivative at the crossing) we can schematize the R → P reaction occurring through the TR crossing as shown in Fig. 5 where A and B stand for either the I or II adiabatic surface index and the TRRA represents the TR chemical state as obtained by the reactive trajectories entering the transition region from RA (i.e. the reactive trajectories moving over an energy surface comprised within the A adiabatic and R diabatic surfaces).
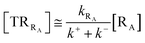
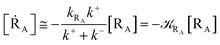
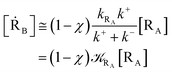
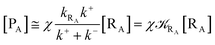
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l values, providing
RA,l values, providing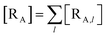
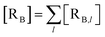
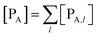
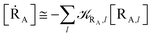
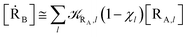
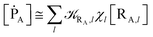
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l and χl (i.e. 〈
RA,l and χl (i.e. 〈![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,lχl〉 ≅ 〈
RA,lχl〉 ≅ 〈![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA,l〉 〈χl〉), thus allowing to write
RA,l〉 〈χl〉), thus allowing to write![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA[RA]
RA[RA]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA(1 − α)[RA]
RA(1 − α)[RA]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RAα[RA]
RAα[RA]
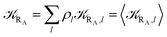
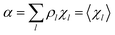
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) RA), as we obtained in previous papers.53,56–58 Moreover, from the ensemble of the diabatic surfaces crossings as provided by the reactive trajectories it is also possible to obtain α = 〈χl〉 by simply evaluating by means of the Landau–Zener approach the adiabatic fraction at each crossing and then averaging over the crossings.
RA), as we obtained in previous papers.53,56–58 Moreover, from the ensemble of the diabatic surfaces crossings as provided by the reactive trajectories it is also possible to obtain α = 〈χl〉 by simply evaluating by means of the Landau–Zener approach the adiabatic fraction at each crossing and then averaging over the crossings.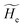 ) within the dipolar approximation
) within the dipolar approximation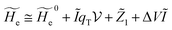
![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) 1]j,j′ = −E⋅〈Φ0e,j|
1]j,j′ = −E⋅〈Φ0e,j|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |Φ0e,j′〉
|Φ0e,j′〉
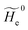 is the unperturbed electronic Hamiltonian matrix (diagonal within the chosen basis set), qT and
is the unperturbed electronic Hamiltonian matrix (diagonal within the chosen basis set), qT and ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) are the QC total charge and dipole operator,
are the QC total charge and dipole operator, ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) and E are the electric potential and field as exerted by the environment on the QC centre of mass and Φ0e,j(ξc, β) becoming parametrically functions of only the QC conformational ξc coordinates when considering also the β coordinates as relaxed to their ξc-dependent energy minimized position as obtained in a reference eigenstate (e.g. the ground state), thus disregarding any explicit quantum vibrational effect73 (note that the use of electronic coordinates within the internal QC reference of frame requires that both
and E are the electric potential and field as exerted by the environment on the QC centre of mass and Φ0e,j(ξc, β) becoming parametrically functions of only the QC conformational ξc coordinates when considering also the β coordinates as relaxed to their ξc-dependent energy minimized position as obtained in a reference eigenstate (e.g. the ground state), thus disregarding any explicit quantum vibrational effect73 (note that the use of electronic coordinates within the internal QC reference of frame requires that both ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) and E must be also expressed within the internal QC reference of frame or, equivalently, that 〈Φ0e,j|
and E must be also expressed within the internal QC reference of frame or, equivalently, that 〈Φ0e,j|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e0b3.gif) |Φ0e,j′〉 be expressed in the reference of frame providing E). Finally, ΔV includes all the other terms treated as a simple short range potential and Ĩ is the identity matrix. Note that we assume, as usual, the R and P quantum vibrational modes as fully defined within the same QC internal coordinates subspace (i.e. the diabatic states share the same QC semiclassical configurational subspace) and thus in both diabatic states the same ξc, β coordinates can be used. The eigenvalues and eigenvectors of
|Φ0e,j′〉 be expressed in the reference of frame providing E). Finally, ΔV includes all the other terms treated as a simple short range potential and Ĩ is the identity matrix. Note that we assume, as usual, the R and P quantum vibrational modes as fully defined within the same QC internal coordinates subspace (i.e. the diabatic states share the same QC semiclassical configurational subspace) and thus in both diabatic states the same ξc, β coordinates can be used. The eigenvalues and eigenvectors of 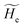 provide the actual perturbed electronic energies and eigenstates (adiabatic electronic states) while its elements corresponding to the diabatic electronic states of the CT reaction of interest (i.e. Φ0e,R, Φ0e,P) can be used to obtain the diabatic electronic energy change (electronic transition energy) Δ
provide the actual perturbed electronic energies and eigenstates (adiabatic electronic states) while its elements corresponding to the diabatic electronic states of the CT reaction of interest (i.e. Φ0e,R, Φ0e,P) can be used to obtain the diabatic electronic energy change (electronic transition energy) Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e
e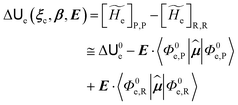
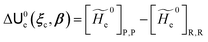
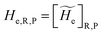
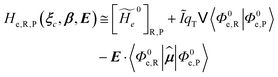
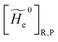 always zero except for the special case Φ0e,R = Φ0e,P (i.e. the diabatic vibronic states involve the same diabatic electronic state and hence 〈Φ0e,R|Φ0e,P〉 = 1 and Δ
always zero except for the special case Φ0e,R = Φ0e,P (i.e. the diabatic vibronic states involve the same diabatic electronic state and hence 〈Φ0e,R|Φ0e,P〉 = 1 and Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e = 0). Such a peculiar condition which is uncommon and requires a specific treatment will not be further discussed and in the following of this paper we will consider only the typical case of diabatic vibronic states involving different (non-degenerate in the unperturbed condition) diabatic electronic states.
e = 0). Such a peculiar condition which is uncommon and requires a specific treatment will not be further discussed and in the following of this paper we will consider only the typical case of diabatic vibronic states involving different (non-degenerate in the unperturbed condition) diabatic electronic states.![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) and, within the Landau–Zener approach, the fraction of adiabatic transitions (χ) in a R → P event involving a given ϕ0v,R,l(ξc, β) → ϕ0v,P,l′(ξc, β) vibrational state transition where ϕ0v,R,l, ϕ0v,P,l′ are, respectively, harmonic-like vibrational states of the diabatic electronic states Φ0e,R and Φ0e,P as obtained within the R and P electronic energy minima relevant for the R → P process (note that the vibrational states are functions of the internal coordinates β and only parametrically functions of the conformational coordinates ξc). Therefore, for a given possible reaction event (i.e. diabatic energy surfaces crossing) the corresponding complete transition energy and diabatic fraction 1 − χ are
and, within the Landau–Zener approach, the fraction of adiabatic transitions (χ) in a R → P event involving a given ϕ0v,R,l(ξc, β) → ϕ0v,P,l′(ξc, β) vibrational state transition where ϕ0v,R,l, ϕ0v,P,l′ are, respectively, harmonic-like vibrational states of the diabatic electronic states Φ0e,R and Φ0e,P as obtained within the R and P electronic energy minima relevant for the R → P process (note that the vibrational states are functions of the internal coordinates β and only parametrically functions of the conformational coordinates ξc). Therefore, for a given possible reaction event (i.e. diabatic energy surfaces crossing) the corresponding complete transition energy and diabatic fraction 1 − χ are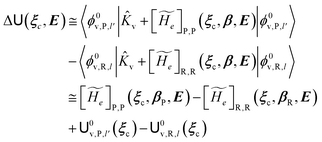
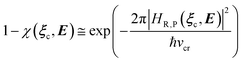
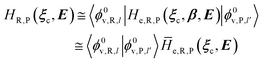
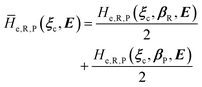
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) v the kinetic energy operator for the nuclear quantum vibrational coordinates,
v the kinetic energy operator for the nuclear quantum vibrational coordinates, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) 0v,R,l,
0v,R,l, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) 0v,P,l′ the unperturbed quantum vibrational energies corresponding to ϕ0v,R,l and ϕ0v,P,l′, respectively (i.e. we disregard the perturbing electric field effects on the vibrational energy difference), βR(ξc) and βP(ξc) the ξc-dependent minimum energy positions of the quantum vibrational coordinates β for the R and P diabatic states and in eqn (24) the crossing velocity vcr (i.e. the absolute value of the transition energy time derivative) as well as the conformational coordinates and the perturbing field are all to be evaluated at the crossing (i.e. when Δ
0v,P,l′ the unperturbed quantum vibrational energies corresponding to ϕ0v,R,l and ϕ0v,P,l′, respectively (i.e. we disregard the perturbing electric field effects on the vibrational energy difference), βR(ξc) and βP(ξc) the ξc-dependent minimum energy positions of the quantum vibrational coordinates β for the R and P diabatic states and in eqn (24) the crossing velocity vcr (i.e. the absolute value of the transition energy time derivative) as well as the conformational coordinates and the perturbing field are all to be evaluated at the crossing (i.e. when Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) = 0) thus providing the constant coupling term for the Landau–Zener formula. Note that typically |〈ϕ0v,R,l|ϕ0v,P,l′〉〈Φ0e,R|
= 0) thus providing the constant coupling term for the Landau–Zener formula. Note that typically |〈ϕ0v,R,l|ϕ0v,P,l′〉〈Φ0e,R|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) |Φ0e,P〉|≪|〈Φ0e,P|
|Φ0e,P〉|≪|〈Φ0e,P|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) |Φ0e,P〉 − 〈Φ0e,R|
|Φ0e,P〉 − 〈Φ0e,R|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) |Φ0e,R〉| thus allowing, within the whole TR, to consider the variation of
|Φ0e,R〉| thus allowing, within the whole TR, to consider the variation of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) R,P as approximately negligible compared to the nearly linear variation of Δ
R,P as approximately negligible compared to the nearly linear variation of Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) . Finally, eqn (25) can be really accurate when the βR and βP minima are close enough to allow considering He,R,P virtually constant within the relevant β range, with He,R,P(ξc, βR, E) ≅ He,R,P(ξc, βP, E) significantly different from zero (i.e. really negligible non-adiabatic coupling).
. Finally, eqn (25) can be really accurate when the βR and βP minima are close enough to allow considering He,R,P virtually constant within the relevant β range, with He,R,P(ξc, βR, E) ≅ He,R,P(ξc, βP, E) significantly different from zero (i.e. really negligible non-adiabatic coupling).
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e =
e = ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,P −
e,P − ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,R where
e,R where ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,R,
e,R, ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) e,P are eigenvalues of the electronic Hamiltonian matrix corresponding to the R and P magnetic state, respectively, and the electronic coupling term corresponding to the R, P element of the perturbed electronic Hamiltonian matrix (including the magnetic interactions) expressed within the diabatic electronic-spin basis set, is given by
e,P are eigenvalues of the electronic Hamiltonian matrix corresponding to the R and P magnetic state, respectively, and the electronic coupling term corresponding to the R, P element of the perturbed electronic Hamiltonian matrix (including the magnetic interactions) expressed within the diabatic electronic-spin basis set, is given by![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) soηP
soηP
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) so is the corresponding matrix and ηRηP the unit vectors representing Φe,RσR and Φe,PσP within the same basis set used to express the spin–orbit matrix (i.e. the unperturbed basis set). Note that typically 〈Φe,RσR|Ĥso|Φe,PσP〉 is only slightly dependent on the perturbation and hence virtually constant within the TR.
so is the corresponding matrix and ηRηP the unit vectors representing Φe,RσR and Φe,PσP within the same basis set used to express the spin–orbit matrix (i.e. the unperturbed basis set). Note that typically 〈Φe,RσR|Ĥso|Φe,PσP〉 is only slightly dependent on the perturbation and hence virtually constant within the TR.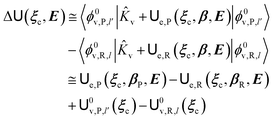
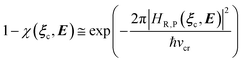
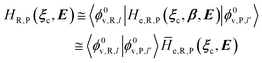
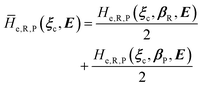
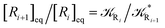 equilibrium constant (i.e. the equilibrium constant must be independent of the diabatic-adiabatic TR traversing behavior).
equilibrium constant (i.e. the equilibrium constant must be independent of the diabatic-adiabatic TR traversing behavior).

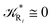 , providing
, providing![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1] −
R1[R1] − ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R2[R2]
R2[R2]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri−1[Ri−1] −
Ri−1[Ri−1] − ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri[Ri]
Ri[Ri]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Rn−1[Rn−1]
Rn−1[Rn−1]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ri ≅ 0 and hence
Ri ≅ 0 and hence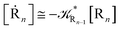
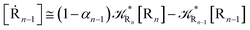
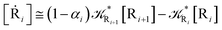
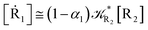
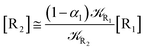
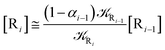
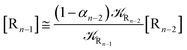
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
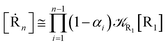
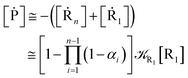
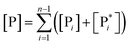 . Similarly, for the Rn → R1 process we have
. Similarly, for the Rn → R1 process we have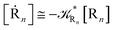
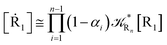
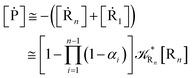
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 with
R1 with 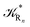 . These last equations can be further simplified considering that from eqn (24), (25), (29) and (30) for each ith reaction step, assuming the R diabatic vibronic state involving the l vibrational state, we have
. These last equations can be further simplified considering that from eqn (24), (25), (29) and (30) for each ith reaction step, assuming the R diabatic vibronic state involving the l vibrational state, we have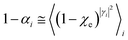
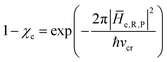
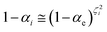
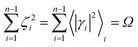 with 0 ≤ Ω ≤ 1. The use of eqn (58) into eqn (49)–(54) then provides for the R1 → Rn kinetics
with 0 ≤ Ω ≤ 1. The use of eqn (58) into eqn (49)–(54) then provides for the R1 → Rn kinetics![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
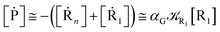
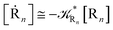
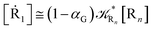
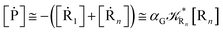
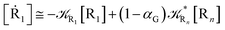
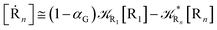
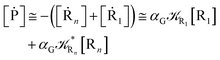

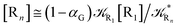 ) we have
) we have![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1[R1]
R1[R1]
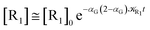
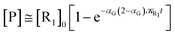
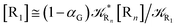 ) we can write
) we can write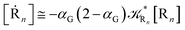
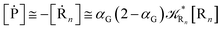
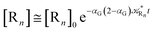
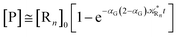
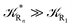 and eqn (74)–(77) implies
and eqn (74)–(77) implies 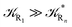 ). Remarkably, eqn (70)–(77) clearly show that within the irreversible reaction step approximation when Ω ≅ 1 and thus 1 − αG ≅ 1 − αe and αG ≅ αe, no explicit vibrational effect is present in the complete reaction kinetics and hence for such a condition in the limit αe → 1 eqn (70)–(77) reduce essentially to the expressions we derived and used in previous papers (ref), based on assuming fully adiabatic ET reactions when neglecting any explicit vibrational effect. Such a result well explains the accuracy of the simpler purely electronic approach utilized previously, indicating that in most typical ET reactions Ω ≈ 1 and αe ≈ 1 thus providing a kinetic behavior equivalent to adiabatic reactions involving purely electronic diabatic states.
). Remarkably, eqn (70)–(77) clearly show that within the irreversible reaction step approximation when Ω ≅ 1 and thus 1 − αG ≅ 1 − αe and αG ≅ αe, no explicit vibrational effect is present in the complete reaction kinetics and hence for such a condition in the limit αe → 1 eqn (70)–(77) reduce essentially to the expressions we derived and used in previous papers (ref), based on assuming fully adiabatic ET reactions when neglecting any explicit vibrational effect. Such a result well explains the accuracy of the simpler purely electronic approach utilized previously, indicating that in most typical ET reactions Ω ≈ 1 and αe ≈ 1 thus providing a kinetic behavior equivalent to adiabatic reactions involving purely electronic diabatic states.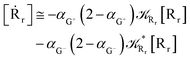
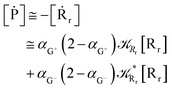
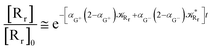
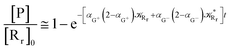




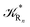 to be used in eqn (74)–(77), corresponding to the purely adiabatic kinetics53 (see Fig. 15) and hence for the complete reaction kinetics model we also need to evaluate the diabatic fraction 1 − αG = (1 − αe)Ω. For the present CT reaction, similarly to most of the typical CT reactions, the initial relevant vibronic crossing involves the P vibronic diabatic state corresponding to the vertical transition, with hence the largest vibrational state overlap, associated to a highly excited and strongly anharmonic P vibrational state. Such a condition avoids the use of any computationally explicit evaluation of the vibrational effects, necessarily based on the assumption of either the harmonic or slightly anharmonic behaviour of the P vibrational states of interest (note that for the R chemical state we consider only the diabatic vibronic state corresponding to the ground vibrational state). Therefore, for the present CT reaction in order to obtain an achievable efficient computational model and on the basis of the high density in energy of the relevant P vibronic states involved in the first reaction steps and corresponding large vibrational state overlaps, we assume Ω ≈ 1 and hence αG ≈ αe thus reducing the evaluation of the diabatic fraction to the purely electronic Landau–Zener factor, see eqn (55)–(60). As discussed in the Theory section such an assumption can be considered a reasonable approximation in typical CT reactions, at least when the initial reaction step involves the P vibronic state corresponding to the R → P vertical transition. From Fig. 15 we obtained
to be used in eqn (74)–(77), corresponding to the purely adiabatic kinetics53 (see Fig. 15) and hence for the complete reaction kinetics model we also need to evaluate the diabatic fraction 1 − αG = (1 − αe)Ω. For the present CT reaction, similarly to most of the typical CT reactions, the initial relevant vibronic crossing involves the P vibronic diabatic state corresponding to the vertical transition, with hence the largest vibrational state overlap, associated to a highly excited and strongly anharmonic P vibrational state. Such a condition avoids the use of any computationally explicit evaluation of the vibrational effects, necessarily based on the assumption of either the harmonic or slightly anharmonic behaviour of the P vibrational states of interest (note that for the R chemical state we consider only the diabatic vibronic state corresponding to the ground vibrational state). Therefore, for the present CT reaction in order to obtain an achievable efficient computational model and on the basis of the high density in energy of the relevant P vibronic states involved in the first reaction steps and corresponding large vibrational state overlaps, we assume Ω ≈ 1 and hence αG ≈ αe thus reducing the evaluation of the diabatic fraction to the purely electronic Landau–Zener factor, see eqn (55)–(60). As discussed in the Theory section such an assumption can be considered a reasonable approximation in typical CT reactions, at least when the initial reaction step involves the P vibronic state corresponding to the R → P vertical transition. From Fig. 15 we obtained 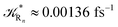 (corresponding to the purely adiabatic mean lifetime of ≈735 fs) and from the first diabatic energy crossing ensemble αG ≈ αe = 0.675 ± 0.035 providing, within our model, the complete rate constant for the reaction
(corresponding to the purely adiabatic mean lifetime of ≈735 fs) and from the first diabatic energy crossing ensemble αG ≈ αe = 0.675 ± 0.035 providing, within our model, the complete rate constant for the reaction 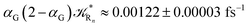 corresponding to a mean lifetime of ≈822 ± 20 fs (the noise indicated is always the estimated standard error). The reported theoretical-computational results reasonably well reproduce the experimental mean lifetime64–66 (≈360 fs), indicating that the employed theoretical-computational model captures the essential physics of the CT reaction.
corresponding to a mean lifetime of ≈822 ± 20 fs (the noise indicated is always the estimated standard error). The reported theoretical-computational results reasonably well reproduce the experimental mean lifetime64–66 (≈360 fs), indicating that the employed theoretical-computational model captures the essential physics of the CT reaction.
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 to be used in eqn (70)–(73), corresponding to the purely adiabatic kinetics53 (see Fig. 18). The complete reaction kinetics model can then be obtained evaluating the diabatic fraction 1 − αG = (1 − αe)Ω where αe is provided by the electronic Landau–Zener factor, see eqn (55)–(60), and Ω includes only the vibrational state overlaps of the S ground state with the T ground and first three excited vibrational states. In order to evaluate the relevant vibrational state overlaps for estimating Ω, we made use of the Duschinsky transformation94 providing the T normal mode coordinates in terms of the S ones. Such a procedure applied to a flexible QC consists, in principle for each fixed QC conformational coordinates configuration and environment perturbation, of the following steps:
R1 to be used in eqn (70)–(73), corresponding to the purely adiabatic kinetics53 (see Fig. 18). The complete reaction kinetics model can then be obtained evaluating the diabatic fraction 1 − αG = (1 − αe)Ω where αe is provided by the electronic Landau–Zener factor, see eqn (55)–(60), and Ω includes only the vibrational state overlaps of the S ground state with the T ground and first three excited vibrational states. In order to evaluate the relevant vibrational state overlaps for estimating Ω, we made use of the Duschinsky transformation94 providing the T normal mode coordinates in terms of the S ones. Such a procedure applied to a flexible QC consists, in principle for each fixed QC conformational coordinates configuration and environment perturbation, of the following steps:![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 ≈ 2αG
R1 ≈ 2αG![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) R1 ≈ 0.0032 ± 0.0004 ps−1 corresponding to a mean lifetime of ≈312 ± 40 ps (the noise indicated is always the estimated standard error). The reported theoretical-computational results well reproduce the experimental mean lifetime67,68 (≈440 ps), indicating that the employed theoretical-computational model captures the essential physics of the ISC reaction. Interestingly, experimental evidences67,68 showed that in cyclohexane (a virtually apolar and very weakly interacting solvent) the FL S → T reaction is strongly accelerated with a reaction mean lifetime of ≈88 ps, indicating the relevant effects of the polar environment perturbation. In order to test the accuracy of our theoretical-computational methodology we performed, similarly to the previous case, MD simulations of the FL QC in vacuo, providing the NonEqMD ensemble for the gas-phase reaction. In this latter case the S diabatic vibronic ground state energy is always initially in between the energies of two T diabatic vibronic states (involving the first excited vibrational states of the T electronic ground state) as a consequence of the relevant increase of the S electronic ground state energy, thus requiring the use of eqn (78)–(81). For the gas-phase condition our results provide for the complete rate constant a corresponding mean lifetime of 16 ± 4 ps, clearly showing the dramatic acceleration of the kinetics due to the missing QC-solvent interaction and therefore possibly well explaining the experimentally observed rate constant increase in cyclohexane.
R1 ≈ 0.0032 ± 0.0004 ps−1 corresponding to a mean lifetime of ≈312 ± 40 ps (the noise indicated is always the estimated standard error). The reported theoretical-computational results well reproduce the experimental mean lifetime67,68 (≈440 ps), indicating that the employed theoretical-computational model captures the essential physics of the ISC reaction. Interestingly, experimental evidences67,68 showed that in cyclohexane (a virtually apolar and very weakly interacting solvent) the FL S → T reaction is strongly accelerated with a reaction mean lifetime of ≈88 ps, indicating the relevant effects of the polar environment perturbation. In order to test the accuracy of our theoretical-computational methodology we performed, similarly to the previous case, MD simulations of the FL QC in vacuo, providing the NonEqMD ensemble for the gas-phase reaction. In this latter case the S diabatic vibronic ground state energy is always initially in between the energies of two T diabatic vibronic states (involving the first excited vibrational states of the T electronic ground state) as a consequence of the relevant increase of the S electronic ground state energy, thus requiring the use of eqn (78)–(81). For the gas-phase condition our results provide for the complete rate constant a corresponding mean lifetime of 16 ± 4 ps, clearly showing the dramatic acceleration of the kinetics due to the missing QC-solvent interaction and therefore possibly well explaining the experimentally observed rate constant increase in cyclohexane.











