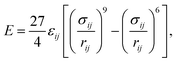Open Access Article
Open Access ArticleMolecular dynamics simulation of droplet nucleation and growth on a rough surface: revealing the microscopic mechanism of the flooding mode
Dong Niu and
GuiHua Tang *
*
MOE Key Laboratory of Thermo-Fluid Science and Engineering, School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, P. R. China. E-mail: ghtang@mail.xjtu.edu.cn; Fax: +86 29 82665445; Tel: +86 29 82665319
First published on 6th July 2018
Abstract
Droplet nucleation and growth have a significant influence on dropwise condensation heat transfer. Controlling the droplet nucleation and growth with a high-precision surface to realize the dropwise condensation heat transfer enhancement is a promising method. Molecular dynamics simulation is employed to investigate the effects of heat flux, surface wettability and adjacent droplet size on the new droplet's nucleation and growth. Simulation results indicate that the high heat flux can lead to droplet nucleation and growth inside the rough structure and finally a Wenzel droplet will form due to the coalescence between the inside droplet and the initial existing droplet. However, for a surface with a larger contact angle, the droplet in the Wenzel state will transfer to the Cassie state due to droplet coalescence. In addition, it is also related to the size of the existing droplet whether or not the nucleation process occurs. For the first time, the droplet nucleation radius is introduced to quantitatively determine the droplet nucleation state (inside or outside the nanostructures) and whether the droplet could achieve the state transition from Wenzel to Cassie or not in the growth process.
1. Introduction
Dropwise condensation heat transfer has been extensively studied because of its high heat transfer coefficient and great potential in industrial applications such as energy conversion,1,2 water recovery,3,4 and electronic device cooling.5 Considering the whole dropwise condensation process including droplet nucleation, growth, coalescence and departure, droplet nucleation and growth play a significant role in dropwise condensation heat transfer as the initial stage of dropwise condensation. To achieve condensation heat transfer enhancement, numerous studies about droplet nucleation and growth have been conducted. To reveal nucleation mechanisms, Yamada et al.6 investigated water vapour condensation on the hybrid hydrophilic–hydrophobic surface. Experimental results demonstrated that droplets would nucleate on the hydrophilic areas under unsaturated conditions, which extended the heterogeneous nucleation theory by considering the water molecules attracted to the hydrophilic area. The effect of microstructures on the heterogeneous nucleation of water droplets was investigated.7 The results indicated that the conical cavities with narrower cone angles would reduce the nucleation free energy barrier compared with apexes or the planar substrate and lead to a relatively higher nucleation capability. The nucleation size distribution model was introduced into the water vapour condensation system to investigate the kinetics of the initial condensation stage.8 The results proved that the growth or decay of a cluster is significantly affected by the cluster size and contact angles of the solid surface. Lv et al.9 explored the vapour condensation on micro-nanostructured superhydrophobic surfaces using an in situ observation technology. Experimental results showed that the droplet preferentially nucleates at the top and the edge of the micropillars. Spatially controlling heterogeneous nucleation by engineering the free energy barrier10 was proved to be able to achieve the rapid and continuous shedding of the condensate on the superhydrophobic surface. Wen et al.11 indicated that the droplet wetting transition and dynamic behaviour on nanostructured superhydrophobic surfaces depend on the synergistic coordination of surface properties and the condensation condition due to the effect of the spatial confinement on droplet nucleation. This can be used to guide the optimization of condensation surface to achieve heat transfer enhancement under a broad range of condensing conditions. For droplet growth mechanism, there also exists an enormous amount of research including the theoretical model and experimental observation. Tanaka12 developed a dropwise condensation heat transfer model by introducing two different mechanisms of droplet growth which are direct vapour condensation and coalescence with adjacent droplets. The mechanism of microdroplet growth on superhydrophobic surface was investigated with optimized environmental scanning electron microscopy imaging and growth simulations.13 The constant contact angle and the constant base growth models were employed to quantify the impact of the growth mode on the microdroplet formation time and average heat transfer rate through the droplet. Sharma et al.14 demonstrated that the individual droplet growth rates vary significantly on the surface textures and this variation in growth rate on the hierarchical texture is mainly controlled by droplet growth dynamics on the nanostructure covering the microstructure.Molecular dynamics simulation was also employed to investigate the droplet behaviour such as the state on the rough surface, nucleation and coalescence-induced jumping. Niu and Tang15 investigated the static and dynamic behaviour of water droplet on solid surfaces with pillar-type nanostructures in the presence of vibration from molecular dynamics simulation. The simulation results showed that the water droplet in the Wenzel or Cassie state depends on the geometric dimensioning of the rough structure and the vibration intensity. Murad and Law16 simulated the droplet collision using molecular dynamics simulation. The simulation results showed that in addition to coalescence and shattering, the bouncing phenomenon also occurs due to the collision within a narrow band of state conditions in which the ambient gas plays a significant role. The reasonable nucleation information including the critical radius and nucleation density17 was obtained by considering the effect of liquid–solid interfacial thermal resistance determined by the molecular dynamics simulation. Furthermore, a new dropwise condensation heat transfer model was established based on the modified nucleation information. Molecular dynamics simulation was also employed to directly investigate the droplet nucleation on the smooth surface.18 The nucleation rate and the critical nucleation size obtained from simulation agreed with classical heterogeneous theory for the smaller cooling rate or less wettable solid. Gao et al.19 carried out molecular dynamics simulation to investigate the coalescence process of two equally sized nanodroplets. Simulation results indicated that the coalescence-induced jumping is also possible for the nanodroplet and the force between surface and droplet plays a significant role.
Although a large number of experiments and simulations have been carried out on the droplet nucleation and growth, it has not been reported for the simultaneous investigation on the nucleation and growth of droplet using molecular dynamics simulation. Most theory or simulation works only focus on the single process, nucleation or growth. In the dropwise condensation heat transfer process, the droplet nucleation and growth are simultaneous and interactional. In this work, we perform the molecular dynamics simulation to study the droplet nucleation and growth synchronously. The effects of heat flux, surface wettability and initial droplet size on the new droplet nucleation and growth are discussed in detail, which may shed light on the mechanism of important phenomena such as droplet state transition and flooding mode in dropwise condensation heat transfer.
2. Simulation details
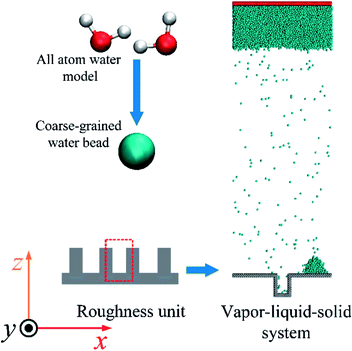
Molecular dynamics simulation is performed using the LAMMPS package.20 To investigate the droplet nucleation and growth, the vapour–liquid–solid system is built firstly with the three dimensions of 196 × 31.36 × 591.92 Å in the x, y and z directions, respectively. The periodic boundary condition is applied for the three dimensions. As shown in Fig. 1, before the heat flux is applied, a droplet has already existed on the top of the rough structure, which means that the droplet prefers to generate on the top of the rough surface as mentioned in the literature.9,21,22 A coarse-grained water model23 in which a coarse-grained bead represents two water molecules as shown in Fig. 1 is employed to reduce the computational cost compared to the all atom model like TIP3P, SPC and TIP4P. These coarse-grained beads interact through a Lennard-Jones 9-6 potential,where ε = 0.0444 eV and σ = 3.760 Å are the characteristic surface energy and the van der Waals radius, respectively. The atoms of the Pt-like rough surface unit with a 23.52 Å width and 39.2 Å height are fixed as a rigid body as shown in Fig. 1. The 9-6 LJ potential is also adopted to describe the interaction between the solid wall and the water molecules using different energy parameters to represent different surface wettabilities.
The Pt-water including the initial droplet system is firstly equilibrated in an NVT ensemble (N is the number of atoms, V is the volume and T is the temperature) at 400 K. The structure after equilibrium as shown in Fig. 1 is adopted as the initial state in next stage in which the heat flux is applied to achieve the droplet nucleation and growth. The liquid film at the top of the simulation box is used as a vapour source as in the macroscale condensation experiment, which was similarly used in our previous study.24 The same intensity of heat flux is injected or extracted in the regions of heat source and heat sink, respectively. In the simulation, the region in the liquid film with a thickness of 15 Å in the z direction is treated as the heat source and the region within a range of 12 Å from the bottom surface is treated as the heat sink where the droplet nucleation or growth occurs due to the extracted energy.
To quantitatively confirm the surface wettability for different energy parameters ε used in the LJ 9-6 potential between the coarse-grained beads and solid surface, droplet on the smooth solid surface is simulated to obtain the contact angle as the wettability reference and the results are shown in Fig. 2. As shown in Fig. 2a, the water droplet is set to be a thin-slab-like cylindrical droplet in the y direction, which was proved to be able to avoid the size-dependent contact angle resulted from the line tension25 and improve the simulation efficiency.26 The contact angle is obtained by the time average for 1 ns by defining the droplet boundary as the contour line with 0.5 g cm−3 in the density field. As shown in Fig. 2b, the range of ε from 0.005 to 0.007 eV is able to cover the surface wetting properties with contact angle range of 151–97°.
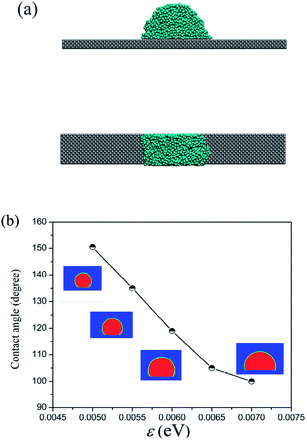 | ||
| Fig. 2 (a) Water droplet on the Pt-like surface in the simulation; (b) contact angles of droplets on the surfaces with different surface wettabilities. | ||
3. Results and discussion
3.1 The effect of heat flux on droplet nucleation and growth
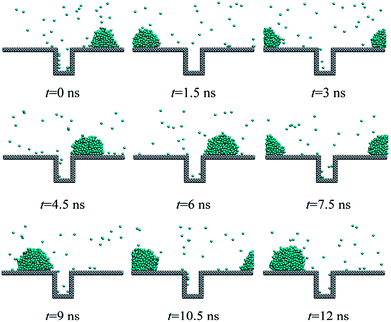
A large number of experimental results have already indicated that large surface subcooling degree or high heat flux would lead to the nucleation-induced flooding condensation.11,21 In this work, different heat fluxes ranging from 0.01 to 0.03 eV ps−1 are applied on the water molecules including the existing droplet and water vapour in the heat sink region. We consider the case that the contact angle of the solid surface is fixed at 97° and the initial existing droplet contains 376 coarse-grained beads.For the heat flux of 0.01 eV ps−1, we cannot observe the birth of new droplet, which means that no nucleation occurs as shown in Fig. 3. On the other hand, the initial existing droplet on the top of the rough structure gradually grows up and consistently stays above the rough structure (keeps in the Cassie state27). In the dropwise condensation experiment on the superhydrophobic surface, the mobile Cassie state of the droplet could ensure high heat transfer coefficient because the Cassie droplet could leave from the surface very fast or even achieve jumping out of the surface due to the droplet coalescence.28,29
In order to observe the droplet nucleation and growth characteristics during the condensation process, the cluster analysis is performed according to the Stillinger criterion.30 A cluster is defined as a set of atoms, each of which is within the cutoff distance from one or more other atoms in the cluster. If an atom has no adjacent atoms within the cutoff distance, it is a 1-atom cluster. Then, all clusters are sorted by the size so that we can distinguish between the newly formed droplet and the initial existing droplet. As shown in Fig. 4, we track the droplet size (molecular number for the cluster) variation of both the maximum droplet (the initial existing droplet) and the second large droplet (the newly generated droplets, if any). We can find that under the case of low heat flux, 0.01 eV ps−1, only the initial existing droplet could keep on growing up and the molecular number of the second large droplet remains around 1, which means that the water vapour molecules keep at a separate state and no nucleation occurs.
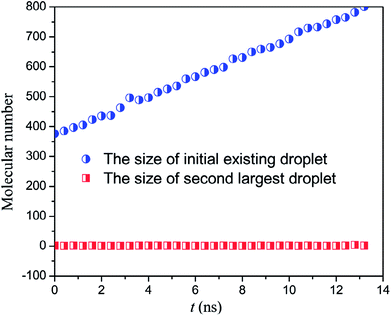 | ||
| Fig. 4 The size of the initial droplet and the second largest droplet under heat flux of 0.01 eV ps−1. | ||
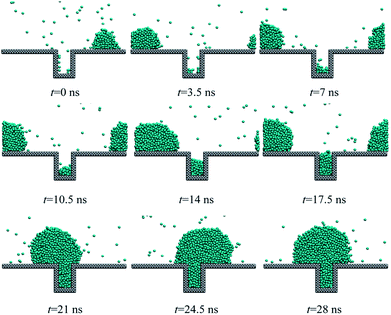
However, for the case of a higher heat flux, 0.02 eV ps−1, new droplet could nucleate at the bottom of the rough structure as shown in Fig. 5. Then, the newly formed droplet and the initial existing droplet continue to grow up until two droplets start to coalesce at about 21 ns after the heat flux is applied as shown in Fig. 6. Next, the coalesced droplet keeps on growing with the Wenzel state.31 As investigated in ref. 32, the Wenzel droplets show increased contact angle hysteresis and thus are difficult to fall off from the superhydrophobic surface. The present simulations also qualitatively validate the previous experimental results21,33,34 in which the large subcooling degree or increased heat flux would lead to the nucleation-induced flooding condensation. Therefore, we can describe the whole process of flooding condensation mode by combining previous experiments and the present simulation results. Firstly, the large subcooling degree or heat flux leads to the extra nucleation inside the nanostructures. Then, the newly formed embryo keeps on growing up and finally coalesces with the existing droplets at the top of the rough structures. The coalescence-induced Wenzel droplets are particularly difficult to fall off from the solid surface, which directly contributes to the flooding condensation mode.
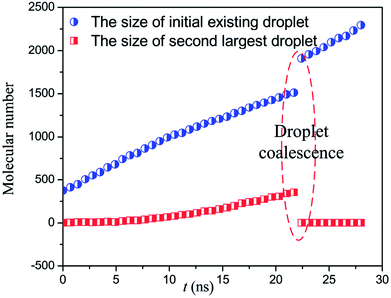 | ||
| Fig. 6 The size of the initial droplet and the second largest droplet under heat flux of 0.02 eV ps−1. | ||
3.2 The effect of surface wettability on droplet nucleation and growth
The surface wettability is adjusted by changing energy parameter ε in the Lennard-Jones 9-6 potential between the solid surface and the coarse-grained beads as shown in Fig. 2. The effect of surface wettability on the droplet nucleation was investigated in previous studies.17,35 According to the classical nucleation theory,36,37 the nucleation capability is evaluated with the nucleation free energy barrier, defined as the Gibbs free energy barrier that has to be overcome to form a nucleus of critical size. Based on previous researches,38 the nucleation free energy on hydrophobic surface is relatively higher compared with the hydrophilic surface, which indicates that the hydrophobicity of the surface makes the nucleation more difficult. In the present study, the effect of the surface wettability on the nucleation and the following droplet behaviour is investigated.As shown in Fig. 7, the droplet nucleation and growth are investigated on the rough surface for three surface wettabilities. The heat fluxes of 0.015, 0.02 and 0.025 eV ps−1 are applied in the heat sink region. The initial droplet on the top of the rough structure contains 87 coarse-grained beads. From the simulation results, we can find that the nucleation at the bottom of the rough structure is more difficult to occur with the increased contact angle under the same heat flux. As shown in Fig. 7a, for the heat flux of 0.015 eV ps−1, the nucleation occurs only on the surface with 97° contact angle and the heat flux is not enough to overcome the nucleation free energy barrier for the solid surfaces with contact angles of 119° and 151°.
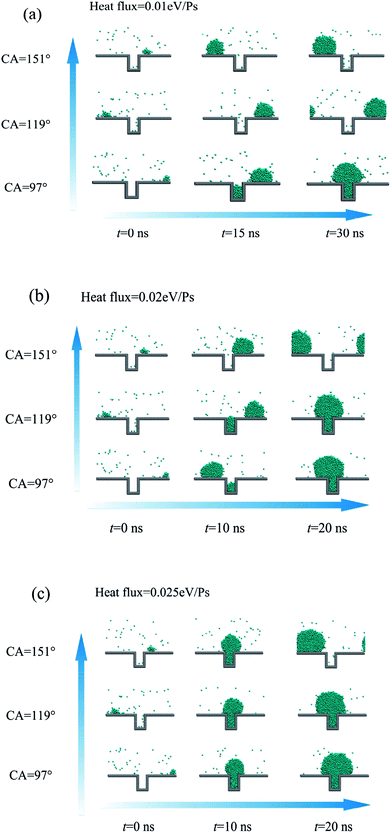 | ||
| Fig. 7 Droplet nucleation and growth on the rough surface for three different contact angles (CA). (a) Heat flux = 0.01 eV ps−1; (b) heat flux = 0.02 eV ps−1; (c) heat flux = 0.025 eV ps−1. | ||
However, with the increase of heat flux, new droplets could gradually generate at the bottom of rough structure on the rough surfaces with contact angles of 119° and 151° as shown in Fig. 7b–c. So enhancing the hydrophobicity of the surface, especially for the bottom of the rough structure, is of great significance to avoid droplet generation (droplet nucleation) inside the rough structures and then prevent the Wenzel droplet formation and the flooding condensation mode. In our previous study,17 we also pointed out that the hydrophobicity would lead to the increase of critical nucleation radius and the reduction of nucleation density due to the liquid–solid interfacial thermal resistance, which is in consistence with the present simulation results.
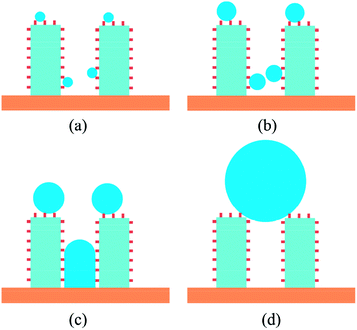
For the surface with contact angle of 151°, the nucleation could occur when the heat flux is high enough to overcome the nucleation free energy barrier, but after the newly formed droplet coalescing with the initial existing droplet, the larger droplet would present state transition from Wenzel state to Cassie state as shown in Fig. 7c. For the surface with contact angles of 97° and 119°, the droplet will keep on growing up remaining the Wenzel state and cannot achieve the state transition from Wenzel state to Cassie state. The previous experimental study for dropwise condensation heat transfer on the superhydrophobic surface14 also observed such a transition. This coalescence results in a sudden increase for the droplet size and leads to a pressure gradient within the droplet, which drives the droplet to escape from the cavity. In addition, the sudden increase of droplet size may induce the instability in the already deformed droplet, which contributes to overcoming the pinning effect from the cavity.
3.3 The effect of the existing droplet size on droplet nucleation and growth
Each droplet experiences the nucleation, growth, coalescence and departure processes in an existence cycle. From nucleation to departure, the droplet size gradually becomes larger due to the vapour direct condensation and droplet coalescence. In this section, we investigate the size effect of the initial existing droplet at the top of the rough structure on the droplet nucleation and growth at the bottom of the rough structure. This will help us better understand the principle of droplet self-organization at the top of the rough structure for dropwise condensation heat transfer enhancement.As shown in Fig. 8, four different sizes of the initial existing droplet are investigated on the surface with contact angle of 97° under the heat flux of 0.015 eV ps−1. From the simulation results, we can find that the new droplet could produce only in the case that the initial existing droplet contains 64 or 172 coarse-grained beads. However, for the case of larger initial droplet, no nucleation and growth could occur in the condensation process. The simulation results indicate that the size of the existing droplet preferentially formed at the top of the rough structure is also a key factor to determine whether the nucleation occurs or not. The occurrence of the nucleation at the bottom of the rough structure requires the supplement of vapour molecules from outside. The inflow vapour molecules will firstly flow across the top of the rough structure. If the initial existing droplet at the top is large enough, the inflow saturated vapour molecules will contact with the existing droplet and condense directly with a higher probability, which restricts the nucleation inside effectively.
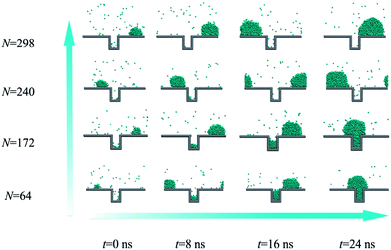 | ||
| Fig. 8 Droplet nucleation and growth on the rough surface for four sizes of initial existing droplet. | ||
So preferential nucleation and growth of the droplet at the top of the rough structure is an important principle for designing high efficient dropwise condensation heat transfer surface due to its restriction to the inside nucleation. Based on this principle, numerous advanced surface treatment technologies39,40 have been developed to prepare the hybrid surface to achieve the droplet self-organization in which the top of the rough structure is hydrophilic and easy to nucleate. This design can guarantee that the large droplets always stay at the top of the rough structure and avoid the inside nucleation or flooding condensation.
3.4 The fundamental mechanism of flooding mode: origin from the droplet nucleation
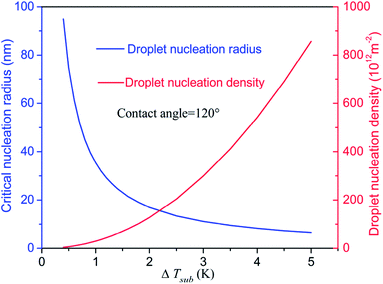
In Section 3.2, we have mentioned that the droplet would present state transition from Wenzel state to Cassie state for the surface with contact angle of 151°. Actually, only cooperation of the hydrophobic coating and rough structure can produce the superhydrophobic surface (CA > 150°). In the present study, we achieved the superhydrophobicity by adjusting the energy parameters used in the LJ 9-6 potential which was a simplified treatment. So considering the real situation of condensation on the micro-nanostructured surface, if the critical nucleation radius rc is less than S (S is half of the spacing between nanostructures), the droplet could nucleate inside the nanostructures as schematic in Fig. 9. In such a situation, the droplet cannot exhibit large contact angle (>150°) because the size of the droplet is less than the minimum size of the rough structure. So when the droplets keep on growth, the state transition will not appear and the Wenzel droplet will form finally. However, in the case of rc > S, the embryo droplet can only suspend on the nanostructures which could exhibit large contact angle (>150°). According to the conclusion in Section 3.2, this type of droplets could achieve state transition from Wenzel state to Cassie state in the process of growth as schematic in Fig. 10.So we could take steps from the droplet nucleation to avoid the flooding mode (Wenzel droplet). The droplet nucleation radius is a particularly important parameter. Based on our previous study17 about the droplet nucleation, the droplet nucleation radius and density for the CA = 120° are shown in Fig. 11. The increase of subcooling degree will lead to a decreased critical radius and an increased nucleation density. So the denser nanostructures are necessary to avoid the nucleation inside the nanostructures and keep a high condensation heat transfer coefficient. Therefore, in the process of surface preparation, the droplet nucleation radius could provide a guide to optimize the surface.
4. Conclusions
The effects of heat flux, surface wettability and size of initial droplet on droplet nucleation and growth on the rough surface were investigated using the molecular dynamics simulation.Results show that the high heat flux could lead to the droplet nucleation and growth inside the rough structure and consequently result in the Wenzel state. For the surface with strong hydrophobicity, contact angle of 151°, although the droplet nucleation and growth can occur under high heat flux, the newly formed droplet after coalescence will exhibit the transition from Wenzel state to Cassie state. In addition, the size of the droplet on the top of the rough structure also affects the droplet nucleation and growth inside. The existence of large droplet on the top will restrict the internal nucleation and thus avoid the Wenzel droplet state or flooding condensation mode.
Actually, the fundamental mechanism of the subcooling degree effect or the surface wettability effect on the dropwise condensation heat transfer is originated from the droplet nucleation stage. The droplet nucleation radius should be introduced to guide the preparation of high efficient surface. Under specific conditions of dropwise condensation, the characteristic size of the spacing between the nanostructures on the condensation surface should be controlled according to the critical nucleation radius. For the chemical homogeneous micro-nanostructured surface, only if the characteristic size of the spacing is less than the critical nucleation radius can the flooding mode be avoided and thus the high condensation heat transfer coefficient can be achieved.
In summary, the droplet nucleation and growth inside the rough structure are related to many factors including the heat flux, surface wettability and adjacent droplet, which need to be taken all into account in developing high efficient surface in dropwise condensation heat transfer. The droplet nucleation radius should also be introduced to achieve the optimal design of condensation surface.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China under grant numbers of 51576156 and 51721004, and the 111 Project under grant number of B16038.Notes and references
- L. R. Glicksman and A. W. Hunt, Int. J. Heat Mass Transfer, 1972, 15, 2251–2269 CrossRef.
- N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2012, 13, 179–187 CrossRef PubMed.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170 CrossRef PubMed.
- H. G. Andrews, E. A. Eccles, W. C. E. Schofield and J. P. S. Badyal, Langmuir, 2011, 27, 3798–3802 CrossRef PubMed.
- X. Chen, J. Wu, R. Ma, M. Hua, N. Koratkar, S. Yao and Z. Wang, Adv. Funct. Mater., 2011, 21, 4617–4623 CrossRef.
- Y. Yamada, T. Ikuta, T. Nishiyama, K. Takahashi and Y. Takata, Langmuir, 2014, 30, 14532–14537 CrossRef PubMed.
- W. Xu, Z. Lan, B. Peng, R. Wen and X. Ma, RSC Adv., 2014, 5, 812–818 RSC.
- W. Xu, Z. Lan, B. Peng, R. Wen and X. Ma, RSC Adv., 2014, 4, 31692–31699 RSC.
- C. Lv, P. Hao, X. Zhang and F. He, ACS Nano, 2015, 9, 12311–12319 CrossRef PubMed.
- C. Lo, C. Wang and M. Lu, Adv. Funct. Mater., 2014, 24, 1211–1217 CrossRef.
- R. Wen, Z. Lan, B. Peng, W. Xu, R. Yang and X. Ma, ACS Appl. Mater. Interfaces, 2017, 9, 13770 CrossRef PubMed.
- H. Tanaka, J. Heat Transfer, 1975, 97, 72–78 CrossRef.
- K. Rykaczewski, Langmuir, 2012, 28, 7720–7729 CrossRef PubMed.
- C. S. Sharma, J. Combe, M. Giger, T. Emmerich and D. Poulikakos, ACS Nano, 2017, 11, 1673 CrossRef PubMed.
- D. Niu and G. H. Tang, Int. J. Heat Mass Transfer, 2014, 79, 647–654 CrossRef.
- S. Murad and C. K. Law, Mol. Phys., 1999, 96, 81–85 CrossRef.
- D. Niu, L. Guo, H. W. Hu and G. H. Tang, Int. J. Heat Mass Transfer, 2017, 112, 333–342 CrossRef.
- T. Kimura and S. Maruyama, Microscale Thermophys. Eng., 2002, 6, 3–13 CrossRef.
- S. Gao, Q. Liao, W. Liu and Z. Liu, J. Phys. Chem. Lett., 2017, 9, 13–18 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef.
- R. Wen, S. Xu, D. Zhao, Y. C. Lee, X. Ma and R. Yang, ACS Appl. Mater. Interfaces, 2017, 9, 44911 CrossRef PubMed.
- C. Lv, X. Zhang, F. Niu, F. He and P. Hao, Sci. Rep., 2017, 7, 42752 CrossRef PubMed.
- X. He, W. Shinoda, R. DeVane and M. L. Klein, Mol. Phys., 2010, 108, 2007–2020 CrossRef.
- D. Niu and G. H. Tang, Sci. Rep., 2016, 6, 19192 CrossRef PubMed.
- J. Rafiee, X. Mi, H. Gullapalli, A. V. Thomas, F. Yavari, Y. Shi and N. A. Koratkar, Nat. Mater., 2012, 11, 217–222 CrossRef PubMed.
- F. C. Wang and H. A. Wu, Soft Matter, 2013, 9, 7974–7980 RSC.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- J. B. Boreyko and C. H. Chen, Phys. Rev. Lett., 2009, 103, 184501 CrossRef PubMed.
- F. Chu, X. Wu, B. Zhu and X. Zhang, Appl. Phys. Lett., 2016, 108, 194103 CrossRef.
- F. H. Stillinger, J. Chem. Phys., 1963, 38, 1486–1494 CrossRef.
- R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef.
- T. Koishi, K. Yasuoka, S. Fujikawa and X. C. Zeng, ACS Nano, 2011, 5, 6834–6842 CrossRef PubMed.
- N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2012, 13, 179–187 CrossRef PubMed.
- R. Wen, Q. Li, J. Wu, G. Wu, W. Wang, Y. Chen, X. Ma, D. Zhao and R. Yang, Nano Energy, 2017, 33, 177–183 CrossRef.
- X. Liu and P. Cheng, Int. J. Heat Mass Transfer, 2015, 83, 833–841 CrossRef.
- A. Dillmann and G. E. A. Meier, J. Chem. Phys., 1991, 94, 3872–3884 CrossRef.
- I. J. Ford, A. Laaksonen and M. Kulmala, J. Chem. Phys., 1993, 99, 764–765 CrossRef.
- W. Xu, Z. Lan, B. L. Peng, R. F. Wen and X. H. Ma, J. Chem. Phys., 2015, 142, 054701 CrossRef PubMed.
- Y. Hou, M. Yu, X. Chen, Z. Wang and S. Yao, ACS Nano, 2014, 9, 71–81 CrossRef PubMed.
- H. W. Hu, G. H. Tang and D. Niu, Int. J. Heat Mass Transfer, 2015, 85, 513–523 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |