Open Access Article
Open Access ArticleNoble-gas-infused neoprene closed-cell foams achieving ultra-low thermal conductivity fabrics†
Jeffrey L. Moran‡
abc,
Anton L. Cottrill‡b,
Jesse D. Benckb,
Pingwei Liub,
Zhe Yuanb,
Michael S. Strano*b and
Jacopo Buongiorno*c
aDepartment of Mechanical Engineering, George Mason University, USA
bDepartment of Chemical Engineering, MIT, USA. E-mail: strano@mit.edu
cDepartment of Nuclear Science and Engineering, MIT, USA. E-mail: jacopo@mit.edu
First published on 18th June 2018
Abstract
Closed-cell foams are widely applied as insulation and essential for the thermal management of protective garments for extreme environments. In this work, we develop and demonstrate a strategy for drastically reducing the thermal conductivity of a flexible, closed-cell polychloroprene foam to 0.031 ± 0.002 W m−1 K−1, approaching values of an air gap (0.027 W m−1 K−1) for an extended period of time (>10 hours), within a material capable of textile processing. Ultra-insulating neoprene materials are synthesized using high-pressure processing at 243 kPa in a high-molecular-weight gas environment, such as Ar, Kr, or Xe. A Fickian diffusion model describes both the mass infusion and thermal conductivity reduction of the foam as a function of processing time, predicting a 24–72 hour required exposure time for full charging of a 6 mm thick 5 cm diameter neoprene sample. These results enable waterproof textile insulation that approximates a wearable air gap. We demonstrate a wetsuit made of ultra-low thermally conductive neoprene capable of potentially extending dive times to 2–3 hours in water below 10 °C, compared with <1 hour for the state-of-the-art. This work introduces the prospect of effectively wearing a flexible air gap for thermal protection in harsh environments.
1. Introduction
Thermally insulating materials are critical for human survival at low temperatures, particularly wearable fabrics. This is especially true in water, where heat loss to the surroundings is more efficient than in air, even across smaller temperature differences. High-performance water-compatible thermally insulating garments are essential for military divers, shipyard and underwater workers, and recreational and professional open-water swimmers and triathletes. In particular, polychloroprene (neoprene) foams are flexible, water-resistant precursors for thermally insulating garments that have been widely investigated.1–4 In general, foam insulation contains a low-thermal conductivity gas dispersed in a relatively low thermal conductivity matrix in an open or closed cell structure.5 The thermal conductivity of the composite is highly influenced by the thermal conductivities of the gas and matrix material; in addition, the cell size and type affect the effective thermal conductivity.5 Traditional thermal insulation materials consist of biopolymer-based materials, such as cork (thermal conductivity between 0.040–0.050 W m−1 K−1)5,6 and cellulose (0.040–0.050 W m−1 K−1),5,6 or fossil-fuel-derived polymeric foams,6 such as expanded polystyrene (EPS) (0.030–0.040 W m−1 K−1),5,7–9 extruded polystyrene (0.030–0.040 W m−1 K−1),5,7,10 polyurethane (0.020–0.030 W m−1 K−1),5,7,9,11,12 and neoprene (0.050–0.060 W m−1 K−1).1 For the purpose of developing thermally insulating garments, however, researchers have focused primarily on neoprene foams due to its flexibility (capability of being shaped into a garment) and its closed cell nature (giving the material water resistance).13 Other closed-cell insulating foams applicable to garment fabrication include thermoplastic polyurethane (TPU) (0.05 W m−1 K−1),14 high performance polyamide (e.g., ZOTEK N) (0.038 W m−1 K−1),15 and polyether block amide (PEBA) (0.038–0.058 W m−1 K−1).16Herein, we develop and model a process for the non-destructive, repeatable fabrication of transient gas insulating materials (GIMs)17 from commercial closed-cell polychloroprene foams. As a demonstration, we modify commercial neoprene in the form factor of a wetsuit and reduce its thermal conductivity by up to 40%. The thermal conductivity of the altered neoprene remains below the control value for more than 12 hours, enabling a potentially dramatic enhancement in insulation performance of foam neoprene-based garments, such as wetsuits. We note that highly insulating open cell and flexible foams, such as silica aerogels operating in the Knudsen regime, have been demonstrated to have thermal conductivities lower than that of air (0.026 W m−1 K−1); however, due to their open cell nature, these foams have limited water resistance capabilities and have also been reported to have both poor mechanical properties and health issues.18 Furthermore, some closed cell foams, for example EPS, have been shown to have thermal conductivities within the range of our lowest-achieved value in this work; however, these materials do not have the flexibility to incorporate into garments.5,7–9
It is well-known that the thermal conductivity of a gas scales linearly with its specific heat and inversely with the square root of its molecular weight.19 Given these criteria, an ideal choice for an insulating gas is a monatomic (low-specific-heat), high-molecular-weight gas that is not radiotoxic and is also inert (e.g., argon, krypton, xenon). Incorporating insulating gases such as monatomic, high-molecular-weight gases, into foams as blowing agents is not a new concept. For example, preliminary studies have been carried out using krypton–xenon mixtures20 and argon21 as blowing agents for foam insulation, but the technique has not become widely adopted. This is likely due to the significant leakage rate and replacement by ambient air that the foams would experience following manufacturing. We overcome this issue by developing a process for the facile infusion of high-molecular-weight noble gases into closed-cell foams in a non-destructive and repeatable fashion at any point post-fabrication. We focus primarily on neoprene foams, since they are often used for extending dive persistence in near 0 °C water.22 However, neoprene foam conducts thermal energy efficiently enough that a wetsuit wearer can only spend less than one hour in near-freezing water before becoming susceptible to hypothermia.22 The ultra-low thermal conductivity garments produced in this work could significantly extend this time by drastically reducing the rate of heat loss from the wearer. Taken together, the results in this work suggest that pressure-induced noble gas infusion is a simple method to dramatically enhance the insulating performance of foam composite materials, which could extend the possible duration of recreational, industrial and military activities in water.
2. Material synthesis
Foam neoprene is a closed-cell elastomeric foam consisting of gaseous cells dispersed within a solid neoprene rubber (polychloroprene) matrix (Fig. 1a). The gaseous phase of neoprene foam typically contains nitrogen or air, with thermal conductivity kg = 0.026 W m−1 K−1 (at 25 °C). Due to the high volume fraction of the gas (typically >70%) and heat partitioning between the gas and rubber phases, the inclusion of the gas phase leads to a reduction in the overall thermal conductivity of the material. However, air is not the most effective insulator among gases at room temperature. Thus, replacement of the air by a better-insulating gas has the potential to significantly improve the insulating performance of neoprene. In this work, we focus on the noble gases argon, xenon, and krypton, and compare their performance with that of air. Xenon (Xe), krypton (Kr) and argon (Ar) all possess lower thermal conductivities than air and are chemically inert, making them attractive candidates to replace air and enhance the insulating capabilities of neoprene foam.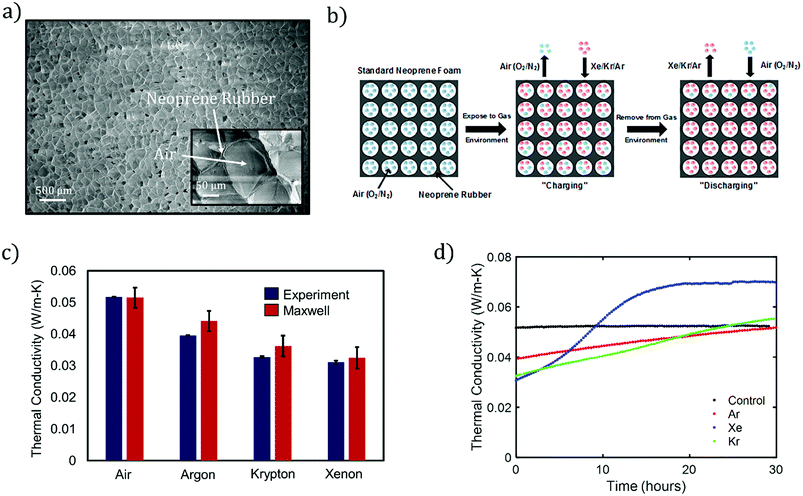 | ||
| Fig. 1 (a) SEM image of unaltered neoprene foam. A magnified SEM is shown in the inset. (b) Process flow for infusing insulating gases into neoprene foam. (c) Experimental thermal conductivities of neoprene foams when infused with the indicated gases. Our experimental measurements are compared with those of the Maxwell's model, eqn (1). Thermal conductivities for the gases considered in this work:17 air (0.026 W m−1 K−1), Ar (0.018 W m−1 K−1), Kr (0.0095 W m−1 K−1), and Xe (0.0055 W m−1 K−1). For experiments, the plotted data represent the average of at least 3 measurements and error bars represent one standard deviation in each direction. For the Maxwell data, error bars reflect uncertainty in the estimate due to uncertainty in the estimate of porosity from SEM images. (d) Measured thermal conductivity of neoprene vs. time for the indicated filling gases, as compared to the control (air). Gas discharge takes place over a time scale that depends mainly on the insulating gas. All measurements are estimated to be within 7% of the actual values. | ||
Fig. 1a shows a scanning electron micrograph (SEM) of a standard, commercial neoprene foam, which is characterized by approximately spherical pores with diameters in the range of 100–200 μm. The pores contain a mixture of nitrogen and oxygen (air) as the filling gas, and the pores are dispersed within a neoprene rubber matrix. We calculate a porosity (gas volume fraction) of 83 ± 2% from image analysis of SEMs of the neoprene foam, such as that shown in Fig. 1a (see also ESI†) for the neoprene foams considered in this work. The thermal conductivities17 of the gases considered in this work, measured at room temperature, are 0.026 W m−1 K−1 (air), 0.018 W m−1 K−1 (Ar), 0.0095 W m−1 K−1 (Kr), and 0.0055 W m−1 K−1 (Xe). The effect of replacing the standard neoprene filling gas with a lower-thermal-conductivity gas can be predicted using Maxwell's homogeneous medium model,23–25 which has been shown to capture the effective thermal conductivity of neoprene foams, kf, reasonably well:1
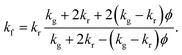 | (1) |
The Maxwell effective medium model was chosen due to its simplicity and relative accuracy. Bardy et al.1 conducted a thorough study of the thermal conductivity as a function of both hydrostatic and uniaxial compressive strain for neoprene foams. At each condition, they measured the thermal conductivity using a thermal conductivity meter that conforms to ASTM C518 and ISO DIS 8301 standards. They compared their measured values to those from various different models for foam materials. As shown in Table 1 of their paper, Maxwell's model generally performed comparably to other (generally more complicated) models, and was typically among the most accurate.
The absolute lower bound on the foam thermal conductivity is determined from setting kg = 0 in eqn (1) above to find kf,kg=0 = 0.0274 W m−1 K−1. When air is present in the pores, the thermal conductivity approximately doubles, suggesting a roughly 50% heat partitioning between air and rubber. The predicted effective thermal conductivities for neoprene foam filled with air, Ar, Xe, and Kr are provided in Fig. 1c. A reduction in thermal conductivity of up to ∼40% is predicted for neoprene foam infused with Xe as compared with standard neoprene foam infused with air.
Fig. 1b illustrates the process flow for fabricating neoprene foams infused with high-molecular-weight, noble gases: starting with standard neoprene consisting of gas cells containing air (blue), the neoprene is immersed in an atmosphere of the insulating gas to be infused (red) at an absolute pressure of 243 kPa (20 psi gauge). The process of gas infusion into a closed-cell foam consists of multiple steps: the insulating gas adsorbs to the outer surface of the neoprene and dissolves in the solid rubber, the gas molecules diffuse through the solid rubber, and the gas desorbs at the inner walls of the gas cells. We term this process “charging.” With the gas infused at room temperature and 243 kPa of pressure, significant reductions in thermal conductivity can be seen in as little as 2 hours, and the maximum possible reduction is attained after approximately 5 days. Eventually, equilibrium is attained such that the pressure of the insulating gas inside the cells is equal to the ambient gas pressure. Foamed neoprene samples with Ar, Xe, and Kr filling gases were fabricated according to the procedure outlined in the Methods section.
The thermal conductivities of charged and unmodified neoprene foams were measured using the Transient Plane Source (TPS) Hot Disk method, which is an established ISO standard transient method for measuring the thermal conductivity of polymeric samples26 (Experimental section and ESI†). The accuracy of the Hot Disk instrument is estimated to be approximately 7%, as quantified by measurements conducted on a NIST thermal conductivity standard material, specifically SRM 1453 (expanded polystyrene board) (ESI†). Almanza et al. presented evidence27 that the TPS method over-predicts the thermal conductivity of polyethylene closed-cell foams compared to a standard steady-state technique. Based on this data, and on the 7% over-prediction of the EPS board, is possible that the TPS method slightly over-predicts the thermal conductivity of neoprene foam as well, and so the values presented in this work may be considered as conservative estimates of the insulation enhancement provided by noble gas infusion. The thermal conductivity measured immediately after removal from the pure-gas environment for Ar-, Kr-, and Xe-infused neoprene foams, is shown in Fig. 1c. A measurement of the thermal conductivity of standard, unmodified neoprene is also provided as a control. We observe a significant reduction in thermal conductivity of neoprene foam, ranging from ∼25% with Ar to 40% with Xe. In addition, the experimental data is in agreement with the Maxwell effective thermal conductivity model assumed throughout this work (Fig. 1c). Error bars indicate the standard deviation of at least 3 individual measurements in each direction. Immediately after removal, we assume that only the noble gas inhabits the pores of the neoprene foam, i.e., the infused gas completely replaces the air in the pores. We gain confirmation of this from finite-element simulations of heat transfer (assuming pure conduction) in simulated neoprene foam, which predict effective thermal conductivities for the neoprene foam that agree well with the experimental values and values predicted by the Maxwell effective thermal conductivity model (Fig. S4 and Table S1†).
The reduction in thermal conductivity due to infusion of a highly insulating gas is transient in nature, as the thermal conductivity returns to and/or surpasses the control value within approximately 12 hours or more (Fig. 1d), reaches a local maximum, and eventually decays back to the control value as the air returns to the pores over time scales of weeks to (in some cases) months. We term this process “discharging.” The increase in thermal conductivity with time after the neoprene samples are removed from the gas environment is attributed to (i) gas exchange between the neoprene sample and the ambient air and (ii) an associated pore shrinkage within the foam, which reduces its porosity. The pore contraction in turn reduces the sample thickness (Fig. 3b) and hence reduces the thermal resistance, since neoprene rubber can be considered incompressible to a good approximation.1,28
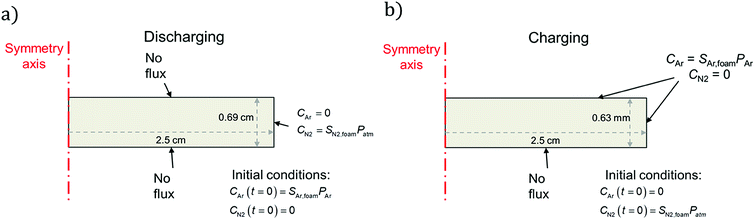 | ||
| Fig. 2 Schematics of (a) discharging and (b) charging simulations undertaken in this work, showing initial and boundary conditions for each case. In the charging case, the neoprene is initially filled with nitrogen (to approximate air) at atmospheric pressure and is placed in a pure atmosphere of Ar at t = 0; in the discharging case the opposite is true, except the Ar is initially at 243 kPa (which is the pressure of the Ar atmosphere to which the neoprene is exposed). Further details on the initial and boundary conditions are provided in the ESI.† | ||
To capture these trends quantitatively and understand how long the neoprene must be exposed to the gas atmosphere for its insulating properties to be noticeably improved, we developed a numerical model of the gas diffusion process, as discussed next.
3. Mathematical modeling of neoprene charging and discharging
The model geometry is based on the experimental setup we employed to measure the thermal conductivity of neoprene foam discs, shown in Fig. 3a, and we focus primarily on Ar-infused neoprene foams. Further details on the experimental apparatus can be found in the Experimental section below.We assume the diffusion process in the neoprene foam to follow Fick's law. In the absence of chemical reactions, the conservation of mass for each gas species becomes:
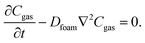 | (2) |
In our model, we also provide initial and boundary conditions for the model that depend on whether the gas is charging or discharging from the neoprene.
For the discharge simulations, the initial condition specifies that only Ar (no nitrogen) fills the pores at a pressure equal to the filling pressure of the gas (∼243 kPa). The boundary conditions dictate negligible flux out of the top and bottom sides and that the sides of the disc instantaneously equilibrate with the surroundings, which contain nitrogen at atmospheric pressure. For the charging simulations, the initial condition specifies only nitrogen in the pores at atmospheric pressure (101 kPa). The boundary conditions specify negligible gas flux on the bottom surface of the disc (it is assumed to lie flat on the bottom of the charging container) and chemical equilibrium between the top and side edges and the surroundings, which contain Ar at 243 kPa. Fig. 2 summarizes the initial and boundary conditions for each simulation and shows the geometry and dimensions of the neoprene disc that serves as the simulation domain.
Finally, we use well-established theories for the thermal conductivity of a gas mixture, combined with Maxwell's eqn (1) to estimate the thermal conductivity as a function of time in both models.
Since the gas cells are (at maximum) 100–200 μm in size (Fig. 1a), the thermal Péclet number is assumed to be negligible throughout the neoprene foam. That is, in this work we assume convective heat transfer within the pores is negligible compared to thermal diffusion. This assumption is justified by the agreement between the experimental measurements (Fig. 1c) and eqn (1), which considers heat transfer by conduction only, and by finite-element simulations of heat transfer in the neoprene that assume pure conduction (ESI†).
To construct a numerical model of gas diffusion in the foam, it is necessary to know the effective diffusion coefficients for the gases in the foam. The diffusion coefficients of several gases, including Ar and nitrogen, in neoprene rubber are tabulated in various sources.29–31 However, the effective diffusivities and solubilities in neoprene foam for the gases of interest here are not documented. To resolve this issue, in this work we derive an “effective foam solubility” Sfoam (details in ESI†); in addition, using a relatively simple permeation apparatus, it is possible to experimentally determine the effective diffusivity of a gas in neoprene foam, Dfoam. In the ESI,† we describe the experimental apparatus and simple curve-fitting procedure that allow us to determine Dfoam for Ar and Xe. Subsequently, we describe the procedure to derive the effective foam solubility for each gas.
During the charging and discharging processes, we expect there to be a mixture of air and the insulating gas in the foam. Thus, the term kg in eqn (1) is generally a function of the relative concentrations of the gases present at a given time.
The thermal conductivity of a gas mixture is not typically a linear function of the mole fraction of each gas. Depending on the difference in polarity between the gas molecules, the resulting mixture may either (i) attain a maximum above the larger of the two thermal conductivities, (ii) attain a minimum below the smaller of the two thermal conductivities, or (iii) vary monotonically with gas composition.32 The thermal conductivity of a gas mixture can be described by the Wassiljewa equation,33
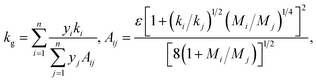 | (3) |
The porosity of the standard neoprene foam samples considered in this work was determined to be approximately 83 ± 2% (see preceding section). Under this assumption, and using the measured values of foam density, the rubber density is estimated from the published relation, ϕ = 1 − ρfoam/ρrubber1 to be ρrubber = 0.51 g cm−3. Since the rubber density is calculated based on the estimated porosity, there is an associated uncertainty in the rubber density. Specifically, the ±2% uncertainty in the porosity implies a range for the rubber density of 0.464 g cm−3 < ρrubber < 0.588 g cm−3.
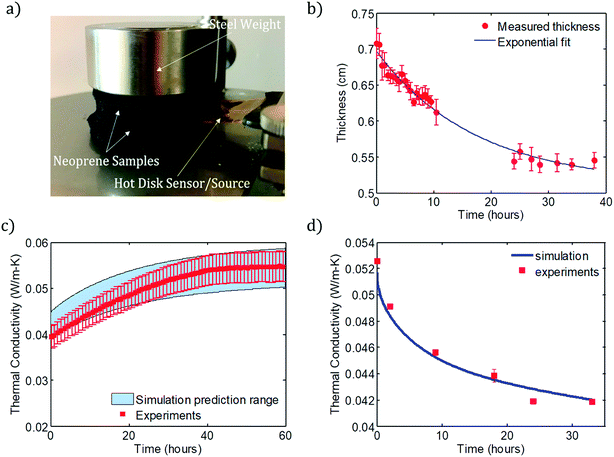
Finally, the overall thermal conductivity of the foam, kf, is computed as the average of kxy over the volume of the foam. The predicted and measured values of kf are plotted in Fig. 3c for discharging and Fig. 3d for charging. The shaded range plotted in Fig. 3c is determined by assuming the minimum and maximum values of the rubber density, which influences the porosity according to ϕ = 1 − ρfoam/ρrubber1 and therefore the thermal conductivity of the foam. The results of the discharging and charging simulations are compared with experiments for Ar-infused neoprene that has been charged for 7 days, and for neoprene charged with Ar for several different filling times (from 2 to 33 hours), respectively.
Fig. 3c shows the simulated and experimentally measured dependence of thermal conductivity on time for Ar-infused neoprene over a 60 hour discharging experiment. Fig. 3d compares the simulation predictions (solid curve) with experimental measurements of neoprene samples that were charged with Ar for various times. In both cases, good agreement is observed between simulations and experiments. We emphasize that both the discharging and charging simulations use the same values of the effective foam diffusivities and effective foam solubilities for nitrogen and Ar. Only the initial and boundary conditions change from the discharging to the charging simulations, as explained above and visualized by comparing Fig. 2a and b. During discharging, there is almost no gas discharge through the top and bottom surfaces (since neoprene pieces are stacked on top of one another, with the metal weight on top and stage on the bottom), and so most of the gas exchange occurs through the outer edges. As a result, we ignore any gas flux that may take place through the top or bottom surfaces. During charging, it is assumed that a neoprene disc is sitting flat on the bottom of the charging container, and so there is very little gas exchange through the bottom surface of the disc (since it touches the bottom of the filling tank), but there is significant gas exchange on the top and outer edge surfaces.
Lastly, it should be noted that effect of charging the neoprene foam at elevated gas temperatures has the potential to significantly accelerate the gas infusion process (Fig. S13†). This will be a major focus of future investigations.
Overall, the simulation and experimental data show that, for these 6 mm thick, 5 cm radius neoprene foam samples, a 20% reduction in thermal conductivity can be achieved within 24 hours of charging. Maximum reduction is observed after roughly 4–5 days – these charging times produced the results shown in Fig. 1c and d.
4. Material performance as a low temperature wetsuit
These flexible, ultra-low-thermal-conductivity materials can be applied to the production of a new class of low-temperature dive suits. First, to determine whether the charging process is repeatable, we subjected two sets of samples to multiple charging steps, one set each in Ar and Xe. Fig. 4a and b show the results of these recharging experiments for Ar and Xe, respectively. In each case, a set of 4 neoprene discs was charged with the indicated gas (over 7 days) and their thermal conductivity measured (“one charge”) using the apparatus shown in Fig. 3a. The same samples are then placed in the same insulating gas a second time (again for 7 days) and their thermal conductivities are measured again. Each panel shows strong evidence that the gas charging process is repeatable using either Ar or Xe as the charging gas. This suggests that garments made from foam neoprene, such as wetsuits, could be charged and recharged multiple times without any reduction in insulation performance.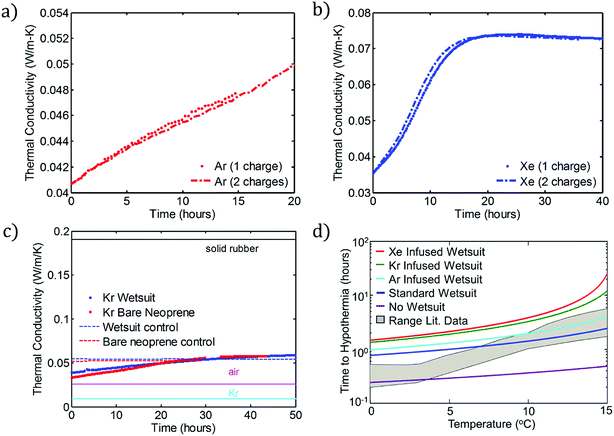 | ||
| Fig. 4 Repeatability and practical benefits of gas charging. (a) Reproducibility of Ar charging. The two data sets show the thermal conductivity vs. time for one set of neoprene coupons, charged and then recharged with the gas. (b) Analogous curves to panel (a), but with a different set of neoprene samples that were charged and recharged using Xe as the charging gas. (c) Thermal conductivity vs. time for bare neoprene charged with Kr compared with data for a full wetsuit, also charged with Kr. (d) Predictions of eqn (6) for the time to hypothermia (i.e., time required for core body temperature Tcore to decrease from the initial value, 37 °C, to Th = 35 °C) as a function of water temperature for no wetsuit and for wetsuits with the indicated gases. These data are compared to experimental data (shaded grey region) reported by Aguilella-Arzo et al.22 (“Range Lit. Data”). Note the logarithmic vertical axis. | ||
Second, we investigate the modification of foamed neoprene in the form of a commercial wetsuit. The process by which an entire neoprene wetsuit is modified is shown schematically in the ESI.† We analyze three wetsuits: a control, a Kr-infused wetsuit, and an Ar-infused wetsuit. Fig. 4c shows the thermal conductivities of the modified (Kr) and unmodified wetsuits stored in air as a function of time. The results for the wetsuit are also compared with the results for the Kr-infused “bare” neoprene samples investigated in the previous sections. As anticipated, the results are quite similar. As a comparison to the elements existing in the systems, thermal conductivities for neoprene rubber, air, and Kr are also provided. Results for the Ar-infused wetsuit are provided in the ESI (Fig. S11b).† Our main conclusion is that an entire wetsuit can be charged to yield similar thermal conductivity reductions to those obtained at a smaller scale.
To quantify the benefit of a better-insulating wetsuit to a diver, we select the time to hypothermia (defined as the time required for the diver's core body temperature to reach 35 °C) as the figure of merit and use a simple thermo-physiological model to calculate it.22 We begin with the first law of thermodynamics applied to the diver,
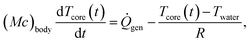 | (4) |
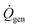 is the diver's metabolic heat generation rate, Twater is the water temperature, and R is the total thermal resistance between the diver's core and the background water. The process of heat transfer from a diver's body to the surrounding water can be modeled with three thermal resistances in series: conduction through the dermis (Rdermis), conduction through the wetsuit, and convection from the outer surface of the wetsuit to the water:
is the diver's metabolic heat generation rate, Twater is the water temperature, and R is the total thermal resistance between the diver's core and the background water. The process of heat transfer from a diver's body to the surrounding water can be modeled with three thermal resistances in series: conduction through the dermis (Rdermis), conduction through the wetsuit, and convection from the outer surface of the wetsuit to the water:
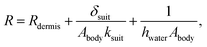 | (5) |
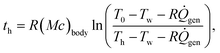 | (6) |
Using typical values for the thermal resistance of the dermis,22 Rdermis = 0.03 K W−1, the surface area of the body35 (Abody = 2 m2), the mass of a typical human body22 (Mbody = 75 kg), the specific heat capacity of the body22 (cbody = 3470 J kg−1 K−1), the heat generation rate22 (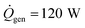 ), the thickness of the suit (δsuit = 7 mm), which varies in general from 5 to 12 mm, and the heat transfer coefficient,36 hwater = 25 W m−2 K−1, we can plot the time to hypothermia as a function of water temperature (Fig. 4d) for wetsuits with thermal conductivities (ksuit) corresponding to the initial measured values in Fig. 1c. As demonstrated by Fig. 4d, the observed reductions in thermal conductivity can enable wetsuits that allow divers to safely spend more time underwater compared to a standard wetsuit, especially in very cold conditions.
), the thickness of the suit (δsuit = 7 mm), which varies in general from 5 to 12 mm, and the heat transfer coefficient,36 hwater = 25 W m−2 K−1, we can plot the time to hypothermia as a function of water temperature (Fig. 4d) for wetsuits with thermal conductivities (ksuit) corresponding to the initial measured values in Fig. 1c. As demonstrated by Fig. 4d, the observed reductions in thermal conductivity can enable wetsuits that allow divers to safely spend more time underwater compared to a standard wetsuit, especially in very cold conditions.
We also investigate the effect of environment on the thermal conductivity of Ar-infused neoprene foam stored in ambient air or water, as shown in the ESI (Fig. S7).† The rate of Ar discharge is significantly reduced for the sample stored in a closed container of stagnant water, enhancing the validity of the dive persistence predictions in Fig. 4d. The rate of discharge is slightly faster (but not as fast as in an air environment) for stirred water, as shown in Fig. S7.†
These results enable waterproof textile insulation that approximates a wearable thermal air gap (the thermal conductivity of air at room temperature is approximately 0.027 W m−1 K−1). As demonstrated in Fig. 4d, these results could enable dives lasting 2–3 hours in water below 10 °C, compared with <1 hour for the state-of-the-art. This advance introduces the prospect of effectively wearing a flexible air gap for thermal protection in harsh environments.
Lastly, as the materials have primarily been characterized under ambient conditions for potential application in a frigid aquatic environment, we also characterize our materials experimentally for their performance in a frigid aquatic environment. Fig. S12† shows the thermal conductivity as a function of time for argon-infused neoprene at room temperature in an air environment, for argon-infused neoprene at 5 °C in an aquatic environment, and for a neoprene control sample at room temperature in an air environment. It is clear that both argon-infused neoprene samples have similar reductions in thermal conductivity as compared with the control. Therefore, the reduction in environmental temperature does not have a strong influence on the composite's thermal conductivity. Furthermore, the leakage rate of argon in the frigid aquatic environment is significantly reduced, which is in agreement with the conclusions obtained from the argon-infused samples stored in an aquatic environment at room temperature (Fig. S7†).
5. Conclusions
We have developed, modeled, and demonstrated a strategy for fabricating highly thermally insulating, water-compatible flexible garments from the infusion of high-molecular-weight noble gases into closed-cell neoprene foams. A reduction in thermal conductivity by up to 40% is measured for neoprene foams infused with high-molecular-weight gases such as Xe, Kr, and Ar. The thermal conductivities measured for the materials closely match analytical predictions from the Maxwell model, suggesting the existence of pure high-molecular-weight noble gases within the foam pores. However, the reduction in thermal conductivity for our materials is transient in nature, with the thermal conductivity returning to, and often surpassing, the control value for unaltered neoprene after a time frame of up to 12 hours. This transient nature motivated the development of a numerical Fickian diffusion model to describe both the charging and discharging processes of our materials. A 6 mm thick neoprene sample can be charged in as little as 24 hours and insulates more effectively than standard neoprene for 12–36 hours after removal from the gas environment. The numerical model matches very well with experimental measurements, and provides a reliable engineering approach to both improving and analyzing the gas charging and discharging processes. The technique introduced in this paper is not limited to neoprene foams. Using a similar strategy, it should be possible to achieve a thermal conductivity below 0.020 W m−1 K−1 in other foams, such as TPU or PEBA. This work was motivated by the need to improve insulation performance of neoprene wetsuits, and thus neoprene has been used as the material with which to demonstrate the concept, but the technique is expected to have a much broader applicability. Lastly, we charge an entire commercial wetsuit with both Ar and Kr gases and demonstrate the thermal insulation enhancements on a larger scale. With a simple thermo-physiological model, we predict a factor of two enhancement in dive persistence before the onset of hypothermia for an average diver in 0 °C water for a wetsuit composed of our material versus standard commercial neoprene.6. Experimental section
Materials
Foamed neoprene (thicknesses = 1.6 mm & 6.4 mm) was purchased from Cleverbrand Inc. (Cheektowaga, NY, USA). Men's medium sized 4/3 mm neoprene wetsuits were purchased from O'Neill (Santa Cruz, CA, USA). Xe and Kr gases were purchased from Concorde Specialty Gases (Eatontown, NJ, USA). Ar gas was obtained from Airgas.Material fabrication
The bare neoprene coupons and wetsuit are placed into a 1.9 L and 19 L sealed container, respectively, which is then filled with the insulating gas until the pressure inside the container reaches 20 psi (gauge). The sealed tanks are attached to the appropriate gas cylinders via pressure regulators, which maintain the pressure for the desired number of days.Thermal characterization
Thermal conductivity was measured in this work using the Hot Disk method, an ISO standard technique (ISO 22007-2:2015(en)). Thermal conductivity measurements were carried out using a Thermtest Hot Disk TPS 2500 S thermal conductivity meter (ThermTest Inc., Fredericton, NB, Canada). For all measurements, the Hot Disk Kapton 5501 sensor (radius = 6.4 mm) acted as both the heat source and temperature measurement sensor. The heating power for each experiment was 15 mW for a period of 80 seconds. Data points 40–200 were analyzed to determine the thermal conductivity. At least four neoprene or wetsuit samples were cut into circles (radius = 2.5 cm) and stacked symmetrically on either side of the planar sensor for each measurement. A mild steel weight (0.3 kg; radius = 2.5 cm; thickness = 2 cm) was also placed on the top of the stacked neoprene samples to minimize the interfacial thermal resistance between samples and the sensor (Fig. 3a). All measurements were performed at ambient temperature (21 °C), with the exception of the data in Fig. S12† (5 °C).Fig. 3a shows the experimental setup for measurement of thermal conductivity. A cylindrical metal weight (mild steel, mass Ms = 0.312 kg, diameter Ds = 5 cm, thickness Hs = 2 cm) is placed on top of the sample to ensure that no air gaps form between the Hot Disk sensor and the neoprene pieces it directly touches. If such gaps were present, heat transfer through the air within them would contaminate the thermal conductivity measurements. The weight imposes a compressive stress of 4Msg/πDs2 = 1.56 kPa, or about 0.015 atm, on the neoprene. From a systematic previous study of neoprene's thermal conductivity as a function of ambient hydrostatic pressure by Bardy et al.,1 the pressure imposed by the steel weight is not enough to significantly alter the thermal conductivity from its nominal value in the absence of compression. The neoprene coupons are cut into circular discs with diameters equal to that of the steel weight, so that the compressive stress is uniform over the neoprene surface, and is consistent for different experiments. A heating power of 15 mW is applied and measurements are collected for 80 s for all data reported in this study.
Microscopic characterization
Thickness and radius vs. time measurements were taken using captured images (analyzed using ImageJ) from a Deluxe Handheld Digital Microscope from Celestron. A single Ar-infused neoprene sample (radius = 2.5 cm) with the mild stainless steel weight (0.3 kg; radius = 2.5 cm; thickness = 2 cm) was imaged over time directly after removal from the pressurized Ar gas environment. The morphology of the neoprene foams was investigated with SEM 6010LA JEOL under high vacuum and operation voltage of 1 kV.Permeation experiments
The Xe and Ar permeation test through neoprene was carried out in a homemade permeation cell, described in detail elsewhere37 where the neoprene foam was clamped between two halves of stainless steel module. A schematic of the operation is shown in the ESI.† Pure xenon or argon gas at a gauge pressure of 445 torr was fed to the neoprene foam. Nitrogen was used as the sweep gas to direct the permeated gas components to the mass spectrometer (MS, Agilent 5977A coupled with Diablo 5000A real-time gas analyzer). The MS was pre-calibrated with respect to the gas composition, yielding a proportional dependence of the MS signal vs. the molar composition (mol%) of gas feed. The MS signal intensities were used to calculate the permeability of each gas species. The pressure on the permeate side was maintained near atmospheric pressure at 1.1 bar.Simulations
Simulations were performed using the finite element software package COMSOL Multiphysics 5.1 (Burlington, MA, USA) on a Sony VAIO personal computer.Conceptual insights
Effective thermal insulation is essential for many applications, including energy conservation and energy harvesting. For example, thermally insulating fabrics are vital for human thermal management and prevention of hypothermia at temperatures below normal physiological range. High-performance insulating garments become even more important in low-temperature water environments, where convective heat losses are very efficient. Herein, we develop, demonstrate, and model a repeatable process for synthesizing ultra-low-thermal-conductivity closed-cell neoprene garments by infusing high-molecular-weight noble gases. We apply this concept to low-temperature dive suits, such as those used by military divers, underwater workers, or open-water swimmers. We employ this processing strategy to develop an ultra-insulating neoprene wetsuit, which we predict can extend safe dive times to 2–3 hours in water below 10 °C, compared to a state-of-the-art wetsuit (<1 hour). Our innovation brings to the materials science field a repeatable process for enhancing the thermal insulation properties of closed-cell foam garments; however, the concept could also be applied to other closed-cell foams to enhance their insulating capabilities.Financial interests
Some of the authors are co-inventors on a provisional patent application entitled “Ultra-Low Thermal Conductivity Diving-Suit Material For Enhanced Persistence In Cold-Water Dives.”Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Matteo Bucci, Kristen Young, and Albert Tianxiang Liu for helpful discussions. The authors acknowledge the Office of Naval Research (ONR), under award N00014-16-1-2144, for their support in developing and analyzing the low thermal conductivity materials for application in low temperature divesuits, and we acknowledge King Abdullah University of Science and Technology (KAUST), under award OSR-2015-Sensors-2700, for their financial support regarding this project. We also acknowledge The US Department of Energy, Office of Science, Basic Energy Sciences under award grant DE-FG02-08ER46488 Mod 0008 is acknowledged for support of mathematical modeling and computation relating to energy systems related to nanomaterials.References
- E. Bardy, J. Mollendorf and D. Pendergast, J. Phys. D: Appl. Phys., 2005, 38, 3832 CrossRef.
- P. B. West, Heat Transfer Eng., 1993, 14, 74–80 CrossRef.
- T. Ohsawa, M. Miwa, N. Goto and A. Nakayama, J. Appl. Polym. Sci., 1979, 23, 1233–1245 CrossRef.
- M. P. Norton and C. Y. L. Chan, Appl. Energy, 1982, 12, 159–176 CrossRef.
- B. P. Jelle, Energy Build, 2011, 43, 2549–2563 CrossRef.
- B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283 CrossRef PubMed.
- D. M. S. Al-Homoud, Build Environ, 2005, 40, 353–366 CrossRef.
- C. V. Vo and A. N. Paquet, J. Cell. Plast., 2004, 40, 205–228 CrossRef.
- S. A. Al-Ajlan, Appl. Therm. Eng., 2006, 26, 2184–2191 CrossRef.
- Z. Zhu, J. H. Zong, C. B. Park and M. Choudhary, J. Heat Transfer, 2009, 131, 052603 CrossRef.
- T. Fishback and C. Reichel, J. Cell. Plast., 1994, 30, 84–89 CrossRef.
- H. Zhang, W.-Z. Fang, Y.-M. Li and W.-Q. Tao, Appl. Therm. Eng., 2017, 115, 528–538 CrossRef.
- E. Bardy, J. Mollendorf and D. Pendergast, J. Phys. D: Appl. Phys., 2006, 39, 1908 CrossRef.
- Infinergy, The first expanded TPU – Small beads, high performance, http://www.polyurethanes.basf.com/pu/solutions/en/function/conversions:/publish/content/group/News_und_Medien/Polyurethan/Infinergy_Flyer_EN.pdf, accessed February 13, 2018.
- V. Izzard, H. Hadavinia, V. Morris, P. Foot, L. Wilson and K. Hewson, Polym. Polym. Compos., 2012, 20, 425 Search PubMed.
- R. C. Willemse, R. Dabbous, A. Fasola, C. Lacroix and M. Mauger, European Patent, EP1828290A1, 2007.
- B. P. Jelle, A. Gustavsen and R. Baetens, J. Build. Phys., 2010, 34, 99–123 CrossRef.
- P. C. Thapliyal and K. Singh, Aerogels as Promising Thermal Insulating Materials, https://www.hindawi.com/journals/jma/2014/127049/abs/, accessed February 13, 2018.
- G. Chen, Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons, Oxford University Press, 2005 Search PubMed.
- T. H. Jensen, US Pat., US5266251A, 1993 Search PubMed.
- S. K. Dey, C. Jacob and M. Xanthos, J. Vinyl Addit. Technol., 1996, 2, 48–52 CrossRef.
- M. Aguilella-Arzo, A. Alcaraz and V. M. Aguilella, Am. J. Phys., 2003, 71, 333–337 CrossRef.
- R. Hamilton and O. Crosser, Ind. Eng. Chem. Fundam., 1962, 1, 187–191 CrossRef.
- C.-W. Nan, R. Birringer, D. R. Clarke and H. Gleiter, J. Appl. Phys., 1997, 81, 6692–6699 CrossRef.
- R. C. Progelhof, J. L. Throne and R. R. Ruetsch, Polym. Eng. Sci., 1976, 16, 615–625 CrossRef.
- S. E. Gustafsson, Rev. Sci. Instrum., 1991, 62, 797–804 CrossRef.
- O. Almanza, M. A. Rodríguez-Pérez and J. A. De Saja, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 1226–1234 CrossRef.
- M. L. Nuckols and W. C. Tucker, Life support systems design: diving and hyperbaric applications, Simon & Schuster Custom Publ., 1996 Search PubMed.
- R. M. Barrer, Trans. Faraday Soc., 1939, 35, 628–643 RSC.
- D. W. van Krevelen and K. Te Nijenhuis, Properties of Polymers: Their Correlation with Chemical Structure; their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier, 2009 Search PubMed.
- R. M. Barrer and H. T. Chio, J. Polym. Sci., Part C: Polym. Symp., 1965, 10, 111–138 CrossRef.
- B. E. Poling, J. M. Prausnitz and J. P. O'connell, The properties of gases and liquids, Mcgraw-hill, New York, 2001, vol. 5 Search PubMed.
- A. Wassiljewa, Phys. Z., 1904, 5, 737 Search PubMed.
- E. A. Mason and S. C. Saxena, Phys. Fluids, 1958, 1, 361–369 CrossRef.
- J. Verbraecken, P. Van de Heyning, W. De Backer and L. Van Gaal, Metabolism, 2006, 55, 515–524 CrossRef PubMed.
- F. Kreith and W. Z. Black, Basic heat transfer, Harper & Row New York, 1980 Search PubMed.
- K. V. Agrawal, J. D. Benck, Z. Yuan, R. P. Misra, A. Govind Rajan, Y. Eatmon, S. Kale, X. S. Chu, D. O. Li, C. Gong, J. Warner, Q. H. Wang, D. Blankschtein and M. S. Strano, J. Phys. Chem. C, 2017, 121, 14312–14321 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04037k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2018 |