Open Access Article
Open Access ArticleSynthesis and properties of novel ammonium-based room-temperature gemini ionic liquids†
Xuzhao Yang ab and
Yun Fang
ab and
Yun Fang *a
*a
aThe Key Laboratory of Synthetic and Biological Colloids, Ministry of Education, School of Chemical and Material Engineering, Jiangnan University, Wuxi 214122, China. E-mail: yunfang@126.com; yangxz@zzuli.edu.cn
bHenan Provincial Key Laboratory of Surface and Interface Science, School of Material and Chemical Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China
First published on 23rd July 2018
Abstract
Ammonium-based room-temperature asymmetrical gemini ionic liquids, 1-trimethylammonium-3-(pyridinium)propane bisdicyanamide ([N111C3Py][DCA]2) and 1-trimethylammonium-3-(1-methylpiperidinium)propane bisdicyanamide ([N111C3MPi][DCA]2) were respectively synthesized and structurally characterized by 1H NMR and 13C NMR. Thermal stability of the gemini ionic liquids was determined by thermogravimetric analysis under a pure nitrogen atmosphere. Densities and viscosities of pure GILs and their binary mixtures with acetonitrile (MeCN) were investigated over the entire range of mole fractions at various temperatures, from 288.15 to 333.15 K, under atmospheric pressure. Moreover, the excess molar volumes (VEm) and the viscosity deviations (Δη) of the binary mixtures were evaluated and well fitted to the Redlich–Kister polynomial expression. The negative values of VEm and Δη result from strong self-association and interaction between the gemini ionic liquid molecules and MeCN. Results are discussed in terms of molecular interactions and structures.
1 Introduction
The pretreatment and transformation of biomass (such as lignocellulosic materials) remain a challenge owing to the complex structure of biomass. Biomass conversion consists of a fair amount of chemical and biological processes which require suitable solvents for the dissolution of various biomass materials. It is difficult to dissolve biomass using traditional organic solvents. Environmentally friendly and biocompatible solvents such as ionic liquids are preferred for use in the biorefining processes due to their unique performance in dissolving whole biomass or selected saccharides such as cellulose, hemicellulose, lignin, glucose and mannose.Ionic liquids (ILs) consisting of only anionic and cationic species have been tailored as replacements for organics commonly used in reactions or separations in the academic and industrial fields due to their negligible volatility, non-flammability, thermal stability, wide electrochemical window, wide liquidus range, recyclability, and so on.1–5 Their unique and tunable physicochemical properties such as melting point, density, viscosity, solubility, heat capacity and surface tension mainly depend on the possible cation and anion combinations. Each cation or anion is associated with an equivalent anion or cation that is either hydrophobic or hydrophilic, providing almost infinite opportunities to design desired ILs with functionalities to fit possible chemical processes and physical applications in materials science and technology.6–9 To date, most investigated ILs are still traditional monocationic ILs. Most IL studies focus on synthesis, properties, the relationships between structure and properties, molecular dynamics, and applications.
Recently, other than the monocationic types, a novel category of ILs, namely gemini ILs (GILs), consisting two cationic head groups linked by a rigid or flexible spacer and two anionic moieties, have gained increasing attention due to their superior properties in terms of thermal stability, tunability and volatility.10 The physicochemical properties such as melting point, density, viscosity, solubility, heat capacity, surface tension and solubility behaviors can thus be altered and engineered to a greater extent than the traditional ILs because of the larger number of possible combinations of numerous cationic moieties, anions, and linkages. Therefore, GILs have been proposed to serve as gas chromatography stationary phases,11,12 solvents for high-temperature reactions,13 and novel high-temperature lubricants14 where conventional ILs fail. Some investigations in GILs have explored their specific and/or desired applications in the field of science and technology.
In the past few years, relatively little attention has been paid to GILs because of the much fewer reports compared with monocationic ILs, and the understanding on GILs is thus lacking. Part of the reason may be that GILs still possess some inconveniences and disadvantages. In some instances, GILs display higher melting points and viscosities in comparison with common monocationic analogues with the same anion. Sometimes, they present as solids even beyond 100 °C (ref. 15) and show higher viscosities even at high temperatures, which may result in decreasing rates of mass transfer and increasing pumping costs, thus limiting their real potential applications to the processes requiring higher temperatures. Some experimental and theoretical efforts to design and synthesize novel GILs with lower melting points and viscosities have been made while our work was in progress.16,17 The most common methodology for lowering the melting point of GILs is to change the counteranions, which thus can alter the solvation properties. According to the literature on this subject, incorporating larger bulky or asymmetrical cationic moieties into the structure of GILs can reduce the cohesive forces and depress ion pairing. Meanwhile, GILs with longer alkane linkage tend to have comparatively lower melting points. As for GILs, it has been proven that employing the longer alkyl chains, introducing specified functional groups, or matching the relatively low symmetry, high flexibility, and weakly coordinating anions can decrease the viscosity. The combination of dicyanamide (DCA), bis(trifluoromethane)sulfonamide (NTf2), or trifluoromethanesulfonate (TfO) anion with cations may form lower-viscosity GILs. Meanwhile, GILs possess the same desirable solvation properties and can dissolve various biomass materials. Therefore, another easy approach to decrease the dynamic viscosity at low temperatures and reduce the costs is to mix GILs with less viscous conventional organic co-solvents or other molecular liquids. The viscosities of pure GILs and their mixtures with other less viscous solvents are essential data, and the knowledge is primordial for industrial and academic processes.
When GILs are applied in academic and industrial fields, it is important to determine and understand their physicochemical properties, namely density, viscosity, thermal behavior, and the relationships between these properties and ionic species and structures. A systematic and precise evaluation of physicochemical properties may be equally important in academic research because it is the required beginning of a comprehensive study of GILs and can help us find optimum GILs for real applications. The accumulation of these data and relationships between the properties and structures may be also an essential step to designing and synthesizing desired GILs. Until now, the systematic and accurate knowledge of physical and chemical properties of GILs and their mixtures with molecular co-solvents are still very lacking compared with conventional monocationic ILs.
To our knowledge, GILs containing DCA anion possess lower melting points and dynamic viscosities due to the coordinating ability of this anion.18–20 In the present work, novel unsymmetrical ammonium-based room-temperature GILs, 1-trimethylammonium-3-(pyridinium)propane bisdicyanamide ([N111C3Py][DCA]2) and 1-trimethylammonium-3-(1-methylpiperidinium)propane bisdicyanamide ([N111C3MPi][DCA]2) were synthesized and characterized by 1H NMR and 13C NMR. The thermal stability of these pure dicationic organics, and the density and dynamic viscosity data of pure GILs together with the binary mixture with acetonitrile, were respectively measured over the entire concentration range in the temperature range from 283.15 to 333.15 K, with 5 K intervals, at atmospheric pressure. In addition, the onset decomposition temperature (Tonset) and the temperature at the maximum rate of weight loss (Tmax) were obtained. Meanwhile, thermal expansion coefficients (α) of the binary mixtures were calculated, and the temperature dependence of the viscosity of pure GILs was correlated using various empirical equations. The excess molar volume (VEm) and dynamic viscosity deviations (Δη) of the binary mixtures were respectively obtained and fitted to the Redlich–Kister (R–K) type polynomials to determine the temperature dependence of VEm and Δη. Results are discussed in terms of molecular interactions and structures to give a better understanding of these interactions between GILs and MeCN.
2 Experimental
2.1. Chemicals
High-grade (3-bromopropyl)trimethylammonium bromide (C6H15Br2N), pyridine (C5H5N), 1-methylpiperidine (C6H13N), sodium dicyanamide (C2N3Na), silver nitrate (AgNO3), acetonitrile (C2H3N) and ethyl acetate (C4H8O2) were all delivered by Aladdin Industrial Inc. All materials were kept in a controlled environment to prevent moisture and contamination, and directly used without further purification. The specifications of these chemicals are presented in Table 1. Deionized water was prepared from an ultrapure water purification system (type UPR-I-5T, Ultrapure Technology Co. Ltd, China).| Chemical name | CAS no. | M.W. | Mass fraction purity | Source |
|---|---|---|---|---|
| Pyridine | 110-86-1 | 79.10 | >99.9% | Aladdin Industrial Inc., China |
| 1-Methylpiperidine | 626-67-5 | 99.17 | 97.0% | Aladdin Industrial Inc., China |
| (3-Bromopropyl)trimethylammonium bromide | 3779-42-8 | 261.00 | >99.0% | Aladdin Industrial Inc., China |
| Methanol | 67-56-1 | 32.04 | >99.9% | Aladdin Industrial Inc., China |
| Ethanol | 64-17-5 | 46.07 | >99.5% | Aladdin Industrial Inc., China |
| Sodium dicyanamide | 1934-75-4 | 89.03 | >96.0% | Aladdin Industrial Inc., China |
| Silver nitrate | 7761-88-8 | 169.87 | >99.0% | Aladdin Industrial Inc., China |
| Ethyl acetate | 141-78-6 | 88.11 | >99.5% | Aladdin Industrial Inc., China |
2.2. Synthesis and characterization
An overview of the synthesis of [N111C3Py][DCA]2 and [N111C3MPi][DCA]2 is depicted in Scheme 1. In order to decrease the water content in GILs, the GIL samples were constantly stored before use under a dry nitrogen atmosphere to prevent absorption of moisture and any organic contamination. The water content of the samples ([N111C3Py][DCA]2 and [N111C3MPi][DCA]2), measured by Karl Fischer titration technique (Aquastar V-200 Titrator, EM Science), is respectively 42 ppm and 47 ppm. Impurity levels of bromide ion in all the desired products were determined by an Oakton Ion 510 Series pH/mV/Ion/°C meter with Cole-Parmer ion specific probes (27502-05 for Br) and were lower than 10 ppm.The structures were identified using 1H NMR and 13C NMR (Bruker AVANCE III 600 MHz Digital NMR Spectrometer). The NMR analysis is presented below.
Solutions containing GIL ([N111C3Py][DCA]2, [N111C3MPi][DCA]2) were prepared gravimetrically using an analytical balance with a precision of ±0.1 mg (type AR224CN, Ohaus) in mass fraction by magnetic stirring. The mixtures were degassed using an ultrasonic bath to remove ubiquitous oxygen. No decomposition was observed at the experimental conditions.
2.3. Thermal stability
The thermal stability of GIL was measured using a simultaneous thermal analysis apparatus (STA 449 F3 Jupiter®, Netzsch, Germany) at a heating rate of 10 K min−1 in an inert atmosphere of nitrogen with a flow rate of 20 mL min−1. A sample of ∼10 mg was placed in a small open platinum pan and heated from room temperature to 1000 °C. The accuracy of the temperature control was found to be ±0.1 °C. The weight loss with respect to temperature was recorded. The scanning differential thermal analysis (DTA) data were obtained simultaneously with the TGA data. The observed decomposition temperatures were determined from the step tangent of the TG curves.2.4. Density measurement
The densities (ρ) of pure GILs, MeCN and their binary mixtures were experimentally determined in the temperature range from 283.15 to 333.15 K at an interval of 5 K, employing an Anton Paar DMA 5000M digital vibrating tube densimeter automatically thermostated within ±0.01 K at ambient pressure. The accuracy and precision of the densimeter were at ±0.000005 g cm−3, and the uncertainty of the measurements was estimated to be better than ±0.000001 g cm−3. Before each measurement, the densimeter was calibrated at 283.15 K, 288.15 K, 293.15 K, 298.15 K, 303.15 K, 308.15 K, 313.15 K, 318.15 K, 323.15 K, 328.15 K and 333.15 K with deionized water and dry air. To reduce the uncertainties in the density values, viscosity corrections needed for GILs with highly viscous liquids are automatically made by the densimeter. Each experimental density value is the average of three measurements at each temperature. The experimental densities of MeCN were compared with the available literature data21–25 to confirm the procedure and reproducibility of our present measurements (see Table S1 in ESI†).2.5. Viscosity measurement
The dynamic viscosities of GILs, MeCN and their binary mixtures at atmospheric pressure from 283.15 to 333.15 K, with an interval of 5 K, were determined through an automatic microviscometer (Lovis 2000 M, Anton Paar, Graz, Austria) by using the rolling-ball principle, which is intended for determining the rolling time of a stainless steel or gold-covered ball in a liquid sample and calculating its viscosity from the rolling time. A ball rolls through a closed, liquid-filled capillary that is inclined at a defined angle. The liquid viscosity is directly related to the time obtained. Calibration was carried out by using deionized water or viscosity standard oils. The microviscometer can keep the temperature variation within ±0.01 K. This apparatus has the viscosity measurement range of 0.3–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mPa s and the accuracy of up to ±0.5%. Each viscosity value is the average of three measurements at each temperature. The experimental viscosities of MeCN were compared with the literature values21–25 (see Table S1 in ESI†).
000 mPa s and the accuracy of up to ±0.5%. Each viscosity value is the average of three measurements at each temperature. The experimental viscosities of MeCN were compared with the literature values21–25 (see Table S1 in ESI†).
3 Results and discussion
3.1. Thermal stability
The changes in weight and the weight loss rate of GILs with increasing temperature, at a heating rate of 10 K min−1, are depicted in Fig. 1. The onset decomposition temperature (Tonset) and temperature at the maximum rate of weight loss (Tmax) of the GILs are listed in Table 2. As shown in Fig. 1 and Table 2, these GILs are thermally more unstable than other GILs, which can be attributed to the weakly coordinating DCA anion. The thermal stabilities for the GILs increase in the following sequence: [N111C3MPi][DCA]2 < [N111C3Py][DCA]2, with [N111C3Py][DCA]2 possessing higher thermal stability. Considering a given anion, the ILs containing [Py]+ cation showed higher decomposition temperature compared with those derived from [MPi]+.26 The thermal stability determined for these GILs is in the reasonable range for various applications. As seen in Fig. 1, the TG curve for each GIL can be divided into four steps. The first step has no obvious mass loss, which shows that these GILs are thermally stable in this temperature range. The second step is the first stage of decomposition, in which the combinations of DCA anions with corresponding cationic moieties may be cleaved, for the reason that the DCA anion is a class of nucleophilic and coordinated anions, which may decompose at lower temperature, leading to corresponding mass loss.27 The third step may be the directed cleavage of C–N bonds between the linkage group and two cationic head groups. The final step may attribute to the decomposition of carbon skeleton in the cations. It has been assumed that the thermal stability of the GILs depends on their structures and the molecular weights of cations and anions.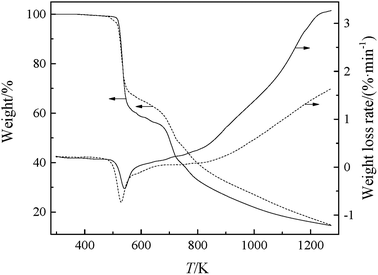 | ||
| Fig. 1 TG-DTG curves of the synthesized GILs: solid line, [N111C3Py][DCA]2; dashed line, [N111C3MPi][DCA]2. | ||
| GIL | Tonset/K | Tmax/K |
|---|---|---|
| [N111C3Py][DCA]2 | 523.12 | 537.89 |
| [N111C3MPi][DCA]2 | 514.91 | 525.58 |
3.2. Density and excess volume
The densities measured for GILs, MeCN and their binary mixtures over the entire composition range at the temperatures ranging from 283.15 to 333.15 K under ambient pressure were systematically determined and are shown in Tables 3 and 4.| x1 | ρ/(g cm−3) | VEm/(cm3 mol−1) | η/(mPa s) | Δη/(mPa s) |
|---|---|---|---|---|
| a Uncertainties are u(T) = 0.01 K, u(p) = 200 Pa, u(x) = 0.00001, u(ρ) = 1 × 10−5 g cm−3, u(η) = 1 × 10−4 mPa s, u(VEm) = 1 × 10−5 cm3 mol−1, u(Δη) = 1 × 10−4 mPa s. | ||||
| 283.15 K | ||||
| 0.0000 | 0.79283 | 0.00000 | 0.4012 | 0.0000 |
| 0.0999 | 0.94085 | −0.97370 | 4.1446 | −751.1908 |
| 0.1999 | 1.02068 | −1.71560 | 14.1880 | −1496.8373 |
| 0.2998 | 1.07022 | −2.34740 | 52.8431 | −2213.1164 |
| 0.3997 | 1.09874 | −2.28366 | 131.4302 | −2889.4636 |
| 0.4999 | 1.11754 | −1.94751 | 245.2401 | −3532.8549 |
| 0.6002 | 1.13081 | −1.46086 | 473.5503 | −4062.5019 |
| 0.7001 | 1.14132 | −1.00940 | 856.9804 | −4434.0060 |
| 0.7998 | 1.15001 | −0.61026 | 1384.9022 | −4659.5089 |
| 0.8997 | 1.15759 | −0.30151 | 2374.5011 | −4424.8430 |
| 1.0000 | 1.16399 | 0.00000 | 7557.3000 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 288.15 K | ||||
| 0.0000 | 0.78748 | 0.00000 | 0.3819 | 0.0000 |
| 0.0999 | 0.93710 | −1.06971 | 3.7453 | −384.1405 |
| 0.1999 | 1.01708 | −1.80523 | 12.2943 | −763.4836 |
| 0.2998 | 1.06687 | −2.44250 | 42.1502 | −1121.1315 |
| 0.3997 | 1.09560 | −2.38204 | 97.8751 | −1452.9104 |
| 0.4999 | 1.11432 | −2.01322 | 174.6311 | −1764.8230 |
| 0.6002 | 1.12773 | −1.52525 | 321.0604 | −2007.4485 |
| 0.7001 | 1.13827 | −1.05804 | 553.7802 | −2162.2324 |
| 0.7998 | 1.14706 | −0.65821 | 848.1505 | −2254.5906 |
| 0.8997 | 1.15467 | −0.33773 | 1335.8011 | −2154.4445 |
| 1.0000 | 1.16099 | 0.00000 | 3879.3002 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 293.15 K | ||||
| 0.0000 | 0.78210 | 0.00000 | 0.3641 | 0.0000 |
| 0.0999 | 0.93325 | −1.16161 | 3.4486 | −215.7600 |
| 0.1999 | 1.01350 | −1.89961 | 10.7510 | −427.5212 |
| 0.2998 | 1.06356 | −2.54413 | 34.4992 | −622.6177 |
| 0.3997 | 1.09248 | −2.48435 | 75.8173 | −800.1442 |
| 0.4999 | 1.11123 | −2.09777 | 129.0504 | −966.4130 |
| 0.6002 | 1.12467 | −1.59225 | 226.4001 | −1088.7837 |
| 0.7001 | 1.13523 | −1.10687 | 371.2505 | −1162.7783 |
| 0.7998 | 1.14414 | −0.70962 | 561.9012 | −1190.5347 |
| 0.8997 | 1.15171 | −0.36192 | 850.2906 | −1120.9892 |
| 1.0000 | 1.15801 | 0.00000 | 2191.0021 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 298.15 K | ||||
| 0.0000 | 0.77670 | 0.00000 | 0.3479 | 0.0000 |
| 0.0999 | 0.92940 | −1.25684 | 3.2052 | −127.5774 |
| 0.1999 | 1.00993 | −1.99789 | 9.5451 | −251.8027 |
| 0.2998 | 1.06026 | −2.64942 | 28.7061 | −363.0764 |
| 0.3997 | 1.08939 | −2.59250 | 59.8222 | −462.3951 |
| 0.4999 | 1.10809 | −2.17645 | 98.1055 | −554.9384 |
| 0.6002 | 1.12162 | −1.66146 | 165.5803 | −618.4203 |
| 0.7001 | 1.13217 | −1.15193 | 263.8207 | −650.6149 |
| 0.7998 | 1.14119 | −0.75440 | 381.8602 | −662.7485 |
| 0.8997 | 1.14879 | −0.39323 | 561.3303 | −613.7131 |
| 1.0000 | 1.15504 | 0.00000 | 1306.0011 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 303.15 K | ||||
| 0.0000 | 0.77127 | 0.00000 | 0.3332 | 0.0000 |
| 0.0999 | 0.92546 | −1.34827 | 3.0028 | −80.2941 |
| 0.1999 | 1.00637 | −2.09932 | 8.5509 | −157.7926 |
| 0.2998 | 1.05698 | −2.75793 | 24.3252 | −224.9822 |
| 0.3997 | 1.08623 | −2.69155 | 48.2821 | −283.9888 |
| 0.4999 | 1.10500 | −2.26048 | 76.3252 | −339.1586 |
| 0.6002 | 1.11858 | −1.72897 | 125.0205 | −373.7594 |
| 0.7001 | 1.12918 | −1.20477 | 192.4303 | −389.3130 |
| 0.7998 | 1.13819 | −0.78296 | 271.0104 | −393.5306 |
| 0.8997 | 1.14587 | −0.41680 | 392.0407 | −355.4642 |
| 1.0000 | 1.15211 | 0.00000 | 830.8034 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 308.15 K | ||||
| 0.0000 | 0.76581 | 0.00000 | 0.3196 | 0.0000 |
| 0.0999 | 0.92152 | −1.44331 | 2.8266 | −53.1763 |
| 0.1999 | 1.00283 | −2.20547 | 7.7113 | −104.0307 |
| 0.2998 | 1.05372 | −2.87052 | 20.9521 | −146.4733 |
| 0.3997 | 1.08309 | −2.79382 | 39.6003 | −183.5086 |
| 0.4999 | 1.10198 | −2.35408 | 61.2755 | −217.6841 |
| 0.6002 | 1.11555 | −1.79623 | 96.7161 | −238.1493 |
| 0.7001 | 1.12619 | −1.25443 | 145.6202 | −244.9286 |
| 0.7998 | 1.13521 | −0.81098 | 200.1906 | −245.9304 |
| 0.8997 | 1.14295 | −0.43465 | 286.2104 | −215.5937 |
| 1.0000 | 1.14921 | 0.00000 | 557.7103 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 313.15 K | ||||
| 0.0000 | 0.76032 | 0.00000 | 0.3071 | 0.0000 |
| 0.0999 | 0.91759 | −1.54292 | 2.6723 | −36.1615 |
| 0.1999 | 0.99930 | −2.31554 | 7.0336 | −70.3655 |
| 0.2998 | 1.05048 | −2.98730 | 18.1521 | −97.7738 |
| 0.3997 | 1.07997 | −2.89941 | 33.2670 | −121.1856 |
| 0.4999 | 1.09893 | −2.44284 | 50.0027 | −143.0950 |
| 0.6002 | 1.11256 | −1.86821 | 76.5772 | −155.1990 |
| 0.7001 | 1.12321 | −1.30274 | 108.6508 | −161.6527 |
| 0.7998 | 1.13227 | −0.84251 | 145.4805 | −163.2723 |
| 0.8997 | 1.14008 | −0.45767 | 212.6704 | −134.6090 |
| 1.0000 | 1.14634 | 0.00000 | 385.9631 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 318.15 K | ||||
| 0.0000 | 0.75479 | 0.00000 | 0.2956 | 0.0000 |
| 0.0999 | 0.91375 | −1.65443 | 2.5404 | −25.7686 |
| 0.1999 | 0.99579 | −2.43121 | 6.4291 | −49.9213 |
| 0.2998 | 1.04725 | −3.10782 | 16.0410 | −68.3228 |
| 0.3997 | 1.07673 | −2.99083 | 28.2121 | −84.1652 |
| 0.4999 | 1.09596 | −2.54328 | 43.4605 | −97.0147 |
| 0.6002 | 1.10959 | −1.94200 | 63.8640 | −104.7363 |
| 0.7001 | 1.12025 | −1.35176 | 89.6683 | −106.9457 |
| 0.7998 | 1.12934 | −0.87169 | 117.5001 | −107.0710 |
| 0.8997 | 1.13719 | −0.47058 | 161.4022 | −91.1844 |
| 1.0000 | 1.14350 | 0.00000 | 280.7116 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 323.15 K | ||||
| 0.0000 | 0.74922 | 0.00000 | 0.2849 | 0.0000 |
| 0.0999 | 0.90992 | −1.77188 | 2.4252 | −18.8302 |
| 0.1999 | 0.99229 | −2.55219 | 5.9133 | −36.3336 |
| 0.2998 | 1.04405 | −3.23519 | 14.1380 | −49.0794 |
| 0.3997 | 1.07349 | −3.08442 | 24.1920 | −59.9960 |
| 0.4999 | 1.09306 | −2.65537 | 36.7422 | −68.4794 |
| 0.6002 | 1.10664 | −2.01914 | 51.7495 | −74.5269 |
| 0.7001 | 1.11738 | −1.41618 | 70.9492 | −76.2975 |
| 0.7998 | 1.12642 | −0.90043 | 91.6491 | −76.5260 |
| 0.8997 | 1.13441 | −0.50423 | 122.6207 | −66.5255 |
| 1.0000 | 1.14068 | 0.00000 | 210.2033 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 328.15 K | ||||
| 0.0000 | 0.74362 | 0.00000 | 0.2750 | 0.0000 |
| 0.0999 | 0.90539 | −1.83606 | 2.3240 | −14.0743 |
| 0.1999 | 0.98889 | −2.68735 | 5.4676 | −27.0702 |
| 0.2998 | 1.04085 | −3.36644 | 12.5480 | −36.1132 |
| 0.3997 | 1.07043 | −3.20431 | 20.9750 | −43.8096 |
| 0.4999 | 1.09015 | −2.76831 | 30.6054 | −50.3513 |
| 0.6002 | 1.10372 | −2.10255 | 43.2911 | −53.8533 |
| 0.7001 | 1.11448 | −1.47543 | 57.6375 | −55.6306 |
| 0.7998 | 1.12358 | −0.94486 | 73.2282 | −56.1307 |
| 0.8997 | 1.13161 | −0.53208 | 95.5920 | −49.8901 |
| 1.0000 | 1.13787 | 0.00000 | 161.6706 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 333.15 K | ||||
| 0.0000 | 0.73797 | 0.00000 | 0.2658 | 0.0000 |
| 0.0999 | 0.90166 | −1.97249 | 2.2332 | −10.6614 |
| 0.1999 | 0.98531 | −2.81029 | 5.0838 | −20.4522 |
| 0.2998 | 1.03768 | −3.50545 | 11.2140 | −26.9508 |
| 0.3997 | 1.06739 | −3.32996 | 18.3542 | −32.4395 |
| 0.4999 | 1.08721 | −2.87872 | 27.6141 | −35.8462 |
| 0.6002 | 1.10082 | −2.18985 | 37.5872 | −38.5526 |
| 0.7001 | 1.11166 | −1.54878 | 48.5280 | −40.2404 |
| 0.7998 | 1.12080 | −0.99949 | 60.3110 | −41.0609 |
| 0.8997 | 1.12887 | −0.56992 | 75.3011 | −38.6997 |
| 1.0000 | 1.13508 | 0.00000 | 126.6806 | 0.0000 |
| x1 | ρ/(g cm−3) | VEm/(cm3 mol−1) | η/(mPa s) | Δη/(mPa s) |
|---|---|---|---|---|
| a Uncertainties are u(T) = 0.01 K, u(p) = 200 Pa, u(x) = 0.00001, u(ρ) = 1 × 10−5 g cm−3, u(η) = 1 × 10−4 mPa s, u(VEm) = 1 × 10−5 cm3 mol−1, u(Δη) = 1 × 10−4 mPa s. | ||||
| 283.15 K | ||||
| 0.0000 | 0.79283 | 0.00000 | ||
| 0.0999 | 0.93640 | −1.36085 | ||
| 0.2001 | 1.00377 | −1.88498 | ||
| 0.3001 | 1.04175 | −2.05646 | ||
| 0.3998 | 1.06511 | −1.94636 | ||
| 0.5002 | 1.08154 | −1.77557 | ||
| 0.6000 | 1.09299 | −1.46325 | ||
| 0.7001 | 1.10148 | −1.06328 | ||
| 0.7996 | 1.10806 | −0.62985 | ||
| 0.8998 | 1.11386 | −0.28797 | ||
| 1.0000 | 1.11889 | 0.00000 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 288.15 K | ||||
| 0.0000 | 0.78748 | 0.00000 | 0.3819 | 0.0000 |
| 0.0999 | 0.93241 | −1.43318 | 3.9949 | −750.8835 |
| 0.2001 | 1.00031 | −1.97687 | 17.4160 | −1494.2247 |
| 0.3001 | 1.03856 | −2.15309 | 56.9202 | −2209.9725 |
| 0.3998 | 1.06199 | −2.02840 | 145.5904 | −2874.2886 |
| 0.5002 | 1.07843 | −1.83548 | 334.0607 | −3444.0914 |
| 0.6000 | 1.09009 | −1.53694 | 678.7513 | −3853.1427 |
| 0.7001 | 1.09859 | −1.11845 | 1177.0028 | −4110.8998 |
| 0.7996 | 1.10511 | −0.65109 | 2304.7011 | −3734.6754 |
| 0.8998 | 1.11098 | −0.30499 | 3991.5051 | −2804.6377 |
| 1.0000 | 1.11602 | 0.00000 | 7552.9043 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 293.15 K | ||||
| 0.0000 | 0.78210 | 0.00000 | 0.3641 | 0.0000 |
| 0.0999 | 0.92841 | −1.50767 | 3.6867 | −446.4707 |
| 0.2001 | 0.99685 | −2.07101 | 15.1392 | −886.1625 |
| 0.3001 | 1.03541 | −2.25572 | 45.9441 | −1305.6011 |
| 0.3998 | 1.05881 | −2.10191 | 111.5906 | −1688.8479 |
| 0.5002 | 1.07538 | −1.90356 | 243.4312 | −2009.0525 |
| 0.6000 | 1.08720 | −1.60992 | 465.9624 | −2235.8656 |
| 0.7001 | 1.09568 | −1.16562 | 729.2211 | −2423.2995 |
| 0.7996 | 1.10223 | −0.68268 | 1390.0052 | −2210.5118 |
| 0.8998 | 1.10812 | −0.32027 | 2477.2033 | −1574.4559 |
| 1.0000 | 1.11318 | 0.00000 | 4502.8071 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 298.15 K | ||||
| 0.0000 | 0.77670 | 0.00000 | 0.3479 | 0.0000 |
| 0.0999 | 0.92442 | −1.58546 | 3.4196 | −278.5217 |
| 0.2001 | 0.99341 | −2.16899 | 13.1605 | −551.2202 |
| 0.3001 | 1.03221 | −2.35320 | 37.6911 | −808.5644 |
| 0.3998 | 1.05574 | −2.19039 | 87.2882 | −1039.9970 |
| 0.5002 | 1.07235 | −1.97315 | 181.4506 | −1228.8377 |
| 0.6000 | 1.08428 | −1.67459 | 322.0602 | −1369.5392 |
| 0.7001 | 1.09278 | −1.21064 | 508.0509 | −1465.7063 |
| 0.7996 | 1.09939 | −0.71785 | 895.2501 | −1358.9721 |
| 0.8998 | 1.10527 | −0.33124 | 1609.8034 | −926.8610 |
| 1.0000 | 1.11037 | 0.00000 | 2819.1027 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 303.15 K | ||||
| 0.0000 | 0.77127 | 0.00000 | 0.3332 | 0.0000 |
| 0.0999 | 0.92044 | −1.66754 | 3.1755 | −180.6008 |
| 0.2001 | 0.98998 | −2.27102 | 11.6030 | −356.1672 |
| 0.3001 | 1.02904 | −2.45647 | 31.3811 | −520.0159 |
| 0.3998 | 1.05280 | −2.29851 | 69.5380 | −664.9347 |
| 0.5002 | 1.06938 | −2.05255 | 139.0803 | −779.7539 |
| 0.6000 | 1.08142 | −1.74937 | 245.8206 | −856.2733 |
| 0.7001 | 1.08992 | −1.26180 | 370.0421 | −915.8636 |
| 0.7996 | 1.09651 | −0.74075 | 623.1633 | −845.4521 |
| 0.8998 | 1.10246 | −0.34783 | 1084.9006 | −567.7061 |
| 1.0000 | 1.10758 | 0.00000 | 1836.6025 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 308.15 K | ||||
| 0.0000 | 0.76581 | 0.00000 | 0.3196 | 0.0000 |
| 0.0999 | 0.91646 | −1.75299 | 2.9790 | −119.5863 |
| 0.2001 | 0.98657 | −2.37770 | 10.3162 | −234.8621 |
| 0.3001 | 1.02588 | −2.56245 | 26.5041 | −341.0421 |
| 0.3998 | 1.04978 | −2.39555 | 56.5374 | −433.0100 |
| 0.5002 | 1.06643 | −2.13406 | 109.3102 | −503.0946 |
| 0.6000 | 1.07851 | −1.81241 | 185.3313 | −549.1979 |
| 0.7001 | 1.08708 | −1.31317 | 274.3805 | −582.6383 |
| 0.7996 | 1.09376 | −0.78797 | 449.3407 | −529.4345 |
| 0.8998 | 1.09966 | −0.36017 | 759.8422 | −341.5472 |
| 1.0000 | 1.10482 | 0.00000 | 1224.0039 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 313.15 K | ||||
| 0.0000 | 0.76032 | 0.00000 | 0.3071 | 0.0000 |
| 0.0999 | 0.91247 | −1.84135 | 2.8089 | −82.9919 |
| 0.2001 | 0.98316 | −2.48769 | 9.2371 | −162.3142 |
| 0.3001 | 1.02274 | −2.67330 | 22.7451 | −234.3855 |
| 0.3998 | 1.04678 | −2.49684 | 46.5810 | −295.8721 |
| 0.5002 | 1.06356 | −2.22902 | 86.9782 | −341.3967 |
| 0.6000 | 1.07563 | −1.88014 | 145.1305 | −368.6528 |
| 0.7001 | 1.08427 | −1.36878 | 210.1421 | −389.3077 |
| 0.7996 | 1.09097 | −0.82296 | 328.5107 | −356.0891 |
| 0.8998 | 1.09690 | −0.37822 | 544.5711 | −225.7796 |
| 1.0000 | 1.10208 | 0.00000 | 856.1032 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 318.15 K | ||||
| 0.0000 | 0.75479 | 0.00000 | 0.2956 | 0.0000 |
| 0.0999 | 0.90850 | −1.93568 | 2.6754 | −59.3758 |
| 0.2001 | 0.97977 | −2.60323 | 8.2623 | −115.7300 |
| 0.3001 | 1.01962 | −2.78885 | 19.6420 | −166.1677 |
| 0.3998 | 1.04379 | −2.60040 | 39.2504 | −208.1917 |
| 0.5002 | 1.06058 | −2.30515 | 70.3852 | −239.1214 |
| 0.6000 | 1.07287 | −1.96819 | 113.8913 | −257.3102 |
| 0.7001 | 1.08149 | −1.42703 | 163.4606 | −269.6195 |
| 0.7996 | 1.08823 | −0.86432 | 246.2922 | −248.2978 |
| 0.8998 | 1.09416 | −0.39463 | 399.5903 | −156.9389 |
| 1.0000 | 1.09937 | 0.00000 | 618.4704 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 323.15 K | ||||
| 0.0000 | 0.74922 | 0.00000 | 0.2849 | 0.0000 |
| 0.0999 | 0.90452 | −2.03419 | 2.5387 | −43.6837 |
| 0.2001 | 0.97640 | −2.72562 | 7.4884 | −84.8095 |
| 0.3001 | 1.01646 | −2.90347 | 17.3140 | −120.9674 |
| 0.3998 | 1.04088 | −2.71874 | 33.3481 | −150.7790 |
| 0.5002 | 1.05761 | −2.38500 | 58.1723 | −172.1224 |
| 0.6000 | 1.07003 | −2.04255 | 91.7744 | −184.4120 |
| 0.7001 | 1.07871 | −1.48556 | 129.8503 | −192.3654 |
| 0.7996 | 1.08553 | −0.91428 | 192.9417 | −175.0290 |
| 0.8998 | 1.09146 | −0.41944 | 302.8822 | −111.1645 |
| 1.0000 | 1.09667 | 0.00000 | 460.1203 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 328.15 K | ||||
| 0.0000 | 0.74362 | 0.00000 | 0.2750 | 0.0000 |
| 0.0999 | 0.90054 | −2.13668 | 2.4270 | −32.8145 |
| 0.2001 | 0.97303 | −2.85127 | 6.8167 | −63.4963 |
| 0.3001 | 1.01333 | −3.02380 | 15.3720 | −89.9425 |
| 0.3998 | 1.03789 | −2.82613 | 28.6281 | −111.5830 |
| 0.5002 | 1.05465 | −2.46556 | 48.6852 | −126.6675 |
| 0.6000 | 1.06705 | −2.08804 | 74.3203 | −135.9640 |
| 0.7001 | 1.07595 | −1.54452 | 104.9515 | −140.3705 |
| 0.7996 | 1.08290 | −0.97541 | 151.8803 | −128.2670 |
| 0.8998 | 1.08877 | −0.44005 | 233.0924 | −82.1285 |
| 1.0000 | 1.09400 | 0.00000 | 350.2906 | 0.0000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| 333.15 K | ||||
| 0.0000 | 0.73797 | 0.00000 | 0.2658 | 0.0000 |
| 0.0999 | 0.89656 | −2.24440 | 2.3198 | −24.8435 |
| 0.2001 | 0.96968 | −2.98310 | 6.1635 | −47.9780 |
| 0.3001 | 1.01025 | −3.15277 | 13.6690 | −67.3970 |
| 0.3998 | 1.03496 | −2.94283 | 24.7680 | −83.1416 |
| 0.5002 | 1.05162 | −2.53274 | 41.5710 | −93.3707 |
| 0.6000 | 1.06408 | −2.13177 | 62.2790 | −99.5333 |
| 0.7001 | 1.07321 | −1.60246 | 85.5210 | −103.2427 |
| 0.7996 | 1.08030 | −1.03658 | 122.0300 | −93.5235 |
| 0.8998 | 1.08610 | −0.45662 | 182.9900 | −59.5417 |
| 1.0000 | 1.09137 | 0.00000 | 269.5100 | 0.0000 |
For pure GILs, the order of the experimental density is [N111C3Py][DCA]2 > [N111C3MPi][DCA]2. [N111C3Py][DCA]2 has higher density value, while [N111C3MPi][DCA]2 possesses lower density over the experimental temperature range. The higher value for [N111C3Py][DCA]2, which contains the [Py]+ cation, is due to the smaller molecular size of the cation compared with the [MPi]+ cation. The densities of GILs increase with the decrease of cation molecular weight and are higher than those of the monocationic analogues reported in the literatures.28,29 The density for [C3Py][DCA] at 298.15 K is 1.08980 g cm−3, lower than that of [N111C3Py][DCA]2 (1.15504 g cm−3), which may be due to the stronger inter-ionic interactions of the GILs than those of the traditional monocationic ILs.9 With the increasing temperature, densities of pure GILs were observed to linearly decrease (see Fig. S1 in ESI†) due to the decrease in the van der Waals forces, which consequently increases the mobility of the ions.30 Molecules are farther apart from each other at higher temperatures, causing the decrease in density.
The density values of binary mixtures containing MeCN as a function of the mole fraction of GIL (x1) at various temperatures (283.15 to 333.15) K are listed in Tables 3 and 4. As expected, the densities of binary mixtures linearly decrease with increasing temperature, while they increase with decreasing MeCN content. A linear model was consequently employed to correlate the experimental densities and temperature.31 Volume expansion properties of GILs and their mixtures may be a prerequisite for understanding their stability in applications, especially those under higher temperature. In the present study, density changes linearly with the temperature change; the value of thermal expansion coefficient (α), a measure of how the volume changes with temperature, can be further quantified from the density data by the following expression:32,33
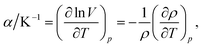 | (1) |
To attain a deeper understanding of the interaction between GIL and the organic solvent, the excess molar volume (VEm), expressing the extent of deviation of mixtures from ideal behavior, of the binary systems ([N111C3Py][DCA]2 + MeCN and [N111C3MPi][DCA]2 + MeCN) were respectively calculated from the experimental density data of the mixtures based on the following expression:34,35
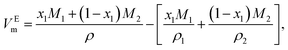 | (2) |
The experimental excess molar volumes can be mathematically represented by the Redlich–Kister polynomial equation:36,37
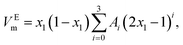 | (3) |
 | (4) |
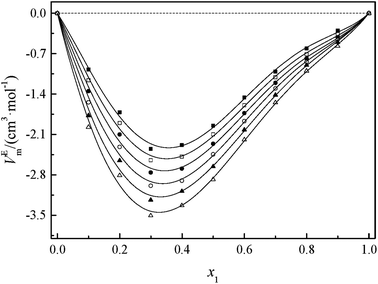
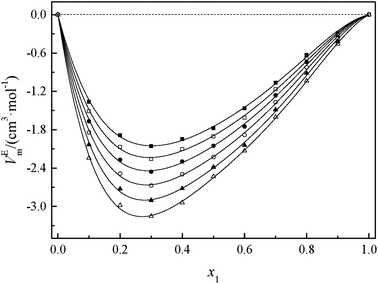
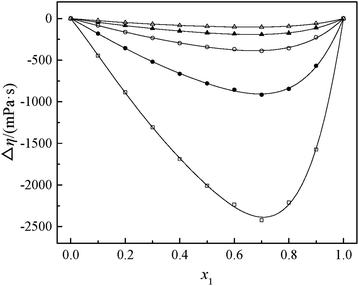
Fig. 2 and 3 show that the variation VEm, as a function of mole fraction of the GIL (x1), is negative over the entire range of composition, suggesting negative deviations from ideal solution behavior. It is more interesting that the VEm in every GIL + MeCN system has minimum values at around x1 ≈ 0.3 for all temperatures investigated, which indicates the strongest interaction. The values of VEm for the system consisting of GILs and relatively polar solvents may mainly depend on the following factors: (1) the dipole–dipole, ion–dipole, and ion–ion interactions between components of the binary mixtures;21 (2) contraction or molecular packing as a consequence of differences in size and shape of molecules (free volume difference of unlike molecules);21 (3) expansion due to the disruption of self-association in the GIL or solvent; (4) contraction owing to specific interaction between the GIL and MeCN; and (5) variation in intermolecular forces between the GIL and solvent molecules that are in contact. This behavior, negative VEm, can be interpreted in several opposing ways. Interactions between like molecules give rise to positive VEm values, while interactions between unlike molecules such as dipole–dipole interaction, dispersion force, or hydrogen bonding lead to negative contributions to VEm.23 As seen in Fig. 2 and 3, the negative values of VEm for the mixtures over the entire investigated range of GIL mole composition and in all analyzed temperatures indicate stronger interactions between GIL and MeCN molecules than those between the pure components. The interactions between unlike molecules, [N111C3Py][DCA]2, MeCN and [N111C3MPi][DCA]2, MeCN, are stronger than those between MeCN molecules, and negative VEm values are observed with the following sequence: [N111C3MPi][DCA]2 > [N111C3Py][DCA]2. GILs can be solvated by MeCN molecules because of a strong ion–dipole interaction, resulting in weakening ion–ion interactions between anions ([DCA]−) and cations in the GILs.18,38 The packing efficiency of MeCN accommodation in the interstice of GIL networks, the difference in the interaction, and hydrogen bonding may be dominant in these binary systems. Meanwhile, the interstitial accommodation and the effect of the condensation of GIL and MeCN make further negative contributions to VEm. In fact, unsymmetrical curves of VEm may be more likely to occur while the components of the binary mixture have large molecular weight and size differences. It is observed that the curves of VEm are asymmetric, indicating a large molar volume difference between the two components (GIL and MeCN) of the binary mixtures.
It can be observed that values of excess molar volume for binary systems of [N111C3Py][DCA]2 + MeCN and [N111C3MPi][DCA]2 + MeCN decrease and become more negative with increased temperature, indicating volume expansion. The variation in VEm with temperature is attributed to the competition of packing efficiency and the hydrogen bonding interaction in the binary mixture. In general, as the temperature increases, the packing efficiency strengthens, leading to decrease of VEm value.39 In the present binary mixtures of [N111C3Py][DCA]2 + MeCN and [N111C3MPi][DCA]2 + MeCN, the variation of VEm with temperature indicates that packing efficiency may play a dominant functional role in the change in value of VEm.
3.3. Viscosity and viscosity deviation
The dynamic viscosity, η, for GILs, MeCN and their binary mixtures at various temperatures over the entire concentration range from 283.15 to 333.15 K was determined (Tables 3 and 4). The viscosities are highest for the pure GIL and significantly decrease with increasing MeCN content. Meanwhile, the viscosities of the binary mixtures decrease with the increasing temperature.The sequence for the experimental viscosities of the two pure GILs is [N111C3MPi][DCA]2 > [N111C3Py][DCA]2. Among the obtained GILs, the viscosity of [N111C3MPi][DCA]2 is remarkably larger than [N111C3Py][DCA]2. The viscosity may be affected by the cation's aromaticity; the aromatic compounds possess lower viscosity values than the non-aromatic ones: [Py]+ < [MPi]+. The viscosity will be greatly affected by the cation's inherent interactions related to the GIL structure and bulk distribution. The π–π interactions in pyridinium GIL were expected to provide higher resistance to shear stress due to a more rigid IL structure and bulk distribution; the results, however, showed the opposite, with lower viscosity for the pyridinium GIL, since the π–π interactions will also lend a more rigid ring structure and induce a more organized bulk distribution compared with the more flexible piperidinium ring, resulting in a relatively flexible structure and a greater entanglement of the rings in the liquid phase.40 The viscosities of GILs are higher than those of the monocationic analogues reported in the literature.18,41 The viscosity of the pure GILs decreases sharply at low temperature when the temperature is increased, while it decreases smoothly at high temperature (see Fig. S2 in ESI†), making the temperature-dependent viscosity of GILs challenging.
The temperature dependence of the viscosity of pure GIL ([N111C3Py][DCA]2 or [N111C3MPi] [DCA]2) can be expressed in the following equations. A common method is by employing the three-parameter Vogel–Tammann–Fulcher (VTF) equation and modified VTF (mVTF) equation:42
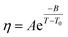 | (5) |
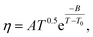 | (6) |
Meanwhile, other expressions, the inverse cubic equation (Litovitz equation)43 and simple linear equation (Ghatee equation)44 can also be used to correlate the viscosity of pure GILs with the temperature:
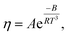 | (7) |
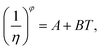 | (8) |
The equation parameters, together with correlation coefficients (R2), can be evaluated (see Table S5 in ESI†). The results indicate that both VTF and mVTF equations can quite accurately correlate the viscosity of pure GILs with temperature. The higher accuracy of the VTF and mVTF equations may be due to the larger number of parameters in the equations.
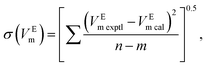
From Tables 3 and 4, it can be observed that the values of dynamic viscosity of the binary systems decreased with the addition of MeCN, as expected. The addition of common organics with higher relative permittivity (e.g. MeCN) may increase the ion solvation (weakening ion–ion interactions) and result in significantly reduced viscosity of the mixture. Deviation of the viscosity, Δη, can be calculated from the viscosity data of the mixtures and pure components based on the following equation:23
| Δη = η − (x1η1 + x2η2), | (9) |
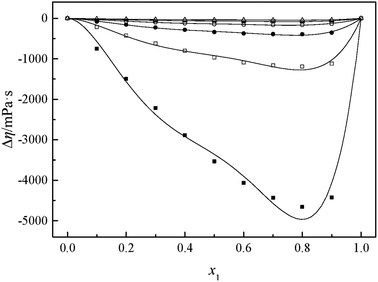
The viscosity of a mixture strongly relies on the liquid's structure. Thus, Δη depends on molecular interactions as well as the size and shape of the molecules. Accordingly, the viscosity deviation of a mixture containing a molecular solvent and an ionic species is the competition of molecular size and molecular interaction (H-bonds, van der Waals interactions).46 The viscosity deviations are negative, provided that the mixture is dominated by intermolecular forces between the solute and the solvent (the van der Waals interactions). On the contrary, the viscosity deviations are positive when the mixture is dominated by strong specific interactions (H-bonds).47 Furthermore, the negative values of Δη for the binary mixtures may also imply that the viscosities of associations formed between unlike molecules are relatively greater than those of the like ones. Negative values of Δη may also occur for the binary mixtures in which dispersion forces are dominant, particularly for the mixtures containing different molecular sizes.48,49 In the present investigation, the negative values of Δη showed that the interaction between cation and anion became weak owing to the solvation interaction between ions (cation and anion) and MeCN molecules. Based on the viscosity deviations shown in Fig. 4 and 5, the negative deviations can be attributed to strong van der Waals interactions and dispersion forces, and weak hydrogen bonding interaction between the molecules of GIL ([N111C3Py][DCA]2, [N111C3MPi][DCA]2) and MeCN.
Viscosity deviation can also be fitted to the Redlich–Kister equation:48
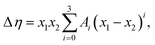 | (10) |
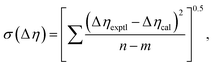 | (11) |
4 Conclusions
Two ammonium-based room-temperature asymmetrical gemini ionic liquids, [N111C3Py][DCA]2 and [N111C3MPi][DCA]2, were synthesized and structurally characterized by 1H NMR and 13C NMR. Thermal stability was determined. Densities and dynamic viscosities for the pure GIL and binary mixture of ([N111C3Py][DCA]2 + MeCN and [N111C3MPi][DCA]2 + MeCN) were respectively measured over the entire composition range from 283.15 to 333.15 K under atmospheric pressure. The densities and viscosities all increase with decreasing temperature and increasing mole fraction of GIL. The values of VEm and Δη are all negative over the entire composition range at the studied temperatures, suggesting the existence of strong self-association and weak hydrogen bonding interaction between the molecules of GIL and MeCN. The Redlich–Kister type expression was employed to correlate VEm and Δη with the mole fraction of GIL. The investigation results are expected to be helpful for a better understanding of the fundamental physicochemical properties of asymmetrical GILs and their further industrial and academic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work was supported by the Science and Technology Planning Project of Henan Province (No. 162102210056), People's Republic of China.References
- X. Cao, L. Qiao, H. Zheng, H. Yang and P. Zhang, RSC Adv., 2018, 8, 170–175 RSC.
- T. Ishida and H. Shirota, J. Phys. Chem. B, 2013, 117, 1136–1150 CrossRef PubMed.
- L. Chen, J. Chen, Z. Song, G. Cui, Y. Xu, X. Wang and J. Liu, J. Chem. Thermodyn., 2015, 91, 292–300 CrossRef.
- H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- A. Corma, S. Iborra and A. Velty, Chem. Rev., 2007, 107, 2411–2502 CrossRef PubMed.
- P. K. Kilaru, R. A. Condemarin and P. Scovazzo, Ind. Eng. Chem. Res., 2008, 47, 900–909 CrossRef.
- P. Kilaru, G. A. Baker and P. Scovazzo, J. Chem. Eng. Data, 2007, 52, 2306–2314 CrossRef.
- B. Kirchner, Ionic liquids from theoretical investigations, in Ionic Liquids, Springer, 2010, pp. 213–262 Search PubMed.
- H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef.
- J. L. Anderson, R. Ding, A. Ellern and D. W. Armstrong, J. Am. Chem. Soc., 2005, 127, 593–604 CrossRef PubMed.
- M. Qi and D. W. Armstrong, Anal. Bioanal. Chem., 2007, 88, 889–899 CrossRef PubMed.
- K. Huang, X. Han, X. Zhang and D. W. Armstrong, Anal. Bioanal. Chem., 2007, 389, 2265–2275 CrossRef PubMed.
- S. S. Bhawal, R. A. Patil and D. W. Armstrong, RSC Adv., 2015, 5, 95854–95856 RSC.
- C. Jin, C. Ye, B. S. Phillips, J. S. Zabinski, X. Liu, W. Liu and J. M. Shreeve, J. Mater. Chem., 2006, 16, 1529–1535 RSC.
- R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792–793 CrossRef PubMed.
- X. Yang, H. Song, J. Wang and W. Zou, RSC Adv., 2016, 6, 29172–29181 RSC.
- X. Yang, H. Song, J. Wang, W. Zou and J. Wu, Korean J. Chem. Eng., 2015, 32, 2369–2374 CrossRef.
- Q. Zhang, Q. Li, D. Liu, X. Zhang and X. Lang, J. Mol. Liq., 2018, 249, 1097–1106 CrossRef.
- R. Fareghi-Alamdari and R. Hatefipour, J. Mol. Liq., 2017, 225, 793–799 CrossRef.
- S. Schneider, T. Hawkins, M. Rosander, G. Vaghjiani, S. Chambreau and G. Drake, Energy Fuels, 2008, 22, 2871–2872 CrossRef.
- N. Anwar and Riyazuddeen, J. Chem. Eng. Data, 2018, 63, 269–289 CrossRef.
- M. d. C. Grande, M. Garcia and C. M. Marschoff, J. Chem. Eng. Data, 2009, 54, 652–658 CrossRef.
- F. Chen, Z. Yang, Z. Chen, J. Hu, C. Chen and J. Cai, J. Mol. Liq., 2015, 209, 683–692 CrossRef.
- N. Saha and B. Das, J. Chem. Eng. Data, 2000, 45, 1125–1128 CrossRef.
- K. Hickey and W. E. Waghorne, J. Chem. Eng. Data, 2001, 46, 851–857 CrossRef.
- J. A. Lazzús, J. Mol. Liq., 2012, 168, 87–93 CrossRef.
- R. Fareghi-Alamdari, F. Ghorbani-Zamani and N. Zekri, RSC Adv., 2016, 6, 26386–26391 RSC.
- J. Klomfar, M. Součková and J. Pátek, J. Chem. Eng. Data, 2011, 56, 3454–3462 CrossRef.
- X. Ma, J. Wei, W. Guan, Y. Pan, L. Zheng, Y. Wu and J. Yang, J. Chem. Thermodyn., 2015, 89, 51–59 CrossRef.
- M. Tariq, P. Forte, M. C. Gomes, J. C. Lopes and L. Rebelo, J. Chem. Thermodyn., 2009, 41, 790–798 CrossRef.
- P. D. Gyan, K. Rajiv and H. Joshi, J. Chem. Thermodyn., 2014, 71, 27–36 CrossRef.
- A. S. Khan, Z. Man, A. Arvina, M. A. Bustam, A. Nasrullah, Z. Ullah, A. Sarwono and N. Muhammad, J. Mol. Liq., 2017, 227, 98–105 CrossRef.
- Z. Y. Gu and J. F. Brennecke, J. Chem. Eng. Data, 2002, 47, 339–345 CrossRef.
- T. Peppel, M. Köckerling, M. Geppert-Rybczyńska, R. V. Ralys, J. K. Lehmann, S. P. Verevkin and A. Heintz, Angew. Chem., Int. Ed., 2010, 49, 7116–7119 CrossRef PubMed.
- B. Mokhtarani, A. Sharifi, H. R. Mortaheb, M. Mirzaei, M. Mafi and F. Sadeghian, J. Chem. Thermodyn., 2009, 41, 323–329 CrossRef.
- J. Wang, Y. Tian, Y. Zhao and K. Zhuo, Green Chem., 2003, 5, 618–622 RSC.
- E. M. Živković, D. M. Bajić, I. R. Radović, S. P. Šerbanović and M. Lj. Kijevčanin, Fluid Phase Equilib., 2014, 373, 1–19 CrossRef.
- N. Zec, M. Bešter-Rogač, M. Vraneš and S. Gadžurić, J. Chem. Thermodyn., 2015, 91, 327–335 CrossRef.
- M. Anouti, A. Vigeant, J. Jacquemin, C. Brigouleix and D. Lemordant, J. Chem. Thermodyn., 2010, 42, 834–845 CrossRef.
- A. Bhattacharjee, P. J. Carvalho and J. A. P. Coutinho, Fluid Phase Equilib., 2014, 375, 80–88 CrossRef.
- L. G. Sánchez, J. R. Espel, F. Onink, G. W. Meindersma and A. B. de Haan, J. Chem. Eng. Data, 2009, 54, 2803–2812 CrossRef.
- O. Ciocirlan and O. Iulian, J. Chem. Eng. Data, 2012, 57, 3142–3148 CrossRef.
- T. A. Litovitz, J. Chem. Phys., 1952, 20, 1088–1089 CrossRef.
- M. H. Ghatee, M. Zare, A. R. Zolghadr and F. Moosavi, Fluid Phase Equilib., 2010, 291, 188–194 CrossRef.
- X. Li, Q. Zhou, X. Lu and S. Zhang, J. Mol. Liq., 2017, 243, 285–292 CrossRef.
- M. Anouti and J. Jacquemin, J. Chem. Eng. Data, 2010, 55, 5719–5728 CrossRef.
- J. Chen, L. Chen and Y. Xu, J. Chem. Thermodyn., 2015, 88, 110–120 CrossRef.
- S. Aznarez, M. M. E. F. de Ruiz Holgado and E. L. Arancibia, J. Mol. Liq., 2016, 124, 78–83 CrossRef.
- R. J. Fort and W. R. Moore, Trans. Faraday Soc., 1966, 62, 1112–1119 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04127j |
| This journal is © The Royal Society of Chemistry 2018 |