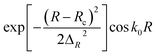DOI:
10.1039/C8RA04305A
(Paper)
RSC Adv., 2018,
8, 22823-22834
Global diabatic potential energy surfaces for the BeH2+ system and dynamics studies on the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction
Received
21st May 2018
, Accepted 14th June 2018
First published on 21st June 2018
Abstract
The Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction has great significance for studying diabatic processes and ultracold chemistry. The first global diabatic potential energy surfaces (PESs) which are correlated with the lowest two adiabatic states 12A′ and 22A′ of the BeH2+ system are constructed by using the neural network method. Ab initio energy points are calculated using the multi-reference configuration interaction method with the Davidson correction and AVQZ basis set. The diabatic energies are obtained from the transformation of ab initio data based on the dipole moment operators. The topographical characteristics of the diabatic PESs are described in detail, and the positions of crossing between the Vd11 and Vd22 are pinpointed. On new diabatic PESs, the time-dependent quantum wave packet method is carried out to study the mechanism of the title reaction. The results of dynamics calculations indicate the reaction has no threshold and the product BeH+ is excited to high vibrational states easily. In addition, the product BeH+ tends to backward scattering at most collision energies.
1 Introduction
In recent decades, the interactions between metal ions and dihydrogen have received considerable attention due to their central roles in chemical reactions at low temperatures,1–4 in hydrogen storage5–8 and in astrophysics9,10 among other fields. For the MH2+ (M = metal atoms) system, there are substantial experimental and theoretical studies concentrated on the spectroscopic properties of the M+–H2 complexes, which have been summarized in a review.11 On the other hand, the reactive collisions between metal ions and molecular hydrogen (M+ + H2) are important objects to study reaction dynamics, and a broad range of M+ ions have been performed by the guide ion beam methods in combination with theoretical calculations.12–15
The BeH2+ system has been widely studied in the related fields of cold and ultracold chemistry. In 2006, Roth et al.2 studied the Be+(2P) + H2 → BeH+ + H reaction by a laser-cooling ion trap apparatus with the millikelvin level translational temperatures of Be+ ions. They measured the rate constant as high as 10−9 cm3 s−1, implying a barrierless reaction pathway. Sawyer et al.16 applied the rotational-state-insensitive dissociation scheme to study photodissociation of BeH+ molecular ions, which were generated by the reaction between laser-cooling Be+ ions and H2. The technique used in this experiment can take away a key limitation for large-scale quantum-information experiments. Moreover, Be+ ions were widely used to sympathetically cool other atomic and molecular ions.17–20 Those experiments may open new approaches for the studies about the coherent manipulation of quantum states and reactions relevant to interstellar molecules.
In contrast, the dynamics calculations for the title reaction have not been carried out. To study the reaction dynamics, the prerequisite is to establish an accurate potential energy surface (PES), which governs the nuclear dynamics. The first PES of the BeH2+ system using self-consistent-field and valence bond configuration interaction methods was reported by Poshusta et al.21 The calculated energies of BeH2+ molecular ions were only in C2v geometries. In 1983, Raimondi and Gerratt22 used the spin-coupled valence bond theory to structure the ground state and several excited states adiabatic PESs for the Be+ + H2 reaction. The results showed that reaction for the ground state is endothermic by 1.57 eV, therefore Be+ ions must be excited to produce BeH+ molecular ions at a low collision energy. Artiukhin et al.23 constructed a ground state adiabatic PES to investigate the structural and spectroscopic properties of the Be+–H2 complexes, the energy points were calculated at the CCSD(T) level. On this PES, the authors identified the T-shape Be+–H2 complex is the minimum energy structure.
For the title reaction, the reactants Be+(2P) + H2(X1Σg+) and the products BeH+(X1Σ+) + H(2S) involve the lowest two adiabatic states (22A′ and 12A′). Namely, the reaction starts from the lowest excited state and then intersects the ground state to enter into the product channel. Therefore, to study the reaction of electronically excited Be+ ion with H2 on diabatic PESs is required. In the diabatic representation, the Born–Oppenheimer approximation breaks down, and the conical intersection appears to connect the two states. As we know, there are no global diabatic PESs which are suited for dynamics studies of the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction up to now. Due to the reaction can occur at very low temperatures, thus the accuracy of dynamics results is especially sensitive to the PES, and the long-range potentials are also very crucial within the low collision energy range. To achieve these requirements above, a mass of high-level ab initio energy points in a large configuration space are calculated and utilized to generate the diabatic energies by a proper diabatization method in this work. The neural network (NN) method is applied to construct the accurate global diabatic PESs for the two states (22A′ and 12A′) of the BeH2+ system. Then, based on the diabatic PESs, the dynamics calculations of the title reaction are implemented using the time-dependent wave packet (TDWP) method.
2 Potential energy surfaces
2.1 Diabatization method
Direct access to the diabatic states of the electronic Hamiltonian would lead to considerable difficulties, so the acquisition of diabatic energies is usually based on the transformation of adiabatic data. The approaches of diabatic transformation can be divided two categories: the derivative-based methods and the molecular property-based methods. The derivative-based methods are the most rigorous approaches for studying diabatic effect, and have been applied to construct some molecular system diabatic PESs.24–27 However, the calculation burden is too heavy to obtain the derivative couplings over a large coordinate space. Making use of suitable molecular properties to characterize the diabatic transformation is also effective methods, which have less computational effect compared to the derivative-based methods. Dipole moment,28–32 angular momentum33–35 and quadrupole moment36 operators have been used to obtain the diabatic energies. The molecular property-based methods are adopted in this work, and a brief description about the diabatization scheme is presented. Considering the coupling of two states, the diabatic wave functions ϕdi are constructed by a representation transformation from the adiabatic wave functions ψai| |
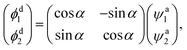 | (1) |
where α is the mixing angle, which is a function of the nuclear coordinates. ϕdi are no longer eigenstates of the electronic Hamiltonian, but the matrix elements of diabatic energies can be expressed as| |
Vd11 = Ea1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + Ea2 α + Ea2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α,
| (2) |
| |
Vd22 = Ea1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + Ea2 α + Ea2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α,
| (3) |
| |
Vd12 = Vd21 = (Ea2 − Ea1)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α,
| (4) |
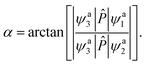
in which Ea1 and Ea2 are the adiabatic energies of 12A′ state and 22A′ state, Vd11 and Vd22 are the diabatic potential energies, and Vd12 and Vd21 are the coupling potential energies between the two states. By comparison, using the dipole moment operators to obtain the mixing angles is the best choice for the BeH2+ system. According to eqn (1), the matrix elements 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa1〉 and 〈ψa3|
|ψa1〉 and 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa2〉 can be calculated as
|ψa2〉 can be calculated as| |
〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa1〉 =〈ψa3| |ψa1〉 =〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉 |ϕd1〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈α + ψa3| 〈α + ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉 |ϕd2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α,
| (5) |
| |
〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa2〉 = 〈−ψa3| |ψa2〉 = 〈−ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉 |ϕd1〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈α + ψa3| 〈α + ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉 |ϕd2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α,
| (6) |
ψa3 is the adiabatic state 12A′′, which does not involve in the electronic mixing. ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) is the dipole moment operator, which is parallel to the molecular axis for collinear HBe+H. A simple manner is to make 〈ψa3|
is the dipole moment operator, which is parallel to the molecular axis for collinear HBe+H. A simple manner is to make 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉 = 0 and 〈ψa3|
|ϕd1〉 = 0 and 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉 = 1 for all geometries, so the mixing angle α can be approximated as
|ϕd2〉 = 1 for all geometries, so the mixing angle α can be approximated as| |
 | (7) |
2.2 Ab initio calculations
The single-point energies of the adiabatic states 12A′ and 22A′ and the dipole moments used for diabatic transformation are carried out at the internally contracted multi-reference configuration interaction (MRCI)37,38 level with a complete active space self-consistent field (CASSCF)39,40 reference wave function, and the Davidson correction (+Q) is used to compensate for the effect of higher-order correlation. Three states (1A′, 2A′ and 1A′′) of BeH2+ are equal weight in the state-averaged CASSCF calculations, and 3 valence electrons are included in 16 active orbitals (12a′ + 4a′′). The augmented correlation-consistent polarization valence quadruple (AVQZ) basis set is adopted for H and Be atoms. A great range of configuration space is employed so that the PESs are suitable for dynamics calculations at low collision energies, and all ab initio points are chosen in the Jacobi coordinates. For the BeH2+ system, the Be+–HH region is defined as 0.6 ≤ rHH/a0 ≤ 18.2, 0 ≤ RBe+–HH/a0 ≤ 45, 0 ≤ θ/degree ≤ 90, and the H–BeH+ region is defined as 2.0 ≤ rBeH+/a0 ≤ 18.2, 0 ≤ RH–BeH+/a0 ≤ 45, 0 ≤ θ/degree ≤ 180. To improve the accuracy of fitting PESs, the interaction region has denser energy points distribution than the asymptotic region, and the discontinuous energy points are eliminated. Finally, 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 conformations in the coordinate space defined above are selected to generate the diabatic energies. In this work, all of the ab initio calculations are performed by MOLPRO program package.41
778 conformations in the coordinate space defined above are selected to generate the diabatic energies. In this work, all of the ab initio calculations are performed by MOLPRO program package.41
2.3 Fitting the diabatic PESs
Various approaches of constructing PESs, such as many-body expansion method42–44 and interpolation method,45,46 have been widely applied. Recent attention has been focused on some more efficient methods based on machine learning to represent global PESs. For example, the NN model47 is considered as an excellent tool with flexible and accurate characteristics for fitting PESs, and it has been used to several reaction systems48–52 in our previous studies. In this work, the diabatic energies are fitted in analytical forms by the NN method, which are obtained from the transformation of ab initio energies using the diabatization method mentioned above. The permutation invariant polynomials (PIP)53,54 are employed for solving the problem of adaptation of permutation symmetry resulted from the two H atoms for the BeH2+ system. A set of functions of internuclear distances are used in the PIP-NN method, which can be written as| | |
Pij = exp(−0.2Rij), (i, j = Be+, Ha, Hb),
| (8) |
where Rij and Pij are the distances between the ith and jth atoms and the corresponding monomials, and then the PIP can be represent as| |
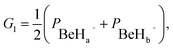 | (9) |
| | |
G2 = (PBeHa+ × PBeHb+),
| (10) |
The G1, G2, G3 are normalized treatment as the input data of NN, which written as
| |
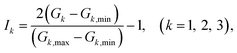 | (12) |
where
Gi,min and
Gi,max are the minimum and maximum values of
Gi. The neuron is the basic unit of neural network. The output signal
yn of a neuron in the
nth layer can be presented as
| |
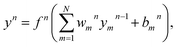 | (13) |
where
N is the number of neurons in the (
n − 1)th layer,
fn is the transfer function,
ωnm are the connection weights and
bnm are the biases. The transfer function used in the output layer is linear, whereas the hyperbolic tangent function as the transfer function is used in the hidden layers, written as
| |
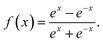 | (14) |
The NN consists of one input layer, which corresponds to the molecular geometries after PIP processing, one output layer that represents energy and two hidden layers of interconnecting neurons. In this work, the Levenberg–Marquardt algorithm55 is applied to optimize the connection weights and biases in the process of fitting. An early stopping and the cross validation are employed to avoid the overfitting of NN. The diabatic data are randomly divided into three sets: training set (90 percent), testing set (5 percent), and validation set (5 percent). The training set is used to train the parameters of NN; the testing set is used to test the generalization ability of the training model and the validation set is used to monitor the performance of fitting. The training should be stopped when the validation set error increases, which usually means the appearance of overfitting. In the training process, 13–14 neurons are included in each hidden layer to fit the diabatic matrix elements. The fitting root mean square errors (RMSEs) for Vd11, Vd22 and Vd12, (Vd21) terms are 0.0101, 0.0130 and 0.0132 eV, respectively.
2.4 Features of the diabatic PESs
The geometries and energies of stationary points on the ground state of the Be+–H2 complexes are listed in Table 1, compared with the previous studies.23,56 In this work, the adiabatic data Ea1 are constructed by diagonalizing the matrices 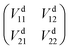 , which are obtained by scanning the three diabatic PESs. The values of energy are relative to the Be+ + H2 dissociation limit. As can be seen, our calculations for the stationary points are good in agreement with Artiukhin PES and the accurate ab initio calculations, especially equilibrium structure. The diabatic PESs can reproduce the adiabatic energies well, supporting the fitting results for the Vd11, Vd22 and Vd12, (Vd21) matrix elements are accurate enough, and the diabatization method used in this work is reliable for the BeH2+ system. Table 2 shows the spectroscopic constants of H2(X1Σg+) and BeH+(X1Σ+) obtained on the diabatic PESs, as compared with the experimental data.57 The approach is to keep the third atom away from the diatomics and then to fit the two-body potential curve. The calculated results of bond length, dissociation energy, vibrational frequencies and anharmonicity constants are coincident with the experimental values, indicating the diabatic PESs could describe the two-body potential energies well. In addition, the long-range potential is crucial for ion-neutral reactions, especially at low reaction temperatures. Fig. 1 presents the potential energy values on the Vd11 and Vd22 surfaces and corresponding ab initio data as function of RBe+–HH for three different θ in a long range of the reactant channel. The rHH is fixed at equilibrium distance. It can be seen that the fitting results are good in agreement with the ab initio calculations, implying the NN PESs are reliable for describing the long-range potential.
, which are obtained by scanning the three diabatic PESs. The values of energy are relative to the Be+ + H2 dissociation limit. As can be seen, our calculations for the stationary points are good in agreement with Artiukhin PES and the accurate ab initio calculations, especially equilibrium structure. The diabatic PESs can reproduce the adiabatic energies well, supporting the fitting results for the Vd11, Vd22 and Vd12, (Vd21) matrix elements are accurate enough, and the diabatization method used in this work is reliable for the BeH2+ system. Table 2 shows the spectroscopic constants of H2(X1Σg+) and BeH+(X1Σ+) obtained on the diabatic PESs, as compared with the experimental data.57 The approach is to keep the third atom away from the diatomics and then to fit the two-body potential curve. The calculated results of bond length, dissociation energy, vibrational frequencies and anharmonicity constants are coincident with the experimental values, indicating the diabatic PESs could describe the two-body potential energies well. In addition, the long-range potential is crucial for ion-neutral reactions, especially at low reaction temperatures. Fig. 1 presents the potential energy values on the Vd11 and Vd22 surfaces and corresponding ab initio data as function of RBe+–HH for three different θ in a long range of the reactant channel. The rHH is fixed at equilibrium distance. It can be seen that the fitting results are good in agreement with the ab initio calculations, implying the NN PESs are reliable for describing the long-range potential.
Table 1 Stationary points of the ground state (12A′) BeH2+
| |
rHH (Bohr) |
RBe+–HH (Bohr) |
E (eV) |
| The adiabatic data Ea1 are obtained by diagonalizing the diabatic matrices in this work. Form ref. 23. Form ref. 56. Energies are relative to the Be+ + H2 dissociation limit. |
| Equilibrium structure, θ = 90° |
| This worka |
1.450 |
3.397 |
−0.384 |
| Artiukhin PESb |
1.451 |
3.356 |
−0.392 |
| MRCI + Qb |
1.450 |
3.390 |
−0.375 |
| CCSD(T)c |
1.450 |
3.354 |
−0.391 |
| CCSDTc |
1.451 |
3.356 |
−0.393 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Saddle point, θ = 0° |
| This worka |
1.442 |
4.146 |
−0.149 |
| Artiukhin PESb |
1.438 |
4.068 |
−0.150 |
| MRCI + Qb |
1.440 |
4.108 |
−0.147 |
Table 2 Spectroscopic constants of H2(X1Σg+) and BeH+(X1Σ+)
| |
|
This work |
Experiment |
| H2(X1Σg+) |
Re (Bohr) |
1.400 |
1.401 |
| De (eV) |
4.732 |
4.747 |
| ωe (cm−1) |
4400.9 |
4401.2 |
| ωexe (cm−1) |
127.70 |
121.33 |
| BeH+(X1Σ+) |
Re (Bohr) |
2.489 |
2.480 |
| De (eV) |
3.160 |
3.140 |
| ωe (cm−1) |
2205.6 |
2221.7 |
| ωexe (cm−1) |
37.20 |
39.79 |
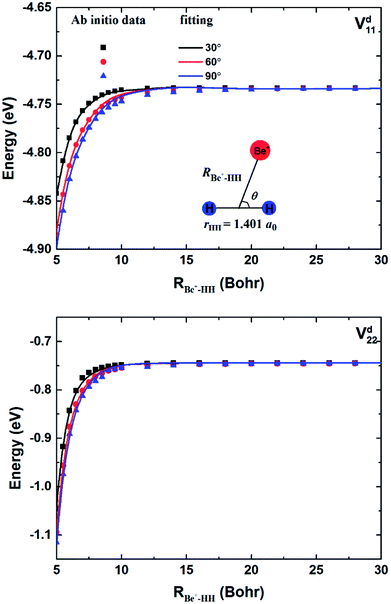 |
| | Fig. 1 Comparison of ab initio data and fitting results in a long range of the reactant channel as function of RBe+–HH at θ = 30.0°, 60.0° and 90.0° for fixed rHH = 1.401a0. | |
Fig. 2 shows the potential energy curves of H2 on the Vd11 and Vd22 surfaces, which are obtained by taking points on the diabatic surfaces when the RBe+–HH is set as 50a0. The electronic coupling is zero when the Be+ is far from H2, thus the diabatic and adiabatic states are same. On the Vd22 surface, there exists a cusp on the potential energy curve of two H atoms, which goes against the fitting. The cusp may be attributed to the intersection of higher state, and the intersection states corresponding to 32A′ and 22A′ electronic states in the adiabatic representation.
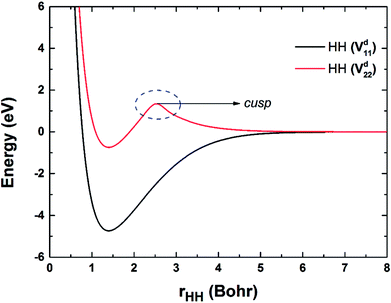 |
| | Fig. 2 Potential energy curves of HH obtained on the Vd11 and Vd22 surfaces. | |
To compare the potential energies in the adiabatic and diabatic representations clearly, Fig. 3 shows an example of the adiabatic and diabatic potential curves near the entrance channel of the title reaction along RBe+–HH for different four angles θ. The internuclear distance of HH is fixed at 2.5a0, which is within the reaction region and could reflect the intersection between the Vd11 and Vd22 well. The diabatic potentials are obtained by scanning the diabatic PESs directly and the adiabatic potentials are obtained by diagonalizing the diabatic matrices. The adiabatic potentials avoid each other near the crossing, whereas the diabatic potentials mix and eventually cross over each other. As the increase of θ, the cross point moves to smaller RBe+–HH, and the difference between two adiabatic potential curves decreases near the cross point. Moreover, for all cases, the adiabatic and diabatic potential curves are overlapping at large RBe+–HH, implying the two states are non-degenerate in the long-range region. Fig. 4(a) and (b) give the corresponding coupling potentials and mixing angles shown in Fig. 3, respectively. Fig. 4(a) shows the value of coupling potential declines rapidly with θ increases and gradually decreases to zero when RBe+–HH value is large enough. It can be explained from eqn (4): as the difference between two adiabatic potential energies increases, the value of coupling potential becomes large. Fig. 4(b) shows the cross point corresponds to the mixing angle of 45°. This conclusion can be obtained from eqn (2) and (3).
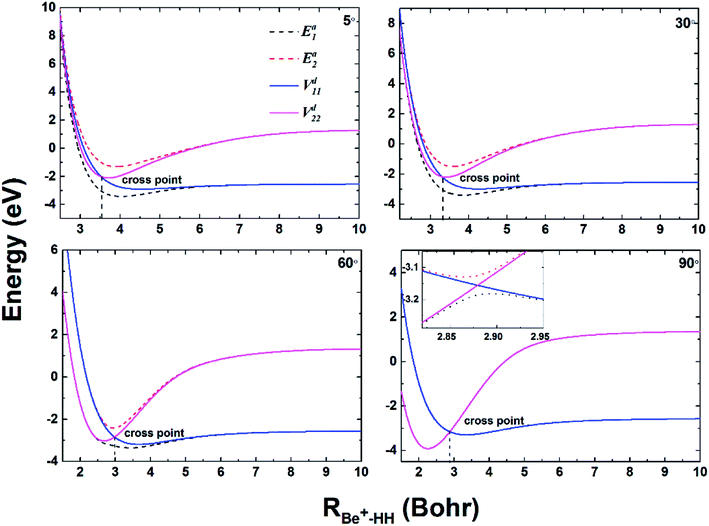 |
| | Fig. 3 Adiabatic and diabatic potential energies as function of RBe+–HH at θ = 5.0°, 30.0°, 60.0° and 90.0° for fixed rHH = 2.5a0. | |
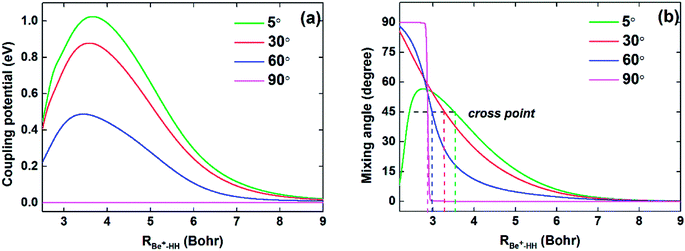 |
| | Fig. 4 (a) Coupling potentials and (b) mixing angles as function of RBe+–HH at θ = 5.0°, 30.0°, 60.0° and 90.0° for fixed rHH = 2.5a0. | |
Fig. 5(a) and (b) show the energy for a Be+ moving around a H2 molecule on the diabatic PESs Vd11 and Vd22, respectively. Two H atoms are symmetrically placed on the x-axis and the bond length is fixed at the equilibrium distance (1.401a0) of the ground state. The energy is set as zero when the Be+ ion is far from the H2 molecule. There is no obvious barrier or well on the Vd11 PES, and the Be+ ion always feels the repulsive force of the H2 molecule. For the Vd22 PES, there exists a 2.48 eV deep well at x = 0.0a0 and y = 2.49a0, which implies the importance of insertion collision on the Vd22 PES. The deep well can attract the Be+ ion to form the metastable complex Be+–H2 and eventually dissociate to the BeH+ + H products.
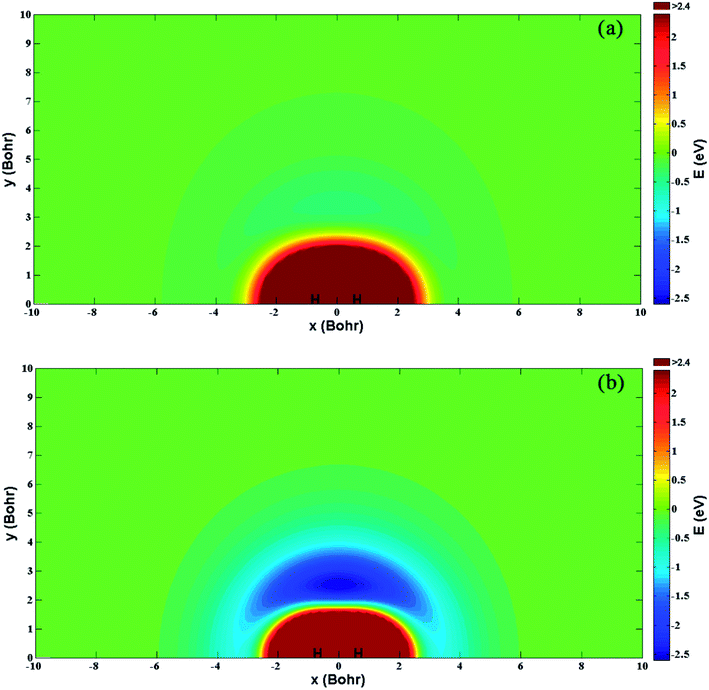 |
| | Fig. 5 Color plots of the potential energy when a Be+ ion moves around the H2 molecule with the bond length fixed at 1.401a0 of the diabatic states (a) Vd11 and (b) Vd22. | |
The three-dimensional diabatic PESs Vd11 and Vd22 at four different Be+–H–H angles (45°, 90°, 135° and 180°) are presented in Fig. 6. The PESs vary smoothly over the coordinate range. For the Vd11 PES, only a valley at the left that corresponds to the Be+(2S) + H2(X1Σg+) channel can be found, and there is no valley in the product region, which indicates the fact that the BeH+ is unstable on the Vd11 surface. For the Vd22 PES, there exist two valleys at the left and right, which correspond to the Be+(2P) + H2(X1Σg+) channel and the BeH+(X1Σ+) + H(2S) channel, respectively. The Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction starts from the lowest excited state and end at the ground state, and the reactant and product channels are both on the Vd22 PES. Moreover, it is evident that the right valley is much lower than the left valley on the Vd22 PES, implying the title reaction has the large exothermicity. In order to describe the region of diabatic transition more clearly, the corresponding contour plots for the difference of (Vd22 − Vd11) are displayed in Fig. 7, and the exact positions of conical intersection between the Vd11 and Vd22 are given in black lines. Fig. 8 depicts the minimum energy paths from H2 to BeH+ at four approaching angles (45°, 90°, 135° and 180°) on the Vd22 PES, which are determined by scanning the PES at different coordinates (RHH − RBeH+) to find the minimum values of energy. The exoergicity of the title reaction is about 2.54 eV when the zero point energy of H2 (0.27 eV) and BeH+ (0.14 eV) are included. For the Be+–H–H angle of 45°, there exists a 0.8 eV deep well on the reaction path, which can support a mass of bound and quasi-bound state complexes. For the Be+–H–H angles of 90°, 135° and 180°, there exist barriers on the reaction paths, and the barrier heights are lower than the energy of reactant channel. The characteristic of the minimum energy paths can reflect that there is no threshold in the title reaction.
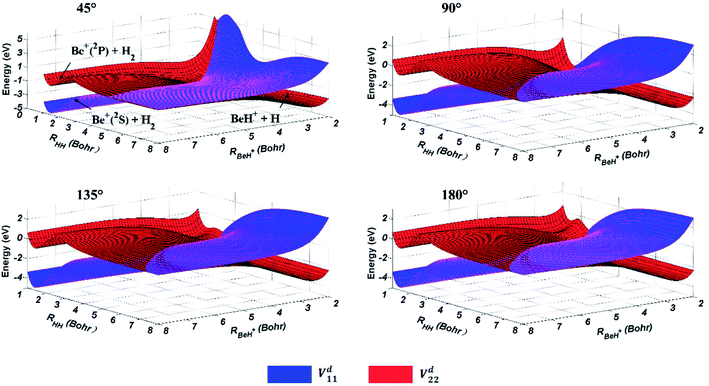 |
| | Fig. 6 Potential energy surfaces of the diabatic states Vd11 and Vd22 for Be+–H–H angles at 45°, 90°, 135° and 180°. | |
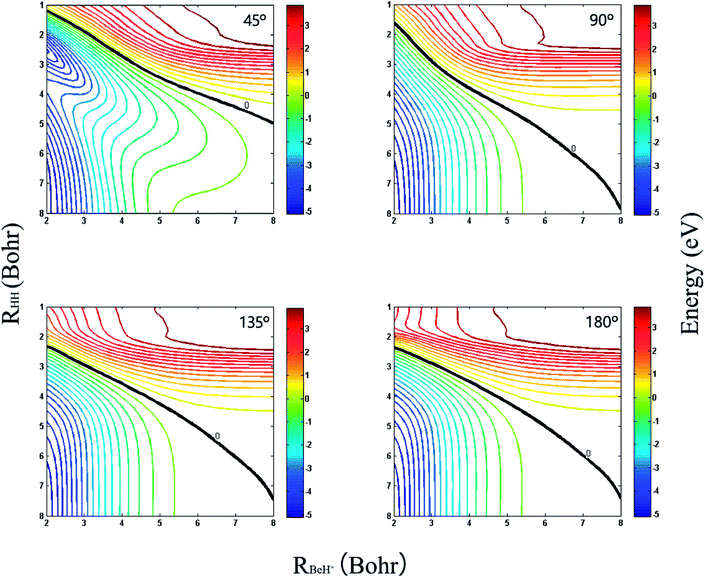 |
| | Fig. 7 Contour plots of the (Vd22 − Vd11) for Be+–H–H angles at 45°, 90°, 135° and 180°. The black lines represent the positions of intersection. | |
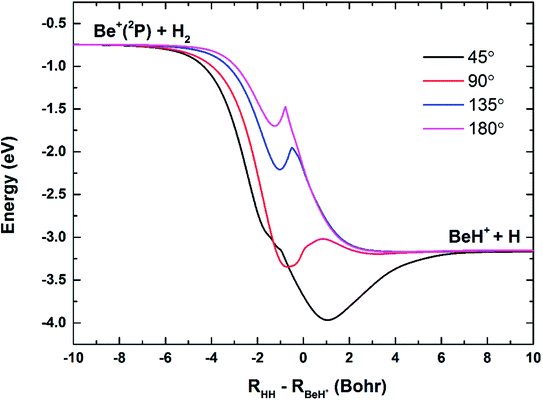 |
| | Fig. 8 Minimum energy paths of the diabatic PES Vd22 for Be+–H–H angles at 45°, 90°, 135° and 180°. | |
3 Dynamics calculations
Based on the diabatic PESs of the BeH2+ system, the dynamics studies of the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction are performed by the TDWP method. The TDWP method is applicable to the diabatic dynamics calculations, and more detailed introduction about this method can be found in previous literatures.58,59 In the TDWP calculations, the Coriolis coupling effect is included. Because of the nonadiabatic transition between two states has been considered, so the Hamiltonian is a 2 × 2 matrix, which can be expressed as| |
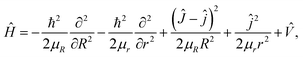 | (15) |
where R and r are the distances of Be+–H2 and HH in the Jacobi coordinates, respectively. μR and μr are the corresponding reduced masses associated with R and r coordinates. Ĵ and ĵ are the angular momentum operators of the BeH2+ system and the diatom molecule H2. ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the potential energies, which is a 2 × 2 matrix. The state-to-state S-matrix is extracted by the reactant coordinate based method,60 and the second-order split operator method is employed in the propagation of wave function. The state-to-state reaction probability is obtained by
is the potential energies, which is a 2 × 2 matrix. The state-to-state S-matrix is extracted by the reactant coordinate based method,60 and the second-order split operator method is employed in the propagation of wave function. The state-to-state reaction probability is obtained by| |
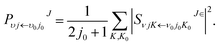 | (16) |
The state-to-state integral cross sections (ICSs) and differential cross sections (DCSs) are calculated by
| |
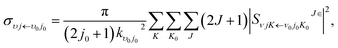 | (17) |
and
| |
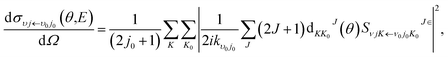 | (18) |
where
kv0j0 is the momenta in the entrance channel,
θ is the scattering angle and
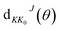
is the element of reduced Wigner rotation matrix.
In the TDWP calculations, the initial rovibrational state of the reactant molecule H2 is chosen as v0 = 0 and j0 = 0. The main parameters used in the TDWP calculations are listed in Table 3.
Table 3 Numerical parameters used in the TDWP calculations
| Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) |
| Grid/basis range and size |
R (Bohr) ∈ [0.01, 22.0], NR = 219 |
| r (Bohr) ∈ [0.5, 16.0], Nr = 159 |
| |
Nj = 139 |
Initial wave packet, 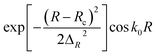 |
Rc = 16.5 Bohr ΔR = 0.20 Bohr k0 = (2E0μR)1/2 with E0 = 0.50 eV |
| Total propagation time |
750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. 000 a.u. |
| Time steps |
15 a.u. |
| Highest J value |
65 |
The reaction probabilities of the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction for five different total angular momentum J values (J = 0, 20, 30, 40 and 50) as a function of collision energy are displayed in Fig. 9. For J = 0, there is no threshold due to the existence of barrierless reaction path. The threshold appears and gets larger with the increase of J value because of the emergence of centrifugal energy barrier. The dominance of the deep potential well on the Vd22 PES leads to some resonance structures in the reaction probability curves, especially at low energies. The oscillations are short-lived and relatively smooth owing to the large exothermicity of the title reaction. The oscillatory amplitude gradually decreases as the collision energy increases, indicating the product escapes the constraint of the potential well more easily.
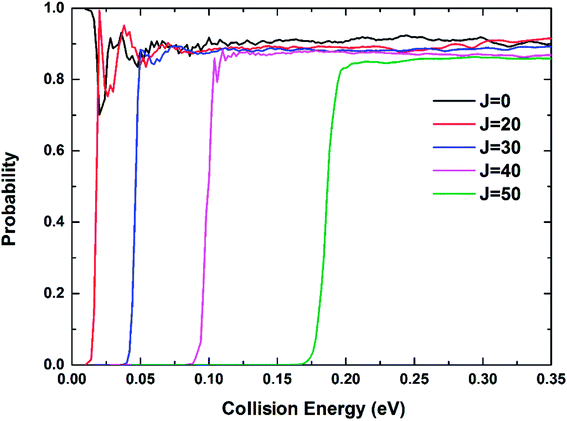 |
| | Fig. 9 Total reaction probabilities of the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction calculated by the TDWP method at J = 0, 20, 30, 40 and 50. | |
The maximum of total angular momentum quantum number used in the TDWP calculations is 65, and the corresponding threshold slightly exceeds 0.35 eV, which is set as the upper collision energy limit in the calculations of the ICSs and DCSs. Fig. 10(a) and (b) show the total and several vibrationally resolved (v′ = 0–10) ICSs of the title reaction, respectively. Compared with the reaction probability curves, no obvious oscillatory structures can be found on the ICS curves due to the oscillations are erased by summing all the partial waves. The total ICS has a high value, and in general, the total ICS curve represents monotonically decreasing collision energy dependence. This feature can be explained by the Vd22 PES. As depicted in Fig. 5(b), the deep well can attract the Be+ ion when the Be+ ion moves around the H2 molecule at a low collision energy, and the system has enough adjustment time to enter the product channel. The adjustment time becomes short when the collision energy increases, thus the ICS value declines. The curves of vibrationally resolved ICSs show an obvious population inversion distribution in the vibrational states of the product BeH+ molecular ion: the highly excited vibrational states (v′ = 6–9) correspond to large ICS values, and the ground vibrational state has the minimum ICS value. This is because the title reaction has the large exothermicity, and the most of energy released from the reactants are transformed into the internal energy of products.
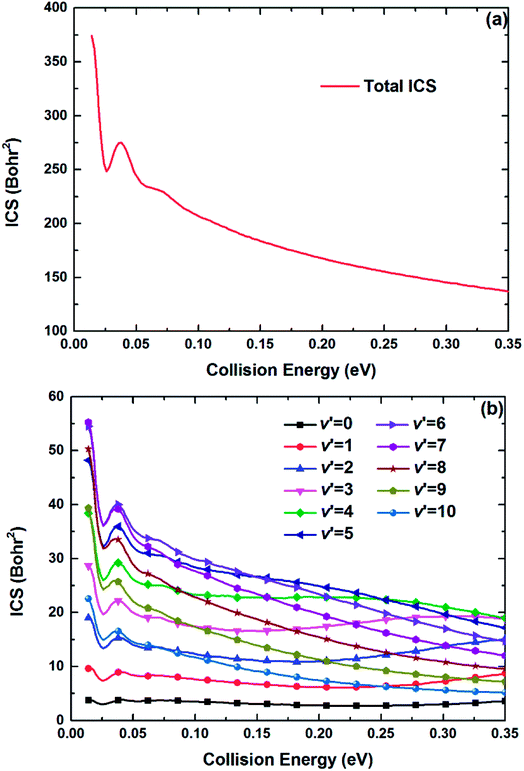 |
| | Fig. 10 (a) Total and (b) vibrationally resolved ICSs of the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction calculated by the TDWP method. | |
The three-dimensional plot of total DCSs for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction as a function of collision energy is displayed in Fig. 11, which describes the angular distribution of the product BeH+. As shown in this figure, the angular distribution of BeH+ is essentially forward–backward symmetric at low collision energy. As the increase of collision energy, the peak at 180° appears, which means the rebound collision becomes obvious for the title reaction. The shapes of DCSs imply the reaction is dominated by a typical direct mechanism, and the product is formed by the short-lived intermediate.
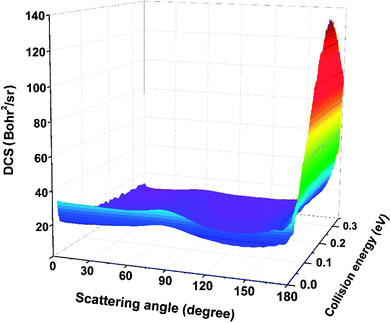 |
| | Fig. 11 Three-dimensional plot of the total DCSs for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction calculated by the TDWP method. | |
4 Conclusion
This work presents the first global diabatic PESs for the lowest two adiabatic states (22A′ and 12A′) of the BeH2+ system. The scheme to obtain the diabatic energies is based on the dipole moment operators. Ab initio energy points are calculated using the MRCI method with the AVQZ basis set. 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 geometries in a large region of configuration space are selected to fit the diabatic PESs by using the NN method. The diabatic PESs can reproduce the adiabatic data well and the spectroscopic constants of diatomics calculated on the diabatic PESs are good in agreement with the experimental values. The diabatic PESs topographical features are accounted in detail and the positions of conical intersection between the Vd11 and Vd22 are pointed. The TDWP calculations for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction are performed on the diabatic PESs. The results of reaction probabilities, ICSs, and DCSs of the title reaction are calculated. The total reaction is no threshold, and there are some oscillatory peaks in the curves of reaction probability. The total ICS has a high value at low collision energy, and the product BeH+ molecular ion is excited to high vibrational states easily. The DCS results show that the product BeH+ molecular ion tends to backward scattering at most collision energies.
778 geometries in a large region of configuration space are selected to fit the diabatic PESs by using the NN method. The diabatic PESs can reproduce the adiabatic data well and the spectroscopic constants of diatomics calculated on the diabatic PESs are good in agreement with the experimental values. The diabatic PESs topographical features are accounted in detail and the positions of conical intersection between the Vd11 and Vd22 are pointed. The TDWP calculations for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction are performed on the diabatic PESs. The results of reaction probabilities, ICSs, and DCSs of the title reaction are calculated. The total reaction is no threshold, and there are some oscillatory peaks in the curves of reaction probability. The total ICS has a high value at low collision energy, and the product BeH+ molecular ion is excited to high vibrational states easily. The DCS results show that the product BeH+ molecular ion tends to backward scattering at most collision energies.
As we know, no more experimental studies can be obtained to examine our work. We anticipate the present results could stimulate future experiments, and further dynamics researches, such as the influence isotopic effect or the title reaction under ultracold conditions, can be carried out on the diabatic PESs.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11774043).
References
- K. Molhave and M. Drewsen, Phys. Rev. A, 2000, 62, 011401 CrossRef.
- B. Roth, P. Blythe, H. Wenz, H. Daerr and S. Schiller, Phys. Rev. A, 2006, 73, 042712 CrossRef.
- P. F. Staanum, K. Hojbjerre, R. Wester and M. Drewsen, Phys. Rev. Lett., 2008, 100, 243003 CrossRef PubMed.
- N. Kimura, K. Okada, T. Takayanagi, M. Wada, S. Ohtani and H. A. Schuessler, Phys. Rev. A, 2011, 83, 033422 CrossRef.
- P. Nachtigall, E. Garrone, G. T. Palomino, M. R. Delgado, D. Nachtigallova and C. O. Arean, Phys. Chem. Chem. Phys., 2006, 8, 2286–2292 RSC.
- M. Felderhoff, C. Weidenthaler, R. von Helmolt and U. Eberle, Phys. Chem. Chem. Phys., 2007, 9, 2643–2653 RSC.
- M. Dinca and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766–6779 CrossRef PubMed.
- S. Q. Ma and H. C. Zhou, Chem. Commun., 2010, 46, 44–53 RSC.
- D. Smith, N. G. Adams, E. Alge and E. Herbst, Astrophys. J., 1983, 272, 365–368 CrossRef.
- A. J. Sauval and J. B. Tatum, Astrophys. J., Suppl. Ser., 1984, 56, 193–209 CrossRef.
- V. Dryza and E. J. Bieske, Int. Rev. Phys. Chem., 2013, 32, 559–587 Search PubMed.
- X. G. Zhang and P. B. Armentrout, J. Chem. Phys., 2002, 116, 5565–5573 CrossRef.
- C. S. Hinton and P. B. Armentrout, J. Chem. Phys., 2010, 133, 124370 CrossRef PubMed.
- C. S. Hinton, M. Citir and P. B. Armentrout, J. Chem. Phys., 2011, 135, 234302 CrossRef PubMed.
- F. X. Li, C. S. Hinton, M. Citir, F. Y. Liu and P. B. Armentrout, J. Chem. Phys., 2011, 134, 024310 CrossRef PubMed.
- B. C. Sawyer, J. G. Bohnet, J. W. Britton and J. J. Bollinger, Phys. Rev. A, 2015, 91, 011401 CrossRef.
- P. Blythe, B. Roth, U. Frohlich, H. Wenz and S. Schiller, Phys. Rev. Lett., 2005, 95, 183002 CrossRef PubMed.
- B. Roth, J. C. J. Koelemeij, H. Daerr and S. Schiller, Phys. Rev. A, 2006, 74, 040501 CrossRef.
- B. Roth, P. Blythe, H. Daerr, L. Patacchini and S. Schiller, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 1241–1258 CrossRef.
- T. Schneider, B. Roth, H. Duncker, I. Ernsting and S. Schiller, Nat. Phys., 2010, 6, 275–278 Search PubMed.
- R. D. Poshusta, D. W. Klint and A. Liberles, J. Chem. Phys., 1971, 55, 252–262 CrossRef.
- M. Raimondi and J. Gerratt, J. Chem. Phys., 1983, 79, 4339–4345 CrossRef.
- D. G. Artiukhin, J. Klos, E. J. Bieske and A. A. Buchachenko, J. Phys. Chem. A, 2014, 118, 6711–6720 CrossRef PubMed.
- R. Abrol and A. Kuppermann, J. Chem. Phys., 2002, 116, 1035–1062 CrossRef.
- X. L. Zhu and D. R. Yarkony, J. Chem. Phys., 2010, 132, 104101 CrossRef PubMed.
- S. Mukherjee, S. Bandyopadhyay, A. K. Paul and S. Adhikari, J. Phys. Chem. A, 2013, 117, 3475–3495 CrossRef PubMed.
- Y. F. Guan, B. N. Fu and D. H. Zhang, J. Chem. Phys., 2017, 147, 224307 CrossRef PubMed.
- H. J. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5802–5807 CrossRef.
- G. Hirsch, R. J. Buenker and C. Petrongolo, Mol. Phys., 1990, 70, 835–848 CrossRef.
- D. R. Yarkony, J. Phys. Chem. A, 1998, 102, 8073–8077 CrossRef.
- M. Boggio-Pasqua, A. I. Voronin, P. Halvick, J. C. Rayez and A. J. C. Varandas, Mol. Phys., 2000, 98, 1925–1938 CrossRef.
- D. He, J. C. Yuan, H. X. Li and M. D. Chen, Sci. Rep., 2016, 6, 25083 CrossRef PubMed.
- M. H. Alexander, J. Chem. Phys., 1993, 99, 6014–6026 CrossRef.
- A. J. Dobbyn and P. J. Knowles, Mol. Phys., 1997, 91, 1107–1123 Search PubMed.
- A. J. Dobbyn, J. N. L. Connor, N. A. Besley, P. J. Knowles and G. C. Schatz, Phys. Chem. Chem. Phys., 1999, 1, 957–966 RSC.
- C. Petrongolo, G. Hirsch and R. J. Buenker, Mol. Phys., 1990, 70, 825–834 CrossRef.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, Wires Comput. Mol. Sci., 2012, 2, 242–253 CrossRef.
- Y. Q. Li, P. Y. Zhang and K. L. Han, J. Chem. Phys., 2015, 142, 124302 CrossRef PubMed.
- Y. Q. Li, F. C. Ma and M. T. Sun, J. Chem. Phys., 2013, 139, 154305 CrossRef PubMed.
- L. Guo, H. Y. Ma, L. L. Zhang, Y. Z. Song and Y. Q. Li, RSC Adv., 2018, 8, 13635–13642 RSC.
- C. X. Xu, D. Q. Xie and D. H. Zhang, Chin. J. Chem. Phys., 2006, 19, 96–98 CrossRef.
- M. A. Collins and D. H. Zhang, J. Chem. Phys., 1999, 111, 9924–9931 CrossRef.
- H. Rabitz and O. F. Alis, J. Math. Chem., 1999, 25, 197–233 CrossRef.
- J. C. Yuan, D. He and M. D. Chen, Phys. Chem. Chem. Phys., 2015, 17, 11732–11739 RSC.
- J. C. Yuan, D. He and M. D. Chen, Sci. Rep., 2015, 5, 14594 CrossRef PubMed.
- D. He, J. C. Yuan, H. X. Li and M. D. Chen, J. Chem. Phys., 2016, 145, 234312 CrossRef PubMed.
- S. F. Wang, J. C. Yuan, H. X. Li and M. D. Chen, Phys. Chem. Chem. Phys., 2017, 19, 19873–19880 RSC.
- J. C. Yuan, D. He, S. F. Wang, M. D. Chen and K. L. Han, Phys. Chem. Chem. Phys., 2018, 20, 6638–6647 RSC.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- M. T. Hagan and M. B. Menhaj, IEEE Trans. Neural Netw. Learn. Syst., 1994, 5, 989–993 CrossRef PubMed.
- A. J. Page, D. J. D. Wilson and E. I. von Nagy-Felsobuki, Phys. Chem. Chem. Phys., 2010, 12, 13788–13797 RSC.
- K. P. Huber and G. Herzberf, Constants of Diatomic Molecules, Springer, 1979 Search PubMed.
- Z. G. Sun, S. Y. Lee, H. Guo and D. H. Zhang, J. Chem. Phys., 2009, 130, 174102 CrossRef PubMed.
- Z. G. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef PubMed.
- Z. G. Sun, X. Lin, S. Y. Lee and D. H. Zhang, J. Phys. Chem. A, 2009, 113, 4145–4154 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Shufen Wang and
Maodu Chen
,
Shufen Wang and
Maodu Chen *
*
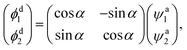
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + Ea2
α + Ea2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α,
α,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2
sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α + Ea2
α + Ea2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α,
α,
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α
α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α,
α,
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa1〉 and 〈ψa3|
|ψa1〉 and 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa2〉 can be calculated as
|ψa2〉 can be calculated as![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa1〉 =〈ψa3|
|ψa1〉 =〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉
|ϕd1〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈α + ψa3|
〈α + ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉
|ϕd2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α,
α,
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ψa2〉 = 〈−ψa3|
|ψa2〉 = 〈−ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉
|ϕd1〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈α + ψa3|
〈α + ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉
|ϕd2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α,
α,
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) is the dipole moment operator, which is parallel to the molecular axis for collinear HBe+H. A simple manner is to make 〈ψa3|
is the dipole moment operator, which is parallel to the molecular axis for collinear HBe+H. A simple manner is to make 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd1〉 = 0 and 〈ψa3|
|ϕd1〉 = 0 and 〈ψa3|![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) |ϕd2〉 = 1 for all geometries, so the mixing angle α can be approximated as
|ϕd2〉 = 1 for all geometries, so the mixing angle α can be approximated as
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 conformations in the coordinate space defined above are selected to generate the diabatic energies. In this work, all of the ab initio calculations are performed by MOLPRO program package.41
778 conformations in the coordinate space defined above are selected to generate the diabatic energies. In this work, all of the ab initio calculations are performed by MOLPRO program package.41
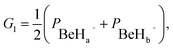
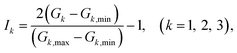
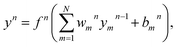
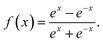
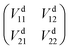 , which are obtained by scanning the three diabatic PESs. The values of energy are relative to the Be+ + H2 dissociation limit. As can be seen, our calculations for the stationary points are good in agreement with Artiukhin PES and the accurate ab initio calculations, especially equilibrium structure. The diabatic PESs can reproduce the adiabatic energies well, supporting the fitting results for the Vd11, Vd22 and Vd12, (Vd21) matrix elements are accurate enough, and the diabatization method used in this work is reliable for the BeH2+ system. Table 2 shows the spectroscopic constants of H2(X1Σg+) and BeH+(X1Σ+) obtained on the diabatic PESs, as compared with the experimental data.57 The approach is to keep the third atom away from the diatomics and then to fit the two-body potential curve. The calculated results of bond length, dissociation energy, vibrational frequencies and anharmonicity constants are coincident with the experimental values, indicating the diabatic PESs could describe the two-body potential energies well. In addition, the long-range potential is crucial for ion-neutral reactions, especially at low reaction temperatures. Fig. 1 presents the potential energy values on the Vd11 and Vd22 surfaces and corresponding ab initio data as function of RBe+–HH for three different θ in a long range of the reactant channel. The rHH is fixed at equilibrium distance. It can be seen that the fitting results are good in agreement with the ab initio calculations, implying the NN PESs are reliable for describing the long-range potential.
, which are obtained by scanning the three diabatic PESs. The values of energy are relative to the Be+ + H2 dissociation limit. As can be seen, our calculations for the stationary points are good in agreement with Artiukhin PES and the accurate ab initio calculations, especially equilibrium structure. The diabatic PESs can reproduce the adiabatic energies well, supporting the fitting results for the Vd11, Vd22 and Vd12, (Vd21) matrix elements are accurate enough, and the diabatization method used in this work is reliable for the BeH2+ system. Table 2 shows the spectroscopic constants of H2(X1Σg+) and BeH+(X1Σ+) obtained on the diabatic PESs, as compared with the experimental data.57 The approach is to keep the third atom away from the diatomics and then to fit the two-body potential curve. The calculated results of bond length, dissociation energy, vibrational frequencies and anharmonicity constants are coincident with the experimental values, indicating the diabatic PESs could describe the two-body potential energies well. In addition, the long-range potential is crucial for ion-neutral reactions, especially at low reaction temperatures. Fig. 1 presents the potential energy values on the Vd11 and Vd22 surfaces and corresponding ab initio data as function of RBe+–HH for three different θ in a long range of the reactant channel. The rHH is fixed at equilibrium distance. It can be seen that the fitting results are good in agreement with the ab initio calculations, implying the NN PESs are reliable for describing the long-range potential.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)






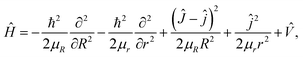
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the potential energies, which is a 2 × 2 matrix. The state-to-state S-matrix is extracted by the reactant coordinate based method,60 and the second-order split operator method is employed in the propagation of wave function. The state-to-state reaction probability is obtained by
is the potential energies, which is a 2 × 2 matrix. The state-to-state S-matrix is extracted by the reactant coordinate based method,60 and the second-order split operator method is employed in the propagation of wave function. The state-to-state reaction probability is obtained by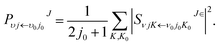
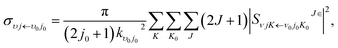
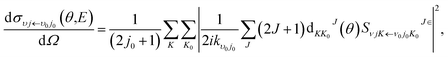
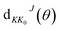 is the element of reduced Wigner rotation matrix.
is the element of reduced Wigner rotation matrix.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 geometries in a large region of configuration space are selected to fit the diabatic PESs by using the NN method. The diabatic PESs can reproduce the adiabatic data well and the spectroscopic constants of diatomics calculated on the diabatic PESs are good in agreement with the experimental values. The diabatic PESs topographical features are accounted in detail and the positions of conical intersection between the Vd11 and Vd22 are pointed. The TDWP calculations for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction are performed on the diabatic PESs. The results of reaction probabilities, ICSs, and DCSs of the title reaction are calculated. The total reaction is no threshold, and there are some oscillatory peaks in the curves of reaction probability. The total ICS has a high value at low collision energy, and the product BeH+ molecular ion is excited to high vibrational states easily. The DCS results show that the product BeH+ molecular ion tends to backward scattering at most collision energies.
778 geometries in a large region of configuration space are selected to fit the diabatic PESs by using the NN method. The diabatic PESs can reproduce the adiabatic data well and the spectroscopic constants of diatomics calculated on the diabatic PESs are good in agreement with the experimental values. The diabatic PESs topographical features are accounted in detail and the positions of conical intersection between the Vd11 and Vd22 are pointed. The TDWP calculations for the Be+(2P) + H2(X1Σg+) → BeH+(X1Σ+) + H(2S) reaction are performed on the diabatic PESs. The results of reaction probabilities, ICSs, and DCSs of the title reaction are calculated. The total reaction is no threshold, and there are some oscillatory peaks in the curves of reaction probability. The total ICS has a high value at low collision energy, and the product BeH+ molecular ion is excited to high vibrational states easily. The DCS results show that the product BeH+ molecular ion tends to backward scattering at most collision energies.