Open Access Article
Open Access ArticleAdsorption behavior of magnetic bentonite for removing Hg(II) from aqueous solutions†
Chenglong Zou ,
Jiyan Liang
,
Jiyan Liang *,
Wei Jiang,
Yinyan Guan and
Yichen Zhang
*,
Wei Jiang,
Yinyan Guan and
Yichen Zhang
School of Science, Shenyang University of Technology, Shenyang, 110870, Liaoning, China. E-mail: liangjiy2017@126.com; Tel: +86 24 25497158
First published on 2nd August 2018
Abstract
Bentonite is a porous clay material that shows good performance for adsorbing heavy metals and other pollutants for wastewater remediation. However, it is very difficult to separate the bentonite from water after adsorption as it forms a stable suspension. In this paper, we prepared magnetic bentonite (M-B) by loading Fe3O4 particles onto aluminum-pillared bentonite (Al-B) in order to facilitate its removal from water. The functional groups, skeleton structure, surface morphology and electrical changes of the prepared material were investigated by FT-IR, XRD, BET, SEM, VSM and zeta potential measurements. It was used as an adsorbent for Hg(II) removal from aqueous solutions and the influence of various parameters on the adsorption performance was investigated. The adsorption kinetics were best fitted by the pseudo-second-order model, and also followed the intra-particle diffusion model up to 18 min. Moreover, adsorption data were successfully reproduced by the Langmuir isotherm, and the Hg(II) adsorption saturation capacity was determined as 26.18 mg g−1. The average adsorption free energy change calculated by the D-R adsorption isotherm model was 11.89 kJ mol−1, which indicated the occurrence of ionic exchange. The adsorption thermodynamic parameter ΔH was calculated as 42.92 kJ mol−1, which indicated chemical adsorption. Overall, the thermodynamic parameters implied that Hg(II) adsorption was endothermic and spontaneous.
1. Introduction
Rapid industrial development has resulted in increased discharge of heavy metal-contaminated wastewater into the environment. This poses a serious safety hazard, owing to the mutagenic, carcinogenic, and teratogenic effects of Hg.1,2 Hg can enter the human body via the inhalation of Hg vapor or the consumption of Hg-contaminated drinking water or fish products.3,4 The non-biodegradability of Hg results in its accumulation in living organisms, which causes serious health problems such as Minamata disease, kidney failure, and neural disorders.5,6 Thus, Hg is a primary pollutant that must be closely monitored and controlled in all countries. At present, a number of Hg removal methods have been developed, e.g., chemical precipitation, electrolytic reduction, membrane filtration, reverse osmosis, adsorption, and ion exchange.6 Among these methods, adsorption shows the most promise because of its high efficiency, convenience, and cost-effectiveness. Bentonite clay is widely used as an adsorbent for wastewater treatment owing to its large surface area, high adsorption capacity, and low cost.7 However, the separation of bentonite from wastewater is challenging, since this adsorbent swells in water and forms very stable colloidal suspensions.Magnetic derivatization of adsorbents is a very useful modification of such materials, which has been shown to improve the manipulation.8,9 By depositing magnetic Fe3O4 particles onto the surfaces of adsorbent powder, it can be effectively separated from wastewater using magnetic separation techniques.10,11 The solvothermal method is effective for preparing high-purity and high-quality magnetic Fe3O4 particles with the desired morphology.12
In this study, a new low-cost magnetic bentonite (M-B) adsorption material was prepared using the solvothermal method. The functional groups, skeleton structure and surface morphology of the prepared material were analysed by Fourier transform infrared (FT-IR) spectroscopy, X-ray diffraction (XRD), Brunauer–Emmett–Teller (BET) surface area analysis, scanning electron microscopy (SEM), vibrating sample magnetometer (VSM) and zeta potential measurements. And its ability to remove Hg(II) from aqueous solutions was evaluated in detail. In particular, the effects of initial Hg(II) concentration, M-B dosage, pH, and temperature on adsorption performance were studied in detail. Moreover, the adsorption mechanism of interaction between Hg(II) ions and M-B was analysed using a number of kinetic/adsorption isotherm models and thermodynamic analysis. Thus, this study is expected to provide a reference and theoretical basis for the treatment of Hg-containing wastewater with M-B materials.
2. Experimental
2.1 Materials and reagents
Sodium bentonite (Na-B; Chaoyang City, Liaoning province, China) was crushed and passed through a 200-mesh sieve after purification and air-drying to afford a light yellow powder. Analytical-grade reagents, including FeCl3·6H2O, AlCl3·6H2O, CH3COONa, (CH2OH)2, NaOH, HCl, and HgCl2, were purchased from Sinopharm Chemical Reagent Co., Ltd. (China) and used in all experiments. All solutions were prepared using deionized water (18 MΩ cm).2.2 Preparation of M-B
The Al-B was prepared using a modification of a recently described method at an Al![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) bentonite ratio of 6 mol kg−1.13 M-B was prepared by loading magnetic Fe3O4 nanoparticles onto Al-pillared bentonite (Al-B) at an Fe
bentonite ratio of 6 mol kg−1.13 M-B was prepared by loading magnetic Fe3O4 nanoparticles onto Al-pillared bentonite (Al-B) at an Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al-B ratio of 6 mol kg−1 using a previously reported solvothermal method.14
Al-B ratio of 6 mol kg−1 using a previously reported solvothermal method.14
2.3 Characterization methods
Infrared spectra of the samples were recorded using a Vertex70 FT-IR spectrometer (Thermo Fisher Scientific, USA). The XRD patterns of samples were obtained using a Rigaku D/Max-2550PC diffractometer (Rigaku, Japan), over a diffraction angle (2θ) range of 10–70°, at a scan rate of 4° min−1. SEM images of the nonmagnetic and magnetic samples were taken using an SU8010N and an S-4800 SEM systems (Hitachi, Japan). The N2 adsorption–desorption isotherms were recorded on a V-Sorb 2800 surface area and porosimetry analyser (Gold APP Instruments Corporation, China). Magnetic characterization was carried out using a magnetic property measurement system (MPMS-7, Quantum Design, USA). zeta potentials of samples in solution were measured by a JS94H zeta potential meter (Powereach, China) at different pH values.2.4 Batch adsorption experiments
In these experiments, we investigated the effects of parameters such as contact time, pH, temperature, adsorbent dosage, and initial Hg(II) concentrations on adsorption performance. The Hg(II) solution was prepared by dissolving HgCl2 in deionized water in the presence of hydrochloric acid. Batch experiments were carried out in a 500 mL conical flask containing 250 mL of test solution. To adjust pH, 0.1 mol L−1 of aqueous HCl or 0.1 mol L−1 of aqueous NaOH was added to the test solution, and the flask was then shaken in an electricity-driven thermostatic water bath oscillator at 170 rpm. When the target temperature was reached, the solution was treated with the required amount of M-B. The adsorbent was separated after the desired contact time using an external magnet. All experiments were conducted in triplicate. Hg(II) concentrations were measured by an AAS novAA 400 hydride generation-atomic absorption spectrometer (Analytik Jena AG, Germany).2.5 Data processing
Hg(II) adsorption efficiencies (r) were calculated using eqn (1):
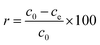 | (1) |
The Hg(II) adsorption capacity of M-B, which is defined as the amount of Hg(II) adsorbed per gram of M-B (mg g−1), was determined using eqn (2):
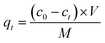 | (2) |
3. Results and discussion
3.1 Characterizations
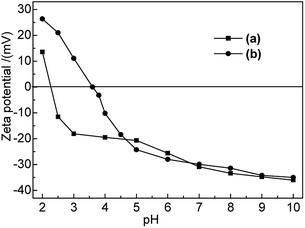
As shown in Fig. 1, the point of zero charge (PZC) of Na-B and M-B corresponded to pH 2.4 and pH 3.6, respectively. The electrochemistry on bentonite surface was changed after modification; the zeta potential of M-B became higher than that of Na-B at pH 2.0–4.7. The zeta potential of M-B was not significantly different with it of Na-B at pH 4.7–10.0.
At pH < pHPZC, M-B exhibited positive zeta potentials, indicating that its surface was positively charged. As pH was increased from 3.6 to 10.0, the functional groups of M-B underwent deprotonation, which decreased its zeta potential from 0 to −35.02 mV and resulted in the build-up of negative surface charge. As a result, the Hg(II) adsorption capacity of M-B increased owing to the electrostatic attraction between Hg(II) ions and the negatively charged M-B surface.
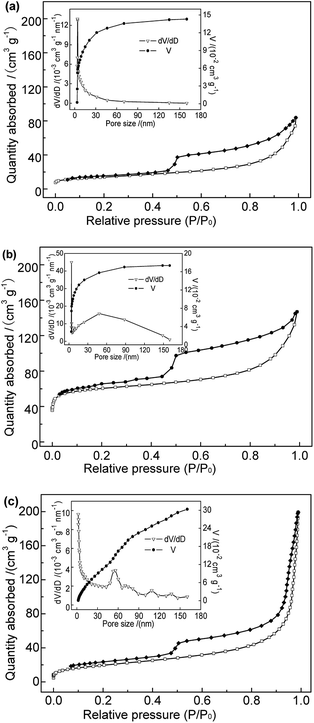 | ||
| Fig. 3 N2 adsorption–desorption isotherms and pore size distributions of (a) Na-B, (b) Al-B, and (c) M-B samples. | ||
| Samples | Na-B | Al-B | M-B |
|---|---|---|---|
| BET surface area (m2 g−1) | 49.56 | 206.71 | 71.35 |
| Microporous surface area (m2 g−1) | 11.35 | 144.49 | 3.18 |
| Total pore volume (cm3 g−1) | 0.139 | 0.174 | 0.308 |
| Micropore volume (cm3 g−1) | 0.005 | 0.066 | 0.001 |
| Average pore size (nm) | 10.45 | 4.40 | 17.28 |
| Average mesopore size (nm) | 6.04 | 5.47 | 13.42 |
3.2 Adsorption properties
To further explore the rate-controlling steps of adsorption and its dynamic characteristics, experimental data were fitted by Lagergren pseudo-first-order and pseudo-second-order kinetic models using the linear equations provided below (eqn (3) and (4)).19 The intra-particle diffusion model proposed by Weber and Morris was applied to analyse the rate-controlling step of adsorption and describe localized adsorption for specific interactions (eqn (5)).20
ln(qe − qt) = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe − k1t qe − k1t
| (3) |
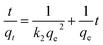 | (4) |
| qt = k3t1/2 + C | (5) |
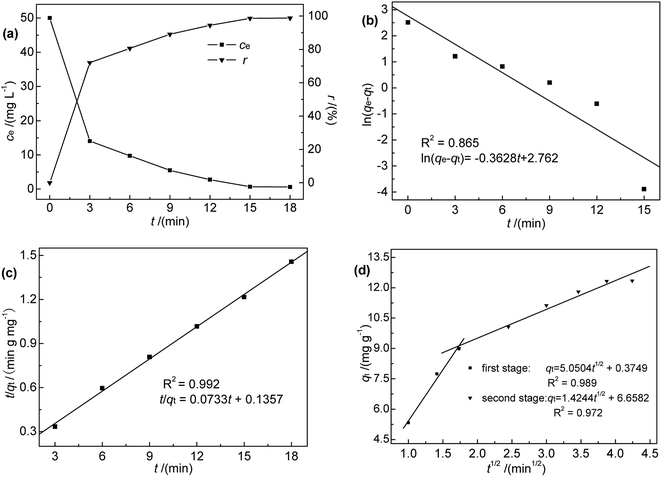
The fits obtained using eqn (3)–(5) are shown in Fig. 4(b)–(d), and the adsorption capacities and rate constants calculated from these plots are listed in Table 2. The results showed that experimental kinetic data were best fitted by the pseudo-second-order model, which also provided a better prediction of the equilibrium adsorption capacity. As the main adsorption-affecting factor of the pseudo-second-order model is the interaction of M-B functional groups with Hg(II), the above findings suggested the occurrence of chemical adsorption.
| Pseudo-first order | Pseudo-second order | ||
|---|---|---|---|
| qe,exp (mg g−1) | 12.35 | qe,exp (mg g−1) | 12.35 |
| qe,cal (mg g−1) | 15.831 | qe,cal (mg g−1) | 13.643 |
| k1 (min−1) | 0.3628 | k2 (g mg−1 min−1) | 0.0396 |
| R2 | 0.865 | R2 | 0.992 |
| Intra-particle diffusion | ||
|---|---|---|
| First step | Second step | |
| C (mg g−1) | 0.375 | 6.658 |
| k3 (mg g−1 min−1/2) | 5.050 | 1.424 |
| R2 | 0.989 | 0.972 |
The fitting adsorption curve of intra-particle diffusion model (Fig. 4(d)) showed two distinct adsorption processes. The first step was related to Hg(II) adsorption on active sites on the surface of M-B (surface adsorption process), while the second step was related to Hg(II) diffusion absorption in the pores of M-B (particle diffusion process). The intercept C of the particle diffusion process was not equal to zero. Hence, the adsorption process was not only controlled by particle diffusion, which is consistent with the analysis of pseudo-second order kinetic.20
As shown in Fig. 5, the removal efficiency of Hg(II) was significantly affected by pH. A rapid and continuous decrease in ce was observed with increasing pH, whereas r steadily increased, reaching a maximum (99.52%) at pH 8 and decreasing slightly thereafter. The above finding was explained as follows. At low pH, Hg2+ ions were the dominant species in the solution and were repelled by the positively charged M-B surface. Additionally, the H3O+ ions abundantly present in solution at low pH strongly competed with Hg(II) ions for adsorption sites on the M-B surface,26 effectively decreasing the amount of adsorbed Hg2+ ions.
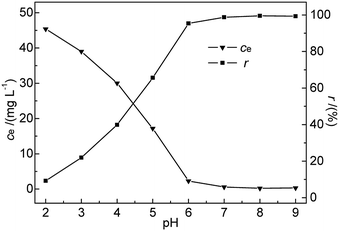 | ||
| Fig. 5 Effect of pH on ce and r (c0 = 50 mg L−1, M-B dosage = 4 g L−1, temperature = 35 °C, contact time = 30 min). | ||
At pH 3.6–7.0, the solution mainly contained Hg(OH)+ and Hg(OH)2 (with hydrated sizes exceeding that of Hg2+) that were strongly bound by the adsorption sites of the sorbent surface, which resulted in enhanced Hg(II) removal efficiency.27,28 At pH > pHPZC, more metal-binding sites on the negatively charged M-B surface were exposed, whereas a certain fraction of Hg(II) in solution was still present as positively charged ions. These conditions favoured the interaction between Hg(II) and the active groups on the M-B surface. With increasing pH, the above interaction was strengthened owing to the concomitantly increasing electronegativity of M-B, which increased its Hg(II) adsorption capacity. However, a further increase in pH to 9 decreased the amount of adsorbed Hg(II) species, which was attributed to the deposition of Hg(II) as Hg(OH)2 (Ksp Hg(OH)2 = 3.13 × 10−26). Finally, excessively high pH values promoted the formation of negatively charged Hg(II)–OH complexes that were electrostatically repelled by the strongly negatively charged M-B surface.29 Therefore, pH 7.0 was selected as the optimal condition.
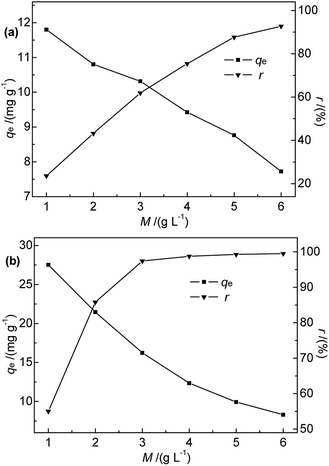 | ||
| Fig. 6 Effect of (a) Na-B and (b) M-B dosage on qe and r (c0 = 50 mg L−1, pH = 7, temperature = 35 °C, contact time = 30 min). | ||
Fig. 6 shows that the adsorption efficiency and adsorption capacity of M-B were significantly higher than that of Na-B with the dosages range 1.0 to 3.0 g L−1. The results indicated that the adsorption performance was improved after modification, which might be due to the several following reasons. After modification, the specific surface area and the total pore volume of bentonite increased, contributing to the active points on the surface increased. Compared with Na-B, the pore size of M-B increased, which was beneficial for the diffusion of particles.
The efficiency of Hg(II) removal sharply increased as the M-B dosage was increased from 1.0 to 4.0 g L−1, which was ascribed to the increasing number of binding sites. Further increases in M-B dosage did not have a significant effect, which was attributed to the insufficient residual metal concentration in solution.30 In addition, the adsorption process followed isothermal adsorption equilibrium theory.
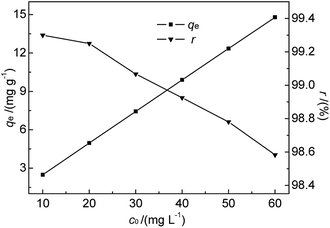 | ||
| Fig. 7 Effect of initial Hg(II) concentration on qe and r (M-B dosage = 4 g L−1, pH = 7, temperature = 35 °C, contact time = 30 min). | ||
As shown in Fig. 7, the amount of adsorbed Hg(II) increased from 2.48 to 14.79 mg g−1 when the initial Hg(II) concentration was increased from 10.0 to 60.0 mg L−1. This increase was almost linear, which was ascribed to the fact that the equilibrium adsorption capacity was lower than the saturated adsorption capacity. However, r slightly decreased with increasing initial Hg(II) concentration. The prepared M-B exhibited a high Hg(II) adsorption ability, although it was difficult to achieve the Hg(II) concentration limit (GB 8978-1996) for high-concentration wastewater with batch-type adsorption. Thus, M-B was concluded to be well suited for the pre-treatment of wastewater contaminated with high concentrations of Hg(II).
To shed further light on the distribution of Hg(II) between the liquid and solid phases at equilibrium, the equilibrium data (amounts of Hg(II) adsorbed per gram of M-B and the equilibrium concentrations of Hg(II); shown in Fig. 8(a)) were fitted using Langmuir and Freundlich isotherms (eqn (6) and (7), respectively).32,33
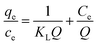 | (6) |
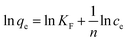 | (7) |
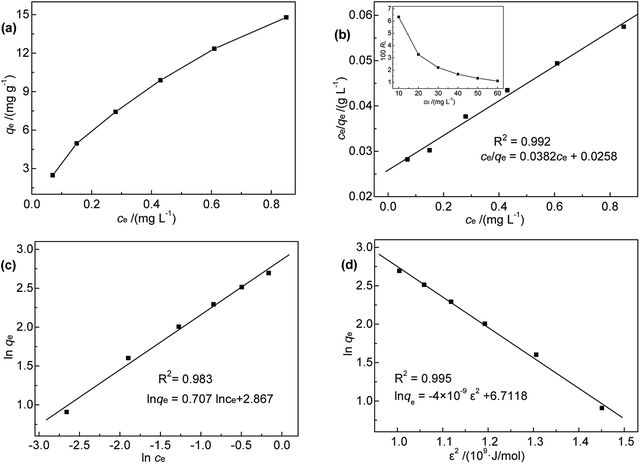 | ||
| Fig. 8 (a) Relationship between qe and ce; (b) Langmuir, (c) Freundlich, and (d) D-R isotherms for Hg(II) adsorption onto M-B. | ||
Fig. 8(b) and (c) show the fits obtained for the above models, indicating that the adsorption of Hg(II) on M-B was best modelled by the Langmuir isotherm. It suggested that this adsorption corresponded to monolayer coverage of Hg(II) on the surface of M-B.34 In addition, the adsorption saturation capacity was determined as 26.18 mg g−1. The value of 1/n = 0.707 (0 < 1/n < 1) was indicative of a material with a heterogeneous surface structure featuring an exponential distribution of active sites. In addition, the high value of Freundlich adsorption constant demonstrated the strong affinity of M-B toward Hg(II).35
The essential characteristics of the Langmuir isotherm can be expressed by a dimensionless constant known as the equilibrium parameter (RL) (eqn (8)).36
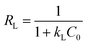 | (8) |
Based on the magnitude of RL, isotherms can be classified as those representing irreversible (RL = 0), favourable (0 < RL < 1), linear (RL = 1), or unfavourable (RL > 1) adsorption.37 In this work, KL was calculated as 0.131 L mg−1 (shown in Table 3). When the initial Hg(II) concentration was increased from 10.0 to 60.0 mg L−1, the RL values (shown in Fig. 8(b)) indicated that Hg(II) ions were favourably adsorbed by M-B.
| Langmuir | Freundlich | D-R | |||
|---|---|---|---|---|---|
| KL (L mg−1) | 1.481 | KF | 17.584 | qm (mg g−1) | 822.05 |
| Q (mg g−1) | 26.18 | n | 1.414 | Es (kJ mol−1) | 11.89 |
| R2 | 0.992 | R2 | 0.983 | R2 | 0.995 |
Additionally, the adsorption mechanism can be deduced from the average adsorption free energy (Es). The magnitude of Es indicates physical adsorption (when the value of Es is lower than 8 kJ mol−1), chemical adsorption (when the value of Es is higher than 16 kJ mol−1) and the presence of ionic exchange (for range between 8 and 16 kJ mol−1).38 The Es is calculated using the Dubinin-Radushkevich (D-R) adsorption isotherm model (eqn (9)–(11)):39
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qm − kdε2 qm − kdε2
| (9) |
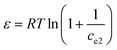 | (10) |
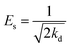 | (11) |
The fits obtained using the linear equation of the D-R model is shown in Fig. 8(d). Based on the obtained kd value, Es was calculated as 11.89 kJ mol−1 using eqn (11). The fact that this value was in the range of 8–16 kJ mol−1 indicated the occurrence of ionic exchange during adsorption process.38,40
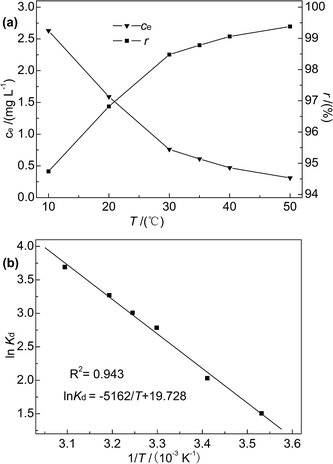
As the temperature increased from 10 to 50 °C, the Hg(II) removal rate slightly increased (from 94.74% to 99.38%), and the Hg(II) equilibrium adsorption capacity and residual concentration at 50 °C were determined as 12.42 mg g−1 and 0.31 mg L−1, respectively. This finding indicated that the adsorption of Hg(II) onto M-B was favoured at high temperature, which suggested that the adsorption process was endothermic. Moreover, thermodynamic analysis revealed the occurrence of chemisorption, the extent of which is known to increase with increasing temperature because of the concomitant facilitation of diffusion.42 In contrast, the reaction temperature had little influence on the adsorption efficiency, which was in agreement with previously obtained results.36
The effect of temperature on Hg(II) adsorption was further studied by thermodynamic analysis using eqn (12)–(15) to determine changes in the Gibbs free energy (ΔG), enthalpy (ΔH), and entropy (ΔS):43,44
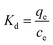 | (12) |
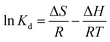 | (13) |
| ΔG = ΔH − TΔS | (14) |
ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd
| (15) |
ΔH and ΔS were obtained from the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd vs. 1/T (Fig. 9(b)), which allows for the determination of ΔG. Table 4 lists the obtained thermodynamic parameters and the calculated correlation coefficients, and shows that the adsorption ΔH was positive and exceeded 40 kJ mol−1. This indicated that the adsorption of Hg(II) onto M-B was endothermic and chemical in nature. The positive value of ΔS suggested that adsorption increased randomness at the solid–liquid interface and reflected the affinity of M-B for Hg(II).37 The ΔG values were negative and decreased with increasing temperature, which indicated that adsorption was spontaneous in nature. Furthermore, the increase in |ΔG| with increasing temperature suggested that the adsorption of Hg(II) onto M-B was more favourable at higher temperatures.45
Kd vs. 1/T (Fig. 9(b)), which allows for the determination of ΔG. Table 4 lists the obtained thermodynamic parameters and the calculated correlation coefficients, and shows that the adsorption ΔH was positive and exceeded 40 kJ mol−1. This indicated that the adsorption of Hg(II) onto M-B was endothermic and chemical in nature. The positive value of ΔS suggested that adsorption increased randomness at the solid–liquid interface and reflected the affinity of M-B for Hg(II).37 The ΔG values were negative and decreased with increasing temperature, which indicated that adsorption was spontaneous in nature. Furthermore, the increase in |ΔG| with increasing temperature suggested that the adsorption of Hg(II) onto M-B was more favourable at higher temperatures.45
| T (K) | ΔG (kJ mol−1) | ΔH (kJ mol−1) | ΔS (J mol−1 K−1) |
|---|---|---|---|
| 283 | −3.54 | 42.92 | 164.03 |
| 293 | −4.94 | ||
| 303 | −7.02 | ||
| 308 | −7.70 | ||
| 313 | −8.51 | ||
| 323 | −9.91 |
4. Conclusions
Magnetic bentonite was prepared in this study and characterized. The results showed that the bentonite structure was not destroyed during the process of modification. The porosity and roughness of the surface increased, and the layers are separated with larger spacing after modification. Fe3O4 spherical nanoparticles were evenly distributed on the surface of Al-B with sizes of ∼40–100 nm. M-B was superparamagnetic with a magnetization saturation value of 22.08 emu g−1.It was successfully used as an adsorbent to remove Hg(II) from aqueous solutions. The effects of several parameters on adsorption capacity and efficiency were studied. Notably, M-B was shown to be an effective Hg(II) adsorbent. Under the optimized conditions (pH 8, contact time = 30 min, temperature = 35 °C, initial Hg(II) concentration = 50 mg L−1, M-B dosage = 4.0 g L−1), the residual concentration and removal efficiency of Hg(II) were determined as 0.24 mg L−1 and 99.52%, respectively.
The adsorption process was best fitted by a pseudo-second-order kinetic model; it followed the intra-particle diffusion model up to 18 min. The Langmuir model was successfully applied to fit the adsorption data, allowing the saturation Hg(II) adsorption capacity of M-B to be calculated as 26.18 mg g−1. Moreover, the adsorption process mainly corresponded to chemical adsorption and ionic exchange. Thermodynamic analysis demonstrated that the adsorption process was endothermic and spontaneous, and was therefore favoured by high temperatures. Thus, M-B was concluded to be a promising low-cost adsorbent for the efficient removal of Hg(II) from liquid waste.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the China Environmental Protection Foundation, Geping Green Action, Liaoning Environmental Research and Education Fund “123 Project” (Grant No. CEPF2014-123-1-6). And, this work was sponsored by “Liaoning BaiQianWan Talents Program”.References
- J. O. Nriagu and J. M. Pacyna, Nature, 1988, 333, 134–139 CrossRef PubMed.
- R. J. Lu, J. A. Hou, J. Xu, T. M. Tang and X. H. Xu, J. Hazard. Mater., 2011, 196(1), 160–165 CrossRef PubMed.
- S. C. Foo and T. C. Tan, Sci. Total Environ., 1998, 209, 185–192 CrossRef PubMed.
- T. M. Tang, J. Xu, R. J. Lu, J. J. Wo and X. H. Xu, Fuel, 2010, 89(12), 3613–3617 CrossRef.
- M. F. Wolfe, S. Schwarzbach and R. A. Sulaiman, Environ. Toxicol. Chem., 2010, 17, 146–160 CrossRef.
- T. W. Clarkson and L. Magos, Crit. Rev. Toxicol., 2006, 36, 609–662 CrossRef PubMed.
- J. Shu, Y. Peng, C. D. Pan, X. Z. Cheng and L. Deng, Adv. Mater. Res., 2013, 781–784, 1977–1980 Search PubMed.
- F. L. Fu and Q. Wang, J. Environ. Manage., 2011, 92, 407–418 CrossRef PubMed.
- J. Xu, X. Liu, G. V. Lowry, Z. Cao, H. Zhao, J. L. Zhou and X. H. Xu, ACS Appl. Mater. Interfaces, 2016, 8, 7333–7342 CrossRef PubMed.
- A. Mockovciaková, Z. Orolínová and J. Skvarla, J. Hazard. Mater., 2010, 180, 274–281 CrossRef PubMed.
- K. Chen, G. Wang, W. B. Li, D. Wan, Q. Hu, L. L. Lu, X. B. Wei and Z. Z. Chen, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2015, 30, 302–306 CrossRef.
- L. S. Tan, J. Xu, X. Q. Xue, Z. M. Lou, J. Zhu, S. A. Baig and X. H. Xu, RSC Adv., 2014, 86, 45920–45929 RSC.
- V. Cabuil, V. Dupuis, D. Talbot and S. Neveu, J. Magn. Magn. Mater., 2011, 323, 1238–1241 CrossRef.
- L. Lian, X. Cao, Y. Q. Wu, D. Z. Sun and D. W. Lou, Appl. Surf. Sci., 2014, 289, 245–251 CrossRef.
- T. K. Sen and D. Gomez, Desalination, 2011, 267, 286–294 CrossRef.
- J. H. Meng, G. Q. Yang, L. M. Yan and X. Y. Wang, Dyes Pigm., 2005, 66, 109–113 CrossRef.
- W. B. Guan, B. X. Zhao, S. Qiu, N. Liu, L. Niu, R. Cheng and Y. Sun, J. Northwest Univ., 2016, 46, 375–380 Search PubMed.
- Q. H. Wang, X. J. Chang, D. D. Li, Z. H. Hu, R. J. Li and Q. He, J. Hazard. Mater., 2011, 186, 1076–1081 CrossRef PubMed.
- A. D. Monfared, M. H. Ghazanfari, M. Jamialahmadi and A. Helalizadeh, Chem. Eng. J., 2015, 281, 334–344 CrossRef.
- N. Sun, W. Shi, L. Ma and S. Yu, RSC Adv., 2017, 7(28), 17095–17106 RSC.
- A. S. Özcan, Ö. Gök and A. Özcan, J. Hazard. Mater., 2009, 161, 499–509 CrossRef PubMed.
- S. Vilvanathan and S. Shanthakumar, Environ. Technol., 2017, 39(4), 1–42 Search PubMed.
- M. M. Liu, L. A. Hou, B. D. Xi, Y. Zhao and X. F. Xia, Appl. Surf. Sci., 2013, 273, 706–716 CrossRef PubMed.
- A. Sari, M. Tuzen, D. Citak and M. Soylak, J. Hazard. Mater., 2007, 148, 387–394 CrossRef PubMed.
- J. Shi, Z. B. Zhao, Z. J. Liang and T. Y. Sun, Water Sci. Technol., 2016, 73, 2422–2429 CrossRef PubMed.
- G. Blázquez, M. A. Martín-Lara, E. Dionisio-Ruiz, G. Tenorio and M. Calero, J. Ind. Eng. Chem., 2012, 18, 1741–1750 CrossRef.
- P. Hadi, M. H. To, C. Hui, C. S. K. Lin and G. Mckay, Water Res., 2015, 73, 37–55 CrossRef PubMed.
- N. Sun, X. Wen and C. J. Yan, Int. J. Biol. Macromol., 2017, 108, 1199–1206 CrossRef PubMed.
- M. Mudasir, K. Karelius, N. H. Aprilita and E. T. Wahyuni, J. Environ. Chem. Eng., 2016, 4, 1839–1849 CrossRef.
- D. Hamane, O. Arous, F. Kaouah, M. Trari, H. Kerdjoudj and Z. Bendjama, J. Environ. Chem. Eng., 2015, 3, 60–69 CrossRef.
- R. R. Pawar, B. H. C. Lalhmunsiama and S. M. Lee, J. Ind. Eng. Chem., 2016, 34, 213–223 CrossRef.
- Y. He, Y. G. Chen and W. M. Ye, Environ. Earth Sci., 2016, 75, 807 CrossRef.
- N. Xue, L. Wang, M. Pei, Y. He, Y. Du and W. Guo, RSC Adv., 2016, 6(101), 98945–98951 RSC.
- Y. H. Song, M. C. Lu, B. Huang, D. L. Wang, G. Wang and L. Zhou, J. Alloys Compd., 2018, 737, 113–121 CrossRef.
- Q. X. Yao, J. J. Xie, J. X. Liu, H. M. Kang and Y. Liu, J. Polym. Res., 2014, 21, 465 CrossRef.
- M. Hamidpour, M. Kalbasi, M. Afyuni, H. Shariatmadari and G. Furrer, Environ. Earth Sci., 2011, 62, 559–568 CrossRef.
- Q. Kang, W. Z. Zhou, Q. Li, B. Y. Gao, J. X. Fan and D. Z. Shen, Appl. Clay Sci., 2009, 45, 280–287 CrossRef.
- M. L. Cantuaria, A. F. D. A. Neto, E. S. Nascimento and M. G. A. Vieira, J. Cleaner Prod., 2015, 112, 1112–1121 CrossRef.
- Y. G. Chen, Z. Sun, W. M. Ye and Y. J. Cui, J. Radioanal. Nucl. Chem., 2017, 311, 1839–1847 CrossRef.
- M. D'Arcy, D. Weiss, M. Bluck and R. Vilar, J. Colloid Interface Sci., 2011, 364, 205–212 CrossRef PubMed.
- I. Daou, O. Zegaoui and A. Amachrouq, Water Sci. Technol., 2017, 75, 1098–1117 CrossRef PubMed.
- K. K. Anoop and T. S. Anirudhan, J. Hazard. Mater., 2002, 92, 161–183 CrossRef.
- S. M. Awadh and F. H. Abdulla, Environ. Earth Sci., 2017, 76, 386 CrossRef.
- H. Chen, Q. S. Chen, B. Huang, S. W. Wang and L. Y. Wang, J. Radioanal. Nucl. Chem., 2018, 316, 71–80 CrossRef.
- H. Moussout, H. Ahlafi, M. Aazza, O. Zegaoui and A. C. El, Water Sci. Technol., 2016, 73, 2199–2210 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra05247f |
| This journal is © The Royal Society of Chemistry 2018 |