Open Access Article
Open Access ArticleTheoretical investigations on azole-fused tricyclic 1,2,3,4-tetrazine-2-oxides†
Teng Fei ,
Yao Du
,
Yao Du ,
Chunlin He* and
Siping Pang
,
Chunlin He* and
Siping Pang *
*
School of Materials Science & Engineering, Beijing Institute of Technology, Beijing 100081, P. R. China. E-mail: chunlinhe@bit.edu.cn; pangsp@bit.edu.cn
First published on 31st July 2018
Abstract
Fused compounds, a unique class of large conjugate structures, have emerged as prime candidates over traditional nitrogen-rich mono-ring or poly-ring materials. Meanwhile, compounds containing catenated nitrogen chains have also attracted attention from scientists due to their high heats of formation. On the other hand, the azoxy [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(O)–] moiety has been found to increase density effectively in the molecular structure of compounds. Therefore, combining fused heterocyclic organic skeletons with the azoxy moiety can be regarded as an effective method for increasing the density and heat of formation, which results in substantial increase in detonation properties. Based on the above-mentioned considerations, in this study, a series of new non-hydrogen-containing 5/6/5 fused ring molecules with azoxy moiety structures are designed. Furthermore, their properties as potential high-energy-density materials, including their density, heats of formation, detonation properties, and impact sensitivity, have been extensively evaluated using thermodynamic calculations and density functional theory. Among the investigated compounds, 1,3,8,10-tetranitrodiimidazo[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (B), 1,10-dinitrobis([1,2,3]triazolo)[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (C) and 2,9-dinitrobis([1,2,4]triazolo)[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (D) display remarkable stabilities and are predicted to be high-performance energetic materials due to their high density (>1.94 g cm−3), detonation velocity (>9616 m s−1), and detonation pressure (>41.1 GPa). In addition, our design strategy, which combines the azoxy moiety and fused tricyclic skeleton to construct nitrogen-rich molecular structures with high density and positive heat of formation, is a valuable approach for developing novel high-energy-density materials with excellent performance and stability.
N(O)–] moiety has been found to increase density effectively in the molecular structure of compounds. Therefore, combining fused heterocyclic organic skeletons with the azoxy moiety can be regarded as an effective method for increasing the density and heat of formation, which results in substantial increase in detonation properties. Based on the above-mentioned considerations, in this study, a series of new non-hydrogen-containing 5/6/5 fused ring molecules with azoxy moiety structures are designed. Furthermore, their properties as potential high-energy-density materials, including their density, heats of formation, detonation properties, and impact sensitivity, have been extensively evaluated using thermodynamic calculations and density functional theory. Among the investigated compounds, 1,3,8,10-tetranitrodiimidazo[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (B), 1,10-dinitrobis([1,2,3]triazolo)[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (C) and 2,9-dinitrobis([1,2,4]triazolo)[1,5-d:5′,1′-f][1,2,3,4]tetrazine 5-oxide (D) display remarkable stabilities and are predicted to be high-performance energetic materials due to their high density (>1.94 g cm−3), detonation velocity (>9616 m s−1), and detonation pressure (>41.1 GPa). In addition, our design strategy, which combines the azoxy moiety and fused tricyclic skeleton to construct nitrogen-rich molecular structures with high density and positive heat of formation, is a valuable approach for developing novel high-energy-density materials with excellent performance and stability.
Introduction
In the pursuit of high-performance energetic materials, nitrogen-rich five- or six-membered heterocycles possessing high densities, high heats of formation, and good oxygen balance are widely sought.1–4 Among these newly emerging structural motifs, the family of fused polycyclic azoles and azines is attracting increasing interests, and these materials have been utilized for designing various highly energetic nitrogen-rich skeletons. Recently, various remarkable novel fused heterocyclic compounds, for example, tetrazino-tetrazine 1,3,6,8-tetraoxide (TTTO),5 4-amino-3,7-dinitrotriazolo-[5,1-c][1,2,4] triazine-4-oxide (DPX-27),6 and 3,6,7-triamino-[1,2,4]triazolo[4,3-b][1,2,4]triazole (TATOT)7 have been reported. Due to their high nitrogen content and planar structure, these energetic molecules exhibit a good balance between high performance and low sensitivity. Significantly, non-hydrogen-containing 5/6/5 fused ring energetic compounds such as 1,2,9,10-tetranitrodipyrazolo[1,5-d:5′,1′-f][1,2,3,4]-tetrazine8 and 2,9-dinitrobis([1,2,4]triazolo)[1,5-d:5′,1′-f][1,2,3,4]tetrazine9 have received considerable attention due to their special molecular structures. In their molecular organization, two dinitropyrazole or dinitrotriazole rings are fused to 1,2,3,4-tetrazine with six concomitant catenated nitrogen atoms. These molecules exhibit clear advantages of thermal stability and excellent energetic performance. Therefore, fused nitrogen-rich heterocycles have been identified as a promising family of organic skeletons for energetic materials.Furthermore, nitrogen-rich heterocycles have become the core motif in the search for new HEDMs, and their compatibility with other energetic functionalized groups is receiving increasing attention.10 During the past decade, several studies have been reported on the potential beneficial energetic properties of the azo group.11–13 The presence of the azo in energetic compounds allows for higher detonation velocities, pressures and densities in azo compounds, as determined by experimental measurements and theoretical calculations. However, the search for new energetic compounds with better properties is ongoing. In addition to introducing the azo group, the introduction of N-oxides is a rather recent methodology. The additional oxygen atom coordinated to the nitrogen system not only enhances density and performance but also tends to stabilize the entire molecule;14–16 for example, 4,4′- bis(nitramino)azofurazan has density of 1.89 g cm−3, detonation velocity of 9517 m s−1, and detonation pressure of 41.1 GPa.17 After the formation of the azoxy compound 4,4′-bis(nitramino)-azoxyfurazan,17 its density and energetic properties are further enhanced; it exhibits density of 1.96 g cm−3, detonation velocity of 9746 m s−1, and detonation pressure of 44.1 GPa. On the basis of the experimental measurements and theoretical calculations, the higher values for detonation velocities and pressures and higher densities for azoxy compounds support the advantages of the presence of an N-oxide moiety in energetic materials.
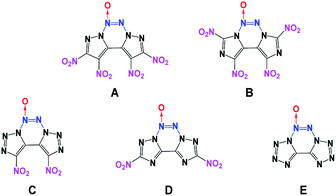
Generally, high density and positive heat of formation result in higher performance.18 Therefore, combining fused heterocyclic organic skeletons with the azoxy moiety can be regarded as an effective method for increasing density and heat of formation. However, among the N-oxide energetic compounds, molecules that contain the azoxy [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(O)–] moiety are hardly reported.17,19 To the best of our knowledge, fused heterocyclic energetic compounds containing an azoxy moiety are rare and particularly, there are no known non-hydrogen-containing 5/6/5 fused tricyclic compounds with the azoxy moiety. Therefore, in this study, five new energetic molecules with fused tricyclic heterocyclic structures containing the azoxy moiety have been designed (Fig. 1). Before their synthesis, it is necessary to predict their performance in advance for security reasons. Fortunately, modern theoretical studies based on quantum chemical treatments have gained acceptance as a useful research tool for screening candidate high-energy-density materials (HEDMs), thereby avoiding expensive and dangerous experimental tests. Such studies can provide an understanding of the relationships between molecular structures and properties, which can then be used to design better and more efficient laboratory tests. The present theoretical investigation may further help the experimental synthesis and testing of these novel energetic compounds.
N(O)–] moiety are hardly reported.17,19 To the best of our knowledge, fused heterocyclic energetic compounds containing an azoxy moiety are rare and particularly, there are no known non-hydrogen-containing 5/6/5 fused tricyclic compounds with the azoxy moiety. Therefore, in this study, five new energetic molecules with fused tricyclic heterocyclic structures containing the azoxy moiety have been designed (Fig. 1). Before their synthesis, it is necessary to predict their performance in advance for security reasons. Fortunately, modern theoretical studies based on quantum chemical treatments have gained acceptance as a useful research tool for screening candidate high-energy-density materials (HEDMs), thereby avoiding expensive and dangerous experimental tests. Such studies can provide an understanding of the relationships between molecular structures and properties, which can then be used to design better and more efficient laboratory tests. The present theoretical investigation may further help the experimental synthesis and testing of these novel energetic compounds.
Computational methods
Theoretical calculations were performed using the Gaussian 09 series of programs.20 The geometric optimization and frequency analyses were completed using the B3LYP functional combined with the 6-311++G** basis set. The single energy points were calculated at the MP2/6-311++G** level of theory. Harmonic vibrational frequencies including IR spectra and thermochemical parameters were obtained at the same levels of theory. Meanwhile, the electronic properties, highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO), and electrostatic potential on the molecular surface of the title compounds were calculated at the B3LYP/6-311++G** level of theory based on their optimized gas-phase structures. For all the compounds, their optimized structures were characterized as true local energy minima on the potential energy surface without imaginary frequencies. The final task was to establish the solid-state heat of formation (ΔHf,solid) for all the synthesized compounds. ΔHf,solid of neutral compounds can be estimated by subtracting the heat of sublimation (ΔHsub) from the gas-phase heat of formation (ΔHf,gas). According to Hess's law of constant heat summation,21 ΔHf,gas and ΔHsub can be used to evaluate ΔHf,solid as follows:| ΔHf,solid = ΔHf,gas − ΔHsub | (1) |
According to Politzer et al.,22,23 ΔHsub can be computed from the corresponding molecular surface area and electrostatic interaction index vσtot2 for energetic compounds. The empirical expression of this approach is
| ΔHsub = aA2 + b(νσtot2)0.5 + c | (2) |
For each neutral compound, the theoretical density was initially determined from the molecular weight (M) divided by Vm, where Vm is the van der Waals volume, which was obtained by Monte Carlo integration using the Multiwfn program. By introducing the interaction index vσtot2, the density of an energetic compound can be corrected according to the following equation, where α = 1.0462, β = 0.0021, and γ = −0.1586.
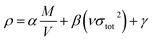 | (3) |
The calculations of the detonation parameters such as detonation velocity (D), detonation pressure (P), heat of detonation (Q) and explosion temperature (Tdet) were performed with the EXPLO5 program package (version 6.01).28
The bond dissociation energy (BDE) can provide useful information for understanding the stability of a molecule. Generally, the smaller the energy for breaking a bond, the weaker the bond, making it easier for the bond to act as a trigger bond. For many organic molecules, the terms “bond dissociation energy” (BDE) and “bond dissociation enthalpy” often appear interchangeably in the literature.29
At 0 K, BDE is given as:
| BDE0(A–B) → E0(A˙) + E0(B˙) − E0(A–B) | (4) |
BDE with a ZPE correction can be calculated using the following equation:
| BDE(A–B)ZPE → BDE0(A–B) + ΔEZPE | (5) |
Mulliken atomic charge analysis of nitro groups is also used to estimate the impact sensitivities of the title compounds. Normally, for the majority of nitro explosives, the R–NO2 (R = N, C or O) bonds are the weakest bonds and their breaking is usually the initial step in decomposition or detonation. The nitro group charge (−QNO2) is calculated by the sum of the net Mulliken atomic charges on the nitrogen and oxygen atoms of the nitro group:
| −QNO2 = QN + QO(1) + QO(2) | (6) |
To investigate the sensitivity of the title compounds, the property–structure relation method, i.e., “generalized interaction property function” was used to estimate the impact sensitivity, h50%. Here, we give four introduced methods, as summarized below:30,31
Method 1: h50% = 9.2 + 8.04 × 102 × exp[−(0.0875 mol kJ−1 × |![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) + − | + − |![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) −||)] −||)]
| (7) |
| Method 2: h50% = 29.3 + 1.386 × 10−3 × exp[48.84ν] | (8) |
| Method 3: h50% = 27.8 + 0.1135 × exp[−(2.6479 g kJ−1 × [Qd − 6.9496 kJ g−1])] | (9) |
| Method 4: h50% = 1.341 × exp[8.1389ν − 1.6234 g kJ−1 × (Qd − 6.166) kJ g−1] | (10) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) + − |
+ − |![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) −|| is the difference between the magnitudes of the averages of the positive and negative values of the electrostatic potential, v is the balance parameter, and Qd is the heat of detonation. To compare with the impact energy when 2.5 kg hammer is used, h50% of 100 cm is equivalent to the impact energy of 24.5 J.32
−|| is the difference between the magnitudes of the averages of the positive and negative values of the electrostatic potential, v is the balance parameter, and Qd is the heat of detonation. To compare with the impact energy when 2.5 kg hammer is used, h50% of 100 cm is equivalent to the impact energy of 24.5 J.32
The electric spark sensitivity shows the degree of sensitivity of an explosive to an electric discharge. The electric spark sensitivity of the title compounds is calculated using the following equation:33
| EES (J) = (−1)n110.16QNO2 − 1.05n1n2ELUMO − 0.20 | (11) |
Results and discussion
Structural design and molecular geometry
For energetic materials, the pursuit of higher energy is a constant goal. Recently, a tricyclic skeleton structure, that is, a non-hydrogen-containing 5/6/5 fused tricyclic structure was reported, in which two five-membered azole heterocycles and a 1,2,3,4-tetrazine are combined via a common C–N bond. From the view of structural design of new energetic compounds, this tricyclic compound offers a potentially promising skeleton for the construction of novel C-nitro-based energetic materials through different nitration reactions. The advantages of this tricyclic skeleton are as follows: (1) the tricyclic structure can provide additional ring strain, thereby making active contribution to the high positive ΔHf,solid of energetic materials; (2) the replacement of the hydrogen atoms with nitro groups in azole heterocycles can greatly increase their oxygen balance (OB) and therefore improve the detonation performance of the resulting compounds. On the other hand, from the viewpoint of molecular design, energetic compounds with high densities (ideally higher than 2.0 g cm−3) are particularly desirable since the detonation pressure and velocity of explosives are directly related to their density (ρ). If ρ can be further enhanced on the basis of this structure, the energetic properties can be further improved. According to calculations and experiments, the presence of an azoxy group in energetic compounds allows for higher D, P and ρ. Therefore, combining the non-hydrogen-containing 5/6/5 fused tricyclic structure with the azoxy moiety can achieve a satisfactory result in theory.In the first design strategy, pyrazole, imidazole, 1,2,3-triazole, 1,2,4-triazole and tetrazole were chosen as potential initial structures for combination with 1,2,3,4-tetrazine via common C–C and C–N bonds, and this resulted in the formation of novel skeletons with fused tricyclic structures. These compounds contained at least six nitrogen atoms with the goal of ensuring a high positive ΔHf,solid value for the resultant molecules. In the second phase, –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(O)– was replaced with the –N
N(O)– was replaced with the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– moiety to form new energetic molecules, which have higher ρ and OB. Considering that the pyrazole, imidazole, 1,2,3-triazole and 1,2,4-triazole moieties have two or four positions that can be further modified, several energetic groups, such as nitroamine and azide functional groups, can be introduced with the goal of ensuring that the resultant new molecules have high energy densities.
N– moiety to form new energetic molecules, which have higher ρ and OB. Considering that the pyrazole, imidazole, 1,2,3-triazole and 1,2,4-triazole moieties have two or four positions that can be further modified, several energetic groups, such as nitroamine and azide functional groups, can be introduced with the goal of ensuring that the resultant new molecules have high energy densities.
Among them, the nitro group is considered to be one of the superior explosophores because of the favorable balance between stability and performance. In comparison, the nitroamino and azido functionalities tend to increase density and detonation properties; however, their molecular stabilities associated with thermal behavior and impact and friction sensitivity are not competitive with those of their nitro-functionalized analogues.34 Therefore, in the third phase, to further enhance the energy level, two or four nitro groups were introduced via C-functionalization. All the designed target compounds have N10 structures (contain 10 nitrogen atoms). Additionally, compounds C and E have 8 and 10 catenated nitrogen atoms in their structures, respectively.
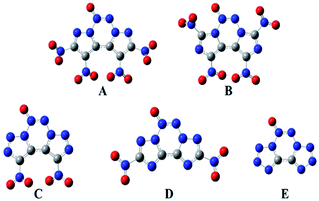
The geometric structures of all the compounds were optimized based on the true local energy minima on the potential energy surface without imaginary frequencies. To help understand the geometric constructions, the optimized structures of A–E are shown in Fig. 2. The surface analyses of A–E are summarized in the ESI.† From Fig. 2, it can be seen that compound D remained coplanar after substitution with nitro groups. However, after nitration of the precursor compounds of A–C, the nitro group and the ring formed a dihedral angle in the range of 35–85°, which may improve their crystal packing. The three heterocycles in the fused tricyclic system and N→O bond were co-planar, whereas the nitro groups deviated from the ring plane, implying that their electronic properties play an important role in their molecular structure.
Electrostatic potentials and frontier molecular orbital energies
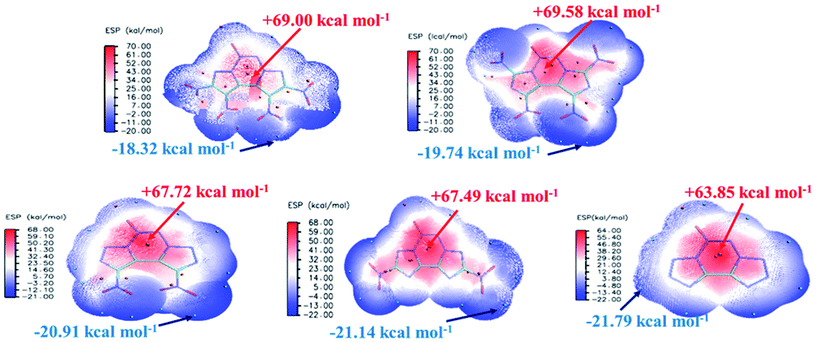
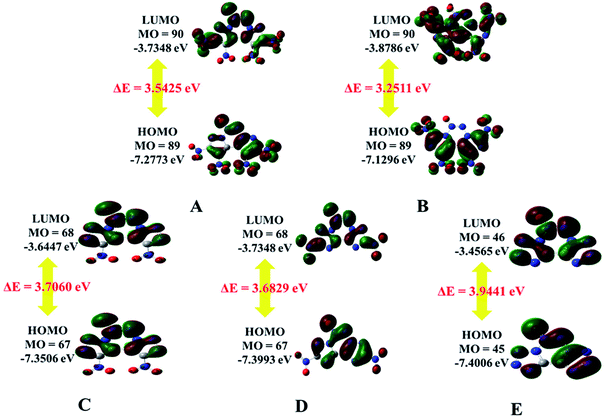
The electrostatic potential (ESP) on a molecular surface can help understand its intermolecular interaction and can also help predict its chemically reactive sites.35 The ESP mapped van der Waals surfaces of compounds A–E are shown in Fig. 3. Only the global minima and maxima on their surfaces are labelled in bold font. The surface areas in each ESP range are plotted in the ESI.† It can be seen that in the A–E unit region, the surface minima of ESP are observed between the oxygen atoms, especially the oxygen atoms of the nitro group bonded to the carbon atom, because of their higher electronegativity, and these are the primary electrophilic sites. The global maxima of ESP on the A–E surfaces range from +63.85 to +69.58 kcal mol−1, corresponding to 1,2,3,4-tetrazine, whereas minima from −18.32 to −21.79 kcal mol−1 correspond to the oxygen atoms of the nitro group. The strongly positive ESP surface (red) is prominent in the center of the molecule, whereas the negative ESP surface (blue) primarily caused by electron-withdrawing groups (–NO2) is in the surrounding of the molecule. These observations are consistent with the atomic charges obtained from the subsequently mentioned natural bond orbital analysis.The highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs) are named as frontier molecular orbitals (FMOs). The energy gap between the HOMO and the LUMO (ΔE) is an important parameter to evaluate molecular stability, especially for compounds with similar skeletons.36,37 A small ΔE value can lead to enhanced reactivity and poor stability with respect to chemical and photochemical processes.38 For example, it causes electrons to transition from the HOMO to LUMO easily, thus leading to the molecule becoming less stable. The HOMOs and LUMOs including the energy gap are depicted in Fig. 4. The red color represents the positive phase, and the green color represents the negative phase. As can be seen from Fig. 4, the HOMOs of all the molecules are localized approximately on the fused tricyclic structure. In addition, ΔE of E (3.9441 eV) is the largest and that of B (3.2511 eV) is the smallest, indicating that the former is more stable than the latter. All the compounds are complete nitrification products (except for E), which indicates that the more nitro groups they possess, the less stable they are. Again, the magnitudes imply that the predicted sequence of stability is B < A < D < C < E, and the order is reversed for the chemical activity of the title compounds.
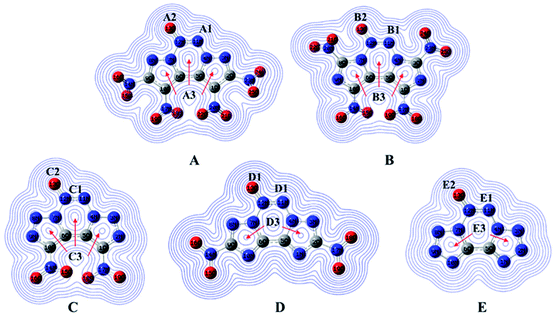
Natural bond orbital charges and electronic density
Natural bond orbital charges (NBO) can provide useful information on the distribution of charges and other chemical properties. Generally, high peaks correspond to the nuclear charge of a heavy nucleus, which improves electron aggregation and displays integral exponential attenuation towards all surrounding atoms.39 The Multiwfn program was used to calculate density, and the contour line maps of the electronic density on A–E are shown in Fig. 5. The electron densities around oxygen and nitrogen atoms are higher than those around other atoms due to their strong electronegativity. Generally, electrons prefer to assemble in the bonding area (such as A1, B1, C1, D1 and E1) because of electron pair sharing between atoms bonded covalently. The electron densities around the oxygen and nitrogen atoms are higher than those around other atoms due to strong electronegativity; the electron densities around O13 are higher than those around other atoms (A2, B2, C2, D2 and E2). Moreover, delocalization also occurs in the fused tricyclic structure, marked as A3 to E3, which may improve the stability of the ring skeleton as well as the molecular structure. To fully investigate the interactions among bonds, their NBO charges40 are summarized in Table 1. Clearly, atom O13 is the most negative since N→O is a strong electron-withdrawing group. The nitro group accommodates higher positive charges because of its strong electronegativity and thus, it attracts electrons towards itself.| A | B | C | D | E | |||||
|---|---|---|---|---|---|---|---|---|---|
| Atom | Charge | Atom | Charge | Atom | Charge | Atom | Charge | Atom | Charge |
| 1C | 0.03844 | 1C | 0.28245 | 1C | 0.24662 | 1N | −0.40933 | 1N | −0.24324 |
| 2C | 0.29824 | 2N | −0.38239 | 2N | −0.18982 | 2C | 0.45835 | 2N | −0.02998 |
| 3N | −0.20285 | 3C | 0.50248 | 3N | −0.00817 | 3C | −0.21354 | 3N | −0.02525 |
| 4N | −0.00205 | 4N | −0.20611 | 4N | −0.02386 | 4C | −0.02407 | 4N | −0.05047 |
| 5C | 0.14488 | 5C | 0.11291 | 5C | 0.09983 | 5N | 0.31421 | 5C | 0.28917 |
| 6C | 0.15709 | 6C | 0.14506 | 6C | 0.14005 | 6C | 0.36744 | 6C | 0.32211 |
| 7N | −0.04202 | 7N | −0.25574 | 7N | −0.06589 | 7N | −0.06832 | 7N | −0.08171 |
| 8N | −0.19494 | 8C | 0.51418 | 8N | 0.00147 | 8N | −0.2087 | 8N | −0.01435 |
| 9C | 0.30618 | 9N | −0.37411 | 9N | −0.17363 | 9C | 0.47063 | 9N | −0.01277 |
| 10C | 0.04704 | 10C | 0.27497 | 10C | 0.2432 | 10N | −0.41328 | 10N | −0.24403 |
| 11N | −0.03583 | 11N | −0.02563 | 11N | −0.03352 | 11N | −0.04001 | 11N | −0.03935 |
| 12N | 0.44867 | 12N | 0.45913 | 12N | 0.45146 | 12N | 0.44692 | 12N | 0.44751 |
| 13O | −0.30751 | 13O | −0.32551 | 13O | −0.30624 | 13O | −0.31165 | 13O | −0.31763 |
| 14N | 0.48666 | 14N | 0.48966 | 14N | 0.48942 | 14N | 0.47294 | — | — |
| 15O | −0.33272 | 15O | −0.36947 | 15O | −0.35975 | 15O | −0.3218 | — | — |
| 16O | −0.30991 | 16O | −0.31006 | 16O | −0.31203 | 16O | −0.32883 | — | — |
| 17N | 0.50622 | 17N | 0.48938 | 17N | 0.48809 | 17N | 0.47248 | — | — |
| 18O | −0.35162 | 18O | −0.30994 | 18O | −0.37328 | 18O | −0.33522 | — | — |
| 19O | −0.31271 | 19O | −0.37635 | 19O | −0.31393 | 19O | −0.3282 | — | — |
| 20N | 0.50409 | 20N | 0.47744 | — | — | — | — | — | — |
| 21O | −0.31787 | 21O | −0.32654 | — | — | — | — | — | — |
| 22O | −0.36784 | 22O | −0.30204 | — | — | — | — | — | — |
| 23N | 0.48726 | 23N | 0.47074 | — | — | — | — | — | — |
| 24O | −0.31447 | 24O | −0.34369 | — | — | — | — | — | — |
| 25O | −0.33242 | 25O | −0.31082 | — | — | — | — | — | — |
Infrared spectra
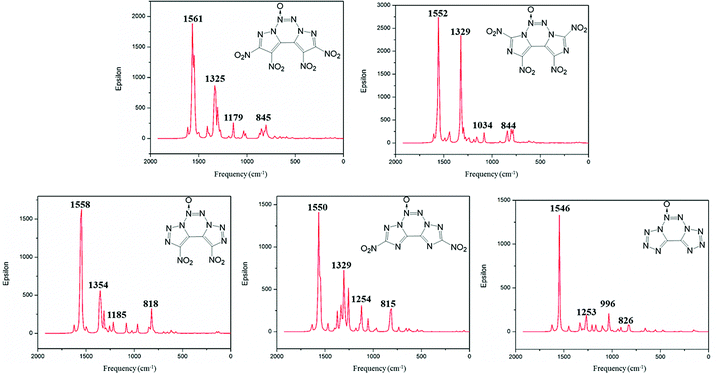
Infrared spectrum (IR) is useful to identify the functional groups of substances. The simulated infrared spectra of A–E are shown in Fig. 6; the horizontal axis represents frequency, and the vertical axis denotes intensity. The frequency value obtained from the DFT calculations is scaled down by a factor of 0.9668.41 The calculated IR results show that the most intense IR peaks are observed at 1561, 1552, 1558, 1550 and 1546 cm−1 for compounds A–E, respectively, which correspond to the stretching vibration of their N→O bonds. The symmetric and asymmetric stretching vibrations of the N–O bond in the nitro groups of compounds A–D vary in the range from 1522 to 1570 cm−1, and these values are very close to those of the stretching vibrations of the N→O bond. Meanwhile, the peaks at 845, 844, 818 and 815 cm−1 correspond to the vibrations of torsion for the nitro group in compounds A–D. The medium intense peaks in the range from 1000 to 1300 cm−1 are mainly due to the stretching vibrations of C–N and N–N bonds in the fused tricyclic skeleton. For compound E, the weak peaks near 826 cm−1 are mainly ascribed to the asymmetric stretching vibration of the tetrazole backbone.Heat of formation
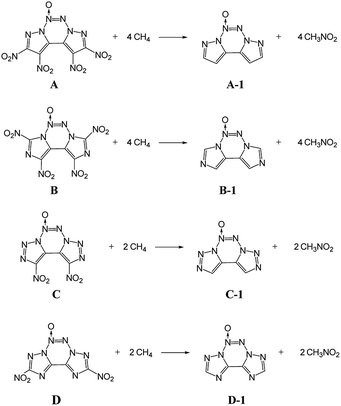
ΔHf,solid is an important property for predicting the detonation properties of energetic materials. Therefore, to estimate D and P of an explosive molecule through theoretical calculations, the ΔHf,solid value must be obtained. To obtain more accurate calculation results, the basic ring skeleton of the parent compound was kept invariable during the designed isodesmic reactions. The designed isodesmic reactions used to obtain ΔHf,gas for the investigated compounds are shown in Scheme 1.Table 2 lists the total energies (E0), ZPEs, thermal corrections (HT), and ΔHf,gas for the reference compounds in the isodesmic reactions. The ΔHf,gas value of each compound was calculated from the atomization reaction at the G2 level. Table 3 summarizes the calculated ΔHf,solid values and the parameters related to ΔHf,solid of all the designed compounds. It has been found that all the title compounds have positive ΔHf,solid values over 580 kJ mol−1 due to a large number of inherently energetic CN and NN bonds in their structures. Among them, compound E has the largest ΔHf,solid of 1092.8 kJ mol−1 due to the ten-nitrogen catenated chain in its structure. Besides, upon comparing these compounds, ΔHf,solid can be summarized as follows: B < A < D < C < E, which indicates that ΔHf,solid is strongly influenced by the length of the nitrogen chains and slightly affected by the number of nitro groups. It is worth noting that the introduction of the azoxy moiety leads to a decrease in ΔHf,solid of this non-hydrogen-containing 5/6/5 fused tricyclic structure. Clearly, compounds A and E have the ΔHf,solid values of 678.06 and 753.81 kJ mol−1, which are reduced to 80 and 34 kJ mol−1, respectively, compared to their non-azoxy structures.8,9
| Comp. | E0 (a.u.) | ZPE (kcal mol−1) | HT (kJ mol−1) | ΔfH (gas) (kJ mol−1) |
|---|---|---|---|---|
| CH4 | −40.38 | 28.11 | 10.01 | −74.62 |
| CH3NO2 | −244.49 | 31.28 | 13.91 | −81.00 |
| A-1 | −633.07 | 70.77 | 25.89 | 783.79 |
| B-1 | −633.07 | 71.17 | 24.68 | 691.53 |
| C-1 | −665.07 | 55.08 | 25.39 | 993.75 |
| D-1 | −665.14 | 56.25 | 25.01 | 834.95 |
| Comp. | ΔHf,gasa (kJ mol−1) | ΔHsubb (kJ mol−1) | ΔHf,solidc (kJ mol−1) | E0 (a.u.) | ZPE (kcal mol−1) | HT (kJ mol−1) |
|---|---|---|---|---|---|---|
| a Calculated gas-phase heat of formation.b Heat of sublimation.c Calculated solid-phase heat of formation. | ||||||
| A | 813.85 | 135.79 | 678.06 | −1449.74 | 76.39 | 53.69 |
| B | 721.59 | 137.86 | 583.73 | −1449.77 | 76.14 | 53.65 |
| C | 1023.81 | 107.31 | 916.5 | −1073.25 | 58.28 | 38.37 |
| D | 865.01 | 111.20 | 753.81 | −1073.54 | 58.96 | 38.31 |
| E | 1172.43 | 79.63 | 1092.8 | −697.09 | 40.34 | 23.64 |
Thermodynamic properties are important for explosives; they are used to describe a chemical system that neither consumes nor releases heat energy and to predict thermal stability in a chemical reaction. On the basis of vibrational analysis and the statistic thermodynamic method, the thermodynamic functions such as thermal correction to internal energy (U), enthalpy (H), free energy (G), standard molar heat capacity (Cv) and standard molar thermal entropy (S) as well as zero-point energy (ZPE) of all the compounds are evaluated and tabulated in Table 4. All these values are obtained at 298.15 K, 1.00 atm. and calculated in units of kcal mol−1 (kcal mol−1 K−1 for S and Cv).
| Comp. | ZPE (kcal mol−1) | U (kcal mol−1) | H (kcal mol−1) | G (kcal mol−1) | S (kcal mol−1 K−1) | Cv (kcal mol−1 K−1) |
|---|---|---|---|---|---|---|
| A | 76.39307 | 88.63139 | 88.632 | 44.12901 | 151.250 | 69.073 |
| B | 76.14081 | 88.37098 | 88.371 | 44.27334 | 149.891 | 69.218 |
| C | 58.27623 | 66.85492 | 66.855 | 31.69867 | 119.900 | 49.940 |
| D | 58.96021 | 67.5251 | 67.525 | 31.45206 | 122.978 | 49.389 |
| E | 40.34325 | 45.40098 | 45.401 | 19.10517 | 90.184 | 30.818 |
Density
Generally, high density results in higher performance.18,42 For example, D of an explosive is proportional to its ρ, and P is proportional to the square of its ρ.43 For an energetic material, a high value ρ means that more energy per unit volume can be packed into a volume-limited space, thereby yielding maximum violent explosion. The molecular volumes, uncorrected densities, and corrected densities are listed in Table 5. The ρ values for the designed compounds were found to be in the range from 1.91 (E) to 199 g cm−3 (A). Among them, compound A exhibited the highest density of 1.99 g cm−3, which was similar to that of CL-20. Clearly, the replacement of the azo moiety with the azoxy moiety led to greater increase in density. This finding illustrated that the incorporation of highly dense groups into high-density skeletons is an effective strategy for obtaining higher density compounds. Overall, all the compounds exhibited higher calculated densities of >1.9 g cm−3 due to the presence of the N→O moiety, indicating that these compounds have potential as new HEDMs.| Comp. | Mw (g mol−1) | Volume (cm3 mol−1) | ρuncorrected (g cm−3) | ρcorrected (g cm−3) |
|---|---|---|---|---|
| A | 356.13 | 178.96 | 2.01 | 1.99 |
| B | 356.13 | 180.23 | 1.98 | 1.97 |
| C | 268.11 | 137.49 | 1.96 | 1.95 |
| D | 268.11 | 138.20 | 1.95 | 1.94 |
| E | 180.09 | 95.29 | 1.93 | 1.91 |
Oxygen balance and detonation performance
Oxygen balance, which indicates the degree to which an explosive can be oxidized, is an important index for identifying the potential of energetic materials as explosives or oxidants. Positive OBs indicate that there is sufficient oxygen to convert all the carbon to carbon monoxide and all the hydrogen to water, whereas negative values indicate that the oxygen content is insufficient for complete oxidation. However, too much oxygen is not favorable for improving the explosive performance of energetic compounds as additional oxygen will produce O2, which consumes a considerable amount of energy during the explosion of energetic materials. Thus, the ideal OB value is equal to zero. All the compounds exhibited OB values between −13.68 and −26.65% mainly due to their relatively high carbon contents. By comparison, the incorporation of more –NO2 groups into a molecule substantially improves its ΔHf,solid and OB, eventually resulting in higher exothermicities for combustion and detonation processes.Detonation velocity and pressure are two important performance parameters for an energetic material. Based on the calculated ΔHf,solid and ρ, the detonation properties of A–E were determined using the EXPLO5 (v 6.01) program,28 as summarized in Table 6 together with a comparison with common explosives. As shown in Table 6, the calculated D values were in the range of 9616–9943 m s−1, and they were remarkably higher than those of RDX (8983 m s−1) and HMX (9221 m s−1). Among the compounds, E exhibited the highest D (9943 m s−1), which exceeded that of CL-20 (9673 m s−1). In terms of P, the P values of the designed compounds were in the range from 41.1 (D) to 44.2 GPa (C). The highest P value (C, 44.2 GPa) was much larger than those of RDX (34.9 GPa) and HMX (39.6 GPa). Overall, the detonation properties of A–E were accordingly predicted to be second only to that of CL-20, and these compounds might be the most powerful energetic materials among the CHNO-containing organic compounds.
| Comp. | Na (%) | OBb (%) | Dc (m s−1) | Pd (GPa) | Qe (kJ kg−1) | Tdetf (K) |
|---|---|---|---|---|---|---|
| a Nitrogen content.b Oxygen balance for CaHbOcNd: 1600 × (c − a − b/2)/Mw, where Mw = molecular weight.c Detonation velocity.d Detonation pressure.e Heat of detonation.f Explosion temperature. | ||||||
| A | 39.33 | −13.48 | 9780 | 44.1 | 6335 | 4785 |
| B | 39.33 | −13.48 | 9614 | 42.2 | 6082 | 4656 |
| C | 52.24 | −17.90 | 9858 | 44.2 | 6553 | 4982 |
| D | 52.24 | −17.90 | 9616 | 41.1 | 6007 | 4631 |
| E | 77.78 | −26.65 | 9543 | 40.7 | 6920 | 5223 |
| RDX15 | 37.84 | −21.26 | 8983 | 38.0 | 6190 | 4232 |
| HMX15 | 37.84 | −21.26 | 9221 | 41.5 | 6185 | 4185 |
| CL-20 (ref. 44) | 38.36 | −10.96 | 9673 | 44.9 | 6130 | — |
Stability
The sensitivity of an energetic material generally refers to its vulnerability to accidental explosion caused by unintended stimuli, and it is directly related to the handling safety as well as potential application.45 The impact sensitivity, as the most commonly used method for assessing the sensitivities of explosives, is measured by the drop height, h50%, where the shorter the drop height, the greater the impact sensitivity. It has been found that impact sensitivity has several strong correlations with various molecular properties.19,46 Using four empirical models based on the properties of electrostatic potential and heat of detonation, as proposed by Rice and Hare,31 the h50% values were estimated, and the results are summarized in Table 7. Methods 1–3 showed relatively consistent results, whereas method 4 overestimated the impact sensitivities derived from the hybrid balance parameter and detonation heat. The h50% values of compounds A and B were even close to that of CL-20, indicating that these two compounds are very sensitive and can be easily triggered by external stimuli such as impact. This may be because these molecules contain four strong electron-withdrawing groups, –NO2, thereby reducing their stabilities to a certain extent. Compounds C–E exhibited relatively acceptable impact sensitivities with the h50% values of about 30 cm, which were comparable with those of RDX (26 cm) and HMX (32 cm). Because of the complexity of the impact sensitivity, these estimates should be regarded as suggestive rather than conclusive results.| Comp. | Bond | Wiberg bond order | BDE (kJ mol−1) | −QNO2 (e) | h50% a (cm) | h50% b (cm) | h50% c (cm) | h50% d (cm) | Exp. | EES (J) |
|---|---|---|---|---|---|---|---|---|---|---|
a Method 1 is related to the GIPF parameters |![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) + − | + − |![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) −||.b Method 2 is related to the GIPF balance parameter ν.c Method 3 is related to the heat of detonation Q.d Method 4 is related to the hybrid model using Q and ν. −||.b Method 2 is related to the GIPF balance parameter ν.c Method 3 is related to the heat of detonation Q.d Method 4 is related to the hybrid model using Q and ν. |
||||||||||
| A | C1–NO2 | 1.075 | 264.68 | 0.19 | 19 | 29 | 30 | 5 | — | 2.9 |
| C2–NO2 | 1.040 | 236.85 | 0.22 | 2.5 | ||||||
| C9–NO2 | 1.039 | 223.91 | 0.22 | 3.1 | ||||||
| C10–NO2 | 1.060 | 254.76 | 0.14 | 3.2 | ||||||
| B | C1–NO2 | 1.066 | 270.58 | 0.26 | 21 | 29 | 32 | 5 | — | 6.3 |
| C3–NO2 | 1.061 | 266.82 | 0.26 | 5.4 | ||||||
| C8–NO2 | 1.040 | 223.91 | 0.29 | 4.5 | ||||||
| C10–NO2 | 1.067 | 271.32 | 0.24 | 5.1 | ||||||
| C | C1–NO2 | 1.077 | 257.33 | 0.25 | 42 | 30 | 34 | 7 | — | 8.6 |
| C10–NO2 | 1.070 | 255.22 | 0.23 | 9.2 | ||||||
| D | C2–NO2 | 1.0488 | 264.68 | 0.25 | 58 | 30 | 36 | 7 | — | 10.2 |
| C9–NO2 | 1.040 | 263.89 | 0.24 | 9.4 | ||||||
| E | — | — | — | — | 88 | 30 | 45 | 9 | — | — |
| RDX | 49 | 31 | 39 | 22 | 28 | — | ||||
| HMX | 21 | 31 | 41 | 22 | 32 | — | ||||
| CL-20 | 16 | 29 | 29 | 3 | 14 | — | ||||
BDEs can provide useful information for understanding the stability of a molecule.29 Generally, smaller BDE corresponds to a weaker bond, which makes it easier for the bond to function as a trigger bond. To investigate the thermal stabilities of the compounds of interest, the C–NO2 bond was considered to be the weakest bond.36,37 In general, if BDE > 80 kJ mol−1, then the compound can be considered as a practical energetic material; otherwise, if BDE > 120 kJ mol−1, then it can be considered as an excellent energetic material, which meets the stability requirements of HEDMs. Compared with TNT (251.16 kJ mol−1), RDX (160.09 kJ mol−1) and TATB (305.79 kJ mol−1), all the designed compounds possess high BDEs and fulfill the requirements of HEDMs.47 Furthermore, by comparing the BDEs of the title compounds, it is observed that the number of nitro groups and substituted positions have strong influence on the BDEs. The computed Wiberg bond order values, −QNO2 values, and trigger lengths of the molecules are summarized in Table 7. The higher the negative charge of the nitro group, the weaker its electron-withdrawing ability and the greater the overall stability of the compound, which lowers its impact sensitivity. Wiberg bond order values also reflect the strength of a trigger bond, where a large Wiberg bond order value indicates that the bond is difficult to rupture and thus, the molecule is stable. The calculated −QNO2 values vary from 0.14 to 0.29 eV, and they are found to be higher than those of CL-20 (0.08 eV), HMX (0.11 eV) and RDX (0.13 eV),48 suggesting that these compounds have very low sensitivity.
Potential HEDM candidates
It is well-known that a good nitrogen-rich HEDM candidate should have not only excellent detonation properties but also good stability. Fig. 7 presents the detonation velocity and pressure, density and impact sensitivity used to evaluate the overall performance of the azoxy-fused tricyclic compounds compared with those of RDX, HMX and CL-20. As far as we know, the challenges in the development of HEDMs include the search for materials with higher performance, better safety, and improved environmental compatibility. However, in most cases, stability decreases as the energy increases. It can be shown that all azoxy-fused tricyclic compounds show relatively high densities and detonation properties when compared with commonly used explosives such as RDX, HMX and CL-20.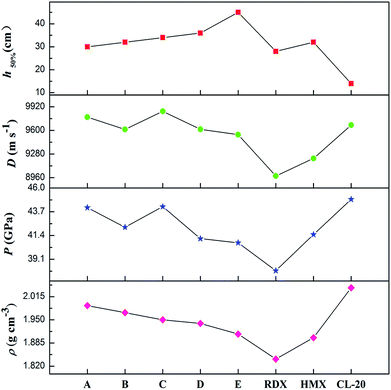 | ||
| Fig. 7 Overall performances of the azoxy-fused tricyclic compounds compared with those of RDX, HMX and CL-20. | ||
This is mainly because these compounds have very high positive ΔHf,solid as nitrogen-rich molecules. Among all the designed compounds, A has the highest ρ value (1.99 g cm−3), whereas it has the lowest h50% value, which limits its application in the future. For compound E, although it has good stability, its energetic properties (P: 40.7 GPa and D: 9543 m s−1) are disadvantageous compared to those of the other four compounds. Fortunately, it is surprising that compounds B–D perform better than HMX similar to CL-20, which results in relative balance between detonation properties and stability. Therefore, B–D may be considered as potential HEDM candidates with improved stability and performance.
Conclusion
In summary, we systematically investigated the molecular structures, electronic structures, heats of formation, energetic properties, and thermal stabilities of five novel azoxy non-hydrogen-containing 5/6/5 fused tricyclic compounds. Their optimized molecular geometries showed that two five-membered azole heterocycles are fused to 1,2,3,4-tetrazine with a common C–N bond. In addition, the three heterocycles in the fused tricyclic system and the N→O bond were coplanar, whereas the nitro groups deviated from the ring plane, implying that their electronic properties play an important role in their molecular structures. Additionally, the surface minima and maxima of ESP displayed a visual representation of their chemically active sites. The theoretical IR spectra data were simulated to confirm the identification of the target compounds. The effects of different skeleton structures on the density, heat of formation, denotation velocity and pressure well as stability of the novel azoxy non-hydrogen-containing 5/6/5 fused tricyclic compounds were also investigated. When the length of the catenated nitrogen chain was elongated in their molecular structures, the heat of formation increased. Among these compounds, compound E exhibited the highest heat of formation of 1092.8 kJ mol−1, and A exhibited the highest density of 1.99 g cm−3.The critical energetic properties and stabilities of all the compounds have been estimated. Their densities range from 1.91 to 1.99 g cm−3. Compared with the azo non-hydrogen-containing 5/6/5 fused compounds, the compounds containing the azoxy moiety can enhance density effectively. However, the azoxy moiety is not beneficial for obtaining energetic molecules with high positive heat of formation in this system, which indicates that the azoxy moiety has both positive and negative effects on their properties, i.e., high densities are obtained, but the heats of formation are low. All the compounds show higher detonation velocities (9543-9858 m s−1) and pressures (40.7–44.1 GPa). By comprehensive analysis, we infer that compounds B–D perform better than HMX similar to CL-20, which results in a relative balance between detonation properties and stability. Therefore, compounds B–D may be considered as potential HEDM candidates with improved stability and performance. In addition, our design strategy, involving the combination of the azoxy moiety and fused tricyclic skeleton for the construction of nitrogen-rich molecular structures with high density and positive HOFs, is a valuable approach for the development of novel HEDMs with excellent performance and stability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (Grant No. 21576026, 21702017).Notes and references
- T. G. Witkowski, E. Sebastiao, B. Gabidullin, A. Hu, F. Zhang and M. Murugesu, ACS Appl. Energy Mater., 2018, 1, 589–593 CrossRef.
- D. E. Chavez, S. K. Hanson, J. M. Veauthier and D. A. Parrish, Angew. Chem., Int. Ed., 2013, 52, 6876–6879 CrossRef PubMed.
- C. L. He, H. X. Gao, G. H. Imler, D. A. Parrish and J. M. Shreeve, J. Mater. Chem. A, 2018, 6, 9391–9396 RSC.
- T. M. Klapötke, P. C. Schmid, S. Schnell and J. Stierstorfer, Chem.–Eur. J, 2015, 21, 9219–9228 CrossRef PubMed.
- M. S. Klenov, A. A. Guskov, O. V. Anikin, A. M. Churakov, Y. A. Strelenko, I. V. Fedyanin, K. A. Lyssenko and V. A. Tartakovsky, Angew. Chem., Int. Ed., 2016, 55, 11472–11475 CrossRef PubMed.
- D. G. Piercey, D. E. Chavez, B. L. Scott, G. H. Imler and D. A. Parrish, Angew. Chem., Int. Ed., 2016, 55, 15315–15318 CrossRef PubMed.
- T. M. Klapötke, P. C. Schmid, S. Simon and J. Stierstorfer, Chem.–Eur. J., 2015, 21, 9219–9228 CrossRef PubMed.
- D. E. Chavez, J. C. Bottaro, M. Petrie and D. A. Parrish, Angew. Chem., Int. Ed., 2015, 54, 12973–12975 CrossRef PubMed.
- Y. Tang, D. Kumar and J. M. Shreeve, J. Am. Chem. Soc., 2017, 139, 13684–13687 CrossRef PubMed.
- P. Yin, J. Zhang, G. H. Imler, D. A. Parrish and J. M. Shreeve, Angew. Chem., Int. Ed., 2017, 56, 8834–8838 CrossRef PubMed.
- Y. Qu and S. P. Babailov, J. Mater. Chem. A, 2018, 6, 1915–1940 RSC.
- Y. Li, C. Qi, S. Li, H. Zhang, C. Sun, Y. Yu and S. Pang, J. Am. Chem. Soc., 2010, 132, 12172–12173 CrossRef PubMed.
- T. M. Klapötke and D. G. Piercey, Inorg. Chem., 2011, 50, 2732–2734 CrossRef PubMed.
- F. Boneberg, A. Kirchner, T. M. Klapötke, D. G. Piercey, M. J. Poller and J. Stierstorfer, Chem.–Asian J., 2013, 8, 148–159 CrossRef PubMed.
- D. Fischer, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, Chem.–Eur. J., 2013, 19, 4602–4613 CrossRef PubMed.
- A. A. Dippold, D. Izsák and T. M. Klapötke, Chem.–Eur. J., 2013, 19, 12042–12051 CrossRef PubMed.
- J. Zhang and J. M. Shreeve, J. Phys. Chem. C, 2015, 119, 12887–12895 CrossRef.
- M. A. Kettner, K. Karaghiosoff, T. M. Klapötke, M. Sućeska and S. Wunder, Chem.–Eur. J., 2014, 20, 7622–7631 CrossRef PubMed.
- J. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437–4445 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Peterssonand et al., Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, U.K., 1982 Search PubMed.
- P. Politzer and J. S. Murray, Cent. Eur. J. Energ. Mater., 2011, 8, 209–220 Search PubMed.
- P. Politzer, P. Lane and J. S. Murray, Cent. Eur. J. Energ. Mater., 2011, 8, 39–52 Search PubMed.
- E. F. C. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005–1013 CrossRef PubMed.
- M. Jaidann, S. Roy, H. Abou-Rachid and L. Lussier, J. Hazard. Mater., 2010, 176, 165–173 CrossRef PubMed.
- F. Wang, H. Du, J. Zhang and X. Gong, J. Phys. Chem. A, 2011, 115, 11852–11860 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef PubMed.
- M. Sućeska, EXPLO5, version 6.01, Brodarski Institute, Zagreb, Croatia, 2013 Search PubMed.
- S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef PubMed.
- P. He, J. Zhang, L. Wu, J. Wu and T. Zhang, J. Phys. Org. Chem., 2017, 30, e3674 CrossRef.
- B. M. Rice and J. J. Hare, J. Phys. Chem. A, 2002, 106, 1770–1783 CrossRef.
- Q. Zhang, J. Zhang, X. Qi and J. M. Shreeve, J. Phys. Chem. A, 2014, 118, 10857–10865 CrossRef PubMed.
- Z. Chunyan, C. Xinlu and Z. Feng, Propellants, Explos., Pyrotech., 2010, 35, 555–560 CrossRef.
- P. Yin and J. M. Shreeve, Angew. Chem., Int. Ed., 2015, 54, 14513–14517 CrossRef PubMed.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 153–163 Search PubMed.
- T. Schmalz, W. A. Seitz, D. J. Klein and G. Hite, J. Am. Chem. Soc., 1988, 110, 1113–1127 CrossRef.
- Z. Zhou and R. G. Parr, J. Am. Chem. Soc., 1989, 111, 7371–7379 CrossRef.
- H. Dong and F. Zhou, High energy explosives and correlative physical properties, Science Press, Beijing, 1989 Search PubMed.
- P. He, J. Zhang, K. Wang, X. Yin, X. Jin and T. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 5840–5848 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42 Search PubMed.
- T. Zhang, L. Liu, C. Li, Y. Zhang, Z. Li and S. Zhang, J. Mol. Struct., 2014, 1067, 195–204 CrossRef.
- T. Fei, Y. Du and S. Pang, RSC Adv., 2018, 8, 10215–10227 RSC.
- J. Zhang, H. Su, Y. Dong, P. Zhang, Y. Du, S. Li, M. Gozin and S. Pang, Inorg. Chem., 2017, 56, 10281–10289 CrossRef PubMed.
- D. Fischer, J. L. Gottfried, T. M. Klapötke, K. Karaghiosoff, J. Stierstorfer and T. G. Witkowski, Angew. Chem., Int. Ed., 2016, 55, 16132–16135 CrossRef PubMed.
- A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–15 CrossRef PubMed.
- F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691 CrossRef PubMed.
- Q. Ma, T. Jiang, X. Zhang, G. Fan, J. Wang and J. Huang, J. Phys. Org. Chem., 2015, 28, 31–39 CrossRef.
- Y. Shu, H. Li, S. Gao and Y. Xiong, J. Mol. Model., 2013, 19, 1583–1590 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of surface analysis and natural population analysis of compound A–E. See DOI: 10.1039/c8ra05274c |
| This journal is © The Royal Society of Chemistry 2018 |