Vibrational properties of isotopically enriched materials: the case of calcite

Abstract

Isotope enrichment is widely used to affect atomic masses, facilitating data acquisition and peak assignments in experiments such as nuclear magnetic resonance and infrared spectroscopy. It is also used for elucidating the origin of weak features in systems where natural isotopic abundances are low. However, it is not possible to always know a priori precisely how vibrational modes change for arbitrary levels of isotopic substitution. Here, we examine this issue by presenting a joint experimental and theoretical study for the important case of ¹³C isotope substitution effects on the infrared spectra of calcite. By systematically varying the ¹³C : ¹²C ratio, we find that the relative positions and intensities of infrared-active vibrational modes can vary, in a non-linear and mode-dependent fashion, with minority isotope content and proximity. This allows us to determine the origin of weak spectral features due to the natural abundance of isotopes and to show that even relatively low levels of substitution are not necessarily within the “dilute limit,” below which isotopic substitutions do not interact.

---

1 Introduction

Isotopic enrichment presents unique and useful opportunities for characterizing the structure and properties of solid materials.^1,2 Isotopic substitution, often known as labeling, affects the atomic mass without introducing changes to the electronic properties of the atoms. This means that it has a significant effect on vibrational properties, as well as any property related to vibrations, such as phonon-mediated superconductivity.³ Isotopic can also affect nuclear magnetic resonance data, by changing the gyromagnetic ratio to increase the sensitivity of the method and dramatically reduce acquisition times.⁴

One important material that has been the subject of many measurements involving isotopic enrichment is calcite (CaCO₃ in the R3̄c structure). Calcite is abundant in natural environments and is of great importance for diverse disciplines, including biology,^5–9 archaeology,^10,11 geology,¹² and planetary science.¹³ In particular, there has been much interest in vibrational spectroscopy of calcite,^5–9 especially because the height and width of various spectral peaks have been shown to correlate with the degree of crystallinity and therefore with calcite origin and process of formation.^14–21 Isotope enrichment methodology was used for the study of calcite crystals with both solid-state nuclear magnetic resonance measurements^22,23 and vibrational spectroscopy.²⁴

Calcite has a natural abundance of isotopic substitution. However, its level is quite low, with a ¹³C : ¹²C ratio of 1% and an even lower ¹⁸O : ¹⁶O ratio of 0.1%.^25,26 Nevertheless, this isotopic presence can still influence the measured vibrational spectrum. Indeed, the origin of weak infrared (IR) spectral features in calcite has been a subject of considerable debate,²⁷ with suggested causes ranging from isotope shifts,^28–31 to a combination of vibration and lattice modes,^32–35 to energy splitting between longitudinal optical (LO) and transverse optical (TO) phonons arising from the carbonate moiety.^35,36

Isotopically-induced peak shifts were identified in the vibrational spectrum of calcite after synthetic enrichment to 50% ¹³C (ref. 28) or to 80% ¹⁸O (ref. 24). Isotopic effects were also studied computationally using density functional theory (DFT).^30,37 The computational studies showed significant (tens of wavenumbers) blue-shift of certain peaks upon complete substitution of all carbon atoms by the ¹³C isotope. Despite this effort, the origin of the above-mentioned weak IR spectral features was not fully elucidated, particularly because extrapolation from high isotopic content to low isotopic content in experimental data of calcite is complicated. Naively, for different isotopic enrichment levels, one could simply assume a linear interpolation between the two end members (calcite with 100% ¹²C or with 100% ¹³C), which is an assumption known in chemical alloys as Vegard's law.^38–40 However, this is not necessarily the case. First, due to the intermixing of smaller and larger masses, Vegard's law does not necessarily hold even if one assumes a uniform distribution of the isotopes. Second, Schauble et al. showed that there is a slight preference for the less-common isotopes of C and O to be found together in the same moiety,⁴¹ an effect known as “isotope clumping.”^42–44 Therefore, a complete analysis of the vibrational data requires a systematic examination of the isotopic effect as a function of isotope concentration, both experimentally and theoretically.

Here, we provide such a systematic examination, for ¹³C enrichment in calcite, by combining Fourier transform infrared (FTIR) spectroscopy with DFT simulations. We show that peak positions and intensity changes cannot be predicted from simple interpolation, based on explanations in terms of effective spring coupling. We also show which weak features discussed above can be assigned definitively to isotope shifts, including isotopic effects on LO–TO peaks. This leads to the conclusion that, even for relatively low levels of substitution, it is not necessarily reasonable to assume that the “dilute limit”, below which the isotopic substitutions do not interact, has been achieved. While these conclusions directly pertain to calcite, the approach is general and can be used for isotopic studies of other materials of interest.

2 Methods

2.1 Experimental approach

Calcite powders were synthesized using a solution-based method described elsewhere.²⁰ Briefly, 25 mL of 5 mM Na₂CO₃ (Sigma-Aldrich, ACS reagent grade) was placed in a flask and immersed in an ultrasonic bath at room temperature. 1 mL of 60 mM CaCl₂ (Sigma-Aldrich, ACS reagent grade) was added every 15 seconds for a total of 25 mL. The suspension was stored at 4 °C for one hour, then centrifuged for 15 minutes at 4200 rpm. The supernatant was then pipetted off. The residual product, comprised of calcite crystallites, was air-dried prior to measurement. To obtain calcite with different concentrations of ¹³C, the usual Na₂¹²CO₃ solution, in which the ¹³C concentration is ∼1%, was mixed with Na₂¹³CO₃ (Sigma-Aldrich) from a solution containing ∼99% ¹³C. Different mixtures of the two solutions allowed for the formation of calcite with different nominal ¹³C isotope concentrations: ∼100%, 50%, 25%, 12.5%, and 1%.

FTIR spectra were obtained using a Bruker Vertex 70v vacuum spectrometer (working pressure <100 Pa) over a wavenumber range of at least 4000 cm⁻¹ to 500 cm⁻¹, with a resolution of 1 cm⁻¹. Measurement in vacuum was essential for eliminating contributions from water vapor, especially in the spectral region containing the calcite v₃ peak. High resolution scans were important for resolving the shoulders on the v₃ absorbance peak and the weak 848 cm⁻¹ peak; a lower resolution (4 cm⁻¹) would have been insufficient for the analyses presented below. All measurements were carried out using a transmission geometry: the synthesized calcite was ground with spectral grade KBr and then pressed into 7 mm diameter pellets using 2 tons of pressure. Before the measurement, the pellets were heated to 350 °C in steps of 110 °C over the course of 3 hours, in order to eliminate the influence of water and other CaCO₃ polymorphs. Bruker's OPUS 7.0 software was used to determine peak positions, heights, widths, and areas.

2.2 Computational approach

Electronic structures, total energies, and geometries were calculated by solving the Kohn–Sham equations of DFT within the generalized gradient approximation (GGA), using the Perdew, Burke and Ernzerhof (PBE) exchange-correlation functional.⁴⁵ All calculations were carried out using the Vienna Ab Initio Simulation Package (VASP),⁴⁶ a plane wave basis code. The ionic cores were described by the projected augmented wave (PAW) method.^46,47

Calculations were performed based on the conventional hexagonal unit cell of calcite, which contains six units of the chemical formula, using different amounts and geometric arrangements of isotopic substitutions. The experimental structure used as a starting point for the geometry optimization of the unit cell was that of Maslen et al.⁴⁸ The planewave energy cutoff used for the calculations was 560 eV. A 7 × 7 × 2 k-point grid sampling of the Brillouin zone was used. All forces of the system were relaxed to 10⁻³ eV Å⁻¹. The optimized geometry (ESI Table 1†) is in excellent agreement with the experimental data: bond lengths and cell parameters are overestimated by ∼1.0–1.5%, a result typical for GGA-based calculations.⁴⁹

The simulation of IR spectra was carried out using an approach described in detail elsewhere.⁵⁰ Briefly, the frozen phonon method^51,52 was used to construct the dynamical matrix based on the variations in atomic forces due to explicit small displacements of the atoms from their equilibrium configuration. Vibrational frequencies and normal modes were then calculated within the harmonic approximation, from the (square root of) eigenvalues and eigenvectors of the dynamical matrix, respectively, evaluated at the Γ point of the Brillouin zone. The numerical precision of the calculated frequencies was better than 1.5 cm⁻¹. IR absorption intensities were calculated, within the framework of the modern theory of polarization,⁵³ based on the crystal response to an external electric field using the Born effective charge tensor.⁵⁴ Finally, in order to facilitate the comparison between experimental and computational data, the latter were broadened by convolution with a Lorentzian.

Longitudinal Optical–Transverse Optical (LO–TO) splittings were calculated using the Phonopy package,⁵⁵ which augments the supercell method using a mixed-space approach.^56,57 Following ref. 52 and 58, it is possible to separate contributions to the dynamical matrix from the Brillouin-zone center (analytical) and from long-range contributions due to dipole–dipole interactions, which depend on the direction of approach to the Brillouin-zone center (non-analytical).^52,58–60 Because calcite is a uniaxial crystal,^35,61 the IR-active modes of the carbonate moiety can be classified into modes with atomic motion along the z direction (v₂) and perpendicular to the z direction (v₁, v₃, v₄). Therefore, two directions of approach to the Γ point should be considered:³¹ the q(x, y) → 0 for the in-plane vibrations and q(z) → 0 for the out-of-plane vibrations. Total and partial phonon densities of states (DOS, PDOS) were also calculated using Phonopy on a 8 × 8 × 8 Γ-centered mesh, which was tested explicitly for convergence.

We note that there is a general tendency of the PBE functional to underestimate the binding energy within the material, which results in generally lower frequencies compared to experiment. In this work, all calculated frequencies are lower than the experimental frequencies by ≈40 cm⁻¹. However, since this is a systematic difference, it does not affect our analysis.

The main reason that we rely on the PBE functional, rather than a hybrid functional such as B3LYP, is that we are interested in peak position shifts due to isotopic substitutions; we do not focus on absolute wavenumber values. Comparing our experimental and calculated peak shifts (ESI Table 2†) shows that the deviation between PBE and experiment is low, on the order of a few wavenumbers, which is close to the experimental precision. Therefore, resorting to hybrid functional calculations (which are more expensive) was not necessary. Furthermore, a recent detailed study of calcite shows that hybrid functionals are more accurate than non-hybrid functionals for some properties, but not all.⁶² Thus, there is no universal reason to prefer a hybrid functional over PBE, even with respect to predictive power.

3 Results and discussion

3.1 Experimental observations of isotope effects

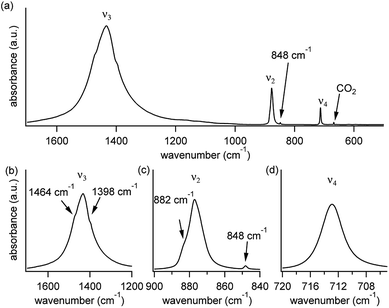
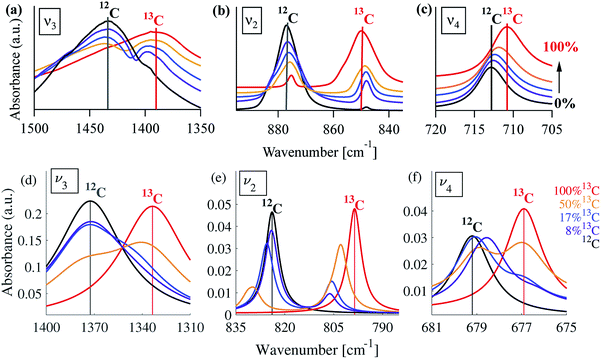
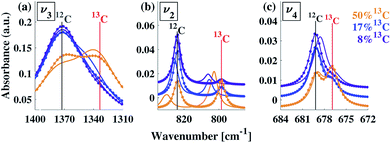
A typical FTIR spectrum of solution-precipitated calcite is shown in Fig. 1a. The mid-IR range exhibits three main absorbance peaks that are related to vibrations within the carbonate moiety:⁶¹ an asymmetric stretch (v₃, Fig. 1b), an out-of-plane bend (v₂, Fig. 1c), and an in-plane bend (v₄, Fig. 1d). Interestingly, there are additional weaker spectral features. Two small shoulders appear on either side of the v₃ peak (Fig. 1b), and the v₂ peak has a blue-shifted shoulder as well as a weak absorbance feature on the low wavenumber tail (Fig. 1c). These features, although small, exceed the noise level and are consistent with previously reported high-resolution IR spectra of calcite.^21,28,36

Fig. 1 (a) A typical IR spectrum of solution-precipitated calcite, exhibiting three main carbonate-related vibrational modes: v₃ (asymmetric stretch), v₂ (out-of-plane bending), and v₄ (in-plane bending). The weak (gas-phase) CO₂ peak is not related to the calcite structure. Panels (b)–(d) focus on each of the three main peaks and reveal weaker, more subtle spectral features.

In order to understand whether the weak spectral features indeed originate from isotopic effects, FTIR spectra of samples with systematically increasing nominal ¹³C isotopic concentrations were measured. They are shown in Fig. 2a–c. The isotopic content affects each calcite vibrational mode differently. The v₃ and v₂ modes exhibit an additional peak that occurs at a wavenumber lower than that of the ¹²C parent peak. For the v₄ mode, the main peak shifts to lower wavenumbers with increasing ¹³C content. A detailed examination of the experimental IR peak positions shows that the intensity of the ¹³C peak increases with increasing ¹³C atomic content, as expected, and that there is a small shift (≤5 cm⁻¹) of the main peak position. Since the v₄ mode occurs in both IR and Raman spectra, this peak can be compared directly and it shows a similar trend in both (ESI Fig. 8†). For the high levels of isotopic enrichment, our experimental FTIR spectra are consistent with earlier available experimental²⁸ and theoretical^30,31 results. Importantly, we observe that the calcite peak positions do not change linearly as a function of the nominal ¹³C concentration.

Fig. 2 Experimental (a–c) and simulated (d–f) IR spectra corresponding to the three main calcite absorbance peaks, for various ¹³C concentrations. For the experimental data, the nominal ¹³C concentrations are 1% (black), 13% (purple), 25% (blue), 50% (orange), and 100% (red). For the simulated spectra, the ¹³C concentrations are 0% (black), 8% (purple), 17% (blue), 50% (orange), and 100% (red). A Lorentzian line shape has been assumed using a full-width half-maximum of 50, 10, and 2 cm⁻¹ for the v₃, v₂ and v₄ peak, respectively. In all panels, vertical lines serve as guides to the eye for peak positions at 1% or 0% (black) and 100% (red) ¹³C concentrations.

3.2 Calculated isotope effects

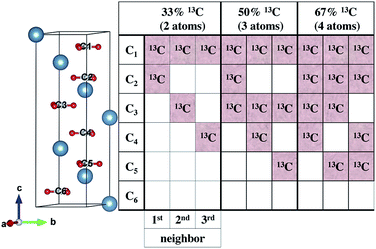
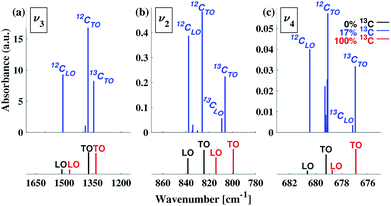
To understand our experimental IR data, we performed first principles calculations of the IR spectra of calcite structures, possessing different levels of ¹³C isotopic substitution. The results are shown in Fig. 2. The isotope containing structures were constructed by replacing selected ¹²C atoms by ¹³C atoms, simply by changing their mass, within the conventional hexagonal unit cell of calcite (for more details see ESI Table 3†).

When substituting ¹²C with ¹³C within a single unit cell, several nonequivalent substitutional arrangements exist. Thus, for all intermediate isotope levels wherein both ¹²C and ¹³C were present, we tested the influence of different geometric arrangements of the isotope sites within the unit cell. These are summarized schematically in tabular form in Fig. 3. For example, to simulate 33% ¹³C isotopic content, two of the six ¹²C atoms in the hexagonal cell were replaced with ¹³C. As shown in Fig. 3, it is possible to substitute the ¹³C atoms next to each other (denoted as 1st neighbors) or to separate them by either one or two atoms of ¹²C (denoted as 2nd or 3rd) neighbor positions, respectively.

Fig. 3 Left: hexagonal unit cell of calcite containing Ca atoms (blue), O atoms (red) and C atoms (gray). Right: schematic tabular representation of the possible arrangements of ¹³C atoms within the calcite unit cell. Each column of the table represents one of the nonequivalent ¹³C substitution arrangements at 33%, 50%, or 67% isotope substitution. Each row in the table corresponds to a carbonate molecular unit position along the c axis within the hexagonal unit cell of calcite. White squares represent unsubstituted ¹²C positions.

Our calculations reveal that the different arrangements of the isotope atoms within the unit cell could influence the IR spectra. We show as an example, in Fig. 4, the calculated IR spectrum for the case of 33% ¹³C; we note that similar trends were observed for the cases of 50% and 67% ¹³C content. For isotope atoms positioned next to each other (1st neighbors), the v₃ mode has spectral features that are different than those obtained for atoms positioned further apart (2nd or 3rd) neighbors, which are very similar for both neighbors. The main difference is in the relative intensity of the ¹²C : ¹³C v₃ peak: for 1st neighbors, the intensity of the ¹²C peak is higher, while for the 2nd or 3rd neighbors, the intensity of the ¹³C peak is higher. We note that the v₂ and v₄ peaks also show some sensitivity to 2nd and 3rd neighbor interactions, but with much smaller magnitudes. We believe that the v₂ sensitivity is smaller because the character of that vibrational mode (out-of-plane) is significantly different than the in-plane character of the v₃ mode, which in turn affects the magnitudes of their responses to distortions of any kind. In the case of the v₄ mode, its response is much weaker, in general. The differences among these three IR-active vibrational modes of calcite are discussed in more detail in earlier work.^17,19

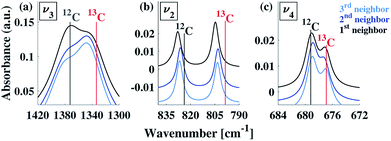Fig. 4 Comparison of calculated IR spectra for different arrangements possible at 33% ¹³C isotopic substitution. Results based on first, second, and third neighbor positions correspond to the arrangements described in Fig. 3. Vertical lines serve as guides to the eye for peak positions at 0% and 100% ¹³C concentrations.

To explore proximity effects for lower isotopic content, we utilized supercell structures of calcite. (Computational details are provided in ESI Fig. 9 and 10†.) The supercell computations revealed that, even at a significantly lower isotopic content (33% vs. 8% ¹³C), the proximity of the neighboring isotope atoms still affects the spectral features in a similar way. In other words, isotopes arranged as 1st neighbors caused a larger intensity for the ¹³C v₃ peak. We note that this is observable only when the peaks are very narrow. Thus, at significantly lower values of ¹³C isotope content, the proximity phenomena may still persist, but it lies below the experimental resolution.

Notably, the above analysis shows that different geometrical arrangements, with different relative proximity of the nearest minority isotopes, result in different spectral features. In particular, the 1st neighbor arrangement yield consistently different results relative to those based on 2nd and 3rd neighbors. We draw on our experimental results, as well as those published by others, and choose to present the computational results that are based on ¹³C isotope-substituted for the 1st neighbor arrangement, for the following considerations:

(1) There is good similarity between the experimentally observed ¹²C : ¹³C v₃ peak ratio and those of the 1st neighbor calculations (at 25% ¹³C isotope substitution).

(2) The probability of finding two neighboring ¹³C atoms is high even for the lowest substitutions we investigated. Assuming random substitution, 33% ¹³C has a 96% likelihood of having two ¹³C atoms as 1st nearest neighbors. This likelihood is 49% for 8% ¹³C substitution levels.

(3) Others have demonstrated that there is a systematic isotopic clumping effect that is common among many different carbonate-based minerals.⁴¹ There is a preference for two heavy isotopes (¹³C and ¹⁸O) to form bonds, based on first-principles lattice dynamics calculations. The effect is small: there is approximately a 0.4‰ (parts per thousand) excess in the amount of ¹³C–¹⁸O bonds, for samples produced at 0 °C. However, there is a pronounced temperature dependence to this effect, decreasing to less than 0.1‰ for samples produced at 300 °C. The scaling was approximately linear: 0.003‰ °C⁻¹. The experimentally observed isotopic clumping effect also favors the 1st neighbor configuration.

3.3 Comparing computed and experimental spectra

Turning to a detailed comparison between the theory and experiment, the simulated results generally reproduce well the trends observed in experiment. In the calculated IR spectra for crystals with pure isotope content, only one peak appears for each vibrational mode. For the mixed-isotope crystals, however, two peaks appear for both the v₃ and the v₂ modes (Fig. 2). These additional peaks have been observed experimentally by others with 50% carbon isotope substitution,²⁸ and by us at intermediate ¹³C isotope substitution levels (Fig. 2). An important observation is that the peak split persists in the simulations even at low ¹³C concentrations. Such peak splitting cannot be observed if one uses a virtual crystal approximation, where an interpolated effective carbon mass is used throughout. Furthermore, previous detailed analyses^32,35 found no viable combination peaks of vibrational modes at wave numbers that are red-shifted with respect to the main peak. This means that the weak shoulder at the right-hand side of the v₃ peak (at 1398 cm⁻¹) and the small peak on the low-wavenumber side of the v₂ peak (at 848 cm⁻¹) can be definitively assigned to the presence of the ¹³C isotope.

Comparison between computed results at 0% and 100% ¹³C indicates that the splitting of the two peak maxima is 38 cm⁻¹ (2.9%, relative to the peak position), 25 cm⁻¹ (3.1%) and 2 cm⁻¹ (0.3%) for v₃, v₂ and v₄, respectively, in good agreement with previous theoretical results.^30,37 Based on our experimental results, the splitting of ¹²C and ¹³C for the v₃ and v₂ peaks is of similar magnitude (41 cm⁻¹ and 27 cm⁻¹, respectively). The much smaller split observed for the calculated v₄ peak precludes its observation in experiment.

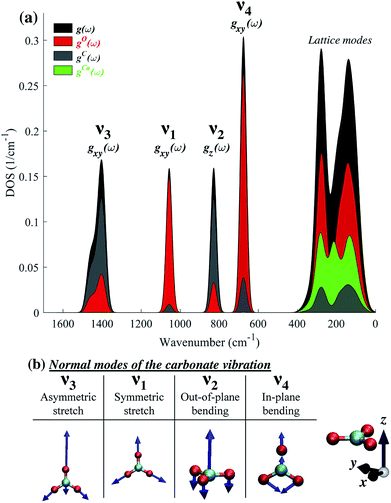
The difference in the degree of peak splitting between different modes can be explained by considering the calculated phonon density of states (DOS) of calcite. Fig. 5a shows a graphical representation of how the energy of each normal mode of vibration is partitioned among different atoms within the calcite unit cell. The DOS can be decomposed into partial contributions from different atoms ((g^O,C,Ca(ω)), depicted by the coloured regions in Fig. 5a. These coloured regions highlight that, even though C and O movements occur in each normal mode, there are different relative amounts of motion for each mode. The atomic motions that make up each of these normal modes are shown schematically in Fig. 5b).

Fig. 5 (a) Calculated phonon density of states (DOS, g(ω), black), along with directional mode information (x, y or z), obtained based on directional partial DOS (PDOS, g_xy(ω) or g_z(ω)). PDOS overlays are based on the contribution of different atoms (g^O,C,Ca(ω) shown in red, gray, and green, respectively). (b) Schematic representation of the computed normal modes of the carbonate moiety.

Fig. 5 illustrates that the v₃ and v₂ modes involve significant contributions from carbon atom vibrations. The v₁ and v₄ modes, however, are dominated by oxygen atom movement and should only be weakly affected by carbon isotope substitution. This matches our experimental data, not only in the case of IR spectra (Fig. 2), but also in Raman spectra (ESI Fig. 8†). Because the natural abundance of ¹⁸O is an order of magnitude lower than that of ¹³C, we do not expect to see any oxygen isotope-related shifts in our spectra. However, these shifts have been observed in oxygen-isotope enriched calcite²⁴ and prior calculations have shown that if ¹⁶O atoms are replaced by ¹⁸O ones, the relative splitting of the v₄ peak (5.7%) becomes much larger than that of v₃ and v₂ peaks (1.4% and 1.3%),³⁰ in agreement with the explanation provided by the calculated phonon DOS (Fig. 5).

Interestingly, the simulated results for intermediate ¹³C concentrations (Fig. 2) cannot be obtained from a simple linear interpolation of the results for 0% and 100% ¹³C. The discrepancy is especially pronounced for the v₂ modes, where the substituted and the interpolated systems differ in both peak position and intensity (Fig. 6).

Fig. 6 Comparison of simulated IR data obtained directly for intermediate ¹³C concentrations and from linear interpolation (dotted lines) of ¹³C and ¹²C data. Vertical lines serve as guides to the eye for peak positions at 0% and 100% ¹³C concentrations. For clarity, plots corresponding to different ¹³C concentrations were shifted vertically with similar shift for both direct and interpolated data.

3.4 Longitudinal optical–transverse optical (LO–TO) splitting

While isotope effects explain the features on the low-frequency side of the main peaks in Fig. 1, they do not explain features on the high-frequency side (near 882 cm⁻¹ for the v₂ peak and near 1464 cm⁻¹ for the v₃ peak, see Fig. 1), because a higher mass can only reduce vibrational frequencies. We use additional computational analyses to demonstrate that these high frequency peaks can be rationalized based on other physical mechanisms, related to LO–TO splitting.^35,61,63

Generally, the contribution of TO phonons to the vibrational modes of a powder sample will be detected by IR spectroscopy regardless of the polarization or incidence angle of the IR beam. The higher-energy LO phonons, however, may be detected only when a component of the IR beam's electric field is parallel to a vibration of interest.⁶⁴ IR experiments on powdered samples probe a large number of particles with arbitrary relative orientation, suggesting that a weak LO contribution could be observable.

The computed LO–TO splittings for 0%, 17% and 100% ¹³C isotope content are given in Fig. 7 (see also ESI Table 4†). For the case of 0% ¹³C, our results are in agreement with previous experimental⁶¹ and computational³¹ results (ESI Table 5†). For both 0% ¹³C and 100% ¹³C, the largest calculated LO–TO splitting (∼140 cm⁻¹) occurs for the v₃ mode, while the smallest (∼2 cm⁻¹) occurs for the v₄ mode. For the intermediate 17% ¹³C content, our calculations suggest that the LO–TO splitting of the ¹³C peaks is significantly smaller that of the ¹²C peaks (see ESI Table 4†) and that the intensity of the ¹³C_LO peak is much lower than the intensity of the corresponding ¹²C_LO modes.

Fig. 7 LO–TO splitting of the v₂, v₃, and v₄ IR peaks of calcite for 17% ¹³C isotope content (blue), as compared with 0% ¹³C (black) and 100% ¹³C (red). Mode assignments are based on normal mode analyses and vibrational visualizations. For clarity, peak positions and intensities are indicated by bars with no broadening.

Comparison of the calculated LO–TO results (Fig. 7) with the experimental data (Fig. 1) suggests that they are sufficient to explain the observations for the v₄ and v₂ features. In the former, no secondary peak is observed. In the latter, the splitting between the main peak and the high-frequency shoulder is consistent with the computed LO–TO splitting (∼10–15 cm⁻¹). For the v₃ peak, the computed splitting of ∼130–140 cm⁻¹ is consistent with previous theoretical results³¹ and some previous experimental results,³⁵ which place the blue-shifted shoulder above ∼1500 cm⁻¹. However, in Fig. 1 as well as in other experimental reports,^21,36 a blue-shifted shoulder appears closer to the main peak (∼1460 cm⁻¹). Thus, for v₃, the observed feature is in qualitative agreement with LO–TO splitting.

As mentioned above, the origin of the blue-shifted weak spectral features in the IR spectrum of calcite has been debated. Some³⁵ suggested that these spectral features could be attributed to combination peaks of different Raman-active and IR-active internal vibrations and lattice modes. An alternative³⁶ suggestion included discussion of possible surface-adsorbed water⁶⁵ on inorganically precipitated calcite, which may result in an asymmetry of both the v₃ and v₂ peaks, leading to features on the high-wavenumber side of the peaks. This effect could be enhanced by small particle sizes, which affect the shape, width, and asymmetry of IR peaks.^21,33,36,64 Importantly, the DFT computations presented in this work are of the bulk solid and inherently do not consider non-linear phonon effects or surface phenomena. Therefore, the results reported here show that we can assign all peaks in our calcite FTIR spectra (500–1700 cm⁻¹) by accounting only for isotopic composition and LO–TO splitting. We note, however, that although surface phenomena and combination modes are not necessary to explain the existence of weak features in the calcite FTIR spectra, they could still be important secondary effects that contribute to poor quantitative agreement in the v₃ peak features.

4 Conclusions

Here, we presented a joint experimental and theoretical study of ¹³C isotope substitution effects on the IR spectra of calcite, a widely studied material. We provide conclusive evidence to determine which weak IR spectral features in calcite can be assigned definitively to isotope shifts. Furthermore, our calculations show that all of the remaining weak features are consistent with LO–TO splittings. These results can put to rest a long-standing question about the origin of weak spectral features in calcite.^{27–35,35,36}

A more general implication of our conclusions is that the relative positions and intensities of various peaks can vary, in a non-linear fashion, with minority isotope content and proximity. This has important experimental implications. Isotopically enriched samples are widely used to increase the signal in systems where natural isotopic abundances are low. They are also used to change the vibrational response of solids, as in the study of phonon-mediated superconductivity. Our results emphasize that it is not possible to know a priori precisely how vibrational modes will change for arbitrary levels of substitution. This is because, even for relatively small levels of substitution, it is not necessarily reasonable to assume that there is a “dilute limit” below which the isotopic substitutions do not interact. Our calculations show that there can be significant effects on vibrational responses when isotopic substitutions are in close proximity to each other. We note that isotopic clumping is not an artificial scenario. It has been observed in mass spectrometry data of ablated solids, including calcite,⁶⁶ and has been backed by theoretical estimates based on fractionation effects.⁴¹ For these reasons, the non-linear variation of peak intensities and positions has the potential to be useful in future studies where identification of clumped isotopes is important, such as for geoscience applications of paleothermometry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

KMP thanks the Natural Science and Engineering Research Council (Canada) for funding.

References

1. P. A. De Groot, Handbook of stable isotope analytical techniques, Elsevier, 2004, vol. 1.
2. A. Kohen and H.-H. Limbach, Isotope effects in chemistry and biology, CRC Press, 2005.
3. S. Bud’ko, G. Lapertot, C. Petrovic, C. Cunningham, N. Anderson and P. Canfield, Phys. Rev. Lett., 2001, 86, 1877.
4. H. S. Atreya, Isotope labeling in biomolecular NMR, Springer Science & Business Media, 2012, vol. 992.
5. J. R. Young and K. Henriksen, Rev. Mineral. Geochem., 2003, 54, 189–215.
6. S. Weiner and P. M. Dove, Rev. Mineral. Geochem., 2003, 54, 1–29.
7. I. Sethmann and G. Wörheide, Micron, 2008, 39, 209–228.
8. J. H. E. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Angew. Chem., Int. Ed., 2012, 51, 11960–11970.
9. A. Van Driessche, M. Kellermeier, L. G. Benning and D. Gebauer, New Perspectives on Mineral Nucleation and Growth: From Solution Precursors to Solid Materials, Springer, 2016.
10. B. Fabbri, S. Gualtieri and S. Shoval, J. Eur. Ceram. Soc., 2014, 34, 1899–1911.
11. E. Boaretto and K. M. Poduska, JOM, 2013, 65, 481–488.
12. A. V. Radha and A. Navrotsky, Rev. Mineral. Geochem., 2013, 77, 73–121.
13. T. Henning, Lect. Notes Phys., 2010, 815, 313–329.
14. E. Beniash, J. Aizenberg, L. Addadi and S. Weiner, Proc. R. Soc. B, 1997, 264, 461–465.
15. G. Falini, S. Albeck, S. Weiner and L. Addadi, Science, 1996, 271, 67–69.
16. F. A. Andersen and L. Brečević, Acta Chem. Scand., 1991, 45, 1018–1024.
17. R. Gueta, A. Natan, L. Addadi, S. Weiner, K. Refson and L. Kronik, Angew. Chem., Int. Ed., 2007, 46, 291–294.
18. L. Regev, K. M. Poduska, L. Addadi, S. Weiner and E. Boaretto, J. Archaeol. Sci., 2010, 37, 3022–3029.
19. K. M. Poduska, L. Regev, E. Boaretto, L. Addadi, S. Weiner, L. Kronik and S. Curtarolo, Adv. Mater., 2011, 23, 550–554.
20. B. Xu and K. M. Poduska, Phys. Chem. Chem. Phys., 2014, 16, 17634–17639.
21. V. Orofino, A. Blanco, S. Fonti, R. Proce and A. Rotundi, Planet. Space Sci., 1998, 46, 1659–1669.
22. B. L. Phillips, Y. J. Lee and R. J. Reeder, Environ. Sci. Technol., 2005, 39, 4533–4539.
23. J. Feng, Y. J. Lee, R. J. Reeder and B. L. Phillips, Am. Mineral., 2006, 91, 957–960.
24. P. Gillet, P. McMillan, J. Schott, J. Badro and A. Grzechnik, Geochim. Cosmochim. Acta, 1996, 60, 3471–3485.
25. T. W. Boutton, Carbon isotope techniques, Elsevier Science, Burlington, 1991, vol. 1, ch. 11, pp. 173–185.
26. C. Slater, T. Preston and L. T. Weaver, Rapid Commun. Mass Spectrom., 2001, 15, 1270–1273.
27. W. B. White, The infrared spectra of minerals, Mineralogical Society, 1974, vol. 4, ch. 12, pp. 227–284.
28. J. C. Decius, O. G. Malan and H. W. Thompson, Proc. R. Soc. London, Ser. A, 1963, 275, 295–309.
29. M. E. Böttcher, P.-L. Gehlken and D. F. Steele, Solid State Ionics, 1997, 101, 1379–1385.
30. M. Prencipe, F. Pascale, C. M. Zicovich-Wilson, V. R. Saunders, R. Orlando and R. Dovesi, Phys. Chem. Miner., 2004, 31, 559–564.
31. L. Valenzano, Y. Noel, R. Orlando, C. M. Zicovich-Wilson, M. Ferrero and R. Dovesi, Theor. Chem. Acc., 2007, 117, 991–1000.
32. M. Donoghue, P. H. Hepburn and S. D. Ross, Spectrochim. Acta, Part A, 1971, 27, 1065–1072.
33. L. Yue, M. Shui and Z. Xu, Spectrosc. Lett., 2001, 34, 793–802.
34. C. Carteret, M. De La Pierre, M. Dossot, F. Pascale, A. Erba and R. Dovesi, J. Chem. Phys., 2013, 138, 014201.
35. K. H. Hellwege, W. Lesch, M. Plihal and G. Schaack, Z. Phys. A: Hadrons Nucl., 1970, 232, 61–86.
36. M. P. Andersson, C. P. Hem, L. N. Schultz, J. W. Nielsen, C. S. Pedersen, K. K. Sand, D. Okhrimenko, A. Johnsson and S. L. S. Stipp, J. Phys. Chem. A, 2014, 118, 10720–10729.
37. L. Valenzano, F. J. Torres, K. Doll, F. Pascale, C. M. Zicovich-Wilson and R. Dovesi, Z. Phys. Chem., 2006, 220, 893–912.
38. L. Vegard, Z. Phys., 1921, 5, 17–26.
39. L. Vegard, Z. Kristallogr. - Cryst. Mater., 1928, 67, 239–259.
40. A. R. Denton and N. W. Ashcroft, Phys. Rev. A, 1991, 43, 3161–3164.
41. E. A. Schauble, P. Ghosh and J. M. Eiler, Geochim. Cosmochim. Acta, 2006, 70, 2510–2529.
42. T. Kluge, C. M. John, A.-L. Jourdan, S. Davis and J. Crawshaw, Geochim. Cosmochim. Acta, 2015, 157, 213–227.
43. K. W. Huntington and A. R. Lechler, Tectonophysics, 2015, 647, 1–20.
44. J. R. Kelson, K. W. Huntington, A. J. Schauer, C. Saenger and A. R. Lechler, Geochim. Cosmochim. Acta, 2017, 197, 104–131.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
47. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
48. E. N. Maslen, V. A. Streltsov and N. R. Streltsova, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 636–641.
49. J. P. Perdew and S. Kurth, A primer in density functional theory, Springer, 2003, vol. 620, ch. 1, pp. 1–55.
50. A. Hirsch, I. Azuri, L. Addadi, S. Weiner, K. Yang, S. Curtarolo and L. Kronik, Chem. Mater., 2014, 26, 2934–2942.
51. G. P. Srivastava, The physics of phonons, CRC Press, 1990.
52. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon Press, Oxford, 1954.
53. R. Resta and D. Vanderbilt, Physics of Ferroelectrics, Springer-Verlag, 2007, pp. 31–68.
54. R. Nunes and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155107.
55. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
56. Y. Wang, J. J. Wang, W. Y. Wang, Z. G. Mei, S. L. Shang, L. Q. Chen and Z. K. Liu, J. Phys.: Condens. Matter, 2010, 22, 202201.
57. Z. Wang, Y. Sun, X.-Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195320.
58. W. Cochran and R. A. Cowley, J. Phys. Chem. Solids, 1962, 23, 447–450.
59. P. Umari, A. Pasquarello and A. Dal Corso, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094305.
60. X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355.
61. V. C. Farmer and A. N. Lazarev, The infrared spectra of minerals, Mineralogical Society, 1974, vol. 4, ch. 4, pp. 51–67.
62. R. Demichelis, P. Raiteri and J. D. Gale, New Perspectives on Mineral Nucleation and Growth, Springer, 2017, pp. 113–135.
63. M. Ishigame, T. Satō and T. Sakurai, Phys. Rev. B: Solid State, 1971, 3, 4388.
64. R. Ruppin and R. Englman, Rep. Prog. Phys., 1970, 33, 149–196.
65. J. Bohr, R. A. Wogelius, P. M. Morris and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2010, 74, 5985–5999.
66. P. Ghosh, J. Adkins, H. Affek, B. Balta, W. Guo, E. A. Schauble, D. Schrag and J. M. Eiler, Geochim. Cosmochim. Acta, 2006, 70, 1439–1456.

---

Footnotes

† Electronic supplementary information (ESI) available: Calcite structural parameters, experimental Raman spectra, computational ¹³C isotope substitution details. See DOI: 10.1039/c8ra06608f

‡ These authors contributed equally to this work.

§ Current address: College of Material Science and Technology, China University of Petroleum (East China).

---