Open Access Article
Open Access ArticleNecessity of two-dimensional visualization of validity in the nanomechanical mapping of atomic force microscopy for sulphur cross-linked rubber†
Takumi Ohashiab,
Tomoyuki Satoa,
Taichi Nakajimaa,
Preeyanuch Junkongbc and
Yuko Ikeda *bd
*bd
aGraduate School of Science and Technology, Kyoto Institute of Technology, Matsugasaki, Sakyo, Kyoto 606-8585, Japan
bCenter for Rubber Science and Technology, Kyoto Institute of Technology, Matsugasaki, Sakyo, Kyoto 606-8585, Japan
cResearch Strategy Promotion Center, Kyoto Institute of Technology, Matsugasaki, Sakyo, Kyoto 606-8585, Japan
dFaculty of Molecular Chemistry and Engineering, Kyoto Institute of Technology, Matsugasaki, Sakyo, Kyoto 606-8585, Japan. E-mail: yuko@kit.ac.jp
First published on 24th September 2018
Abstract
The importance of the two-dimensional (2D) visualization of validity for nanomechanical mapping in atomic force microscopy (AFM) for sulphur cross-linked rubber is emphasized for accurately interpreting the nanoscale physical properties on the surface of the soft material. The “R-factor,” evaluated to be the difference between the experimental and theoretical force–deformation curves, was considered to be the reliability index of the AFM analysis for all data points on the sample surface. A small R-factor corresponds to high accuracy. The advantage of the R-factor mapping method is demonstrated using nanomechanical mapping data of the inhomogeneous isoprene rubber network by the Johnson–Kendall–Roberts and the Derjaguin, Muller, and Toporov contact mechanics models. The 2D R-factor mapping clearly and correctly supported the roles of sulphur cross-linking reagents to control the network morphology of vulcanizates. Additionally, the blanket effect, which is induced by the rubber layer on the hard part and influences experimental force–deformation curves, is firstly proposed in this study. Nanomechanical mapping with 2D reliability indexes is expected to contribute to an advance in AFM studies on soft matter such as rubber materials, leading to a more accurate understanding of the structural characteristics of the rubber networks. Thus, this validity confirmation method is necessary for developing rubber science and technology.
1. Introduction
Since its invention in 1986,1 atomic force microscopy (AFM) has emerged as a powerful tool to image the surface topographies of an extensive range of materials.2,3 AFM is suitable for confirming the nanoscale characterization of surfaces and interfaces, and the image resolution ranges from tens of micrometers to 1 nm. Generally, the selective staining that is required for transmission electron microscopy is not necessary for AFM. AFM can be easily conducted under various conditions (e.g., under vacuum, in air, or in liquid, and at low or high temperatures). Additionally, to characterise different materials, numerous types of AFM measurements, including amplitude-modulation mode (a tapping mode also referred to as dynamic mode or intermittent contact mode), force mode (e.g., nanoindentation and nanomechanical mapping), and conductive mode, can be conducted. These advantages increase the versatility of AFM which has given rise to numerous discoveries and technologies, and has opened new doors in various fields such as physics, chemistry, materials science, and biology.4,5In polymer materials science, AFM has been extensively utilized to evaluate the morphological characteristics of plastics, rubbers and fibres, because several polymeric materials are observed to possess inhomogeneous structures on a nanometer scale.3,6,7 Particularly, conventional rubber materials are comprised of cross-linked network structures and filler particles. Thus, imaging the morphologies of these materials on a nanoscale resolution is becoming increasingly important. In general, the phase image of the tapping mode is used to reveal the different components in the sample surface.8 This is because the phase contrast is mainly governed by the various mechanical properties of the regions or components on the sample surface, and is highly sensitive to the sample heterogeneity. However, the phase image can be visualized differently depending on the measurement conditions. For example, the reversal of phase contrast possibly occurs when a set point ratio was increased.3 Therefore, a quantitative AFM image became necessary to characterise the morphologies of soft materials. For this purpose, the AFM nanomechanical mapping9 or nano-palpation10 has been used, where the nanomechanical properties of the material surface were evaluated by analyzing the AFM data using contact mechanics, and followed by mapping as a two-dimensional (2D) image.
Presently, many techniques of AFM nanomechanical mapping are well-known. The methods are categorized into the non-vibrating and the vibrating systems. The representative case of the former is the force volume (FV) imaging firstly proposed by Heinz et al.11 This method is to collect an array of force curves over the surface and to assemble those curves into FV data. It possesses some advantages of the simple principal of the measurement and easy interpretation of the data. Furthermore, an indentation depth can be controlled, which allows us to acquire the sample information in the depth direction. On the other hand, the method which is used in the vibrating system is further separated into two types; vibrations of the cantilever and the sample. The former is the system where the cantilever is vibrating, such as the PeakForce™ quantitative nanomechanical mapping (QNM)12 and the multifrequency force microscopy.13 The latter is the system where the sample is vibrating, such as the atomic force acoustic microscope (AFAM)14 and the contact resonance.15 Among these techniques, especially in the FV imaging and PeakForce™ QNM methods, the Young's moduli are calculated by analyzing force–sample deformation curves with contact mechanics models for their fitting process or a two-point method. In many cases, however, the 2D Young's modulus image was shown without any evaluation on a deviation between experimental and theoretical force–deformation curves at all measured points. This deviation should not be ignored, especially for soft matters such as rubber materials due to the inhomogeneity of hardness in the sample.
Up to now, several contact mechanics models, including the Hertzian, Johnson–Kendall–Roberts (JKR), Derjaguin, Muller, and Toporov (DMT), and Maugis–Dugdale (MD) models, have been used in AFM studies on rubber materials. For example, Glebova et al. investigated the morphology of a vulcanized butadiene–styrene rubber containing ZnO particles by employing AFM nanomechanical mapping with the DMT and Hertzian models; their results confirmed that the rubber surrounding the ZnO particles exhibited a high Young's modulus and a small hysteresis.16 Xue et al. also found the domain and interfaces of ZnO in NR vulcanizates by AFM nanomechanical mapping with the JKR model.17 Wang et al. successfully combined the JKR model and a two-point method with AFM to visualize the nanomechanical mapping of a natural rubber (NR) nanocomposite filled with carbon nanotubes (CNTs); the authors quantitatively characterised the CNT and NR regions in the nanocomposites.9,18 Lu et al. also investigated the Young's moduli of interface between CNTs and NR at nanoscale resolution using the DMT model in the PeakForce™ QNM method.19 However, the AFM measurements used to perform nanomechanical mapping have been known to be affected by several factors, including tip geometry, instrument calibration errors, the presence of extrinsic mechanical heterogeneities and the physical justifications of the contact mechanics models of materials.18,20–24 Therefore, evaluating the validity of AFM data becomes necessary for developing scientific techniques.
In the recent AFM studies, a confirmation of the validity of force curve analysis by contact mechanics models has been achieved only by naked eyes.10,16–18,25,26 In addition, only a few points were used for the confirmation, i.e., many authors did not ensure that good agreements with the contact mechanics models at all points of the measurement. Thus, a quantitative analytical method that provides a reliability index for all the AFM data is required to ensure an accurate interpretation of data. However, the all point's evaluation for the validity of nanomechanical properties has been scarcely discussed in the academic publications, although the commercial software for AFM mapping may be available. Only one paper reported the goodness of fit R2 images together with mappings of tip–sample contact potential difference and capacitance second derivative of indium tin oxide and poly(3-hexylthiophene) nanowires by electrostatic force microscopy (EFM or a conductive AFM).27 Therefore, in this study, the 2D mapping of reliability indexes for nanomechanical mapping is reported for the first time.
The objective of this study is to show a necessity of a quantitative and reliable evaluation process for the fitting quality of all data points in the elasticity (Young's modulus) mapping. The 2D mapping image of the reliability index in the AFM nanomechanical mapping is demonstrated for a sulphur cross-linked rubber and its importance is emphasized for the first time as far as we have concerned. The quantitative and reliable Young's modulus map will become an evidence to correctly support a new concept for the vulcanization mechanism which we found in the studies by small-angle neutron scattering (SANS)28 and synchrotron X-ray absorption fine structure (XAFS)29–32 The novel mechanism was expected to be a key to develop rubber science and technology as described in the ACS News Service Weekly PressPac in 2015.33
2. Experimental
2.1 Preparation of sulphur cross-linked isoprene rubber
The sulphur cross-linked isoprene rubber, abbreviated as SIR was obtained by heat pressing at 140 °C of its compound prepared by conventional milling as follow: the isoprene rubber (IR2200 supplied from JSR Co.) was mixed with 1 part per hundred rubber by weight (phr) of zinc oxide (ZnO, average diameter 0.29 μm purchased from Sakai Chemical Industry Co., Ltd.), 1 phr of N-(1,3-benzothiazol-2-ylsulfanyl)cyclohexanamine (CBS, Sanceler CM-G supplied from Sanshin Chemical Industry Co., Ltd.) and 1.5 phr of elemental sulphur (S8, powder, 150 mesh purchased from Hosoi Chemical Industry Co., Ltd.), respectively. All reagents were commercial grades for rubber processing and used as received. Network-chain density of SIR determined by the swelling test in toluene at 25 °C was 1.00 × 10−4 mol cm−3. The detail of swelling experiment can be followed in our previous study.282.2 AFM measurement
The AFM measurement in this study was performed using a commercial AFM system (Shimadzu, SPM-9700) with a contact mode under ambient condition. For a preparation of the sample surface, the sulphur cross-linked rubber sheet was cut by an ultra-microtome (MT-XL CR-X, RMC Boeckeler Instruments, Inc., AZ, USA) at about −80 °C to prepare the flat surface. A cantilever used in this mode was made of SiN (OMCL-RC800PSA, Olympus, Japan) with a nominal spring constant of 0.76 N m−1 and a tip radius of 15 nm. Before the measurement, an actual spring constant of the cantilever was measured by Sader's method.34 The AFM measurement was operated with very small applied force of 1.4 nN as trigger set point for acquiring only the surface information, preventing the damage of sample surface and contamination of the cantilever. A loading speed was set at 6720 nm s−1.2.3 Force volume (FV) measurement for SIR
Force–distance curves were randomly collected over the selected surfaces area of 2 μm × 2 μm with a resolution of 64 × 64 pixels. Simultaneously, z-displacement values of the piezo scanner under 0.49 nN as the relative operating point were recorded to construct an “apparent height” image. Each force–distance curve was converted to the force–deformation curve according to the method proposed by Nakajima et al.10 as shown in Fig. S1.†2.4 Theoretical basis
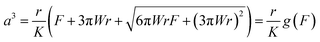 | (1) |
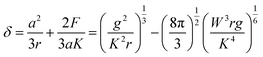 | (2) |
By combining eqn (1) with eqn (2), the sample deformation (δ) becomes in a function of F. Then, the JKR theoretical force–deformation curves can be calculated using the experimental force. Here, K is the elastic coefficient, which can be expressed by eqn (3),
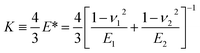 | (3) |
In the case of rubber materials, the Young's modulus of the cantilever (E2) is generally much larger than that of the sample (E1).37 In addition, the Poisson's ratio of an unfilled rubber sample is almost 0.5 in general.38 Thus, eqn (3) can be approximated as eqn (4).
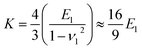 | (4) |
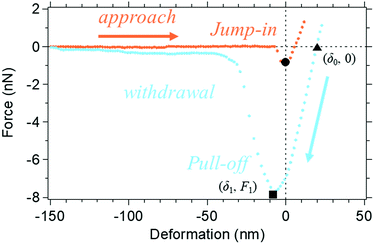
In the case of the JKR two-point method,39 it is possible to determine K and W as shown in eqn (5) and (6) from the max-adhesion point (δ1, F1) and the balance point (δ0, 0) obtained in each experimental force–deformation curve, respectively (Fig. 3). Note that the point where the attractive force and the repulsive force become equivalent is defined as the “balance point” (δ0, 0), and the point where adhesive force becomes maximum is defined as the “max-adhesion point” (δ1, F1). By combining eqn (4) and (5), the Young's modulus of the sample, E1 can be obtained.
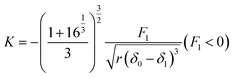 | (5) |
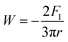 | (6) |
Note that the relationship between sample deformation at max-adhesion point (δ1) and sample deformation at balance point (δ0) in withdrawing process based on the JKR theory was considered as the following equation10
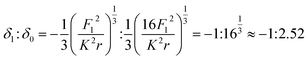 | (7) |
Therefore, the origin of sample deformation in withdrawing force–deformation curve (δ′) can be calculated as shown in eqn (8).
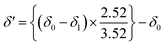 | (8) |
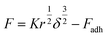 | (9) |
The DMT theory is simply considered as the Hertzain equation 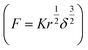 , in which the spherical tip of the cantilever is regarded, added by the term of an adhesive force (Fadh). When the sample deformation follows Hertzian prediction, F is assumed to be proportional to
, in which the spherical tip of the cantilever is regarded, added by the term of an adhesive force (Fadh). When the sample deformation follows Hertzian prediction, F is assumed to be proportional to 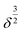 .37,40 Importantly, this assumption should be also used for the DMT theory. Therefore, in this study, the fitting range for the DMT theory was set in the range of δ < r, where F is still proportional to
.37,40 Importantly, this assumption should be also used for the DMT theory. Therefore, in this study, the fitting range for the DMT theory was set in the range of δ < r, where F is still proportional to 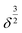 and spherical tip of the cantilever can be assumed.41 The jump-in-contact point is regarded as the origin of sample deformation in approaching process. However, the minimum point before the substantial increase of cantilever deflection is decided to be an origin of sample deformation for the complicate approaching force curve, e.g., existing a few jump-in-contact points.
and spherical tip of the cantilever can be assumed.41 The jump-in-contact point is regarded as the origin of sample deformation in approaching process. However, the minimum point before the substantial increase of cantilever deflection is decided to be an origin of sample deformation for the complicate approaching force curve, e.g., existing a few jump-in-contact points.
2.5 Calculation of a reliability index (R-factor)
The accuracy of nanomechanical mapping using AFM is determined as a matching degree between experimental and theoretical force–deformation curves in this study. It is represented as a dimensionless error parameter or R-factor which has general form as shown in eqn (10).
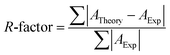 | (10) |
3. Results and discussion
3.1 Selection of a contact mechanics model for SIR
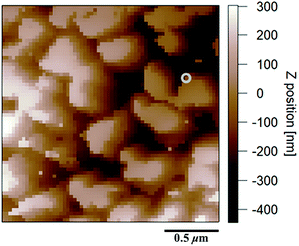
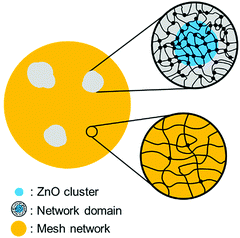
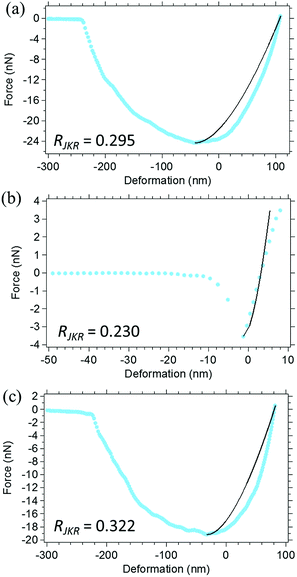
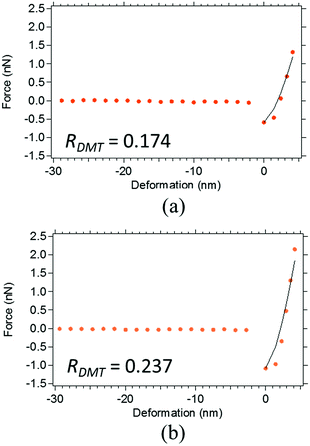
Fig. 1 depicts an apparent-height image of SIR obtained from the force volume (FV) measurements from which the high and low regions on the surface can be clearly detected. This experimental mode suggests that the soft parts were more easily and extensively deformed than the hard parts on the surface. Therefore, the high and low regions in Fig. 1 depict the hard and soft parts in the SIR, respectively. Specifically, the apparent-height image clearly indicates that the SIR possesses an inhomogeneous network structure. In our previous study,28 we detected an inhomogeneous network structure by SANS even for vulcanizates prepared without stearic acid. Thus, the apparent-height image of SIR may be related to the two-phase inhomogeneous network structure illustrated in Fig. 2 where two phases with high and low network-chain densities are predicted to be present. The former and the latter are referred to as a network domain and a mesh network in this study, respectively, among which the network domain is proposed to be embedded in a matrix of the mesh network.28Measurement of the Young's moduli of SIR by AFM may provide a powerful tool to quantitatively confirm its network morphology. Note that an adequate contact mechanics model must be applied to the results of FV measurements to accurately determine each Young's modulus. Thus, selection of an appropriate contact mechanics model becomes important. For this purpose, in the present study, the presence or absence of an adhesive force was first evaluated from the force–deformation curves of AFM measurements. For example, Fig. 3 depicts the force–deformation curves corresponding to a gray circle in Fig. 1. The force at the jump-in-contact in the approaching curve (●) and at the pull-off in the withdrawing curve (■) were observed to be the adhesive forces of the approaching and withdrawing curves, respectively. Other points were also confirmed to represent the adhesive forces in both the approaching and withdrawing processes even the adhesive forces were very small in several points (Fig. 4(a) and (b)).
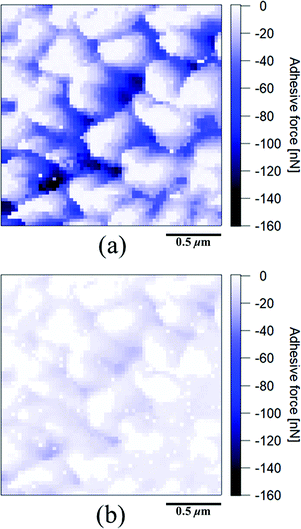 | ||
| Fig. 4 (a) An adhesive force mapping image from the withdrawing curves, (b) an adhesive force mapping image from the approaching curves of SIR (the scan size is 2.0 μm). | ||
The experimental force–deformation curves require a contact model that includes adhesion. Thus, the JKR and DMT models were investigated as candidates for use in the AFM analysis in this study. Because the JKR model36 has been well utilized to determine the Young's moduli of soft matters, including cross-linked rubbers,15,18,44,45 we initially selected this model for the force–curve mapping of SIR.
3.2 Two-dimensional visualization of the reliability of Young's moduli determined by the JKR theory
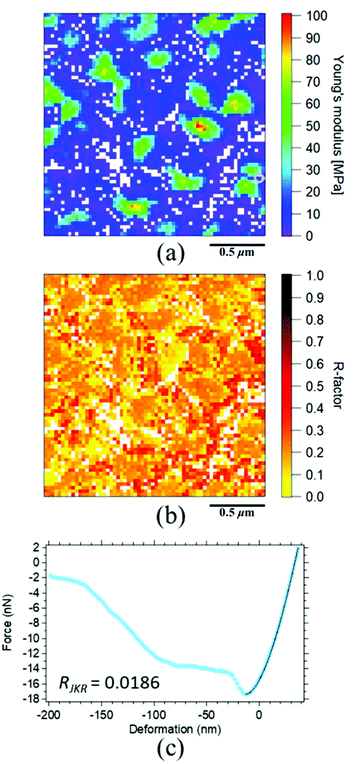
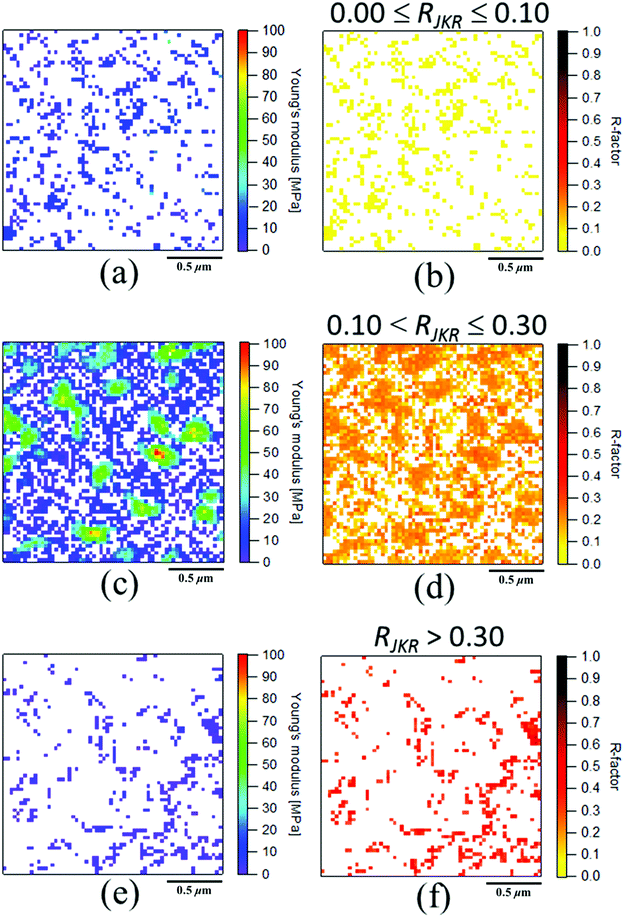
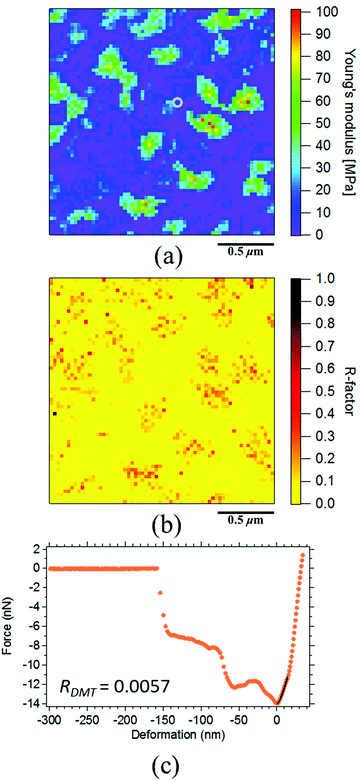
Fig. 5(a) depicts the Young's modulus mapping image of SIR calculated using the JKR theory, where the colour variation from purple to red corresponds to an increase in the modulus from low to high. The obtained Young's moduli of all the points in SIR were clearly observed to be related to the apparent heights. However, confirmation of the accuracy of all the Young's moduli in the mapping was necessary because the values were obtained by the JKR two-point method.39 To evaluate the reliability of these Young's modulus values, we compared the experimental and the theoretical JKR force–deformation curves. For example, two JKR force–deformation curves corresponding to the gray circle in Fig. 5(a) are depicted in Fig. 5(c). The experimental curve was well superimposed on a theoretical curve, with negligible differences. However, such a good agreement may not have been obtained for all the measurement points. Therefore, we should carefully consider the results in Fig. 5(a). Further, we should also verify whether it is possible to discuss the Young's modulus mapping image of SIR in detail without any evidence.To confirm the reliability of all the modulus mapping results, a matching degree between the experimental and the theoretical force–deformation curves (i.e., the “R-factor”) was conducted in this study. All R-factors were quantitatively calculated on the basis of eqn (10) for each experimental and theoretical force–deformation curve, and the obtained R-factors were visualized in a two-dimensional manner for all the points, as depicted in Fig. 5(b). To the best of our knowledge, the imaging of reliability for all the moduli in the cross-linked rubber was reported for the first time in this study. The index is abbreviated as RJKR where the JKR theoretical deformation (δJKR) and the experimental deformation (δExp) under a given force were used for ATheory and AExp in eqn (10), respectively. Note that the range of the calculation was set between the maximum adhesive force and the maximum loading force in the withdrawing force–deformation curve. In Fig. 5(b), the variation of colour from yellow to black indicates the variation from a small error to a large error. Thus, the reliability of the Young's modulus values increases with the increasing yellow area in the image. Note that the missing Young's moduli are denoted by the white points in Fig. 5(a). These white points were ascribed to the severe experimental conditions. Specifically, the balance point (δ0, 0), which is required for the JKR two-point method, as depicted in Fig. 3 (▲), could not be obtained in these white points, partially because the loading force was set to be as small as possible to minimize the sample deformation. Their points were strictly eliminated as invalid points from the Young's modulus mapping in this study. Overall, the reliability of the Young's moduli for the surface of SIR was concluded to be poor, as detected in Fig. 5(b). Before going to the application of other model, a reason of the mismatch in the JKR analysis is considered next using extracted mapping images. As shown in Fig. 6, a classification of R-factor ranges may give us not only a reliable Young's modulus mapping image but also important information on the poor agreement between the experimental and the theoretical curves.
The Young's modulus and R-factor mappings are visualized in Fig. 6 based on each given R-factor range for our discussion. Namely, the RJKR in Fig. 5(b) was categorized into three groups in this study as shown in Fig. 6(b), (d) and (f), i.e., 0 ≤ RJKR ≤ 0.1, 0.1 < RJKR ≤ 0.3 and RJKR > 0.3, respectively. Note that the classification of R-factors can be freely conducted by researchers depending on the objective of their discussion. Fig. 6(a) shows the points which could be fully explained by the JKR theory and whose Young's moduli were approximately 10 MPa. Principally, only these points can be used for characterization of the sample, because the Young's moduli in Fig. 6(c) and (e) were not much reliable. However, the best extracted Young's modulus mapping with the low RJKR in Fig. 6(a) was insufficient to fully explain the total elastic properties of SIR due to a few points. In order to obtain the more reliable Young's modulus mapping, an elucidation for the large RJKR was conducted as follows.
In the regions of RJKR > 0.3, the representative experimental force–deformation curves of SIR significantly showed the deviation from the theoretical curves. When all deviations were investigated, the large RJKR was mainly ascribed to the sharper slope of F–δ at the initial stage of the withdrawal than the prediction by the JKR theory as shown in Fig. 7(c) as one typical example. This suggests that the reason of large RJKR was mostly the high viscous response from the matrix of SIR. This response is generally difficult to be explained by the elastic contact mechanic models.46 In the regions of 0.1 < RJKR ≤ 0.3, the two types of representative force–deformation curves of SIR were observed. The first deviation type due to the high viscosity was also observed similarly in the region of RJKR > 0.3 as shown in Fig. 7(a). The second deviation type was not simply explained, because the slope of tangential line of experimental curve was not continuously changed. For example, as shown in Fig. 7(b), the slope of tangential line of experimental curve was suddenly increased around δ = 5 nm during withdrawal. Therefore, it cannot be explained by one theoretical curve. The discontinuous change of the slope of tangential line of experimental curve was possibly supposed to occur by the different responses of SIR against the indentation depth during withdrawal.
It is worth noting that the two main types of deviation were distinguished using this 2D R-factor mapping technique by separating the RJKR regions. However, the analysis to get a better agreement between the experimental–theoretical JKR force–deformation curves for both deviation types in SIR as presented in Fig. 7 will be considered in near future. At least, here, it was thought that the viscosity effect is possibly avoided. The technique to change the scanning speed was reported to be useful.25 However, this technique requires very slow or high scanning speed, and was not so practical for our AFM machine. Therefore, the force–deformation curve during approaching was utilized for the analysis of AFM nanomechanical mapping in this study, because the viscous response of the material surfaces is known to be less explicit in the approaching process than the withdrawing process in general. Then, the DMT theory, where the elastic behaviour of the surfaces is considered in the approaching process, was subsequently used to evaluate the Young's moduli for all the points on SIR. As demonstrated above, the introduction of R-factor mapping to AFM studies is highly useful in materials science.
3.3 Two-dimensional visualization of the reliability of the Young's moduli determined by the DMT theory
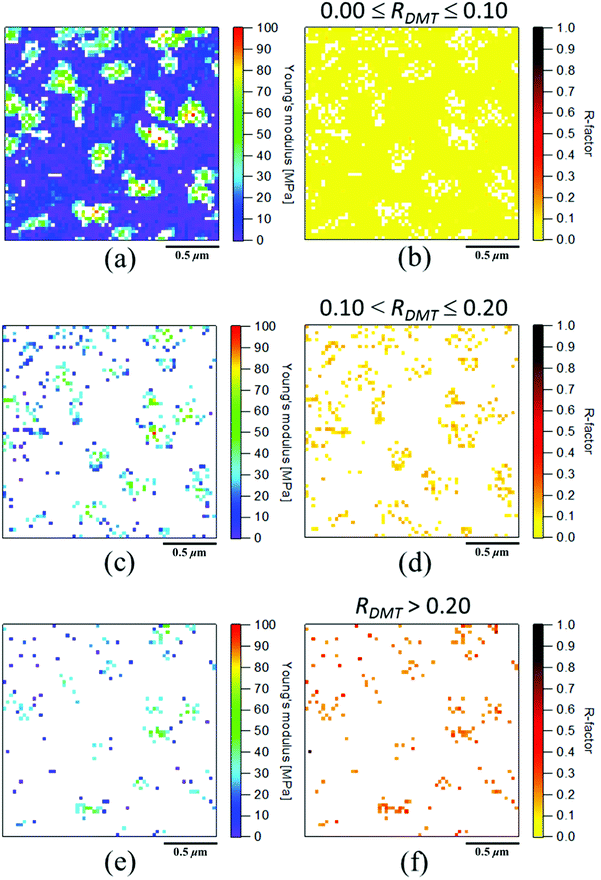
Young's modulus mapping calculated by the DMT theory and the corresponding R-factor mapping images for SIR are presented in Fig. 8(a) and (b), respectively. The R-factor in the DMT theory (RDMT) was calculated using eqn (10), where the DMT-calculated force (FDMT) and the experimental force (FExp) under a given sample deformation were used as ATheory and AExp in eqn (10), respectively, in the range of 0 < δ < r for the DMT force–deformation curve. Fig. 8(b) clearly depicts that the R-factors in several points of SIR were less than 0.1 and that the validity of all the modulus mapping results was considerable.The low R-factors (for example, R-factors less than 0.1) exhibited a greater increase in reliability during the application of the DMT theory to the FV measurements than upon the application of the JKR theory for this sample. For example, Fig. 8(c) depicts a good agreement between the experimental and the theoretical DMT force–deformation curves corresponding to the gray circle in Fig. 8(a). However, all of the Young's moduli did not always result in low R-factors; some of the values were greater than 0.2 even when the DMT theory was used to perform the analysis. Therefore, the evaluation of the Young's moduli of SIR in Fig. 8(a) was carefully conducted using their R-factors in the next section.
To obtain a reliable Young's modulus map by the DMT theory, the classification of Young's modulus mapping based on the R-factor range was conducted. Here, the R-factors were separated into three groups for ease of discussion: 0 ≤ RDMT ≤ 0.1, 0.1 < RDMT ≤ 0.2, and RDMT > 0.2 (Fig. 9(b), (d) and (f), respectively). The extracted Young's modulus image in Fig. 9(a) depicts that almost all of the points can be completely explained by the DMT theory (0 ≤ RDMT ≤ 0.1), which is sufficiently reliable for quantitative discussion of the morphology of the SIR.
In contrast, large R-factors of greater than 0.1 were detected at the points at which a very small deformation occurred even when the same loading force was applied for all the points, as depicted in Fig. 10(a) and (b). For example, δ was ca. 30 nm in Fig. 8(c) but was ca. 3 nm in Fig. 10(b) even though the loading force was 1 nN in both cases. The latter was assumed to be related to the deformation of hard parts, such as the ZnO clusters, in SIR. In addition, the slope of the experimental force–deformation curve was suggested to vary. For example, the slope of tangential line of the experimental curve was suddenly increased at around δ = 2 nm during approaching. These phenomena were similar to the effect of multiple components in force–deformation curves of SIR by JKR theory as shown in Fig. 7(b). The gentle and keen experimental slopes were possibly attributed to the soft and hard phases, respectively (Fig. 10(a) and (b)). The observation indicates the presence of multiple layers in the depth direction within the region for analysis, which was assumed to contribute to the mismatch between the experimental curves and those predicted by the DMT and JKR theories in both approaching and withdrawing processes.
3.4 Effect of multiple layers on the force–deformation curves
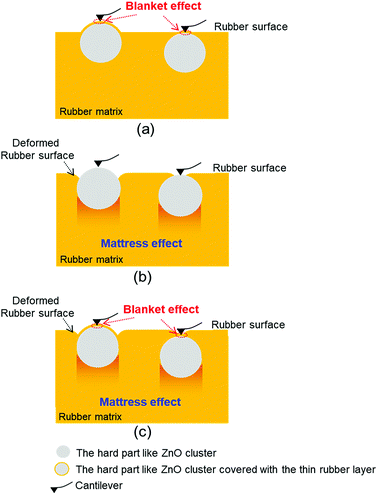
To explain the complicated experimental force–deformation curves, we consider the phenomena ascribed to the multiple layers from viewpoints of a “blanket effect” and a “mattress effect”, respectively, according to Fig. 11. As previously described, the gentler experimental slope during the initial stage of the approaching process (Fig. 10(a) and (b)) indicate a presence of a soft phase; a small adhesive force was also detected during the measurement. Therefore, the observed hard parts were predicted to be a thin rubber-coated ZnO particle and not a naked ZnO particle surface. The effect induced by this thin rubber layer on the ZnO particle is the aforementioned blanket effect. Our previous SANS study on the formation of a two-phase network structure in the vulcanizates in 2009 (ref. 28) supports this interpretation, where sulphur and an accelerator, CBS, were reported to be easily adsorbed onto the surface of ZnO, followed by a cross-linking reaction around the ZnO particle to form a network structure with a high network-chain density. Specifically, the presence of a network on ZnO was feasible based on the vulcanization reaction. For example, recently, using a scanning electron microscope equipped with an energy-dispersive X-ray spectrometer, Glebova et al. detected a strong signal that can be attributed to the carbon on the surface of a ZnO particle even though they did not discuss the phenomena in detail.16 This result clearly supports our interpretation of the blanket effect on the ZnO particles in SIR. In fact, the presence of blanket effect was confirmed by the change of slope from the gentle one in the initial stage to the keen one during approaching in the experimental force–deformation curve of SIR as depicted in Fig. 8(c), 10(a) and (b).On the other hand, as shown in Fig. 5(c), the Young's modulus calculated by the force–deformation curve in the seemingly hard part near ZnO was in an order of megapascals, but not the gigapascals47 expected for naked ZnO particles in the rubber matrix. This observation clearly suggests that the ZnO particles are embedded in the soft rubber phase in a manner similar to that of the objects lying on a mattress in the two-phase network morphology of the vulcanizates. In this study, the phenomenon resulting from the rubber phase under the hard part is the aforementioned mattress effect. Similar phenomena have been reported by other authors. For example, Nakajima et al.46 reported that their calculated Young's modulus of the ZnO region was smaller than the predicted value of raw ZnO particles in a vulcanized rubber blend system. Wang et al.18 reported that the Young's modulus of CNTs on an NR matrix was much smaller than the typical Young's modulus of the CNTs. In both the cases, the hard material region exhibited a lower elastic modulus than the predicted modulus because the rubber phase around ZnO was deformed. Note that they did not report the validity in their nanomechanical mappings for all points.
Till now, only the mattress effect has been hypothesized to explain the phenomena mentioned above.18,46 Our research is the first report to emphasize the presence of the blanket effect as far as we know. Further, a question arises as to whether the blanket effect or the mattress effect is influential for the nanomechanical mapping of AFM. This question is difficult to answer in the case of heterogeneous rubber materials. It can be thought that the experimental force–deformation curve containing multiple components within the region for analysis may not be explained using only one theoretical force–deformation curve. However, our experimental results pointed out that the blanket effect evidently existed with the mattress effect, particularly when the approaching process with the very small force applied is considered. Therefore, this finding suggested that the blanket effect should be carefully considered more for the analysis of nanomechanical AFM data based on FV measurement.
3.5 Characterization of network morphology in SIR using good R-factors
The Young's modulus map based on the DMT theory with the R-factors having less than 10% error is illustrated in Fig. 9(a), which was the most acceptable result of nanomechanical mapping for SIR in the present study. A two-phase inhomogeneous network structure corresponding to our previously proposed structure based on SANS28 was apparently visualized for SIR. It means that the inhomogeneous network structure in the vulcanized isoprene rubber was clearly observed in both the swollen state by SANS and the dry state by AFM measurement. The morphology of SIR was acceptable, where the domains of high network-chain density were embedded in the matrix of mesh network as proposed in Fig. 2. Note that it is supposed that network-chain density of the mesh network was very small because stearic acid was not added in SIR in this study. This consideration is based on our previous SANS study: the size of mesh network is controlled by the concentration of solubilized zinc stearate, which was generated by the reaction of stearic acid and ZnO in the rubber matrix upon milling and heat-pressing the rubber compound. The generated zinc stearate further reacts with sulphur and the accelerator in the rubber matrix to form sulphur crosslinks. The accurate Young's modulus map apparently supported our consideration about the formation of network domains in the rubber matrix: As predicted by the SANS results, sulphur and the accelerator were adsorbed on the ZnO clusters, and followed by sulphur crosslinking on the surface area of ZnO clusters. Since stearic acid was not mixed in this study, the sulphur cross-linking reaction mainly and significantly occurred around the ZnO particles to result in the formation of network with a high network-chain density near ZnO.28,29 Consequently, the very low Young's moduli in the order of a few megapascals were observed in the matrix of the SIR, and the dispersed phases with Young's moduli (>50 MPa) greater than the Young's moduli of the matrix were detected.By this two-dimensional and highly accurate Young's moduli in the AFM nanomechanical mapping, we could reconfirm the aforementioned consideration. The results also supported the important concept for the vulcanization:28 sulphur cross-linking reagents play a role in controlling not only the cross-linking reaction but also the morphology of the rubber network. Namely, the combination and composition of ZnO with the other reagents are crucial to control the structural network inhomogeneity in the vulcanizate. After this publication,28 several studies on the inhomogeneous structures of vulcanizates by AFM have been reported.10,16–18 However, the validity of nanomechanical mapping was not confirmed for all data points. Therefore, it is emphasized that a confirmation of reliability for the morphology obtained by AFM nanomechanical mapping is important in order to reveal the complicated vulcanization mechanism of rubbers by AFM.
4. Conclusion
Necessity of the two-dimensional visualization to confirm the validity of AFM nanomechanical mapping for all data points in the sulphur cross-linked rubber was shown for the first time for accurately interpreting the nanoscale physical properties of the typical soft matter. The quality of fitting was evaluated on the basis of the reliability indexes (R-factors) to depict the difference between the theoretical and the experimental force–deformation curves of the materials. By separating the poor R-factor regions, this method enabled us to obtain a reliable Young's modulus mapping image that was completely explained by contact mechanics. As a result, the most reliable Young's modulus mapping by DMT theory was achieved to reveal the role of sulphur cross-linking reagents on the two-phase inhomogeneous network formation of vulcanized rubber in this study. To the best of our knowledge, this present study is the first report to consider the vulcanization mechanisms in the inhomogeneous rubber network for both the network domain and mesh network phases based on AFM study.Moreover, the classification of R-factors in this 2D validity mapping, two effects of a thin rubber layer on the particles and a soft rubber phase under the particles were apparently detected and found to decrease the Young's moduli of virgin zinc oxide. To explain the phenomena, the “blanket effect” and the “mattress effect” were named and used for the discussion, especially the idea of blanket effect is the first report as far as we know. The presence of blanket and mattress effects as well as the effect of high viscous response from the rubber matrix within the region for analysis were ascribed to the reason of the deviation of experimental results from the theoretical ones.
The usefulness and importance of 2D R-factor mapping for the soft matter were confirmed as aforementioned. Notably, this method for all fitting quality is also highly required for hard materials. Because various techniques in AFM are now available, the 2D mapping method of reliability indexes can be a powerful tool not only for AFM nanomechanical mapping but also for other AFM analysis modes when experimental and theoretical values are compared. Therefore, this method should be much more used for developing AFM technology that will advance science.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JST ALCA Grant Number JPMJAL1501, Japan.Notes and references
- G. Binning, C. F. Quate and Ch. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef PubMed.
- P. Eaton and P. West, Atomic Force Microscopy, Oxford University Press, Oxford, 2010 Search PubMed.
- R. A. Meyers, Encyclopedia of Analytical Chemistry, John Wiley & Sons Ltd., Chichester, 2000 Search PubMed.
- C. Gerber and H. P. Lang, Nat. Nanotechnol., 2006, 1, 3–5 CrossRef PubMed.
- Y. F. Dufrêne, T. Ando, R. Garcia, D. Alsteens, D. Martinez-Martin, A. Engel, C. Gerber and D. J. Müller, Nat. Nanotechnol., 2017, 12, 295–307 CrossRef PubMed.
- D. Wang and T. P. Russell, Macromolecules, 2018, 51, 3–24 CrossRef.
- D. M. Ridgley and J. R. Barone, ACS Nano, 2013, 7, 1006–1015 CrossRef PubMed.
- R. García, R. Magerle and R. Perez, Nat. Mater., 2007, 6, 405–411 CrossRef PubMed.
- D. Wang, S. Fujinami, K. Nakajima, K. Niihara, S. Inukai, H. Ueki, A. Magario, T. Noguchi, M. Endo and T. Nishi, Carbon, 2010, 48, 3708–3714 CrossRef.
- K. Nakajima, M. Ito, D. Wang, H. Liu, H. K. Nguyen, X. Liang, A. Kumagai and S. Fujinami, Microscopy, 2014, 63, 193–208 CrossRef PubMed.
- W. F. Heinz and J. H. Hoh, Trends Biotechnol., 1999, 17, 143–150 CrossRef PubMed.
- T. J. Young, M. A. Monclus, T. L. Burnett, W. R. Broughton, S. L. Ogin and P. A. Smith, Meas. Sci. Technol., 2011, 22, 125703 CrossRef.
- M. Kocun, A. Labuda, W. Meinhold, I. Revenko and R. Proksch, ACS Nano, 2017, 11, 10097–10105 CrossRef PubMed.
- D. Passeri, A. Bettucci and M. Rossi, Anal. Bioanal. Chem., 2010, 396, 2769–2783 CrossRef PubMed.
- D. G. Yablon, A. Gannepalli, R. Proksch, J. Killgore, D. C. Hurley, J. Grabowski and A. H. Tsou, Macromolecules, 2012, 45, 4363–4370 CrossRef.
- Y. Glebova, V. Reiter-Scherer, S. Suvanto, T. Korpela, T. T. Pakkanen, N. Severin, V. Shershnev and J. P. Rabe, Polymer, 2016, 107, 102–107 CrossRef.
- X. Xue and Z. Wang, Mater. Sci. Forum, 2016, 852, 520–524 Search PubMed.
- D. Wang, S. Fujinami, K. Nakajima, S. Inukai, H. Ueki, A. Magario, T. Noguchi, M. Endo and T. Nishi, Polymer, 2010, 51, 2455–2459 CrossRef.
- N. Ning, T. Mi, G. Chu, L. Zhang, L. Liu, M. Tian, H. Yu and Y. Lu, Eur. Polym. J., 2018, 102, 10–18 CrossRef.
- K. L. Johnson and J. A. Greenwood, J. Colloid Interface Sci., 1997, 192, 326–333 CrossRef PubMed.
- M. Kopycinska-Müller, R. H. Geiss and D. C. Hurley, Ultramicroscopy, 2006, 106, 466–474 CrossRef PubMed.
- M. Vandamme and F. J. Ulm, Int. J. Solids Struct., 2006, 43, 3142–3165 CrossRef.
- M. E. Dokukin and I. Sokolov, Macromolecules, 2012, 45, 4277–4288 CrossRef.
- M. Chyasnavichyus, S. L. Young and V. V. Tsukruk, Langmuir, 2014, 30, 10566–10582 CrossRef PubMed.
- S. Nagai, S. Fujinami, K. Nakajima and T. Nishi, Nihon Reoroji Gakkaishi, 2008, 36, 99–106 CrossRef.
- P. L. Chandran, E. K. Dimitriadis, E. L. Mertz and F. Horkay, Soft Matter, 2018, 14, 2879–2892 RSC.
- S. Lilliu, C. Maragliano, M. Hampton, M. Elliott, M. Stefancich, M. Chiesa, M. S. Dahlem and J. E. Macdonald, Sci. Rep., 2013, 3, 3352 CrossRef PubMed , 1–7.
- Y. Ikeda, N. Higashitani, K. Hijikata, Y. Kokubo, Y. Morita, M. Shibayama, N. Osaka, T. Suzuki, H. Endo and S. Kohjiya, Macromolecules, 2009, 42, 2741–2748 CrossRef.
- Y. Yasuda, S. Minoda, T. Ohashi, H. Yokohama and Y. Ikeda, Macromol. Chem. Phys., 2014, 215, 971–977 CrossRef.
- Y. Ikeda, Y. Yasuda, T. Ohashi, H. Yokohama, S. Minoda, H. Kobayashi and T. Honma, Macromolecules, 2015, 48, 462–475 CrossRef.
- Y. Sakaki, R. Usami, A. Tohsan, P. Junkong and Y. Ikeda, RSC Adv., 2018, 8, 10727–10734 RSC.
- A. Tohsan, Y. Yasuda, R. Usami, T. Ohashi, Y. Sakaki, P. Junkong and Y. Ikeda, Kautsch. Gummi Kunstst., 2018, 6, 111–115 Search PubMed.
- ACS News Service Weekly PressPac, https://www.acs.org/content/acs/en/pressroom/presspacs/2015/acs-presspac-february-11-2015/new-insight-into-how-rubber-is-made-could-improve-tires-reduce-air-pollution.html, accessed July 2018.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef.
- D. Maugis and M. Barquins, J. Phys., Lett., 1981, 42, 95–97 CrossRef.
- K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. A, 1971, 324, 301–313 CrossRef.
- M. Salerno, S. Dante, N. Patra and A. Diaspro, Microsc. Res. Tech., 2010, 73, 982–990 Search PubMed.
- Y. Ikeda, Y. Yasuda, K. Hijikata, M. Tosaka and S. Kohjiya, Macromolecule, 2008, 41, 5876–5884 CrossRef.
- Y. Sun, B. Akhremitchev and G. C. Walker, Langmuir, 2004, 20, 5837–5845 CrossRef PubMed.
- B. V. Derjaguin, V. M. Muller and Y. U. P. Toporov, J. Colloid Interface Sci., 1975, 53, 314–326 CrossRef.
- N. Bouchonville, M. Meyer, C. Gaude, E. Gay, D. Ratel and A. Nicolas, Soft Matter, 2016, 12, 6232–6239 RSC.
- M. S. Weiss, J. Appl. Crystallogr., 2000, 34, 130–135 CrossRef.
- M. S. Weiss and R. Hilgenfeld, J. Appl. Crystallogr., 1997, 30, 203–205 CrossRef.
- S. Nagai, S. Fujinami, K. Nakajima and T. Nishi, Compos. Interfaces, 2009, 16, 13–25 CrossRef.
- K. Nakajima, H. Liu, M. Ito and S. Fujinami, J. Vac. Soc. Jpn., 2013, 56, 258–266 CrossRef.
- S. Fujinami, K. Nakajima and T. Nishi, Nippon Gomu Kyokaishi, 2011, 84, 171–175 CrossRef.
- G. Stan, C. V. Ciobanu, P. M. Parthangal and R. F. Cook, Nano Lett., 2007, 7, 3691–3697 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: A conversion of force–distance curve to force–deformation curve. See DOI: 10.1039/c8ra06669h |
| This journal is © The Royal Society of Chemistry 2018 |