DOI:
10.1039/C8RA06768F
(Paper)
RSC Adv., 2018,
8, 35735-35743
Retention and diffusion of transmutation H and He atoms in Be12Ti: first-principles calculations
Received
12th August 2018
, Accepted 5th October 2018
First published on 19th October 2018
Abstract
The beryllide Be12Ti is considered to be the most promising candidate material for advanced plasma facing materials in future fusion reactors because of its excellent performance. In this work, first-principles calculations were conducted to gain insight into the retention and diffusion behavior of transmutation H and He atoms in Be12Ti. The solution energy and migration energy of single impurity H/He atoms were computed to study the behavior of their retention and diffusion. Among seven stable interstitial sites, H atoms preferentially occupy the octahedral interstitial site, Ioct, whereas He atoms preferentially occupy the dodecahedral interstitial site, Idode. The solubility of H is much higher than that of He in Be12Ti. When monovacancy is generated, H atoms preferentially stay in the vicinity of Be1 vacancies, while He atoms tend to reside in the center of Ti vacancies. The migration energy barrier of a single He atom between first near-neighbor Idode sites is 0.35 eV. For H atoms, the migration energy barrier from Idode to Itetra2 is 0.45 eV. The barrier along the paths Itri1–Idode–Itri1 is 0.38 eV. When a Be3 vacancy is introduced as the neighbour of Itri1, the migration energy barrier increases to 0.77 eV. These results indicate that vacancies can trap impurity atoms and may act as seeds for bubble formation.
1 Introduction
For future nuclear applications – such as the DEMO reactor – plasma facing materials (PFMs) would experience high flux particles (H isotopes and He), high-energy neutron irradiation, heat flux, thermomechanical stress, surface sputtering and erosion, etc. The blanket material may need to withstand the severe conditions of high temperatures up to 600–900 °C, high neutron doses of ∼50 dPa, and high He generation (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 appm).1 Therefore, advanced PFMs are urgently desired and beryllium intermetallic compounds (beryllides) have been proposed as candidate materials. Be12X (X is Ti, V, Mo, or W) was pre-selected as one of the candidate materials due to the low radioactivity and high melting point of Ti, V, Mo, and W metals. Besides, the structure of Be12X has good oxidation resistance and high Be content.2–4 Of the pre-selected beryllides, the main research has been focused on Be12Ti due to its relatively easy fabrication.5,6 It was indicated that the compatibility between Be12Ti and the structural material SS316LN was much better than that of Be and SS316LN.7 On the other hand, the swelling of Be12Ti was expected to be smaller than that of Be under high temperature neutron irradiation.8 Be12Ti had fewer irradiation defects than Be under He ion and electron irradiation.9 Furthermore, it was indicated that the amount of tritium retained in Be12Ti was much smaller than that in Be.10
000 appm).1 Therefore, advanced PFMs are urgently desired and beryllium intermetallic compounds (beryllides) have been proposed as candidate materials. Be12X (X is Ti, V, Mo, or W) was pre-selected as one of the candidate materials due to the low radioactivity and high melting point of Ti, V, Mo, and W metals. Besides, the structure of Be12X has good oxidation resistance and high Be content.2–4 Of the pre-selected beryllides, the main research has been focused on Be12Ti due to its relatively easy fabrication.5,6 It was indicated that the compatibility between Be12Ti and the structural material SS316LN was much better than that of Be and SS316LN.7 On the other hand, the swelling of Be12Ti was expected to be smaller than that of Be under high temperature neutron irradiation.8 Be12Ti had fewer irradiation defects than Be under He ion and electron irradiation.9 Furthermore, it was indicated that the amount of tritium retained in Be12Ti was much smaller than that in Be.10
However, the irradiation response of Be12Ti has not yet been completely clarified due to the lack of an accessible fusion environment. More work must be carried out to identify the fundamental processes occurring during irradiation damage. In particular, it is vitally important to understand how the defects are generated and lead to macroscopic changes not only by means of experiments but also with numeric simulations. First-principles density functional theory (DFT) is a powerful and reliable tool for exploring the atomistic behavior of defects in materials.11,12 So far, there has been relatively little theoretical effort devoted to the study of the performance of Be12Ti in nuclear reactors. Jackson et al. have investigated the stability of intrinsic point defects (self-interstitial atoms and vacancies) and the interactions between them in Be12X using DFT simulations.13 Peng et al. have conducted theoretical investigations on the structural, elastic and electronic properties under pressure.14,15
In addition, H and He impurities are inevitably generated in the blanket materials due to transmutation reactions. The aggregation and accumulation of them will result in the formation of H/He bubbles, and finally the degradation of the mechanical properties, such as swelling, creep, and embrittlement, which have been validated in various metals.16–19 Unfortunately, so far there have been few theoretical simulation studies on the behaviour of the impurity H and He atoms in Be12Ti. Only the solution energy of H in Be12Ti has been determined using first-principles electronic structure methods.20 Atomistic simulations are helpful for a better understanding of the properties of defects due to inaccessible observation from experiments.
In order to better understand the behavior of H and He atoms in Be12Ti, the fundamental properties of retention and diffusion processes for H and He atoms have to be studied from first principles. In the present work, the primary research concentrates on the stable positions of interstitial H and He atoms and individual H and He atoms within monovacancies, the lowest-energy diffusion path and corresponding migration energies. This paper is organized as follows: in Section 2, after a brief description of the computational methodology including parameter settings, the crystal structure of Be12Ti is described; the detailed simulation results and discussion are presented in Section 3; and a brief conclusion is given in Section 4.
2 Computational methodology
All first-principles calculations were performed using the Vienna Ab initio Simulation Package (VASP)21,22 using the plane-wave pseudo-potential approach.23,24 The projector-augmented wave (PAW) potentials25,26 for the ion–electron interaction and the generalized gradient approximation (GGA) with a PW91 functional27 for the exchange–correlation interaction are adopted. A tetragonal supercell of 2 × 2 × 2 containing 208 atoms was used for all defect calculations. The Brillouin zone was sampled with 2 × 2 × 4 k-point meshes generated with the Monkhorst–Pack scheme28 and a cutoff energy of 500 eV was employed to describe the interactions of impurity H/He atoms in Be12Ti. During geometry optimization, all atomic positions were fully relaxed at a constant cell volume until there were energy changes on each atom of less than 1 × 10−6 eV and forces on each atom of less than 0.001 eV Å−1. These parameters, including k-point and cutoff energy convergence, have been proved to be sufficient to give a well-converged total energy. The climbing image nudged elastic band (CI-NEB) method29,30 was used to determine the minimum energy paths and the migration barriers of impurity H/He atoms in bulk Be12Ti.
The crystal structure of Be12Ti shows tetragonal symmetry with the space group I4/mmm.31 Ti atoms occupy the Wyckoff position of the 2a lattice site (0,0,0), Be atoms occupy three symmetrically distinct sites within the structure, here labeled Be1, Be2, and Be3, which occupy the Wyckoff positions of 8f (0.25,0.25,0.25), 8i (0.361,0,0), and 8j (0.277,0.5,0), respectively. The structure of the unit cell for tetragonal Be12Ti is shown in Fig. 1, where red balls, yellow balls, orange balls, and green balls denote Be1 atoms, Be2 atoms, Be3 atoms, and Ti atoms, respectively. In our calculations, the equilibrium lattice parameters of tetragonal Be12Ti were a = b = 7.33 Å and c = 4.14 Å, which are in good agreement with the experimental values (a = b = 7.35 Å and c = 4.19 Å)32 and the CASTEP calculation results (a = b = 7.361 Å and c = 4.163 Å).13 This ensures the accuracy of the present first-principles calculations.
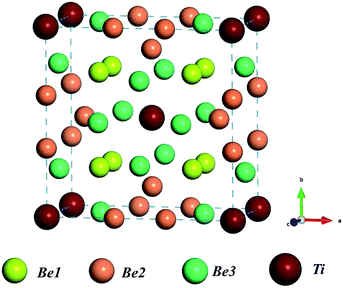 |
| | Fig. 1 Schematic of the unit cell of the Be12Ti crystal structure; red balls, yellow balls, orange balls, and green balls denote Be1 atoms, Be2 atoms, Be3 atoms, and Ti atoms, respectively. | |
3 Results and discussion
3.1 Individual H and He in bulk Be12Ti
To investigate the solution state of H/He impurity atoms in the Be12Ti lattice, we chose 20 sets of interstitial sites in the unit cell of Be12Ti as the initial locations of H/He atoms. After relaxation, seven stable interstitial sites were found, as shown in Fig. 2: an octahedral interstitial site (Ioct) surrounded by four Be3 atoms and two Ti atoms, a tetrahedral interstitial site (Itetra1) surrounded by four Be2 atoms, a trigonal-bipyramid interstitial site (Itri1) surrounded by five atoms (two Be1 atoms, two Be2 atoms, and one Ti atom), a tetrahedral interstitial site (Itetra2) surrounded by four atoms (Ti atom, Be1 atom, and two Be3 atoms), a trigonal-bipyramid interstitial site (Itri2) surrounded by four Be2 atoms and one Be3 atom, a dodecahedral interstitial site (Idode) surrounded by six Be2 atoms and two Be3 atoms, and another tetrahedral interstitial site (Itetra3) surrounded by four atoms (two Be1 atoms, one Be2 atom, and one Be3 atom). To determine the most preferential site for impurity H/He atoms, the solution energies of H/He atoms in these interstitial sites were calculated by:33| | |
EsH(int) = E(nA + H) − E(nA) − E(H2)/2
| (1) |
and| | |
EsHe(int) = E(nA + He) − E(nA) − E(He)
| (2) |
respectively, where A denotes the host lattice of Be12Ti, n is the number of atoms in a supercell without defects; E(nA) is the energy of a perfect supercell; E(nA + H/He) is the energy of a supercell with an interstitial H/He atom; E(H2)/2 is one half of the energy of a gas-phase H2 molecule, which is −3.385 eV according to our calculation; E(He) is the energy of an isolated He atom. By definition, a positive solution energy denotes endothermicity, while a negative solution energy denotes exothermicity. The zero-point energy (ZPE) should be taken into consideration in the system involving light elements, which is calculated by 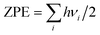 , where h is the Planck constant and ν is the real normal mode frequency. The ZPE-corrected H solution energy should be defined as:34
, where h is the Planck constant and ν is the real normal mode frequency. The ZPE-corrected H solution energy should be defined as:34| | |
EsH(int)ZPE = EsH(int) + ΔZPE = EsH(int) + {ZPE(nA + H) − ZPE(nA) − ZPE(H2)/2}
| (3) |
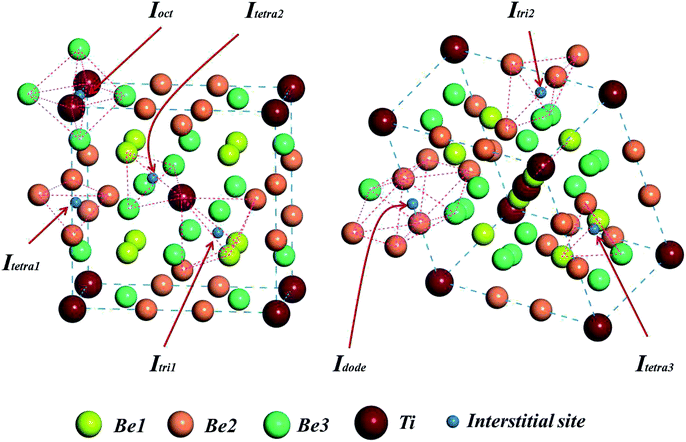 |
| | Fig. 2 Seven energetically favorable interstitial configurations within a unit cell of the Be12Ti structure. | |
Since the vibrations of the bulk metal are negligible compared to those of atomic H in an interstitial site, ZPE(nA) was ignored and ZPE(nA + H) was replaced with ZPE(H) in our calculations. ZPE(H2) is 0.28 eV. The ZPE-corrected He solution energy is similar to eqn (3). ZPE(He) is about 0.01 eV. The solution energies of interstitial H/He atoms and the corresponding ZPE-corrected solution energies are all shown in Table 1. As we can see, the solution energies of interstitial H/He atoms are positive, which means that the incorporation of impurity H/He atoms is always an endothermic process. Since He atoms have a closed-shell electronic structure and bonding interactions are small, its solubility in materials is extremely low.35,36 The solubility of H atoms in materials can vary as the phase structure changes. For example, the solutions of H atoms in Fe, Ni, W, Be, Pt, Cu, Ag and Au are endothermic, while those in V, Ti, Nb, Ta and Pd are exothermic.34 The solution energies of He atoms are 4.03 eV, 4.38 eV, 4.53 eV, and 4.87 eV for Idode, Itetra1, Ioct and Itri1, respectively. After relaxation, He atoms at Itetra2, Itetra3, and Itri2 interstitial sites have been proved to be unstable: the interstitial He atom at Itetra2 or Itetra3 will diffuse to Idode and the He atom at Itri2 will diffuse to Ioct. It is indicated that Idode is the most energetically favorable site for a single He atom in Be12Ti. The dodecahedron has a larger volume than other polyhedra, which provides a lower charge density for the accommodation of He atoms. For interstitial H atoms, the sequence of solution energies is Ioct < Itetra2 < Itri2 < Itetra1 < Itri1 < Itetra3 < Idode. The solution energy is lowest at Ioct, with 0.50 eV. However, the solution energy is largest at Idode, with 1.30 eV. It is indicated that H atoms preferentially occupy Ioct. Itetra1, Itri1 and Itri2 have nearly equal solution energies. Ioct sites are surrounded by four Be3 atoms and two Ti atoms. Idode sites are surrounded by six Be2 atoms and two Be3 atoms. The solution of H atoms into Be metal is endothermic, while the solution of H atoms in Ti metal is exothermic, that is the interactions of H atoms with Ti atoms are stronger those that of H atoms with Be atoms, so H atoms preferentially occupy the Ioct site. As a distinct difference between the interstitial H and He, the solution energy of H is substantially lower than that of He, indicating that the solubility of H in Be12Ti is much higher than that of He, which is similar to that of Be metal.37 In addition, the effect of ZPE on the solution energies of interstitial H/He varies from 0.03 to 0.11 eV, and the preferential site for H/He atoms in bulk Be12Ti remains unchanged after ZPE correction.
Table 1 Solution energies of single H and He atoms in Be12Ti
| Configuration |
Ioct |
Idode |
Itetra1 |
Itetra2 |
Itetra3 |
Itri1 |
Itri2 |
| EsH(int) |
0.50 |
1.30 |
0.94 |
0.80 |
1.20 |
0.98 |
0.92 |
| EsH(int)ZPE |
0.57 |
1.40 |
1.06 |
0.93 |
1.36 |
1.07 |
1.05 |
| EsHe(int) |
4.53 |
4.03 |
4.38 |
— |
— |
4.87 |
— |
| EsHe(int)ZPE |
4.58 |
4.10 |
4.42 |
— |
— |
4.98 |
— |
To interpret the difference of H/He occupation in perfect Be12Ti, Fig. 3 shows the site-projected electronic density of states (DOS) of H/He interstitial defects and the nearest-neighbor metal atom in Be12Ti. As we can see from Fig. 3(a) and (b), the embedded H/He atoms cause distortion of the DOS of the neighboring Ti and Be metal atoms, which indicates ongoing hybridization. Larger distortion of the DOS at the metal site corresponds to the larger solution energy of H/He defects. Fig. 3(c) shows the s-projected DOS of H at Ioct, Idode, Itetra1, and Itetra2. Fig. 3(d) shows the p-projected DOS of He at Ioct, Idode, Itetra1, and Itri1. The position of the Fermi energy level relative to the peaks in the DOS determines the occupation of the states and the nature of the bonding.38 The lower the DOS at the Fermi energy level, the more energetically favorable the corresponding defect configuration. It can be seen from Fig. 3(c) that the interaction of Ioct H with its neighbor metal atoms leads to a lower DOS at the Fermi energy level than that of other H interstitials, which indicates the stronger bonding at the Ioct site. The DOSs of He interstitials at the Fermi energy level rank in a sequence of Idode < Itetra1 < Ioct < Itri1, which is in agreement with the order of the site preference of He in Be12Ti.
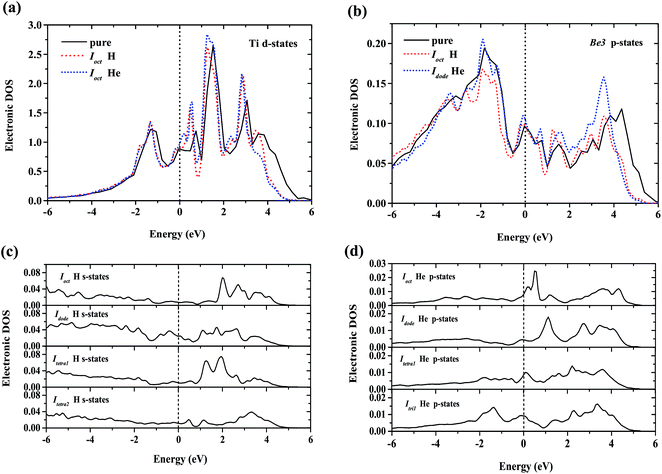 |
| | Fig. 3 (a) Local DOS for H/He nearest-neighbor Ti atom; (b) local DOS for H/He nearest-neighbor Be3 atom; (c) local DOS for interstitial H atoms – the s-projected DOS of H at Ioct, Idode, Itetra1, and Itetra2; (d) local DOS for interstitial He atoms – the p-projected DOS of He at Ioct, Idode, Itetra1, and Itri1. The Fermi energy of the supercell with the H/He defect is 0.00 eV. | |
3.2 Individual H/He within a monovacancy in Be12Ti
As a PFM for nuclear energy applications, Be12Ti is inevitably subject to high temperatures and particle fluxes that induce the generation of large numbers of vacancies. Four types of vacancy can be formed in bulk Be12Ti under irradiation. The formation energies of the vacancies were calculated using the following formula:| | |
EfVA = E((n − 1)A) − E(nA) + E(Be/Ti)
| (4) |
where E((n − 1)A) is the energy of a supercell with a vacancy and E(Be/Ti) is the chemical potential of the Be or Ti host. Hexagonal close-packed bulk Be and Ti are adopted as the reference elemental Be and Ti solids, respectively. The formation energies of the vacancies are listed in Table 2. It can be seen that the Be2 vacancy has the lowest formation energy of 1.44 eV, which indicates that the Be2 vacancy is easier to form than the other types of vacancy in Be12Ti. The formation energy of the Ti vacancy of 3.92 eV is much larger than that of the Be vacancies, indicating that the formation of Ti vacancies is very difficult in Be12Ti. The present results are in good agreement with the previous CASTEP results.13
Table 2 Vacancy (VA) formation energies (EfVA) in Be12Ti
| Configuration |
VABe1 |
VABe2 |
VABe3 |
VATi |
| This work |
1.65 |
1.44 |
1.56 |
3.92 |
| Previous work13 |
1.60 |
1.43 |
1.53 |
4.10 |
The theoretical and experimental research demonstrates that vacancies can reduce the charge density of their vicinity, leading to the aggregation and binding of impurity atoms at these sites.39,40 Thus, it is important to shed light on the capacity of the four types of vacancy to trap H/He atoms. The solution energies for single H/He atoms within monovacancies in Be12Ti are computed as follows:
| | |
EsH(VA) = E((n − 1)A + H) − E((n − 1)A) − E(H2)/2
| (5) |
and
| | |
EsHe(VA) = E((n − 1)A + He) − E((n − 1)A) − E(He)
| (6) |
respectively. What is the most preferential position for a single H/He atom in a Be
12Ti solid containing a monovacancy? Several possible initial positions were considered: vacancy centers and the adjacent interstitial sites of vacancies. These configurations and the corresponding solution energies of H/He are illustrated in
Fig. 4 and
6, respectively, where (a)–(d) show that the H/He atoms are initially placed at a vacancy center, and (e)–(h) show that H/He atoms are initially placed at stable or metastable interstitial sites near the vacancies. The hollow circles of different colours represent corresponding vacancies; pink balls denote H atoms and dark blue balls denote He atoms. The plane direction of each schematic is labeled. In
Fig. 4(a), the solution energy of H atoms at Ti vacancy centers is 2.03 eV, which is less favorable than that of interstitial H sites in perfect Be
12Ti. When placing H at an
Ioct site near a Ti vacancy, its solution energy reduces to 0.17 eV as shown in
Fig. 4(e). After relaxation, a H atom at
Itetra2 close to a Be1 vacancy moves 0.35 Å towards the Be1 vacancy with
Es = −0.26 eV, which is much lower than that of H staying at the Be1 vacancy center (
Es = 0.78 eV) as shown in
Fig. 4(b) and (f). A H atom within a Be2 vacancy center moves towards a Ti atom by a distance of 0.765 Å with a solution energy of 0.06 eV, as shown in
Fig. 4(c). When putting H at an
Itetra2 site near a Be2 vacancy, it shifts towards the Be2 vacancy by 1.24 Å with
Es = −0.17 eV, as shown in
Fig. 4(g). A H atom at a Be3 vacancy center moves to
Ioct with
Es = −0.01 eV, as shown in
Fig. 4(d). In conclusion, H atoms preferentially occupy the neighbouring interstitial sites of the vacancy rather than the vacancy center. The capacity for vacancy trapping single H atoms follows the order VA
Be1 > VA
Be2 > VA
Be3 > VA
Ti.
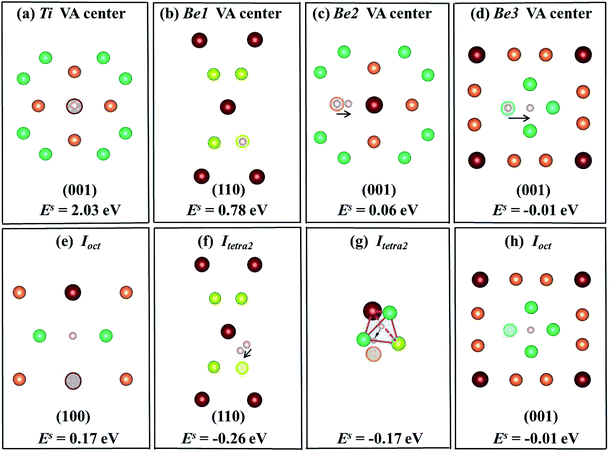 |
| | Fig. 4 Schematic diagrams and corresponding solution energies of a single H atom in the vacancy centers ((a)–(d)) and interstitial sites near vacancies ((e)–(h)) in the Be12Ti solid. The hollow circles of different colours represent the corresponding vacancies and pink balls denote H atoms. | |
To describe the behaviour of H preferentially occupying the neighbouring interstitial sites of a vacancy rather than the vacancy center, we have computed the local densities of states (LDOS) of selected H and their nearest-neighbor metal atoms. As shown in Fig. 5(a), the p-projected DOSs of Be3 for the H in the center of VATi and Ioct H within VATi produce distortion compared to that of the pure material with a VATi, and the DOS of Be3 for the H in the center of VATi deforms more than that of Ioct H within VATi. The s-projected DOS of H at the Fermi energy level for H in the center of VATi is larger than that of Ioct H within VATi, as shown in Fig. 5(b). It is indicated that H in the VATi center is less energetically stable than Ioct H within VATi. The deformation of the d-projected DOSs of Ti for the H in the center of VABe1 and Itetra2 H within VABe1 compared with that of the pure material with a VABe1, as shown in Fig. 5(a), is visible, and the s-projected DOS of H at the Fermi energy level for H in the center of VABe1 is slightly larger than that of Itetra2 H within VABe1, as shown in Fig. 5(b).
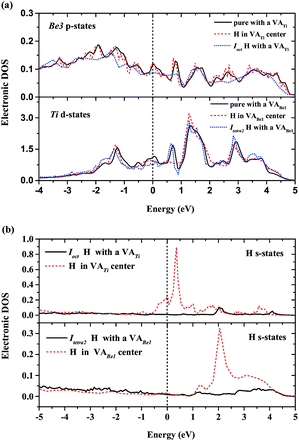 |
| | Fig. 5 (a) Local DOS for vacancy nearest-neighbor Ti and Be3 atoms; (b) local DOS for interstitial H atoms within VATi and VABe1. The Fermi energy of the supercell with the H defect is 0.00 eV. | |
The most energetically preferable site for one He atom is the Ti vacancy center with the lowest solution energy of 0.94 eV (Fig. 6(a)). After relaxation, He atoms at nearest neighbouring interstitial sites, Ioct, spontaneously move into the Ti vacancy centers with an athermal process as shown in Fig. 6(e). The solution energy is 3.10 eV when the He atom is placed at the Be1 vacancy center (Fig. 6(b)), but the He atom at the Itri1 site shifts 0.74 Å towards the Be1 vacancy with a solution energy of 2.81 eV (Fig. 6(f)), which is smaller than that at the Be1 vacancy center. The He atom at the Be2 vacancy center moves to an interstitial site, which is very close to Idode with a distance of only 0.37 Å. The He atom at the Idode site moves nearly the same distance of 0.36 Å towards the Be2 vacancy. The solution energies in these two cases are 1.90 eV, as shown in Fig. 6(c) and (g), respectively. When a He atom is initially placed at the Be3 vacancy center, it moves 0.667 Å towards an adjacent Idode site (Fig. 6(d)). As shown in Fig. 6(h), a He atom is initially located at an Idode site close to the Be3 vacancy and it moves towards the Be3 vacancy and finally arrives at a position, which is 0.687 Å from the Be3 vacancy center. The two cases have the same solution energy of 2.73 eV. It follows that the capacity of vacancies for trapping single He atoms satisfies the sequence VATi > VABe2 > VABe3 > VABe1. It was found that He atoms preferentially occupy Ti vacancy centers, which is different to H. Such trends are similar to the behaviour of H and He inside a hcp Be solid.37 The solution energies of H/He within a monovacancy in the stable states are much lower than those in a perfect supercell, indicating that the impurity atoms are preferentially trapped by vacancies. This is accordance with the fact that a larger volume of vacancy is available for the accommodation of impurity atoms.
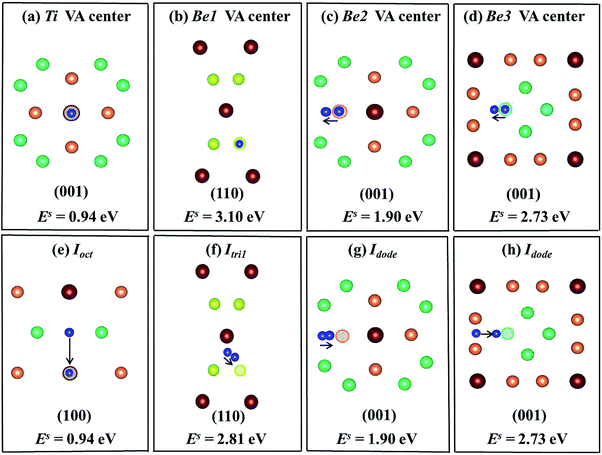 |
| | Fig. 6 Schematic diagrams and corresponding solution energies of a single He atom in the vacancy centers ((a)–(d)) and interstitial sites near vacancies ((e)–(h)) in the Be12Ti solid. The hollow circles of different colours represent corresponding vacancies and dark blue balls denote He atoms. | |
3.3 The diffusion of a single H/He atom in Be12Ti
Concerning the kinetics of H/He atoms in the Be12Ti solid, we mainly examined the diffusion of interstitial H/He atoms, which is relevant to the initial stage after implantation or production of impurity H/He atoms. The diffusion mechanism of impurity H/He atoms was studied in terms of possible diffusion paths and the corresponding migration energies using the CI-NEB method. Here, we studied the diffusion of a single H/He atom between the relatively stable interstitial sites in a perfect Be12Ti solid and the diffusion of a single H/He atom from a monovacancy to a stable interstitial site. Idode is the most energetically favorable interstitial site of He. Fig. 7 shows a path from one Idode site to its first nearest-neighbor (1nn) Idode site passing through an Itetra1 site in perfect Be12Ti (Idode–Itetra1–Idode). The migration energy barrier is 0.35 eV, which is nearly equal to the migration energy of a single He along the BT–CN–BT path in Be metal.41
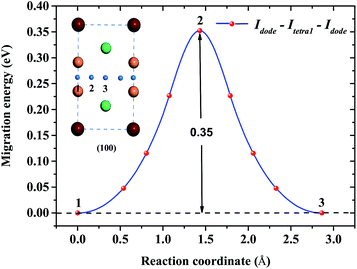 |
| | Fig. 7 Diffusion path between two 1nn Idode sites passing through an Itetra1 site for He atoms and its migration energy profile. | |
For a single H atom, Ioct is the most energetically favorable interstitial site. Fig. 8(a) shows a diffusion path from Ioct to its nearest-neighbor, Itetra2. The migration energy barrier is 0.45 eV. It can be seen from Fig. 8(b) that Ioct is more stable than Itetra2 by 0.30 eV, which is in agreement with their solution energies. In Fig. 9, another diffusion path between metastable interstitial sites (Itri1–Idode–Itri1) is also considered, where Idode is the transition state. The migration energy barrier is 0.38 eV and the saddle point of the path is exactly right at the Idode site. When a Be3 vacancy is introduced as the neighbour of Itri1, the H atom shifts 0.23 Å towards the Be3 vacancy. The diffusion path and corresponding migration energy profile are also depicted in Fig. 9 for comparison. The migration energy increases to 0.77 eV, but the barrier of the H atom from the Idode site to the Be3 vacancy is 0.20 eV. As we can see, the migration energy barrier increases when the H atom migrates from the vacancy to the interstitial site, which is attributed to the vacancy trapping of H atoms. These results imply that the diffusion of impurity atoms is relatively fast in the perfect Be12Ti solid. When vacancy defects exist, the diffusion of impurity atoms is impeded so that they cannot easily migrate, but to some extent segregate to form bubbles.
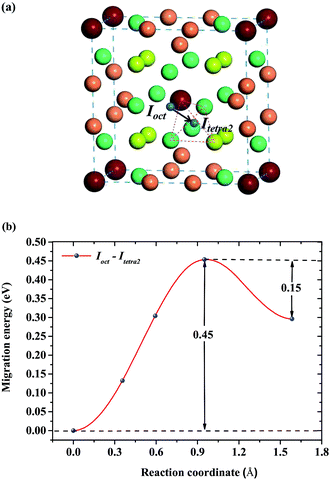 |
| | Fig. 8 (a) Diffusion path from Ioct to its nearest-neighbor Itetra2 for H atoms. (b) Corresponding migration energy profile. | |
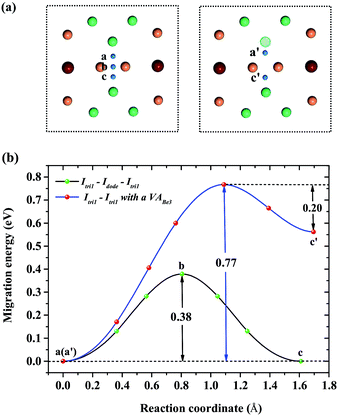 |
| | Fig. 9 (a) Diffusion paths Itri1–Idode–Itetra1 and Itri1–Itetra1 with a VABe3 for H atoms. (b) Corresponding migration energy profiles. | |
4 Summary and conclusions
The retention and diffusion behavior of H/He impurities in Be12Ti solid has been investigated using first-principles calculations. Among seven stable interstitial sites, H atoms preferentially occupy the octahedral interstitial site, Ioct, with a solution energy of 0.5 eV, whereas He atoms preferentially occupy the dodecahedral interstitial site, Idode, with a solution energy of 4.03 eV. The effect of ZPE on the solution energies of H/He varies from 0.03 to 0.11 eV, and the preferential sites for H/He atoms remain unchanged after ZPE correction. The solution energy of H atoms is much lower than that of He atoms, indicating that the solubility of H atoms in Be12Ti is much higher than that of He atoms. When monovacancies are present in Be12Ti, H atoms tend to stay in the vicinity of the Be1 vacancy with a solution energy of −0.26 eV, while He atoms will reside in the Ti vacancy center with a solution energy of 0.94 eV. The capacities of four types of vacancy to trap impurity atoms are different: it follows the sequence VABe1 > VABe2 > VABe3 > VATi for single H atoms, and VATi > VABe2 > VABe3 > VABe1 for single He atoms. The solution energies of H/He within a monovacancy in the stable states are much lower than that in a perfect supercell, indicating that the impurity atoms are preferentially trapped by vacancies. The migration energy barrier of a single He atom between first near-neighbor Idode sites passing through Idode is 0.35 eV. For a single H atom, the migration energy barriers from Ioct to its nearest-neighbor Itetra2 is 0.45 eV. It can be seen that the diffusion of single H/He in perfect Be12Ti is relatively fast due to the lower migration energy barriers. The migration energy barrier along the diffusion path Itri1–Idode–Itetra1 for a single H atom is 0.38 eV. When a Be3 vacancy is introduced as the neighbour of Itri1, the barrier increases to 0.77 eV. These results imply that vacancies can trap impurity atoms and may act as seeds for bubble formation. The current first-principles results can provide the fundamental parameters for and microscopic effects of impurity H and He atoms on Be12Ti, and are helpful to better understand the aggregation of impurity atoms and bubble formation in the early stages of irradiation damage.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grant No. 2016YFB0200504), the Bureau of International Cooperation, Chinese Academy of Foreign Cooperation Key Projects (Grant No. 113462KYSB20160040), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA21010202) and the National Natural Science Foundation of China (Grant No. 11747306).
References
- K. Tsuchiya, T. Hoshino, H. Kawamura, Y. Mishima, N. Yoshida, T. Terai, S. Tanaka, K. Munakata, S. Kato, M. Uchida, M. Nakamichi, H. Yamada, D. Yamaki and K. Hayashi, Nucl. Fusion, 2007, 47, 1300–1306 CrossRef CAS.
- H. Yamada, Y. Nagao, H. Kawamura, M. Nakao, M. Uchida and H. Ito, Fusion Eng. Des., 2003, 69, 269–273 CrossRef CAS.
- H. Kawamura, H. Takahashi, N. Yoshida, V. Shestakov, Y. Ito, M. Uchida, H. Yamada, M. Nakamichi and E. Ishitsuka, Fusion Eng. Des., 2002, 61–62, 391–397 CrossRef CAS.
- P. Kurinskiy, A. Moeslang, V. Chakin, M. Klimenkov, R. Rolli, S. van Til and A. A. Goraieb, Fusion Eng. Des., 2013, 88, 2198–2201 CrossRef CAS.
- M. Nakamichi and K. Yonehara, J. Nucl. Mater., 2011, 417, 765–768 CrossRef CAS.
- M. Nakamichi and J.-H. KimFusion, Fusion Eng. Des., 2014, 89, 1304–1308 CrossRef CAS.
- H. Kawamura, M. Uchida and V. Shestakov, J. Nucl. Mater., 2002, 307–311, 638–642 CrossRef CAS.
- M. Uchida, E. Ishitsuka and H. Kawamura, J. Nucl. Mater., 2002, 307–311, 653–656 CrossRef CAS.
- H. Takahashi, T. Shibayama, M. Uchida, H. Kawamura and Y. Ito, JAERI-Rev., 2002, 2002-011, 142–152 Search PubMed.
- N. Yoshida, H. Iwakiri, H. Kawamura and Y. Ito, JAERI-Rev., 2002, 2002-011, 58–69 Search PubMed.
- T. W. He, Y. H. Jiang, R. Zhou and J. Feng, RSC Adv., 2016, 6, 45250–45258 RSC.
- J. Z. Duan, J. R. Zhang, C. L. Wang, Y. Qiu, W. S. Duan and L. Yang, RSC Adv., 2014, 79, 42014–42021 RSC.
- M. L. Jackson, P. A. Burr and R. W. Grimes, Nucl. Fusion, 2017, 57, 086049 CrossRef.
- X. K. Liu, W. Zhou, X. Liu and S. M. Peng, RSC Adv., 2015, 5, 59648 RSC.
- S. M. Peng, J. Nucl. Mater., 2015, 464, 230–235 CrossRef CAS.
- S. T. Yang, N. W. Hu, X. Q. Gou, C. L. Wang, X. L. Zhu, W. S. Duan and L. Yang, RSC Adv., 2016, 6, 59875 RSC.
- F. Scaffidi-Argentina, G. Piazza and R. Rolli, Fusion Eng. Des., 2003, 69, 505 CrossRef CAS.
- V. P. Chakin, A. O. Posevin and I. B. Kupriyanov, J. Nucl. Mater., 2007, 367–370, 1377–1381 CrossRef CAS.
- S. P. Vagin, P. V. Chakrov, B. D. Utkelbayev, L. A. Jacobson, R. D. Field and H. Kung, J. Nucl. Mater., 1998, 258–263, 719–723 CrossRef CAS.
- Y. Fujii, M. Miyamoto, J.-H. Kim, M. Nakamichi, N. Murayoshi and H. Iwakiri, Nuclear Materials and Energy, 2016, 9, 233–236 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohna and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. E. Bląğochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- G. Henkelman and H. Jonsson, J. Phys. Chem., 2000, 113, 9978 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Phys. Chem., 2000, 113, 9901 CrossRef CAS.
- E. Gillam, H. P. Rooksby and L. D. Brownlee, Acta Crystallogr., 1964, 17, 762–763 CrossRef CAS.
- A. Zalkin, D. E. Sands, R. G. Bedford and O. H. Krikorian, Acta Crystallogr., 1961, 14, 63–65 CrossRef CAS.
- C. Freysoldt, B. Grabowski, T. Hickel and J. Neugebauer, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- K. Lee, M. Yuan and J. Wilcox, J. Phys. Chem. C, 2015, 119, 19642–19653 CrossRef CAS.
- T. Seletskai, Y. Osetsky, R. E. Stoller and G. M. Stocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 78, 134103 CrossRef.
- X. T. Zu, L. Yang, F. Gao, S. M. Peng, H. L. Heinisch, X. G. Long and R. J. Kurtz, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 054104 CrossRef.
- P. B. Zhang, J. J. Zhao and B. Wen, J. Phys.: Condens. Matter, 2012, 24, 095004 CrossRef PubMed.
- R. Pentcheva and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155418 CrossRef.
- J. K. Nø rskov, F. Besenbacher, J. Bøttiger, B. B. Nielsen and A. A. Pisarev, Phys. Rev. Lett., 1982, 49, 1420 CrossRef.
- F. Besenbacher, J. K. Nørskov, M. J. Puska and S. Holloway, Phys. Rev. Lett., 1985, 55, 852 CrossRef CAS PubMed.
- P. B. Zhang, J. J. Zhao and B. Wen, J. Nucl. Mater., 2012, 423, 164–169 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Xingming Zhangc,
Huiqiu Dengd,
Wenshan Duan*a and
Lei Yangb
ab,
Xingming Zhangc,
Huiqiu Dengd,
Wenshan Duan*a and
Lei Yangb
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 appm).1 Therefore, advanced PFMs are urgently desired and beryllium intermetallic compounds (beryllides) have been proposed as candidate materials. Be12X (X is Ti, V, Mo, or W) was pre-selected as one of the candidate materials due to the low radioactivity and high melting point of Ti, V, Mo, and W metals. Besides, the structure of Be12X has good oxidation resistance and high Be content.2–4 Of the pre-selected beryllides, the main research has been focused on Be12Ti due to its relatively easy fabrication.5,6 It was indicated that the compatibility between Be12Ti and the structural material SS316LN was much better than that of Be and SS316LN.7 On the other hand, the swelling of Be12Ti was expected to be smaller than that of Be under high temperature neutron irradiation.8 Be12Ti had fewer irradiation defects than Be under He ion and electron irradiation.9 Furthermore, it was indicated that the amount of tritium retained in Be12Ti was much smaller than that in Be.10
000 appm).1 Therefore, advanced PFMs are urgently desired and beryllium intermetallic compounds (beryllides) have been proposed as candidate materials. Be12X (X is Ti, V, Mo, or W) was pre-selected as one of the candidate materials due to the low radioactivity and high melting point of Ti, V, Mo, and W metals. Besides, the structure of Be12X has good oxidation resistance and high Be content.2–4 Of the pre-selected beryllides, the main research has been focused on Be12Ti due to its relatively easy fabrication.5,6 It was indicated that the compatibility between Be12Ti and the structural material SS316LN was much better than that of Be and SS316LN.7 On the other hand, the swelling of Be12Ti was expected to be smaller than that of Be under high temperature neutron irradiation.8 Be12Ti had fewer irradiation defects than Be under He ion and electron irradiation.9 Furthermore, it was indicated that the amount of tritium retained in Be12Ti was much smaller than that in Be.10

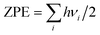 , where h is the Planck constant and ν is the real normal mode frequency. The ZPE-corrected H solution energy should be defined as:34
, where h is the Planck constant and ν is the real normal mode frequency. The ZPE-corrected H solution energy should be defined as:34







