Open Access Article
Open Access ArticleThe adsorption and aggregation properties of dendritic cationic tetrameric surfactants†
Yangchun Xiea,
Jie Li *a,
Zuofeng Lib,
Tong Suna,
Yipeng Wanga and
Guangmiao Qua
*a,
Zuofeng Lib,
Tong Suna,
Yipeng Wanga and
Guangmiao Qua
aCollege of Chemistry and Chemical Engineering, Northeast Petroleum University, Daqing, 163318, P. R. China. E-mail: lijie838@nepu.edu.cn
bNatural Gas Branch Testing Center, Daqing Oil Field Co. Ltd., Daqing, 163321, China
First published on 23rd October 2018
Abstract
A series of dendritic cationic tetrameric surfactants (4CntetraQ, n = 12, 14, 16) were synthesized with raw materials that are commercially available. The adsorption and aggregation properties of the synthesized surfactants were studied using the Wilhelmy plate method, electrical conductivity, fluorescence spectra and dynamic light scattering techniques, and surface chemical parameters and thermodynamics parameters were obtained, respectively. These surfactants have higher surface activities than those of the corresponding monomeric and dimeric surfactants and are more prone to self-assembling in aqueous solution than adsorption at the surface. The thermodynamics parameters reflect that both adsorption and micellization processes of 4CntetraQ are spontaneous, and that the micellization process is entropy-driven. Both adsorption and micellization of 4CntetraQ have a tendency to occur with increasing alkyl chain length or temperature. DLS measurements show that there exist large aggregates at the concentration of 10 times the CMC.
1. Introduction
Gemini surfactants, also called dimeric surfactants, contain two polar head groups and two hydrophobic groups linked by a rigid or flexible spacer.1–3 These surfactants display unusual properties in contrast with the conventional (monomeric) surfactants, for instance, lower critical micelle concentration (CMC), higher efficiency to reduce surface tension, and special aggregation behaviors.4–8 So far, extensive research has been carried out on cationic dimeric surfactants because of their simple synthesis and broad application prospects, for instance, in gene and drug delivery,9,10 nano-materials preparation,11 emulsion polymerization,12 corrosion inhibitors13 and antimicrobial materials.14 The excellent properties of the cationic dimeric surfactants led researchers to synthesize higher oligomeric surfactants, for example, trimeric or tetrameric surfactants,15–18 which consist of three or more hydrophobic and polar head groups connected by different spacers.However, limited research on synthesis and applications of higher oligomeric surfactants was conducted in comparison with dimeric surfactants, probably due to the difficulties in the synthesis.19,20 This, in turn, inspires and stimulates researchers to study synthesis and physicochemical properties of novel kinds of oligomeric surfactants. Now, there have been some research groups working in this area, such as Zana,21 Esumi,22 Laschewsky,23 Menger,28 Ikeda,29 Yoshimura30 and Y. L. Wang,34,35 and many fundamental studies have begun to spring up.
The oligomeric surfactants may be divided into three main types, line-type, dendritic or star-type and ring-type, according to the features of their spacer structures. Zana et al.21 reported synthesis of trimeric and tetrameric surfactants with line-type structures, and they found that the CMC values of these surfactants were lower than those of analogous monomeric or dimeric surfactants. Esumi et al.22 improved the above synthetic method and synthesized the similar trimeric surfactants by one step reaction. Laschewsky23 synthesized three series of line-type trimeric and tetrameric surfactants with rigid spacers, which were characterized of benzene ring or unsaturated double bond in the spacers. With cyanuric chloride as a core, Esumi et al.24 further synthesized the anionic ring-type trimeric surfactants (3CnNAc-Tz, n = 4, 10) which show unique physicochemical properties in alkali solution. Grau et al.25,26 prepared a series of sulfate-type tetrameric surfactants with multiple-ring spacers by three-step reactions from cheap tetraols. A series of ring-type surfactants were synthesized by Regen27 via the quaternization reaction, in which the starting materials could be bought commercially. Menger's group28 synthesized three series of cationic dendritic tetrameric surfactants, referred to as the multiarmed surfactants, in which the key reaction was characteristic of introducing α-carbonyl bromide group in the spacer by acylation reaction. Ikeda29 reported the synthesis of sulfonate-type dendritic trimeric surfactants containing three hydroxyl groups. Yoshimura et al.30 reported the synthesis of anionic-type trimeric surfactants (3CntaAm, n = 8, 10, 12) with tris(2-aminoethyl)amine as a spacer, in which the carbonyl groups were reduced to the methylene groups. To reduce the reaction procedure, they conducted methylation of three primary amine groups in the spacer, then carried out quaterisation and prepared the star-shaped cationic trimeric surfactants (3CntrisQ, n = 8, 10, 12, 14).31 Uner et al.32 synthesized the star-shaped octameric surfactants by copper(I)-catalysed azide–alkyne cycloaddition(CuAAC) click reaction under mild reaction conditions. Tan et al.33 prepared the polyether-type branched tetrameric surfactant (TPE) by anion polymerization with propylene oxide (PO) and ethylene oxide (EO), and the product has good surface activities and may be used as a chemical demulsifier for crude oil emulsions. Wang and co-worker16,17,34–37 synthesized a series of oligomeric surfactants and studied their physicochemical properties in the solution, in which the star-shaped hexameric quaternary ammonium surfactant (PAHB) is a potential condensing agent for gene transfection.19
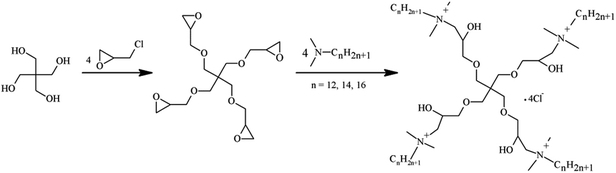
In previous work, the dendritic cationic tetrameric surfactant with alkyl chain of 12 (4C12tetraQ) was synthesized by a simple two-step reaction using commercially available materials.38 This tetrameric surfactant shows good surface activity, emulsifying ability, foam performance, and application prospects. To more understand adsorption and self-assembly behaviors of the cationic tetrameric surfactants with dendritic structures, the paper synthesized this type of surfactants (4CntetraQ, n = 12, 14, 16). Their physicochemical properties were studied by Wilhelmy plate method, electrical conductivity, fluorescence spectra and dynamic light scattering technique.
2. Experimental
2.1 Materials
Ethanol and acetone were purchased from Tianjin Kermel Chemical Reagents Development Centre. Pyrene was purchased from Sigma-Aldrich and recrystallized thrice before use.2.2 Synthesis
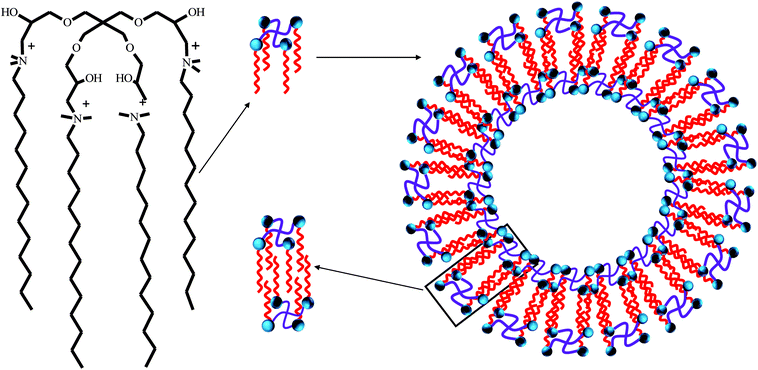
The synthesis route of dendritic cationic tetrameric surfactants with different alkyl chains (4CntetraQ, n = 12, 14, 16) was shown in Fig. 1. The detailed synthesis procedure was listed in the literature.38 Fourier transform infrared (FT-IR) spectra were obtained using a Perkin Elmer Spectrum One (U.S.) by KBr disk method. 1H NMR measurements were carried out using a Bruker Avance III 400 spectrometer (Switzerland) operating at 400 MHz, in which deuteroxide (D2O) was used as a solvent. The elemental analysis measurements were conducted using a Vario EL-III CHNOS instrument (Germany).2.3 Surface tension measurements
Surface tension measurements were carried out using the QBZY-2 automatic tensionmeter (Shanghai Fangrui Instrument Co., Ltd., China) by Wilhelmy plate method. The surfactant solution was aged for 12 hours before measurement. The average of three surface tension measurements of pure water was 71.80 ± 0.04 mN m−1 at 25 °C.2.4 Conductivity measurements
Conductivity measurements of the surfactant solution were conducted by a DDS-11A digital conductimeter (Shanghai Kangyi Instruments Co., Ltd, China). The variations of conductivity vs. concentration of surfactants at different temperature were seen in Fig. 3, and the results were given in Table 2.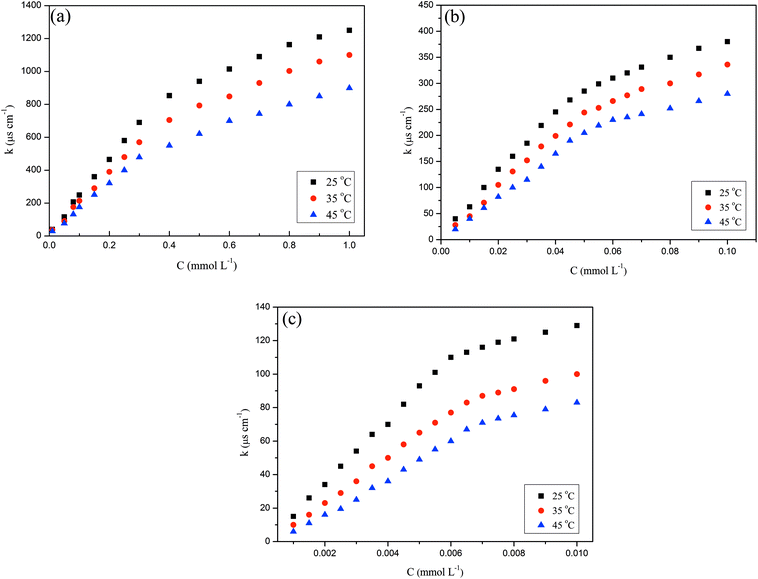 | ||
| Fig. 3 Variations of electrical conductivity (κ) vs. concentration of 4CntetraQ at different temperature: (a), 4C12tetraQ; (b), 4C14tetraQ; (c), 4C16tetraQ. | ||
2.5 Steady-state fluorescence measurements
Steady-state fluorescence measurements were conducted by a PerkinElmer LS-55 spectrofluorometer (PerkinElmer Co., Ltd., U.K.) at 25 °C. All the measurement parameters were given as follows: the excitation wave length, 335 nm; the slit widths of the excitation and emission: 4.5, 2.5 nm, respectively; the range of the emission spectra: 345–460 nm; the scan speed: 20 nm min−1; the concentration of fluorescence probe (pyrene): 1 × 10−7 mol L−1. The intensity ratio (I1/I3) between the first peak (around 372 nm) and the third peak (around 384 nm) may be used to determine the CMC of surfactants and estimate the micellar micropolarity sensed by pyrene.2.6 Dynamic light scattering measurements
Dynamic light scattering (DLS) measurements were performed to investigate the size distribution of surfactants using a Malvern Instruments Zetasizer Nano-ZS90 (Malvern Instrument Ltd, English) at 25 °C. All the experiments were made thrice at a scattering angle of 90° and the wavelength of 633 nm. The sample aqueous solution was filtered by a filter of 0.22 μm (mixed cellulose ester).3. Results and discussion
3.1 Characterization
The chemical structures of the synthesized tetrameric surfactants were confirmed by FTIR, 1H NMR and elemental analysis, and FTIR and 1H NMR spectra were provided in the ESI.†3.2 Surface activity
| Compounds | CMC (mmol L−1) | γCMC (mN m−1) | Γmax/10−6 (mol m−2) | Amin (nm2) | ΠCMC (mN m−1) | pC20 | CMC/C20 | ||
|---|---|---|---|---|---|---|---|---|---|
| n = 4 | n = 5 | n = 4 | n = 5 | ||||||
| a Values are taken from ref. 51.b Values are taken from ref. 52.c Values are taken from ref. 30. | |||||||||
| 4C12tetraQ | 0.39 | 30.29 | 1.09 | 0.88 | 1.52 | 1.89 | 41.51 | 4.40 | 9.79 |
| 4C14tetraQ | 0.0501 | 27.68 | 1.24 | 0.99 | 1.34 | 1.67 | 44.12 | 5.11 | 6.45 |
| 4C16tetraQ | 0.0063 | 26.76 | 1.73 | 1.39 | 0.96 | 1.20 | 45.40 | 5.78 | 3.80 |
| DTAB | 15.7a | 38.9a | 3.17b | 0.52b | 33.2b | 2.18a | 2.37a | ||
| 12-2-12c | 0.9c | 31.4c | 2.31c | 0.72c | — | — | — | ||
| 12-2-12-2-12c | 0.08c | 36.4c | 1.29c | 1.28c | — | — | — | ||
| 3C12trisQc | 0.139c | 32.3c | 0.82c | 2.03c | — | — | — | ||
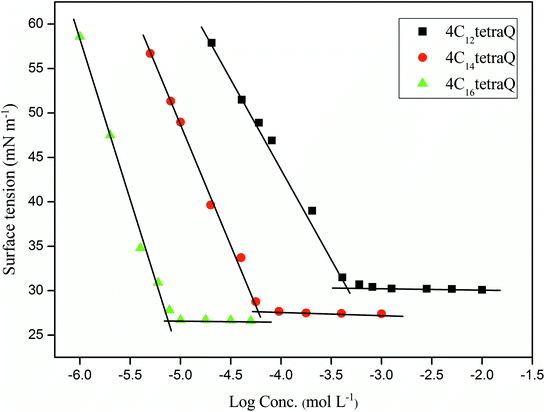
It is obviously that the CMC of 4CntetraQ decreases by 1–3 order of magnitude than those of analogous monomeric surfactant (for instance, DTAB) and dimeric surfactant (Gemini, 12-2-12), and their values are close to the values of the cationic trimeric surfactants having the line or star type structure (12-2-12-2-12 and 3C12trisQ, respectively). This may be due to strong hydrophobic interaction among four hydrophobic chains in the same molecule, which also demonstrates that the synthesized surfactants have an excellent ability of the micelle formation in comparison with the monomeric or dimeric surfactants. These results are accordance with those obtained from star-like cationic trimeric surfactants reported by Liu et al.39
The minimum surface area (Amin) and the surface excess concentration (Γmax) could be calculated by the Gibbs adsorption equation as follows,40 and the calculated results were given in Table 1.
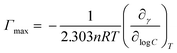 | (1) |
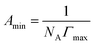 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C is the slope of surface tension curves at surfactant concentration below the CMC. n is the number of species at the air/solution interface.21 It is well known that the value of n is 2 for a univalent surfactant in calculating Γ, but for an ionic dimeric surfactant, there are different views (n = 2 or n = 3).41–44 The same problem arises for ionic tetrameric surfactants consisting of a tetravalent surfactant ion and four univalent counterions.25 Thus, the values of Γmax in the paper were calculated by n = 4 or n = 5, respectively. The n value (n = 4 or 5) has effect on calculating Γmax and Amin, while it has not bearing on the way Γmax and Amin vary with the alkyl carbon number. Thus, the conclusions inferred from these variations do not be affected by the change of the n value.
C is the slope of surface tension curves at surfactant concentration below the CMC. n is the number of species at the air/solution interface.21 It is well known that the value of n is 2 for a univalent surfactant in calculating Γ, but for an ionic dimeric surfactant, there are different views (n = 2 or n = 3).41–44 The same problem arises for ionic tetrameric surfactants consisting of a tetravalent surfactant ion and four univalent counterions.25 Thus, the values of Γmax in the paper were calculated by n = 4 or n = 5, respectively. The n value (n = 4 or 5) has effect on calculating Γmax and Amin, while it has not bearing on the way Γmax and Amin vary with the alkyl carbon number. Thus, the conclusions inferred from these variations do not be affected by the change of the n value.
As shown in Table 1, the increase of Γmax and the decrease of Amin of these tetrameric surfactants are with an increase of length of alkyl chain from 12 to 16. This shows that the tetrameric surfactants with longer alkyl chains have higher packing densities at the air/solution interface, which may be due to that the longer alkyl tails are more prone to stretch45 and have stronger hydrophobic interaction between each other.46
pC20 = −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C20 C20
| (3) |
| ΠCMC = γ0 − γCMC | (4) |
As seen in Table 1, the values of pC20 and ΠCMC of 4CntetraQ increase with increasing length of hydrophobic chain. The pC20 values of tetrameric surfactants are two or more higher than that of DTAB, indicating that 4CntetraQ molecules are more prone to adsorption at the air/solution interface than those of the analogue monomeric surfactant. The ratio of CMC/C20 can evaluate the structural factors in the process of adsorption or formation of aggregates.5 The higher the CMC/C20 is, the greater the tendency of surfactant molecules adsorbing at the interface rather than forming aggregates is.50 Thus, these dendritic tetrameric surfactants are more prone to self-assemble in aqueous solution rather than adsorb at the surface.
3.3 Thermodynamics parameters
Electrical conductivity of surfactant solution may be used to investigate thermodynamic properties of micellization. As shown in Fig. 3, the pre-micellar slope (S1 = dκ/dC) and the post-micellar slope (S2 = dκ/dC) are obtained from the curves of electrical conductivity (κ) vs. 4CntetraQ concentration. The concentration of the break point between the two straight lines in the plots may be regarded as the CMC. As can be given in Table 2, the CMC values increase with increasing temperature. These values are slightly larger than those from surface tension measurements, which is in accordance with the results obtained from other cationic oligomeric surfactants.53,54| Compounds | T (°C) | CMC (mmol L−1) | β | ΔGomic (kJ mol−1) | ΔHomic (kJ mol−1) | ΔSomic (kJ mol−1 K−1) | −TΔSomic (kJ mol−1) | ΔGoads (kJ mol−1) | |
|---|---|---|---|---|---|---|---|---|---|
| n = 4 | n = 5 | ||||||||
| 4C12tetraQ | 25 | 0.412 | 0.66 | −26.64 | −1.48 | 0.0844 | −25.16 | −30.45 | −31.36 |
| 35 | 0.422 | 0.65 | −27.17 | −1.538 | 0.0831 | −25.63 | |||
| 45 | 0.430 | 0.63 | −27.38 | −1.63 | 0.0809 | −25.75 | |||
| 4C14tetraQ | 25 | 0.0484 | 0.69 | −32.16 | −1.17 | 0.1039 | −30.98 | −35.72 | −36.62 |
| 35 | 0.0490 | 0.66 | −32.50 | −1.22 | 0.1015 | −31.28 | |||
| 45 | 0.0501 | 0.64 | −32.76 | −1.27 | 0.099 | −31.49 | |||
| 4C16tetraQ | 25 | 0.0063 | 0.71 | −38.05 | −4.24 | 0.1134 | −33.81 | −40.68 | −41.32 |
| 35 | 0.0067 | 0.69 | −38.36 | −4.44 | 0.11 | −33.92 | |||
| 45 | 0.0070 | 0.67 | −38.65 | −4.63 | 0.1069 | −34.02 | |||
Micelle ionization degree (α) may be represented by the ratio between the pre-micellar slope and the post-micellar slope (α = S2/S1), and the degree of counterion binding (β) is calculated by the equation (β = 1 − α).55 β may represent the number of counterions contained in the Stern layer in order to balance the electrostatic force that can inhibit the formation of micelles.56
The β values increase with the increasing of alkyl tail length, which is due to that the increase of charge densities of aggregate surface is with the increasing of alkyl tail length. This means that the polar head groups of surfactant molecules with longer chains in the aggregates can bind relatively more counterions.57,58
Thermodynamic parameters at 25, 35 and 45 °C were calculated by the following equation,45,59,60 and the results were seen in Table 2.
ΔGomic = RT(0.25 + β)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XCMS XCMS
| (5) |
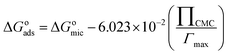 | (6) |
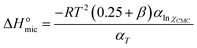 | (7) |
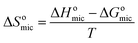 | (8) |
As shown in Table 2, the changes of the free energy of adsorption (ΔGoads) and micellization (ΔGomic) are negative, which means that both processes are spontaneous.61 Therefore, the adsorption at the air/solution interface or aggregation in the bulk solution is more favorable than distribution of surfactant molecules in water. The values of ΔGoads of 4CntetraQ are bigger than those of ΔGomic, showing that adsorption process favorably occurs until all the air/solution interface is occupied, and then surfactant molecules begin to aggregate and form micelles in the bulk solution.53,62 The values of ΔGoads and ΔGomic in the negative direction increase with the increase of the hydrophobic chain or solution temperature. The increase of the hydrophobic chain length of the surfactant make its hydrophobicity become strong, which can destroy the structure of water and increase free energy of the system, resulting in the migration of surfactant molecules to the air/solution interface and/or the formation of micelles in bulk solution. This behavior can make energy of the surfactant system decrease, and thus the values of ΔGoads and ΔGomic are more negative. The temperature rise of the surfactant system can make the decrease of hydration around hydrophilic groups, which results in the increase of the system energy, so the surfactant molecules are more favorable to adsorption in the interface and formation of micelle in order to decrease energy of the surfactant system.63
The positive sign of ΔSomic suggests that entropy change is favorable to aggregate in clusters for surfactant molecules in bulk solution.64 The decrease of ΔSomic with the temperature rise is due to that iceberg structure around hydrophilic groups diminishes in size or becomes easier to curl. The negative sign of ΔHomic shows that the micellization process is exothermic.53 As shown in Table 2, the values of ΔHomic are far lower than those of −TΔSomic, showing that micellization processes of these surfactant molecules are entropy-driven.53,65
3.4 Microenvironment
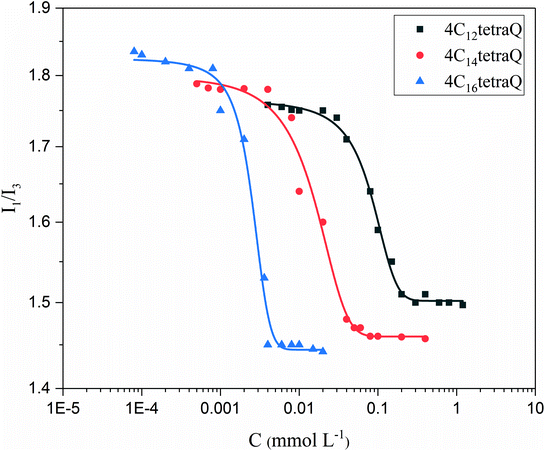
As is well known that the useful information on the micellization of surfactants is obtained from the fluorescence measurements, in which pyrene as a fluorescence probe can be solubilized in the palisade layer of aggregates when the surfactant concentrations are above the CMC.66 The intensity ratio between the first and third vibrational peaks (I1/I3) in the fluorescence spectrum is a sensitive parameter characterizing the polarity of the probe's microenvironment.67 The ratio of I1/I3 decrease when pyrene is moved from a polar region to a nonpolar region (aggregates).39Fig. 4 shows variations of the pyrene polarity ratio (I1/I3) vs. surfactant concentration at 25 °C. The value of I1/I3 changes slightly with the increase of initial surfactant concentration, showing that pyrene has no interaction with surfactants at the beginning.64,68 Then, the I1/I3 value decreases abruptly with the increase of the surfactant concentration, which suggests that a spot of aggregates begin to form, and that pyrene is solubilized in the inner hydrophobic region of aggregates.69 Thereafter, the ratio of I1/I3 is almost constant because the micellar microenvironment in the surfactant system is no change. The minimum ratio of I1/I3 decreases with the increment of the hydrophobic chain length, implying that hydrophobic interaction among longer alkyl tails makes the palisade layer arrange more compact and result in a reduction for polarity.64,70 The plots in Fig. 4 were sigmoidal (Boltzmann type) in nature, and thus the CMC may be obtained in terms of the procedure proposed by Zana et al.71–74 The CMC values for 4C12tetraQ, 4C14tetraQ and 4C16tetraQ were found to be 0.16, 0.048, and 0.0043 mmol L−1, which are approximately in agreement with the results obtained from electrical conductivities and surface tension measurements.
3.5 Aggregate behavior
The critical packing parameter (P) may be used to estimate the geometric construction of surfactant aggregates and calculated by the following equations.75–77
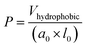 | (9) |
| V = (27.4 + 26.9m) × 10−3 nm3 | (10) |
| l0 = (0.15 + 0.1265m) nm | (11) |
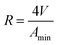 | (12) |
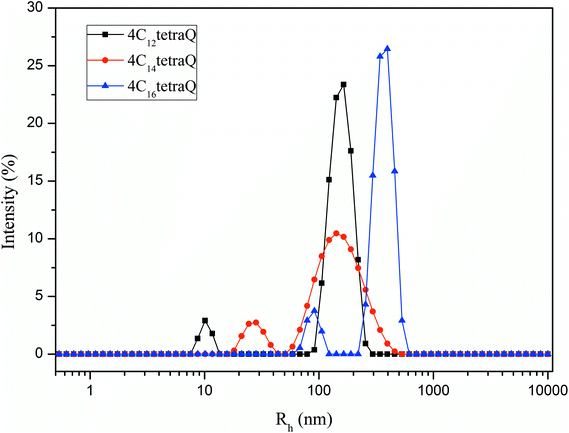
According to the theory of critical packing parameter, for spherical aggregates the p value is less than 0.333; for non-spherical aggregates, 0.33 ≤ P < 0.50; for vesicles or bilayers, 1/2 < P ≤ 1.75,76 As seen in the Table 3, the P values of these three surfactants are mostly above 0.5, suggesting that they can aggregate and may be possible to form vesicles structure. To further investigate aggregation behavior of these tetrameric surfactants at the concentration of 10 times of CMC, their size distributions were studied by DLS, and the measurement results were shown in Fig. 5. As shown in Fig. 5, two apparent hydrodynamic radius (Rh) distributions were detected, and the average Rh varies in the range of 10–500 nm. This indicates that there exist large aggregates in the surfactant solution, which should be assigned to vesicles.21,77–79 The formation of these vesicles may be due to that there are four larger hydrophilic head groups, four hydroxyl groups in the spacer, and smaller counterions bound by these aggregates in comparison with traditional cationic surfactants.70,80 It is clearly that these tetrameric surfactants in aqueous solution have a strong tendency to aggregate and form aggregates with large size distribution as hydrocarbon chain length of 4CntetraQ increases, due to the strong hydrophobic interaction among four alkyl chains.21 However, these results are not completely accordance with those obtained from star-like cationic trimeric surfactants.39 And their results from DLS and Transmission Electron Microscopy (TEM) measurements show that there exist small globule micelles and large ellipsoidal vesicles, and that the numbers of large vesicles decrease with increasing alkyl chain length.
| Surfactants | Vhydrophobic (nm3) | l0 (nm) | Rrange | P | R (nm) | |||
|---|---|---|---|---|---|---|---|---|
| n = 4 | n = 5 | n = 4 | n = 5 | n = 4 | n = 5 | |||
| 4C12tetraQ | 1.40 | 1.67 | 0.92–1.84 | 1.48–2.22 | 0.55 | 0.44 | 3.68 | 2.96 |
| 4C14tetraQ | 1.62 | 1.92 | 1.21–2.41 | 0.97–1.94 | 0.63 | 0.50 | 4.84 | 3.88 |
| 4C16tetraQ | 1.83 | 2.17 | 1.91–3.81 | 1.53–3.05 | 0.89 | 0.70 | 7.63 | 6.10 |
In addition, there is an exception that the p value of 4C12tetraQ (where P = 0.44) is not incompletely accordance with the results from the DLS measurements, which may be due to that the calculated value of average parking area (a0) of polar head groups of 4C12tetraQ is larger than its practical value.75 To explore arrangement of the alkyl chains in the vesicular region, the length ranges of hydrophobic chains (Rmax and Rmin) can be calculated by Tanford's equation.
For 4CntetraQ, the length of their alkyl chain fully extended is smaller than Rmin or falls in between Rmax and Rmin, which indicates that these tetrameric surfactant molecules present face-to-face attitude and easily interdigitate.75 Thus, the bilayer thickness of vesicles is less than twice the length of the hydrophobic chain, and the possible aggregate model was given in Fig. 6.
4. Conclusions
A series of dendritic cationic tetrameric surfactants were synthesized with raw materials that are commercially available. The synthesized surfactants have better surface activities than those of the corresponding monomeric and dimeric surfactants, and are more prone to self-assemble in the aqueous solution than adsorb at the air/solution surface. The thermodynamic parameters (ΔGomic, ΔHomic, ΔSomic, ΔGoads) obtained from electrical conductivity measurements show that both processes of adsorption and micellization of 4CntetraQ are spontaneous, and that the micellization processes of these surfactants are entropy-driven. Both adsorption and micellization of 4CntetraQ are inclined to occur with the increase of alkyl chain length or temperature. The DLS measurements reflect that there exist large aggregates, assigned to vesicles, at the concentration of 10 times of the CMC, which is incompletely accordance with the critical packing parameters (P) obtained by Tanford's expression. Given few reports on oligomeric surfactants, the paper helps to understand physicochemical properties of tetrameric surfactants with dendritic structure, aid the design synthesis of novel oligomeric surfactants, and study their structure–performance relationship.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the financial support from the National Natural Science Foundation of China (Grant No. 51674085). The authors acknowledge the assistance of Northwest University in performing elemental analysis experiments.References
- R. Domínguez, A. Rodríguez, A. Maestre, I. Robina and M. L. Moyá, J. Colloid Interface Sci., 2012, 386, 228–239 CrossRef PubMed.
- L. Y. Wang, Y. Zhang, L. M. Ding, J. Liu, B. Zhao, Q. G. Deng and T. Yan, RSC Adv., 2015, 5, 74764–74773 RSC.
- A. K. Tiwari, Sonu and S. K. Saha, J. Chem. Thermodyn., 2014, 70, 24–32 CrossRef CAS.
- M. A. Migahed, M. M. Shaban, A. A. Fadd, T. A. Ali and N. A. Negm, RSC Adv., 2015, 5, 104480–104492 RSC.
- T. Zhang, X. Cao, X. Wang and C. Song, J. Mol. Liq., 2017, 230, 505–510 CrossRef CAS.
- T. Jiao, X. Liu, X. Wang, Y. Wang and J. Niu, Colloids Surf., A, 2016, 498, 30–41 CrossRef CAS.
- A. Bhadani and S. Singh, Langmuir, 2011, 27, 14033–14044 CrossRef CAS PubMed.
- L. Zhou, X. Jiang, Y. Li, Z. Chen and X. Hu, Langmuir, 2007, 23, 11404–11408 CrossRef CAS PubMed.
- H. Wang, T. Kaur, N. Tavakoli, J. Joseph and S. Wettig, Phys. Chem. Chem. Phys., 2013, 15, 20510–20516 RSC.
- K. Wang, D. S. Guo, X. Wang and Y. Liu, ACS Nano, 2011, 5, 2880–2894 CrossRef CAS PubMed.
- Q. Chen, Y. Sakamoto, O. Terasaki and S. Che, Microporous Mesoporous Mater., 2007, 105, 24–33 CrossRef CAS.
- P. V. D. Voort, M. Mathieu, A. F. Mees and E. F. Vansant, J. Phys. Chem. B, 1998, 102, 8847–8851 CrossRef.
- V. Branzoi, F. Branzoi and M. Baibarac, Mater. Chem. Phys., 2000, 65, 288–297 CrossRef CAS.
- W. Li, H. Chen, Z. He, C. Han, S. L. Liu and Y. Li, LWT--Food Sci. Technol., 2015, 62, 39–47 CrossRef CAS.
- L. Wattebled, A. Laschewsky, A. Moussa and J. Habib-Jiwan, Langmuir, 2006, 22, 2551–2557 CrossRef CAS PubMed.
- Y. B. Hou, M. W. Cao, M. L. Deng and Y. L. Wang, Langmuir, 2008, 24, 10572–10574 CrossRef CAS PubMed.
- Y. B. Hou, Y. C. Han, M. L. Deng and J. F. Xiang, Langmuir, 2010, 26, 28–33 CrossRef CAS PubMed.
- X. Li, F. L. Xing, Q. Xu, X. L. Sun, Y. P. Wang, L. Y. Wang and P. L. Wang, J. Surfactants Deterg., 2016, 19, 129–135 CrossRef CAS.
- R. L. Qi, M. N. Wang, L. Y. Zhu, Z. Liu and Y. L. Wang, Langmuir, 2017, 33, 7271–7280 CrossRef CAS PubMed.
- N. Sun, L. Shi, F. Lu, S. T. Xie, P. P. Sun and L. Q. Zheng, Langmuir, 2015, 31, 2281–2287 CrossRef CAS PubMed.
- I. Martin, B. Veronique, A. C. Olivier and R. Zana, Langmuir, 2000, 16, 141–148 CrossRef.
- T. Yoshimura, H. Yoshida, A. Ohno and K. Esumi, J. Colloid Interface Sci., 2003, 267(1), 167–172 CrossRef CAS PubMed.
- A. Laschewsky, L. Wattebled, M. J. L. Arotçaréna, J. L. Habib-Jiwan and R. H. Rakotoaly, Langmuir, 2005, 21, 7170–7179 CrossRef CAS PubMed.
- T. Yoshimura and K. Esumi, Langmuir, 2003, 19, 3535–3538 CrossRef CAS.
- M. C. Murguía, M. I. Cabrera, J. F. Guastavino and R. J. Grau, Colloids Surf., A, 2005, 262, 1–7 CrossRef.
- M. C. Murguía and R. J. Grau, Synlett, 2001, 8, 1229–1232 CrossRef.
- D. H. McCullough, V. Janout, J. W. Li, J. T. Hsu, Q. Truong, E. Wilusz and S. L. Regen, J. Am. Chem. Soc., 2004, 126, 9916–9917 CrossRef CAS PubMed.
- F. M. Menger and V. A. Migulin, J. Org. Chem., 1999, 64, 8916–8921 CrossRef CAS PubMed.
- Y. Sumida, T. Oki, A. Masuyama, H. Maekawa, M. Nishiura, T. Kida, Y. Nakatsuji, I. Ikeda and M. Nojima, Langmuir, 1998, 14, 7450–7455 CrossRef CAS.
- T. Yoshimura, N. Kimura, E. Onitsuka, H. Shosenji and K. Esumi, J. Surfactants Deterg., 2004, 7, 67–74 CrossRef CAS.
- T. Yoshimura, T. Kusano, H. Iwase, M. Shibayama, T. Ogawa and H. Kurata, Langmuir, 2012, 28, 9322–9331 CrossRef CAS PubMed.
- A. Uner, E. Doganci, M. A. Tasdelen, F. Yilmaz and A. G. Gürek, Polym. Int., 2017, 66, 1610–1616 CrossRef CAS.
- Z. W. Li, Z. Y. Shi, S. L. Zhao, S. Yin, G. R. Tan, B. Jing and Y. B. Tan, J. Surfactants Deterg., 2016, 19, 1107–1120 CrossRef CAS.
- C. X. Wu, Y. B. Hou, M. L. Deng, X. Huang, D. F. Yu, J. F. Xiang, Y. Liu, Z. B. Li and Y. L. Wang, Langmuir, 2010, 26(11), 7922–7927 CrossRef CAS PubMed.
- Y. X. Fan, Y. B. Hou, J. F. Xiang, D. F. Yu, C. X. Wu, M. Z. Tian, Y. C. Han and Y. L. Wang, Langmuir, 2011, 27, 10570–10579 CrossRef CAS PubMed.
- D. Wang, M. W. Cao, Y. Chen, Z. Liu, C. X. Wu, H. Xu, S. Wang and Y. L. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 30811–30823 CrossRef PubMed.
- N. Kampf, C. X. Wu, Y. L. Wang and J. Klein, Langmuir, 2016, 32, 11754–11762 CrossRef CAS PubMed.
- Y. C. Xie, J. Li, T. Sun, Y. Han, G. M. Qu and R. X. Niu, J. Dispersion Sci. Technol., 2017, 39, 1153–1159 CrossRef.
- X. G. Liu, X. J. Xing and Z. N. Gao, Colloids Surf., A, 2014, 457, 374–381 CrossRef CAS.
- E. M. Kandeel, J. Dispersion Sci. Technol., 2013, 33, 949–954 CrossRef.
- E. Alami, G. Beinert, P. Marie and R. Zana, Langmuir, 1993, 9, 1465–1467 CrossRef CAS.
- Q. Zhang, Z. N. Gao, F. Xu, S. X. Tai, X. G. Liu, S. B. Mo and F. Niu, Langmuir, 2012, 28, 11979–11987 CrossRef CAS PubMed.
- M. Q. Ao, G. Y. Xu, Y. Y. Zhu and Y. Bai, J. Colloid Interface Sci., 2008, 326, 490–495 CrossRef CAS PubMed.
- L. H. Zhuang, K. H. Yu, G. W. Wang and C. Yao, J. Colloid Interface Sci., 2013, 408, 94–100 CrossRef CAS PubMed.
- M. Zhou, Z. Huang, S. Yu, Y. Yang, Y. S. Huang, D. Qiu and J. Z. Zhao, Tenside, Surfactants, Deterg., 2016, 53, 134–139 CrossRef CAS.
- O. Kaczerewska, B. Brycki, I. Ribosa, F. Comelles and M. T. Garcia, J. Ind. Eng. Chem., 2018, 59, 141–148 CrossRef CAS.
- M. U. H. Mir, N. Maurya, I. Beg, A. B. Khan and R. Patel, Colloids Surf., A, 2016, 507, 36–45 CrossRef.
- I. Aiad, M. A. Riya, S. M. Tawfik and M. A. Abousehly, Egypt. J. Pet., 2016, 25, 299–307 CrossRef.
- M. Abo-Riya, A. Tantawy and W. El-Dougdoug, J. Mol. Liq., 2016, 221, 642–650 CrossRef CAS.
- K. Taleb, M. Mohamed-Benkada, N. Benhamed, S. Saidi-Besbes, Y. Grohens and A. Derdour, J. Mol. Liq., 2017, 241, 81–90 CrossRef CAS.
- J. W. Guo, X. Zhong, H. Zhu and L. J. Feng, Chin. Chem. Lett., 2o13, 23, 653–656 Search PubMed.
- A. Sokołowski, A. Bieniecki, K. A. Wilk and B. Burczyk, Colloids Surf., A, 1995, 98, 73–82 CrossRef.
- C. L. Dai, S. S. Fang, M. Hu, X. J. He, M. W. Zhao, X. P. Wu, S. Yang and Y. N. Wu, J. Ind. Eng. Chem., 2017, 54, 226–233 CrossRef CAS.
- J. Darija, H. Ivan and F. C. Nada, Colloids Surf., A, 2010, 368, 119–128 CrossRef.
- P. Patial, A. Shaheen and I. Ahmad, J. Surfactants Deterg., 2014, 17, 253–260 CrossRef CAS.
- X. Zhong, J. Guo, L. Feng, X. Xu and D. Zhu, Colloids Surf., A, 2014, 441, 572–580 CrossRef CAS.
- L. F. Zhi, Q. X. Li, Y. L. Li and Y. Q. Sun, Colloids Surf., A, 2014, 456, 231–237 CrossRef CAS.
- R. Kamboj, S. Singh, A. Bhadani, H. Kataria and G. Kaur, Langmuir, 2012, 28, 11969–11978 CrossRef CAS PubMed.
- G. H. Sayed, F. M. Ghuiba, M. I. Abdou, E. A. A. Badr, S. M. Tawfik and N. A. M. Negm, J. Surfactants Deterg., 2012, 15, 735–743 CrossRef CAS.
- N. Azum, M. A. Rub, A. M. Asiri and W. A. Bawazeer, Colloids Surf., A, 2017, 522, 183–192 CrossRef CAS.
- I. Aiad, M. M. E. Sukkary, E. A. Soliman, M. Y. E. Awady and S. M. Shaban, J. Ind. Eng. Chem., 2014, 20, 1633–1640 CrossRef CAS.
- S. M. Shaban, A. S. Foud, M. A. Elmorsi, T. Fayed and O. Azazy, J. Mol. Liq., 2016, 216, 284–292 CrossRef CAS.
- S. M. Shaban, A. S. Foud, S. M. Rashwan, H. E. Ibrahim and M. F. El-Bhrawy, J. Mol. Liq., 2016, 221, 224–234 CrossRef CAS.
- D. Q. Xu, X. Y. Ni, C. Y. Zhang, J. Mao and C. C. Song, J. Mol. Liq., 2017, 240, 542–548 CrossRef CAS.
- G. Y. Liu, D. M. Gu, H. Y. Liu, W. Ding, H. X. Luan and Y. M. Lou, J. Colloid Interface Sci., 2012, 375, 148–153 CrossRef CAS PubMed.
- Y. Bao, J. Guo, J. Ma, M. Li and X. L. Li, J. Mol. Liq., 2017, 242, 8–15 CrossRef CAS.
- G. B. Ray, I. Chakraborty and S. P. Moulik, Colloid Interface Sci., 2006, 294, 248–254 CrossRef PubMed.
- N. Azum, M. A. Rub, A. M. Asiri, K. A. Alamry and H. M. Marwani, J. Dispersion Sci. Technol., 2014, 35, 358–363 CrossRef CAS.
- K. Esumi, K. Taguma and Y. Koide, Langmuir, 1996, 12, 4039–4041 CrossRef CAS.
- V. Chauhan, S. Singh, R. Mishra and G. Kaur, J. Colloid Interface Sci., 2014, 436, 122–131 CrossRef CAS PubMed.
- A. Rodríguez, M. M. Graciani and M. L. Moya, Langmuir, 2008, 24, 12785–12792 CrossRef PubMed.
- R. Zana and H. Lévy, Colloids Surf., A, 1997, 127, 229–232 CrossRef CAS.
- C. H. Hsu, S. M. Shau, R. J. Jeng, H. C. Chiu, S. H. A. Dai, E. D. Conted and S. Y. Suen, Microchem. J., 2013, 110, 48–53 CrossRef CAS.
- J. Aguiar, P. Carpena, J. A. Molina-Bolívar and C. C. Ruiz, J. Colloid Interface Sci., 2003, 258, 116–122 CrossRef CAS.
- B. Li, Q. Zhang, Y. Xia and Z. N. Gao, Colloids Surf., A, 2015, 470, 211–217 CrossRef CAS.
- K. Maiti, S. C. Bhattachary, S. P. Moulik and A. K. Panda, Colloids Surf., A, 2010, 355, 88–98 CrossRef CAS.
- G. Y. Wang, Q. W. Yin, J. X. Shen, Y. Y. Bai, X. Y. Ma, Z. P. Du and W. X. Wang, J. Mol. Liq., 2017, 234, 142–148 CrossRef CAS.
- G. Wang, P. Li, Z. Du, W. Wang and G. Li, Langmuir, 2015, 31, 8235–8242 CrossRef CAS PubMed.
- Z. T. Liu, Y. F. Ge, Q. Zhang, X. Gao, X. Cai, M. Y. Chen and X. C. Yu, J. Surfactants Deterg., 2017, 20, 765–775 CrossRef CAS.
- B. Dong, X. Y. Zhao, L. Q. Zheng, J. Zhang, N. Li and T. Inoue, Colloids Surf., A, 2008, 317, 666–672 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra06900j |
| This journal is © The Royal Society of Chemistry 2018 |