Open Access Article
Open Access ArticleMolecular dynamics derived life times of active substrate binding poses explain KM of laccase mutants†
Rukmankesh Mehra ab,
Anne S. Meyer
ab,
Anne S. Meyer *b and
Kasper P. Kepp
*b and
Kasper P. Kepp *a
*a
aTechnical University of Denmark, DTU Chemistry, Building 206, 2800 Kgs. Lyngby, Denmark. E-mail: kpj@kemi.dtu.dk
bTechnical University of Denmark, DTU Bioengineering, Building 221, 2800 Kgs. Lyngby, Denmark. E-mail: asme@dtu.dk
First published on 1st November 2018
Abstract
Fungal laccases (EC 1.10.3.2) are important multi-copper oxidases with broad substrate specificity. Laccases from Trametes versicolor (TvL) are among the best-characterized of these enzymes. Mutations in the substrate-binding site of TvL substantially affect KM, but a molecular understanding of this effect is missing. We explored the effect of TvL mutations on KM for the standard laccase substrate 2,6-dimethoxyphenol using 4500 ns of molecular dynamics, docking, and MMGBSA free energy computations. We show that changes in KM due to mutation consistently correlate with the dynamics of the substrates within the substrate-binding site. We find that KM depends on the lifetime (“dynamic stability”) of the enzyme-substrate complex as commonly assumed. We then further show that MMGBSA-derived free energies of substrate binding in the active pose consistently reproduce large vs. small experimental KM values. Our results indicate that hydrophobic packing of the substrate near the T1 binding site of the laccase is instrumental for high turnover via KM. We also address the more general question of how enzymes such as laccases gain advantage of lower KM despite the Sabatier principle, which disfavors a stable enzyme–substrate complex. Our data suggest that the observed KM relates directly to the lifetime of the active substrate pose within a protein. In contrast, the thermochemical stability of the enzyme–substrate complex reflects an ensemble average of all enzyme–substrate binding poses. This distinction may explain how enzymes work by favoring longer residence time in the active pose without too favorable general enzyme–substrate interactions, a principle that may aid the rational design of enzymes.
Introduction
Laccases (EC 1.10.3.2) are multi-copper oxidases found in plants, fungi, bacteria and insects.1,2 They catalyze the transfer of four electrons from substrates to catalytic copper centers in protein and reduce molecular oxygen to water.3–5 They have broad activity toward organic electron donors and catalyze the oxidation of a range of phenols, acids, anilines, ketones and lignin.6–10 Laccases perform diverse functions based on their origin;1,11 in some plants, they perform lignin biosynthesis, whereas in fungi and bacteria they appear to perform lignin modification.1,11 Accordingly, laccases are important industrial biocatalysts with potential for lignocellulose processing.12–17Structurally, fungal laccases consist of three different domains (1, 2 and 3) and four Cu atoms distributed within two sites: The T1 Cu site, and the tri-nuclear cluster consisting of T2 Cu, T3 α Cu, and T3 β Cu.8,18–20 The T1 Cu site is situated near the surface of domain 3 and directly interacts with the substrates in the presumed active binding poses, via a histidine hydrogen bond.21 The four electrons are transferred from substrates to T1 Cu one at a time, and then from T1 to the tri-nuclear cluster.1,3,22,23 This cluster of three copper ions is located at the buried interface between domains 1 and 3 and is responsible for the 4-electron reduction of molecular oxygen to water.3 It is accessed by water and oxygen channels, and can be inhibited by small anions such as cyanide and fluoride.24
Site-directed mutagenesis has been widely applied to study and improve laccases for particular types of reactivity.25–28 Two central studies reported the effect on the Michaelis constant KM of specific mutations within the substrate-binding site of Trametes versicolor laccase (TvL),25,26 suggesting order-of-magnitude effects on KM due to mutation of only one amino acid. Madzak et al. mutated Asp-206,25 which interacts directly with many laccase substrates.21 They prepared the D206E, D206A and D206N mutants and evaluated KM, kcat and kcat/KM for 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulphonic acid) (ABTS) and 2,6-dimethoxyphenol (2,6-DMP) at pH 3.4. While little effect on ABTS activity was observed, a major increase in KM of 2,6-DMP was seen for two specific mutants, D206A and D206N. Galli et al. studied the effect of mutating phenylalanine at positions 162, 265, 332 and 337 within the substrate binding site.26 Again, no major change was observed for ABTS whereas for 2,6-DMP, KM increased from 17 ± 5 μM in the wild-type protein (WT) to 165 ± 5 μM in F332A. Very low initial oxidation of 2,6-DMP was reported for the mutant F337A and therefore, no kinetic data were reported in this case.26
These experimental studies thus open the door to a more detailed molecular investigation of the substrate–protein interactions that contribute to the observed enzymatic turnover and KM. Such studies using molecular dynamics (MD) simulations to confer the substrate dynamics of enzyme catalysis have been applied successfully to other enzymes.29,30 In this process, one should note that the Michaelis constant KM is not trivially interpretable as a stability constant of the enzyme–substrate complex.31 Generally, higher turnover numbers are associated with higher kcat/KM. Thus, lower KM is presumably desirable for high turnover, but this would violate the Sabatier principle,32 which states that too stable intermediates, in this case the enzyme–substrate complex, impair turnover. Then how do enzymes such as laccases gain advantage of lower KM in light of the Sabatier principle? Understanding the molecularly “active” substrate-protein poses that actually lead to product formation therefore seems to be of major interest not just for understanding and improving laccase activity but also for understanding the molecular determinants of KM more generally.
To understand the molecular determinants of KM, its modulation, and whether the effect can be reproduced computationally, we performed a detailed analysis of 2,6-DMP in complex with TvL using both explicit MD simulations of the combined substrate–protein complexes and dynamically averaged MMGBSA calculations on the active enzyme–substrate conformations. Our simulations consistently recover the high stability of 2,6-DMP associated with the T1 site of the WT protein at both the assay pH values. In contrast, the same type of MD simulations consistently produce release of the substrate quite early in the studied mutants with high KM values. Third, the MMGBSA method, which provides estimates of the binding affinity of ligands to proteins with higher accuracy than conventional docking scores, consistently separates the large and small experimental KM values. Our results thus show that the binding affinity of the substrate to the protein in the active (productive) pose largely contribute to real observed KM in a way that enables a robust protocol for KM optimization of laccases. In a broader sense, the fact that relative magnitudes of KM are largely recoverable from combined MD and MMGBSA studies, which are normally used primarily for protein inhibitor studies, should be of substantial interest in future enzyme design.
Methods
Studied dataset
The studied dataset consists of the experimentally reported KM for WT TvL and four of its mutants25,26 reported at two pH values (3.4 and 5.0). We were interested in understanding the large effects observed for 2,6-DMP compared to the other non-phenolic standard laccase substrate ABTS, and these data were accordingly investigated, as summarized in Table 1. The positions of the T1 binding site and the experimentally mutated residues, Asp-206, Phe-332, and Phe-337 are shown in Fig. 1.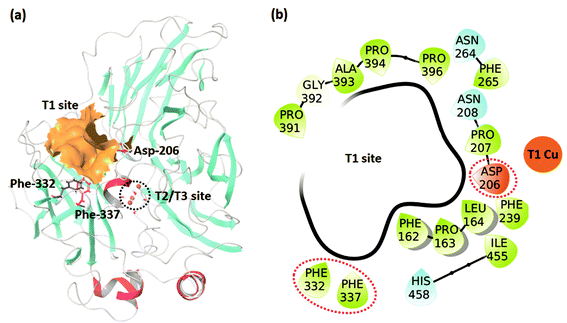 | ||
| Fig. 1 (a) The TvL structure showing the T1 and T2/T3 sites and the residues where mutations occurred in the studied data. (b) Residues forming the T1 binding site. | ||
Preparation of wild-type and mutant laccases
The TvL structure with PDB code 1KYA33,34 was used for the preparation of the WT and mutant laccases as it has a substrate (2,5-xylidine) bound and thus represents a protein–ligand complex better than the commonly used 1GYC structure.35 The same resting oxidized (RO) state3 of the WT and mutants were prepared at the specific pH of each assay as mentioned in Table 1. To ensure adequate reference states for the WT protein, we studied the WT in parallel at both pH values using otherwise identical setups. The RO state contains all four copper atoms in oxidation state (Cu2+). The 1KYA structure contains four Cu2+ atoms, but it does not contain all the water molecules known to coordinate with these Cu atoms.36 Therefore, the PDB structure 1GYC,35 which is assumed to be in this RO state, was used to consistently produce this state for all the studied proteins. The four Cu2+ atoms and water molecules within 5 Å of these were copied from 1GYC to 1KYA. The 1KYA structure was then prepared using the Protein Preparation Wizard. Missing side chains of the residues and hydrogens (which are not available in the crystal structure) were added using Prime.37 All hydrogen bonds of the proteins were optimized for proper alignment. In addition, we performed local structure optimization to remove close contacts of the amino acid side chains without changing the backbone atom coordinates. A WT structure and the mutants D206A and D206N were prepared at pH 3.4, and another WT structure, F332A, and F337A were prepared at pH 5.Substrate structures, molecular docking and MMGBSA computations
2,6-DMP was prepared at pH 3.4 and 5.0 using the LigPrep module of Schrodinger.38 For each of the protein structures, we generated a grid similar in size to the co-crystallized ligand of the 1KYA structure. Docking of 2,6-DMP was then performed on this grid using the XP scoring function of Glide39 with default parameters and using the specific structures generated at pH 3.4 and 5. At both these pH values, the ligand protonation state and pose were similar. The output pose from the Glide docking, which was ensured to represent an active pose with close contact to T1 as required for optimal electron transfer, was subsequently used to compute the MMGBSA binding affinity with fixed protein structure.37,40Molecular dynamics simulations of protein–substrate complexes
In order to qualitatively analyze the binding of 2,6-DMP to the TvL variants, four simulations were performed for each of the six protein–substrate systems: one standard simulation for 50 ns (run 1), two additional longer simulations for 200 ns (run 2 and 3) and one final simulation for 300 ns (run 4) using the Desmond MD program.41,42 Previous MD simulations on laccases have shown that this is necessary and sufficient to obtain equilibrated ensembles for these enzymes.43,44 To ensure independency of the simulations, we used random seeds and random velocities for runs 1, 2 and 3. Run 4 was performed using the same seed as run 1 but for longer simulation time. Each protein–substrate complex obtained from Glide docking was solvated with SPC water in an orthorhombic box. The volume of each box was ∼487![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Å3 with approximately 45
000 Å3 with approximately 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, including ∼12
000 atoms, including ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 water molecules (ESI Table S1†). These systems were neutralized by adding counter-ions, and additional ions up to a total concentration of 0.15 M NaCl were added to each structure using random placement (ESI Table S1†).
500 water molecules (ESI Table S1†). These systems were neutralized by adding counter-ions, and additional ions up to a total concentration of 0.15 M NaCl were added to each structure using random placement (ESI Table S1†).
The systems were prepared using the System Builder tool of Desmond,42 and the OPLS2005 force field was applied,45 which is based on the free-energy derived force fields developed by Jorgensen and co-workers.46–48 All system energies were minimized using a combination of steepest descent and Broyden–Fletcher–Goldfarb–Shanno optimization. MD simulation was then performed within the NPT ensemble at 300 K and 1.0013 bar using an integration time-step of 2 femtoseconds for the multistep protocol as implicated in Desmond.41 Energies were recorded at intervals of 1.2 picoseconds (ps), and trajectories were noted with an interval of 50 ps for the six 50 ns simulations, 200 ps for the twelve 200 ns simulations, and 300 ps for the six 300 ns simulations, thereby generating 1002 snapshots in each simulation. Steady temperature and pressure values were maintained using the Nose–Hoover chain thermostat49 and the Martyna–Tobias–Klein barostat50 as commonly applied. Ewald mesh summation was used to determine the long-range electrostatic interactions.51 The default interpolating function was applied for electrostatic interactions with a cut-off of 9.0 Å.
MMGBSA computation on MD trajectories
In order to estimate the binding affinities of the substrate to the various laccase variants, we computed MMGBSA calculations using Prime.37 Because these calculations are likely to be sensitive to the exact choice of protein–substrate coordinates, and because protein properties are generally very sensitive to the exact choice of static structure used as input for computation,44,52,53 we performed the calculations both on the top pose produced by Glide as commonly applied, but also exhaustively on 402 snapshots from the last 20 ns of the 50 ns MD trajectories (run 1). For each protein–substrate complex, we compared the average free energy of binding obtained from these computations, the associated standard deviation, and the maximum and minimum values.Results and discussion
Docking and MMGBSA analysis
The comparison of the experimental pKm values and the MMGBSA binding affinities (kcal mol−1) calculated using the docked protein–ligand complexes generated directly from Glide indicates some trend agreement between these parameters (of the WT and mutated complexes; ESI Table S2†), albeit not very strongly. This free energy represents a simple estimate of the substrate affinity towards the enzyme for only one, fixated and static enzyme–substrate conformation. We speculated that a more informative estimate of this affinity is obtainable from a complete dynamic averaging over the MD trajectories of all the six proteins, as explored further below.Qualitative analysis of 2,6-DMP binding in WT and mutated complexes
Based on the four MD trajectories of each protein-substrate complex (viz. one 50 ns, two 200 ns, and one 300 ns), the root-mean-square deviation (RMSD) in the protein structure relative to the initial structure is shown in ESI Fig. S1–S4† (additional data of RMSF plots in ESI Fig. S5–S8†). All trajectories were dynamically stable as indicated by the dominance of horizontal RMSD values in the final parts of the trajectories (except for the mutants F332A in run 4 and F337A in run 2 and 4 where the substrate loss affects the RMSD substantially, which was a desired observation as we are looking for substrate loss in the mutant systems).Analysis of the ligand RMSD during the four runs showed that in all the WT complexes the ligand spanned more time at the T1 pocket than their mutants (except F337A, only in run 4) as shown in Table 2 and ESI Fig. S9–S12.† The ligand in the mutants moved away from the T1 site either very early or after some initial residence time (ESI Fig. S9–S12†). In all simulations, the substrate spent more time at the T1 sites of the WT proteins, except for F337A in run 4, where the ligand was stable for ∼148 ns near the T1 site (Table 2 and ESI Fig. S12†). However, in runs 1, 2 and 3, the substrate left the T1 site of the F337A mutant early during the simulation (Table 2 and ESI Fig. S9–S11†). Altogether, there are four mutant-WT comparisons for each set of simulations, giving a total of 16 mutant-WT comparisons; in 15 of these 16 simulations we observed that the substrate left the T1 site earlier in the respective mutant than in the WT protein.
| Mutation | KM25,26 (μM) | Analysis of the ligand movement from T1 site | |||
|---|---|---|---|---|---|
| Run 1 (50 ns) | Run 2 (200 ns) | Run 3 (200 ns) | Run 4 (300 ns) | ||
| WT (pH 3.4) | 190 | Ligand remains at T1 site | Moves away at ∼198 ns | Moves away at ∼100 ns | Moves away at ∼70 ns |
| D206A | 1630 | Moves away at ∼30 ns | Moves very early | Moves very early | Unstable trajectory (moves away at ∼23 ns then moves in and out up to ∼60 ns) |
| D206N | 3280 | Moves very early | Moves away at ∼44 ns | Moves very early | Moves away very early |
| WT (pH 5.0) | 17 ± 5 | Remains at T1 site | Ligand remains at T1 site | Moves away at ∼155 ns | Moves away at ∼110 ns |
| F332A | 165 ± 5 | Moves away at ∼20 ns | Moves very early | Moves very early | Moves away very early |
| F337A | N/A | Moves very early | Moves very early | Moves away at ∼13 ns early | Moves away at ∼148 ns |
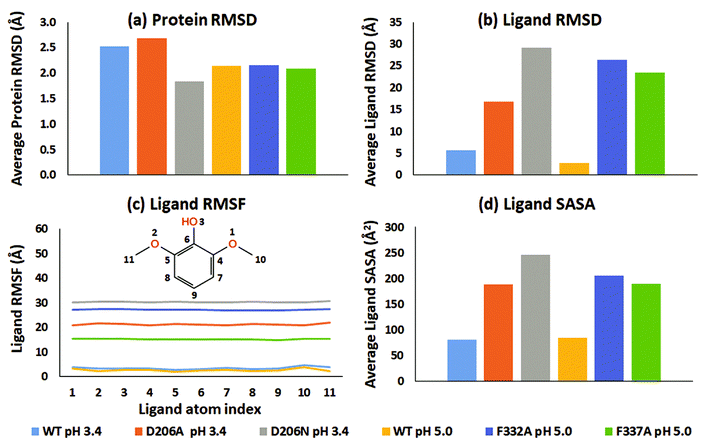
From an analysis of the specific substrate trajectories, it is clear that the lifetime of the T1-bound substrate state is longer in WT than in the mutants; since the general behavior is very consistent (except one of the four F337A simulations mentioned above), we focus our further analysis on run 1 (50 ns), which provides better clarity of presentation. Fig. 2a shows the average of the protein RMSD during run 1. Fig. 2b shows the corresponding ligand-only average RMSD. For both WT complexes at pH 3.4 and 5.0, the ligand RMSD values were low, indicating stable dynamics throughout the simulations, whereas the substrates undergo major changes in all the mutants (ESI Fig. S9†). Importantly, although the two WT simulations were statistically independent, the ligand RMSD was similar, up to 10 Å in both simulations and generally smaller than this. In contrast, all mutants displayed unstable trajectories for the ligand dynamics: in the D206A mutant complex (pH 3.4), the substrate moved up to ∼54 Å during the simulation. In the D206N mutant complex (pH 3.4), the ligand RMSD reached values of ∼64 Å. A similar magnitude of fluctuations was seen for the F332A variant (pH 5.0), although 2,6-DMP eventually attained a stable RMSD trajectory at ∼30–45 Å, indicating movement to a secondary binding site on the surface of the protein, as explored further below. Finally, the F337A variant (pH 5.0) also displayed features of an unstable ligand–protein complex, with the substrate RMSD values up to ∼50 Å relative to the initial active pose.
In all six simulations of run 1, the RMSD analysis consistently shows that the substrate relocates from the binding site in the mutants but remains in the binding site in the WT proteins. These results were supported by the root-mean-square fluctuations (RMSF) of the substrates, which directly relate to the structural disorder of the protein-bound ligand (Fig. 2c). Whereas the two WT structures consistently show low disorder (RMSF < 5 Å), the mutants consistently showed much higher ligand RMSF values. In order of D206N (pH 3.4), F332A (pH 5.0), D206A (pH 3.4), and F337A (pH 5.0) the average RMSF values were 30.3 Å, 27.1 Å, 21.2 Å, and 15.2 Å.
In the WT complexes at pH 3.4 and 5.0 (run 1), 2,6-DMP interacted with 21 and 18 residues, respectively, during the simulation time (ESI Fig. S13a and d†). The substrate maintained contact with the same ∼1–5 residues most of the time in the WT structures (ESI Fig. S14 and S15†). However, in the mutant complexes, 2,6-DMP consistently interacted with 33–64 different residues during the simulations (ESI Fig. S13b, c, e and f†), with relatively fewer persistent interactions (ESI Fig. S16–S19†). We conclude from the interaction analysis that the substrate moved away from the substrate-binding site of all mutated proteins whereas the two WT structures maintained tight association with the substrate during the entire simulation within the same binding cavity.
To explore further the displacement occurring distinctly in the mutant structures, the solvent accessible surface area (SASA) of 2,6-DMP was assessed over the full MD trajectory (Fig. 2d and ESI Fig. S20†). In WT structures at both pH 3.4 and 5.0, the SASA of 2,6-DMP was <100 Å2 during most of the simulation time. In contrast, large departures from this regime took place consistently for all four mutant simulations. In both D206A and D206N at pH 3.4, the substrate SASA increased beyond 300 Å2 during large parts of the simulation. In the F332A mutant at pH 5.0, the substrate SASA exceeded 300 Å2 for ∼14 ns. In F337A (pH 5.0), the substrate SASA was mostly 100–200 Å2 but exceeded 300 Å2 for ∼7 ns. Thus, SASA values for 2,6-DMP consistently showed increased solvent exposure during the simulations of the mutant proteins, which is indicative of impaired binding to the protein, to be further analyzed below.
Substrate relocation during MD simulation correlates with experimental KM
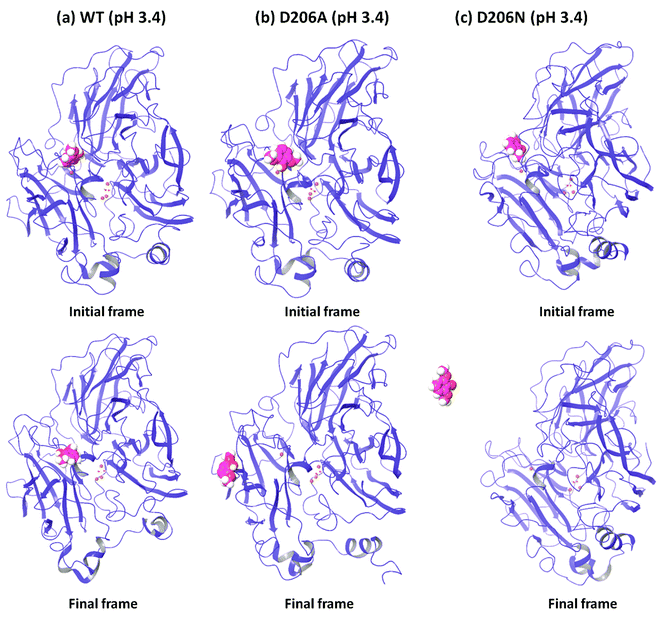
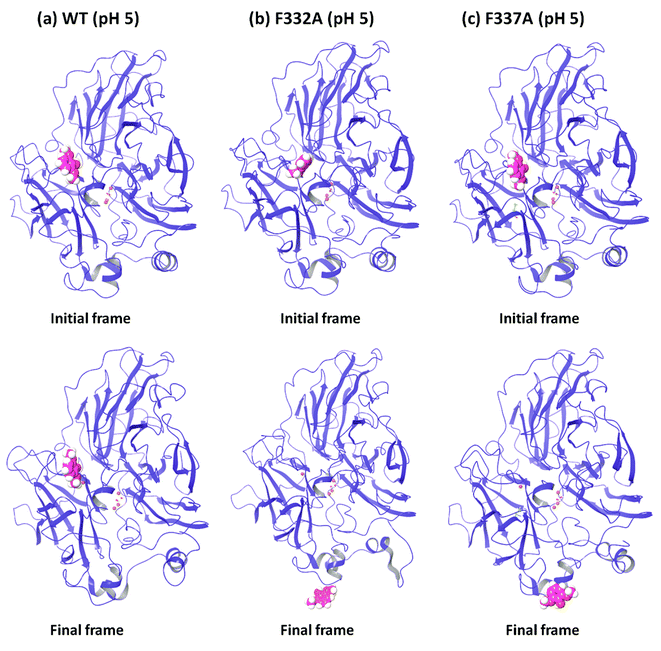
In order to understand the dynamic changes described above in terms of molecular structure, we inspected the protein and the substrate poses of the initial and final frames of the 50 ns MD simulations (run 1) as shown in Fig. 3 and 4. Since the early event of substrate release from the mutant proteins is a consistent feature producing most of the observations in the overall RMSD and fluctuations, the overall behavior is well represented by the simulation at only 50 ns; although we required the longer multiple MD simulations to actually realize this. In case of the WT complexes at both pH 3.4 (Fig. 3a) and 5.0 (Fig. 4a), the ligand remained in the initial binding pocket throughout the simulation time. However, in the mutated complexes D206A (pH 3.4), D206N (pH 3.4), and F332A (pH 5.0), 2,6-DMP moved away from the initial binding site (T1) and became exposed to the solvent. In F337A (pH 5.0), the substrate moved from the T1 site to different cavities of the protein and sometimes outside the protein, and therefore, formed contacts with very many residues of the protein (ESI Fig. S13†). Table 3 shows a summary of this MD trajectory analysis. Thus, the MD simulations clearly represent a case of stronger substrate–protein binding for the WT laccase and weaker binding for the mutated proteins as directly reflected in the full-atom dynamics of the various proteins.| Mutation | KM25,26 (μM) | Analysis of the MD trajectory | |||||
|---|---|---|---|---|---|---|---|
| Ligand RMSD (Å) | Average ligand RMSF (Å) | Protein–ligand contacts | Ligand–protein contacts (>30%) | SASA (Å2) | Ligand moved from T1 site | ||
| WT (pH 3.4) | 190 | ≤9 | 3.5 | Mostly ≥1 | 2 | Mostly <100 | No |
| D206A | 1630 | ≤54 | 21.2 | No contact for ∼15 ns | No | >300 during ∼28–45 ns | Yes |
| D206N | 3280 | ≤64 | 30.3 | No contact for ∼15 ns | No | >300 for ∼15 ns | Yes |
| WT (pH 5.0) | 17 ± 5 | ≤9 | 2.7 | Mostly 2–5 | 4 | Mostly ≤100 | No |
| F332A | 165 ± 5 | ≤64 | 27.1 | No contact for ∼14 ns | No | >300 for ∼14 ns | Yes |
| F337A | N/A | ≤50 | 15.2 | Mostly ≥1 | No | >100 | Yes |
In order to further confirm the high dynamic stability of 2,6-DMP at the T1 site of the WT, we performed an additional replication of the WT (pH 3.4) simulation with a different substrate pose (produced by Glide) using the same methodology as described above for 50 ns and 150 ns. Analysis revealed very similar results as those discussed above for the two other WT systems (ESI Fig. S21–S24†). The 150 ns run reproduced the 50 ns run, and the substrate remained at the T1 site throughout the entire 150 ns of time (ESI Fig. S24†). The average binding affinity for the last 20 ns of the 50 ns run was −35.9 kcal mol−1 and its range was −44.0 to −27.5 kcal mol−1.
We conclude that 2,6-DMP forms favorable contacts with the WT at both pH 3.4 and 5.0 and that this leads to a longer residence time of the substrate within the T1 pocket, which will increase the effective concentration of active poses that lead to product formation. However, in the absence of the crucial binding residues, favorable protein–substrate contacts are missing and the substrate displaces from the T1 site to reduce the lifetime of the productive conformation. This dynamic stability (defined here as the lifetime measured in the MD trajectory) of the active protein–substrate conformations is arguably an important real reason for the observed KM in experimental assays, as explored further below. The consistent observation for all these statistically independent simulations suggests that explicit protein–substrate molecular dynamics effectively discriminate large vs. small KM, which is very encouraging.
Dynamically averaged MMGBSA binding affinities reproduce experimental KM
As discussed above, the dynamic stability of the protein–substrate complexes as deduced from MD simulations reproduce the experimentally observed low vs. high KM values for WT and mutant laccases. The question now arises whether this dynamic stability of the active conformations that lead to product formation also relate to the thermodynamic stability of these protein–substrate complexes. To explore this, we evaluated the MMGBSA binding affinities over the full last 20 ns of the 50 ns MD trajectories (run 1), to avoid artifacts of the initial equilibration of the structures. Interestingly, the average MMGBSA energy correlated well with the experimental KM values (Table 4), and showed a better binding energy difference than for Glide poses. This indicates that MMGBSA calculations averaged over equilibrated MD snapshots gives semi-quantitative, accurate information on overall KM.| Mutation | pH | KM25,26 (μM) | MMGBSA binding free energies (kcal mol−1) | ||
|---|---|---|---|---|---|
| Average | SD | Range | |||
| WT (YL4) | 3.4 | 190 | −26.3 | 3.3 | −36.8 to −16.3 |
| D206A | 3.4 | 1630 | −4.3 | 7.9 | −25.7 to 0.8 |
| D206N | 3.4 | 3280 | −11.3 | 7.7 | −30.6 to 0.5 |
| WT (YL4) | 5.0 | 17 ± 5 | −30.4 | 4.1 | −38.4 to −8.9 |
| F332A | 5.0 | 165 ± 5 | −15.3 | 8.4 | −29.4 to 1.6 |
| F337A | 5.0 | N/A | −18.4 | 5.7 | −30.5 to 0.3 |
Many of the configurations in the mutants represent substrate configurations far from the active site, illustrating a real dynamic molecular situation where low-affinity substrates diffuse on the surfaces of the proteins and do not remain statically fixated within the active site. We believe, based on the correlation to experimental KM of these data and the MD simulations discussed above, that our simulations capture a molecular interpretation of the KM parameter as reflecting the subset of active conformations that actually lead to product formation. In contrast, the many low-affinity sites on the surface of the proteins, which are relatively more important when the substrate-binding site has been impaired by mutation, reflect unproductive conformations. Accordingly, we argue that KM does not simply reflect the stability of the protein–substrate complex, but only the active conformation of this complex. In contrast, the measured thermochemical stability of the protein–substrate complex (i.e. the substrate affinity for the protein) reflects an ensemble average of all the conformations encountered. In laccases, this active conformation is well defined by restrictions on the electron transfer distance,21 making it an ideal case study for understanding Michaelis–Menten kinetics.
The pattern of maximal and minimal binding affinities also correlated well with the experimental KM values in all cases. The minimal and maximal binding energy values were in all cases smaller for the WT proteins than for the mutants. The upper range of the free energy of binding for both the WT complexes were negative, whereas they were positive (indicating no net binding) for the mutant complexes. The maximum binding affinity of both the WT complexes (pH 3.4 and 5.0) clearly represented the affinity at the T1 site, because the ligand remained at the T1 site in both these complexes throughout the simulations.
In addition, the standard deviation (SD) values represented the variation in the binding energy over last 20 ns. SD of both the WT complexes was also consistently smaller than their mutated complexes, which reflects a consistency of binding affinity in WT complexes.
Active pose of 2,6-dimethoxyphenol
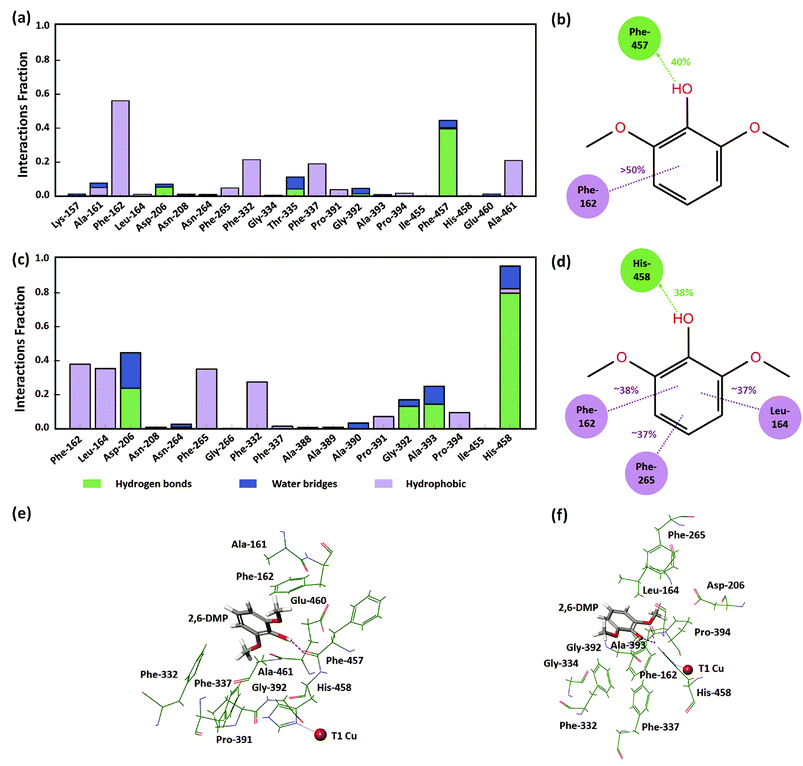
In order to understand the identified active protein–substrate conformation that explains the observed KM, we analyzed in detail the conformation in the WT complex at pH 3.4 during run 1 (50 ns). 2,6-DMP maintained hydrogen bonding and hydrophobic interactions with Phe-457 and Phe-162 for more than 30% of the simulation time (Fig. 5a, b and 5e). The ligand phenolic OH donated a hydrogen bond to the backbone carbonyl O-atom of Phe-457 and maintained this contact for ∼40% of the total 50 ns (Fig. 5b and e). Phe-162 formed hydrophobic contacts with 2,6-DMP for about >50% time, including π–π stacking (∼24% time). In addition, the residues Ala-161, Asp-206, Phe-265, Phe-332, Thr-335, Phe-337, Gly-392, and Ala-461 formed crucial contacts with 2,6-DMP during the simulation (Fig. 5a). Ala-161 formed hydrophobic contacts and water bridges. Asp-206, Thr-335 and Gly-392 formed hydrogen bonds and water bridges with the ligand. Asp-206 formed a hydrogen bond with the phenolic OH group and water bridges with the OH and OCH3 groups of 2,6-DMP. The residues Phe-265, Phe-332, Phe-337 and Ala-461 were involved in hydrophobic interactions with the protein.In WT complex at pH 5.0 (run 1–50 ns), 2,6-DMP showed similar prominent hydrophobic interaction with Phe-162 and Phe-332 residues as in WT pH 3.4; however, the interaction with Phe-457 was not found. In contrast to WT complex at pH 3.4, the prominent interactions in WT at pH 5.0 occurred with Leu-164, Asp-206, Phe-265 and His-458 residues. 2,6-DMP formed and maintained favorable contacts with Phe-162, Leu-164, Phe-265 and His-458 for more than 30% of the simulation time (Fig. 5c, d and f). Nε H-atom of His-458 donated a hydrogen bond to the OH group of 2,6-DMP and maintained this interaction for 38% of the time (Fig. 5d and f). It also formed hydrogen bonding with the two ortho OCH3 groups of the ligand for 17% and 23% time. His-458 also formed water bridges with OH and OCH3 groups and π–π stacking with the phenyl ring of the ligand. The residues Leu-164, Phe-265 formed and maintained crucial hydrophobic contacts. Asp-206, which formed contacts for a very small duration in WT at pH 3.4, formed prominent hydrogen bonds or water bridges for >40% of the simulation in WT pH 5.0. The carboxyl group of Asp-206 accepted a hydrogen bond from the OH group for ∼23% time and additional water bridges with the OH and OCH3 groups of 2,6-DMP. In addition, Pro-391 and Pro-394 formed hydrophobic contacts, and Gly-392 and Ala-393 formed hydrogen bonding and water bridges with 2,6-DMP.
In contrast to 2,6-DMP, another substrate in the dataset – ABTS25,26 showed similar experimental KM in the mutated and the WT laccases. The plausible reason for this is that the ABTS lacks the phenolic OH and OCH3 groups, and therefore does not form hydrogen bonding between these atoms and Asp-206 (ESI Fig. S25†). However, it mainly forms π–π stacking (hydrophobic) interaction with Phe-265. In addition, ABTS (molecular weight: 514.603 g mol−1) is comparatively larger than 2,6-DMP (molecular weight: 154.165 g mol−1), and therefore maintains different prominent interactions than 2,6-DMP (ESI Fig. S25†).
From this detailed overview, we conclude that the active poses that explain the observed KM of the assays involve direct hydrogen bonding between Asp-206/His-458 and 2,6-DMP and additional water bridges that illustrate the role of solvent in substrate–laccase interaction at the T1 site. At pH 5 both ortho methoxy groups of the substrate maintained hydrogen bond interactions with the His-458 for 23% and 17% of the time. However, His-458 also formed hydrogen bond with the OH group for 38% of the time. The residues Phe-162, Leu-164, Phe-265, Phe-332 and Phe-337 provide excellent hydrophobic packing of the substrate to keep it near the T1 site, and thus maximizes the residence time of the substrate's active pose that enables electron transfer to T1. In the absence of this strong hydrophobic interaction, the active pose of 2,6-DMP becomes dynamically instable. The reduced prevalence of this pose thus leads to a reduction in turnover of the enzyme regardless of the affinity of the substrate for the protein in other non-productive poses.
Rationalization of the observed KM effects of laccase mutants
Our computations suggest that Asp-206 is engaged in important interactions with the substrate in the active pose that leads to enzymatic turnover and thus underlies the measured KM. When this residue is replaced with the very hydrophobic Ala, the important stabilizing hydrogen bond is lost. Instead, Ala-206 forms mainly hydrophobic interactions with the ligand together with several other residues (viz. Y152, F162, F265 and F457) that are not strong enough to keep the substrate in the active pose for longer simulation time (ESI Fig. S13 and S16†). This suggests that the D206A mutation disrupts the important hydrogen-bond interaction of Asp-206 and destabilizes the ligand at T1 site, even though some hydrophobic residues work to maintain the ligand at T1 site.In another mutant, Asp-206 was replaced with the similar-sized Asn residue, which neutralizes a negative charge in the binding cavity (Asp-206 could in principle be protonated at the studied pH but the protonation protocol did not indicate so, and the agreement with experiment does not suggest so either). In these simulations, the substrate moved away from the T1 site (ESI Fig. S17†), indicating that the optimal hydrogen bonding is also lost in this mutant, consistent with the expected weaker hydrogen bond accepting ability of the amide group.
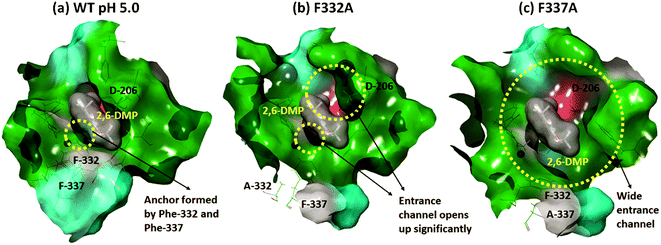
In contrast, Phe-332 and Phe-337 act as anchors that fixate the substrate within the T1 binding site. These residues are present at the entrance of the T1 site as shown in Fig. 1a and 6. They form hydrophobic interactions with 2,6-DMP in the WT complexes (pH 3.4 and 5.0) (Fig. 5). When Phe was replaced by the much smaller Ala residue, the substrate-anchoring function was lost and the T1 entrance channel opened up significantly (Fig. 6), which further reduced the affinity of the ligand for the active site. In the F332A mutant, Ala-332 formed mainly hydrophobic interactions initially for some time during the MD run. The residues Phe-162 and Phe-337 also formed hydrophobic interactions that stabilize this pose of the substrate; however, this interaction was lost during the run and the substrate moved away from the T1 site (ESI Fig. S13 and S18†). In the mutant F337A, the substrate could not maintain any contacts with the T1 site and immediately left the T1 site during simulation (ESI Fig. S19†).
We conclude that the hydrogen bonding between Asp-206 and 2,6-DMP as well as hydrophobic anchoring by the phenylalanines are important interactions that orient the substrate for productive turnover (electron transfer) at the T1 site.
Conclusions
We have reported the results of a computational study of the molecular causes of the experimentally observed KM values of laccase mutants. Using docking, MMGBSA and molecular dynamics simulations, we identify what we consider the “active” pose of the substrate 2,6-DMP within the laccase, located close to the T1 copper and optimally positioned for electron transfer, enabled by hydrogen bonds between the ortho methoxy groups and OH group and His-458. We show that MD lifetimes of the protein–substrate complexes and MMGBSA binding free energies consistently reproduce the separation of the mutants with high experimental KM values from the WT proteins with low KM values.We find that the Asp-206 and hydrophobic Phe-332 and Phe-337 residues are crucial for maintaining the substrate in the active pose that leads to turnover. Mutation of these residues leads to premature diffusion of the substrate away from the T1 site to impair turnover; these observations in all cases correlated with the experimental KM values from two different assays.
One may speculate on the reasons for the success of this procedure. First of all, the dynamic stability of the active poses of the substrate that supposedly engage in enzymatic turnover must necessarily require an energy-balanced force field that enables observation of both the bound and free ligand states, as we see here. Thus, part of the success of the protocol described here probably relates to the fact that we used OPLS2005,45 which is well suited to produce a balanced description of drug–protein interactions because of its origin in experimental free energies rather than merely quantum mechanical calculations.46–48 We expect unbalanced force fields to favor either too much or too little the active pose of the substrate. The fact that we observe both prevalence and loss of this pose indicates that the applied force field is balanced, justifying its use in this protocol, which we consider encouraging for further studies of this type. We observed the expected stochastic behavior of MD simulations, as different runs of the same system yielded distinct residence times, but the overall behavior of the 4500 nanoseconds of simulations were similar, with 15 of the 16 mutant-WT comparisons consistently showing earlier release of substrate in the mutants. This shows that one should perform several MD runs of such systems before making strong conclusions, as the substrate release depends, among other things, on the initial velocity seeds of the MD simulations.
We also note that the MMGBSA binding affinity averaged over the MD trajectory displays a good trend agreement with the experimental KM. While MMGBSA binding affinities are commonly used to predict drug inhibitory constants, they can also estimate KM values for enzymes. Our results suggest that MMGBSA is a good scoring function to qualitatively distinguish between high and low KM values of an order of magnitude difference; this finding should be of interest to enzyme design and optimization.
In its standard interpretation, KM reflects the concentration of substrate required to reach half the maximum activity of the enzyme.54 However, the Michaelis constant is often assumed to quantify the strength of the protein–substrate interaction. Yet, in the limit of very strong association, the turnover would be impaired as described by the Sabatier principle,32 and thus the normal interpretation of KM as simply the protein–substrate affinity cannot be universally true.31,54 We show in this work that KM relates directly to the lifetime of the active substrate pose within the protein, a conformation that is largely determined by the electron transfer distance from the substrate to the T1 copper site, rather than the total ensemble-averaged stability of the enzyme–substrate complex. While the lifetime arising from the specific stability of the active pose substantially contributes to KM, additional factors probably contribute, as KM also carries some information relating to the actual electron transfer step.
In contrast, the measured thermochemical stability of the protein–substrate complex (i.e. the substrate affinity for the protein) reflects an ensemble average of all the conformations encountered. These findings are in good agreement with the discussion of the Michaelis–Menten parameters by Northrop.31 Thus, one cannot generally expect substrate affinities for various docked poses to correlate well with KM, whereas we argue here that those of active poses do.
MD simulations have been carried out previously for other proteins to understand the active site dynamics showing the value of this approach.29,30,55 The present study shows that for laccases, which are complex multi-copper electron transfer proteins, relative experimental KM values (i.e. larger vs. smaller KM) can be accurately estimated from a group of comparative MD simulations allowing for substrate release according to our protocol. In laccases, the relevant active conformation is well-defined by restrictions on the electron transfer distance,21 and thus it is an ideal case study for understanding the contribution of substrate residence time to experimental KM.
Author contributions
R. M. and K. P. K. planned the work. R. M. performed the computations and wrote the first draft of the paper. A. M. and K. P. K. contributed to analysis of the data and writing the final paper.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This study was supported by The Danish Council for Independent Research (Project ref. DFF-4184-00355).References
- A. K. Sitarz, J. D. Mikkelsen and A. S. Meyer, Crit. Rev. Biotechnol., 2016, 36, 70–86 CrossRef CAS PubMed.
- E. I. Solomon, U. M. Sundaram and T. E. Machonkin, Chem. Rev., 1996, 96, 2563–2606 CrossRef CAS PubMed.
- E. I. Solomon, D. E. Heppner, E. M. Johnston, J. W. Ginsbach, J. Cirera, M. Qayyum, M. T. Kieber-Emmons, C. H. Kjaergaard, R. G. Hadt and L. Tian, Chem. Rev., 2014, 114, 3659–3853 CrossRef CAS PubMed.
- S. M. Jones and E. I. Solomon, Cell. Mol. Life Sci., 2015, 72, 869–883 CrossRef CAS PubMed.
- C. Galli, C. Madzak, R. Vadalà, C. Jolivalt and P. Gentili, ChemBioChem, 2013, 14, 2500–2505 CrossRef CAS PubMed.
- U. N. Dwivedi, P. Singh, V. P. Pandey and A. Kumar, J. Mol. Catal. B: Enzym., 2011, 68, 117–128 CrossRef CAS.
- A. I. Cañas and S. Camarero, Biotechnol. Adv., 2010, 28, 694–705 CrossRef PubMed.
- P. Giardina, V. Faraco, C. Pezzella, A. Piscitelli, S. Vanhulle and G. Sannia, Cell. Mol. Life Sci., 2010, 67, 369–385 CrossRef CAS PubMed.
- R. Pogni, M. C. Baratto, A. Sinicropi and R. Basosi, Cell. Mol. Life Sci., 2015, 72, 885–896 CrossRef CAS PubMed.
- L. Munk, M. L. Andersen and A. S. Meyer, Enzyme Microb. Technol., 2017, 106, 88–96 CrossRef CAS PubMed.
- D. K. Sandhu and D. S. Arora, Experientia, 1985, 41, 355–356 CrossRef CAS.
- A. Kunamneni, S. Camarero, C. García-Burgos, F. J. Plou, A. Ballesteros and M. Alcalde, Microb. Cell Fact., 2008, 7, 32, DOI:10.1186/1475-2859-7-32.
- K. Koschorreck, S. M. Richter, A. Swierczek, U. Beifuss, R. D. Schmid and V. B. Urlacher, Arch. Biochem. Biophys., 2008, 474, 213–219 CrossRef CAS PubMed.
- C. Pezzella, L. Guarino and A. Piscitelli, Cell. Mol. Life Sci., 2015, 72, 923–940 CrossRef CAS PubMed.
- P. Giardina and G. Sannia, Cell. Mol. Life Sci., 2015, 72, 855–856 CrossRef CAS PubMed.
- D. M. Mate and M. Alcalde, Biotechnol. Adv., 2015, 33, 25–40 CrossRef CAS PubMed.
- L. Munk, A. M. Punt, M. A. Kabel and A. S. Meyer, RSC Adv., 2017, 7, 3358–3368 RSC.
- N. Hakulinen and J. Rouvinen, Cell. Mol. Life Sci., 2015, 72, 857–868 CrossRef CAS PubMed.
- M. E. P. Murphy, P. E. Lindley and E. T. Adman, Protein Sci., 1997, 6, 761–770 CrossRef CAS PubMed.
- K. Nakamura and N. Go, Cell. Mol. Life Sci., 2005, 62, 2050–2066 CrossRef CAS PubMed.
- N. J. Christensen and K. P. Kepp, J. Mol. Catal. B: Enzym., 2014, 100, 68–77 CrossRef CAS.
- L. P. Christopher, B. Yao and Y. Ji, Frontiers in Energy Research, 2014, 2, 12, DOI:10.3389/fenrg.2014.0001.
- L. Rulísek and U. Ryde, Coord. Chem. Rev., 2013, 257, 445–458 CrossRef.
- K. P. Kepp, Inorg. Chem., 2015, 54, 476–483 CrossRef CAS PubMed.
- C. Madzak, M. C. Mimmi, E. Caminade, A. Brault, S. Baumberger, P. Briozzo, C. Mougin and C. Jolivalt, Protein Eng., Des. Sel., 2006, 19, 77–84 CrossRef CAS PubMed.
- C. Galli, P. Gentili, C. Jolivalt, C. Madzak and R. Vadalà, Appl. Microbiol. Biotechnol., 2011, 91, 123–131 CrossRef CAS PubMed.
- G. Macellaro, M. C. Baratto, A. Piscitelli, C. Pezzella, F. Fabrizi De Biani, A. Palmese, F. Piumi, E. Record, R. Basosi and G. Sannia, Appl. Microbiol. Biotechnol., 2014, 98, 4949–4961 CrossRef CAS PubMed.
- F. Xu, Biochemistry, 1996, 35, 7608–7614 CrossRef CAS PubMed.
- G. Jiménez-Osés, S. Osuna, X. Gao, M. R. Sawaya, L. Gilson, S. J. Collier, G. W. Huisman, T. O. Yeates, Y. Tang and K. N. Houk, Nat. Chem. Biol., 2014, 10, 431–436 CrossRef PubMed.
- S. Osuna, G. Jiménez-Osés, E. L. Noey and K. N. Houk, Acc. Chem. Res., 2015, 48, 1080–1089 CrossRef CAS PubMed.
- D. B. Northrop, J. Chem. Educ., 1998, 75, 1153–1157 CrossRef CAS.
- P. Sabatier, Ber. Dtsch. Chem. Ges., 1911, 44, 1984–2001 CrossRef CAS.
- T. Bertrand, C. Jolivalt, P. Briozzo, E. Caminade, N. Joly, C. Madzak and C. Mougin, Biochemistry, 2002, 41, 7325–7333 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Wessig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- K. Piontek, M. Antorini and T. Choinowski, J. Biol. Chem., 2002, 277, 37663–37669 CrossRef CAS PubMed.
- D. E. Heppner, C. H. Kjaergaard and E. I. Solomon, J. Am. Chem. Soc., 2014, 136, 17788–17801 CrossRef CAS PubMed.
- Prime, Schrödinger, LLC, New York, NY, 2017 Search PubMed.
- LigPrep, Schrödinger, LLC, New York, NY, 2017 Search PubMed.
- R. A. Friesner, R. B. Murphy, M. P. Repasky, L. L. Frye, J. R. Greenwood, T. A. Halgren, P. C. Sanschagrin and D. T. Mainz, J. Med. Chem., 2006, 49, 6177–6196 CrossRef CAS PubMed.
- W. W. Bhat, N. Dhar, S. Razdan, S. Rana, R. Mehra, A. Nargotra, R. S. Dhar, N. Ashraf, R. Vishwakarma and S. K. Lattoo, PLoS One, 2013, 8, e73804 CrossRef CAS PubMed.
- K. J. Bowers, F. D. Sacerdoti, J. K. Salmon, Y. Shan, D. E. Shaw, E. Chow, H. Xu, R. O. Dror, M. P. Eastwood, B. A. Gregersen, J. L. Klepeis, I. Kolossvary and M. A. Moraes, in Proceedings of the 2006 ACM/IEEE conference on Supercomputing - SC ’06, 2006, p. 84 Search PubMed.
- Desmond Molecular Dynamics System, version 2016-4, Schrödinger, LLC, and D. E. Shaw Research, New York, US, 2016 Search PubMed.
- N. J. Christensen and K. P. Kepp, PLoS One, 2013, 8, e61985 CrossRef CAS PubMed.
- N. J. Christensen and K. P. Kepp, J. Chem. Theory Comput., 2013, 9, 3210–3223 CrossRef CAS PubMed.
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed.
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- K. P. Kepp, Biochim. Biophys. Acta, Proteins Proteomics, 2015, 1854, 1239–1248 CrossRef CAS PubMed.
- K. P. Kepp, J. Phys. Chem. B, 2014, 118, 1799–1812 CrossRef CAS PubMed.
- B. P. English, W. Min, A. M. van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. C. Kou and X. S. Xie, Nat. Chem. Biol., 2005, 2, 87–94 CrossRef PubMed.
- E. L. Noey, N. Tibrewal, G. Jiménez-Osés, S. Osuna, J. Park, C. M. Bond, D. Cascio, J. Liang, X. Zhang, G. W. Huisman, Y. Tang and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E7065–E7072 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: System preparation used for MD simulation (Table S1), binding affinity analysis of the docked ligand–protein complexes (Table S2), protein RMSD plots of run 1–4 (Fig. S1–S4), protein RMSF plots of run 1–4 (Fig. S5–S8), ligand RMSD plots of run 1–4 (Fig. S9–S12), ligand-protein interactions during run 1 MD simulations (Fig. S13–S19), SASA plots of run 1 (Fig. S20), MD simulation analysis of another pose of 2,6-DMP in complex with WT (pH 3.4) structure (Fig. S21–S24), and ABTS interaction with WT (pH 3.4) TvL (Fig. S25). See DOI: 10.1039/c8ra07138a |
| This journal is © The Royal Society of Chemistry 2018 |