A novel optical diffuser based on polymer micro-balls-filled nematic liquid crystal composite film

Abstract

In this study, optical diffusers based on epoxy resin/thiol/nematic liquid crystal composites were prepared using different curing temperatures, curing times and curing agents (thiols). Additionally, the effects of the curing temperatures, the curing times and the thiols on the polymer ball microstructures and the optical properties of optical diffusers were investigated systematically. For applications of optical diffusers, the optimized curing temperature has been achieved by combining the high transmittance and high haze. A novel optical diffuser with ultrahigh transmittance (>94.0%), ultrahigh haze (>94.0%) and excellent diffusing ability has been obtained, of which the polymer morphology is single polymer micro-balls without aggregation.

---

1. Introduction

Liquid crystal displays (LCDs) are widely applied in cell-phones, laptops and computers, and optical diffusers are essential constituents of LCDs that enable high performance light management with independent control of light distribution patterns.^1–5 Transmission and haze are two main indices used to characterize optical diffusers, and two broad types of optical diffusers in the LCDs are the top diffuser film and the bottom diffuser film. In general, the top diffuser film requires high transmission and low haze,⁶ while the bottom diffuser needs high transmission and high haze, which have been focused and investigated recently. One method to achieve the bottom diffuser with high transmission, high haze and excellent diffusing ability is doping inorganic or organic particles into a polymer substrate and another method involves building periodic structures onto a polymer substrate.⁷ However, both methods have disadvantages. The dispersibility of particles is critical for the optical properties of optical diffusers in the former method,⁸ while the complex preparation of the periodic structure is the most important factor in the latter method.^9,10 Recently, polymer/liquid crystal (LC) composite films have been focused on in order to avoid the abovementioned problems.¹¹ First, the preparation of the polymer/LC composite films is simple, diversified and cost-effective. Additionally, the polymer/LC composite films can be phase separated and are tunable. Thus, high transmittance and highly scattering films are easily obtained.^12–16

In principle, a polymer/LC composite film consists of micron-size liquid crystals and polymers, where the LC droplets disperse in the polymer matrix by means of a thermally or an ultraviolet (UV) irradiation induced phase separation in a homogeneous solution of LCs and monomers; thus, the film appears to be in a scattering state and can be applied as an optical diffuser.¹⁷ LC droplets dispersed in polymer networks have been investigated, using various approaches such as the Rayleigh–Gans approximation for smaller LC droplets and the anomalous diffraction approximation and the geometrical optical theory for larger LC droplets.¹⁸ We have also studied these three scattering theories, and when the size of LC droplets is about 3.0 μm, the haze and the transmittance of an optical diffuser can reach 88.5% and nearly 90.0%,¹⁹ respectively. Additionally, we have investigated that films with a combined morphology of polymer network and polymer balls has high transmission (>93.0%) and high haze (>95.0%). The curing agent for this type of films consists of thiol and polyamine and their weight ratio is 3 : 1.^20–23

Herein, to obtain a novel optical diffuser with ultrahigh transmission and ultrahigh haze, the same epoxy system described in a previous study was applied. However, only thiol is used the curing agent, and a curing accelerator is used in the system for saving curing time.²⁴ Consequently, we designed an optical diffuser with high transmission (>94.0%) and high haze (>94.0%) filled with uniform polymer micro-balls and nematic LCs. Furthermore, the influences of the curing temperatures, the curing times and the curing agent thiols on the morphologies of the polymer balls and the optical properties of the films were investigated intensively.

2. Experimental

2.1 Materials and methods

The nematic liquid crystal SLC1717 (T_NI = 365 K, Δn = 0.201, n_o = 1.519, n_e = 1.720) was used in the system, which was purchased from Shijiazhuang Chengzhi Yonghua Display Materials Co. Ltd. Commercial. The epoxy monomers used in this study were commercial epoxy resin E-51 and resorcinol diglycidyl ether (RDE), which were both purchased from Heowns Biochem Technologies. Trimethylopropane tris(3-mercaptopropionate) (TTMP) and dipentaerythritol hexakis(3-mercaptopropionate) (DHMP) are thiols without rigid groups, and are both produced by Heowns Biochem Technologies. 4-Dimethylaminopyridine (DMAP) was used as a curing accelerator for the reaction of the epoxy resin and thiol. Chemical structures of the materials are shown in Fig. 1. All the materials were used without further purification.

Fig. 1 The chemical structures of E-51, RDE, TTMP, DHMP and DMAP.

The composite mixtures were prepared according to the data shown in Table 1, and the 20.0 μm-thick glass micro-bead (0.5 wt% of the total weight of the mixtures) was additionally added to control the film thickness. Then, the mixtures were treated by sonicating for 10.0 min to form a homogenous solution, followed by being pressed between two pieces of poly(ethylene terephthalate) (PET substrates, thickness = 50.0 μm). Finally, the mixtures were cured in an oven at defined temperatures for the determined time to obtain the optical diffusers.

Table 1 The composites of the optical diffusers A1–A9 and C1–C9

Sample ID^a	E-51	RDE	TTMP	SLC1717	DMAP
a Sample ID (curing time, curing temperature): A1 (0.5 h, 343.15 K); A2 (0.5 h, 358.15 K); A3 (0.5 h, 373.15 K); A4 (1.0 h, 343.15 K); A5 (1.0 h, 358.15 K); A6 (1.0 h, 373.15 K); A7 (1.5 h, 343.15 K); A8 (1.5 h, 358.15 K); A9 (1.5 h, 373.15 K).b Sample ID (curing time, curing temperature): C1 (0.5 h, 343.15 K); C2 (0.5 h, 358.15 K); C3 (0.5 h, 373.15 K); C4 (1.0 h, 343.15 K); C5 (1.0 h, 358.15 K); C6 (1.0 h, 343.15 K); C7 (1.5 h, 343.15 K); C8 (1.5 h, 358.15 K); C9 (1.5 h, 373.15 K).
A1–A9	0.10 g	0.30 g	0.40 g	0.80 g	0.0080 g

---

Sample ID^b	E-51	RDE	DHMP	SLC1717	DMAP
C1–C9	0.10 g	0.30 g	0.40 g	0.80 g	0.0080 g

---

2.2 Measurements of optical diffusers

Optical properties of optical diffusers include the total transmission and transmission haze, which were examined by UV-vis-NIR spectrophotometry (America, PE Lambda 950) in the visible region (400–800 nm). By adding the integrating spheres, the UV-vis-NIR spectra of optical diffusers were obtained in compliance with ASTM D1003. The optical diffusing abilities of optical diffusers were measured by a light intensity distribution measuring instrument. The distance between the optical diffuser and the light source (CIE illuminant C) was 4.0 cm, while the distance between the photo detector and the optical diffuser is 40.0 cm. By rotating the optical diffuser and the light source synchronously from −60.0° to 60.0°, the corresponding light intensity per degree was detected.

In order to observe the morphologies of optical diffusers, the optical diffusers were dipped into cyclohexane for two weeks at room temperature to remove the LCs. Then, they were dried for 4.0 hours at 353.15 K under vacuum and sputtered with gold coating. The morphologies of the polymers in the optical diffusers were examined by scanning electron microscopy (SEM, HITACHI S-4800).

3. Results and discussions

3.1 The effect of the curing temperature and the curing time on the polymer micro-balls in films A1–A9

As we can see in Fig. 2, when the curing time is 0.5 h, the curing temperature has a profound effect on the morphologies of samples A1–A3. With the increase in the curing temperature, the average size of the polymeric balls increases due to the higher activation energy. At curing temperature 373.15 K, the average size of the polymeric balls in film A2 is about 8.45 μm and that in film A3 is about 14.40 μm. When the curing temperature is 358.15 K, the polymeric balls are still bonded to each other. When the curing temperature is 343.15 K, the energy is relatively lower, and film A1 is isotropic without the formed polymer balls.

Fig. 2 The polymer morphologies of optical diffusers A1–A9.

As the curing time extends to 1.0 h, similar to films A1–A3, the curing temperature also has a profound effect on the polymer morphologies of films A4–A6. Due to the incomplete polymerization, irregular polymer balls are formed in film A4. When the curing temperature is 358.15 K, connected regular polymer balls are formed in film A5 and their average size is 5.55 μm. When the curing temperature increases to 373.15 K, the regular polymer micro-balls in film A6 become smaller, with an average size of 3.33 μm.

Upon prolonging the curing time to 1.5 h, the density of the polymer ball aggregate in film A7 increased with the curing temperature of 343.15 K. Increasing the curing temperature to 358.15 K causes the shape of the polymer balls nearly spherical, as observed for film A8. Upon increasing the curing temperature to 373.15 K, the size of the single polymer ball increased in film A9 compared with that of film A6, which is 10.50 μm.

The microstructures of films A3, A6 and A9, which were prepared at the same temperature while increasing the curing time, were compared. First, with shorter curing time for film A3, the average size of polymer micro-balls is the largest and the micro-balls are poly-dispersed. With the longer curing time in film A6, the micro-balls are uniform and the smallest. When the curing time is set as 1.5 h, the size of the polymer micro-balls increase in film A9, such that they are larger than the limit for light scattering.

3.2 The effect of the curing temperature and the curing time on the polymer micro-balls in films C1–C9

When thiols with the highest degree of functionality were applied as the curing agent in the epoxy resin system, unlike with the film A1, the polymer micro-balls were not formed. First, large polymer ball aggregation occurs and virtually no single polymer balls exist in film C1 when the film is cured at 343.15 K for 0.5 h. On extending the curing time to 1.0 h, the average size of the polymer micro-balls is smaller in film C2, which was cured at 358.15 K for 0.5 h. Continually increasing the curing time to 373.15 K for 1.5 h, the average size of the polymer-balls in the film C3 decreases compared with that in film C2.·In conclusion, the density of the polymer micro-balls of the film increases with the increase in the curing temperature (Fig. 3).

Fig. 3 The polymer morphologies of optical diffusers C1–C9.

By providing the system with a higher degree of functionality, the polymer micro-ball aggregation occurs at the low temperature of 343.15 K for 1.0 h, as observed in the film C4. The density of the polymer micro-balls in film C4 is higher than that in film C1 due to the extended curing time. By raising the curing temperature to 358.15 K for 1.0 h, higher density polymer micro-ball aggregate formed in film C5 compared with that in the film C2. On further increasing the curing temperature to 373.15 K for 1.0 h, the density of the polymer-ball aggregate greatly increased in film C6. Additionally, the average diameter of the polymer micro-balls that grew into polymer micro-ball aggregates decreased.

On increasing the curing time to 1.5 h, the density of the polymer micro-ball aggregate in film C7 increased at the low temperature 343.15 K compared with that in films C1 and C4. Moreover, the average size of the polymer micro-ball aggregate in film C8 decreases with the increase in curing temperature to 358.15 K for 1.5 h. Similarly, on increasing the curing temperature to 373.15 K for 1.5 h, the density of polymer micro-ball aggregate in film C9 was the largest and the average size was the smallest compared with those in films C7 and C8.

3.3 The effect of the curing temperature and the curing time on the optical properties of films

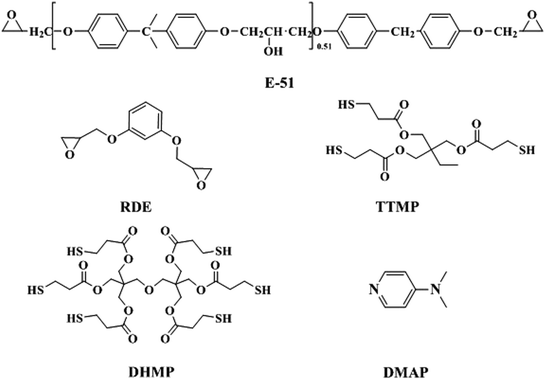
As shown in Fig. 2, the average size of the polymer micro-balls in film A2 is smaller than that in film A3. Moreover, the polymer balls are typically bonded with each other, and the interfaces between the polymer balls and LCs in film A2 are less. Thus, the haze of film A3 is the highest, as shown in Fig. 4(B). Additionally, due to the smaller polymer micro-balls in the film A2, the haze of film A2 is less than that of film A3. As there exists no phase separation in film A1, and the haze of film A1 is the lowest due to the least interfaces between the LCs and the polymer. In case of the transmission of films A1–A3 (shown in Fig. 4(A)), due to the smaller polymer micro-balls in film A2, light can transmit from the film more, so the transmission of film A2 is the highest. Contrary to films A2 and A3, the polymer forms a flat film without polymer micro-balls, and the scattering of the LC droplets leads to a decrease in the transmission in film A1. In summary, in terms of high transmission (>90.0%) and haze (>90.0%), film A2 can meet the needs of the system when the curing time is fixed at 0.5 h and the curing temperature is fixed at 358.15 K.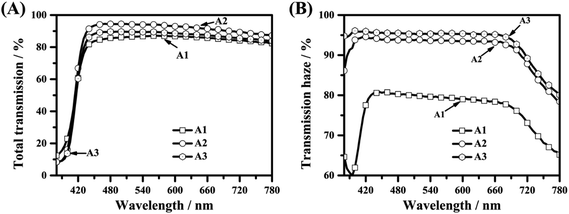

Fig. 4 The optical properties of optical diffusers A1–A3; (A) total transmissions of optical diffusers A1–A3; (B) transmission hazes of optical diffusers A1–A3.

As shown in Fig. 5(B), due to the non-uniform polymer balls in film A5, the haze of film A5 (over 95.0%) is higher than that of film A6 because of the interfacial scattering between the LCs and polymer balls. Due to the irregular and larger polymer micro-balls, the haze of film A4 is the smallest. Due to the high transmission of the smallest regular polymer balls, the transmission of film A6 is the highest, as shown in Fig. 5(A). As transmissions of films A4 and film A5 both decrease with the fortified light scattering between the LCs and the irregular polymer balls, their transmissions are lower than that of film A6. In summary, film A6 displays ultrahigh transmission and ultrahigh haze and hence, it can be widely applied as an excellent optical diffuser.

Fig. 5 The optical properties of optical diffusers A4–A6; (A) total transmissions of optical diffusers A4–A6; (B) transmission hazes of optical diffusers A4–A6.

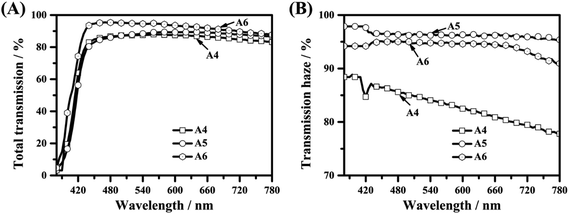
With a curing time of 1.5 h, the hazes of films A8 and A9 are both above 90%, as depicted in Fig. 6(B), which mainly depends on the scattering of the larger polymer balls. As the polymer balls are interconnected in film A7, the light scattering decreased. Referring to the transmissions in films A7–A9 deriving from high transmission of polymer balls, transmissions of film A8 and film A9 are relatively higher than that of film A7, as described in Fig. 6(A).

Fig. 6 The optical properties of optical diffusers A7–A9; (A) total transmissions of optical diffusers A7–A9; (B) transmission hazes of optical diffusers A7–A9.

Considering the transmissions and hazes of films A1–A9 at light wavelength λ = 560.0 nm, as shown in Fig. 7, with shortened curing time, the optimal curing temperature is 358.15 K for obtaining simultaneously high transmission and haze that are. Upon extending the curing time, the film haze increases with the increase in curing temperature while maintaining a high transmission. By continually increasing the curing time, the transmission of the film increases. Additionally, the haze of the film decreases when the film is cured at higher temperatures. In conclusion, the optical diffuser A6 obtains a high transmittance (94.72%) and high haze (94.87%); thus, it can be expected to be a novel optical diffuser.

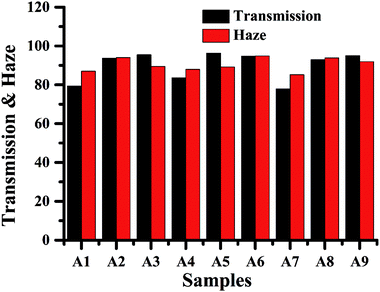Fig. 7 The transmissions and hazes of optical diffusers A1–A9 when the light wavelength is 560.0 nm.

The relationship between the average size of the polymer balls in film A3, film A6 and film A9 and the optical properties of these films has been investigated, as shown in Fig. 8(A). With the increase in average size of the polymer balls, the haze of the film decreases and the transmission of the film increases. Generally, the scattering theories, such as the Rayleigh–Gans approximation and the anomalous diffraction approximation, are applied in investigations of polymer/LC composites based on polymer networks and nematic LCs.^25–35 Herein, as the polymer network becomes micro-size anisotropic polymer balls, the Mie scattering theory was applied in the system, which inferred that the scattering intensity of the film is inversely proportional to the size of the scatters. The experimental result shown in Fig. 8(A) conforms to the scattering theory. Comparing the light diffusing abilities of film A3, A6 and A9, as shown in Fig. 8(B), the light diffusing abilities of films A6 and A9 are better than that of film A3.

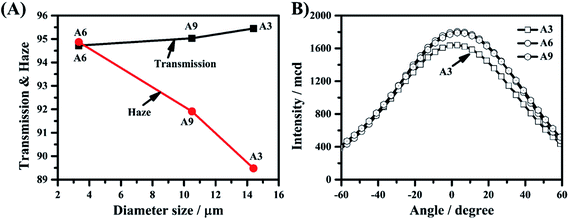Fig. 8 (a) The relationship between the transmissions and hazes of optical diffusers A3, A6 and A9 and their diameter sizes; (b) the diffusing abilities of optical diffusers A3, A6 and A9.

3.4 The effect of the functionality of the curing agent on the optical properties of films

The polymer balls in films C1–C3 formed high density aggregates. Thus, the hazes of films C1–C3 are basically maintained at 95.0% due to the multiple light scattering of the polymer ball aggregates,^25–35 as shown in Fig. 9(B). Owing to the strong scattering in films C1–C3, the transmissions of films C1–C3 decreased to 80.0%. Similar to the case for films A1–A3, among films C1–C3, film C2 shows the highest transmission (just over 80.0%), as depicted in Fig. 9(A). Consequently, to obtain films with high transmission (>90.0%) and high haze (>90.0%), they should be cured at 358.15 K.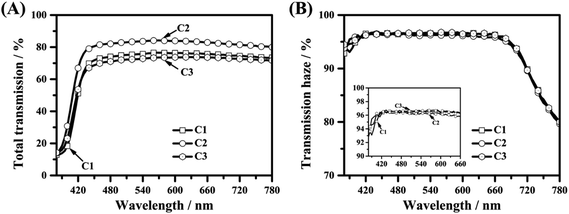

Fig. 9 The optical properties of optical diffusers C1–C3; (A) total transmissions of optical diffusers C1–C3; (B) transmission hazes of optical diffusers C1–C3.

When the curing agent functionality is primarily thiol, the polymer balls became polymer aggregates. The hazes of films C4–C6, unlike those of films A4–A6, are not consistently over 90.0% when the light wavelength is lower than 660.0 nm, as depicted in Fig. 10(B). Due to the highest density of polymer aggregates, film C6 has the highest haze. The transmissions of films C4–C6 decreased with the increase in haze and the transmission of film C4 was the highest, as shown in Fig. 10(A). Herein, the film with high transmission (>90.0%) and haze (>90.0%) was achieved at the lowest temperature.

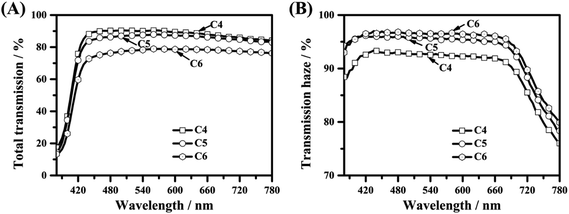Fig. 10 The optical properties of optical diffusers C4–C6; (A) total transmissions of optical diffusers C4–C6; (B) transmission hazes of optical diffusers C4–C6.

The transmissions and hazes of films C7–C9 are presented in Fig. 11(A) and (B). It is easily observed that the transmissions of the films decrease with the increase in curing temperature in films C7–C9, while the hazes of the films increase. Due to the enhanced high-density polymer ball aggregates in films C7–C9 obtained on increasing the curing temperature, light scattering increases between the interfaces of the LCs and polymer ball aggregates.

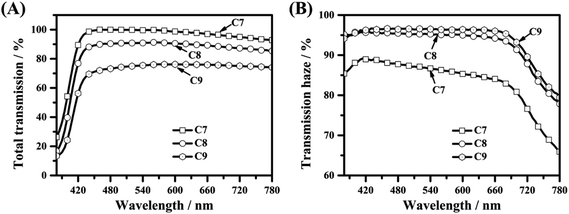Fig. 11 The optical properties of optical diffusers C7–C9; (A) total transmissions of optical diffusers C7–C9; (B) transmission hazes of optical diffusers C7–C9.

Fig. 12 shows the transmissions and hazes of films C1–C9 when the light wavelength is 560.0 nm. With shorter curing time, the transmissions of the films are ultrahigh, while the hazes are relatively low. On curing the films for longer times, the haze of films decreases with the increase in curing temperature due to the smaller polymer ball aggregates. On curing the films with increasing curing time, the haze of the film reaches the highest at the lower curing temperature, but the haze of the film decreases with the increase in curing temperature, while the transmission of film increases. Therefore, the optimal curing temperature is 358.15 K with the longest curing time (1.5 h), due to which film C8 simultaneously obtains high transmission (95.08%) and high haze (91.25%). Therefore, to obtain a high-performance optical diffusers, film A6 is the best choice due to the single uniform 3.33 μm polymer balls in the film.

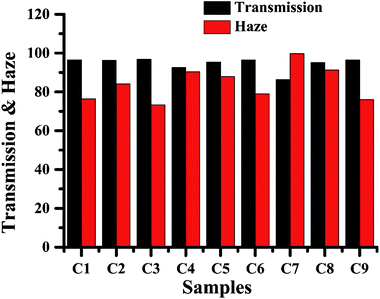Fig. 12 The transmissions and hazes of optical diffusers C1–C9 when the light wavelength is 560.0 nm.

3.5 The comparison of optical diffusers based on polymer micro-balls and optical diffusers based on composite polymer networks/polymer micro-balls

In our lab, we proposed for the first time the preparation of optical diffusers based on polymer/nematic LCs composite films. Haipeng et al. fabricated several optical diffusers based on polymer networks/nematic LCs composite films, which can be named type A optical diffusers.¹⁹ When the size of the spherically dispersed LC droplets in the polymer networks is about 3.0 μm, the haze of the optical diffuser can reach 88.5% and the transmission is nearly 90.0%. When the size of spherically dispersed LC droplets in the polymer networks is about 10.0 μm, the haze of the optical diffuser can reach 39.2% and the transmission is 90.2%. To obtain optical diffusers with higher transmission and higher haze, our former study focused on an optical diffuser with a combined polymer morphology of polymer networks and polymer balls.²³ The haze of the optical diffuser can reach 95% and the transmission of the optical diffuser can reach 93% when the average diameter size of the polymer balls in the optical diffuser is 2.67 μm and the average diameter of the dispersed LC droplets in the polymer networks is 1.99 μm. These can be regarded as type B optical diffusers. Herein, to investigate optical diffusers with polymer micro-balls/nematic LCs composite films, we applied a tertiary amine as an accelerator and used a thiol as the curing agent. By coherently controlling the functionality of thiol in the curing agent (choosing TTMP as the curing agent), the curing time (1.0 h) and the curing temperature (373.15 K), an optical diffuser with high transmission and high haze was fabricated, whose transmission can reach 94% and haze can reach 94%. Compared with the type B optical diffuser, the transmission of this optical diffuser is slightly high and the haze is slightly low as the average diameter of the polymer micro-balls in the optical diffuser is 3.33 μm. This optical diffuser can be called type C optical diffuser. Although there is a minor difference between the optical properties of the type B optical diffuser and the type C optical diffuser, their polymer morphologies are different and the light scattering theories in the type B optical diffuser and the type C optical diffuser differ, which has great significance for the design of optical diffusers.

3.6 The potential mechanism of light scattering in the optical diffuser based on polymer micro-balls/nematic liquid crystals

Early observations of light scattering were made by Lord Rayleigh, who attributed it for the blue color of the sky.^36,37 According to Maxwell's equations, the light scattering of a plane electromagnetic wave by a homogeneous sphere is one boundary.^38–40 In 1908, G. Mie provided a solution for the spherical wave function, which accurately predicts sphere scattering for all sizes of spheres.^41,42 The Rayleigh approximation can be applied when the size of the particle is smaller than the wavelength of the incident light.^43–45 Meeten et al. considered the results for isotropic and anisotropic spherical droplets and observed that the Rayleigh–Gans approximation and anomalous diffraction approximation can be applied for anisotropic spheres with a mean refractive index close to that of the polymer.^46–50 The basic theories for LC droplets were developed by Stein and Rhodes, Meeten and Navard, Zumer, Whitehead, Yang, Montgomery and others.^36–50 S. Zumer theoretically studied the light scattering from a single spherical birefringent droplet. For LC droplets that are much smaller than the wavelength of the light, the Rayleigh–Gans approximation describes the scattering, while for LC droplets that are comparable in size to the incident light wavelength, the anomalous diffraction approach is more appropriate.^41,43 It is well known that light scattering of polymer/nematic LCs is an important issue and many studies have focused on the issue.^51–54 As for the light scattering of polymer/nematic LC composite films, there are many models focusing on single scattering and multiple scattering in the polymer/nematic LC composite films.^55–63

In this study, we prepared optical diffusers based on polymer micro-balls/nematic LCs. As the average diameter size of polymer micro-balls was larger than the incident light wavelength, Mie scattering was applied in the system. According to many theoretical simulations of Mie scattering,^64–70 generally, the light scattering intensity increases with the decrease in the size of the polymer balls. Additionally, because the anisotropic LC droplets are not confined by the polymer micro-balls, the transmission of the film increases.

4. Conclusions

In summary, we have demonstrated a simple, innovative, and cost-effective optical diffuser based on a polymer/LC composite. The polymer micro-balls formed automatically in the polymer/LC composites were critical for fabricating optical diffusers. When the average size of uniform spherical polymer balls was about 3.33 μm, an excellent optical diffuser with high light transmission, high haze and good diffusion ability was fabricated.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 51333001, 51573006 and 51573003), the Key International Cooperation Project (Grant No. 51720105002), NSFC International Cooperation and Exchanges Projects (Grant No. 51561135014) and the National Natural Science Foundation of China (Grant No. 51602007).

References

1. J. Hu and Y. Zhou, The properties of nano (ZnO–CeO₂)@polysiloxane core–shell microspheres and their application for fabricating optical diffusers, Appl. Surf. Sci., 2016, 365, 166–170.
2. J. Hu, Y. Zhou and T. Zhang, The novel optical diffusers based on the fillers of boehmite hollow microspheres, Mater. Lett., 2014, 136, 114–117.
3. J.-H. Wang, S.-Y. Lien, J.-R. Ho, T.-K. Shih, C.-F. Chen, C.-C. Chen and W.-T. Whang, Optical diffusers based on silicone emulsions, Opt. Mater., 2009, 32, 374–377.
4. J. Zhu, Y. Liu, S. Su and J. Wu, Fabrication of engineered particle-doped light diffuser with a soft transparent mold of UV-curable polymer, Opt. Mater., 2017, 73, 234–240.
5. J. Hu, Y. Zhou and X. Sheng, Optical diffusers with enhanced properties based on novel polysiloxane@CeO₂@PMMA fillers, J. Mater. Chem. C, 2015, 3, 2223–2230.
6. J. Hu, Y. Zhou and X. Sheng, Hydrothermal synthesis of ZnO@polysiloxane microspheres and their application in preparing optical diffusers, RSC Adv., 2015, 5, 17064–17069.
7. J. Hu, Y. Zhou, M. Wang, M. Yang and G. Yan, Optical diffusers based on the novel fillers of polysiloxane@boehmite core–shell microspheres, Mater. Lett., 2016, 165, 107–110.
8. H.-G. Park and D.-Y. Khang, High-performance light diffuser films by hierarchical buckling-based surface texturing combined with internal pores generated from physical gelation induced phase separation of binary polymer solution, Polymer, 2016, 99, 1–6.
9. W. Suthabanditpong, C. Takai, M. Fuji, R. Buntem and T. Shirai, Improved optical properties of silica/UV-cured polymer composite films made of hollow silica nanoparticles with a hierarchical structure for light diffuser film applications, Phys. Chem. Chem. Phys., 2016, 18, 16293–16301.
10. J. Hu, Y. Zhou, M. He and X. Yang, Novel multifunctional microspheres of polysiloxane@CeO₂-PMMA: optical properties and their application in optical diffusers, Opt. Mater., 2013, 36, 271–277.
11. J. Zhu, Y. Liu, S. Shen and J. Wu, Fabrication of engineered particle-doped light diffuser with a soft transparent mold of UV-curable polymer, Opt. Mater., 2017, 73, 234–240.
12. T. Alqurashi, P. Penchev, A. K. Yetisen, A. Sabouri, R. M. Ameen, S. Dimov and H. Butt, Femtosecond laser directed fabrication of optical diffusers, RSC Adv., 2017, 7, 18019–18023.
13. A. Colombo, F. Tassone, F. Santolini, N. Contiello, A. Gambirasio and R. Simonutti, Nanoparticle-doped large area PMMA plates with controlled optical diffusion, J. Mater. Chem. C, 2013, 1, 2927–2934.
14. Z. Fang, H. Zhu, W. Bao, C. Preston, Z. Liu, J. Dai, Y. Li and L. Hu, Energy Environ. Sci., 2014, 7, 3313–3319.
15. H. Butt, A. K. Yetisen, A. A. Khan, K. M. Knowles, M. M. Qasim, S. H. Yun and T. D. Wilkinson, Electrically Tunable Scattering from Devitrite-Liquid Crystal Hybrid Devices, Adv. Opt. Mater., 2017, 5, 1600414.
16. T. Ohzono, K. Suzuki, T. Yamaguchi and N. Fukuda, Tunable Optical Diffuser Based on Deformable Wrinkles, Adv. Opt. Mater., 2013, 1, 374–380.
17. H. M. J. Boots, J. H. M. Neijzen, F. A. M. A. Paulissen, M. B. Van Der Mark and H. J. Cornelissen, Multiple Light Scattering from Polymer-Dispersed Liquid Crystals, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 303, 37–40.
18. K.-J. Yang, S.-J. Sung, B. D. Choi and J. K. Kang, Light Scattering Characteristics of Newly Designed Polymer Dispersed Liquid Crystals Films, Mol. Cryst. Liq. Cryst., 2009, 513, 38–44.
19. H. Ma, L. Zhou, C. Han, C. Zhang and L. Zhang, The fabrication of novel optical diffuser based on UV-cured polymer dispersed liquid crystals, Liq. Cryst. DOI:10.1080/02678292.2018.1477210.
20. H. Nomura, et al., Interfacial Interaction between Nematic Liquid Crystal and Polymer in the Composite Film Consisting of Nematic Liquid Crystal and Connected Polymer Microspheres, J. Appl. Phys., 1991, 30, 327–330.
21. H. Nomura, S. Suzuki and Y. Atarashi, Electro-optical properties of films consisting of nematic liquid crystals and connected polymer microspheres, J. Appl. Phys., 1990, 68, 2922–2926.
22. S. J. Chang, C. M. Lin and A. Y. G. Fuh, Studies of polymer ball type polymer dispersed liquid crystal films, Liq. Cryst., 1996, 21, 19–23.
23. L. Zhou, H. Ma, C. Han, W. Hu, S. Zhang, L. Zhang and H. Yang, A novel light diffuser based on the combined morphology of polymer networks and polymer balls in a polymer dispersed liquid crystals film, RSC Adv., 2018, 8, 21690–21698.
24. Y. Gao, P. Song, T. Zhang, W. Yao, H. Ding, J. Xiao, S. Zhu, H. Cao and H. Yang, Effects of a triethylamine catalyst on curing time and electro-optical properties of PDLC films, RSC Adv., 2013, 3, 23533–23538.
25. B.-G. Wu, J. L. West and J. William Doane, Angular discrimination of light transmission through polymer-dispersed liquid-crystal films, J. Appl. Phys., 1987, 62, 3925–3931.
26. N. A. Vaz and G. Paul Montgomery, Refractive indices of polymer-dispersed liquid-crystal film materials: epoxy-based systems, J. Appl. Phys., 1987, 62, 3161–3172.
27. P. S. Drzaic, Polymer dispersed nematic liquid crystal for large area displays and light valves, J. Appl. Phys., 1986, 60, 2142–2148.
28. S. J. Cox, V. Y. Reshetnyak and T. J. Sluckin, Effective medium theory of light scattering in polymer dispersed liquid crystal films, J. Phys. D: Appl. Phys., 1998, 31, 1611–1625.
29. P. S. Drzaic and A. M. Gonzales, Refractive index gradients and light scattering in polymer-dispersed liquid crystal films, Appl. Phys. Lett., 1993, 62, 1332–1334.
30. J. Kelly, W. Wu and P. Palffy-muhoray, Wavelength Dependence of Scattering in PDLC Films: Droplet Size Effects, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1992, 223, 251–261.
31. V. A. Loiko and V. I. Molochko, Polymer-Dispersed Liquid Crystal Droplets: Calculations of Light Scattering, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 331, 541–548.
32. L. Leclercq, Light scattering from acrylate-based polymer dispersed liquid crystals: theoretical considerations and experimental examples, Liq. Cryst., 1991, 26, 415–425.
33. S. Stallinga, M. M. Wittebrood, D. H. Luijendijk and Th. Rasing, Light Scattering by Thin Nematic Liquid Crystal Films, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 304, 231–234.
34. W. Li, Z. Cheng, G. Pan, H. Liu, H. Cao, Y. Zhou and H. Yang, Effects of the mixture composition on the microstructure of polymer matrix and light scattering properties of liquid crystal/photo-polymerizable monomers composites, Opt. Mater., 2008, 31, 434–439.
35. D. Sinclair, Light Scattering by Spherical Particles, J. Opt. Soc. Am., 1947, 37, 475–480.
36. J. R. Stevens, I. C. Bowell and J. L. Hunt, Light scattering from isotropic polymeric solids, J. Appl. Phys., 1972, 43, 4354.
37. S. R. Aragón and R. Pecora, Theory of dynamic light scattering from polydisperse systems, J. Chem. Phys., 1976, 64, 2395–2404.
38. V. Mazzacurati, M. Nardone and G. Signorelli, Light scattering from disordered media, Mol. Phys., 1979, 38, 1379–1391.
39. S. Asano and M. Sato, Light scattering by randomly oriented spheroidal particles, Appl. Opt., 1980, 19, 962–974.
40. R. S. Stein and S. Mohan, Fifty Years of Light Scattering: A Perspective, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 2003–2010.
41. S. Žumer and J. W. Doane, Light scattering from a small nematic droplet, Phys. Rev. A, 1986, 34, 3373–3386.
42. R. Schiffer, Light Scattering by Composite Rough Surfaces, J. Mod. Opt., 1987, 34, 1145–1168.
43. S. Žumer, Light scattering from nematic droplets: anomalous-diffraction approach, Phys. Rev. A, 1988, 37, 4006–4015.
44. G. P. Montgomery Jr, Angle-dependent scattering of polarized light by polymer-dispersed liquid-crystal films, J. Opt. Soc. Am. B, 1988, 5, 774–784.
45. G. P. Montgomery Jr and N. A. Vaz, Light-scattering analysis of the temperature-dependent transmittance of a polymer-dispersed liquid crystal film in its isotropic phase, Phys. Rev. A, 1989, 40, 6580–6591.
46. P. S. Drzaic and A. Muller, Droplet shape and reorientation fields in nematic droplet/polymer films, Liq. Cryst., 1989, 5, 1467–1475.
47. H. Zhang, Approximate calculation of extinction coefficient, J. Phys. D: Appl. Phys., 1990, 23, 1735–1737.
48. G. P. Montgomery Jr, J. L. West and W. Tamura-Lis, Light-Scattering from Polymer-Dispersed Liquid Crystal Films-Droplet Size Effects, J. Appl. Phys., 1991, 69, 1605–1612.
49. R. Graaff, J. G. Aarnoudse, J. R. Zijp, P. M. A. Sloot, F. F. M. de Mul, J. Greve and M. H. Koelink, Reduced light-scattering properties for mixtures of spherical particles: a simple approximation derived from Mie calculations, Appl. Opt., 1992, 31, 1370–1376.
50. J. R. Kelly and W. Wu, Multiple scattering effects in polymer dispersed liquid crystals, Liq. Cryst., 1993, 14, 1683–1694.
51. J. B. Whitehead Jr, S. Žumer and J. W. Doane, Light scattering from a dispersion of aligned nematic droplets, J. Appl. Phys., 1993, 73, 1057–1065.
52. P. S. Drzaic and A. M. Gonzales, Refractive index gradients and light scattering in polymer-dispersed liquid crystal films, Appl. Phys. Lett., 1993, 62, 1332.
53. K. Muinonen, Light Scattering by Gaussian Random Particles: Rayleigh and Rayleigh–Gans Approximation, J. Quant. Spectrosc. Radiat. Transfer, 1996, 55, 603–613.
54. K. Muinonen, T. Nousiainen, P. Fast, K. Lumme and J. I. Peltoniemi, Light Scattering by Gaussian Random Particle: Ray Optics Approximation, J. Quant. Spectrosc. Radiat. Transfer, 1996, 55, 577–601.
55. S. Tahata, A. Tsumura, M. Mizunuma, H. Koyama, A. Tamatani and T. Masumi, Light Scattering Properties of Polymer Dispersed Liquid Crystals, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1996, 275, 99–106.
56. A. I. Vanin, Light Scattering by groups of spherical particles, J. Appl. Spectrosc., 1997, 64, 242–245.
57. S. Stallinga, M. M. Wittebrood, D. H. Luijendijk and Th. Rasing, Light Scattering by Thin Nematic Liquid Crystal Films, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 304, 231–234.
58. J. H. M. Neijzen, H. M. J. Boots, F. A. M. A. Paulissen, M. B. M. Van Der and H. J. Cornelissen, Multiple scattering of light from polymer dispersed liquid crystal material, Liq. Cryst., 1997, 22, 255–264.
59. G. Chidichimo, Z. Huang, C. Caruso, G. De Filpo and F. P. Nicoletta, Angular Transmission of Polymer Dispersed Liquid Crystals Films, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1997, 299, 379–387.
60. J. W. Doane, N. A. Vaz, B. G. Wu and S. Žumer, Field controlled light scattering from nematic microdroplets, Appl. Phys. Lett., 1998, 48, 269.
61. V. A. Loiko and V. I. Molochko, Polymer-Dispersed Liquid Crystal Droplets: Calculations of Light Scattering, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 331, 541–548.
62. L. Leclercq, U. Maschke, B. Ewen, X. Coqueret, L. Mechernene and M. Benmoun, Light scattering from acrylate-based polymer dispersed liquid crystals: theoretical considerations and experimental examples, Liq. Cryst., 1999, 26, 415–425.
63. V. A. Loiko and V. V. Berdnik, Investigation of Multiple Scattering in Polymer-Dispersed Liquid Crystal Films on the Base of Radiative Transfer Equation, Mol. Cryst. Liq. Cryst., 2002, 375, 511–523.
64. E. G. Rawson, Calculation of Mie Scattering by Spherical Particles in Low-Loss Glasses for Optical Waveguides, Appl. Opt., 1971, 10, 2778–2779.
65. Y. Yang, Z. Zhang and D. Jiang, Numerical Calculation of Mie Scattering, J. Appl. Opt., 1997, 38, 81–85.
66. R.-J. Zhu, J. Wang and G.-F. Jin, Mie scattering calculation by FDTD employing a modified Debye model for Gold material, Optik, 2005, 116, 419–422.
67. A. R. Jones, Calculation of the ratios of complex Riccati–Bessel functions for Mie scattering, J. Phys. D: Appl. Phys., 1983, 16, L49–L52.
68. H. Du, Mie-scattering calculation, Appl. Opt., 2004, 43(9), 1951–1956.
69. V. E. Cachorro and L. L. Salcedo, New Improvements for Mie Scattering Calculations, J. Electromagnet. Wave., 1991, 5, 913–926.
70. H. Y. Zhang, W. J. Zhao, De. M. Ren, Q. U. Yan-Chen and B. A. Song, Improved Algorithm of Mie Scattering Parameter Based on Matlab, Chinese Journal of Light Scattering, 2008, 20, 102–110.

---