Insights into Ag(I)-catalyzed addition reactions of amino alcohols to electron-deficient olefins: competing mechanisms, role of catalyst, and origin of chemoselectivity

Abstract

The competing mechanisms of Ag(I)-catalyzed chemoselective addition reactions of amino alcohols and electron-deficient olefins leading to the O-adduct or N-adduct products were systematically studied with density functional theory methods. Calculations indicate that the AgHMDS/dppe versus AgOAc/dppe catalytic systems can play different roles and thereby generate two different products. The AgHMDS/dppe system works as a Brønsted base to deprotonate the amino alcohol OH to form the Ag–O bond, which leads to formation of the O-adduct. In contrast, the AgOAc/dppe system mainly acts as a Lewis acid to coordinate with O and N atoms of the amino alcohol, but it cannot act as the Brønsted base to further activate the OH group because of its weaker basicity. Therefore, the AgOAc/dppe catalyzed reaction has a mechanism that is similar to the non-catalyzed reaction, and generates the same N-adduct. The obtained insights will be important for rational design of the various kinds of cooperatively catalyzed chemoselective addition reactions, including the use of the less nucleophilic hydroxyl groups of unprotected amino alcohols.

---

1. Introduction

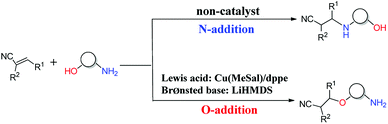
The oxa-Michael reaction is an efficient method for the construction of carbon–oxygen bonds.^1–3 These oxygen-containing natural products, such as glycosides, amino acids, and polycyclic ethers, have many important bioactivities. Although this kind of reaction is a highly atom-economic transformation for the construction of carbon–oxygen bonds and has attracted considerable attention from the synthetic community,^4–7 it has some drawbacks such as low reactivity, reversibility issues, and a lack of control in selectivity. Thus, the development of the oxa-Michael reaction with atomic economy and high selectivity is highly desirable.

Recently, a number of studies were reported to have solved these questions.^5–12 In 2006, Gunnoe and coauthors^8,9 reported the determination method of reaction rates of O vs. N nucleophiles in the Cu(I) catalyzed Michael addition. Subsequently, the Ohshima group^10–12 reported that a series of soft Lewis acids (Cu(I) and Ag(I) salt) catalyzed the chemoselective conjugate addition reactions of amino alcohols to electron-deficient olefins (an oxa-Michael reaction), which enabled the chemoselective deprotonation of the hydroxyl group (OH) of the amino alcohol. As shown in Scheme 1, the Ohshima group reported the first example of the Lewis acid and base cooperatively catalyzed conjugate addition reaction of amino alcohols to α,β-unsaturated nitriles in 2014.¹⁰ Generally, the nucleophilicity of the NH₂ group is stronger than that of the OH group in amino alcohols, and N-addition should be the preferred process. Interestingly, the cooperative nature of the catalyst (Cu(MeSal)/dppe and LiHMDS) enabled chemoselective activation of alcohols over amines, leading to the O-addition reaction. Then the Ohshima group reported the addition reaction of amino alcohol to α,β-unsaturated sulfonyl derivatives,¹¹ as shown in Scheme 2, gave varied reaction products according to different reaction conditions. The AgHMDS/dppe system and the cooperative catalyst system (Ag(OAc)/dppe and KHMDS) enabled chemoselective activation of alcohols over amines to induce the O-addition reaction, but the AgOAc/dppe catalyst cannot reverse the innate activity order of OH and NH₂ groups of amino alcohols. In 2017, the Ohshima group reported the chemoselective conjugate addition of an amino alcohol to an α,β-unsaturated ester,¹² as shown in Scheme 3, in which the cooperative catalyst achieved chemoselective addition of the hydroxyl group over the amino group, and favored chemoselective conjugate addition over transesterification. These reactions not only contribute to atom and step economy,¹³ but also reverse the innate activity order of OH and NH₂ groups of amino alcohols.

Scheme 1 The different O- and N-additions of amino alcohols to α,β-unsaturated nitriles.

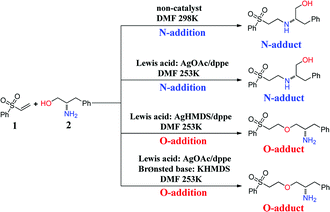Scheme 2 The different O- and N-additions of amino alcohols to α,β-unsaturated sulfonyl derivatives controlled by different catalysts.

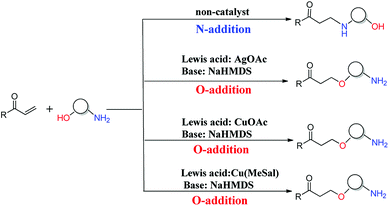Scheme 3 The different O- and N-additions of amino alcohols to α,β-unsaturated esters controlled by different catalysts.

The reactions discussed in Schemes 1–3 are very convenient and unique, therefore, the detailed reaction mechanisms should be worthy to disclose, and the origin of switchable chemoselectivities is urgent to confirm and explore deeply in theory. Prompted by the interesting experimental observations and our interest in catalysis mechanisms,¹⁴ we selected and investigated the addition reactions of amino alcohols and olefins based on the different catalytic systems in Scheme 2 as model reactions. In the present study, we sought to provide exact pictures of the detailed reaction mechanisms, explore the roles of the different catalysts, and find the origin of the chemoselectivity. All the calculations were carried out using density functional theory (DFT), which has been confirmed to be a powerful tool for investigating enzyme-catalyzed,¹⁵ organocatalytic,¹⁶ and transition metal-catalyzed¹⁷ reaction mechanisms and other theoretical studies.¹⁸

2. Results and discussion

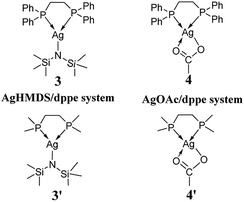
We started our investigation using the model reaction between L-phenylalaninol (1) and unsubstituted phenyl vinyl sulfone (2), as shown in Scheme 2. As depicted in Scheme 4, we constructed two model catalysts (3′ and 4′) for this mechanistic study. It is noteworthy that the phenyl groups of dppe in AgHMDS/dppe (3) and AgOAc/dppe (4) systems were replaced by methyl groups to save computing resources. To explore the roles of different catalysts, we examined four main scenarios to discuss the calculated results, including addition reaction pathways in the absence of catalyst and use of the different catalyst systems.

Scheme 4 The catalyst systems.

2.1 Addition reaction pathways in the absence of catalyst

The processes of direct addition of 1 to 2 to give the O-adduct and N-adduct in the absence of catalyst were investigated, and the corresponding free-energy profiles are shown in Fig. 1. The energy profile of O-addition pathway was shown in red color, while that of N-addition pathway was shown in blue color, and the same colors were used in the following figures. Both addition processes are compatible with the anti-Markovnikov rule, with the N or O atom of 1 adding to the C2 atom of 2 while the H atom of 1 adds to the C1 atom of 2. This is a 1,2-addition process, and is preferred because the 1,4-addition process is very difficult using the benzenesulfonyl group. Fig. 1 suggests that the reactivity of the NH₂ group is higher than that of the OH group, because the N-adduct is easy to obtain at room temperature with an energy barrier of 19.8 kcal mol⁻¹ via transition state TS1-N-non, whereas the O-adduct is difficult to obtain because of the extremely high energy barrier (31.5 kcal mol⁻¹) via transition state TS1-O-non. These calculated results are consistent with the experimental results depicted in Scheme 2.¹¹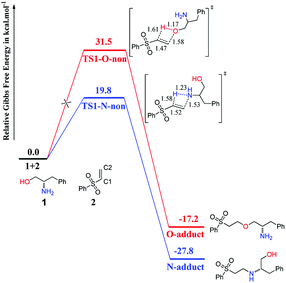

Fig. 1 Computed Gibbs free-energy profiles (298 K) for chemoselective addition reactions without catalyst.

2.2 Addition reaction pathways catalyzed by AgHMDS/dppe 3 and 3′ systems

The computed free-energy profiles of the addition reaction pathways catalyzed by 3′ are depicted in Fig. 2, and the optimized three-dimensional (3-D) structures of the transition states are shown in Fig. 3. This catalysis system reverses the chemoselectivity of the addition reaction and provides the O-adduct. The first step is chemoselective deprotonation of the OH group. Catalyst 3′ approaches reactant 1 and works as a Brønsted base to capture a proton from the OH or NH₂ group. These respective processes go through TS1-O or TS1-N with free energies of 11.8 and 17.9 kcal mol⁻¹ above the reactants, respectively, which indicates that the OH group has the stronger Brønsted acidity. In TS1-O, the hydrogen atom is transferred from the OH group (distance D_O–H = 1.28 Å) to the HMDS⁻ (distance D_N–H = 1.25 Å), and the Ag atom coordinates to the O atom of the substrate to form the Ag–O bond. TS1-O evolves towards ADD2-O (adduct 2-O), where the HHMDS species is weakly bound to other parts through the hydrogen bond (1.83 Å). TS1-N evolves towards ADD2-N, which is thermodynamically disfavored because it is 10.0 kcal mol⁻¹ above the reactants in free energy. The HMDS⁻ is a strong base with an approximate pK_a value of 26 (this value would be slightly different when it is coordinating with different alkali metals), indicating it can deprotonate both –O⁺H– group in intermediate ADD1-O and –N⁺H₂– in intermediate ADD1-N.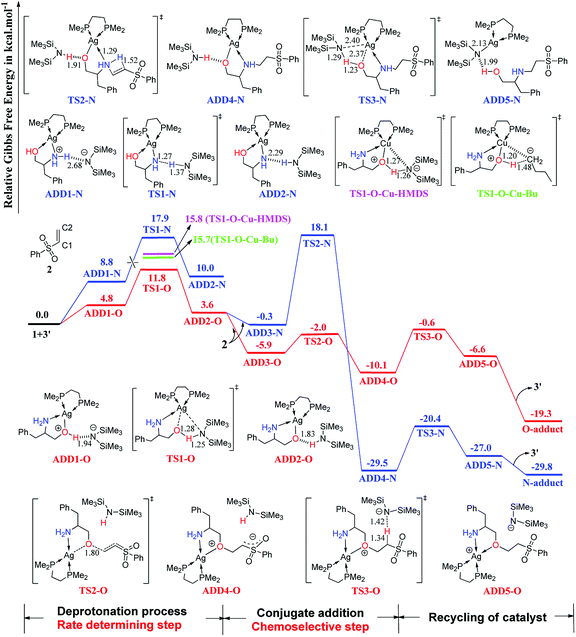

Fig. 2 Computed Gibbs free-energy profiles (253 K) for chemoselective addition reactions catalyzed by 3′ system (distances in Å).

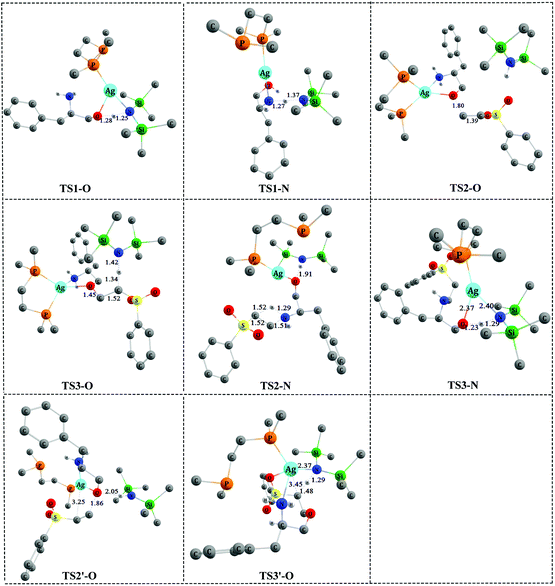Fig. 3 The optimized 3-D structures of the transition states in Fig. 2 and 4. Some H atoms are omitted for clarity (distances in Å).

As depicted in Fig. 2, phenyl vinyl sulfone 2 approaches ADD2-O to undergo the O- or N-addition process via the transition states TS2-O or TS2-N with the relative free energy of −2.0 or 18.1 kcal mol⁻¹, respectively. For the O-addition process, the C2 atom of 2 undergoes nucleophilic attack by the O atom of the Ag–O group via the transition state TS2-O with a relative free-energy difference of −2.0 kcal mol⁻¹. In TS2-O, the O–C bond distance is 1.80 Å, and HHMDS locates close to the carbanion of the C=C bond. TS2-O evolves towards ADD4-O in which the C–O bond has been formed with a carbanion based on the C=C bond. HHMDS then works as a Brønsted acid to return a proton to the carbanion of the C=C bond via transition state TS3-O with a relative free-energy difference of −0.6 kcal mol⁻¹. ADD5-O is 6.6 kcal mol⁻¹ below the reactant energy level. Separation of the O-adduct and regeneration of catalyst 3′ is favorable on the free-energy scale; the overall exergonicity of the whole process is 19.3 kcal mol⁻¹.

For the N-addition process, the C=C bond of 2 undergoes nucleophilic attack by the NH₂ group of ADD2-O via a four-membered ring transition state TS2-N with a relative free-energy difference of 18.1 kcal mol⁻¹. In TS2-N, the HHMDS group is weakly bonded to the substrate with the hydrogen bond (1.91 Å). The N-addition process leads to ADD4-N, and then HHMDS works as a Brønsted acid to return a proton to the O atom of the substrate via four-membered ring TS3-N with an energy barrier of 9.1 kcal mol⁻¹. In TS3-N, a proton is transferred from the N atom of HHMDS to the O atom with a N–H distance of 1.29 Å and an O–H distance of 1.23 Å, while breaking of the Ag–O bond (2.37 Å) is coupled with formation of Ag–N (2.40 Å). TS3-N evolves towards ADD5-N, in which the N-adduct is weakly bound to catalyst 3′ through a hydrogen bond (1.99 Å).

As shown in Fig. 2, catalyst 3′ works as a Brønsted base to capture a proton from the OH group and form the Ag–O bond to attain ADD2-O before phenyl vinyl sulfone 2 approaches ADD2-O to undergo the O- or N-addition process. We then considered whether the Ag–O group can attack the C=C bond of 2 together to form the four-membered ring, which is a similar process to the N-addition process via TS2-N. This process is depicted in Fig. 4, and the optimized 3-D structures of the transition states are shown in Fig. 3. As shown in Fig. 4, the Ag–O bond adds to the C=C bond of 2 to form the four-membered ring transition state TS2′-O. In TS2′-O, the HHMDS group is weakly bound to the substrate via the hydrogen bond (2.05 Å). This new process leads to ADD4′-O, and then HHMDS returns a proton to the C atom of the substrate through four-membered ring TS3′-O. In TS3′-O, a proton is transferred from the N atom of HHMDS to the C atom of the substrate (N–H, 1.29 Å; C–H, 1.48 Å), and the Ag–C bond is broken to form the Ag–N bond. This process is not favored because of the high energy barrier of 21.9 kcal mol⁻¹ (energy difference between ADD4′-O and TS3′-O). Therefore, for the O-addition process, the four-membered ring TS2′-O formed by the Ag–O group direct attack of the C=C bond of 2 is unsuitable.

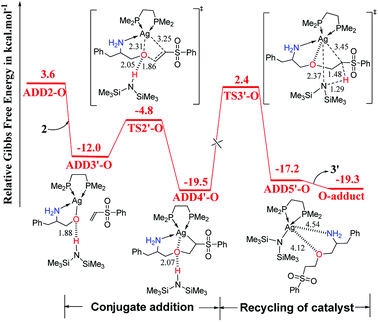Fig. 4 Computed Gibbs free-energy profiles (253 K) for the possible reaction pathways via TS2′-O and TS3′-O catalyzed by 3′ (distances in Å).

If catalyst 3′ only acts as a Lewis acid and does not work as a Brønsted base, the mechanism should proceed in only one step as shown in Fig. S1 of ESI.† Initially, reactant 1 approaches catalyst 3′ to form ADD1′, and a hydrogen bond forms between the N atom of HMDS⁻ and the OH group of 1 (1.90 Å). Afterwards, the approach of 2 to ADD1′ results in N-addition or O-addition through the respective transition states TS1′-N or TS1′-O. TS1′-N and TS1′-O are four-membered ring transition states with relative free energies of 17.4 and 33.3 kcal mol⁻¹, respectively. In TS1′-N depicted in Fig. S1,† the NH₂ group adds to the vinyl group to form the N-addition product (N-adduct), while for TS1′-O, the OH group adds to the vinyl group to form the O-addition product (O-adduct). The energy difference indicates that the Lewis acid-catalyzed N-addition pathway is more energetically favorable than the Lewis acid-catalyzed O-addition pathway, but this is not consistent with the experimental observations depicted in Scheme 2.¹¹ Therefore, the mechanism via TS1′-N and TS1′-O for which catalyst 3′ only works as a Lewis acid cannot be the most favorable pathway for this system.

As shown in Fig. 2, the O-addition reaction pathway associated with transition states TS1-O, TS2-O, and TS3-O should be the most favorable pathway with an energy barrier of 9.5 kcal mol⁻¹. In this case, the AgHMDS/dppe catalyst not only acts as a Lewis acid to coordinate with the O and N atom of the substrate, but also works as a Brønsted base to capture a proton from the OH group to form the Ag–O bond and as a Brønsted acid to return a proton to recycle itself. Comparing the structure of TS2-O with those of TS1′-N and TS2-N, the O atom of the Ag–O group is more suitable than the N atom of the NH₂ group for nucleophilic addition to the C=C bond of 2. This is probably because the O atom of Ag–O has a stronger nucleophilicity than the N atom of NH₂ groups, which is discussed in the Parr function analysis. This factor is responsible for the chemoselectivity of the addition reaction and O-adduct formation.

In the overall Gibbs free-energy profiles (Fig. 2, 4, and S1†), the second step (conjugate addition process) determines the chemoselectivity of O- and N-addition through TS2-O, TS2-N, and TS1′-N. The energy of TS2-O is much lower than those of TS2-N and TS1′-N, which indicates that the chemoselectivity of O-addition is preferred in this system, and is consistent with the experimental observations shown in Scheme 2.¹¹ To compare the effects of the real and model AgHMDS/dppe system (i.e., 3 and 3′) on the chemoselectivity of the reaction, we additionally constructed and optimized TS2-O-real, TS2-N-real, and TS1′-N-real with the actual dppe ligand by employing catalyst 3. As shown in Fig. 5, the energy of transition state TS2-O-real associated with O-addition is still lower than those of TS2-N-real and TS1′-N-real associated with the N-addition. We also reproduced Fig. 2 with the actual dppe ligand by using catalyst 3 (see the Fig. S2 of ESI†). The computed Gibbs free-energy profiles and energy barriers showed the same trend and conclusions as the calculated results of the model systems. This indicates that the selected models and the computed results should be suitable and reliable.

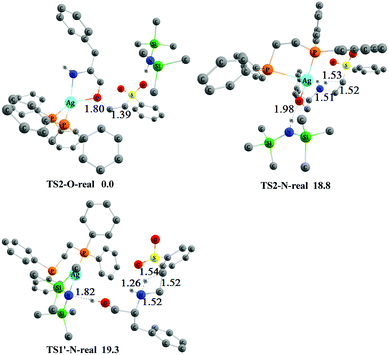Fig. 5 The optimized 3-D structures and relative free energies (253 K, kcal mol⁻¹) of TS2-O-real, TS2-N-real and TS1′-N-real. Some H atoms are omitted for clarity (distances in Å).

In the favored O-addition reaction pathway, the deprotonation process is the rate-determining step. We computed the TS1-O–Cu-HMDS and TS1-O–Cu-Bu transition states with CuHMDS/dppe and CuBu/dppe as catalysts, in which the phenyl groups of dppe were replaced by methyl groups. As shown in Fig. 2, the free energies related to the separate reactants of TS1-O–Cu-HMDS and TS1-O–Cu-Bu are higher than that of TS1-O, indicating that the rate of Ag(I)-catalyzed addition would be faster than that of the Cu(I)-catalyzed addition. This is consistent with the experimental observations described in Ohshima's report.¹¹ To test the impact of different computational methods on the calculated results, we additionally computed the rate-determining step by using different computational methods. As summarized in Table S1 (ESI),† the free energies calculated by the different methods are very close and have small differences, which indicate that the calculated results should be reliable by using the selected computational method.

2.3 Addition reaction catalyzed by AgOAc/dppe 4 and 4′ systems

The addition reaction catalyzed by the AgOAc/dppe system prefers the N-adduct, and the detailed mechanism was studied using catalyst 4′. We tried without success to locate the transition state of the deprotonation of the OH group by OAc⁻ of the catalyst. We then scanned the energy changes along with the deprotonation processes of OH and NH₂ group mediated by OAc⁻ ligand of the catalyst. As shown in Fig. 6, the energies of both deprotonation processes increase with the elongating distances of O1–H and N1–H, and the protons always returned after the optimizations. Therefore, we concluded that the OAc⁻ group cannot capture a proton from the OH or NH₂ group, but rather forms hydrogen bonds with them. The computed results indicated that the AgOAc/dppe system only acts as a Lewis acid to coordinate with the O and N atom of the substrate but does not work as a Brønsted base to capture a proton from these groups.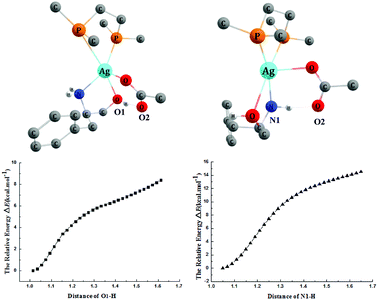

Fig. 6 The energy scans of the deprotonation processes along with the distance changes and 3-D structures. Some H atoms are omitted for clarity (distances in Å).

The detailed mechanisms of the addition reaction catalyzed by 4′ and the corresponding energy profiles are shown in Fig. 7. Initially, L-phenylalaninol 1 approaches catalyst 4′ to form ADD1-OAc, and two hydrogen bonds are formed between the oxygen atom of OAc⁻ and the OH and NH₂ group with distances of 1.79 Å and 1.92 Å. ADD1-OAc sits only 0.03 kcal mol⁻¹ above the reactants in energy, and afterwards the approach of 2 to ADD1-OAc results in two separate conjugate addition processes (O-addition and N-addition) through transition states TS1-N–OAc and TS1-O–OAc. Both TS1-N–OAc and TS1-O–OAc are four-membered ring transition states. In TS1-N–OAc depicted in Fig. 7, the NH₂ group adds to the vinyl group to form the N-addition product (N-adduct) via nucleophilic attack of the N atom on the C2 atom of 2 and electrophilic attack of the H atom on the C1 atom of 2. Similarly, in TS1-O–OAc (Fig. 7), the OH group adds to the vinyl group to form the O-addition product (O-adduct) via addition of the O atom to the C2 atom of 2 while the H atom adds to the C1 atom of 2. The free energies of transition states TS1-N–OAc and TS1-O–OAc are 17.0 and 33.8 kcal mol⁻¹, respectively, relative the reactants. This energy difference indicates that the N-addition process is preferred, while the O-addition process is difficult because of the much higher free-energy barrier of 33.8 kcal mol⁻¹. The N-addition process mainly leads to ADD2-N–OAc, in which the N-adduct is weakly bound to catalyst 4′ through hydrogen bonds (1.71 Å and 2.38 Å) and Ag–O through a coordination bond (2.49 Å). ADD2-N–OAc sits 22.5 kcal mol⁻¹ below the reactants in energy terms. Separation of the main N-adduct product and regeneration of catalyst 4′ can proceed smoothly with an overall exergonicity of 29.8 kcal mol⁻¹.

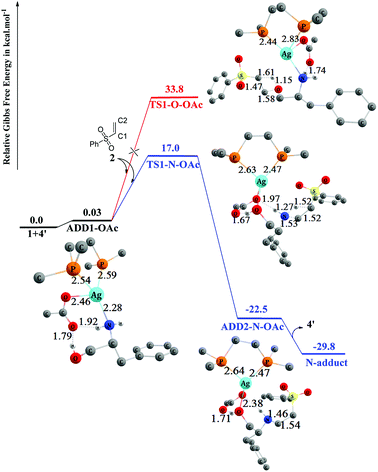Fig. 7 Computed free-energy profiles (253 K) and optimized 3-D structures for the chemoselective addition reactions catalyzed by 4′. Some H atoms are omitted for clarity (distances in Å).

Comparing the structure of TS1-N–OAc with that of TS1-N-non depicted in Fig. 1, the Ag atom is coordinated with O and N atoms of the substrate and two hydrogen bonds are formed (1.67 Å and 1.97 Å) between the OAc⁻ group and the OH and NH₂ groups in TS1-N–OAc. This interaction would cause the energy barrier to be lower than that via TS1-N-non. Therefore, the rate of reaction catalyzed by the AgOAc/dppe system is higher than that without the presence of the catalyst. According to the above discussion, the transition states TS1-N–OAc and TS1-O–OAc would be the key to determining the chemoselectivity of the preferred N-adduct.

In addition, we found that the chemoselectivity has the same trend by constructing and computing the key transition states TS1-N–OAc-real and TS1-O–OAc-real catalyzed by AgOAc/dppe 4. As shown in Fig. 8, transition state TS1-O–OAc-real associated with the O-addition process is higher than transition state TS1-N–OAc-real associated with the N-addition process by 15.4 kcal mol⁻¹. This is close to the energy difference of 16.8 kcal mol⁻¹ between TS1-N–OAc and TS1-O–OAc depicted in Fig. 7. Therefore, the N-addition process still has the energy advantage for the AgOAc/dppe 4 system, and the chemoselectivity of the N-addition product is consistent with the experimental observations shown in Scheme 2.¹¹

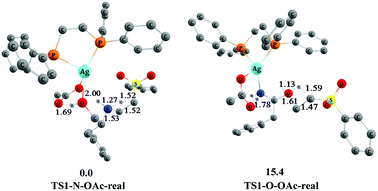Fig. 8 The optimized 3-D structures and relative free energies (253 K, kcal mol⁻¹) of TS1-N–OAc-real and TS1-O–OAc-real. Some H atoms are omitted for clarity (distances in Å).

As discussed above, the AgOAc/dppe system only acts as a Lewis acid to form the coordination bonds with the O and N atoms of the substrate during the addition, but does not work as a Brønsted base to capture a proton from the OH and NH₂ group. When compared with the AgHMDS/dppe system, AgOAc/dppe does not enable the deprotonation of the OH group to form the Ag–O bond, and cannot change the innate reactivity of the OH and NH₂ groups. This means that the origin of chemoselectivity in the addition reaction is the same as the non-catalyst reaction depicted in Fig. 1, which leads to the N-adduct.

In brief, we can conclude that the AgOAc/dppe only works as Lewis acid, and the strong base (such as KHMDS, NaHMDS, LiHMDS) works as Brønsted base. Therefore, the whole system should be a cooperatively catalytic system in the favorable O-addition pathway. Obviously, both of the Ag(I) salt and the strong base additives should be necessary, which is in agreement with the experimental observation that the O-adduct is the main product with the presence of AgOAc/dppe and the strong base (such as KHMDS, LiHMDS, NaHMDS).¹¹

2.4 Parr function analysis

As discussed above, the chemoselectivity of the addition reaction catalyzed by the different systems is dictated by the order of nucleophilicity of N- and O-sites in the substrate. To further prove this point, we computed the electrophilic and nucleophilic Parr functions (P_k⁺ and P_k⁻)¹⁹ to predict the local nucleophilicity of the different sites in the substrate. The local nucleophilic P_k⁻ and electrophilic P_k⁺ Parr functions of the neutral system were obtained by the Mulliken atomic spin density (ASD) of the radical cation and anion of the optimized neutral geometry. This approach has been proved to be a good choice to measure the nucleophilicities and electrophilicities of different sites.²⁰

It is noteworthy that reactant 1, intermediate ADD2-O (Fig. 2), and ADD1-OAc (Fig. 7) all have two reactive nucleophilic sites: the O atom of OH (denoted as 1-O) and the N atom of NH₂ (denoted as 1-N) in reactant 1, the O atom of Ag–O (denoted as ADD2-O–O) and the N atom of NH₂ (denoted as ADD2-O–N) in ADD2-O, and the O atom of OH (denoted as ADD1-OAc-O) and the N atom of NH₂ (denoted as ADD1-OAc-N) in ADD1-OAc. For these species, the question of relative site reactivity was addressed by a simple calculation of Parr functions (P_k⁺ and P_k⁻).

As summarized in Table 1, the order of nucleophilic Parr function (P_k⁻) in reactant 1 is 1-N (0.0359) > 1-O (0.0092). This assessment reflects how the innate reactivity of the NH₂ group is stronger than the OH group of the amino alcohol, and why the N-addition process is preferred in the absence of catalyst. The order of nucleophilic Parr function (P_k⁻) in ADD2-O is ADD2-O–O (0.5570) > ADD2-O–N (0.1034). This comparison confirms that the nucleophilic reactivity of the O atom of Ag–O is stronger than the N atom of NH₂ in ADD2-O, and helps to explain why the O-addition process is preferred with the 3′ catalyst system. For ADD1-OAc, the order of nucleophilic Parr function (P_k⁻) is ADD1-OAc-N (0.0014) > ADD1-OAc-O (0.0013), indicating that the nucleophilic reactivity order of NH₂ and OH does not change with the 4′ catalyst system, and that the N-addition process is still preferred. These results suggest that we can successfully predict the most nucleophilic reactive site by the Parr function analysis using a simple single-point calculation.

Table 1 Electrophilic and nucleophilic Parr functions (P_k⁺ and P_k⁻) at the O and N atoms of reactant 1, ADD2-O, and ADD1-OAc

Parr function	1-O	1-N	ADD2-O–O	ADD2-O–N	ADD1-OAc-O	ADD1-OAc-N
Pk^+	−0.0015	−0.0061	−0.0099	0.0237	0.0011	0.0235
Pk^−	0.0092	0.0359	0.5570	0.1034	0.0013	0.0014

---

3. Conclusions

The competing reaction mechanisms for the addition of amino alcohols to electron-deficient olefins catalyzed by different Ag(I) catalysts including AgHMDS/dppe and AgOAc/dppe were systematically studied for the first time using DFT methods. In the AgHMDS/dppe system, the most energetically favorable reaction mechanism consists of three steps. The first step is deprotonation of the OH group of the amino alcohol by AgHMDS/dppe. The conjugate addition process with the olefin then proceeds, which is the chemoselective step. The third step is the separation of the product and AgHMDS/dppe catalyst. In the whole process, the AgHMDS/dppe catalyst not only acts as a Lewis acid to coordinate with an O atom, but also works as a Brønsted base to capture a proton from the OH group to form the Ag–O bond and subsequently as a Brønsted acid to provide a proton to the carbanion of the olefin. Parr function analysis also indicated that the innate nucleophilicity order of the O and N atoms of the amino alcohol can be reversed to control the chemoselectivity.

However, the calculated results suggested that AgOAc/dppe catalyst can only act as the Lewis acid to coordinate with O and N atoms of the substrate, but cannot work as the Brønsted base to enable deprotonation of the OH group to form the Ag–O bond. This means that the reaction catalyzed by Lewis acid AgOAc/dppe has the same mechanism and chemoselectivity as the uncatalyzed reaction via the direct four-membered ring transition state. Through this original research of Ag(I)-catalyzed chemoselective addition reactions, we reasonably expect that the obtained insights will be useful for rational design of more efficient addition reactions of olefins with OH and NH₂ groups with special selectivities.

4. Computational details

All calculations were performed using the Gaussian09 package,²¹ while Chemcraft was used for molecule visualization.²² Geometry optimizations and frequency calculations were carried out with the B3LYP²³ function. Ag and Cu atoms were described by the effective core potentials of the Stuttgart/Dresden (SDD) basis set,²⁴ while the polarized 6-31G(d) basis set²⁵ was used for all remaining atoms (C, H, O, N, S, Si, and P). The natures of the stationary points as minima or transition states were confirmed by frequency calculations at the respective experimental temperatures of 298 K and 253 K. The connectivity between the transition state and the associated minima was confirmed by intrinsic reaction coordinate calculations to determine two corresponding minima. Then single-point calculations were performed based on the optimized gas phase geometries using the solvent model density method²⁶ at the M06 (ref. 27) level with the SDD basis set for Ag and Cu, and the 6-311+G (d,p) basis set for all remaining atoms. N,N-Dimethylformamide (dielectric constant 37.219) was used as solvent. The potential energies in solution were taken directly from the self-consistent reaction field calculation, and the free energies in solution were obtained from the additional introduction of the gas phase entropy corrections. Natural bond orbital analyses were carried out at the same level of theory to obtain the values of Parr functions (P_k⁺ and P_k⁻).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work described in this paper was supported by the National Natural Science Foundation of China (No. 21703195, 31601447, 21773214), the Foundation of Henan Educational Committee of China (No. 17B150013, 17A150050) and Henan Scientific Committee of China (No. 172102210466).

Notes and references

1. C. F. Nising and S. Bräse, Chem. Soc. Rev., 2008, 37, 1218–1228.
2. L. Hintermann, Top. Organomet. Chem., 2010, 3, 123–155.
3. C. F. Nising and S. Bräse, Chem. Soc. Rev., 2012, 41, 988–999.
4. F. Loydl, Justus Liebigs Ann. Chem., 1878, 192, 80–89.
5. (a) C. D. Vanderwal and E. N. Jacobsen, J. Am. Chem. Soc., 2004, 126, 14724–14725; (b) S. Bertelsen, P. Dinér, R. L. Johansen and K. A. Jørgensen, J. Am. Chem. Soc., 2007, 129, 1536–1537; (c) D. R. Li, A. Murugan and J. R. Falck, J. Am. Chem. Soc., 2008, 130, 46–48; (d) X. Xiong, C. Ovens, A. W. Pilling, J. W. Ward and D. J. Dixon, Org. Lett., 2008, 10, 565–567; (e) L. Wang, X. Liu, Z. Dong, X. Fu and X. Feng, Angew. Chem., Int. Ed., 2008, 47, 8670–8673; (f) A. J. Boersma, D. Coquière, D. Geerdink, F. Rosati, B. L. Feringa and G. Roelfes, Nat. Chem., 2010, 2, 991–995; (g) H. Fuwa, K. Noto and M. Sasaki, Org. Lett., 2010, 12, 1636–1639.
6. (a) M. M. Biddle, M. Lin and K. A. Scheidt, J. Am. Chem. Soc., 2007, 129, 3830–3831; (b) C. M. Reisinger, X. Wang and B. List, Angew. Chem., Int. Ed., 2008, 47, 8112–8115; (c) E. Reyes, G. Talavera, J. L. Vicario, D. Badía and L. Carrillo, Angew. Chem., Int. Ed., 2009, 48, 5701–5704; (d) E. M. Phillips, M. Riedrich and K. A. Scheidt, J. Am. Chem. Soc., 2010, 132, 13179–13181; (e) C. Grondal, M. Jeanty and D. Enders, Nat. Chem., 2010, 2, 167–178; (f) Q. Gu, Z. Q. Rong, C. Zheng and S. L. You, J. Am. Chem. Soc., 2010, 132, 4056–4057; (g) B. Ravindra, S. Maity, B. G. Das and G. Prasanta, J. Org. Chem., 2015, 80, 7008–7018; (h) B. Parhi, J. Gurjar, S. Pramanik, A. Midya and P. Ghorai, J. Org. Chem., 2016, 81, 4654–4663.
7. (a) B. Mondal, R. Maity and S. C. Pan, J. Org. Chem., 2018, 83, 8645–8654; (b) A. Yadav, J. Banerjee, S. K. Arupula, S. M. Mobin and S. Samanta, Asian J. Org. Chem., 2018, 7, 1595–1599; (c) K. C. Nicolaou, D. Rhoades and S. M. Kumar, J. Am. Chem. Soc., 2018, 140, 8303–8320; (d) K. Sakurai, M. Sasaki and H. Fuwa, Angew. Chem., Int. Ed., 2018, 57, 5143–5146; (e) M. Kumar, P. Chauhan, S. J. Bailey, E. Jafari, C. v. Essen, K. Rissanen and D. Enders, Org. Lett., 2018, 20, 1232–1235; (f) S. S. Wang, J. He and Z. An, Chem. Commun., 2017, 53, 8882–8885.
8. C. Munro-Leighton, E. D. Blue and T. B. Gunnoe, J. Am. Chem. Soc., 2006, 128, 1446–1447.
9. C. Munro-Leighton, S. A. Delp, E. D. Blue and T. B. Gunnoe, Organometallics, 2007, 26, 1483–1493.
10. S. Uesugi, Z. Li, R. Yazaki and T. Ohshima, Angew. Chem., Int. Ed., 2014, 53, 1611–1615.
11. Z. Li, R. Yazaki and T. Ohshima, Org. Lett., 2016, 18, 3350–3353.
12. Z. Li, M. Tamura, R. Yazaki and T. Ohshima, Chem. Pharm. Bull., 2017, 65, 19–21.
13. (a) B. M. Trost, Science, 1991, 254, 1471–1477; (b) P. A. Wender, V. A. Verma, T. J. Paxton and T. H. Pillow, Acc. Chem. Res., 2008, 41, 40–49.
14. (a) Y. Wang, D. H. Wei and M. S. Tang, J. Org. Chem., 2017, 82, 13043–13050; (b) Y. Wang, Y. Qiao, D. H. Wei and M. S. Tang, Org. Chem. Front., 2017, 4, 1987–1998; (c) Y. Y. Wang, D. H. Wei, Y. Wang, W. J. Zhang and M. S. Tang, ACS Catal., 2016, 6, 279–289.
15. (a) D. H. Wei, B. L. Lei, M. S. Tang and C. G. Zhan, J. Am. Chem. Soc., 2012, 134, 10436–10450; (b) D. H. Wei, X. Q. Huang, J. J. Liu, M. S. Tang and C. G. Zhan, Biochemistry, 2013, 52, 5145–5154; (c) D. H. Wei, L. Fang, M. S. Tang and C. G. Zhan, J. Phys. Chem. B, 2013, 117, 13418–13434; (d) D. H. Wei, X. Q. Huang, Y. Qiao, J. J. Rao, L. Wang, F. Liao and C. G. Zhan, ACS Catal., 2017, 7, 4623–4636.
16. (a) Y. Reddi and R. B. Sunoj, ACS Catal., 2017, 7, 530–537; (b) M. Pareek and R. B. Sunoj, ACS Catal., 2016, 6, 3118–3126; (c) A. E. Fraley, M. Garcia-Borràs, A. Tripathi, D. Khare, E. V. Mercado-Marin, H. Tran, Q. Dan, G. P. Webb, K. R. Watts, P. Crews, R. Sarpong, R. M. Williams, J. L. Smith, K. N. Houk and D. H. Sherman, J. Am. Chem. Soc., 2017, 139, 12060–12068; (d) P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042–5137; (e) T. Liu, S. Han, Y. Li and S. Bi, J. Org. Chem., 2016, 81, 9775–9784; (f) R. T. Larson, R. P. Pemberton, J. M. Franke, D. J. Tantillo and R. Thomson, J. Am. Chem. Soc., 2015, 137, 11197–11204; (g) C. Liu, M. Besora and F. Maseras, Chem.–Asian J., 2016, 11, 411–416; (h) Y. X. Shao, J. Y. Zhang, Y. W. Li, Y. Liu and Z. F. Ke, Org. Lett., 2018, 20, 1102–1105.
17. (a) S. Chen, X. Huang, E. Meggers and K. N. Houk, J. Am. Chem. Soc., 2017, 139, 17902–17907; (b) R. V. Hoveln, B. M. Hudson, H. B. Wedler, D. M. Bates, G. Le Gros, D. J. Tantillo and J. M. Schomaker, J. Am. Chem. Soc., 2015, 137, 5346–5354; (c) I. Funes-Ardoiz and F. Maseras, Chem.–Eur. J., 2018, 24, 12383–12388; (d) M. E. de Orbe, L. Amenós, M. S. Kirillova, Y. Wang, V. López-Carrillo, F. Maseras and A. Echavarren, J. Am. Chem. Soc., 2017, 139(30), 10302–10311; (e) S. J. Li and D. C. Fang, Organometallics, 2018, 37, 1373–1380; (f) W. H. Mu, R. J. Cheng, D. C. Fang and G. A. Chass, Dalton Trans., 2018, 47, 6494–6498; (g) B. Lian, L. Zhang, S. J. Li, L. L. Zhang and D. C. Fang, J. Org. Chem., 2018, 83, 3142–3148; (h) X. Xu, X. Chen, Y. X. Shao, H. S. Xie, Y. F. Deng, Z. F. Ke, H. F. Jiang and W. Zeng, ACS Catal., 2018, 8, 1308–1312; (i) H. S. Xie, Z. R. Ye, Z. F. Ke, H. F. Jiang and W. Zeng, Chem. Sci., 2018, 9, 985–989; (j) Y. Li, C. Hou, J. Jiang, Z. Zhang, C. Zhao, A. Page and Z. F. Ke, ACS Catal., 2016, 6, 1655–1662.
18. (a) M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862; (b) X. Li, Y. Zhu, C. Liu, X. Lin, W. Zhang and M. Tang, Struct. Chem., 2017, 28, 1631–1644; (c) V. M. Fernández-Álvarez, M. Nappi, P. Melchiorre and F. Maseras, Org. Lett., 2015, 17, 2676–2679; (d) S. J. Li and D. C. Fang, Phys. Chem. Chem. Phys., 2016, 18, 30815–30823.
19. L. R. Domingo, P. Pérez and J. A. Sáez, RSC Adv., 2013, 3, 1486–1494.
20. (a) X. Li, M. S. Tang, Y. Y. Wang, Y. Wang, Z. J. Li, L. B. Qu and D. H. Wei, Chem.–Asian J., 2018, 13, 1710–1718; (b) Y. X. Li, Y. Y. Zhu, W. J. Zhang, D. H. Wei, Y. Y. Ran, Q. L. Zhao and M. S. Tang, Phys. Chem. Chem. Phys., 2014, 16, 20001–20008; (c) Q. Q. Shi, Y. Wang and D. H. Wei, Org. Biomol. Chem., 2018, 16, 2301–2311; (d) X. Li, D. H. Wei and Z. J. Li, ACS Omega, 2017, 2, 7029–7038.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision C.01), Wallingford, CT, 2010.
22. ChemCraft, https://www.chemcraftprog.com.
23. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
24. (a) P. Fuentealba, H. Preuss, H. Stoll and L. v. Szentpály, Chem. Phys. Lett., 1982, 89, 418–422; (b) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872; (c) G. Igel-Mann, H. Stoll and H. Preuss, Mol. Phys., 1988, 65, 1321–1328; (d) D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chem. Acc., 1990, 77, 123–141.
25. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (b) G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
26. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
27. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1, Fig. S1–S3, Cartesian coordinates, absolute energies and imaginary frequency of the computed structures. See DOI: 10.1039/c8ra09065c

---