Open Access Article
Open Access ArticleComparative studies on structure, sensitivity and mechanical properties of CL-20/DNDAP cocrystal and composite by molecular dynamics simulation†
Binghui Duan a,
Yuanjie Shu*ab,
Ning Liu
a,
Yuanjie Shu*ab,
Ning Liu *ab,
Yingying Lua,
Bozhou Wangab,
Xianming Luab and
Jiaoqiang Zhangc
*ab,
Yingying Lua,
Bozhou Wangab,
Xianming Luab and
Jiaoqiang Zhangc
aXi'an Modern Chemistry Research Institute, Xi'an, 710065, People's Republic of China. E-mail: Syj1204172675@163.com; flackliu@sina.com
bState Key Laboratory of Fluorine & Nitrogen Chemicals, Xi'an 710065, People's Republic of China
cDepartment of Applied Chemistry, School of Science, Northwestern Polytechnical University, Xi'an 710129, People's Republic of China
First published on 9th October 2018
Abstract
Molecular dynamics simulation was performed on 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20), 2,4-dinitro-2,4-diazapentane (DNDAP), and CL-20/DNDAP cocrystal and composite under COMPASS force field at different temperatures. The binding energy (Ebind), radial distribution function (RDF), trigger bond length, cohesive energy density (CED) and mechanical properties were studied and compared. The results show that the binding energy of the cocrystal is evidently higher than that of the composite at the same temperature. RDF analysis reveals that hydrogen bonds and vdW forces between CL-20 and DNDAP exist in both CL-20/DNDAP cocrystal and composite, and the interactions in the cocrystal are stronger than those in the composite. The maximum trigger bond length decreases in the order ε-CL-20 > CL-20/DNDAP composite > CL-20/DNDAP cocrystal. Moreover, the rigidity and stiffness of the cocrystal and composite decrease compared to that of CL-20, while the ductility and elasticity are better than that of the two pure components. These results demonstrate that CL-20/DNDAP cocrystal might be very promising in explosive applications.
1. Introduction
Energetic materials (EMs) which can store and release considerable amounts of chemical energy on demand under certain conditions have occupied an important place in civilian and military areas.1–6 Modern EMs are required to have excellent energetic properties and acceptable stability for safe handling simultaneously.7,8 However, the contradiction between energy density and sensitivity for traditional EMs has existed for a long time, i.e., powerful EMs are mostly not safe.9–11 Of late, cocrystallization has appeared as an efficient method to address the contradiction to some extent.By combining two or more different molecules through non-covalent interactions, cocrystallization aims to achieve explosives with desirable detonation performance, nice stability and improved mechanical properties.12–17 These non-covalent interactions include hydrogen bonding, van der Waals (vdW) interactions, π–π stacking and electrostatic interactions.18–20 In this way, cocrystallization exhibits great superiority to decrease the sensitivity of the existing energetic compounds without markedly reducing their detonation performance. 2,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) is a representative high energy density compound (HEDC) with a better oxygen balance, higher detonation velocity than 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX) and 1,3,5-trinitro-1,3,5-triazine (RDX) that are extensively used as high energy explosives.21–24 Unfortunately, its high mechanical sensitivity has a negative effect on manufacture and storage, and thus limits its further applications.25,26 The introduction of cocrystallization to EMs inspired lots of efforts to get CL-20-based cocrystals with tunable physicochemical properties. For example, Bolton and his coworkers obtained CL-20/TNT cocrystal in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio, and found it has excellent detonation performance and approximately double impact stability of pure CL-20.27 More and more CL-20-based cocrystals were prepared in succession after this breakthrough with other explosives like BTF, DNT, DNP, MTNP, etc.28–33 Furthermore, theoretical studies have been performed to screen proper coformers and investigate the formation driving force and decreased sensitivity for CL-20-based energetic cocrystals. These co-formers are usually equivalent to or smaller than CL-20, characterized as planar molecules with nitro and amino groups.34–39 Hang et al.40 pointed out that molar ratio played a non-negligible role in the binding energy and stability of the cocrystals and the low molar ratio is common among the observed cocrystals. Taylor et al. found that cocrystallization is almost always a thermodynamically favorable process and more densely packed cocrystals with stronger hydrogen bonding tend to be more stable.41 Many researchers point out that intermolecular interactions play a vital role in determining molecular conformation and crystal framework, and then affect the stability of cocrystal system.42–45 Zhou and his coworkers confirmed that hydrogen bonding and vdW forces are the main driving forces for CL-20-based cocrystals.11 In addition, C–NO2 and N–NO2 bonds are considered as trigger bonds (i.e., the chemical bond with the lowest energy and initially ruptured with external stimuli) in nitramine explosives, which has been confirmed experimentally to be the first step in the thermal decomposition among many of them.46–48 Thus the length of trigger bond can be a measurement of the bond strength and correlate with the explosive sensitivity.
1 molar ratio, and found it has excellent detonation performance and approximately double impact stability of pure CL-20.27 More and more CL-20-based cocrystals were prepared in succession after this breakthrough with other explosives like BTF, DNT, DNP, MTNP, etc.28–33 Furthermore, theoretical studies have been performed to screen proper coformers and investigate the formation driving force and decreased sensitivity for CL-20-based energetic cocrystals. These co-formers are usually equivalent to or smaller than CL-20, characterized as planar molecules with nitro and amino groups.34–39 Hang et al.40 pointed out that molar ratio played a non-negligible role in the binding energy and stability of the cocrystals and the low molar ratio is common among the observed cocrystals. Taylor et al. found that cocrystallization is almost always a thermodynamically favorable process and more densely packed cocrystals with stronger hydrogen bonding tend to be more stable.41 Many researchers point out that intermolecular interactions play a vital role in determining molecular conformation and crystal framework, and then affect the stability of cocrystal system.42–45 Zhou and his coworkers confirmed that hydrogen bonding and vdW forces are the main driving forces for CL-20-based cocrystals.11 In addition, C–NO2 and N–NO2 bonds are considered as trigger bonds (i.e., the chemical bond with the lowest energy and initially ruptured with external stimuli) in nitramine explosives, which has been confirmed experimentally to be the first step in the thermal decomposition among many of them.46–48 Thus the length of trigger bond can be a measurement of the bond strength and correlate with the explosive sensitivity.
Our previous work reported a cocrystal of CL-20 and 2,4-dinitro-2,4-diazapentane (DNDAP) with a molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
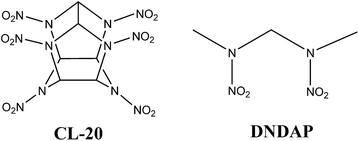
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and found the cocrystal possesses high explosive power and features reduced sensitivity relative to that of CL-20.49 Consequently, CL-20/DNDAP may be another novel high energy density insensitive explosive. With this in mind, theoretical investigations are needed to explain the properties of the cocrystal and as a complement to experimental work. The molecules of CL-20 and DNDAP are shown in Fig. 1.
1 and found the cocrystal possesses high explosive power and features reduced sensitivity relative to that of CL-20.49 Consequently, CL-20/DNDAP may be another novel high energy density insensitive explosive. With this in mind, theoretical investigations are needed to explain the properties of the cocrystal and as a complement to experimental work. The molecules of CL-20 and DNDAP are shown in Fig. 1.
CL-20 has four distinct crystalline forms: α, β, γ and ε. In these forms, ε-CL-20 is the most stable conformation at room conditions.21,23 Herein, ε-CL-20 was chosen for analysis. In this paper, we constructed the models of pure ε-CL-20, DNDAP, CL-20/DNDAP cocrystal and composite. Molecular dynamics (MD) simulations were conducted to simulate structures and predict the property parameters at different temperatures. The binding energy (Ebind) and radial distribution function (RDF) analysis were used to probe the intermolecular interactions of CL-20/DNDAP cocrystal and composite. The trigger bond lengths and cohesive energy density (CED) of CL-20/DNDAP cocrystal and composite at different temperatures were also provided in regard to the relationship with sensitivity and thermal stability. At the end, mechanical properties of pure CL-20, DNDAP, CL-20/DNDAP cocrystal and composite were all discussed for comparison. These studies aim to provide some insights for the design of cocrystal explosive and a better understanding of the cocrystal formation mechanism.
2. Computational details
2.1 Construction of models
Based on the crystal parameters derived from X-ray diffraction,21,49,50 the initial models of ε-CL-20, DNDAP and CL-20/DNDAP cocrystal were constructed corresponding to (2 × 3 × 3), (2 × 1 × 2) and (2 × 2 × 2) unit cells, respectively. ε-CL-20 supercell contains 72 CL-20 molecules, equivalent to a total of 2592 atoms and DNDAP supercell possesses 128 DNDAP molecules, 2432 atoms. CL-20/DNDAP cocrystal belongs to monoclinic system with P2/1c space group and the cell parameters are a = 1.3022(2) nm, b = 2.2619(4) nm, c = 1.2962(2) nm, α = 90°, β = 104.648(3)°, γ = 90°. A single crystal cell holds 8 CL-20 molecules and 4 DNDAP molecules. There are 64 CL-20 molecules, 32 DNDAP molecules, totally 2912 atoms in (2 × 2 × 2) cocrystal supercell. Cell parameters of CL-20/DNDAP cocrystal at different temperatures are tabulated in Table S1.† It can be seen that the predicted lattice parameters agree reasonably with the experimental data, indicating that (2 × 2 × 2) unit cell of CL-20/DNDAP cocrystal and the simulation methods are proper and reasonable to perform MD simulation.The original model of CL-20/DNDAP composite was built according to the number and proportion of the molecules in the cocrystal supercell. 64 CL-20 molecules and 32 DNDAP molecules were placed in a cubic periodic box with a side length of 100 Å. Minimizations were conducted for 5000 iterations to equilibrate the system, and then, MD simulation was performed with NVT ensemble until the system obtained thermal equilibrium. Afterwards, the periodic box was compressed and the above processes were repeated until the system approached its theoretical density. The theoretical density was predicted according to the corresponding components' weight percent. It was believed then that this box size is suitable for the following MD simulation.
2.2 Choice of force field
Choosing a reasonable calculation method is crucial to the reliability of calculation results. It is necessary to verify a proper force field for MD simulation. COMPASS (condensed-phase optimized molecular potentials for atomistic simulation studies) force field is popular as the first ab initio force field of quantum mechanics.51,52 It has been parameterized to precisely predict various properties for molecules in isolation and in condensed phase.53,54 COMPASS force field was chosen to optimize the primitive cells of CL-20 and DNDAP, and the experimental lattice parameters of the two compounds are shown in Table 1. From Table 1, we can find that most relative errors are within 5%.| Cell parameters | CL-20 | DNDAP | ||||
|---|---|---|---|---|---|---|
| Exp.b | Comp. | Relative error/% | Exp.c | Comp. | Relative error/% | |
| a The experimental values were obtained at 298 K.b Cited from ref. 21.c Cited from ref. 50. | ||||||
| a/Å | 8.85 | 8.80 | −0.56 | 20.82 | 21.52 | 3.36 |
| b/Å | 12.56 | 12.45 | −0.88 | 43.43 | 45.58 | 4.95 |
| c/Å | 13.39 | 13.31 | −0.60 | 6.24 | 6.36 | 1.92 |
| α/(°) | 90.00 | 90.28 | 0.31 | 90.00 | 90.06 | 0.07 |
| β/(°) | 106.82 | 105.32 | −1.40 | 90.00 | 89.67 | −0.37 |
| γ/(°) | 90.00 | 89.82 | −0.20 | 90.00 | 90.80 | 0.89 |
| ρ/(g cm−3) | 2.04 | 2.07 | 1.47 | 1.54 | 1.46 | −5.19 |
The validation of COMPASS force field could also be checked by calculating the lattice energy of CL-20 and DNDAP. The lattice energy (Elatt) is defined as the total internal energy of the molecule in the crystal minus the corresponding energy of the molecule in the gas-phase.55 It could also be determined from experimental enthalpy of sublimation (ΔHsub) by the following equation:56
| Elatt = −ΔHsub − 2RT − K0 | (1) |
2.3 MD simulations
Firstly, the models constructed were optimized with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps by smart algorithm. The quality of geometry optimization was “Fine”. And then an anneal task was executed during 5 temperature cycles (150–500–150 K) under NVT ensemble in order to eliminate the unreasonable conformations and get a fully relaxed system. Andersen58 was set as the temperature control method. Next, MD simulations were conducted on in NPT ensemble, namely, the number of molecules, pressure (1 atm), temperature were constant in the whole process. Parrinello59 was employed as the pressure control method and Andersen as temperature control method. The summation methods for electrostatic and van der Waals were Ewald and atom-based, respectively. The interactions were determined within the cutoff distance of 15.5 Å. A fixed time step size of 1 fs was considered in all cases. An MD simulation with a simulation time of 500 ps was performed to equilibrate the system. Then another MD simulation with a period of 500 ps would be carried out and the trajectory was used for statistical analysis. All the MD simulations were conducted by Forcite module, Materials Studio software (MS), 2014.
000 steps by smart algorithm. The quality of geometry optimization was “Fine”. And then an anneal task was executed during 5 temperature cycles (150–500–150 K) under NVT ensemble in order to eliminate the unreasonable conformations and get a fully relaxed system. Andersen58 was set as the temperature control method. Next, MD simulations were conducted on in NPT ensemble, namely, the number of molecules, pressure (1 atm), temperature were constant in the whole process. Parrinello59 was employed as the pressure control method and Andersen as temperature control method. The summation methods for electrostatic and van der Waals were Ewald and atom-based, respectively. The interactions were determined within the cutoff distance of 15.5 Å. A fixed time step size of 1 fs was considered in all cases. An MD simulation with a simulation time of 500 ps was performed to equilibrate the system. Then another MD simulation with a period of 500 ps would be carried out and the trajectory was used for statistical analysis. All the MD simulations were conducted by Forcite module, Materials Studio software (MS), 2014.
3. Results and discussion
3.1 Judgment of system equilibrium
The system is required to reach an equilibration before MD simulation. Generally speaking, when the fluctuations of temperature, energy, cell length and cell angle are within 5–10%, the system is believed to proceed at an equilibrium state. Fig. S1† shows the typical fluctuation curves of CL-20/DNDAP cocrystal at 298 K for the first 500 ps. It can be seen from Fig. S1a† that the temperature quickly increases at the beginning, and then fluctuates around a relative stable value within ±15 K when the system reaches an equilibration. As can be seen from Fig. S1b,† the potential energy and non-bond energy fluctuate within a tiny range of less than 5%. Moreover, the cell length and cell angle are all reaching to relative stable values. These results confirm an equilibration of the system. Other systems all come to an equilibrium state based on the criteria. As an exemplification, the equilibrium structures of CL-20/DNDAP cocrystal and composite are shown in Fig. 2.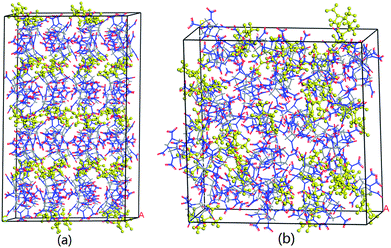 | ||
| Fig. 2 Equilibrium structures of CL-20/DNDAP cocrystal (a) and composite (b) at 298 K (DNDAP in yellow). | ||
3.2 Intermolecular interactions between CL-20 and DNDAP of CL-20/DNDAP cocrystal and composite
| Ebind = −Einter = −(Etotal − ECL-20 − EDNDAP) | (2) |
| Sample | T/K | Etotal/(kJ mol−1) | ECL-20/(kJ mol−1) | EDNDAP/(kJ mol−1) | Ebind/(kJ mol−1) |
|---|---|---|---|---|---|
| Cocrystal | 198 | −90971.20 | −80118.85 | −5219.24 | 5633.11 |
| 248 | −89382.01 | −78945.52 | −4871.10 | 5565.39 | |
| 298 | −87364.26 | −77414.95 | −4495.89 | 5453.42 | |
| 348 | −85233.52 | −75708.36 | −4164.65 | 5360.51 | |
| 398 | −83255.28 | −74254.98 | −3878.66 | 5121.64 | |
| Composite | 198 | −88842.11 | −79343.33 | −5464.27 | 4034.51 |
| 248 | −87144.84 | −78043.45 | −5139.67 | 3961.73 | |
| 298 | −85281.00 | −76674.28 | −4762.44 | 3844.28 | |
| 348 | −83319.34 | −75199.56 | −4417.80 | 3701.98 | |
| 398 | −81641.05 | −73757.61 | −4298.52 | 3584.92 |
From the data in Table 2, the binding energy of CL-20/DNDAP cocrystal is obviously higher than that of the composite at the same temperature, that is to say, the cocrystal structure is more thermally stable. This is mainly because that layers of CL-20 alternate with bilayers of DNDAP in the cocrystal forming a zigzag network and there may be expected to exist extensive interactions between CL-20 and DNDAP molecules due to their close contacts. While for the composite, CL-20 and DNDAP molecules distribute randomly, which can be proofed from Fig. 2, thus they share a smaller interaction area in the composite. In addition, it is found that the binding energies of CL-20/DNDAP cocrystal and composite exhibit a decreasing variation tendency with the increasing temperature. The decrease of the binding energy indicates that the compatibility and stability of the systems deteriorate.
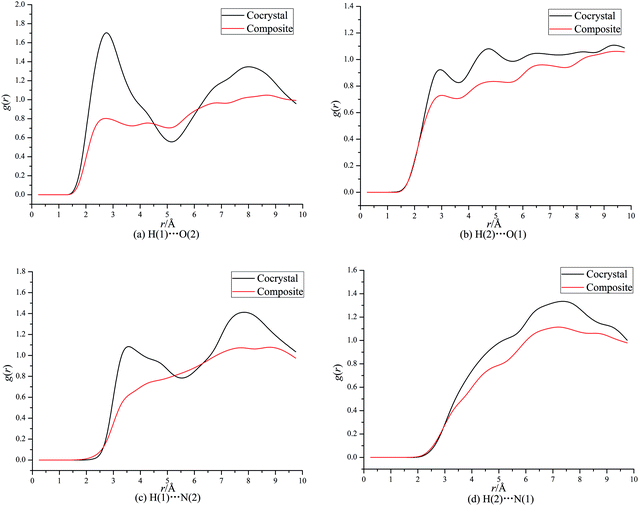
From Fig. 3a, it can be seen that a maximum of g(r) at about 2.5 Å denotes strong interaction between H of CL-20 and O of DNDAP both for the cocrystal and composite, which can be figured out as hydrogen bonding interaction. Similarly, the first peaks of g(r) at about 2.8 Å in Fig. 3b indicate hydrogen bonding interaction between O of CL-20 and H of DNDAP. It is necessary to note that the former peaks in Fig. 3a are higher than the latter in Fig. 3b during the hydrogen bond range, suggesting that the hydrogen bonding is primarily derived from H of CL-20 and O of DNDAP. From Fig. 3c, it is found that the first peak of the cocrystal locates at about 3.4 Å, implying strong vdW interaction between H of CL-20 and N of DNDAP. There are no evident strong vdW forces examined in the composite. Also, weak vdW interaction between N of CL-20 and H of DNDAP can be confirmed from the curves in Fig. 3d. It is noteworthy that the value of g(r) of CL-20/DNDAP cocrystal is mostly higher than that of the composite, suggesting stronger intermolecular interactions lying in cocrystal structure.
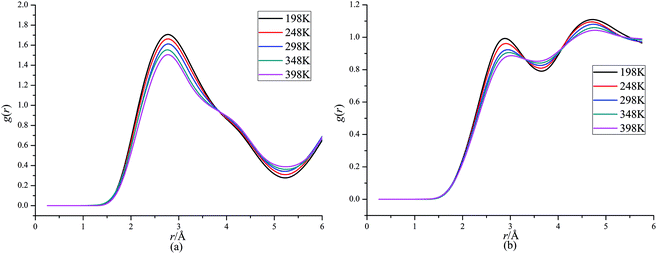
Fig. 4 presents RDFs for H⋯O in CL-20/DNDAP cocrystal at different temperatures. It can be seen that the peak height decreases and it has a slightly change to right as the temperature increases, which can be ascribed to the reinforcement of atomic thermal motion with the increasing temperature. It can be deduced that the intermolecular interaction forces between CL-20 and DNDAP decrease gradually with the increasing temperature, which is in agreement with the conclusion from binding energy analysis.
3.3 Sensitivity
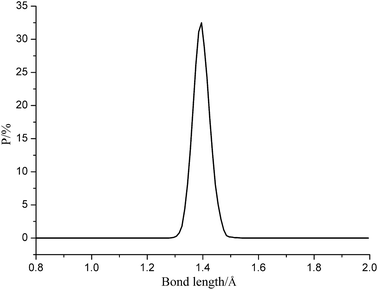
Fig. 5 gives the representative bond length distribution of ε-CL-20 at 298 K. According to Fig. 5, N–NO2 bond exhibits symmetric Gaussian distribution. Despite of the tiny proportion of Lmax, it is easy to be broken during the reactions and initiate decomposition and explosion. Table 3 tabulates the trigger bond lengths of ε-CL-20, CL-20/DNDAP cocrystal and composite at different temperatures. It is found from Table 3 that the averaged length of trigger bond (Lave) shows a little change with the increasing temperature, whereas Lmax displays an obvious increasing tendency. The result is in accordance with the fact that the stability of the explosive gets poor as the temperature increases, thus it is reasonable to set Lmax as a criterion to measure the explosive sensitivity. Moreover, one observes that Lmax at the same temperature decreases in the order of ε-CL-20 > CL-20/DNDAP composite > CL-20/DNDAP cocrystal, indicating that N–NO2 bond is more difficult to be ruptured and the sensitivity of the systems decreases in the sequence of ε-CL-20 > CL-20/DNDAP composite > CL-20/DNDAP cocrystal. Hence we can deduce that adding DNDAP into CL-20 explosives may be an effective method to enhance the stability of the explosive and the effect of cocrystallization is more significant.
| Sample | Bond length/Å | Temperature/K | ||||
|---|---|---|---|---|---|---|
| 198 | 248 | 298 | 348 | 398 | ||
| ε-CL-20 | Lave | 1.397 | 1.397 | 1.398 | 1.399 | 1.400 |
| Lmax | 1.465 | 1.494 | 1.530 | 1.542 | 1.565 | |
| Composite | Lave | 1.394 | 1.394 | 1.395 | 1.396 | 1.397 |
| Lmax | 1.461 | 1.485 | 1.515 | 1.529 | 1.540 | |
| Cocrystal | Lave | 1.391 | 1.391 | 1.392 | 1.392 | 1.393 |
| Lmax | 1.451 | 1.479 | 1.488 | 1.513 | 1.517 | |
| CED = (Hv − RT)/Vm | (3) |
| Sample | T/K | van der Waals/(kJ cm−3) | Electrostatic/(kJ cm−3) | CED/(kJ cm−3) |
|---|---|---|---|---|
| a Deviations are listed in the parentheses. | ||||
| Cocrystal | 198 | 0.368(0.001) | 0.465(0.002) | 0.844(0.002) |
| 248 | 0.358(0.001) | 0.451(0.002) | 0.821(0.002) | |
| 298 | 0.352(0.001) | 0.435(0.002) | 0.800(0.002) | |
| 348 | 0.343(0.002) | 0.411(0.002) | 0.765(0.001) | |
| 398 | 0.336(0.001) | 0.399(0.002) | 0.746(0.003) | |
| Composite | 198 | 0.304(0.001) | 0.341(0.002) | 0.655(0.002) |
| 248 | 0.293(0.002) | 0.334(0.002) | 0.636(0.004) | |
| 298 | 0.288(0.001) | 0.327(0.002) | 0.624(0.002) | |
| 348 | 0.283(0.001) | 0.322(0.002) | 0.614(0.002) | |
| 398 | 0.270(0.002) | 0.298(0.003) | 0.577(0.004) | |
As can be seen from Table 4, CED is mainly consisted of vdW and electrostatic energy density. Electrostatic force accounts for a larger proportion of CED value, and thus giving a more influence to the formation of the cocrystal and composite. Combining Table 4 and Fig. S2,† it can be found that CED, vdW energy, electrostatic energy of CL-20/DNDAP cocrystal and composite all decrease gradually as the temperature increases. It follows that lower energy is required by the explosive to turn into gas phase and cause explosion, indicating that the sensitivity of the system increases with temperature rising. Meanwhile, the CED value of CL-20/DNDAP cocrystal is much higher than that of the composite at the same temperature, implying that the cocrystal structure remarkably diminishes the sensitivity of CL-20 and features a better thermal stability.
3.4 Mechanical properties
Mechanical properties are some of the most important properties of energetic materials as they relates to the preparation, machining, transport and usage of energetic materials closely. Explosives are expected to possess lower rigidity and better ductility. There are four parameters to characterize the mechanical properties, namely tensile modulus E, bulk modulus K, shear modulus G and Poisson's ratio ν. Each material is isotropic according to the assumption of the static method in MS and herein two Lamé coefficients called λ and μ are correlated with the mechanical properties. These parameters could be illustrated as follows:66,67
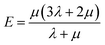 | (4) |
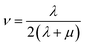 | (5) |
| G = μ | (6) |
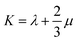 | (7) |
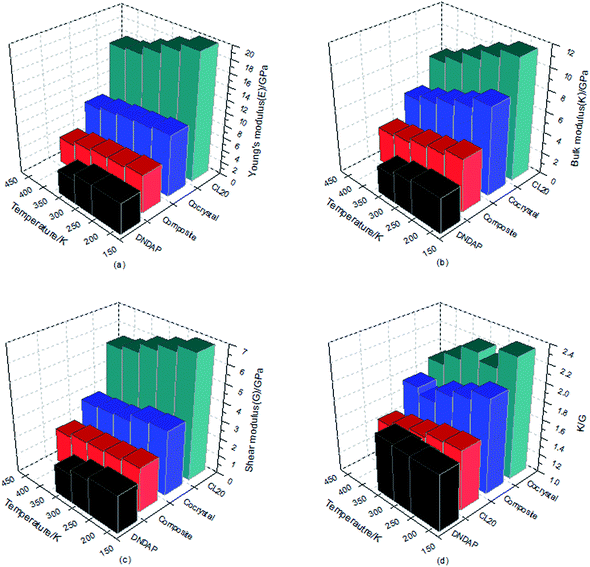
The larger the values of K, G and E are, the greater the hardness and stiffness of explosives are. Additionally, the ratio of K to G is an indication of the ductility of materials, the higher the value, the better the ductility. Poisson's ratio is an elastic constant that reflects the plasticity of materials and commonly, the value of ν is 0.2–0.4 for a plastic. The mechanical parameters obtained based on the equilibrium trajectory documents from dynamics simulation were summarized and depicted in Table 5 and Fig. 6. In view of the melting point of DNDAP (327.5 K), the calculation of DNDAP only performed at the first three temperatures (198, 248, 298 K).
| Sample | T/K | Mechanical modulus | ||||
|---|---|---|---|---|---|---|
| E/GPa | K/GPa | G/GPa | ν | K/G | ||
| ε-CL-20 | 198 | 19.95 | 11.40 | 6.86 | 0.34 | 1.66 |
| 248 | 18.83 | 10.67 | 6.51 | 0.34 | 1.64 | |
| 298 | 17.41 | 9.78 | 6.18 | 0.34 | 1.58 | |
| 348 | 16.06 | 8.75 | 5.67 | 0.33 | 1.54 | |
| 398 | 15.71 | 8.06 | 5.45 | 0.33 | 1.48 | |
| Cocrystal | 198 | 9.70 | 8.30 | 3.56 | 0.30 | 2.33 |
| 248 | 9.26 | 7.38 | 3.47 | 0.29 | 2.13 | |
| 298 | 8.97 | 6.73 | 3.06 | 0.30 | 2.21 | |
| 348 | 8.51 | 6.08 | 2.96 | 0.30 | 2.06 | |
| 398 | 7.95 | 5.52 | 2.88 | 0.31 | 1.92 | |
| Composite | 198 | 5.98 | 4.96 | 2.43 | 0.30 | 2.04 |
| 248 | 5.57 | 4.41 | 2.27 | 0.28 | 1.94 | |
| 298 | 5.41 | 4.10 | 2.19 | 0.29 | 1.87 | |
| 348 | 4.96 | 3.65 | 2.12 | 0.29 | 1.72 | |
| 398 | 4.16 | 3.38 | 1.89 | 0.30 | 1.79 | |
| DNDAP | 198 | 4.89 | 3.34 | 2.06 | 0.26 | 1.62 |
| 248 | 4.82 | 3.07 | 1.88 | 0.24 | 1.63 | |
| 298 | 3.78 | 2.57 | 1.56 | 0.22 | 1.65 | |
As can be seen from Table 5 and Fig. 6, E, K, G values of CL-20, DNDAP, CL-20/DNDAP cocrystal and composite all show a downward trend with the increasing temperature, indicating that the rigidity and stiffness of the crystals decrease, the ductility and elasticity are strengthened and thus, the sensitivity of the system is weakened, which appear to be in contradiction with the fact that the thermal stability becomes poor when the temperature increases. In fact, the sensitivity is influenced by many factors. As temperature rises, the acceleration of molecular motion leads to a significant change in structure (such as the maximum trigger bond length) and energy of the system, whose effects become prominent with regard to the sensitivity of the system. It is worthy to note that the E, K, G values of the cocrystal are larger than that of DNDAP, but smaller compared to CL-20. The ν values of the crystals range between 0.2–0.4 and hardly vary with temperature, indicating a stable plasticity of the crystals. Meanwhile, the K/G values of CL-20/DNDAP cocrystal and composite are larger than that of pure components at the same temperature, suggesting improved ductility and acceptable capability to reduce vibration towards mechanical stimuli of the systems, whereas the elastic properties of the composite decline too much compared to the pure components.
4. Conclusions
In this study, the structures, sensitivity and mechanical properties of CL-20/DNDAP cocrystal and composite were analyzed by molecular dynamics simulation. The binding energies of CL-20/DNDAP cocrystal and composite exhibit a decreasing tendency with the increasing temperature, indicating that the compatibility and stability of the systems deteriorate. Hydrogen bonding and vdW interactions are the main driving force for the formation of the cocrystal and composite based on RDF analysis and the cocrystal structure possesses stronger intermolecular interactions. Adding DNDAP into CL-20 explosives can enhance the stability of the explosive and the effect of cocrystallization is more significant based on the maximum trigger bond length and CED analyses. The ductility and elasticity of the cocrystal and composite are strengthened compared to pure components, whereas the elastic properties of the composite decrease too much.In a word, the cocrystal structure improves the high sensitivity defect of CL-20 and possesses better mechanical properties than the composite. The conclusions drawn based on MD simulations help provide guidance for the application of CL-20/DNDAP cocrystal explosive and the formulation design of novel cocrystal explosives.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support for this work by the National Natural Science Foundation of China (Grant No. 21703168).References
- D. M. Badgujar, M. B. Talawar, S. N. Asthana and P. P. Mahulikar, J. Hazard. Mater., 2008, 151, 289–305 CrossRef CAS PubMed.
- Q. Ma, M. P. Wen, B. H. Zheng, H. J. Huang, D. B. Liu and J. S. Li, RSC Adv., 2015, 5, 33755–33761 RSC; P. Politzer and J. S. Murray, Propellants, Explos., Pyrotech., 2016, 41, 414–425 CrossRef CAS.
- Z. Zeman, Chem. Heterocycl. Compd., 2017, 1, 13–17 Search PubMed.
- K. Liu, G. Zhang, Z. Chen, J. Luan and M. Xu, Chem. Anal. Meterage, 2014, 23, 139–143 CAS.
- A. K. Sikder and N. Sikder, J. Hazard. Mater., 2004, 112, 1–15 CrossRef CAS PubMed.
- P. F. Pagoria, G. S. Lee, A. R. Mitchell and R. D. Schmidt, Thermochim. Acta, 2002, 384, 187–204 CrossRef CAS.
- D. D. Dlott, Met. Sci. J., 2013, 22, 463–473 Search PubMed.
- T. Grecu, Virtual Cocrystal Screening, University of Sheffield Press, Sheffield, U.K., 2014 Search PubMed.
- N. Zohari, M. H. Keshavarz and S. A. Seyedsadjadi, Cent. Eur. J. Energ. Mater., 2013, 10, 135–147 CAS.
- T. B. Brill and K. J. James, Chem. Rev., 1993, 93, 2667–2692 CrossRef CAS.
- J. H. Zhou, L. W. Shi, C. Y. Zhang, H. Z. Li, M. B. Chen and W. M. Chen, J. Mol. Struct., 2016, 1116, 93–101 CrossRef CAS.
- M. Sowa, K. Ślepokura and E. Matczak-Jon, J. Mol. Struct., 2014, 1058, 114–121 CrossRef CAS.
- B. M. Gu, H. Lin and S. G. Zhu, J. Appl. Phys., 2014, 115, 6468–6471 CrossRef.
- Z. Yang, H. Li, X. Zhou, C. Zhang, H. Huang, J. Li and F. Nie, Cryst. Growth Des., 2012, 12, 5155–5158 CrossRef CAS.
- S. Roy, G. Mahata and K. Biradha, Cryst. Growth Des., 2015, 9, 5006–5008 CrossRef.
- S. Xiong, S. Chen, S. Jin, Z. Zhang, Y. Zhang and L. Li, RSC Adv., 2017, 7, 6795–6799 RSC.
- C. An, H. Li, B. Ye and J. Wang, J. Nanomater., 2017, 2017, 7 CrossRef.
- H. Yamashita, Y. Hirakura, M. Yuda, T. Teramura and K. Terada, Pharm. Res., 2013, 30, 70 CrossRef CAS PubMed.
- W. Zhu, X. Wang, J. Xiao, W. Zhu, H. Sun and H. Xiao, J. Hazard. Mater., 2009, 167, 810–816 CrossRef CAS PubMed.
- K. Thanigaimani, N. C. Khalib, E. Temel, S. Arshad and I. A. Razak, J. Mol. Struct., 2015, 1099, 246–256 CrossRef CAS.
- X. Q. Zhao and N. C. Shi, Chin. Sci. Bull., 1995, 40, 2158–2160 Search PubMed.
- O. Bolton, L. R. Simke, P. F. Pagoria and A. J. Matzger, Cryst. Growth Des., 2012, 12, 4311 CrossRef CAS.
- M. Keshavarz, A. Afzali, K. Esmaeilpour, S. Damiri and Z. Hadi, Cent. Eur. J. Energ. Mater., 2016, 13, 845–858 CrossRef.
- Z. Liu, Q. Wu, W. Zhu and H. Xiao, RSC Adv., 2015, 5, 34216–34225 RSC.
- T. Sun, J. Xiao, Q. Liu, F. Zhao and H. Xiao, J. Mater. Chem. A, 2014, 2, 13898–13904 RSC.
- H. M. Xiao, Z. Y. Wang and J. M. Yao, Acta Chim. Sin., 1985, 43, 1–24 Search PubMed.
- O. Bolton and A. J. Matzger, Angew. Chem., 2011, 50, 8960–8963 CrossRef CAS PubMed.
- K. Liu, G. Zhang, J. Luan, Z. Chen, P. Su and Y. Shu, J. Mol. Struct., 2016, 1110, 91–96 CrossRef CAS.
- H. Xu, X. Duan, H. Li and C. Pei, RSC Adv., 2015, 5, 95764–95770 RSC.
- S. R. Anderson, D. J. AmEnde, J. S. Salan and P. Samuels, Propellants, Explos., Pyrotech., 2015, 39, 637–640 CrossRef.
- C. L. Wu, S. H. Zhang, F. D. Ren, R. J. Gou and G. Han, J. Theor. Comput. Chem., 2017, 16, 19 Search PubMed.
- S. F. Zhu, S. H. Zhang, R. J. Gou, G. Han, C. L. Wu and F. D. Ren, J. Mol. Model., 2017, 23, 353 CrossRef PubMed.
- S. F. Zhu, S. H. Zhang, R. J. Gou, C. L. Wu, G. Han and H. Y. Jia, Cryst. Res. Technol., 2018, 53, 1700299 CrossRef.
- M. Sowa, K. Ślepokura and E. Matczak-Jon, Acta Crystallogr., 2013, 69, 1267–1272 CAS.
- H. M. B. Sethsmith, S. J. Rosser, A. Basran, E. R. Travis, E. R. Dabbs, S. Nicklin and N. C. Bruce, Appl. Environ. Microbiol., 2002, 68, 4764–4771 CrossRef CAS.
- X. J. Xu, H. M. Xiao, X. H. Ju, X. D. Gong and W. H. Zhu, J. Phys. Chem. A, 2006, 110, 5929 CrossRef CAS PubMed.
- W. P. Lai, P. Lian, Y. Z. Liu, T. Yu, W. L. Zhu, Z. X. Ge and J. Lv, J. Mol. Model., 2014, 20, 2479 CrossRef PubMed.
- D. S. Viswanath, T. K. Ghosh and V. M. Boddu, Emerging Energetic Materials: Synthesis, Physicochemical, and Detonation Properties, Springer, Dordrecht, 2018 Search PubMed.
- T. M. Klapötke, C. Pflüger and M. W. Reintinger, Eur. J. Inorg. Chem., 2016, 2016, 138–147 CrossRef.
- G. Y. Hang, W. L. Yu, T. Wang, J. T. Wang and Z. Li, J. Mol. Struct., 2017, 1141, 577–583 CrossRef CAS.
- C. R. Taylor and G. M. Day, Cryst. Growth Des., 2018, 18, 892–904 CrossRef CAS PubMed.
- P. Yin and J. N. M. Shreeve, Angew. Chem., Int. Ed. Engl., 2016, 54, 14513–14517 CrossRef PubMed.
- J. K. Miller, J. O. Mares, I. E. Gunduz, S. F. Son and J. F. Rhoads, J. Appl. Phys., 2016, 119, 24903 CrossRef.
- T. Leyssens, G. Springuel, R. Montis, N. Candoni and S. Veesler, Cryst. Growth Des., 2012, 12, 1520–1530 CrossRef CAS.
- T. L. Qiang, J. J. Xiao, F. Zhao and H. M. Xiao, Acta Chim. Sin., 2014, 72, 1036 CrossRef.
- Y. Y. Lu, Y. J. Shu, N. Liu, X. M. Lu and M. H. Xu, RSC Adv., 2018, 8, 4955 RSC.
- D. A. Mathieu, Ind. Eng. Chem. Res., 2017, 56, 29 CrossRef.
- J. Liu, W. Jiang, Q. Yang, J. Song, G. Z. Hao and L. I. Feng, Def. Technol., 2014, 10, 184–189 CrossRef.
- N. Liu, B. H. Duan, X. M. Lu, H. C. Mo, M. H. Xu, Q. Zhang and B. Z. Wang, CrystEngComm, 2018, 20, 2060–2067 RSC.
- D. Spitzer, B. Wanders, M. R. Schäfer and R. Welter, J. Mol. Struct., 2003, 644, 37–48 CrossRef CAS.
- H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- M. J. Mcquaid, H. Sun and D. Rigby, J. Comput. Chem., 2004, 25, 61–71 CrossRef CAS PubMed.
- T. S. Asche, P. Behrens and A. M. Schneider, J. Sol-Gel Sci. Technol., 2016, 3, 1–10 Search PubMed.
- G. Chen, C. Y. Chen, M. Z. Xia, W. Lei, F. Y. Wang and X. D. Gong, RSC Adv., 2015, 5, 25581–25589 RSC.
- L. Qiu, W. H. Zhu, J. J. Xiao, W. Zhu, H. M. Xiao, H. Huang and J. S. Li, J. Phys. Chem. B, 2007, 111, 1559–1566 CrossRef CAS PubMed.
- A. J. Pertsin and A. I. Kitaigorodsky, The Atom-Atom Potential Method, Applications to Organic Molecular Solids, Springer-Verlag, Berlin, 1987 Search PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J. Tao, X. F. Wang, S. X. Zhao, X. Q. Diao, C. L. Wang and Z. X. Han, Chin. J. Energ. Mater., 2016, 4, 324–330 Search PubMed.
- R. J. Gou, Y. Y. Zhao, X. Ding, S. H. Zhang, W. S. Yang and H. F. Gao, J. Sichuan Univ., 2016, 4, 852–858 Search PubMed.
- C. Zhang, Z. Yang, X. Zhou, C. Zhang, Y. Ma, J. Xu, Q. Zhang, F. Nie and H. Li, Cryst. Growth Des., 2014, 14, 3923–3928 CrossRef CAS.
- S. Xiong, S. Chen and S. Jin, J. Mol. Graphics Modell., 2017, 74, 171 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, J. Mol. Model., 2015, 21, 25 CrossRef PubMed.
- J. J. Xiao, L. Zhao, W. Zhu, J. Chen, G. F. Ji, F. Zhao, Q. Wu and H. M. Xiao, Sci. China: Chem., 2012, 55, 2587–2594 CrossRef CAS.
- B. Li, C. Dong, J. G. Yu, Q. X. Zhang, H. Y. Zhou and R. Liu, RSC Adv., 2018, 8, 22127–22135 RSC.
- L. Qiu, W. H. Zhu, J. J. Xiao, W. Zhu, H. M. Xiao, H. Huang and J. S. Li, J. Phys. Chem. B, 2007, 111, 1559 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Cell parameters of CL-20/DNDAP cocrystal at different temperatures, the balanced curves of CL-20/DNDAP cocrystal at 298 K and CED curves of CL-20/DNDAP cocrystal at different temperatures. See DOI: 10.1039/c8ra07387b |
| This journal is © The Royal Society of Chemistry 2018 |